Abstract
To improve the voltage gain of step-up converters, the cascaded technique is considered as a possible solution in this paper. By considering the concept of cascading two Z-source networks in a conventional boost converter, the proposed topology takes the advantages of both impedance source and cascaded converters. By applying some modifications, the proposed converter provides high voltage gain while the voltage stress of the switch and diodes is still low. Moreover, the low input current ripple of the converter makes it absolutely appropriate for photovoltaic applications in expanding the lifetime of PV panels. After analyzing the operation principles of the proposed converter, we present the simulation and experimental results of a 100 W prototype to verify the proposed converter performance.
1. Introduction
Given the lack of energy and the climate changes due to increasing fossil fuel consumption over the last few decades, using renewable energies could be a way to help the planet Earth survive in a future energy crisis [1]. However, in order to utilize the renewable energies, power electronics converters are inevitably essential to produce the required voltage and current for different applications. Among different types of renewable energies, solar energy is more popular as a limitless source of energy, which is spread all over the world. Although the output voltage of photovoltaic (PV) cells are relatively low, applying high step-up DC–DC converters can lead to increasing the voltage level without connecting in series numerous PV panels to enhance the operation of photovoltaic systems, especially in low-power applications [2].
Research on high step-up converters in recent years has led to the present diverse topologies that are used to resolve existing drawbacks such as high voltage stress of semiconductor devices, reverse-recovery problem of diodes, and intense spike on switches which mostly appear in conventional boost converters by increasing the duty cycle [3,4]. Consequently, the topological alteration of the conventional boost converter was proposed by researchers to extend the input-to-output voltage ratio while the circuit operation is enhanced as well. To overcome the drawbacks of boost converters with high efficiency and their simple control scheme, boost converters based on different techniques were proposed by researchers, such as a coupled inductor based boost converter, switched-capacitor based boost converter, cascaded boost converter, and interleaved boost converter [5]. All introduced converters have some weaknesses and strengths that make them restricted for specific applications. A better performance of a high step-up converter may be obtained if it could be possible to apply different techniques in a converter.
Inserting coupled inductors into the DC–DC converters is an effective method to increase the voltage gain by adjusting the turn ratio between the windings in a topology. Although by increasing the leakage inductance, the reverse-recovery problem of diodes can be reduced effectively due to inserting coupled inductors, the leakage energy induces high voltage spikes across the semiconductor switches. One approach in order to solve this problem is employing a switched-capacitor technique as an active clamp circuit in order to recycle the leakage energy [6]. To reduce the topology complexity and cost, passive clamps are also considered as a possible solution. In [7], a passive clamp was replaced with an active clamp in a flyback converter to enhance the performance of the converter by alleviating the reverse-recovery problem and lowering the circulating current into the clamp circuit. Switched-capacitor converters are able to provide high voltage ratio for high power applications; however, the high input ripple current in these converters make them inappropriate for solar PV applications [5].
The other step-up converter topologies, such as cascaded boost converters, interleaved boost converters, and three-level boost converters, can effectively take the advantages of the mentioned techniques such as coupled inductors, switched capacitors, and switched-inductors to cover the mentioned weaknesses and improve their performance. For instance, the reverse-recovery problem of cascaded boost converters can be compromised with the coupled-inductor technique, although the converter efficiency in cascaded converters will be decreased due to the two-time energy processing [8,9,10,11,12,13,14,15,16,17,18]. Moreover, low input current ripple of interleaved converters can effectively employ switched-capacitor configurations to improve their static voltage gain and alleviate the adverse effect of their pulsating input current [9]. In [10], a three-level boost converter was proposed by employing coupled inductors to increase the voltage gain and an active clamp to recycle the leakage inductance energy of the coupled inductors. Consequently, it can be observed how incorporating step-up techniques can appropriately influence the operation of different step-up topologies.
Impedance source converters are the other recent popular methods that are used widely in power electronic converters by inserting an impedance network between the power source and main circuit. The first impedance source converter was proposed by authors in [11] in 2003 for implementing DC–AC, AC–DC, DC–DC, and AC–AC power conversion. The impedance source converters are able to totally change the operational characteristics of the main converter [11,12]. An impedance network could provide the following features for high step-up DC–DC converters [13]: high voltage gain, low voltage stress for semiconductor devices, inherent short circuit immunity, and inherent open circuit immunity. An impedance source network consists of inductors, capacitors, and diodes with different configurations, such as Z-source, Y-source, Δ-source, T-source, Γ-source, TZ-source, sigma-Z-source, and so on [14]. A Y-shaped impedance network by a coupled-inductor implementation in order to obtain high voltage gain in small duty ratio was presented in [15]. In [16], a Δ-source converter was investigated by employing three coupled inductors and comparing it with a Y-source impedance network. The investigation demonstrated that in a Δ-source converter, smaller magnetizing current and winding loss can be attained compared with a Y-source converter. Moreover, the adverse effect of leakage inductance caused by coupled inductors is reduced significantly in a Δ-source converter. In [19], the other Z-source high step-up converter was presented by utilizing two cores for two sets of coupled inductors. Although the voltage conversion ratio increased in the mentioned proposed converter in [19], the core loss of the ferrite reduced the efficiency of the converter. In [13], different topologies of a galvanically isolated impedance source DC–DC converter with a wide range of input voltage and load regulation for distributed generation systems were surveyed. By contrast, the operating principle of a common grounded Z-source DC–DC converter for photovoltaic applications was proposed in [17]. The proposed converter with a common ground for the input and output resulted in having a low cost and a small-sized step-up converter compared with the isolated ones.
Investigation in different types of high step-up converters resulted in the proposal of a novel impedance source converter by cascading two Z-source networks and employing switched-capacitor-inductor cells in order to obtain a converter with high voltage gain ratio, low voltage stress on semiconductor devices, and low input current ripple, as expected from impedance source converters. However, the conventional configuration of cascading two Z-source networks between input source and main converter leads to the system suffering from very high input current ripple and high voltage stress for the switch. By modifying the proposed configuration, the converter can become appropriate for high step-up applications with low input current ripple. Furthermore, further research can be done to find out how cascading other impedance network configurations could affect the converter operation.
In this paper, after elaborating the topology of the proposed converter and investigating the operational modes in Section 2, the analysis and design consideration of the proposed converter are given in Section 3 in order to find out the voltage conversion ratio and voltage stresses of the switch and diodes. Finally, Section 4 presents the experimental results of a prototype converter to validate the theoretical analysis.
2. Proposed Converter and Principle of Operation
As it can be seen from Figure 1, the proposed high step-up DC–DC impedance source based boost converter includes two cascaded Z-source networks and two switched-capacitor-inductor cells. The converter hires a single ferrite core with six coupled inductors, which are part of the impedance network and cells. The very high input current ripple and the high voltage stress of the switch are two main problems in this converter. Therefore, some inevitable alterations are required in order to make the converter practically applicable. Although by adding a capacitor as shown in Figure 2, the voltage stress of the switch clamps at a specific value, the high input current ripple is still considered as a drawback in this converter. The dashed line in Figure 2 represents how the KVL (Kirchhoff’s Voltage Law) loop clamps the switch voltage at a specific value. Eventually, the final modification into the converter configuration resulted in obtaining a high step-up converter with low input current ripple and low voltage stress for semiconductor devices. Figure 3 shows the modified proposed high step-up impedance source converter with an equivalent circuit of coupled inductors. The proposed converter is composed of a single switch Q1; one diode D1 in the impedance network; two diodes in the cells D2 and D3; and one output diode D4; six coupled inductors L1, L2, L3, L4, L5, and L6; four capacitors C1, C2, C3, and C4 in the impedance network; two switched-capacitors C5 and C6; and output capacitor C7.
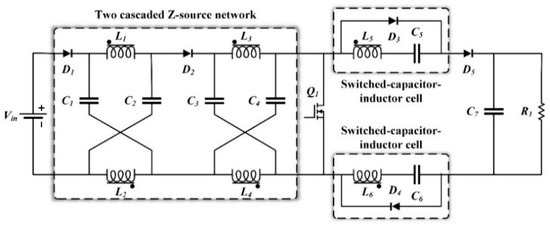
Figure 1.
Two cascaded Z-source high step-up converter.
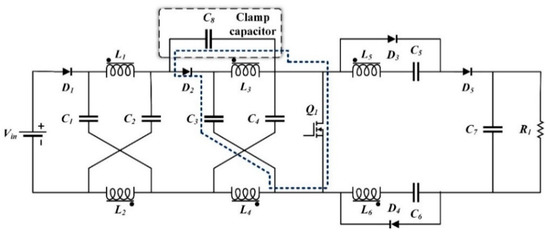
Figure 2.
Modified converter by a clamp capacitor.
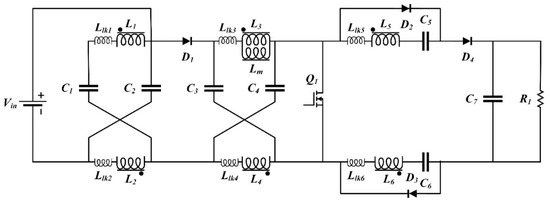
Figure 3.
Circuit diagram of proposed converter with equivalent circuit of coupled inductors.
The converter has four time intervals within a switching cycle in the steady state operation. Figure 4 illustrates the equivalent circuits for each operating interval; the capacitor C2 can be considered not in the circuit due to being in parallel with input voltage source, and Figure 5 is provided to show the theoretical waveforms of the proposed converter. To simplify the steady state analysis, the following assumptions are made:
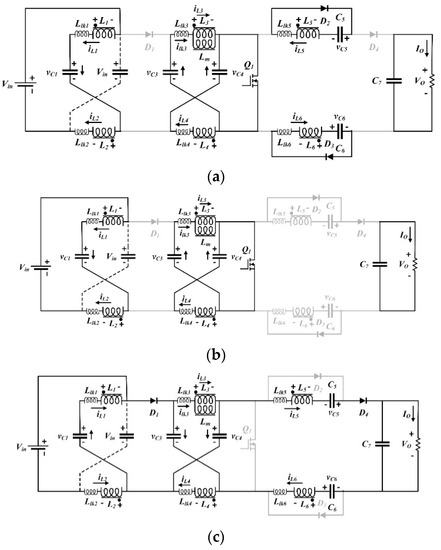
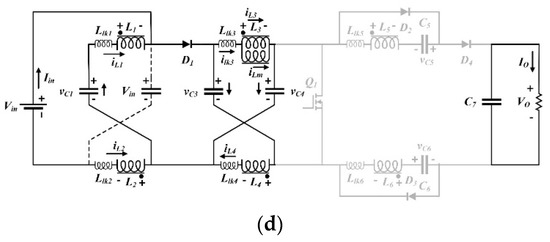
Figure 4.
Equivalent circuits of the proposed converter for each operation mode. (a) interval 1, (b) interval 2, (c) interval 3, (d) interval 4.
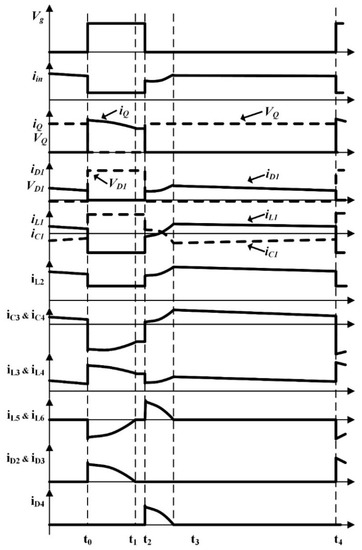
Figure 5.
Theoretical waveforms of the proposed converter.
- The converter operates in continuous conduction mode (CCM);
- The switch, diodes, and all inductors and capacitors are assumed ideal;
- The magnetizing inductance is large enough to ignore its current ripple;
- The leakage inductances of all windings are equal;
- The output capacitor C7 is large enough to make the output voltage constant;
- The switching capacitors C5 and C6 are equal.
Operation Principles
Interval 1 [t0 < t < t1] (Figure 4a): Before the t0 input, diode D1 is conducting, and the other semiconductor devices are off. At t0, the switch Q turns on, diode D1 becomes reverse-biased, and (2 + n)VC − Vin is applied across it. In addition, the current direction of capacitors C3 and C4 become reverse. In this operation mode, the capacitor voltage of C3 and C4 applies to inductors L3 and L4, and consequently this voltage will be induced to other coupled inductors L1, L2, L5, and L6 by considering the turn ratio. In this stage, the energy of leakage inductances L1 and L2 are recycled to the input voltage source, and the energy of leakage inductances L5 and L6 are absorbed by switched-capacitors C5 and C6. The following equations are established in this time interval:
where n is the turn ratio of coupled inductors:
VC5(t0) and VC6(t0) are less than the coupled inductor’s voltage in their corresponding cells, so a resonance occurs between the leakage inductances and both C4 and C5 to charge the capacitors through D2 and D3 over the half resonance period. The current and voltage of capacitor C5 can be expressed as:
where and .
The capacitor C3 and switch Q current are determined as:
where iC5 is given by (5).
This mode ends after a half resonance period once the current direction changes. Therefore, the diodes D2 and D3 turn off at zero current.
Interval 2 [t1 < t < t2] (Figure 4b): At this operation mode, the switch Q is still on and all diodes are at the off state. In addition, the magnetizing inductance Lm is still charging by C3 and C4. Diodes D2 and D3 are off in this stage due to reversing the current of inductors L5 and L6, which are blocked by diodes D2 and D3, respectively. Therefore, the stored magnetic energy of the transformer leads to slightly increasing the current of other coupling windings. This mode ends when the switch Q turns off. The current of inductor L1 can be expressed as:
where , , and regarding Equation (5), I1 is also equal to iC4(t1) by considering the turn ratio.
Interval 3 [t2 < t < t3] (Figure 4c): At t = t2, the switch Q turns off, diodes D1 and D4 turn on, and the energy transfers from the input to the output during this stage. The stored energy of the magnetizing inductance and of capacitors C5 and C6 also transfers to the load, and capacitors C3 and C4 will be charged through diode D1; however, capacitor C1 is discharged in this operation mode. The resonance between leakage inductance L5 and C5 and also leakage inductance L6 and C6 occurs during the maximum time of the half-resonant interval. This stage ends when the resonant current of iC5 becomes zero and provide the ZCS (zero current switching) turn-off for diode D4. In the following, the corresponding voltage and current equations are expressed:
Interval 4 [t3 < t < t4] (Figure 4d): In this stage, the switch is still off and the output diode D4 is also off by reversing the current of L5, which occurred in the previous operation mode. However, the input diode D1 remains on in this stage, which causes the capacitors C3 and C4 to keep their charging state on from the previous stage. In addition, capacitor C1 is discharged the same way as operation mode 3. The current of L1 can be stated as:
where I3 is equal to iC4(t3) by considering the turn ratio.
Moreover, the other current equations can be expressed as:
This operation mode ends when the switch is turned on again.
3. The Proposed Converter Analysis and Design Considerations
In this section, different features of the proposed converter, such as voltage gain and voltage stresses of the switch and diodes, are discussed and compared with other high step-up converters. Then, in order to compare the performance of the proposed converter’s features, some graphs and tables are provided.
3.1. Conversion Ratio
When the input diode D1 is on, the capacitors C3 and C4 charge by the input voltage source through magnetizing inductance Lm. However, at the on-state of switch Q, the capacitors C3 and C4 discharge themselves to Lm, which causes the voltage gain of the converter to increase. By applying the magnetizing inductor Lm, the voltage-second balance equation VC can be calculated as:
According to interval 3, by applying a KVL the output voltage can be obtained as:
where the VC5 and VC6 can be expressed as:
Therefore, the voltage gain of the proposed converter is equal to:
Figure 6 shows the voltage gain of the proposed converter by variation of the duty cycle for different turn ratios of the coupled inductors. As it can be seen, although by increasing the turn ratio of the coupled inductors a larger voltage gain can be obtained at a lower duty cycle, the duty cycle range for the step-up purpose in the Z-source converter will be restricted. In fact, the following equation represents the range of duty cycle for the proposed impedance source converter in a step-up operation mode:
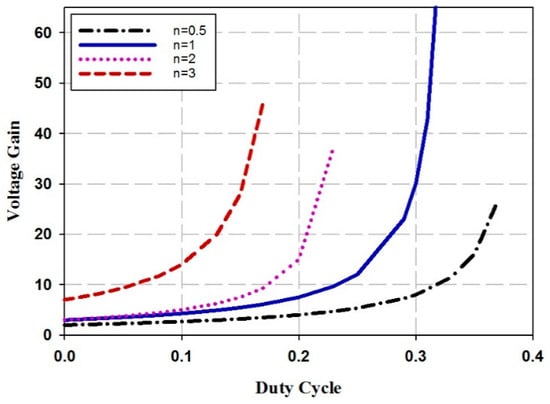
Figure 6.
Voltage gain of the proposed converter for different turn ratio of coupled inductors.
Moreover, a higher turn ratio results in higher power loss due to increasing the leakage inductance of coupled inductors. Moreover in Figure 7, the voltage gain of the proposed converter is compared with converters in [12,18,19]. As it can be observed, the voltage gain of proposed converter is higher than that of the other three converters for variation of duty cycle from 0 to 0.33 due to considering the unity turn ratio of the coupled inductors.
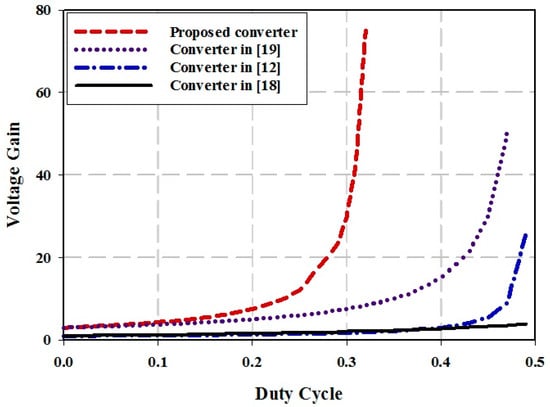
Figure 7.
Voltage gain of the proposed converter vs. converters in [12,18,19].
3.2. Voltage Stresses of Switch and Diodes
By considering the corresponding time interval of the converter operation mode, the voltage stress of the semiconductor devices can be calculated. According to the interval 1, voltage stress of D1 and D4 can be determined as:
In addition, the voltage stress of diodes D2 and D3 can be determined by considering interval 2 as:
To calculate the voltage stress of switch Q, a KVL is applied by considering interval 3; therefore, the following equation is obtained:
According to Equation (16), the voltage stress of the switch can be expressed as:
Figure 8 shows the voltage stress of the switch for different turn ratios of coupled inductors by varying the duty cycle; as it can be observed, by increasing the turn ratio, the voltage stress increases as well. Moreover, Figure 9 demonstrates the voltage stress of the proposed converter compared with converters in [12,18,19]. The voltage gain varies from 5 to 15, and the voltage stresses of the switch for the converters are compared with each other. As it can be seen from Figure 9, the stress voltage of the switch in the proposed converter and the converter in [19] is lower than that of the two other converters.
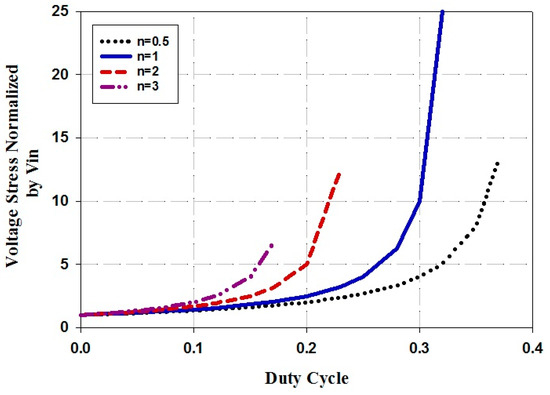
Figure 8.
Voltage stress of the switch for different turn ratios of coupled inductors.
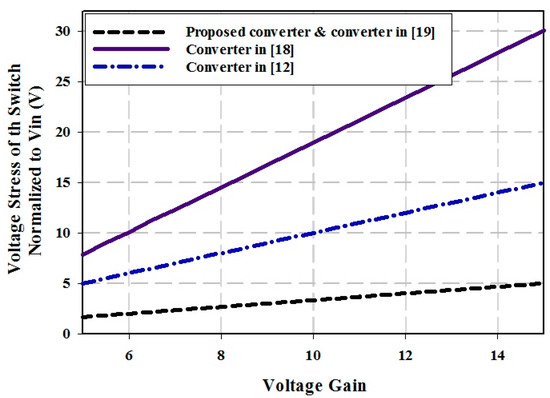
Figure 9.
Voltage stress of the switch in the proposed converter and the converters in [12,18,19].
3.3. Converter Analysis and Design Guideline
The ZCS occurs for the diodes D2, D3 and D4 for the sake of resonance between leakage inductances of L5 (or L6) and C5 (or C6). The full-resonance can be done if the following equation is satisfied:
In order to stabilize the input current, Equation (26) is not satisfied in the proposed converter. However, the ZCS condition is still established because even just the beginning part of the resonant waveform will be affected.
In addition, diode D4 is conducting current only in time interval 3 (t2 < t < t3). Therefore, it can be concluded that the average current of D4 is equal to the output current:
Consequently, the leakage inductance can be calculated as:
The duration t3 − t2 can be considered as the maximum DTSW. In addition, the magnetizing inductance can be also calculated as the following by considering the desirable current ripple :
Moreover, capacitor C3 can be calculated with regard to the current flow over the switched-on interval:
The other capacitors in the impedance network have the same value as capacitor C3.
3.4. High Step-up Converters Comparison
In Table 1 the performance of the proposed converter is compared with the other high step-up converters in [12,18,19]. As observed, the proposed converter provides a higher voltage gain meanwhile the voltage stress of the switch is lower than that of others. Moreover, the proposed converter employs a single ferrite core which make the converter more efficient due to reducing the core loss of the transformer in comparison with the converter in [18,19] with two ferrite cores and the converter in [12] with three ferrite core. In addition, the input current of proposed converter is continuous with a low current ripple; however, the input current of the other compared converters are discontinuous.

Table 1.
Comparison of proposed converter with other Z-source DC–DC converters.
4. Experimental Results
To compare the performance of the proposed converter in practice, a real prototype of the converter was implemented, and experimental results are provided in order to verify the theoretical analysis. Figure 10 shows the real implemented prototype. The implemented converter operated at 50 kHz to convert the 25 V input voltage to 300 V with a nominal power of 100 W for the load.

Figure 10.
Implemented prototype of the proposed converter.
Table 2 reports the parameters of the designed converter. The drain-to-source breakdown voltage of the selected MOSFET was much lower than the output voltage, and therefore a low RDS of the MOSFET resulted in low conduction power loss.

Table 2.
Important parameters of the implemented prototype.
Experimental waveforms of the implemented prototype are illustrated in Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15. The input current and voltage of the converter are shown in Figure 11; the low input current ripple can be observed in this figure. Figure 12 shows the voltage and current of diode D1; the voltage and current waveforms of the switch are shown in Figure 13. It can be seen that regarding the output voltage of 300 V, which is illustrated in Figure 15, the stress voltage of MOSFET is 100 V. Finally, the voltage and current of diode D4 can be seen in Figure 14.
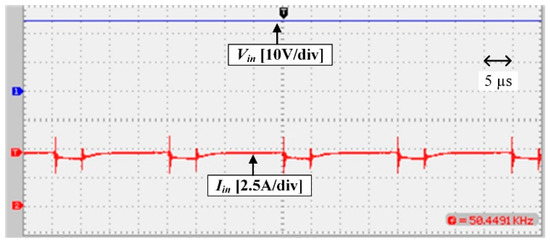
Figure 11.
Input Voltage and current of the converter.
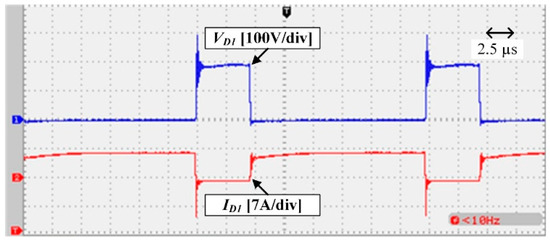
Figure 12.
Voltage and current waveform of the diode D1.
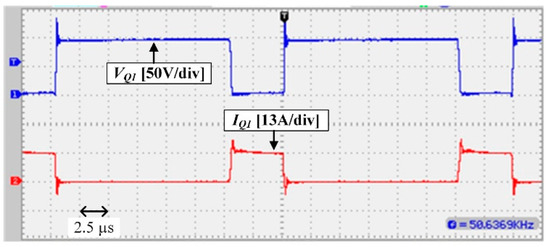
Figure 13.
Voltage and current waveform of the switch Q.
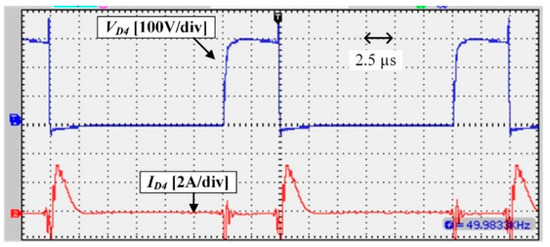
Figure 14.
Voltage and current waveform of the diode D4.
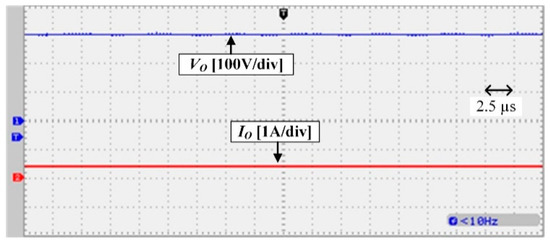
Figure 15.
Output voltage and current waveform of the high step-up converter.
The efficiency of the proposed converter was calculated by measuring the input and output current and voltage of the converter by means of DC current and voltage meters, respectively. Figure 16 shows the efficiency of the implemented proposed converter from 50% to 100% of a full load condition and it is compared with the converter in [19]. As it can be observed, by increasing the output power, conduction losses increase as well and lead to dropping the efficiency slightly. Moreover, under a full load condition, the measured efficiency is 93%.
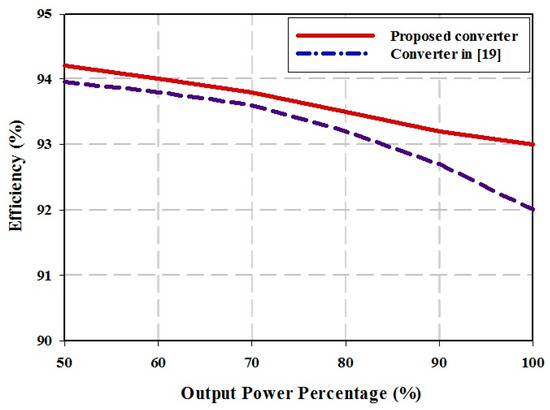
Figure 16.
Efficiency plot of the implemented prototype under different load conditions.
5. Conclusions
Among the different step-up techniques that were applied on boost converters in order to improve the input-to-output voltage ratio, the cascaded technique was chosen in this paper in order to cascade two Z-source networks and take advantage of both the cascade and impedance source converters. All inductors were coupled together in the proposed converter; therefore, the voltage gain increased only by utilizing a single core in the proposed configuration. A low duty cycle of the switch lead to reducing the reverse-recovery problem of the output diode significantly and results in enhancing the efficiency due to a reduction of power loss of the switch and diodes. Furthermore, diodes D2, D3, and D4 turn off under a ZCS condition. The low input current ripple of this converter makes it appropriate to apply in renewable energy sources. A laboratory prototype of the proposed converter in order to justify the theoretic analysis was built, and experimental waveforms were presented for a 100 W output power converter.
Author Contributions
Conceptualization, N.S.; methodology, N.S.; software, N.S.; validation, N.S., H.M.-G., and G.V.-Q.; investigation, N.S.; data curation, N.S.; writing—original draft preparation, N.S.; writing—review and editing, N.S., H.M.-G., and G.V.-Q.; supervision, H.M.-G. and G.V.-Q. All authors have read and agreed to the published version of the manuscript.
Funding
This research and the APC was funded by the Spanish Ministerio de Ciencia, Innovación y Universidades (MICINN)-Agencia Estatal de Investigación (AEI) and the European Regional Development Funds (FEDER), by means of project PGC2018-098946-B-I00.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bugaje, I. Renewable energy for sustainable development in Africa: A review. Renew. Sustain. Energy Rev. 2006, 10, 603–612. [Google Scholar] [CrossRef]
- Wai, R.-J.; Wang, W.-H.; Lin, C.-Y. High-Performance Stand-Alone Photovoltaic Generation System. IEEE Trans. Ind. Electron. 2008, 55, 240–250. [Google Scholar] [CrossRef]
- Liu, H.; Hu, H.; Wu, H.; Xing, Y.; Batarseh, I. Overview of High-Step-Up Coupled-Inductor Boost Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 689–704. [Google Scholar] [CrossRef]
- Forouzesh, M.; Siwakoti, Y.P.; Gorji, S.A.; Blaabjerg, F.; Lehman, B. Step-Up DC–DC Converters: A Comprehensive Review of Voltage-Boosting Techniques, Topologies, and Applications. IEEE Trans. Power Electron. 2017, 32, 9143–9178. [Google Scholar] [CrossRef]
- Tofoli, F.L.; De Paula, W.J.; Júnior, D.D.S.O.; Pereira, D.D.C. Survey on non-isolated high-voltage step-up dc–dc topologies based on the boost converter. IET Power Electron. 2015, 8, 2044–2057. [Google Scholar] [CrossRef]
- Salehi, N.; Mirtalaei, S.M.M.; Mirenayat, S.H. A high step-up DC–DC soft-switched converter using coupled inductor and switched capacitor. Int. J. Electron. Lett. 2017, 6, 260–271. [Google Scholar] [CrossRef]
- Zhao, Q.; Lee, F. High-efficiency, high step-up DC-DC converters. IEEE Trans. Power Electron. 2003, 18, 65–73. [Google Scholar] [CrossRef]
- Kim, K.-D.; Kim, J.-G.; Jung, Y.-C.; Won, C.-Y. Improved non-isolated high voltage gain boost converter using coupled inductors. In Proceedings of the 2011 International Conference on Electrical Machines and Systems, Beijing, China, 20–23 August 2011; pp. 1–6. [Google Scholar]
- Prudente, M.; Pfitscher, L.L.; Emmendoerfer, G.; Romaneli, E.F.; Gules, R. Voltage Multiplier Cells Applied to Non-Isolated DC–DC Converters. IEEE Trans. Power Electron. 2008, 23, 871–887. [Google Scholar] [CrossRef]
- Poorali, B.; Jazi, H.M.; Adib, E. Single-core soft-switching high step-up three-level boost converter with active clamp. IET Power Electron. 2016, 9, 2692–2699. [Google Scholar] [CrossRef]
- Peng, F.Z. Z-Source Inverters. IEEE Trans. Ind. Appl. 2003, 39, 504–510. [Google Scholar] [CrossRef]
- Galigekere, V.P.; Kazimierczuk, M.K. Analysis of PWM Z-Source DC-DC Converter in CCM for Steady State. IEEE Trans. Circuits Syst. I Regul. Pap. 2011, 59, 854–863. [Google Scholar] [CrossRef]
- Chub, A.; Vinnikov, D.; Blaabjerg, F.; Peng, F.Z. A Review of Galvanically Isolated Impedance-Source DC–DC Converters. IEEE Trans. Power Electron. 2015, 31, 2808–2828. [Google Scholar] [CrossRef]
- Siwakoti, Y.P.; Peng, F.Z.; Blaabjerg, F.; Loh, P.C.; Town, G.E. Impedance-Source Networks for Electric Power Conversion Part I: A Topological Review. IEEE Trans. Power Electron. 2014, 30, 699–716. [Google Scholar] [CrossRef]
- Siwakoti, Y.P.; Loh, P.C.; Blaabjerg, F.; Town, G.E. Y-source impedance network. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition—APEC 2014, Fort Worth, TX, USA, 16–20 March 2014; pp. 3362–3366. [Google Scholar]
- Hakemi, A.; Sanatkar-Chayjani, M.; Monfared, M. Δ-Source Impedance Network. IEEE Trans. Ind. Electron. 2017, 64, 7842–7851. [Google Scholar] [CrossRef]
- Shen, H.; Zhang, B.; Qiu, D.; Zhou, L. A Common Grounded Z-Source DC–DC Converter With High Voltage Gain. IEEE Trans. Ind. Electron. 2016, 63, 2925–2935. [Google Scholar] [CrossRef]
- Luo, F.; Ye, H. Positive output cascade boost converters. IEE Proc. Electr. Power Appl. 2004, 151, 590–606. [Google Scholar] [CrossRef]
- Poorali, B.; Torkan, A.; Adib, E. High step-up Z-source DC–DC converter with coupled inductors and switched capacitor cell. IET Power Electron. 2015, 8, 1394–1402. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).