Investigation of Scale Conversion for Inductive Power Transfer in Series-Series Configuration
Abstract
1. Introduction
2. Materials and Methods
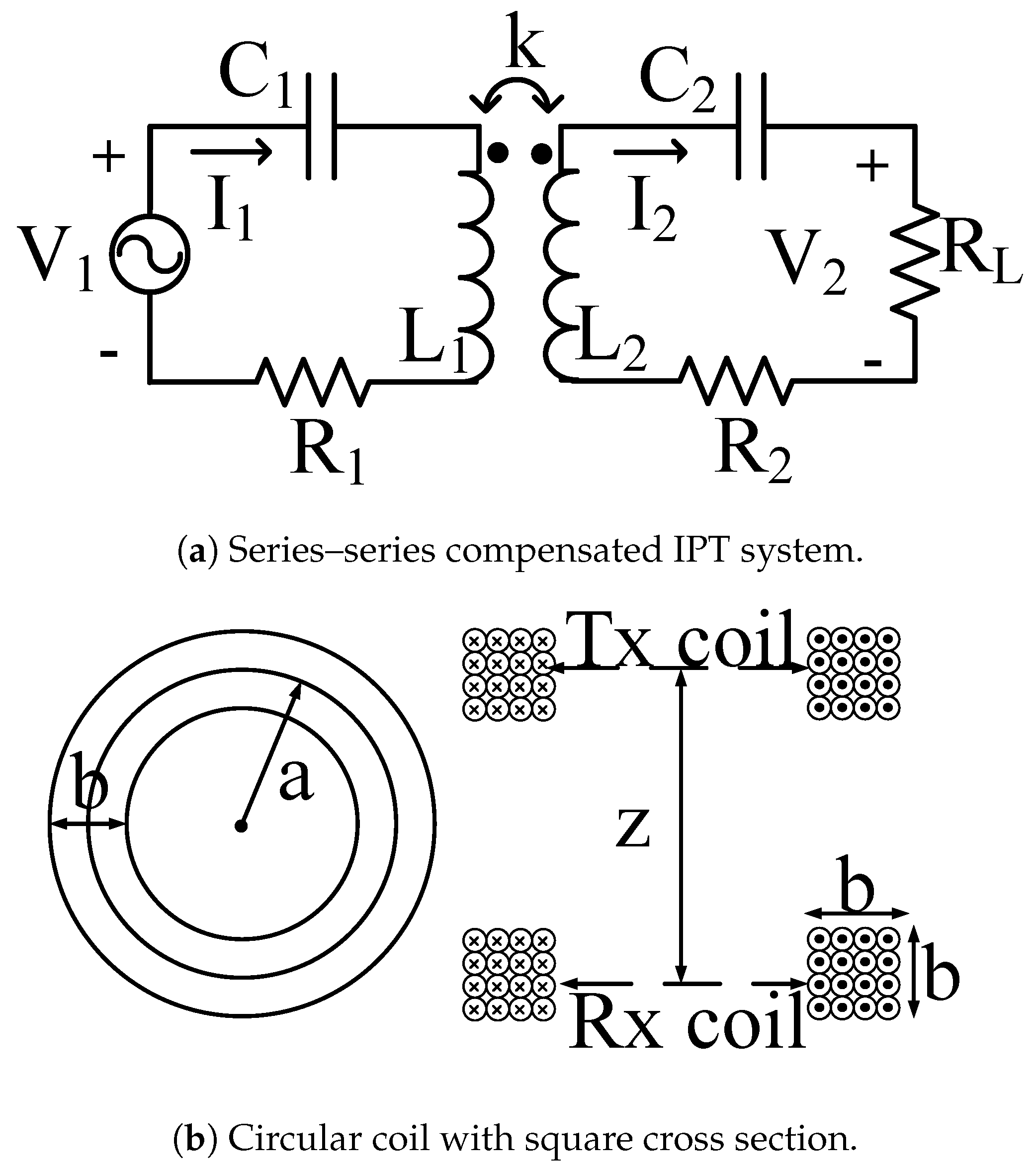
2.1. Target System and Performance Indices
2.2. Proposed Scaling Rules
2.2.1. Geometric Scaling and Circuit Parameters
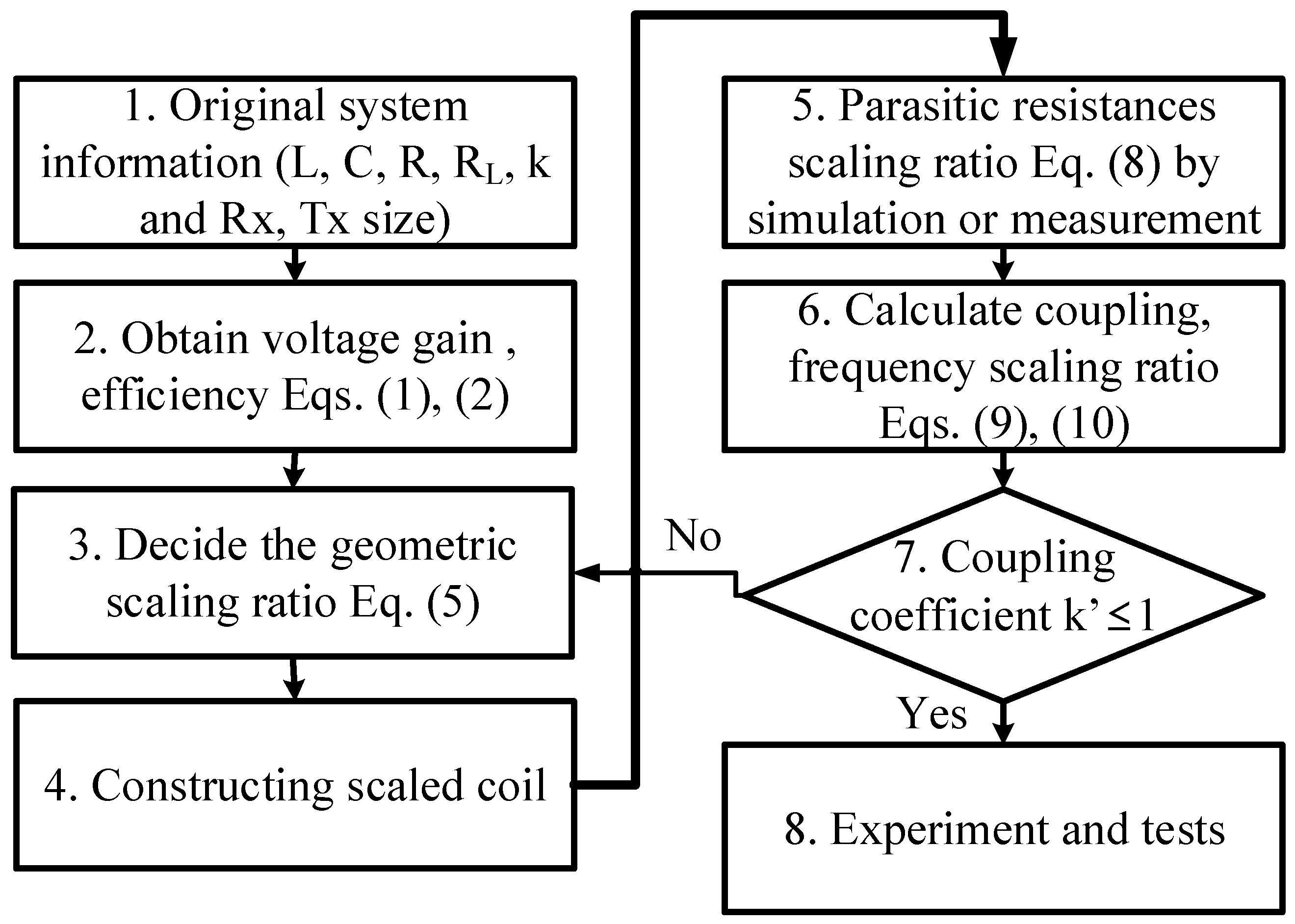
2.2.2. Design Procedure for the Proposed Scale Conversion
3. Prototype Design and Experimental Results
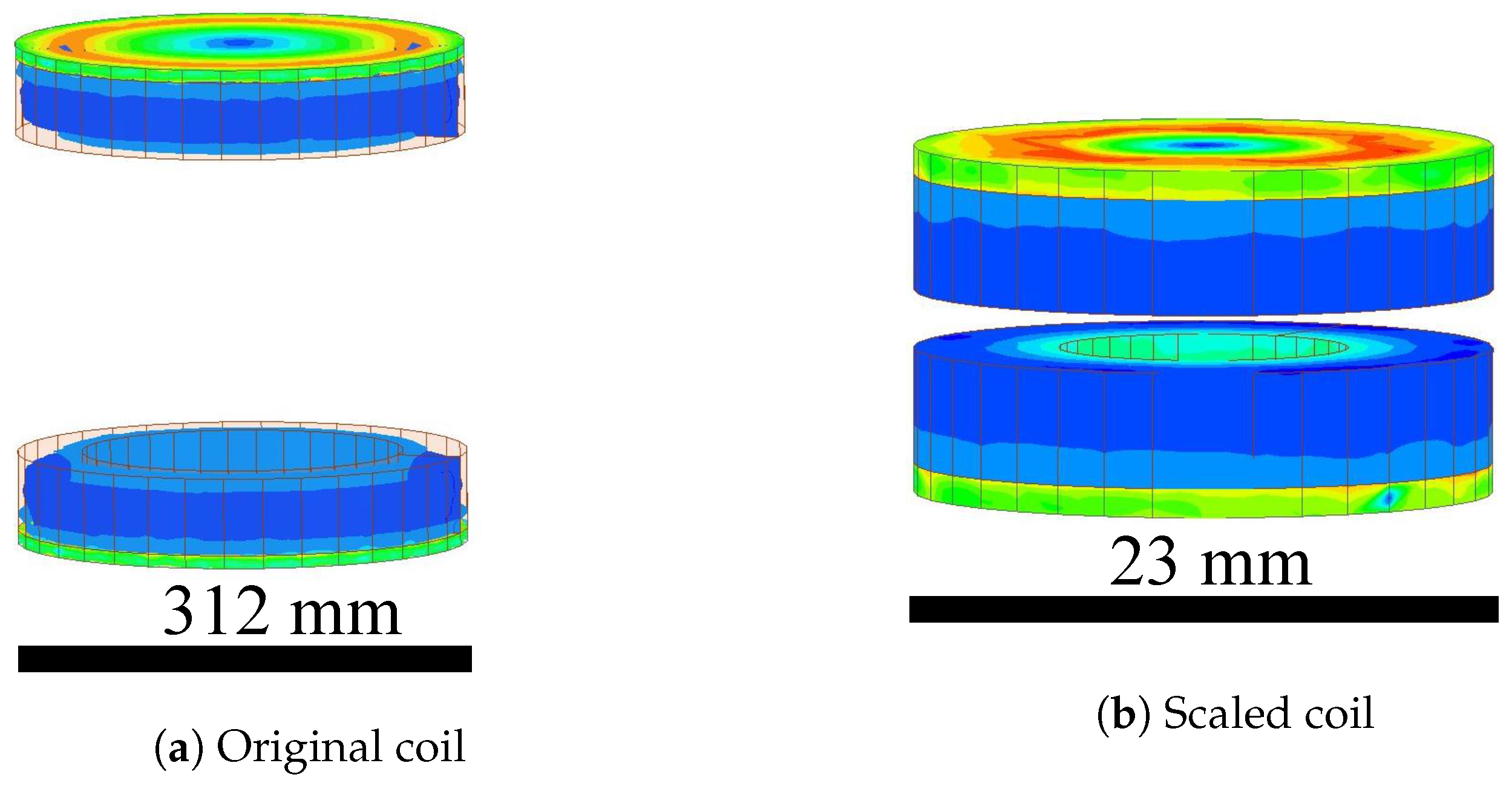
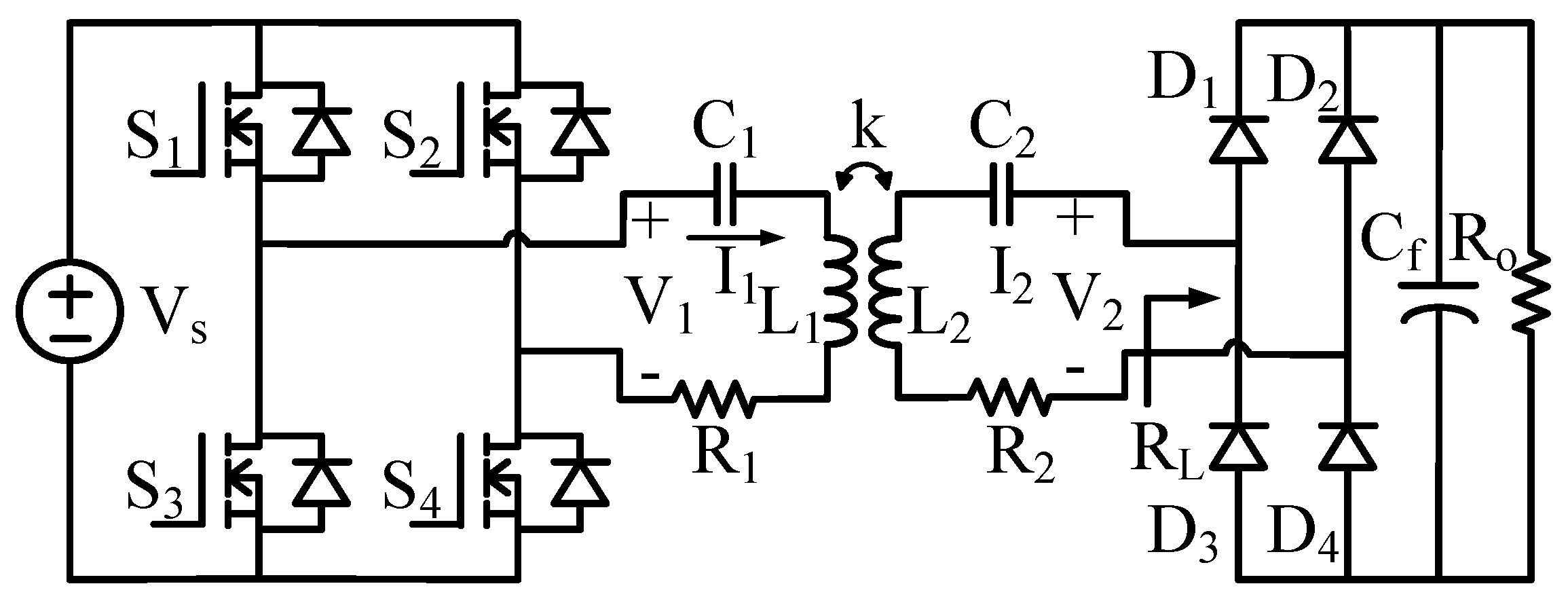
3.1. Prototype Design
3.2. Experimental Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Derivation of Performance Indices
References
- Kurs, A.; Karalis, A.; Moffatt, R.; Joannopoulos, J.D.; Fisher, P.; Soljačić, M. Wireless power transfer via strongly coupled magnetic resonances. Science 2007, 317, 83–86. [Google Scholar] [CrossRef]
- Covic, G.A.; Boys, J.T. Inductive power transfer. Proc. IEEE 2013, 101, 1276–1289. [Google Scholar] [CrossRef]
- Guidi, G.; Suul, J.A.; Jenset, F.; Sorfonn, I. Wireless Charging for Ships: High-Power Inductive Charging for Battery Electric and Plug-In Hybrid Vessels. IEEE Electrif. Mag. 2017, 5, 22–32. [Google Scholar] [CrossRef]
- Gao, J. Inductive power transmission for untethered micro-robots. In Proceedings of the 31st Annual Conference of IEEE Industrial Electronics Society, IECON 2005, Raleigh, NC, USA, 6–10 November 2005; p. 6. [Google Scholar]
- Foote, A.; Onar, O.C. A review of high-power wireless power transfer. In Proceedings of the 2017 IEEE Transportation Electrification Conference and Expo (ITEC), Chicago, IL, USA, 22–24 June 2017; pp. 234–240. [Google Scholar]
- Bosshard, R.; Kolar, J.W. Multi-Objective Optimization of 50 kW/85 kHz IPT System for Public Transport. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 1370–1382. [Google Scholar] [CrossRef]
- Bosshard, R.; Iruretagoyena, U.; Kolar, J.W. Comprehensive Evaluation of Rectangular and Double-D Coil Geometry for 50 kW/85 kHz IPT System. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 1406–1415. [Google Scholar] [CrossRef]
- Zaheer, A.; Hao, H.; Covic, G.A.; Kacprzak, D. Investigation of Multiple Decoupled Coil Primary Pad Topologies in Lumped IPT Systems for Interoperable Electric Vehicle Charging. IEEE Trans. Power Electron. 2015, 30, 1937–1955. [Google Scholar] [CrossRef]
- Budhia, M.; Covic, G.A.; Boys, J.T. Design and Optimization of Circular Magnetic Structures for Lumped Inductive Power Transfer Systems. IEEE Trans. Power Electron. 2011, 26, 3096–3108. [Google Scholar] [CrossRef]
- Chen, X.; Fu, X.; Jiang, C.; Pei, C.; Liu, F. Magnetic-field-model and circuit-model based analysis of three-phase magnetically coupled resonant wireless power transfer systems with cylinder-shaped coils. J. Power Electron. 2018, 18, 1154–1164. [Google Scholar]
- Zhu, G.; Gao, D.; Lin, S. Leakage Magnetic Field Suppression Using Dual-Transmitter Topology in EV Wireless Charging. J. Power Electron. 2019, 19, 625–636. [Google Scholar]
- Chen, X.; Chen, L.; Ye, W.; Zhang, W. Three-coil magnetically coupled resonant wireless power transfer system with adjustable-position intermediate coil for stable transmission characteristics. J. Power Electron. 2019, 19, 211–219. [Google Scholar]
- Meng, Y.; Wang, Z.; Jiang, P.; Wang, W.; Chen, F.; Yan, G. Optimization and analysis of Helmholtz-like three-coil wireless power transfer system applied in gastrointestinal robots. J. Power Electron. 2020, 20, 1088–1098. [Google Scholar] [CrossRef]
- Zhu, G.; Gao, D. Highly effective leakage magnetic field suppression by using a reactive coil in perfectly aligned EV wireless charging systems. J. Power Electron. 2020, 20, 11–21. [Google Scholar] [CrossRef]
- Wang, C.-S.; Stielau, O.H.; Covic, G.A. Design considerations for a contactless electric vehicle battery charger. IEEE Trans. Ind. Electron. 2005, 52, 1308–1314. [Google Scholar] [CrossRef]
- Zhong, W.X.; Hui, S.Y.R. Maximum Energy Efficiency Tracking for Wireless Power Transfer Systems. IEEE Trans. Power Electron. 2015, 30, 4025–4034. [Google Scholar] [CrossRef]
- Chen, C.; Zhou, H.; Deng, Q.; Hu, W.; Yu, Y.; Lu, X.; Lai, J. Modeling and Design of Zero-Voltage-Switching Controller for Wireless Power Transfer Systems Based on Closed-Loop Dominant Pole. J. Power Electron. 2019, 19, 1235–1247. [Google Scholar]
- Lee, B.H. Wireless Power Transfer via Magnetic Resonance Coupling (MRC) with Reduced Standby Power Consumption. J. Power Electron. 2019, 19, 637–644. [Google Scholar]
- Iwasa, Y.; Brown, W.; Wallace, C. An operational 1/25-scale magneplane system with superconducting coils. IEEE Trans. Magn. 1975, 11, 1490–1492. [Google Scholar] [CrossRef]
- Stipetic, S.; Zarko, D.; Popescu, M. Scaling laws for synchronous permanent magnet machines. In Proceedings of the 2015 Tenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, Monaco, 31 March–2 April 2015; pp. 1–7. [Google Scholar]
- Reichert, T.; Nussbaumer, T.; Kolar, J.W. Torque scaling laws for interior and exterior rotor permanent magnet machines. A A 2009, 3, 1. [Google Scholar]
- Guillod, T.; Kolar, J.W. Medium-frequency transformer scaling laws: Derivation, verification, and critical analysis. CPSS Trans. Power Electron. Appl. 2020, 5, 18–33. [Google Scholar] [CrossRef]
- Azurza Anderson, J.; Zulauf, G.; Papamanolis, P.; Hobi, S.; Miric, S.M.; Kolar, J.W. Three Levels Are Not Enough: Scaling Laws for Multi-Level Converters in AC/DC Applications. IEEE Trans. Power Electron. 2020, 1. [Google Scholar] [CrossRef]
- Kasper, M.; Bortis, D.; Kolar, J.W. Scaling and balancing of multi-cell converters. In Proceedings of the 2014 International Power Electronics Conference (IPEC-Hiroshima 2014–ECCE ASIA), Hiroshima, Japan, 18–21 May 2014; pp. 2079–2086. [Google Scholar]
- Sudhoff, S.D.; Shane, G.M.; Suryanarayana, H. Magnetic-equivalent-circuit-based scaling laws for low-frequency magnetic devices. IEEE Trans. Energy Convers. 2013, 28, 746–755. [Google Scholar] [CrossRef]
- Zowarka, R. Physical scale modeling to verify energy storage inductor parameters. IEEE Trans. Magn. 1984, 20, 219–222. [Google Scholar] [CrossRef]
- Cirimele, V.; Freschi, F.; Guglielmi, P. Scaling Rules at Constant Frequency for Resonant Inductive Power Transfer Systems for Electric Vehicles. Energies 2018, 11, 1754. [Google Scholar] [CrossRef]
- Nagai, C.; Inukai, K.; Kobayashi, M.; Tanaka, T.; Abumi, K.; Imura, T.; Hori, Y. Scaling law of coupling coefficient and coil size in wireless power transfer design via magnetic coupling. Electr. Eng. Jpn. 2018, 202, 21–30. [Google Scholar] [CrossRef]
- Sampath, J.; Alphones, A.; Kenneth, L.; Vilathgamuwa, D. Analysis on normalized distance and scalability in designing wireless power transfer. In Proceedings of the 2015 IEEE PELS Workshop on Emerging Technologies: Wireless Power (2015 WoW), Daejeon, Korea, 5–6 June 2015; pp. 1–6. [Google Scholar]
- Jiang, Y.; Wang, L.; Wang, Y.; Liu, J.; Wu, M.; Ning, G. Analysis, Design, and Implementation of WPT System for EV’s Battery Charging Based on Optimal Operation Frequency Range. IEEE Trans. Power Electron. 2019, 34, 6890–6905. [Google Scholar] [CrossRef]
- Si, P.; Hu, A.P.; Malpas, S.; Budgett, D. A frequency control method for regulating wireless power to implantable devices. IEEE Trans. Biomed. Circuits Syst. 2008, 2, 22–29. [Google Scholar] [CrossRef]
- Liu, X.; Clare, L.; Yuan, X.; Wang, J.; Wang, C.; Liu, J. Constant Output Power Control Methods for Variable-Load Wireless Power Transfer Systems. J. Power Electron. 2018, 18, 533–546. [Google Scholar]
- Li, Y.; Liu, L.; Zhang, C.; Yang, Q.; Li, J.; Zhang, X.; Xue, M. Improved particle swarm optimization algorithm for adaptive frequency-tracking control in wireless power transfer systems. J. Power Electron. 2018, 18, 1470–1478. [Google Scholar]
- Wu, Q.; Wang, L.; Ju, D.; Chen, C.; Chang, C. Design of efficient optimized wireless power transfer system. J. Power Electron. 2020, 20, 1121–1129. [Google Scholar] [CrossRef]
- Bosshard, R.; Kolar, J.W.; Mühlethaler, J.; Stevanović, I.; Wunsch, B.; Canales, F. Modeling and η-α-Pareto Optimization of Inductive Power Transfer Coils for Electric Vehicles. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 50–64. [Google Scholar] [CrossRef]
- Zhang, W.; Wong, S.; Tse, C.K.; Chen, Q. Design for Efficiency Optimization and Voltage Controllability of Series–Series Compensated Inductive Power Transfer Systems. IEEE Trans. Power Electron. 2014, 29, 191–200. [Google Scholar] [CrossRef]
- Song, K.; Li, Z.; Jiang, J.; Zhu, C. Constant Current/Voltage Charging Operation for Series–Series and Series–Parallel Compensated Wireless Power Transfer Systems Employing Primary-Side Controller. IEEE Trans. Power Electron. 2018, 33, 8065–8080. [Google Scholar] [CrossRef]
- Bosshard, R.; Mühlethaler, J.; Kolar, J.W.; Stevanović, I. Optimized magnetic design for inductive power transfer coils. In Proceedings of the 2013 Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 17–21 March 2013; pp. 1812–1819. [Google Scholar]
- Jeong, C.H.; Choi, S.J. Graphical Design Plane Analysis for Series-Compensated Resonant Energy Links of Inductive Wireless Power Transfer Systems. J. Power Electron. 2019, 19, 1440–1448. [Google Scholar]
- Thompson, M.T. High Temperature Superconducting Magnetic Suspension for Maglev. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1997. [Google Scholar]
- Grover, F.W. Inductance Calculations: Working Formulas and Tables; Courier Corporation: North Chelmsford, MA, USA, 2004. [Google Scholar]
- Wang, X.; Sun, P.; Deng, Q.; Wang, W. Evaluation of AC resistance in litz wire planar spiral coils for wireless power transfer. J. Power Electron. 2018, 18, 1268–1277. [Google Scholar]
- Wojda, R.; Kazimierczuk, M. Winding resistance of litz-wire and multi-strand inductors. IET Power Electron. 2012, 5, 257–268. [Google Scholar] [CrossRef]
- Sullivan, C.R. Winding loss calculation with multiple windings, arbitrary waveforms, and two-dimensional field geometry. In Proceedings of the Conference Record of the 1999 IEEE Industry Applications Conference, Thirty-Forth IAS Annual Meeting (Cat. No.99CH36370), Phoenix, AZ, USA, 3–7 October 1999; Volume 3, pp. 2093–2099. [Google Scholar]
- Rosu, M.; Zhou, P.; Lin, D.; Ionel, D.M.; Popescu, M.; Blaabjerg, F.; Rallabandi, V.; Staton, D. Multiphysics Simulation by Design for Electrical Machines, Power Electronics and Drives; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Steigerwald, R.L. A comparison of half-bridge resonant converter topologies. IEEE Trans. Power Electron. 1988, 3, 174–182. [Google Scholar] [CrossRef]
- Yang, L.; Li, X.; Xu, Z.; Liu, S.; Dong, Z.; Wu, Y. Analysis and design of a high-efficiency three-coil WPT system with constant current output. IET Electr. Power Appl. 2020, 14, 1933–1943. [Google Scholar] [CrossRef]


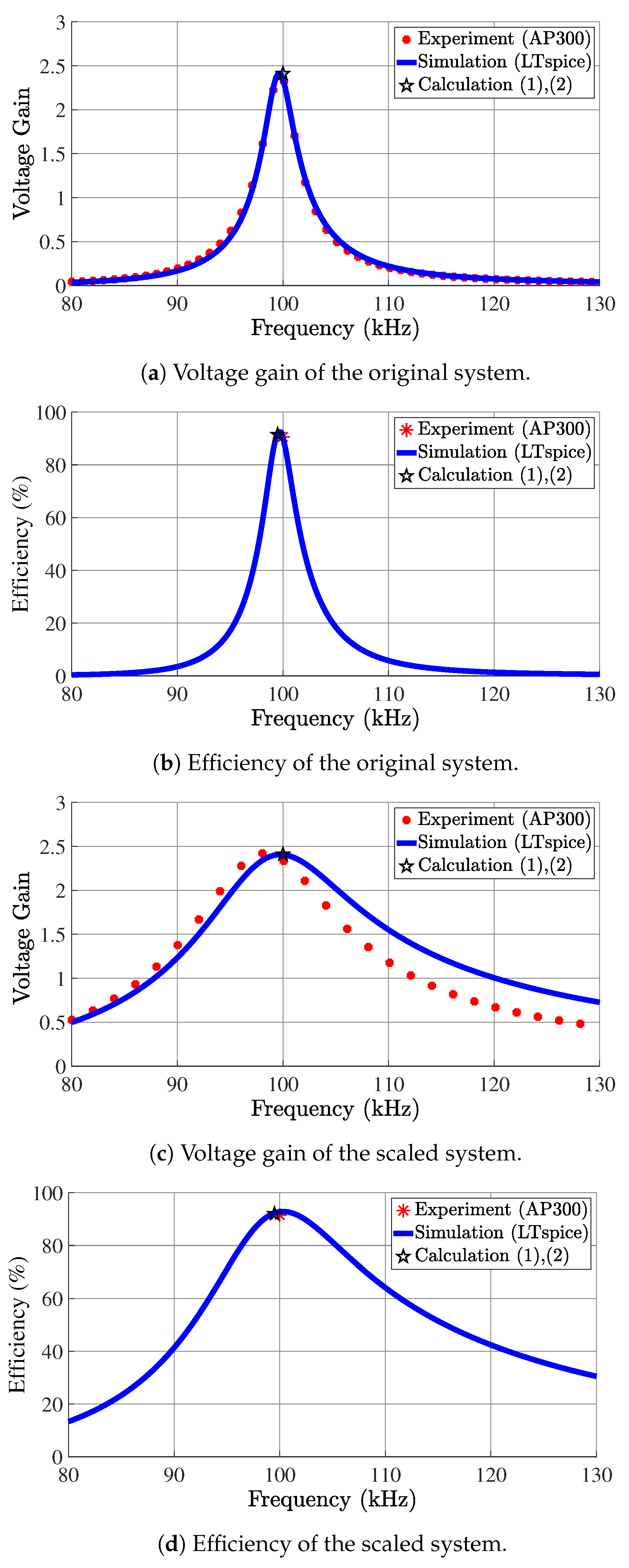
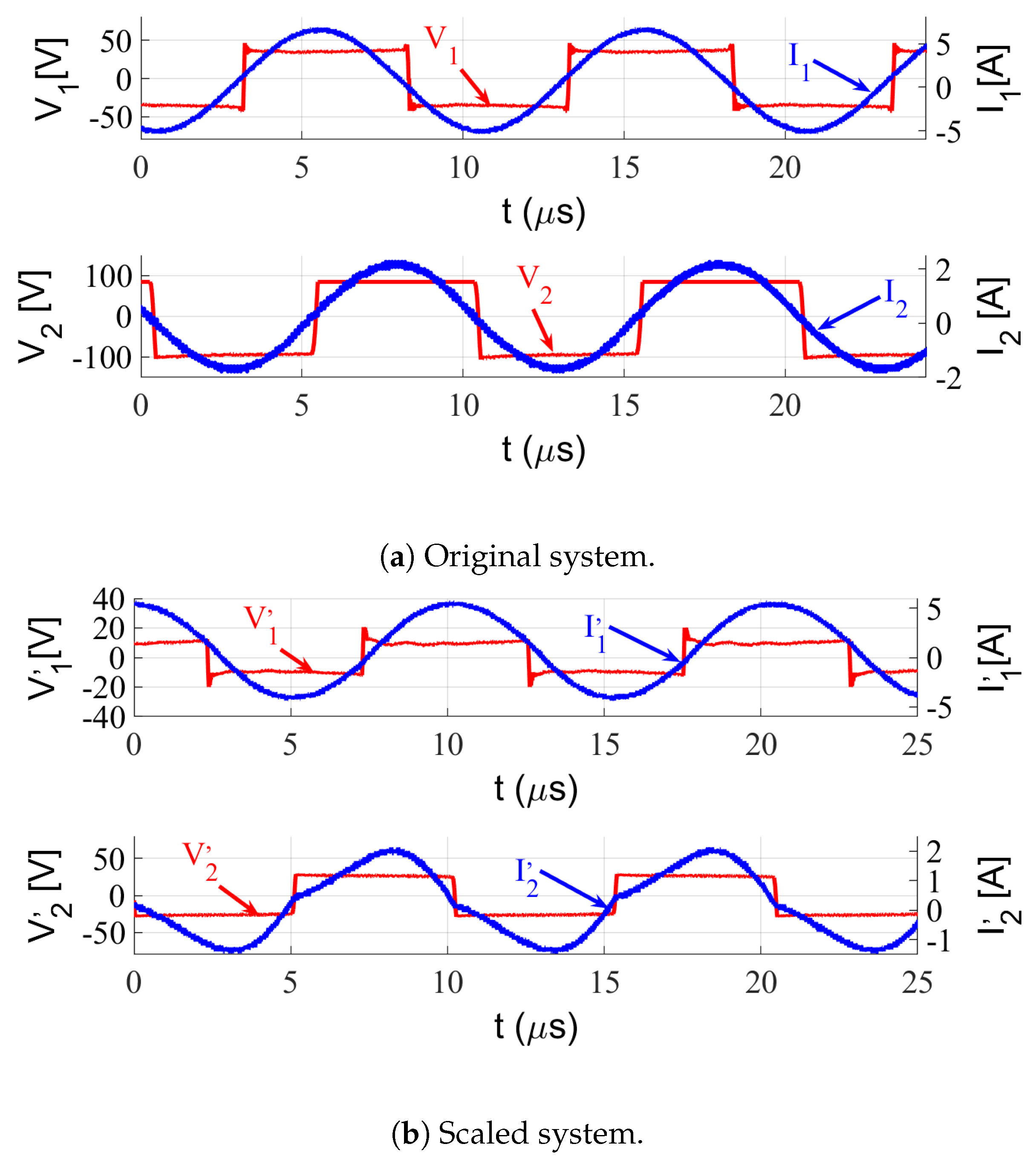
| Symbol | Parameters | Calculation | Experiment |
|---|---|---|---|
| Geometric scale | 0.067 | 0.065 | |
| Parasitic resistance scale | 0.31 | 0.327 | |
| Coupling coefficient scale | 5.16 | 5.11 | |
| Frequency scale | 1 | 1 |
| Symbol | Parameters | Original | Scaled | Unit |
|---|---|---|---|---|
| Inductance | 618, 619 | 40.1, 40.3 | ||
| Parasitic resistance | 352, 364 | 115, 117 | m | |
| Capacitance | 4.12, 4.14 | nF | ||
| k | Coupling coefficient | 0.06 | 0.31 | - |
| Resistance of load | 60 | 20 | ||
| Input voltage | 35 | 10 | V | |
| Output power | 115 | 25 | W | |
| Frequency switching | 100 | 100 | kHz | |
| Voltage gain | 2.73 | 2.27 | - | |
| Efficiency | 0.922 | 0.925 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Truong, C.-T.; Choi, S.-J. Investigation of Scale Conversion for Inductive Power Transfer in Series-Series Configuration. Electronics 2020, 9, 1851. https://doi.org/10.3390/electronics9111851
Truong C-T, Choi S-J. Investigation of Scale Conversion for Inductive Power Transfer in Series-Series Configuration. Electronics. 2020; 9(11):1851. https://doi.org/10.3390/electronics9111851
Chicago/Turabian StyleTruong, Chanh-Tin, and Sung-Jin Choi. 2020. "Investigation of Scale Conversion for Inductive Power Transfer in Series-Series Configuration" Electronics 9, no. 11: 1851. https://doi.org/10.3390/electronics9111851
APA StyleTruong, C.-T., & Choi, S.-J. (2020). Investigation of Scale Conversion for Inductive Power Transfer in Series-Series Configuration. Electronics, 9(11), 1851. https://doi.org/10.3390/electronics9111851





