Temporal Auditory Coding Features for Causal Speech Enhancement
Abstract
1. Introduction
2. Materials and Methods
2.1. Problem Formulation
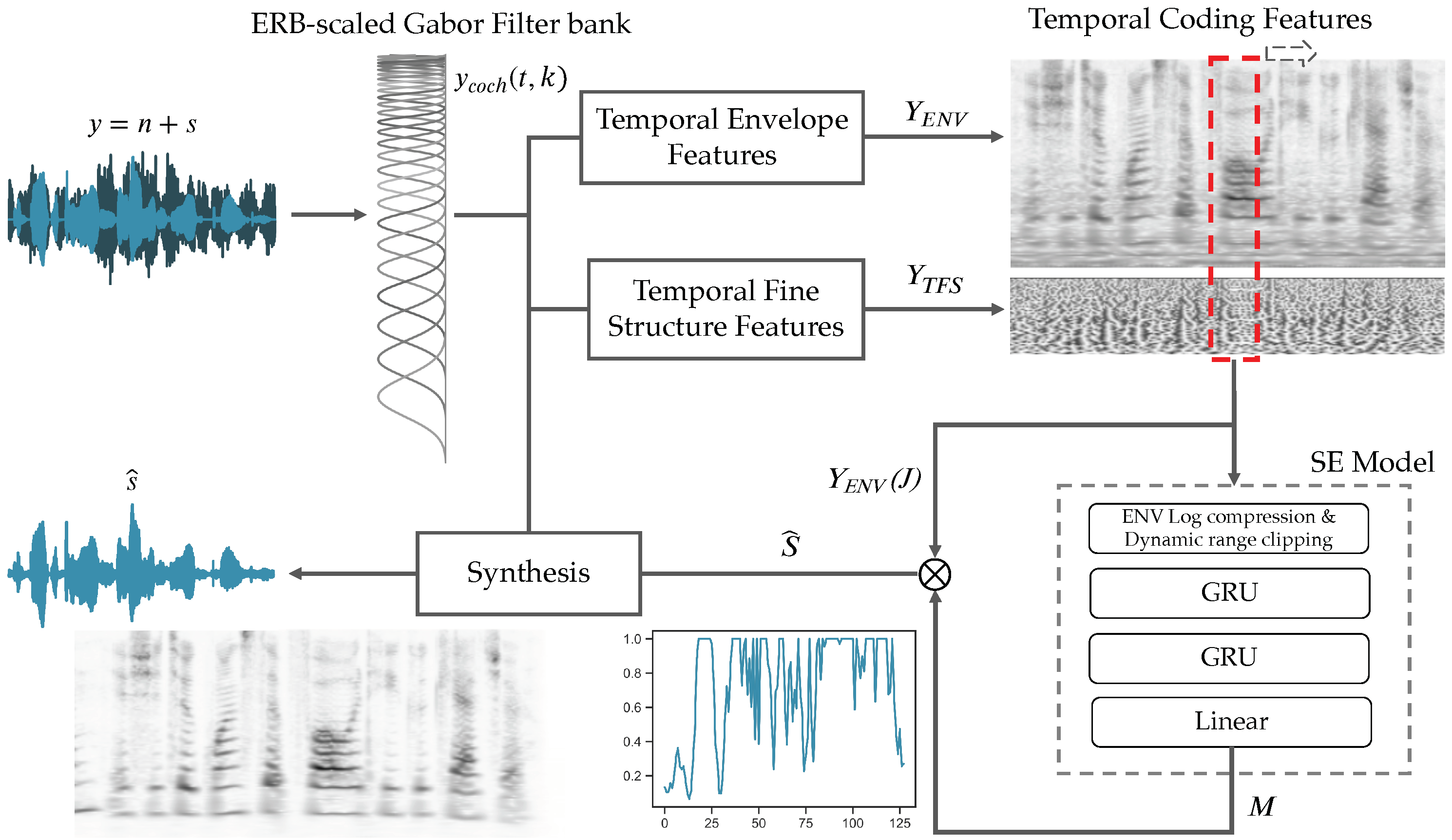
2.2. Temporal Auditory Processing: Features and Targets
2.2.1. ERB-Scaled Gabor Filter Bank: Analysis Framework
2.2.2. Temporal Envelope Features
2.2.3. Temporal Fine Structure Features
2.2.4. Synthesis Framework
2.3. Model Architecture & Training
2.4. Dataset
2.5. Objective Evaluation Criteria
2.6. Experimental Setup
3. Results
3.1. Reconstruction from Envelope Spectrogram
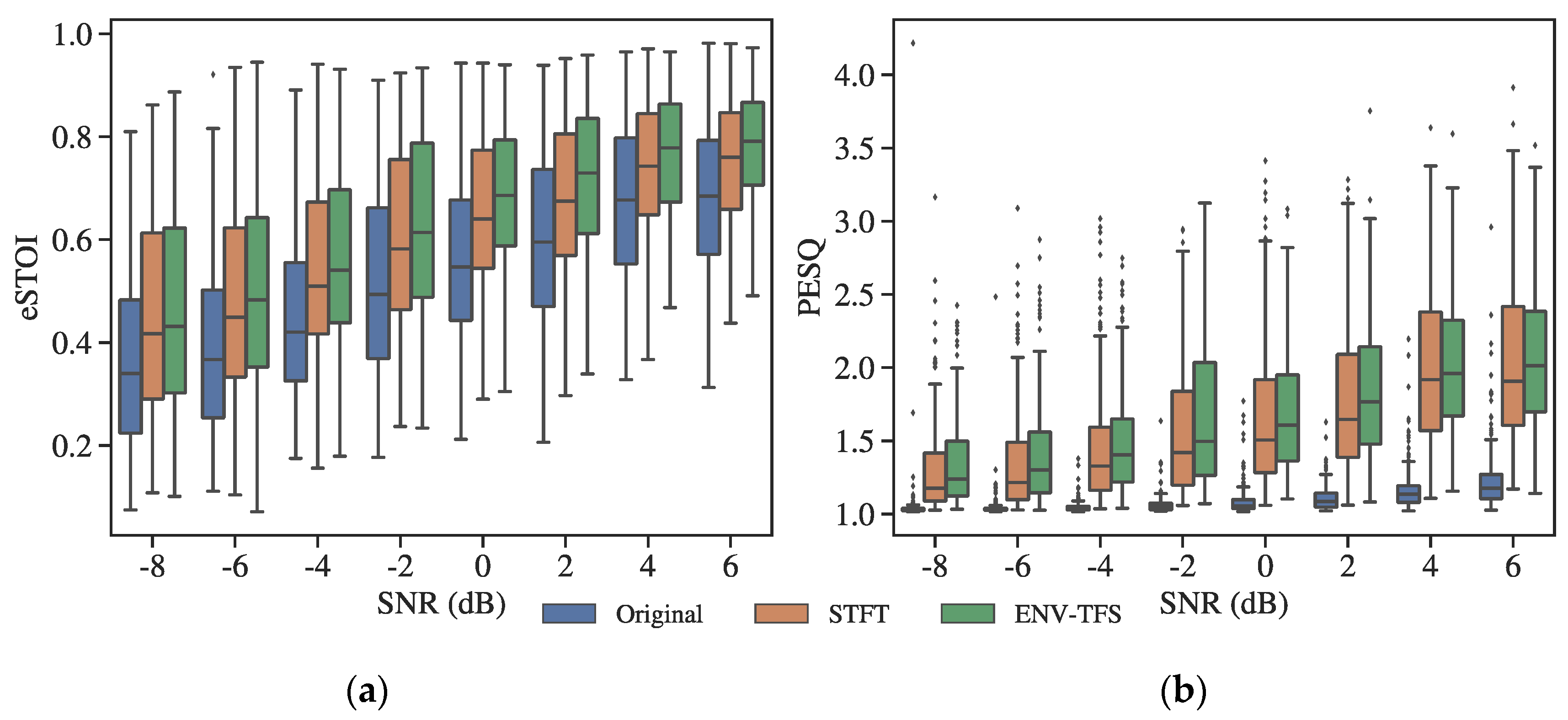
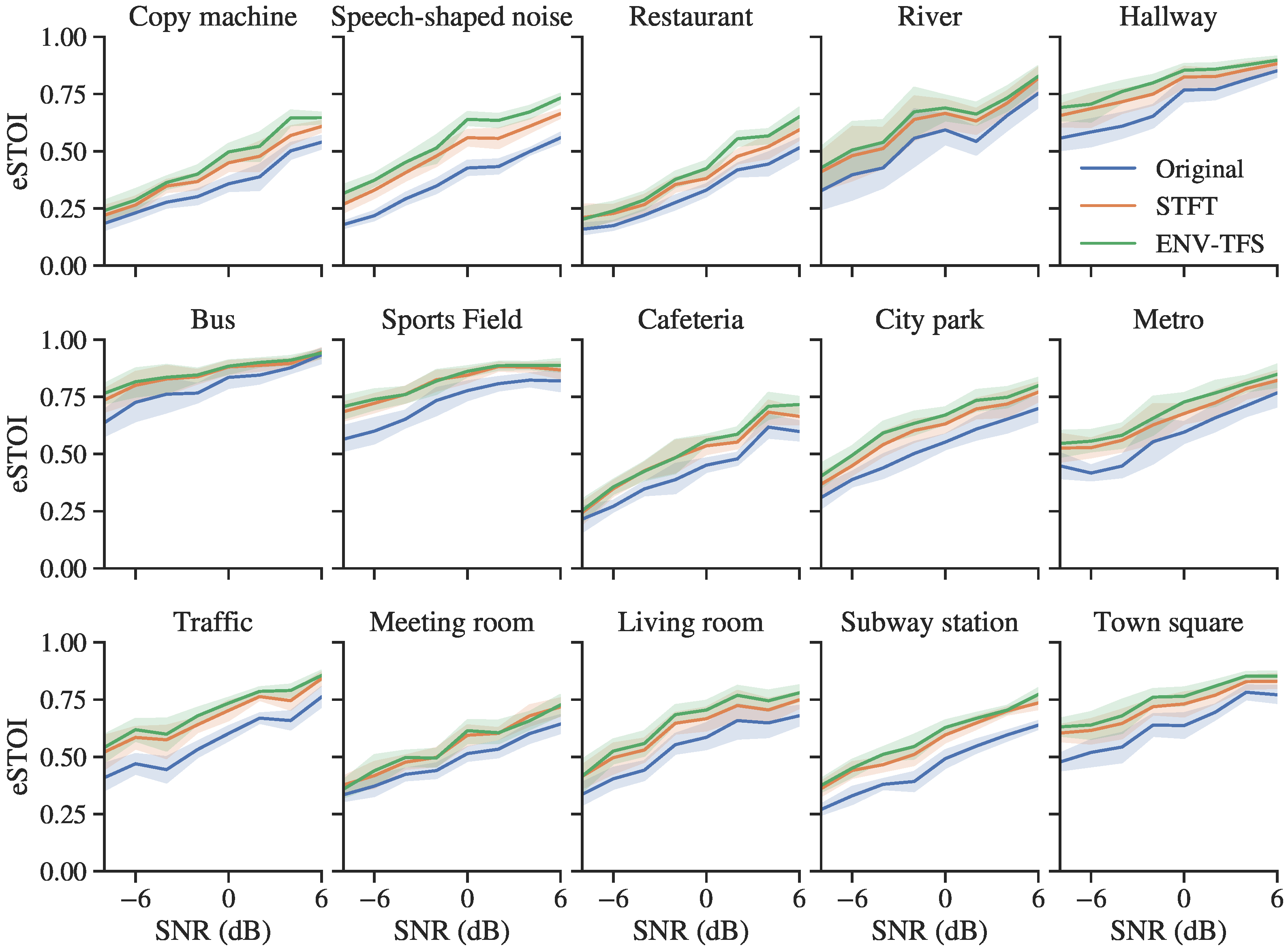
3.2. Objective Evaluation for Normal-Hearing Listeners
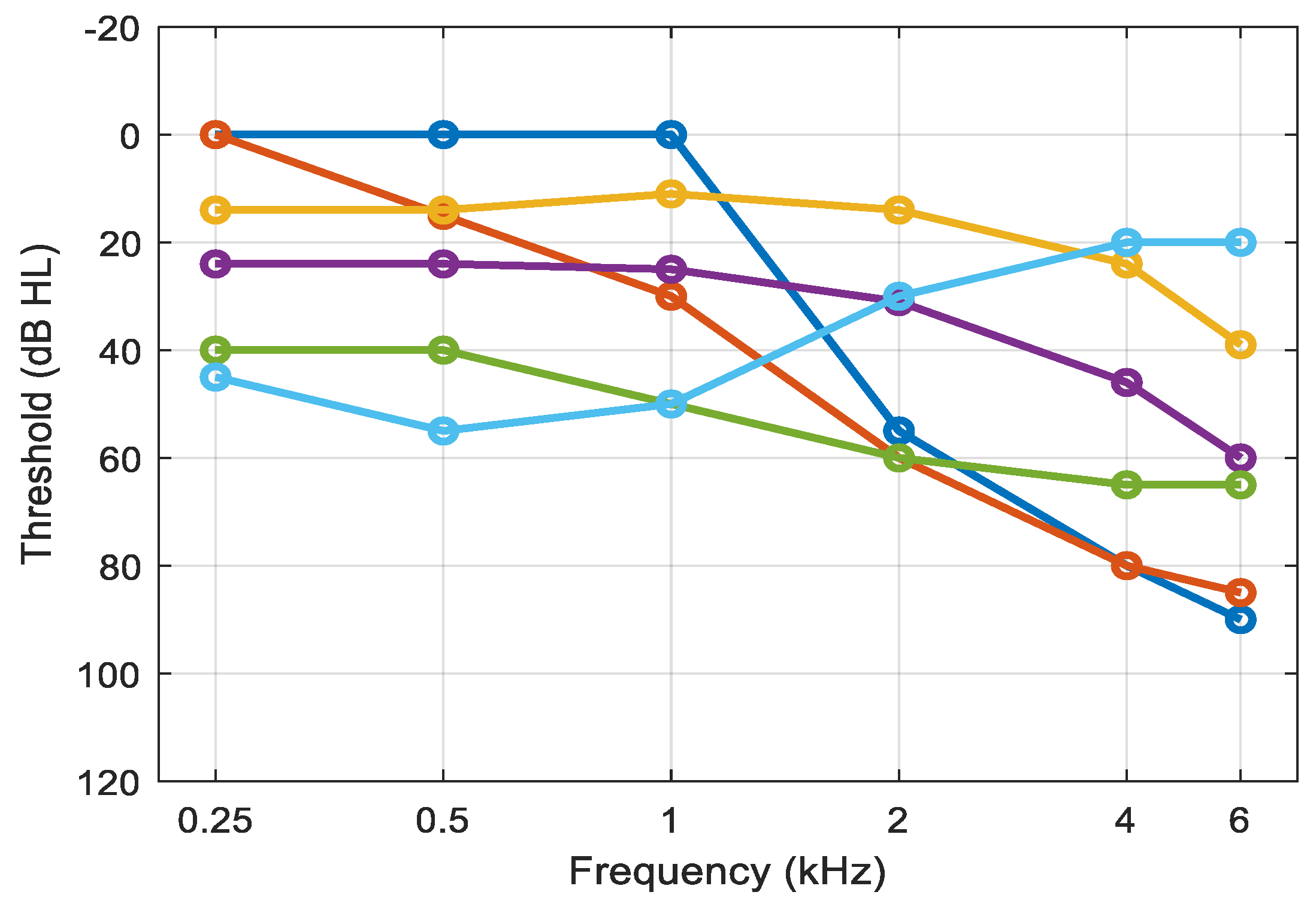
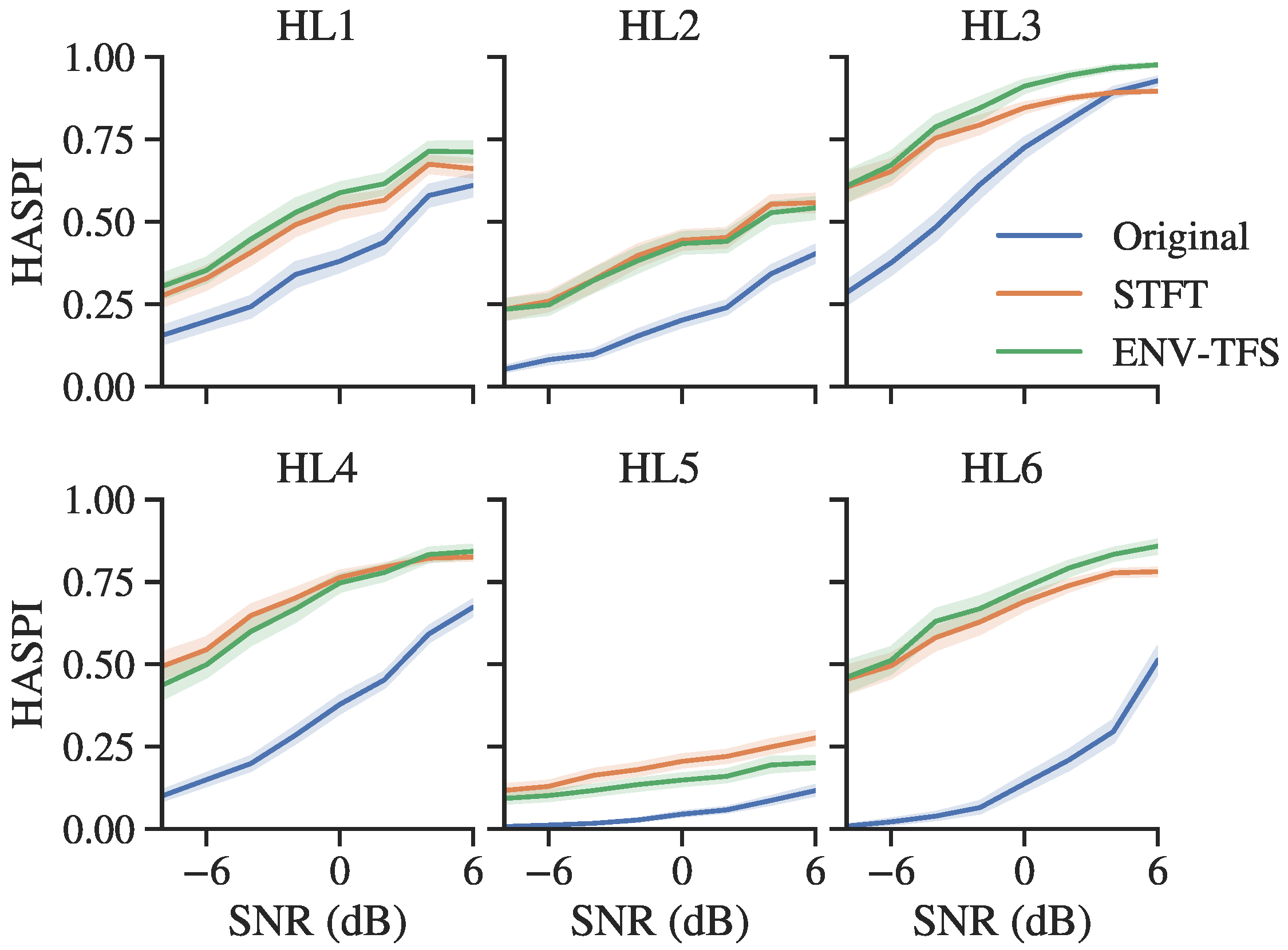
3.3. Objective Evaluation for Hearing-Impaired Listeners
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pardede, H.; Ramli, K.; Suryanto, Y.; Hayati, N.; Presekal, A. Speech Enhancement for Secure Communication Using Coupled Spectral Subtraction and Wiener Filter. Electronics 2019, 8, 897. [Google Scholar] [CrossRef]
- Rix, A.W.; Hollier, M.P.; Hekstra, A.P.; Beerends, J.G. Perceptual Evaluation of Speech Quality (PESQ) The New ITU Standard for End-to-End Speech Quality Assessment Part I—Time-Delay Compensation. J. Audio Eng. Soc. 2002, 50, 755–764. [Google Scholar]
- Srinivasan, S.; Roman, N.; Wang, D. Binary and ratio time-frequency masks for robust speech recognition. Speech Commun. 2006, 48, 1486–1501. [Google Scholar] [CrossRef]
- Czyzewski, A.; Kulesza, M. Speech Codec Enhancements Utilizing Time Compression and Perceptual Coding. In Audio Engineering Society Convention 122; Audio Engineering Society: New York, NY, USA, 2007. [Google Scholar]
- Park, G.; Cho, W.; Kim, K.-S.; Lee, S. Speech Enhancement for Hearing Aids with Deep Learning on Environmental Noises. Appl. Sci. 2020, 10, 6077. [Google Scholar] [CrossRef]
- Loizou, P.C. Speech Enhancement: Theory and Practice; CRC Press: Boca Raton, FL, USA, 2013; ISBN 1466504218. [Google Scholar]
- Boll, S. Suppression of acoustic noise in speech using spectral subtraction. IEEE Trans. Acoust. 1979, 27, 113–120. [Google Scholar] [CrossRef]
- Tsoukalas, D.E.; Mourjopoulos, J.; Kokkinakis, G. Perceptual filters for audio signal enhancement. J. Audio Eng. Soc. 1997, 45, 22–36. [Google Scholar]
- Ephraim, Y.; Malah, D. Speech enhancement using a minimum-mean square error short-time spectral amplitude estimator. IEEE Trans. Acoust. 1984, 32, 1109–1121. [Google Scholar] [CrossRef]
- Purwins, H.; Li, B.; Virtanen, T.; Schlüter, J.; Chang, S.; Sainath, T. Deep Learning for Audio Signal Processing. IEEE J. Sel. Top. Signal Process. 2019, 13, 206–219. [Google Scholar] [CrossRef]
- Korvel, G.; Kurowski, A.; Kostek, B.; Czyzewski, A. Speech analytics based on machine learning. In Machine Learning Paradigms; Springer: Cham, Switzerland, 2019; pp. 129–157. [Google Scholar]
- Vrysis, L.; Tsipas, N.; Thoidis, I.; Dimoulas, C. 1D/2D Deep CNNs vs. Temporal Feature Integration for General Audio Classification. J. Audio Eng. Soc. 2020, 68, 66–77. [Google Scholar] [CrossRef]
- Vryzas, N.; Vrysis, L.; Matsiola, M.; Kotsakis, R.; Dimoulas, C.; Kalliris, G. Continuous Speech Emotion Recognition with Convolutional Neural Networks. J. Audio Eng. Soc. 2020, 68, 14–24. [Google Scholar] [CrossRef]
- Vrysis, L.; Thoidis, I.; Dimoulas, C.; Papanikolaou, G. Experimenting with 1D CNN Architectures for Generic Audio Classification. In Audio Engineering Society Convention 148; Audio Engineering Society: New York, NY, USA, 2020. [Google Scholar]
- Thoidis, I.; Giouvanakis, M.; Papanikolaou, G. Audio-based detection of malfunctioning machines using deep convolutional autoencoders. In Audio Engineering Society Convention 148; Audio Engineering Society: New York, NY, USA, 2020. [Google Scholar]
- Goehring, T.; Keshavarzi, M.; Carlyon, R.P.; Moore, B.C.J. Using recurrent neural networks to improve the perception of speech in non-stationary noise by people with cochlear implants. J. Acoust. Soc. Am. 2019, 146, 705–718. [Google Scholar] [CrossRef] [PubMed]
- Lee, G.W.; Kim, H.K. Multi-Task Learning U-Net for Single-Channel Speech Enhancement and Mask-Based Voice Activity Detection. Appl. Sci. 2020, 10, 3230. [Google Scholar] [CrossRef]
- Czyzewski, A.; Kostek, B.; Bratoszewski, P.; Kotus, J.; Szykulski, M. An audio-visual corpus for multimodal automatic speech recognition. J. Intell. Inf. Syst. 2017, 49, 167–192. [Google Scholar] [CrossRef]
- Chen, J.; Wang, Y.; Yoho, S.E.; Wang, D.; Healy, E.W. Large-scale training to increase speech intelligibility for hearing-impaired listeners in novel noises. J. Acoust. Soc. Am. 2016, 139, 2604–2612. [Google Scholar] [CrossRef] [PubMed]
- Lang, H.; Yang, J. Speech enhancement based on fusion of both magnitude/phase-aware features and targets. Electronics 2020, 9, 1125. [Google Scholar] [CrossRef]
- Bae, S.H.; Choi, I.; Kim, N.S. Disentangled feature learning for noise-invariant speech enhancement. Appl. Sci. 2019, 9, 2289. [Google Scholar] [CrossRef]
- Rao, A.; Carney, L.H. Speech enhancement for listeners with hearing loss based on a model for vowel coding in the auditory midbrain. IEEE Trans. Biomed. Eng. 2014, 61, 2081–2091. [Google Scholar] [CrossRef][Green Version]
- Oord, A.v.D.; Dieleman, S.; Zen, H.; Simonyan, K.; Vinyals, O.; Graves, A.; Kalchbrenner, N.; Senior, A.; Kavukcuoglu, K. Wavenet: A generative model for raw audio. arXiv 2016, arXiv:1609.03499. [Google Scholar]
- Thoidis, I.; Vrysis, L.; Pastiadis, K.; Markou, K.; Papanikolaou, G. Investigation of an encoder-decoder lstm model on the enhancement of speech intelligibility in noise for hearing impaired listeners. In Audio Engineering Society Convention 146; Audio Engineering Society: New York, NY, USA, 2019. [Google Scholar]
- Rosen, S.; Carlyon, R.P.; Darwin, C.J.; Russell, I.J. Temporal information in speech: Acoustic, auditory and linguistic aspects. Philos. Trans. R. Soc. London. Ser. B Biol. Sci. 1992, 336, 367–373. [Google Scholar] [CrossRef]
- Van Tasell, D.J.; Soli, S.D.; Kirby, V.M.; Widin, G.P. Speech waveform envelope cues for consonant recognition. J. Acoust. Soc. Am. 1987, 82, 1152–1161. [Google Scholar] [CrossRef]
- Souza, P.E.; Wright, R.A.; Blackburn, M.C.; Tatman, R.; Gallun, F.J. Individual sensitivity to spectral and temporal cues in listeners with hearing impairment. J. Speech Lang. Hear. Res. 2015, 58, 520–534. [Google Scholar] [CrossRef]
- Shannon, R.V.; Zeng, F.-G.; Kamath, V.; Wygonski, J.; Ekelid, M. Speech recognition with primarily temporal cues. Science 1995, 270, 303–304. [Google Scholar] [CrossRef]
- Grose, J.H.; Mamo, S.K.; Hall III, J.W. Age effects in temporal envelope processing: Speech unmasking and auditory steady state responses. Ear Hear. 2009, 30, 568. [Google Scholar] [CrossRef]
- Hopkins, K.; Moore, B.C.J. The contribution of temporal fine structure to the intelligibility of speech in steady and modulated noise. J. Acoust. Soc. Am. 2009, 125, 442–446. [Google Scholar] [CrossRef] [PubMed]
- Koutsogiannaki, M.; Francois, H.; Choo, K.; Oh, E. Real-Time Modulation Enhancement of Temporal Envelopes for Increasing Speech Intelligibility. Interspeech 2017, 1973–1977. [Google Scholar] [CrossRef]
- Langhans, T.; Strube, H. Speech enhancement by nonlinear multiband envelope filtering. In Proceedings of the ICASSP’82. IEEE International Conference on Acoustics, Speech, and Signal Processing, Paris, France, 3–5 May 1982; Volume 7, pp. 156–159. [Google Scholar]
- Apoux, F.; Tribut, N.; Debruille, X.; Lorenzi, C. Identification of envelope-expanded sentences in normal-hearing and hearing-impaired listeners. Hear. Res. 2004, 189, 13–24. [Google Scholar] [CrossRef]
- Anderson, M.C.; Arehart, K.H.; Kates, J.M. The effects of noise vocoding on speech quality perception. Hear. Res. 2014, 309, 75–83. [Google Scholar] [CrossRef]
- Shetty, H.N. Temporal cues and the effect of their enhancement on speech perception in older adults—A scoping review. J. Otol. 2016, 11, 95–101. [Google Scholar] [CrossRef] [PubMed]
- Shetty, H.N.; Mendhakar, A. Deep band modulation and noise effects: Perception of phrases in adults. Hear. Balance Commun. 2015, 13, 111–117. [Google Scholar] [CrossRef]
- Wang, D.; Chen, J. Supervised speech separation based on deep learning: An overview. IEEE ACM Trans. Audio Speech Lang. Process. 2018, 26, 1702–1726. [Google Scholar] [CrossRef] [PubMed]
- Moore, B.C.J.J.; Glasberg, B.R. A revision of Zwicker’s loudness model. Acta Acust. United Acust. 1996, 82, 335–345. [Google Scholar]
- Maganti, H.K.; Matassoni, M. Auditory processing-based features for improving speech recognition in adverse acoustic conditions. EURASIP J. Audio Speech Music Process. 2014, 2014, 21. [Google Scholar] [CrossRef]
- Chou, K.F.; Dong, J.; Colburn, H.S.; Sen, K. A Physiologically Inspired Model for Solving the Cocktail Party Problem. J. Assoc. Res. Otolaryngol. 2019, 20, 579–593. [Google Scholar] [CrossRef] [PubMed]
- Glasberg, B.R.; Moore, B.C.J. Derivation of auditory filter shapes from notched-noise data. Hear. Res. 1990, 47, 103–138. [Google Scholar] [CrossRef]
- Necciari, T.; Holighaus, N.; Balazs, P.; Průša, Z.; Majdak, P.; Derrien, O. Audlet filter banks: A versatile analysis/synthesis framework using auditory frequency scales. Appl. Sci. 2018, 8, 96. [Google Scholar] [CrossRef]
- Velasco, G.A.; Holighaus, N.; Dörfler, M.; Grill, T. Constructing an invertible constant-Q transform with nonstationary Gabor frames. In Proceedings of the 14th International Conference on Digital Audio Effects (DAFx), Paris, France, 19–23 September 2011; Volume 33, pp. 93–100. [Google Scholar]
- Abolhassani, M.D.; Salimpour, Y. A human auditory tuning curves matched wavelet function. In Proceedings of the 2008 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, BC, Canada, 20–24 August 2008; pp. 2956–2959. [Google Scholar]
- Necciari, T.; Balazs, P.; Holighaus, N.; Søndergaard, P.L. The ERBlet transform: An auditory-based time-frequency representation with perfect reconstruction. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 498–502. [Google Scholar]
- Apoux, F.; Millman, R.E.; Viemeister, N.F.; Brown, C.A.; Bacon, S.P. On the mechanisms involved in the recovery of envelope information from temporal fine structure. J. Acoust. Soc. Am. 2011, 130, 273–282. [Google Scholar] [CrossRef]
- Chi, T.; Ru, P.; Shamma, S.A. Multiresolution spectrotemporal analysis of complex sounds. J. Acoust. Soc. Am. 2005, 118, 887–906. [Google Scholar] [CrossRef]
- Gabor, D. Theory of communication. Part 1: The analysis of information. J. Inst. Electr. Eng. III Radio Commun. Eng. 1946, 93, 429–441. [Google Scholar] [CrossRef]
- Sheft, S.; Yost, W.A. Temporal integration in amplitude modulation detection. J. Acoust. Soc. Am. 1990, 88, 796–805. [Google Scholar] [CrossRef]
- Wang, K.; Shamma, S. Self-normalization and noise-robustness in early auditory representations. IEEE Trans. Speech Audio Process. 1994, 2, 421–435. [Google Scholar] [CrossRef]
- Yang, X.; Wang, K.; Shamma, S.A. Auditory representations of acoustic signals. IEEE Trans. Inf. Theory 1992, 38, 824–839. [Google Scholar] [CrossRef]
- Elhilali, M.; Shamma, S.A. A cocktail party with a cortical twist: How cortical mechanisms contribute to sound segregation. J. Acoust. Soc. Am. 2008, 124, 3751–3771. [Google Scholar] [CrossRef] [PubMed]
- Cariani, P. Temporal coding of periodicity pitch in the auditory system: An overview. Neural Plast. 1999, 6. [Google Scholar] [CrossRef] [PubMed]
- Palmer, A.R.; Russell, I.J. Phase-locking in the cochlear nerve of the guinea-pig and its relation to the receptor potential of inner hair-cells. Hear. Res. 1986, 24, 1–15. [Google Scholar] [CrossRef]
- Ewert, S.D.; Paraouty, N.; Lorenzi, C. A two-path model of auditory modulation detection using temporal fine structure and envelope cues. Eur. J. Neurosci. 2020, 51, 1265–1278. [Google Scholar] [CrossRef] [PubMed]
- Cui, X.; Chen, Z.; Yin, F. Speech enhancement based on simple recurrent unit network. Appl. Acoust. 2020, 157, 107019. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Zue, V.; Seneff, S.; Glass, J. Speech database development at MIT: TIMIT and beyond. Speech Commun. 1990, 9, 351–356. [Google Scholar] [CrossRef]
- Salamon, J.; Jacoby, C.; Bello, J.P. A dataset and taxonomy for urban sound research. In Proceedings of the 22nd ACM international conference on Multimedia, Orlando, FL, USA, 3–7 November 2014; pp. 1041–1044. [Google Scholar]
- Thiemann, J.; Ito, N.; Vincent, E. The diverse environments multi-channel acoustic noise database: A database of multichannel environmental noise recordings. J. Acoust. Soc. Am. 2013, 133, 3591. [Google Scholar] [CrossRef]
- Jensen, J.; Taal, C.H. An algorithm for predicting the intelligibility of speech masked by modulated noise maskers. IEEE/ACM Trans. Audio Speech Lang. Process. 2016, 24, 2009–2022. [Google Scholar] [CrossRef]
- ITU-T P.862.2 Wideband extension to Recommendation P.862 for the assessment of wideband telephone networks and speech codecs. Telecommun. Stand. Sect. ITU 2007, 12. [CrossRef]
- Beerends, J.G.; Hekstra, A.P.; Rix, A.W.; Hollier, M.P. Perceptual evaluation of speech quality (pesq) the new itu standard for end-to-end speech quality assessment part ii: Psychoacoustic model. J. Audio Eng. Soc. 2002, 50, 765–778. [Google Scholar]
- Kates, J.M.; Arehart, K.H. The hearing-aid speech perception index (HASPI). Speech Commun. 2014, 65, 75–93. [Google Scholar] [CrossRef]
- Kates, J.M.; Arehart, K.H. The hearing-aid speech quality index (HASQI) version 2. AES J. Audio Eng. Soc. 2014, 62, 99–117. [Google Scholar] [CrossRef]
- Thoidis, I.; Vrysis, L.; Markou, K.; Papanikolaou, G. Development and evaluation of a tablet-based diagnostic audiometer. Int. J. Audiol. 2019, 58, 476–483. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
| Method | eSTOI | PESQ | ||
|---|---|---|---|---|
| ENV | STFT | ENV | STFT | |
| Noisy (unprocessed) | 0.54 ± 0.17 | 0.54 ± 0.17 | 1.19 ± 0.15 | 1.19 ± 0.15 |
| Target | 0.88 ± 0.05 | 0.90 ± 0.05 | 2.73 ± 0.25 | 3.11 ± 0.37 |
| Target | 0.86 ± 0.06 | 0.89 ± 0.05 | 2.71 ± 0.25 | 3.06 ± 0.37 |
| Clean (reconstructed) | 0.99 ± 0.00 | 1.00 ± 0.00 | 3.90 ± 0.17 | 4.20 ± 0.15 |
| Method | eSTOI | PESQ |
|---|---|---|
| Original | 0.529 ± 0.20 | 1.101 ± 0.16 |
| STFT | 0.608 ± 0.20 | 1.668 ± 0.48 |
| ENV | 0.610 ± 0.19 | 1.638 ± 0.51 |
| ENV-TFS | 0.635 ± 0.20 | 1.687 ± 0.49 |
| HASPI | HASQI | |||||
|---|---|---|---|---|---|---|
| Config. | Original | STFT | ENV-TFS | Original | STFT | ENV-TFS |
| HL1 | 36.5 ± 28.4 | 49.0 ± 27.1 | 53.0 ± 29.3 | 14.3 ± 9.0 | 24.0 ± 12.6 | 26.8 ± 13.0 |
| HL2 | 19.4 ± 17.9 | 40.0 ± 24.3 | 38.8 ± 25.9 | 11.2 ± 6.4 | 25.7 ± 12.1 | 22.8 ± 10.2 |
| HL3 | 63.5 ± 31.5 | 78.8 ± 21.2 | 83.7 ± 25.0 | 20.6 ± 12.0 | 34.5 ± 16.5 | 35.4 ± 17.3 |
| HL4 | 35.0 ± 25.4 | 69.7 ± 23.1 | 67.3 ± 27.9 | 15.6 ± 8.3 | 33.5 ± 14.2 | 29.9 ± 13.4 |
| HL5 | 4.6 ± 6.4 | 19.2 ± 14.2 | 14.3 ± 13.6 | 6.6 ± 4.9 | 28.7 ± 9.9 | 19.7 ± 7.7 |
| HL6 | 15.8 ± 23.9 | 64.1 ± 24.0 | 68.3 ± 28.0 | 5.1 ± 6.0 | 19.0 ± 7.4 | 22.4 ± 8.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thoidis, I.; Vrysis, L.; Markou, D.; Papanikolaou, G. Temporal Auditory Coding Features for Causal Speech Enhancement. Electronics 2020, 9, 1698. https://doi.org/10.3390/electronics9101698
Thoidis I, Vrysis L, Markou D, Papanikolaou G. Temporal Auditory Coding Features for Causal Speech Enhancement. Electronics. 2020; 9(10):1698. https://doi.org/10.3390/electronics9101698
Chicago/Turabian StyleThoidis, Iordanis, Lazaros Vrysis, Dimitrios Markou, and George Papanikolaou. 2020. "Temporal Auditory Coding Features for Causal Speech Enhancement" Electronics 9, no. 10: 1698. https://doi.org/10.3390/electronics9101698
APA StyleThoidis, I., Vrysis, L., Markou, D., & Papanikolaou, G. (2020). Temporal Auditory Coding Features for Causal Speech Enhancement. Electronics, 9(10), 1698. https://doi.org/10.3390/electronics9101698







