Road-Based Multi-Metric Forwarder Evaluation for Multipath Video Streaming in Urban Vehicular Communication
Abstract
1. Introduction
- (1)
- A link connectivity strategy for forwarder vehicle selection considering vehicle density on the road and vehicle trajectory.
- (2)
- An enhanced link connectivity considering response time evaluation based on hello message receive rate for forwarder vehicle selection.
- (3)
- Improved link quality estimation by employing accessible bandwidth estimation and signal to interference plus noise ratio.
- (4)
- Dynamic self-weighting score for multi-metric forwarder vehicle selection evaluation.
- (5)
- Validation based on extensive simulation results and critical analysis in comparison with state-of-the-art techniques.
2. Related Works
2.1. Cross-Layer Oriented Video Streaming
2.2. Multi-Metric Oriented Video Streaming
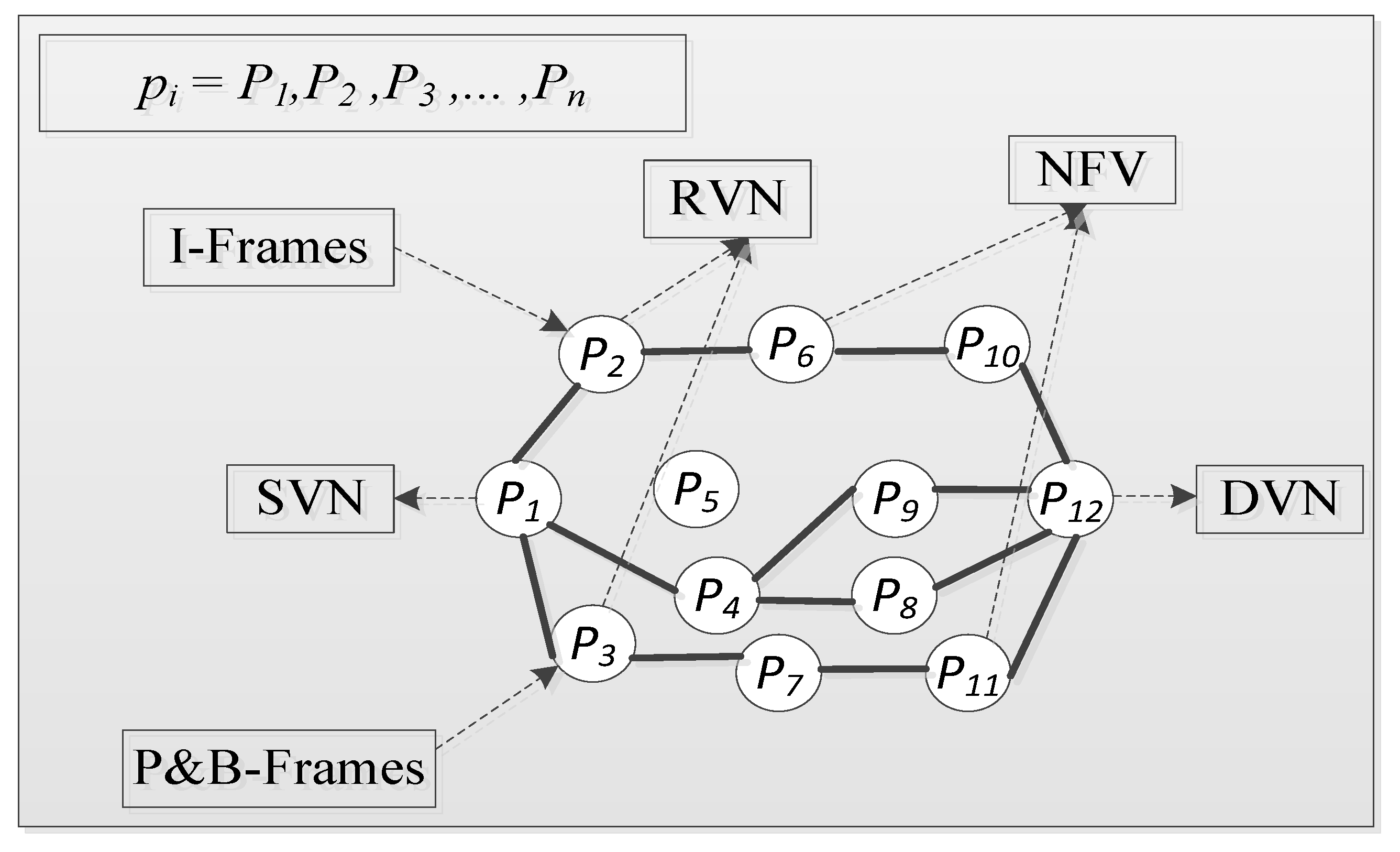
3. Road-Based Multi-Metric Forwarder Evaluation Scheme
3.1. Information Collection Stage
3.1.1. Vehicle Density of the Road Estimation
3.1.2. Vehicle Trajectory
3.1.3. Hello Message Receive Rate
3.1.4. Accessible Bandwidth Estimation
3.1.5. Signal to Interference Plus Noise Ratio
3.2. Multi-Metric Video Streaming with Dynamic Self-Weigthting Score
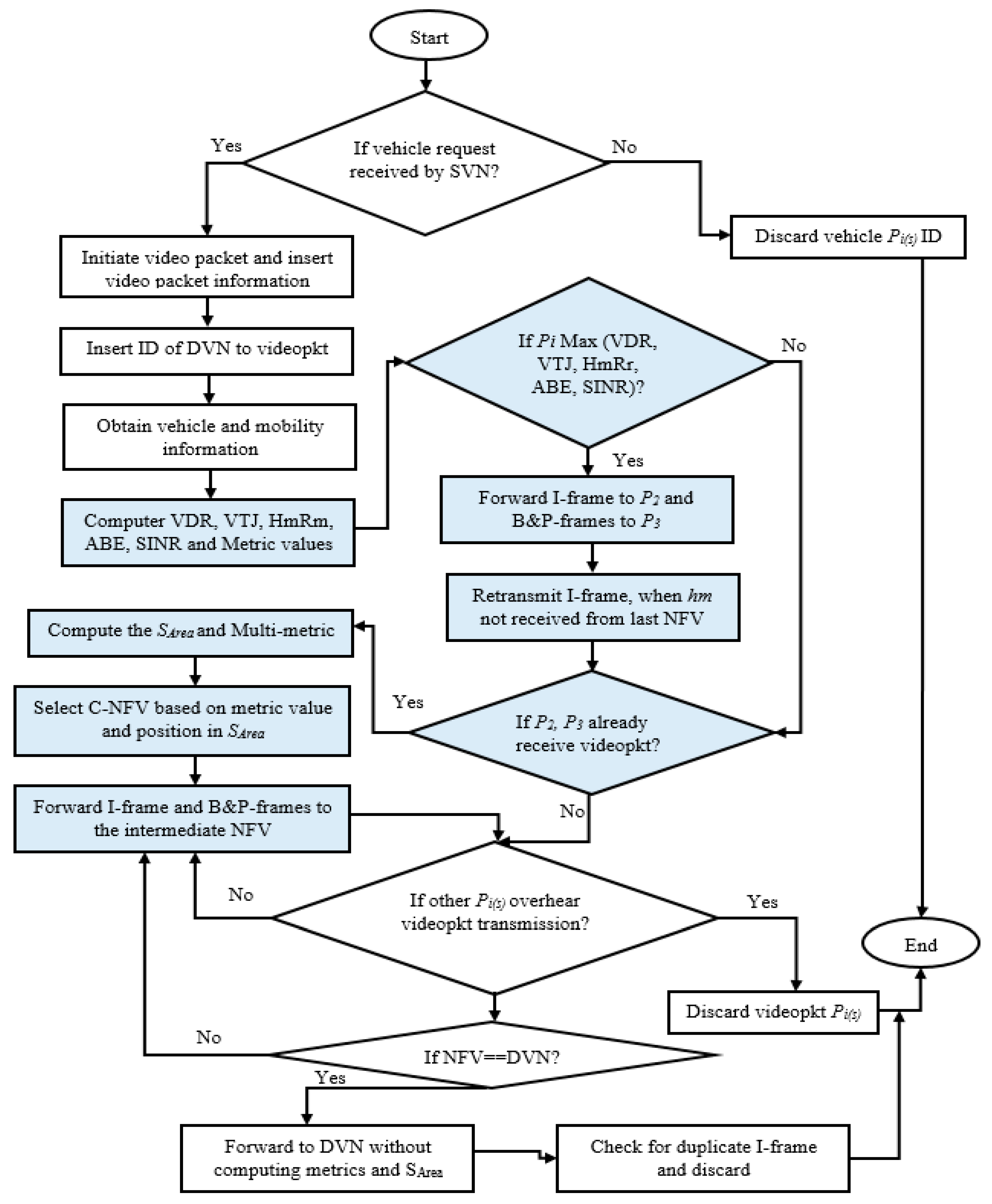
3.2.1. Multi-Metric Video Streaming without Dynamic Self-Weighting Score
| Algorithm 1. Multi-metric Video Streaming Forwarding |
1: 2: 3: 4: 5: 6: 7: 8: 9: 10: 11: 12: 13: 14: 15: 16: 17: 18: 19: 20: 21: 22: 23: 24: 25: 26: 27: 28: 29: 30: 31: 32: 33: 34: 35: 36: 37: 38: 39: 40: |
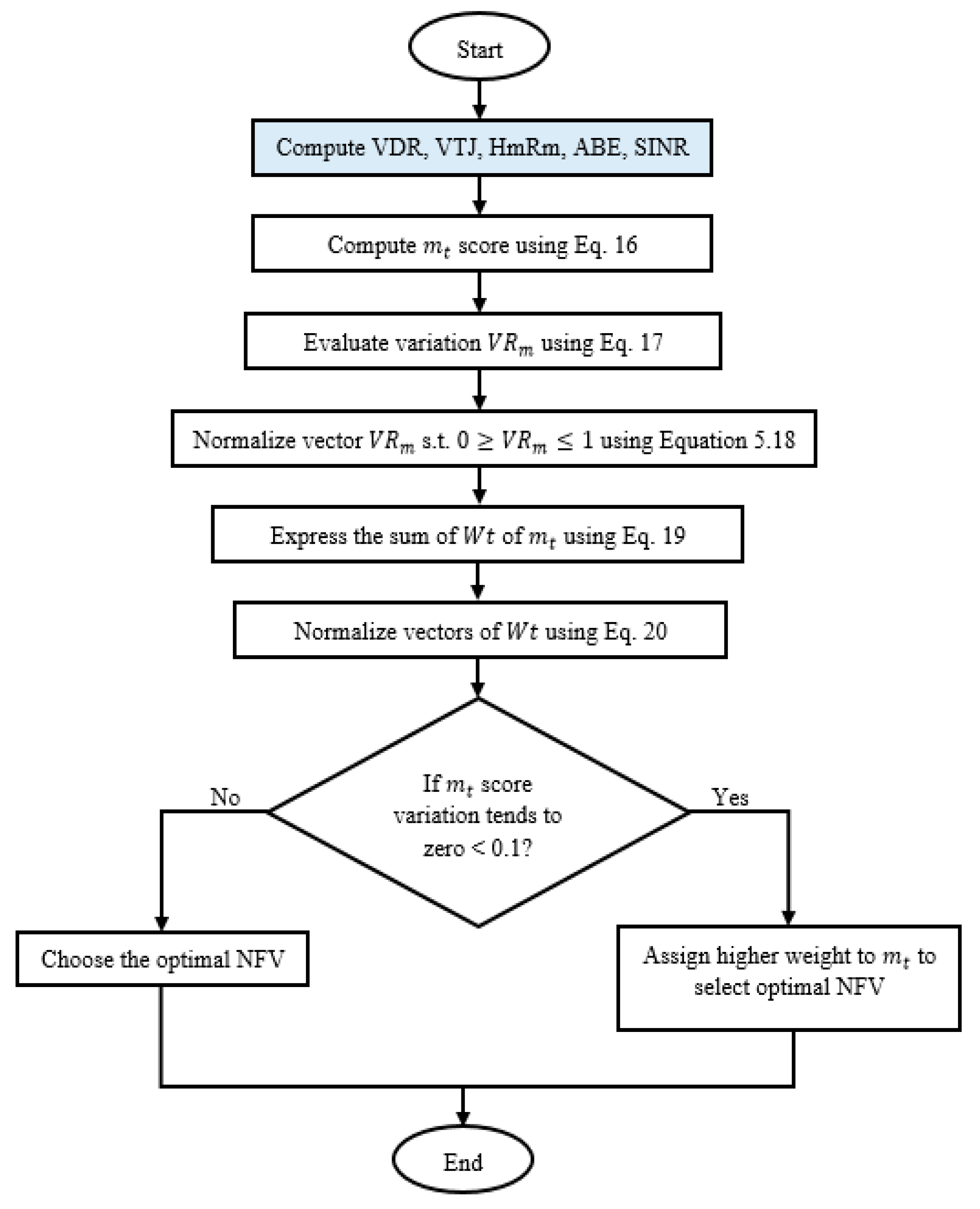
3.2.2. Multi-Metric Video Streaming with Dynamic Self-Weighting Score
| Algorithm 2. Dynamic Self-Weighting Score |
Output: Dynamic self-weighting score for NFV selection 1: 2: 3: 4: 5: 6: 7: 8: 9: 10: 11: 12: 13: |
4. Performance Evaluation
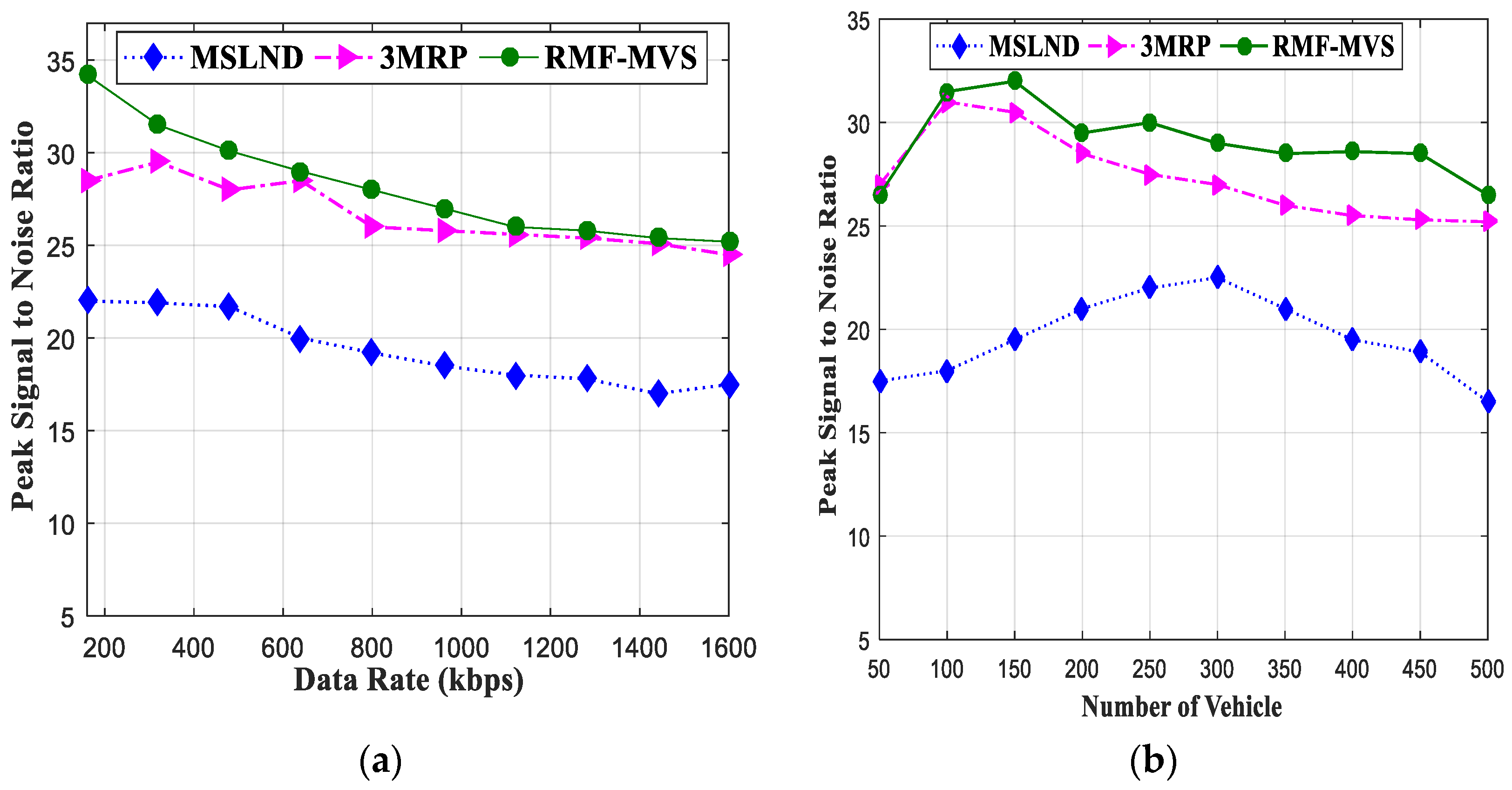
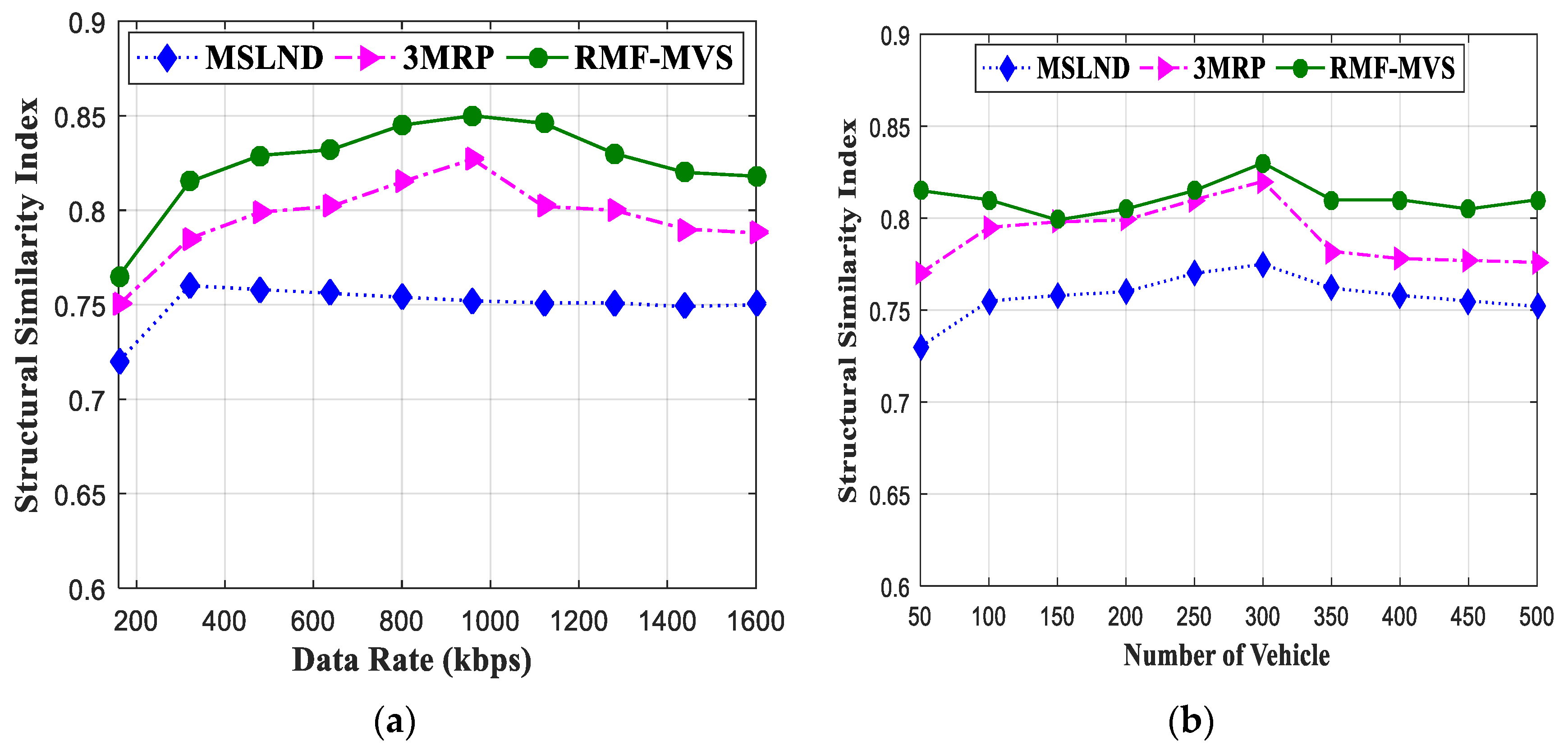
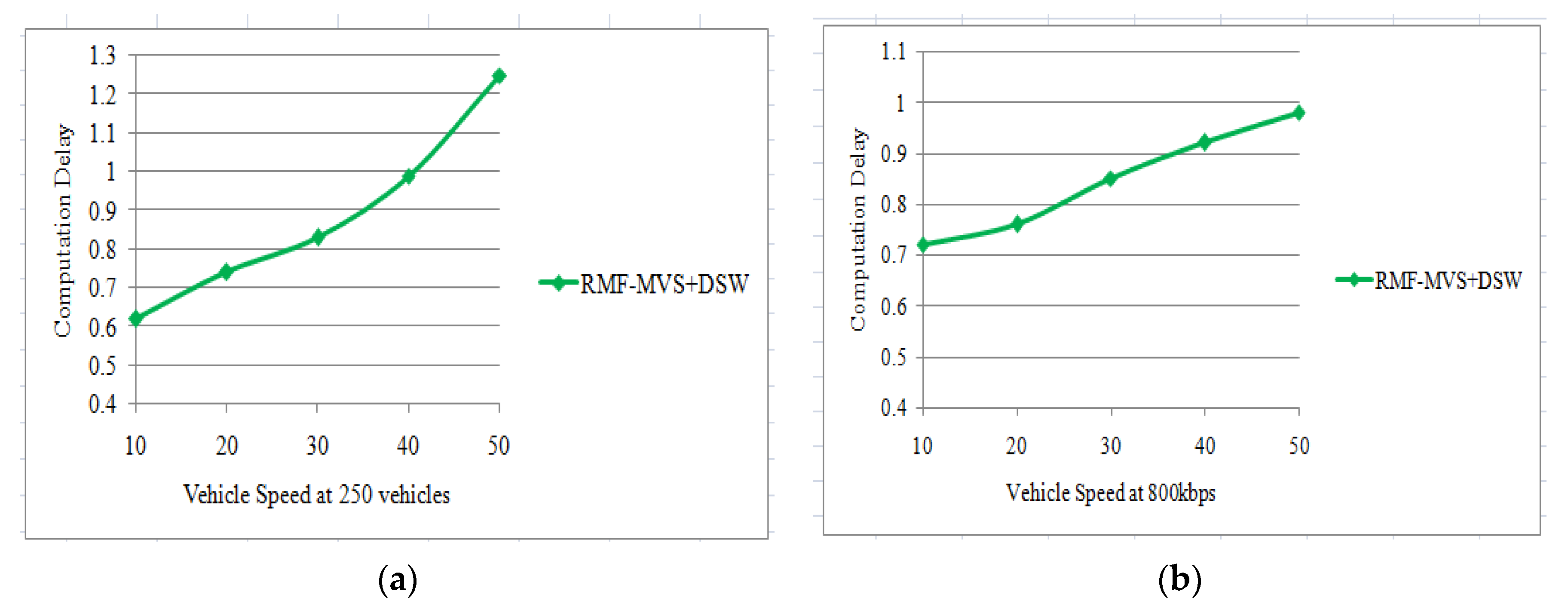
4.1. Result Analysis of RMF-MVS
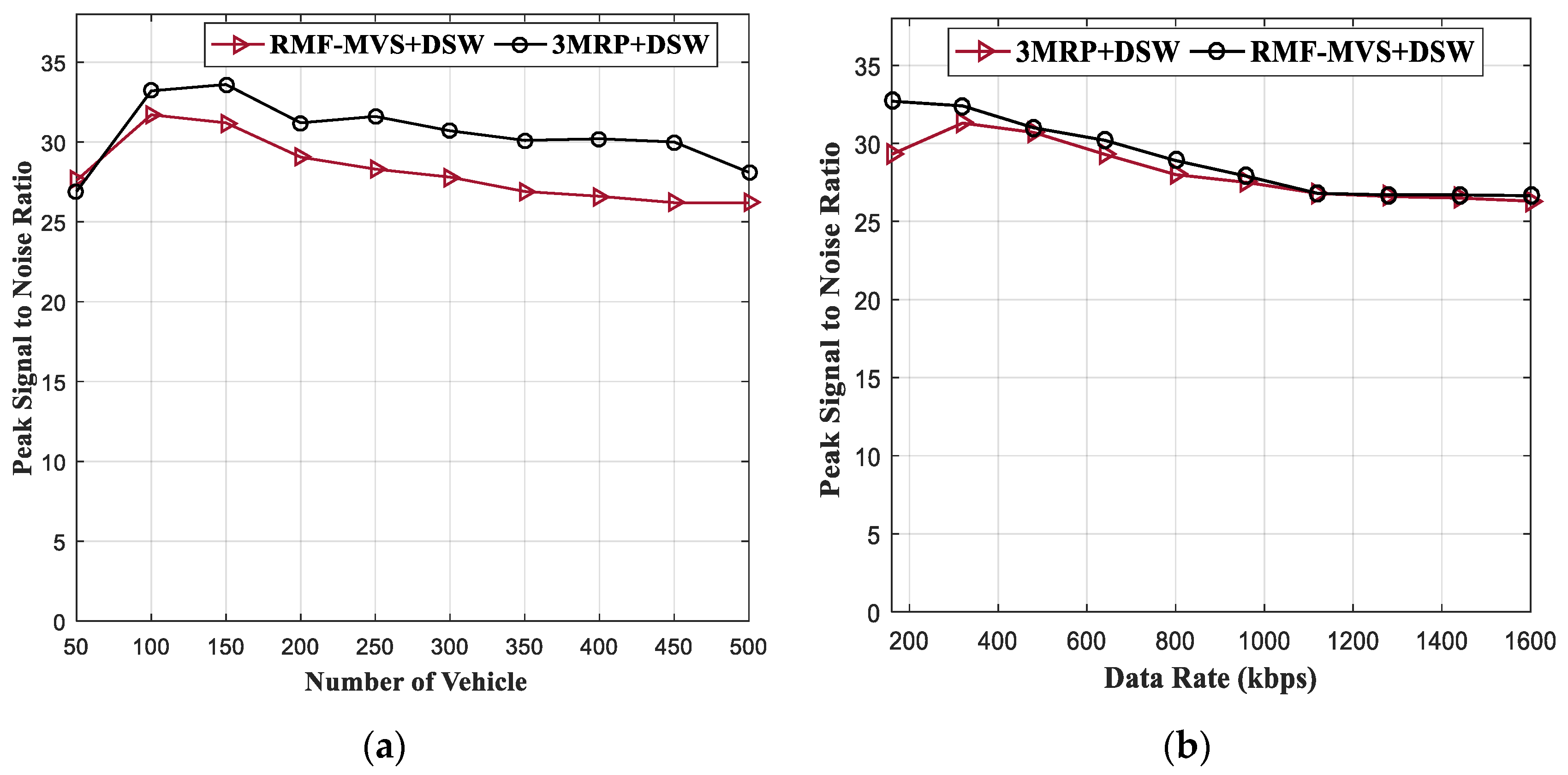
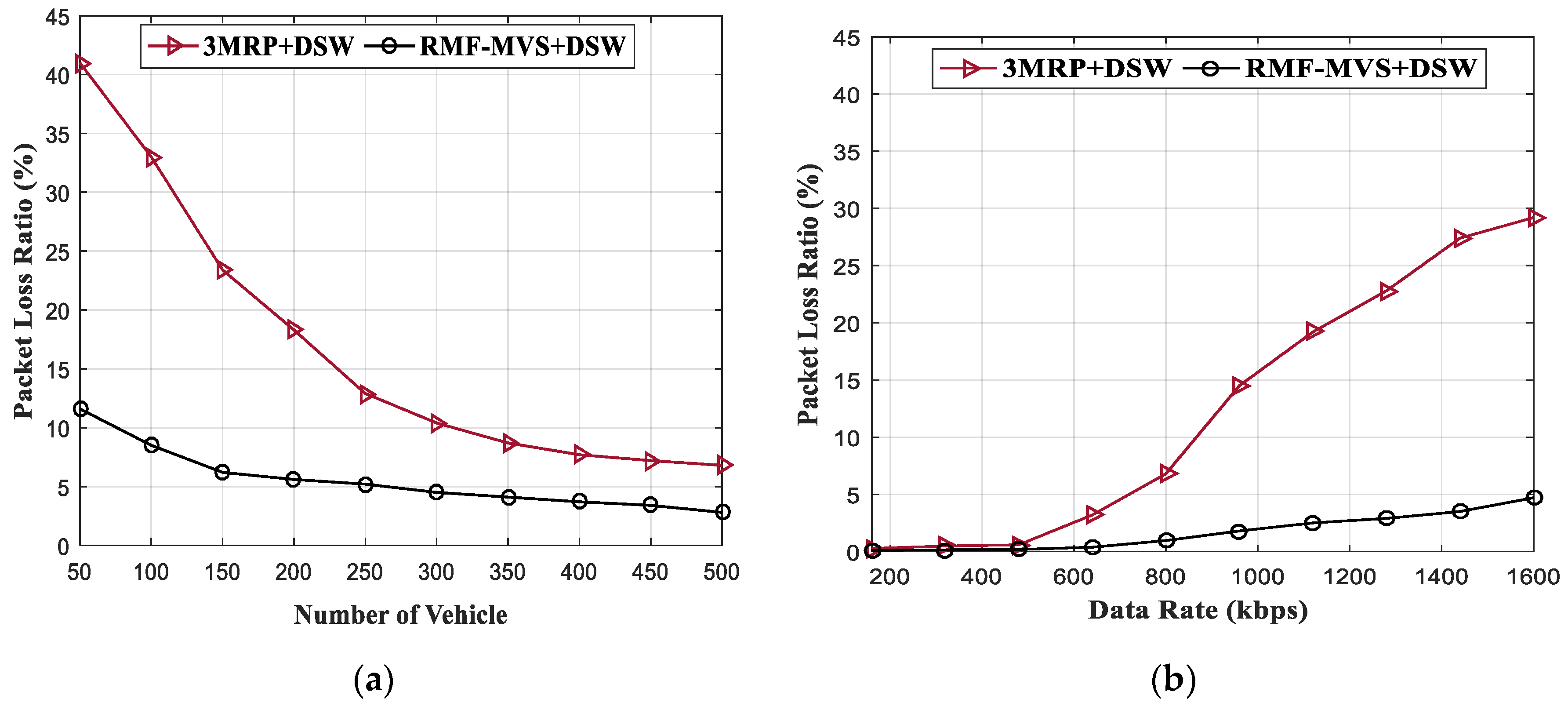
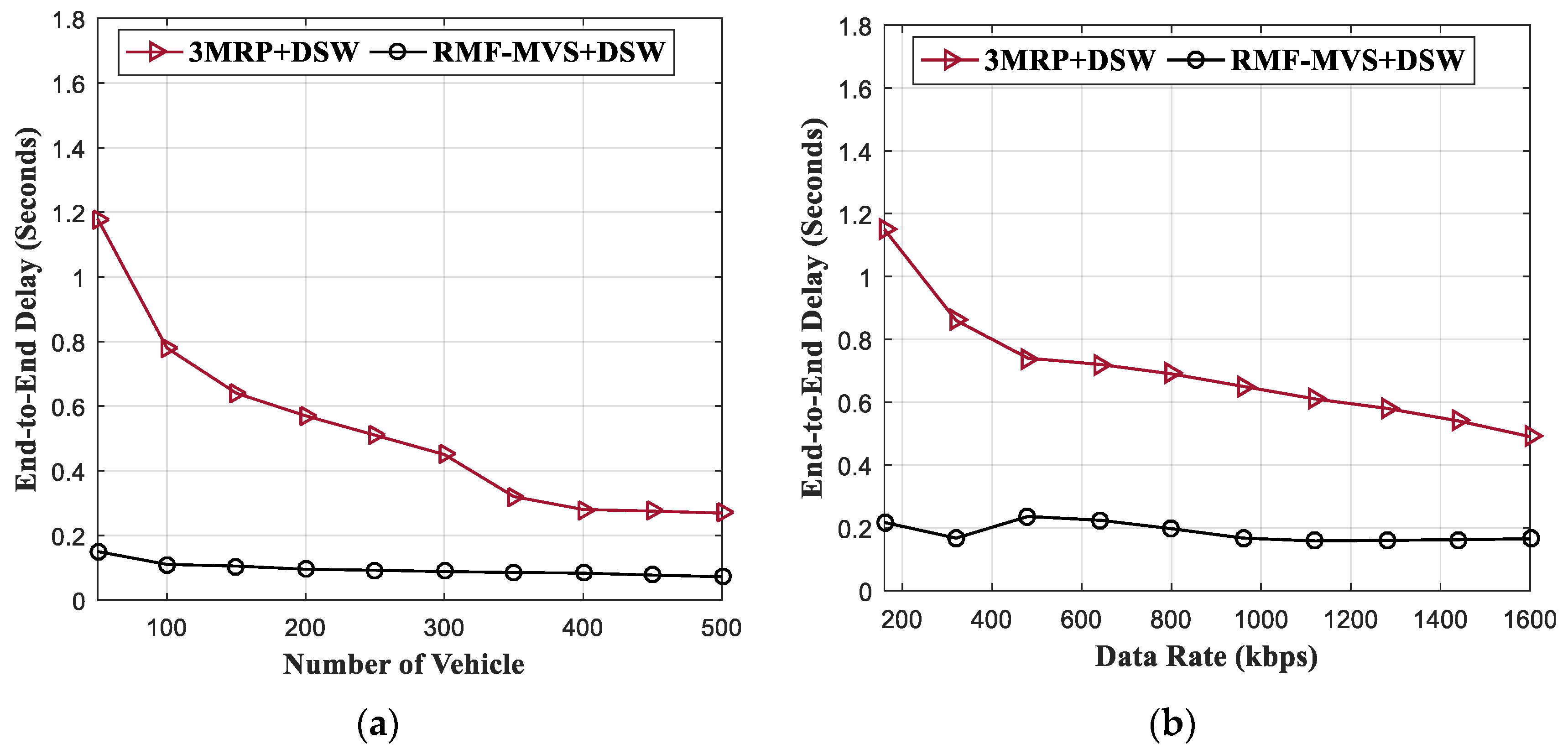
4.2. Result Analysis of RMF-MVS + DSW
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Kaiwartya, O.; Kumar, S. Enhanced caching for geocast routing in vehicular Ad Hoc network. In Intelligent Computing, Networking, and Informatics; Springer: NewDelhi, India, 2014; pp. 213–220. [Google Scholar]
- Aliyu, A.; Abdullah, A.H.; Kaiwartya, O.; Cao, Y.; Usman, M.J.; Kumar, S.; Lobiyal, D.; Raw, R.S. Cloud Computing in VANETs: Architecture, Taxonomy, and Challenges. IETE Tech. Rev. 2018, 35, 523–547. [Google Scholar] [CrossRef]
- Hassan, A.N.; Abdullah, A.H.; Kaiwartya, O.; Sheet, D.K.; Aliyu, A. Geographic forwarding techniques: Limitations and future challenges in IVC. In Proceedings of the Student Project Conference (ICT-ISPC), 2017 6th ICT International, Skudai, Malaysia, 23–24 May 2017; pp. 1–5. [Google Scholar]
- Bali, R.S.; Kumar, N.; Rodrigues, J.J. Clustering in vehicular ad hoc networks: Taxonomy, challenges and solutions. Veh. Commun. 2014, 1, 134–152. [Google Scholar] [CrossRef]
- Kaiwartya, O.; Kumar, S. Guaranteed geocast routing protocol for vehicular ad hoc networks in highway traffic environment. Wirel. Pers. Commun. 2015, 83, 2657–2682. [Google Scholar] [CrossRef]
- Aliyu, A.; Abdullah, A.H.; Kaiwartya, O.; Ullah, F.; Joda, U.M.; Hassan, A.N. Multi-Path video streaming in vehicular communication: Approaches and challenges. In Proceedings of the Student Project Conference (ICT-ISPC), 2017 6th ICT International, Skudai, Malaysia, 23–24 May 2017; pp. 1–4. [Google Scholar]
- Kaiwartya, O.; Kumar, S. Geocasting in vehicular ad hoc networks using particles warm optimization. In Proceedings of the International Conference on Information Systems and Design of Communication, Lisbon, Portugal, 16–17 May 2014; pp. 62–66. [Google Scholar]
- Aliyu, A.; Abdullah, A.; Kaiwartya, O.; Cao, Y.; Lloret, J.; Aslam, N.; Joda, U. Towards video streaming in IoT Environments: Vehicular communication perspective. Comput. Commun. 2018, 118, 93–119. [Google Scholar] [CrossRef]
- Xie, H.; Boukerche, A.; Loureiro, A.A. A multipath video streaming solution for vehicular networks with link disjoint and node-disjoint. IEEE Trans. Parallel Distrib. Syst. 2015, 26, 3223–3235. [Google Scholar] [CrossRef]
- Tripp-Barba, C.; Urquiza-Aguiar, L.; Igartua, M.A.; Rebollo-Monedero, D.; de la Cruz Llopis, L.J.; Mezher, A.M.; Aguilar-Calderón, J.A. A multimetric, map-aware routing protocol for VANETs in urban areas. Sensors 2014, 14, 2199–2224. [Google Scholar] [CrossRef] [PubMed]
- Mezher, A.M.; Igartua, M.A. Multimedia Multimetric Map-aware Routing protocol to send video-reporting messages over VANETs in smart cities. IEEE Trans. Veh. Technol. 2017, 66, 10611–10625. [Google Scholar] [CrossRef]
- Puangpronpitag, S.; Kasabai, P.; Suwannasa, A. Cross-layer optimization of Vehicle-to-Vehicle video streaming for overtaking maneuver assistance systems. In Proceedings of the Ubiquitous and Future Networks (ICUFN), 2013 Fifth International Conference, Da Nang, Vietnam, 2–5 July 2013; pp. 345–349. [Google Scholar]
- Quadros, C.; Cerqueira, E.; Santos, A.; Gerla, M. Amulti-flow-driven mechanism to support live video streaming on VANETs. In Proceedings of the Computer Networks and Distributed Systems (SBRC), Florianopolis, Brazil, 5–9 May 2014; pp. 468–476. [Google Scholar]
- Granelli, F.; Boato, G.; Kliazovich, D.; Vernazza, G. Enhanced gpsr routing in multi-hop vehicular communications through movement awareness. IEEE Commun. Lett. 2007, 11, 781–783. [Google Scholar] [CrossRef]
- Granelli, F.; Boato, G.; Kliazovich, D. MORA: A movement-based routing algorithm for vehicle ad hoc networks. In IEEE Workshop on Automotive Networking and Applications (AutoNet 2006); IEEE: San Francisco, CA, USA, 2006. [Google Scholar]
- Vinel, A.; Belyaev, E.; Lamotte, O.; Gabbouj, M.; Koucheryavy, Y.; Egiazarian, K. Video transmission over IEEE 802.11 p: Real-world measurements. In Proceedings of the Communications Workshops (ICC), 2013 IEEE International Conference, Budapest, Hungary, 9–13 June 2013; pp. 505–509. [Google Scholar]
- Bradai, A.; Ahmed, T. ReViV: Selective rebroadcast mechanism for video streaming over VANET. In Proceedings of the Vehicular Technology Conference (VTC Spring), 2014 79th IEEE, Seoul, Korea, 18–21 May 2014; pp. 1–6. [Google Scholar]
- Jiang, X.; Cao, X.; Du, D.H. Multihop transmission and retransmission measurement of real-time video streaming over DSRC devices. In Proceedings of the IEEE International Symposium on a World of Wireless, Mobile and Multimedia Networks 2014, Sydney, Australia, 19 June 2014; pp. 1–9. [Google Scholar]
- Xie, H.; Boukerche, A.; Loureiro, A.A. MERVS: A Novel Multichannel Error Recovery VideoS treaming Protocolfor Vehicle AdHoc Networks. IEEE Trans. Veh. Technol. 2016, 65, 923–935. [Google Scholar] [CrossRef]
- Kumar, N.; Zeadally, S.; Rodrigues, J.J. QoS-aware hierarchical web caching scheme for online video streaming applications in internet-based vehicular adhoc networks. IEEE Trans. Ind. Electron. 2015, 62, 7892–7900. [Google Scholar] [CrossRef]
- Asefi, M.; Mark, J.W.; Shen, X.S. Amobility-aware and quality-driven retransmission limit adaptation scheme for video streaming over VANETs. IEEE Trans. Wirel. Commun. 2012, 11, 1817–1827. [Google Scholar] [CrossRef]
- Darwish, T.S.; Bakar, K.A.; Haseeb, K. Reliable Intersection-Based Traffic Aware Routing Protocol for Urban Areas Vehicular Ad Hoc Networks. IEEE Intell. Transp. Syst. Mag. 2018, 10, 60–73. [Google Scholar] [CrossRef]
- Tripp-Barba, C.; AguilarIgartua, M.; UrquizaAguiar, L.; Mezher, A.M.; Zaldívar-Colado, A.; Guérin-Lassous, I. Available bandwidth estimation in GPSR for VANETs. In Proceedings of the Third ACM International Symposium on Design and Analysis of Intelligent Vehicular Networks and Applications, Barcelona, Spain, 3–8 November 2013; pp. 1–8. [Google Scholar]
- Sarr, C.; Chaudet, C.; Chelius, G.; Lassous, I.G. Bandwidth estimation for IEEE 802.11-based ad hoc networks. IEEE Trans. Mob. Comput. 2008, 7, 1228–1241. [Google Scholar] [CrossRef]
- Blaszczyszyn, B.; Mühlethaler, P.; Toor, Y. Maximizing throughput of Linear Vehicular Ad-hoc NETworks (VANETs)—Astochastic approach. In Proceedings of the Wireless Conference, EW 2009. European, Aalborg, Denmark, 17–20 May 2009; pp. 32–36. [Google Scholar]
- Chen, Q.; Schmidt-Eisenlohr, F.; Jiang, D.; Torrent-Moreno, M.; Delgrossi, L.; Hartenstein, H. Overhaul of IEEE 802.11 modeling and simulation in ns-2. In Proceedings of the 10th ACM Symposium on Modeling, Analysis, and Simulation of Wireless and Mobile Systems, Chania, Crete Island, Greece, 22–26 October 2007; pp. 159–168. [Google Scholar]
- Krajzewicz, D.; Hertkorn, G.; Rössel, C.; Wagner, P. Sumo (simulation of urban mobility). In Proceedings of the 4th Middle East Symposium on Simulation and Modelling, Naples, Italy, 27–29 October 2003; pp. 183–187. [Google Scholar]
- Klaue, J.; Rathke, B.; Wolisz, A. Evalvid–A framework for video transmission and quality evaluation. In Proceedings of the International Conference on Modelling Techniques and Tools for Computer Performance Evaluation, Urbana, IL, USA, 2–5 September 2003; pp. 255–272. [Google Scholar]
- Karnadi, F.K.; Mo, Z.H.; Lan, K.-C. Rapid generation of realistic mobility models for VANET. In Proceedings of the Wireless Communications and Networking Conference, WCNC 2007, Kowloon, China, 11–15 March 2007; pp. 2506–2511. [Google Scholar]
- Xie, F.; Hua, K.A.; Wang, W.; Ho, Y.H. Performance study of live video streaming over highway vehicular ad hoc networks. In Proceedings of the Vehicular Technology Conference, VTC-2007 Fall, 2007 66th IEEE, Baltimore, MD, USA, 30 September–3 October 2007; pp. 2121–2125. [Google Scholar]
- Piñol, P.; López, O.; Martínez, M.; Oliver, J.; Malumbres, M.P. Modeling video streaming over VANETs. In Proceedings of the 7th ACM Workshop on Performance Monitoring and Measurement of Heterogeneous Wireless and Wired Networks, Paphos, Cyprus, 21–22 October 2012; pp. 7–14. [Google Scholar]
- Immich, R.; Cerqueira, E.; Curado, M. Shielding video streaming against packet losses over VANETs. Wirel. Netw. 2016, 22, 2563–2577. [Google Scholar] [CrossRef]
- Razzaq, A.; Mehaoua, A. Video transport over VANETs: Multi-stream coding with multi-path and network coding. In Proceedings of the Local Computer Networks (LCN), 2010 35th IEEE Conference, Denver, CO, USA, 10–14 October 2010; pp. 32–39. [Google Scholar]
- Yang, Z.; Li, M.; Lou, W. Codeplay: Live multimer diastreaming in vanets using symbol-level network coding. In Proceedings of the Network Protocols (ICNP), 2010 18th IEEE International Conferenceon, Kyoto, Japan, 5–8 October 2010; pp. 223–232. [Google Scholar]
- Zaidi, S.; Bitam, S.; Mellouk, A. Hybrid error recovery protocol for video streaming in vehicle adhoc networks. Veh. Commun. 2018, 12, 110–126. [Google Scholar]
- Yadav, R.; Zhang, W.; Kaiwartya, O.; Singh, P.R.; Elgendy, I.A.; Tian, Y.C. Adaptive energy-aware algorithms for minimizing energy consumption and SLA violation in cloud computing. IEEE Access 2018, 6, 55923–55936. [Google Scholar] [CrossRef]
- Ahmed, M.N.; Abdullah, A.H.; Chizari, H.; Kaiwartya, O. F3TM: Flooding Factor based Trust Management Framework for secure data transmission in MANETs. J. King Saud Univ. Comput. Inf. Sci. 2017, 29, 269–280. [Google Scholar] [CrossRef]
- Ullah, F.; Abdullah, A.H.; Kaiwartya, O.; Cao, Y. TraPy-MAC: Traffic priority aware medium access control protocol for wireless body area network. J. Med. Syst. 2017, 41, 93. [Google Scholar] [CrossRef] [PubMed]
- Khasawneh, A.; Latiff, M.S.B.A.; Kaiwartya, O.; Chizari, H. Next forwarding nodes election in underwater wireless sensor networks (UWSNs): Techniques and challenges. Information 2017, 8, 3. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |


| Parameters | Values |
|---|---|
| Urban simulation area | 1000 1000 m2 |
| Simulation time | 600 s |
| Vehicle speed | 2.78 to 13.89 m/s (10 to 50 km/h) |
| Number of vehicles | 50 to 500 |
| MAC protocol | IEEE 802.11p |
| Video resolution | 352 288 |
| Video play duration | 139 s |
| Transmission range | 250 m |
| Frequency Bandwidth | 5.9 GHz |
| Propagation model | Shadowing |
| Antenna model | Omni-directional |
| Traffic type | Constant Bit Rate |
| Channel type | Wireless |
| Transmission Protocol | UDP |
| Hello packet timeout | 1 s |
| Scenarios | High-density urban scenario |
| Comparison protocol | MSLND, 3MRP and 3MRP + DSW |
| Metrics | PSNR, SSIM index, PLR and E2ED |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aliyu, A.; Abdullah, A.H.; Isnin, I.F.; Radzi, R.Z.R.M.; Kumar, A.; Darwish, T.S.J.; Joda, U.M. Road-Based Multi-Metric Forwarder Evaluation for Multipath Video Streaming in Urban Vehicular Communication. Electronics 2020, 9, 1663. https://doi.org/10.3390/electronics9101663
Aliyu A, Abdullah AH, Isnin IF, Radzi RZRM, Kumar A, Darwish TSJ, Joda UM. Road-Based Multi-Metric Forwarder Evaluation for Multipath Video Streaming in Urban Vehicular Communication. Electronics. 2020; 9(10):1663. https://doi.org/10.3390/electronics9101663
Chicago/Turabian StyleAliyu, Ahmed, Abdul Hanan Abdullah, Ismail Fauzi Isnin, Raja Zahilah Raja Mohd. Radzi, Arvind Kumar, Tasneem S. J. Darwish, and Usman Mohammed Joda. 2020. "Road-Based Multi-Metric Forwarder Evaluation for Multipath Video Streaming in Urban Vehicular Communication" Electronics 9, no. 10: 1663. https://doi.org/10.3390/electronics9101663
APA StyleAliyu, A., Abdullah, A. H., Isnin, I. F., Radzi, R. Z. R. M., Kumar, A., Darwish, T. S. J., & Joda, U. M. (2020). Road-Based Multi-Metric Forwarder Evaluation for Multipath Video Streaming in Urban Vehicular Communication. Electronics, 9(10), 1663. https://doi.org/10.3390/electronics9101663





