Simplified Swarm Optimization for the Heterogeneous Fleet Vehicle Routing Problem with Time-Varying Continuous Speed Function
Abstract
:1. Introduction
2. Literature Review
2.1. Time Dependent Vehicle Routing Problem with Time-Varying Speeds
2.2. Heterogeneous Fixed Fleet Vehicle Routing Problem
3. Problem Statement
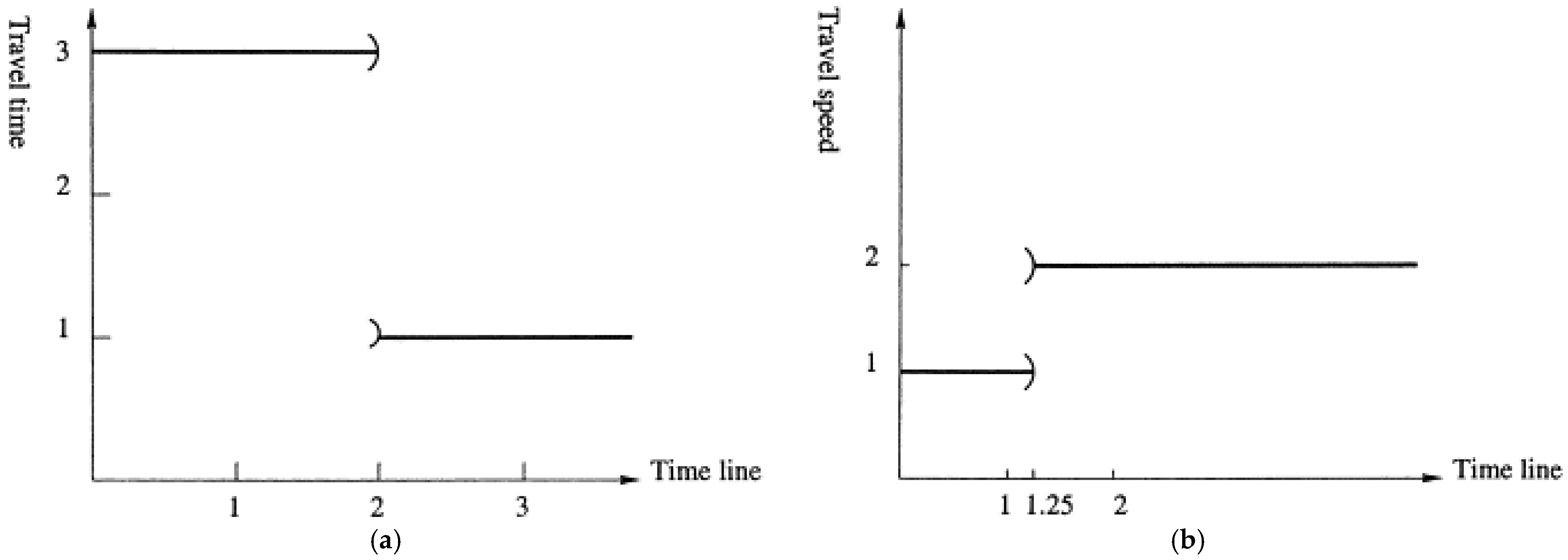
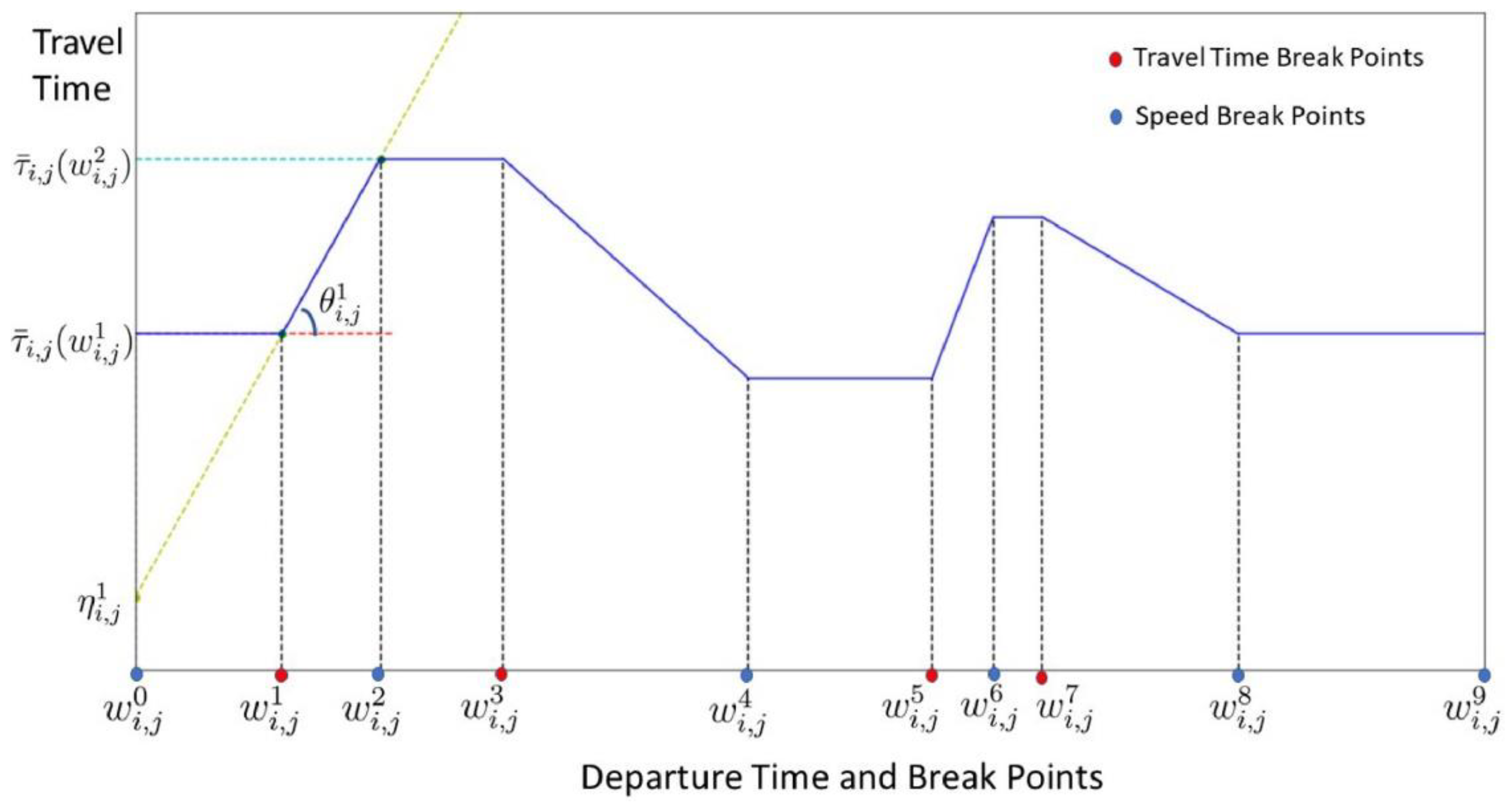
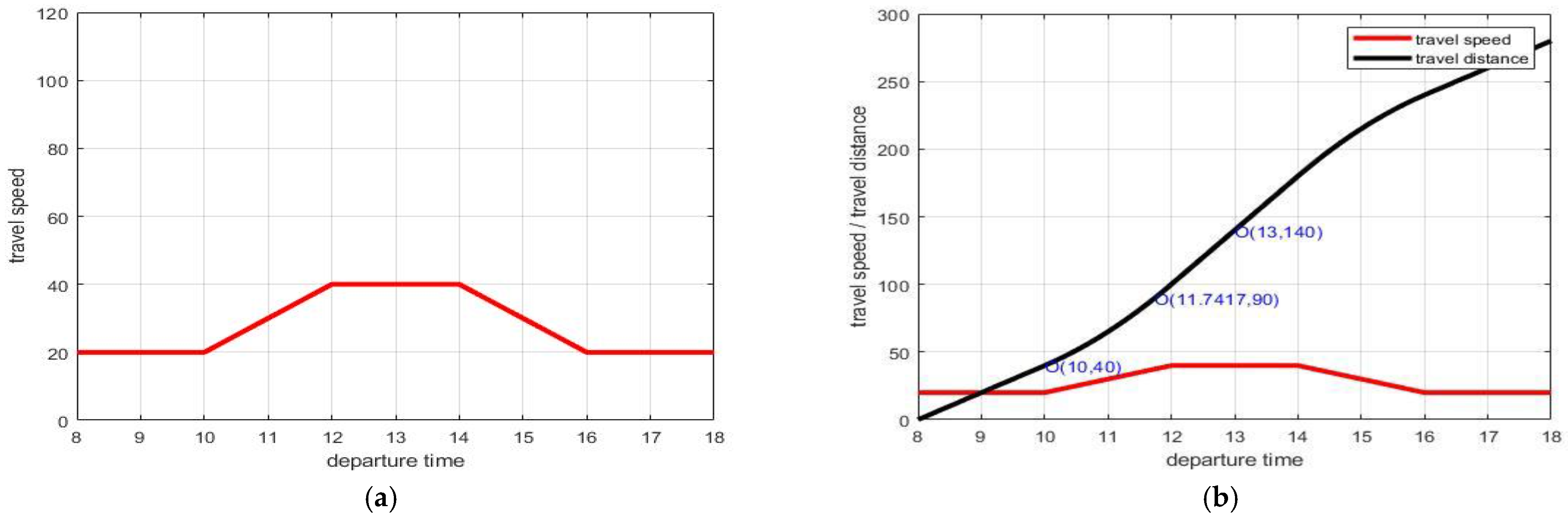
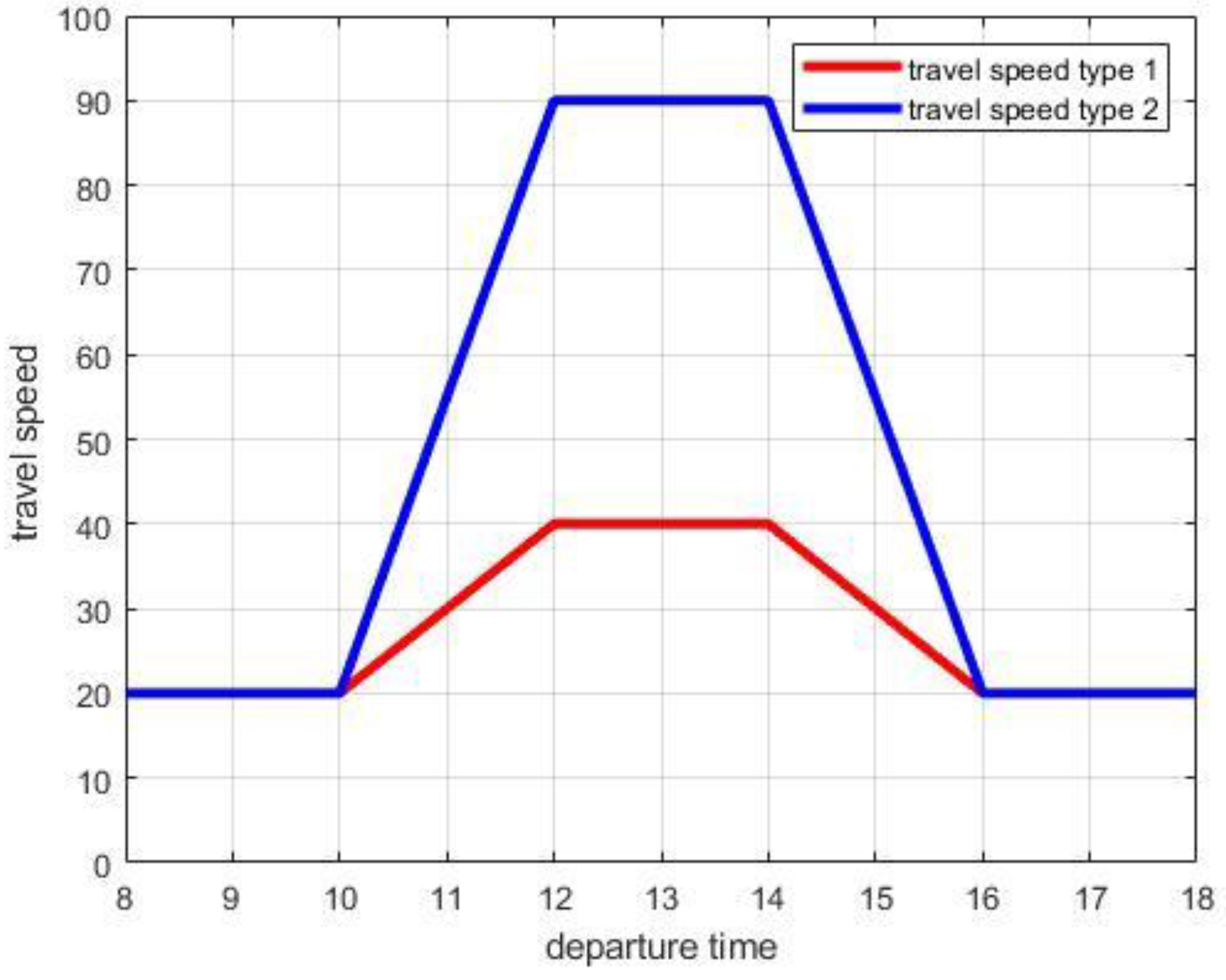
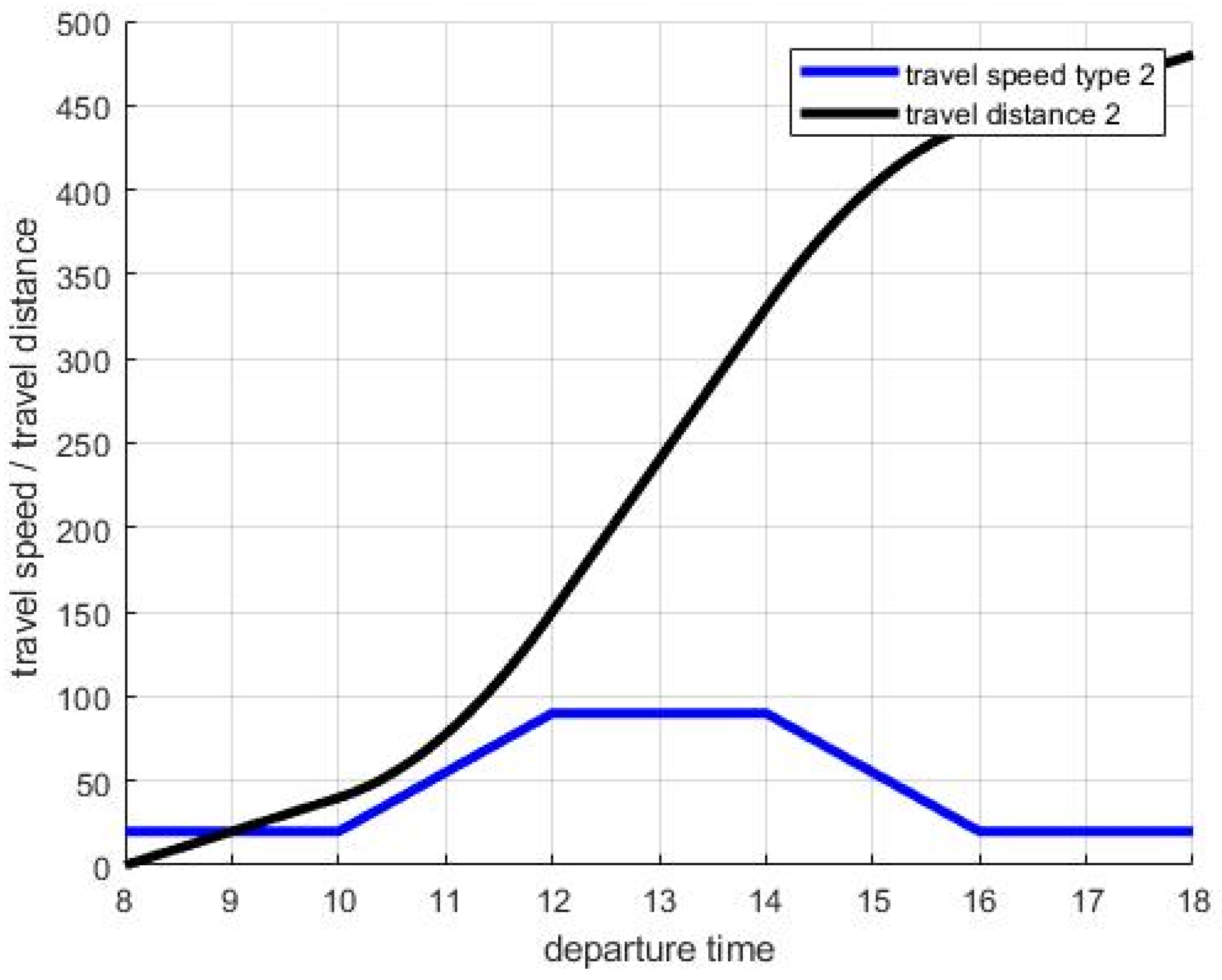
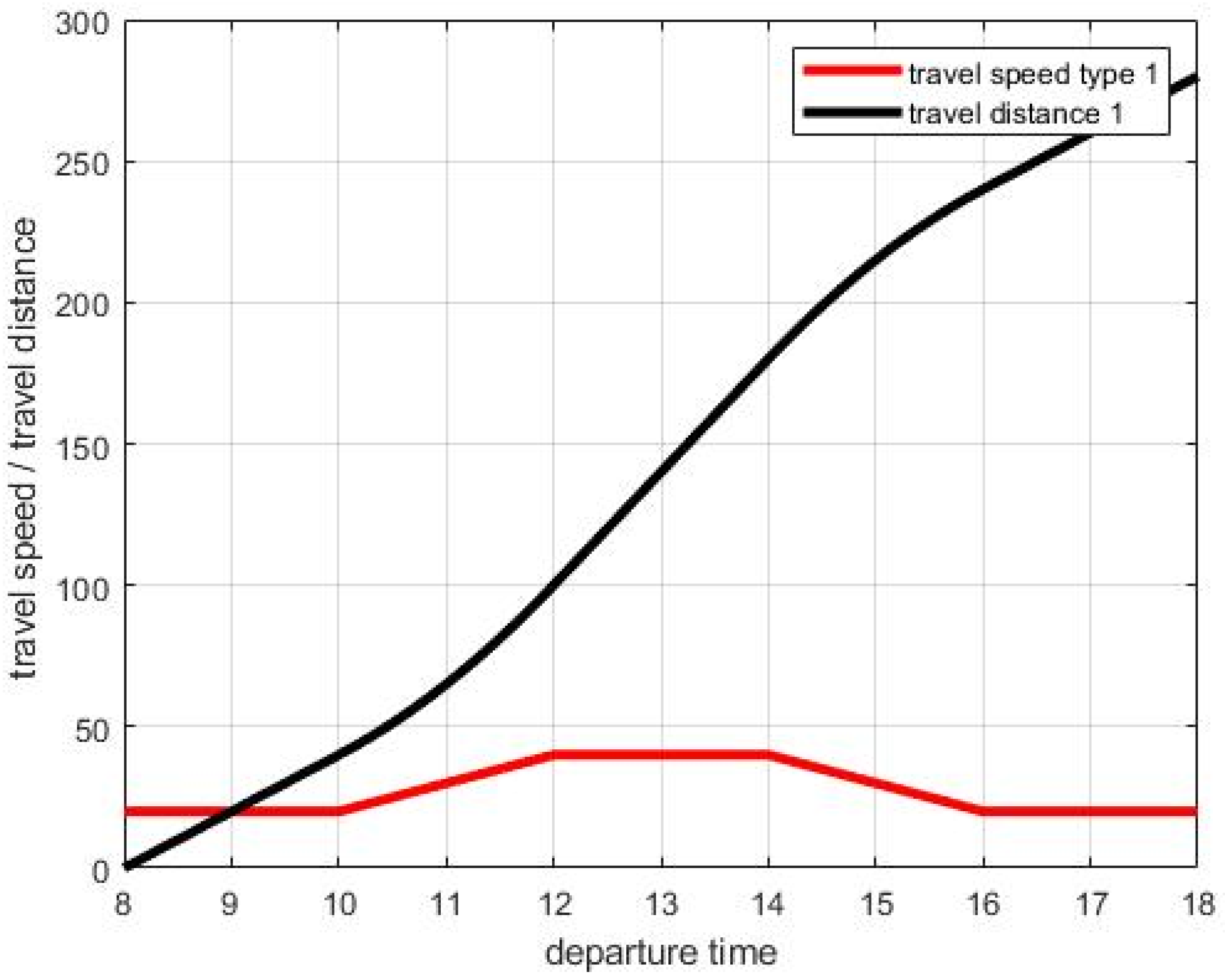
3.1. Time Dependent Vehicle Routing Problem with Time-Varying Speeds of Continuous Function
3.2. Heterogeneous Fixed Fleet Vehicle Routing Problem
- The depot has a demand equal to zero
- Each customer location is serviced from only one vehicle
- Each customer’s delivery must arrive within the time window
- The number of each type of vehicle in routing cannot exceed each type of vehicle; the maximum available number is
- Each vehicle shall not exceed its maximum load capacity
- The total delivery time of each vehicle shall not exceed 9 h
3.3. Fitness Function and Mathematical Model
4. Simplified Swarm Optimization
4.1. Simplified Swarm Optimization
4.2. Example for Code and Decode
4.3. SSO Algorithm Pseudo Code
| STEP 0. Initialize parameters; let , randomly initial solution . |
| Each variable for is , there are in total vehicles, subscript n stands for n customer nodes, subscript m stands for m particle size, stands for customer i needs, stands for customer i time window. |
| STEP 1. Let , first row of solution matrix. |
| STEP 1.1 Let |
| STEP 1.2 Find |
| STEP 1.3.1 Rank get , then read the distance link node i and node j, add the vehicle fix cost; |
| STEP 1.3.2 calculate arrive time for each node, and departure time check whether the arrival time is in the time window. |
| STEP 1.3.3 calculate variable cost for each node, |
| STEP 1.3.4 check total weight not over |
| STEP 1.4 Calculate for vehicle |
| STEP 1.5 |
| if |
| , go back to STEP 1.2 |
| Otherwise |
| Calculate |
| If |
| Otherwise |
| STEP 2. |
| if |
| , go back to STEP 1.1 |
| Otherwise |
| If |
| Otherwise |
| STEP 3. |
| if and CPU time is not met, randomly |
| switch |
| Case1 |
| Case2 |
| Case3 |
| go back to STEP1 |
| Otherwise |
| Halt |
5. Computational Experiments
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| D | Dem | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D | 0 | 83 | 80 | 32 | 86 | 79 | 57 | 57 | 44 | 86 | 61 | 0 | 0 | 9 |
| 82 | 0 | 25 | 88 | 135 | 9 | 87 | 47 | 97 | 96 | 29 | 403 | 1.45 | 7.16 | |
| 80 | 24 | 0 | 90 | 113 | 31 | 98 | 28 | 80 | 111 | 37 | 411 | 0.73 | 6.12 | |
| 32 | 88 | 90 | 0 | 117 | 82 | 48 | 75 | 74 | 77 | 64 | 596 | 0.75 | 6.29 | |
| 86 | 135 | 112 | 116 | 0 | 139 | 140 | 91 | 44 | 169 | 125 | 582 | 0.24 | 6.1 | |
| 78 | 9 | 32 | 82 | 139 | 0 | 79 | 49 | 98 | 87 | 23 | 212 | 0.26 | 5.73 | |
| 58 | 87 | 98 | 48 | 140 | 79 | 0 | 95 | 98 | 39 | 65 | 330 | 0.96 | 6.28 | |
| 57 | 47 | 28 | 75 | 91 | 49 | 94 | 0 | 55 | 113 | 38 | 687 | 0.45 | 5.91 | |
| 43 | 97 | 78 | 73 | 44 | 98 | 97 | 55 | 0 | 126 | 83 | 210 | 0.89 | 6.55 | |
| 87 | 96 | 111 | 77 | 169 | 86 | 39 | 113 | 127 | 0 | 78 | 330 | 0.88 | 6.19 | |
| 59 | 30 | 38 | 62 | 124 | 22 | 63 | 39 | 83 | 76 | 0 | 697 | 0.84 | 6.51 |
| D | Dem | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D | 0 | 93 | 53 | 48 | 34 | 63 | 80 | 99 | 51 | 16 | 31 | 0 | 0 | 9 |
| 93 | 0 | 46 | 55 | 106 | 106 | 139 | 9 | 140 | 109 | 124 | 187 | 0.96 | 6.47 | |
| 53 | 46 | 0 | 33 | 73 | 92 | 114 | 47 | 98 | 67 | 84 | 806 | 0.33 | 6.12 | |
| 48 | 54 | 33 | 0 | 53 | 62 | 86 | 59 | 96 | 63 | 77 | 672 | 1.16 | 6.62 | |
| 34 | 106 | 73 | 53 | 0 | 38 | 50 | 110 | 67 | 40 | 41 | 465 | 1.01 | 6.42 | |
| 63 | 106 | 92 | 61 | 38 | 0 | 34 | 114 | 103 | 76 | 77 | 628 | 1.16 | 6.94 | |
| 80 | 139 | 113 | 86 | 50 | 34 | 0 | 143 | 113 | 87 | 86 | 735 | 1.1 | 6.55 | |
| 99 | 9 | 47 | 59 | 110 | 114 | 143 | 0 | 144 | 113 | 129 | 207 | 1.23 | 6.7 | |
| 51 | 140 | 98 | 96 | 67 | 103 | 113 | 145 | 0 | 35 | 29 | 824 | 0.3 | 5.9 | |
| 16 | 108 | 67 | 63 | 40 | 76 | 87 | 113 | 35 | 0 | 18 | 348 | 0.97 | 6.19 | |
| 31 | 124 | 83 | 77 | 42 | 77 | 87 | 130 | 29 | 19 | 0 | 672 | 0.23 | 5.79 |
| D | Dem | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D | 0 | 48 | 51 | 34 | 95 | 59 | 32 | 71 | 14 | 97 | 59 | 0 | 0 | 9 |
| 48 | 0 | 91 | 14 | 120 | 71 | 16 | 95 | 38 | 119 | 101 | 691 | 1.49 | 6.92 | |
| 51 | 91 | 0 | 78 | 137 | 51 | 77 | 113 | 64 | 150 | 24 | 692 | 0.67 | 6.48 | |
| 34 | 14 | 78 | 0 | 106 | 65 | 3 | 81 | 25 | 106 | 88 | 190 | 0.85 | 6.04 | |
| 95 | 119 | 138 | 106 | 0 | 150 | 103 | 25 | 84 | 30 | 136 | 613 | 0.65 | 6.28 | |
| 58 | 71 | 51 | 64 | 152 | 0 | 66 | 127 | 66 | 152 | 72 | 528 | 0.28 | 5.62 | |
| 32 | 16 | 77 | 3 | 104 | 66 | 0 | 78 | 22 | 103 | 87 | 375 | 1.3 | 6.56 | |
| 71 | 94 | 113 | 81 | 25 | 124 | 78 | 0 | 59 | 35 | 111 | 718 | 1.15 | 6.59 | |
| 14 | 38 | 64 | 25 | 84 | 66 | 22 | 59 | 0 | 85 | 73 | 203 | 1.34 | 6.46 | |
| 97 | 118 | 149 | 105 | 30 | 151 | 102 | 35 | 85 | 0 | 151 | 414 | 0.86 | 6.35 | |
| 59 | 100 | 25 | 88 | 136 | 73 | 86 | 111 | 73 | 150 | 0 | 168 | 0.95 | 6.31 |
| D | Dem | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D | 0 | 50 | 24 | 34 | 49 | 86 | 24 | 28 | 52 | 73 | 93 | 0 | 0 | 9 |
| 51 | 0 | 36 | 19 | 33 | 115 | 39 | 32 | 45 | 115 | 124 | 169 | 0.56 | 5.91 | |
| 24 | 36 | 0 | 22 | 31 | 83 | 6 | 20 | 48 | 84 | 92 | 508 | 0.92 | 6.22 | |
| 35 | 19 | 22 | 0 | 30 | 102 | 27 | 13 | 33 | 99 | 112 | 702 | 1.09 | 6.55 | |
| 49 | 33 | 31 | 30 | 0 | 105 | 35 | 36 | 61 | 111 | 116 | 406 | 0.66 | 6.17 | |
| 86 | 117 | 84 | 103 | 106 | 0 | 80 | 101 | 128 | 59 | 12 | 269 | 0.39 | 5.63 | |
| 25 | 40 | 6 | 27 | 36 | 79 | 0 | 25 | 52 | 80 | 88 | 279 | 1.02 | 6.62 | |
| 28 | 32 | 20 | 13 | 35 | 100 | 25 | 0 | 31 | 96 | 109 | 659 | 1.36 | 6.76 | |
| 51 | 45 | 48 | 33 | 60 | 128 | 52 | 31 | 0 | 123 | 137 | 215 | 0.19 | 5.62 | |
| 73 | 114 | 84 | 99 | 111 | 58 | 80 | 96 | 123 | 0 | 66 | 589 | 0.71 | 6.19 | |
| 94 | 126 | 93 | 112 | 117 | 13 | 89 | 109 | 137 | 66 | 0 | 541 | 1.32 | 6.97 |
| D | Dem | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D | 0 | 76 | 53 | 84 | 35 | 76 | 63 | 31 | 80 | 63 | 74 | 0 | 0 | 9 |
| 77 | 0 | 95 | 26 | 55 | 141 | 22 | 50 | 92 | 78 | 148 | 575 | 0.37 | 6.12 | |
| 53 | 94 | 0 | 113 | 42 | 111 | 91 | 76 | 128 | 32 | 97 | 675 | 1.13 | 6.57 | |
| 84 | 26 | 113 | 0 | 73 | 142 | 22 | 53 | 72 | 101 | 153 | 194 | 1.33 | 6.92 | |
| 35 | 55 | 43 | 73 | 0 | 108 | 52 | 41 | 97 | 35 | 99 | 438 | 0.63 | 6.05 | |
| 76 | 141 | 111 | 143 | 108 | 0 | 122 | 92 | 94 | 131 | 39 | 147 | 1.09 | 6.26 | |
| 63 | 25 | 91 | 26 | 51 | 123 | 0 | 33 | 73 | 79 | 130 | 651 | 0.82 | 6.51 | |
| 31 | 50 | 76 | 53 | 41 | 91 | 33 | 0 | 58 | 75 | 97 | 712 | 1 | 6.77 | |
| 80 | 92 | 127 | 72 | 97 | 94 | 70 | 58 | 0 | 130 | 110 | 533 | 0.93 | 6.46 | |
| 64 | 77 | 32 | 101 | 34 | 131 | 79 | 75 | 130 | 0 | 119 | 298 | 0.7 | 6.07 | |
| 74 | 149 | 97 | 154 | 99 | 40 | 132 | 97 | 111 | 118 | 0 | 125 | 0.41 | 5.95 |
| D | Dem | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D | 0 | 94 | 29 | 65 | 71 | 87 | 99 | 100 | 42 | 73 | 18 | 0 | 0 | 9 |
| 94 | 0 | 76 | 150 | 150 | 10 | 9 | 44 | 69 | 46 | 82 | 697 | 1.09 | 6.54 | |
| 29 | 76 | 0 | 74 | 98 | 69 | 81 | 92 | 49 | 69 | 34 | 816 | 0.2 | 5.89 | |
| 65 | 149 | 73 | 0 | 94 | 144 | 155 | 164 | 105 | 137 | 81 | 110 | 0.58 | 6.16 | |
| 71 | 150 | 98 | 93 | 0 | 142 | 159 | 135 | 82 | 112 | 72 | 413 | 0.6 | 6.15 | |
| 87 | 10 | 69 | 144 | 142 | 0 | 18 | 43 | 61 | 38 | 75 | 343 | 0.6 | 6.12 | |
| 100 | 9 | 81 | 155 | 159 | 19 | 0 | 44 | 78 | 56 | 91 | 146 | 1.14 | 6.48 | |
| 100 | 44 | 92 | 163 | 135 | 43 | 44 | 0 | 61 | 28 | 83 | 335 | 0.51 | 6.02 | |
| 41 | 69 | 49 | 104 | 82 | 61 | 78 | 61 | 0 | 35 | 24 | 366 | 0.81 | 6.57 | |
| 73 | 46 | 69 | 137 | 112 | 38 | 55 | 28 | 35 | 0 | 57 | 146 | 0.83 | 6.07 | |
| 18 | 83 | 34 | 81 | 72 | 75 | 90 | 84 | 24 | 57 | 0 | 668 | 0.84 | 6.73 |
| D | Dem | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D | 0 | 54 | 97 | 71 | 88 | 48 | 68 | 48 | 79 | 73 | 38 | 0 | 0 | 9 |
| 54 | 0 | 139 | 109 | 139 | 98 | 94 | 39 | 97 | 75 | 54 | 629 | 0.52 | 6.01 | |
| 96 | 139 | 0 | 134 | 43 | 50 | 58 | 138 | 163 | 92 | 133 | 114 | 0.62 | 5.69 | |
| 71 | 110 | 135 | 0 | 109 | 87 | 135 | 76 | 39 | 143 | 55 | 475 | 1.39 | 7.15 | |
| 88 | 139 | 43 | 109 | 0 | 42 | 76 | 132 | 137 | 109 | 118 | 370 | 0.72 | 6.35 | |
| 48 | 98 | 51 | 88 | 41 | 0 | 51 | 94 | 116 | 75 | 83 | 596 | 0.5 | 6.3 | |
| 69 | 94 | 58 | 136 | 77 | 52 | 0 | 109 | 146 | 36 | 106 | 679 | 0.38 | 6.15 | |
| 48 | 39 | 139 | 75 | 132 | 94 | 108 | 0 | 63 | 102 | 21 | 512 | 1.26 | 6.6 | |
| 79 | 97 | 164 | 39 | 137 | 114 | 146 | 63 | 0 | 150 | 45 | 781 | 0.34 | 5.9 | |
| 73 | 75 | 92 | 143 | 109 | 75 | 36 | 102 | 149 | 0 | 105 | 392 | 1.38 | 6.82 | |
| 38 | 55 | 133 | 55 | 118 | 82 | 105 | 21 | 45 | 105 | 0 | 771 | 0.72 | 6.39 |
| D | Dem | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D | 0 | 91 | 45 | 36 | 97 | 89 | 72 | 63 | 74 | 95 | 75 | 0 | 0 | 9 |
| 91 | 0 | 111 | 87 | 145 | 36 | 121 | 117 | 32 | 49 | 144 | 486 | 1.32 | 6.78 | |
| 45 | 111 | 0 | 24 | 41 | 91 | 38 | 19 | 104 | 94 | 31 | 682 | 0.59 | 6.2 | |
| 35 | 87 | 24 | 0 | 63 | 70 | 39 | 32 | 86 | 75 | 61 | 533 | 1.46 | 7.1 | |
| 97 | 145 | 41 | 63 | 0 | 113 | 26 | 49 | 147 | 111 | 10 | 556 | 1.37 | 6.78 | |
| 89 | 36 | 90 | 69 | 112 | 0 | 89 | 85 | 58 | 15 | 111 | 257 | 0.56 | 6.01 | |
| 73 | 122 | 37 | 39 | 26 | 89 | 0 | 24 | 123 | 93 | 23 | 227 | 0.75 | 6.15 | |
| 63 | 117 | 19 | 33 | 49 | 85 | 24 | 0 | 117 | 88 | 47 | 128 | 1.08 | 6.61 | |
| 74 | 32 | 104 | 86 | 147 | 58 | 123 | 117 | 0 | 72 | 146 | 365 | 0.27 | 5.56 | |
| 95 | 49 | 94 | 75 | 111 | 14 | 92 | 88 | 72 | 0 | 115 | 126 | 1.49 | 7.08 | |
| 75 | 144 | 31 | 61 | 10 | 112 | 23 | 47 | 145 | 115 | 0 | 404 | 0.92 | 6.16 |
| D | Dem | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D | 0 | 57 | 65 | 38 | 100 | 82 | 59 | 93 | 38 | 86 | 59 | 0 | 0 | 9 |
| 57 | 0 | 9 | 80 | 122 | 107 | 54 | 39 | 45 | 126 | 101 | 431 | 1.23 | 6.95 | |
| 66 | 9 | 0 | 88 | 130 | 115 | 57 | 33 | 54 | 135 | 110 | 236 | 1.38 | 6.86 | |
| 37 | 79 | 88 | 0 | 84 | 62 | 75 | 116 | 54 | 49 | 22 | 426 | 0.27 | 5.73 | |
| 100 | 122 | 130 | 84 | 0 | 22 | 79 | 141 | 77 | 61 | 89 | 550 | 1.16 | 6.76 | |
| 82 | 107 | 115 | 62 | 23 | 0 | 70 | 129 | 64 | 42 | 66 | 687 | 0.72 | 6.14 | |
| 59 | 54 | 57 | 75 | 79 | 70 | 0 | 60 | 22 | 100 | 96 | 578 | 0.19 | 6.06 | |
| 94 | 39 | 33 | 117 | 138 | 127 | 60 | 0 | 70 | 155 | 138 | 403 | 1.48 | 6.86 | |
| 38 | 45 | 53 | 54 | 77 | 63 | 22 | 70 | 0 | 83 | 74 | 409 | 0.43 | 5.71 | |
| 86 | 127 | 136 | 49 | 62 | 42 | 100 | 159 | 83 | 0 | 41 | 597 | 1.43 | 7.15 | |
| 59 | 101 | 109 | 21 | 89 | 67 | 95 | 138 | 74 | 41 | 0 | 441 | 1.07 | 6.73 |
| Dataset | Object | Runtime | Dataset | Object | Runtime | Dataset | Object | Runtime |
|---|---|---|---|---|---|---|---|---|
| UK10_1 | 4579.4 | 28.02 | UK10_5 | 3800.175 | 28.66 | UK10_9 | 4404.37 | 31.04 |
| 4578.21 | 29.21 | 3626.59 | 30.17 | 4694.27 | 30.46 | |||
| 4857.73 | 26.86 | 3916.33 | 27.38 | 4167.22 | 29.78 | |||
| 4650.555 | 30.03 | 3636.265 | 29.52 | 4125.075 | 28.61 | |||
| 5056.05 | 29.67 | 3952.075 | 29.86 | 3996.045 | 30.7 | |||
| UK10_2 | 4990.565 | 29.78 | UK10_6 | 4277.8 | 31.49 | UK10_10 | 5374.835 | 27.83 |
| 4423.505 | 30.36 | 4618.615 | 29.93 | 5444.72 | 30.14 | |||
| 4848.19 | 28.71 | 4776.03 | 27.87 | 5243.825 | 29.49 | |||
| 4918.935 | 28.97 | 4426.16 | 29.12 | 5399.75 | 29.27 | |||
| 4930.825 | 30.55 | 4233.62 | 28.89 | 5596.515 | 28.14 | |||
| UK10_3 | 5283.625 | 29.06 | UK10_7 | 3665.455 | 28.96 | |||
| 5532.12 | 27.72 | 3859.02 | 30.25 | |||||
| 5106.665 | 27.83 | 3727.06 | 28.77 | |||||
| 5178.215 | 31.24 | 3979.495 | 29.8 | |||||
| 4676.6 | 30.5 | 3666.08 | 29.37 | |||||
| UK10_4 | 4438.18 | 31.17 | UK10_8 | 5821.58 | 30.58 | |||
| 4925.145 | 29.44 | 5944.335 | 29.17 | |||||
| 4617.705 | 30.74 | 5556.985 | 29.87 | |||||
| 4536.81 | 30.38 | 5550.52 | 29.34 | |||||
| 4576.975 | 30.16 | 5803.02 | 30.17 |
| Dataset | Object | Runtime | Dataset | Object | Runtime | Dataset | Object | Runtime |
|---|---|---|---|---|---|---|---|---|
| UK10_1 | 5299.55 | 20.34 | UK10_5 | 3942.56 | 18.93 | UK10_9 | 4372.21 | 18.34 |
| 4991.555 | 20.92 | 4660.105 | 19.12 | 4416.71 | 18.67 | |||
| 5005.5 | 19.68 | 3983.105 | 20.31 | 4248.505 | 19.03 | |||
| 5130.775 | 20.55 | 3864.295 | 19.56 | 4342.815 | 20.29 | |||
| 4999.415 | 21.06 | 3919.825 | 19.42 | 4365.025 | 19.74 | |||
| UK10_2 | 5045.55 | 21.65 | UK10_6 | 4537.515 | 18.97 | UK10_10 | 5539.805 | 20.31 |
| 5104.19 | 20.92 | 4452.69 | 19.77 | 5476.845 | 19.72 | |||
| 4849.96 | 19.68 | 4477.275 | 20.05 | 5426.95 | 19.86 | |||
| 4748.23 | 20.55 | 4464.92 | 19.94 | 5621.52 | 18.81 | |||
| 5049.005 | 21.06 | 4562.27 | 20.35 | 5636.43 | 19.83 | |||
| UK10_3 | 5412.62 | 22.27 | UK10_7 | 3978.84 | 20.33 | |||
| 5416.275 | 19.76 | 3863.26 | 18.67 | |||||
| 5451.84 | 21.66 | 4011.7 | 20.1 | |||||
| 5221.17 | 20.46 | 4107.485 | 19.85 | |||||
| 5176.115 | 19.94 | 4051.87 | 19.74 | |||||
| UK10_4 | 4942.085 | 21.52 | UK10_8 | 5564.86 | 19.76 | |||
| 4788.575 | 20.12 | 5762.02 | 20.3 | |||||
| 4947.73 | 22.02 | 5663.74 | 19.45 | |||||
| 5062.86 | 19.97 | 5657.115 | 19.23 | |||||
| 5057.325 | 20.75 | 5760.365 | 19.55 |
| Dataset | Object | Runtime | Dataset | Object | Runtime | Dataset | Object | Runtime |
|---|---|---|---|---|---|---|---|---|
| UK10_1 | 4729.38 | 19.05 | UK10_5 | 3862.26 | 19.82 | UK10_9 | 3998.045 | 19.12 |
| 4664.14 | 17.68 | 3851.745 | 20.58 | 3998.045 | 19.36 | |||
| 4664.14 | 19.25 | 3877.2 | 18.21 | 3998.045 | 19.07 | |||
| 4664.14 | 18.73 | 3877.2 | 18.23 | 3786.95 | 19.42 | |||
| 4948.695 | 17.68 | 3862.26 | 19.67 | 3998.045 | 18.33 | |||
| UK10_2 | 4423.505 | 18.53 | UK10_6 | 4357.945 | 18.97 | UK10_10 | 5393.96 | 20.34 |
| 4554.775 | 20.1 | 4319.66 | 20.1 | 5316.535 | 18.78 | |||
| 4753.095 | 19.58 | 4316.145 | 19.03 | 5320.675 | 19.23 | |||
| 4423.505 | 18.79 | 4444.69 | 18.42 | 5554.535 | 19.36 | |||
| 4708.27 | 19.17 | 4290.77 | 18.5 | 5329.32 | 18.73 | |||
| UK10_3 | 4876.6 | 18.11 | UK10_7 | 3727.06 | 18.67 | |||
| 4876.6 | 19.51 | 3727.06 | 18.39 | |||||
| 4768.49 | 18.76 | 3727.06 | 17.89 | |||||
| 4876.6 | 19.29 | 3777.7 | 19.02 | |||||
| 4885.03 | 18.01 | 3727.06 | 18.37 | |||||
| UK10_4 | 4639.595 | 18.11 | UK10_8 | 5655.395 | 19.02 | |||
| 4858.115 | 19.51 | 5624.36 | 17.88 | |||||
| 4854.055 | 18.76 | 5724.765 | 19.27 | |||||
| 4676.96 | 20.29 | 5610.88 | 18.76 | |||||
| 4762.76 | 18.01 | 5750.38 | 19.41 |
References
- Cattaruzza, D.; Absi, N.; Feillet, D.; González-Feliu, J. Vehicle routing problems for city logistics. EURO J. Transp. Logist. 2017, 6, 51–79. [Google Scholar] [CrossRef]
- Dantzig, G.; Ramser, J. The Truck Dispatching Problem. Manag. Sci. 1959, 80–91. [Google Scholar] [CrossRef]
- Clarke, G.; Wright, J.W. Scheduling of vehicles from a central depot to a number of delivery points. Oper. Res. 1964, 12, 568–581. [Google Scholar] [CrossRef]
- Malandraki, C.; Daskin, M.S. Time dependent vehicle routing problems: Formulations, properties and heuristic algorithms. Transp. Sci. 1992, 26, 185–200. [Google Scholar] [CrossRef]
- Ichoua, S.; Gendreau, M.; Potvin, J.-Y. Vehicle dispatching with time-dependent travel times. Eur. J. Oper. Res. 2003, 144, 379–396. [Google Scholar] [CrossRef] [Green Version]
- Margiotta, R.; Eisele, B.; Short, J. Freight Performance Measure Approaches for Bottlenecks, Arterials, and Linking Volumes to Congestion Report. 2015. Available online: https://rosap.ntl.bts.gov/view/dot/41268 (accessed on 1 June 2021).
- Jha, K.; Eisele, B. Freight Multimodal Performance Measures. 2015. Available online: https://static.tti.tamu.edu/tti.tamu.edu/documents/TTI-2015-19.pdf (accessed on 1 June 2021).
- Baldacci, R.; Battarra, M.; Vigo, D. Routing a heterogeneous fleet of vehicles. In The Vehicle Routing Problem: Latest Advances and New Challenges; Springer: Berlin/Heidelberg, Germany, 2008; pp. 3–27. [Google Scholar]
- Taillard, É.D. A heuristic column generation method for the heterogeneous fleet VRP. RAIRO Oper. Res. Rech. Opér. 1999, 33, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Wen, P. Optimization of a low-carbon two-echelon heterogeneous-fleet vehicle routing for cold chain logistics under mixed time window. Sustainability 2020, 12, 1967. [Google Scholar] [CrossRef] [Green Version]
- Anh, P.T.; Cuong, C.T.; Phuc, P.N.K. The vehicle routing problem with time windows: A case study of fresh food distribution center. In Proceedings of the 2019 11th International Conference on Knowledge and Systems Engineering (KSE), Da Nang, Vietnam, 24–26 October 2019; pp. 1–5. [Google Scholar]
- Adriano, D.D.; Montez, C.; Novaes, A.G.; Wangham, M. DMRVR: Dynamic milk-run vehicle routing solution using fog-based vehicular ad hoc networks. Electronics 2020, 9, 2010. [Google Scholar] [CrossRef]
- Yuan, Z.; Yang, Z.; Lv, L.; Shi, Y. A Bi-Level Path Planning Algorithm for Multi-AGV Routing Problem. Electronics 2020, 9, 1351. [Google Scholar] [CrossRef]
- Wang, Y.; Assogba, K.; Fan, J.; Xu, M.; Liu, Y.; Wang, H. Multi-depot green vehicle routing problem with shared transportation resource: Integration of time-dependent speed and piecewise penalty cost. J. Clean. Prod. 2019, 232, 12–29. [Google Scholar] [CrossRef]
- Emde, S.; Schneider, M. Just-in-time vehicle routing for in-house part feeding to assembly lines. Transp. Sci. 2018, 52, 657–672. [Google Scholar] [CrossRef]
- Liu, L.; Li, K.; Liu, Z. A capacitated vehicle routing problem with order available time in e-commerce industry. Eng. Optim. 2017, 49, 449–465. [Google Scholar] [CrossRef]
- Nakazawa, T.; Tang, S.; Obana, S. CCN-based inter-vehicle communication for efficient collection of road and traffic information. Electronics 2020, 9, 112. [Google Scholar] [CrossRef] [Green Version]
- Sujaree, K.; Samattapapong, N. A Hybrid Chemical Based Metaheuristic Approach for a Vaccine Cold Chain Network. Oper. Supply Chain Manag. Int. J. 2021, 14, 351–359. [Google Scholar] [CrossRef]
- Lenstra, J.K.; Kan, A.R. Complexity of vehicle routing and scheduling problems. Networks 1981, 11, 221–227. [Google Scholar] [CrossRef] [Green Version]
- Cordeau, J.-F.; Gendreau, M.; Laporte, G.; Potvin, J.-Y.; Semet, F. A guide to vehicle routing heuristics. J. Oper. Res. Soc. 2002, 53, 512–522. [Google Scholar] [CrossRef]
- Xu, Z.; Elomri, A.; Pokharel, S.; Mutlu, F. A model for capacitated green vehicle routing problem with the time-varying vehicle speed and soft time windows. Comput. Ind. Eng. 2019, 137, 106011. [Google Scholar] [CrossRef]
- Cao, S.; Liao, W.; Huang, Y. Heterogeneous fleet recyclables collection routing optimization in a two-echelon collaborative reverse logistics network from circular economic and environmental perspective. Sci. Total Environ. 2021, 758, 144062. [Google Scholar] [CrossRef]
- Fan, H.; Zhang, Y.; Tian, P.; Lv, Y.; Fan, H. Time-dependent multi-depot green vehicle routing problem with time windows considering temporal-spatial distance. Comput. Oper. Res. 2021, 129, 105211. [Google Scholar] [CrossRef]
- Alinaghian, M.; Ghazanfari, M.; Norouzi, N.; Nouralizadeh, H. A novel model for the time dependent competitive vehicle routing problem: Modified random topology particle swarm optimization. Netw. Spat. Econ. 2017, 17, 1185–1211. [Google Scholar] [CrossRef]
- Iswari, T.; Asih, A.M.S. Comparing genetic algorithm and particle swarm optimization for solving capacitated vehicle routing problem. IOP Conf. Ser. Mater. Sci. Eng. 2018, 337, 012004. [Google Scholar] [CrossRef]
- Yeh, W.-C. A hybrid heuristic algorithm for the multistage supply chain network problem. Int. J. Adv. Manuf. Technol. 2005, 26, 675–685. [Google Scholar] [CrossRef]
- Yeh, W.-C. A two-stage discrete particle swarm optimization for the problem of multiple multi-level redundancy allocation in series systems. Expert Syst. Appl. 2009, 36, 9192–9200. [Google Scholar] [CrossRef]
- Yeh, W.-C.; Chuang, M.-C. Using multi-objective genetic algorithm for partner selection in green supply chain problems. Expert Syst. Appl. 2011, 38, 4244–4253. [Google Scholar] [CrossRef]
- Malandraki, C.; Dial, R.B. A restricted dynamic programming heuristic algorithm for the time dependent traveling salesman problem. Eur. J. Oper. Res. 1996, 90, 45–55. [Google Scholar] [CrossRef]
- Çimen, M.; Soysal, M. Time-dependent green vehicle routing problem with stochastic vehicle speeds: An approximate dynamic programming algorithm. Transp. Res. Part D Transp. Environ. 2017, 54, 82–98. [Google Scholar] [CrossRef]
- Soysal, M.; Çimen, M. A simulation based restricted dynamic programming approach for the green time dependent vehicle routing problem. Comput. Oper. Res. 2017, 88, 297–305. [Google Scholar] [CrossRef]
- Sun, P.; Veelenturf, L.P.; Dabia, S.; Van Woensel, T. The time-dependent capacitated profitable tour problem with time windows and precedence constraints. Eur. J. Oper. Res. 2018, 264, 1058–1073. [Google Scholar] [CrossRef]
- Liu, C.; Kou, G.; Zhou, X.; Peng, Y.; Sheng, H.; Alsaadi, F.E. Time-dependent vehicle routing problem with time windows of city logistics with a congestion avoidance approach. Knowl. Based Syst. 2020, 188, 104813. [Google Scholar] [CrossRef]
- Pan, B.; Zhang, Z.; Lim, A. A hybrid algorithm for time-dependent vehicle routing problem with time windows. Comput. Oper. Res. 2021, 128, 105193. [Google Scholar] [CrossRef]
- Pan, B.; Zhang, Z.; Lim, A. Multi-trip time-dependent vehicle routing problem with time windows. Eur. J. Oper. Res. 2021, 291, 218–231. [Google Scholar] [CrossRef]
- Gmira, M.; Gendreau, M.; Lodi, A.; Potvin, J.-Y. Tabu search for the time-dependent vehicle routing problem with time windows on a road network. Eur. J. Oper. Res. 2021, 288, 129–140. [Google Scholar] [CrossRef]
- Xiao, Y.; Konak, A. The heterogeneous green vehicle routing and scheduling problem with time-varying traffic congestion. Transp. Res. Part E Logist. Transp. Rev. 2016, 88, 146–166. [Google Scholar] [CrossRef]
- Huang, C.-L.; Jiang, Y.-Z.; Tan, S.-Y.; Yeh, W.-C.; Chung, V.Y.Y.; Lai, C.-M. Simplified swarm optimization for the time dependent competitive vehicle routing problem with heterogeneous fleet. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Koç, Ç.; Bektaş, T.; Jabali, O.; Laporte, G. Thirty years of heterogeneous vehicle routing. Eur. J. Oper. Res. 2016, 249, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Golden, B.; Assad, A.; Levy, L.; Gheysens, F. The fleet size and mix vehicle routing problem. Comput. Oper. Res. 1984, 11, 49–66. [Google Scholar] [CrossRef]
- Micheli, G.J.; Mantella, F. Modelling an environmentally-extended inventory routing problem with demand uncertainty and a heterogeneous fleet under carbon control policies. Int. J. Prod. Econ. 2018, 204, 316–327. [Google Scholar] [CrossRef]
- Afshar-Nadjafi, B.; Afshar-Nadjafi, A. A constructive heuristic for time-dependent multi-depot vehicle routing problem with time-windows and heterogeneous fleet. J. King Saud Univ. Eng. Sci. 2017, 29, 29–34. [Google Scholar] [CrossRef] [Green Version]
- Vincent, F.Y.; Redi, A.P.; Jewpanya, P.; Lathifah, A.; Maghfiroh, M.F.; Masruroh, N.A. A simulated annealing heuristic for the heterogeneous fleet pollution routing problem. In Environmental Sustainability in Asian Logistics and Supply Chains; Springer: Berlin/Heidelberg, Germany, 2019; pp. 171–204. [Google Scholar]
- Wang, Z.; Qi, M.; Cheng, C.; Zhang, C. A hybrid algorithm for large-scale service network design considering a heterogeneous fleet. Eur. J. Oper. Res. 2019, 276, 483–494. [Google Scholar] [CrossRef]
- De, M.; Giri, B. Modelling a closed-loop supply chain with a heterogeneous fleet under carbon emission reduction policy. Transp. Res. Part E Logist. Transp. Rev. 2020, 133, 101813. [Google Scholar] [CrossRef]
- Soman, J.T.; Patil, R.J. A scatter search method for heterogeneous fleet vehicle routing problem with release dates under lateness dependent tardiness costs. Expert Syst. Appl. 2020, 150, 113302. [Google Scholar] [CrossRef]
- Ropke, S.; Cordeau, J.F. Branch and cut and price for the pickup and delivery problem with time windows. Transp. Sci. 2009, 43, 267–286. [Google Scholar] [CrossRef] [Green Version]
- Ben Ticha, H.; Absi, N.; Feillet, D.; Quilliot, A. Vehicle routing problems with road-network information: State of the art. Networks 2018, 72, 393–406. [Google Scholar] [CrossRef]
- Crainic, T.G.; Frangioni, A.; Gendron, B. Bundle-based relaxation methods for multicommodity capacitated fixed charge network design. Discret. Appl. Math. 2001, 112, 73–99. [Google Scholar] [CrossRef]
- Shelbourne, B.C.; Battarra, M.; Potts, C.N. The vehicle routing problem with release and due dates. INFORMS J. Comput. 2017, 29, 705–723. [Google Scholar] [CrossRef]
- Xu, Z.; Ming, X.; Zheng, M.; Li, M.; He, L.; Song, W. Cross-trained workers scheduling for field service using improved NSGA-II. Int. J. Prod. Res. 2015, 53, 1255–1272. [Google Scholar] [CrossRef]
- Vidal, T.; Crainic, T.G.; Gendreau, M.; Lahrichi, N.; Rei, W. A hybrid genetic algorithm for multidepot and periodic vehicle routing problems. Oper. Res. 2012, 60, 611–624. [Google Scholar] [CrossRef]
- Zhong, S.-Q.; Du, G.; He, G.-G. Study on open vehicle routing problem with time windows limits and its genetic algorithm. Jisuanji Gongcheng Yu Yingyong Comput. Eng. Appl. 2006, 42, 201–204. [Google Scholar]
- Wang, M.; Yeh, W.-C.; Chu, T.-C.; Zhang, X.; Huang, C.-L.; Yang, J. Solving multi-objective fuzzy optimization in wireless smart sensor networks under uncertainty using a hybrid of IFR and SSO algorithm. Energies 2018, 11, 2385. [Google Scholar] [CrossRef] [Green Version]
- Yeh, W.-C.; Lai, C.-M.; Peng, Y.-F. Multi-objective optimal operation of renewable energy hybrid CCHP system using SSO. J. Phys. Conf. Ser. 2019, 1411, 012016. [Google Scholar] [CrossRef]
- Lai, C.-M.; Chiu, C.-C.; Liu, W.-C.; Yeh, W.-C. A novel nondominated sorting simplified swarm optimization for multi-stage capacitated facility location problems with multiple quantitative and qualitative objectives. Appl. Soft Comput. 2019, 84, 105684. [Google Scholar] [CrossRef]
- Yeh, W.-C.; Lin, Y.-P.; Liang, Y.-C.; Lai, C.-M. Convolution Neural Network Hyperparameter Optimization Using Simplified Swarm Optimization. arXiv 2021, arXiv:2103.03995. [Google Scholar]
- Yeh, W.-C. A novel boundary swarm optimization method for reliability redundancy allocation problems. Reliab. Eng. Syst. Saf. 2019, 192, 106060. [Google Scholar] [CrossRef]
- Yeh, W.-C.; Su, Y.-Z.; Gao, X.-Z.; Hu, C.-F.; Wang, J.; Huang, C.-L. Simplified swarm optimization for bi-objection active reliability redundancy allocation problems. Appl. Soft Comput. 2021, 106, 107321. [Google Scholar] [CrossRef]
- Yeh, W.-C. New parameter-free simplified swarm optimization for artificial neural network training and its application in the prediction of time series. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 661–665. [Google Scholar] [PubMed]
- Yeh, W.-C. Optimization of the disassembly sequencing problem on the basis of self-adaptive simplified swarm optimization. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2011, 42, 250–261. [Google Scholar] [CrossRef]
- Yeh, W.-C. Simplified swarm optimization in disassembly sequencing problems with learning effects. Comput. Oper. Res. 2012, 39, 2168–2177. [Google Scholar] [CrossRef]
- Lin, P.; Cheng, S.; Yeh, W.; Chen, Z.; Wu, L. Parameters extraction of solar cell models using a modified simplified swarm optimization algorithm. Sol. Energy 2017, 144, 594–603. [Google Scholar] [CrossRef]
| Paper | Speed | HF | TW | Test Problem | Veh Type | Tp | Objective | Solution Method | ||
|---|---|---|---|---|---|---|---|---|---|---|
| D | C | F | V | |||||||
| Çimen and Soysal [30] | √ | - | - | - | - | Pollution-Routing Problem Instance Library | homo | 4 | carbon | Approximate Dynamic Programming (ADP) based heuristic algorithm |
| Soysal and Çimen [31] | √ | - | - | - | - | Pollution-Routing Problem InstanceLibrary | homo | 4 | carbon | Simulation Based Restricted Dynamic Programming (RDP) algorithm |
| Sun, Veelenturf, Dabia and Van Woensel [32] | √ | - | - | - | √ | Instances proposed by Ropke et al. [47] | homo | 5 | max profit | Tailored labeling algorithm |
| Wang, Assogba, Fan, Xu, Liu and Wang [14] | √ | - | - | - | √ | Pollution-Routing Problem Instance Library | homo | 5 | carbon and cost | Clarke and Wright Saving, Sweep algorithm, and multi-objective PSO |
| Adriano, Montez, Novaes and Wangham [12] | - | - | - | - | √ | Self-generated | homo | not TD | cost | Dynamic milk-run vehicle routing solution |
| Liu, Kou et al. [33] | √ | - | - | - | √ | Solomon dataset | homo | 3 | cost | Ant colony algorithm |
| Pan, Zhang et al. [34] | √ | - | - | - | √ | Solomon dataset | homo | 5 | time | Tabu search |
| Pan, Zhang et al. [35] | √ | - | - | - | √ | Solomon dataset | homo | 5 | dis | Tabu search |
| Gmira, Gendreau et al. [36] | √ | - | - | - | √ | NEWLET coming from [48] | homo | 5 | dis | Tabu search |
| Afshar-Nadjafi and Afshar-Nadjafi [42] | √ | - | - | √ | √ | Self-generated | 4 | 3 | cost | Simulated annealing |
| Vincent, Redi et al. [43] | - | - | - | √ | - | Pollution-Routing Problem Instance Library | 3 | not TD | cost | Simulated annealing |
| Wang, Qi et al. [44] | - | - | - | √ | - | Instances proposed by [49] | 10 | not TD | cost | Linear solution provided by the column-and-cut generation with local search |
| Soman and Patil [46] | - | - | - | √ | - | Instances proposed by [50] | 2 | not TD | cost | Scatter search |
| De and Giri [45] | - | - | - | √ | - | Self-generated | 3 | not TD | carbon and cost | Mixed integer linear programming |
| Cao, Liao et al. [22] | - | - | √ | √ | - | Self-generated | 3 | not TD | cost | Genetic algorithm |
| Huang, Jiang et al. [38] | - | √ | - | √ | √ | Self-generated | 3 | 5 | cost | Simplified swarm optimization |
| Xu, Elomri et al. [21] | - | √ | - | √ | √ | Instances proposed by [51] | 12 | 4 | fuel | Genetic algorithm |
| Fan, Zhang et al. [23] | - | √ | √ | √ | √ | MDVRP by [52], MDVRPTW by [53] | 3 | 4 | cost | Genetic algorithm |
| Our study | - | √ | √ | √ | √ | Pollution-Routing Problem Instance Library | 3 | 5 | cost | Simplified swarm optimization |
| Sets and Indices | |
| V | are customers |
| i,j | |
| A | is the arcs set linking node i and node j |
| the set of vehicles with m types | |
| m | |
| Parameters | |
| demand of i customer | |
| time window of i customer | |
| service time of i customer | |
| T | time period |
| the arrive time of node i | |
| the departure time from node i to node j | |
| the travel time from node i to node j | |
| the distance linking node i and node j | |
| time-varying speed function of m type vehicle | |
| time-varying travel time function of m type vehicle | |
| each type of vehicle, maximum available number | |
| maximum load capacity of m type vehicle | |
| fixed cost of m type vehicle | |
| variable cost of m type vehicle | |
| amount carried using type m vehicle from i to j | |
| Decision variable | |
| one if a type m vehicle travels from node i to j; otherwise, zero | |
| Notation | Description | Typical Values of a Type of m Vehicle | ||
|---|---|---|---|---|
| Vehicle Type 1 | Vehicle Type 2 | Vehicle Type 3 | ||
| Maximum load capacity of m type vehicle | 1000 | 2000 | 3650 | |
| Variable cost of m type vehicle (£/m) | 0.0001 | 0.00015 | 0.0002 | |
| D | Demand | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| D | 0 | 41,150 | 25,680 | 23,000 | 32,450 | 22,500 | 0 | 0 | 22,400 | 0 |
| 40,660 | 0 | 51,980 | 40,000 | 23,000 | 32,000 | 900 | 752 | 21,289 | 200 | |
| 25,010 | 51,780 | 0 | 30,000 | 32,000 | 23,000 | 727 | 270 | 24,050 | 2000 | |
| 20,000 | 30,000 | 300,000 | 0 | 23,000 | 25,000 | 800 | 250 | 22,500 | 1500 | |
| 32,500 | 23,000 | 32,000 | 23,000 | 0 | 30,000 | 580 | 700 | 28,000 | 200 | |
| 22,500 | 32,000 | 23,000 | 25,000 | 30,000 | 0 | 600 | 300 | 27,000 | 300 |
| 1.2 | 2.1 | 5.3 | 5.2 | 5.1 |
| From to | Distance | Travel time | Arrive T | TW | Service Time | Departure T |
|---|---|---|---|---|---|---|
| 0–2 | 25,680 | 10,272 | 10,272 | 2000 | 12,272 | |
| 2–5 | 23,000 | 920 | 13,192 | 300 | 13,492 | |
| 5–1 | 32,000 | 1280 | 14,772 | 200 | 14,972 | |
| 1–4 | 23,000 | 920 | 15,892 | 200 | 16,092 | |
| 4–3 | 23,000 | 920 | 17,012 | 1500 | 18,512 | |
| 3–0 | 20,000 | 800 | 19,312 | 0 | / |
| Notation | Description | Typical Values of a Type of m Vehicle | ||
|---|---|---|---|---|
| Vehicle Type 1 | Vehicle Type 2 | Vehicle Type 3 | ||
| Maximum load capacity of m type vehicle | 1000 | 2000 | 3650 | |
| ) | 0.00002 | 0.000015 | 0.00001 | |
| Fixed cost of m type vehicle | 50 | 100 | 180 | |
| From to | Distance | Total Dis | Variable Cost | Demand | Total VC |
|---|---|---|---|---|---|
| 0–5 | 22,500 | - | 0.00002 | 600 | 270 |
| 5–0 | 22,500 | - | 1 | 0.45 | |
| 0–2 | 25,680 | - | 0.000015 | 727 | 280.0404 |
| 2–0 | 25,010 | - | 1 | 0.3752 | |
| 0–4 | 32,450 | - | 0.000015 | 580 | 282.315 |
| 4–0 | 32,500 | - | 1 | 0.4875 | |
| 0–3 | 23,000 | - | 0.00001 | 800 | 184 |
| 3–1 | 30,000 | 53,000 | 900 | 477 | |
| 1–0 | 40,660 | - | 1 | 0.4066 | |
| 1924.6995 | |||||
| D | Dem | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D | 0 | 41 | 26 | 54 | 95 | 16 | 89 | 74 | 26 | 88 | 66 | 0 | 0 | 9 |
| 41 | 0 | 52 | 33 | 100 | 42 | 76 | 64 | 24 | 72 | 26 | 721 | 0.60 | 6.15 | |
| 25 | 52 | 0 | 62 | 74 | 13 | 69 | 53 | 43 | 73 | 77 | 814 | 0.18 | 5.85 | |
| 54 | 33 | 62 | 0 | 77 | 52 | 43 | 32 | 49 | 40 | 30 | 620 | 0.29 | 5.67 | |
| 95 | 100 | 74 | 77 | 0 | 81 | 56 | 46 | 112 | 62 | 106 | 311 | 1.42 | 6.73 | |
| 16 | 43 | 13 | 52 | 81 | 0 | 78 | 61 | 34 | 82 | 68 | 167 | 0.65 | 6.03 | |
| 89 | 76 | 69 | 43 | 55 | 78 | 0 | 17 | 92 | 7 | 69 | 513 | 1.02 | 6.70 | |
| 73 | 63 | 52 | 32 | 46 | 61 | 17 | 0 | 76 | 21 | 61 | 568 | 1.22 | 6.96 | |
| 26 | 24 | 44 | 50 | 112 | 34 | 91 | 76 | 0 | 89 | 49 | 763 | 0.97 | 6.76 | |
| 88 | 72 | 73 | 39 | 61 | 82 | 7 | 21 | 88 | 0 | 64 | 558 | 1.04 | 6.68 | |
| 65 | 26 | 77 | 29 | 106 | 67 | 69 | 61 | 49 | 64 | 0 | 636 | 1.47 | 7.28 |
| GA | PSO | SSO | ||||
|---|---|---|---|---|---|---|
| Average | Runtime | Average | Runtime | Average | Runtime | |
| 1 | 4744.389 | 28.758 | 5085.359 | 20.51 | 4734.099 | 18.478 |
| 2 | 4822.404 | 29.674 | 4959.387 | 20.772 | 4572.63 | 19.234 |
| 3 | 5155.445 | 29.27 | 5335.604 | 20.818 | 4856.664 | 18.736 |
| 4 | 4618.963 | 30.378 | 4959.715 | 20.876 | 4758.297 | 18.936 |
| 5 | 3786.287 | 29.118 | 4073.978 | 19.468 | 3866.133 | 19.302 |
| 6 | 4466.445 | 29.3425 | 4498.934 | 19.816 | 4345.842 | 19.004 |
| 7 | 3779.422 | 29.43 | 4002.631 | 19.738 | 3737.188 | 18.468 |
| 8 | 5735.288 | 29.826 | 5681.62 | 19.658 | 5673.156 | 18.868 |
| 9 | 4277.396 | 30.118 | 4349.053 | 19.214 | 3955.826 | 19.06 |
| 10 | 5411.929 | 28.9 | 5540.31 | 19.706 | 5383.005 | 19.288 |
| average | 4679.797 | 29.48145 | 4845.599 | 20.0576 | 4589.337 | 18.9374 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yeh, W.-C.; Tan, S.-Y. Simplified Swarm Optimization for the Heterogeneous Fleet Vehicle Routing Problem with Time-Varying Continuous Speed Function. Electronics 2021, 10, 1775. https://doi.org/10.3390/electronics10151775
Yeh W-C, Tan S-Y. Simplified Swarm Optimization for the Heterogeneous Fleet Vehicle Routing Problem with Time-Varying Continuous Speed Function. Electronics. 2021; 10(15):1775. https://doi.org/10.3390/electronics10151775
Chicago/Turabian StyleYeh, Wei-Chang, and Shi-Yi Tan. 2021. "Simplified Swarm Optimization for the Heterogeneous Fleet Vehicle Routing Problem with Time-Varying Continuous Speed Function" Electronics 10, no. 15: 1775. https://doi.org/10.3390/electronics10151775
APA StyleYeh, W.-C., & Tan, S.-Y. (2021). Simplified Swarm Optimization for the Heterogeneous Fleet Vehicle Routing Problem with Time-Varying Continuous Speed Function. Electronics, 10(15), 1775. https://doi.org/10.3390/electronics10151775







