CENNA: Cost-Effective Neural Network Accelerator
Abstract
1. Introduction
2. Background and Related Works
2.1. Convolutional Neural Network (CNN)
2.2. Key Issues in CNN Accelerator Implementation
2.2.1. Computation Complexity
2.2.2. Data Reuse
3. Cost-Effective Neural Network Accelerator (CENNA) Architecture
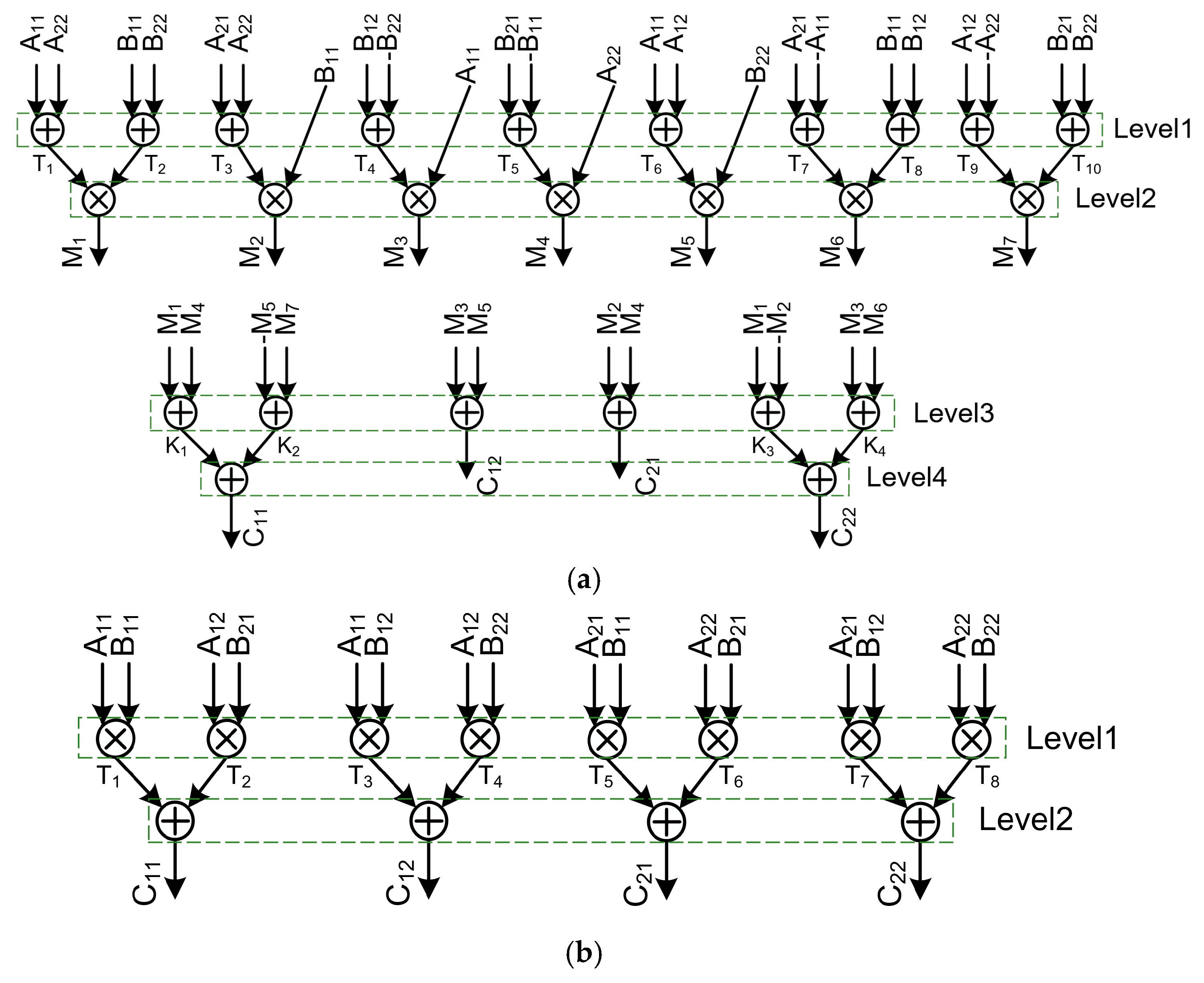
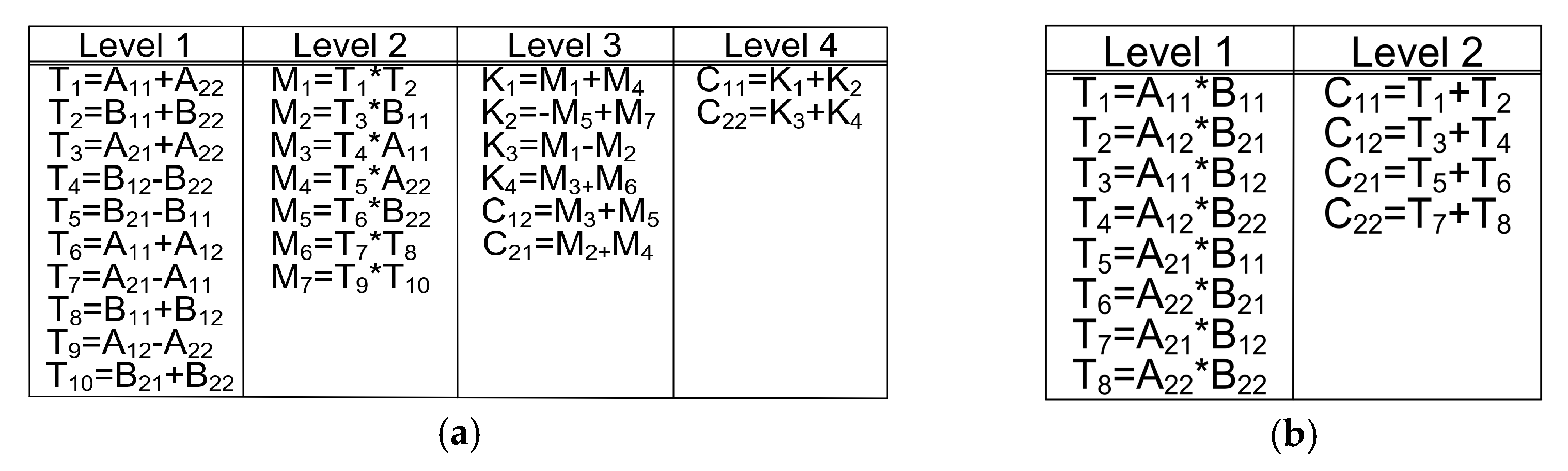
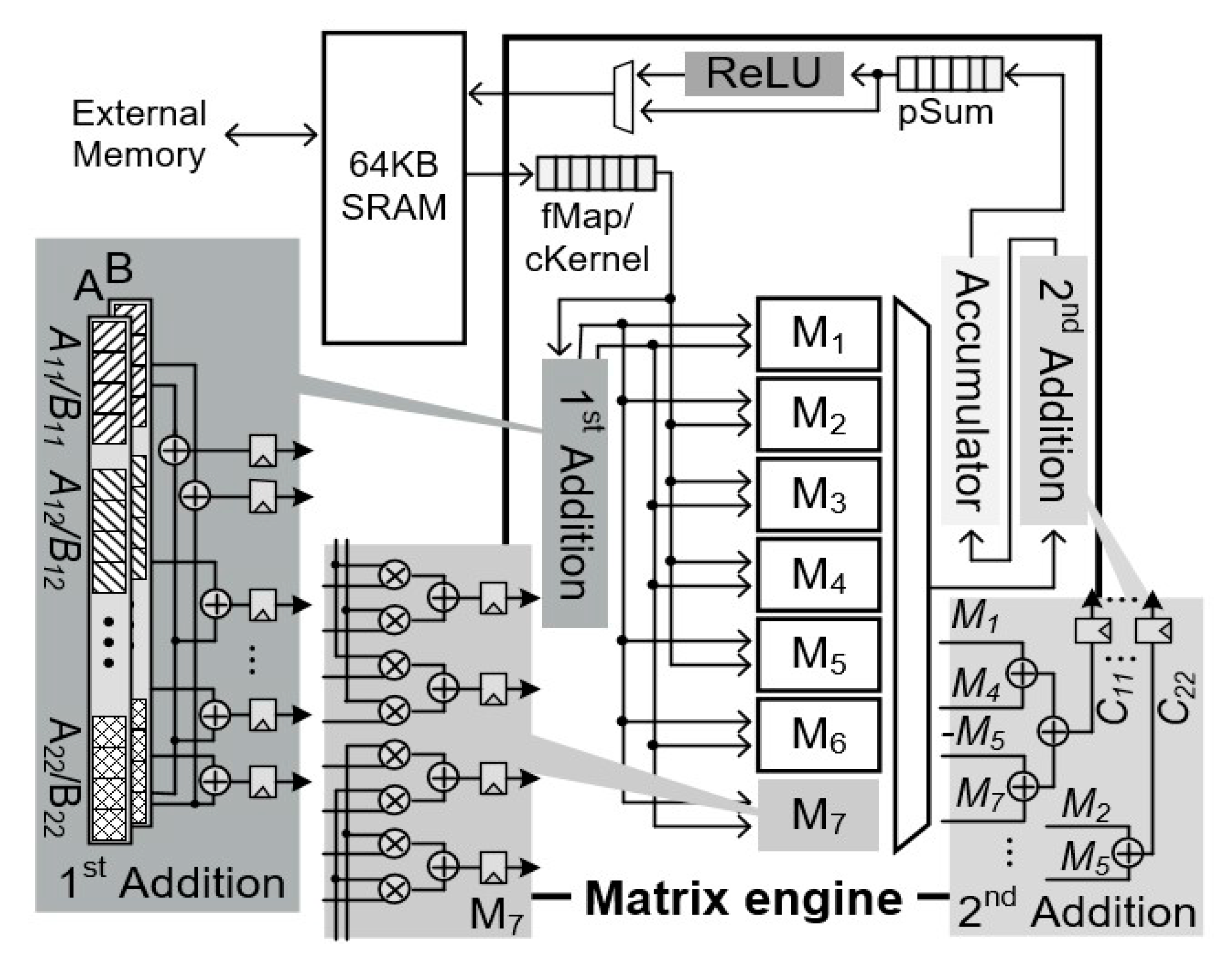
3.1. Proposed Matrix Multiplication Engine
3.2. CENNA Architecture
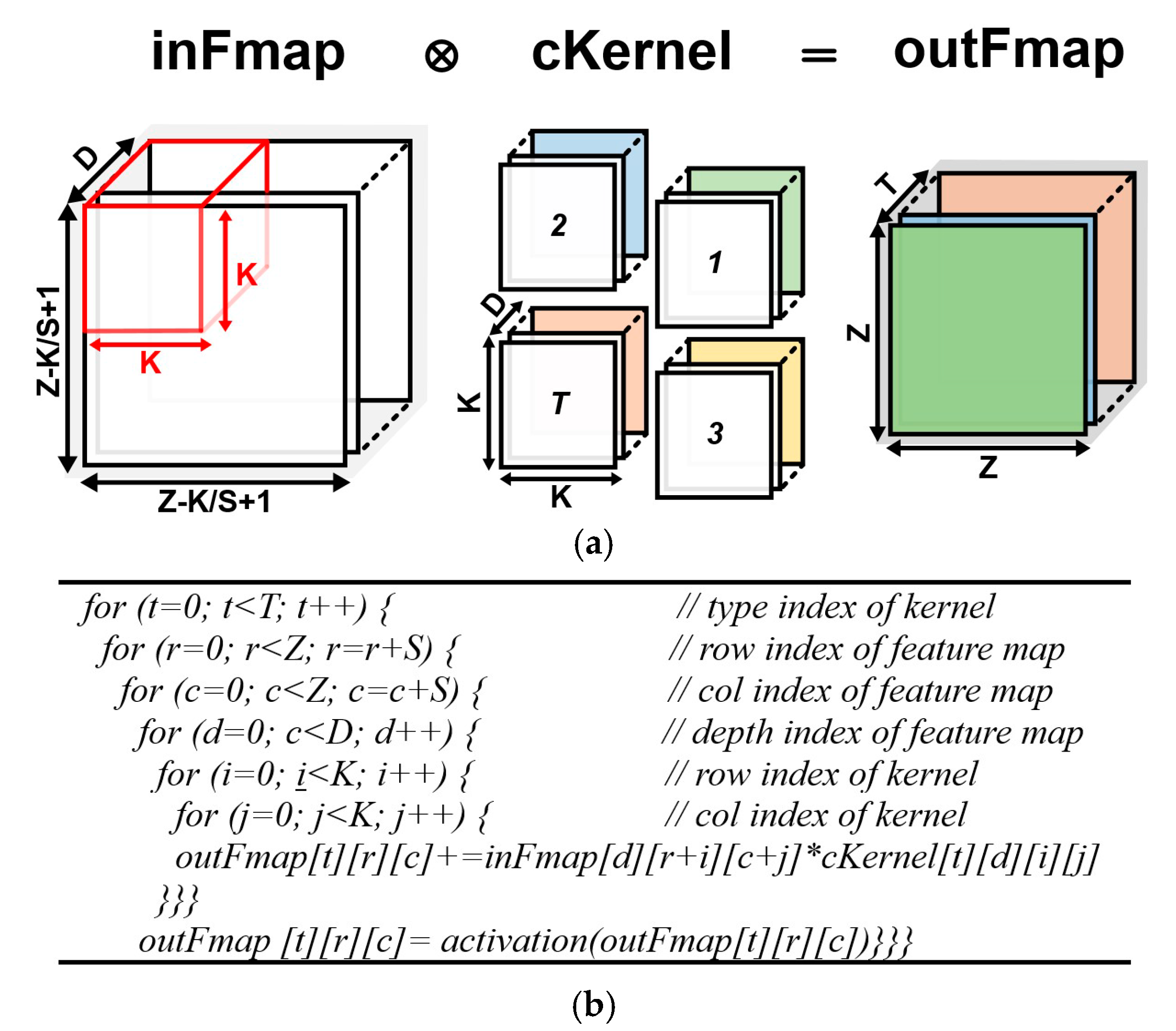
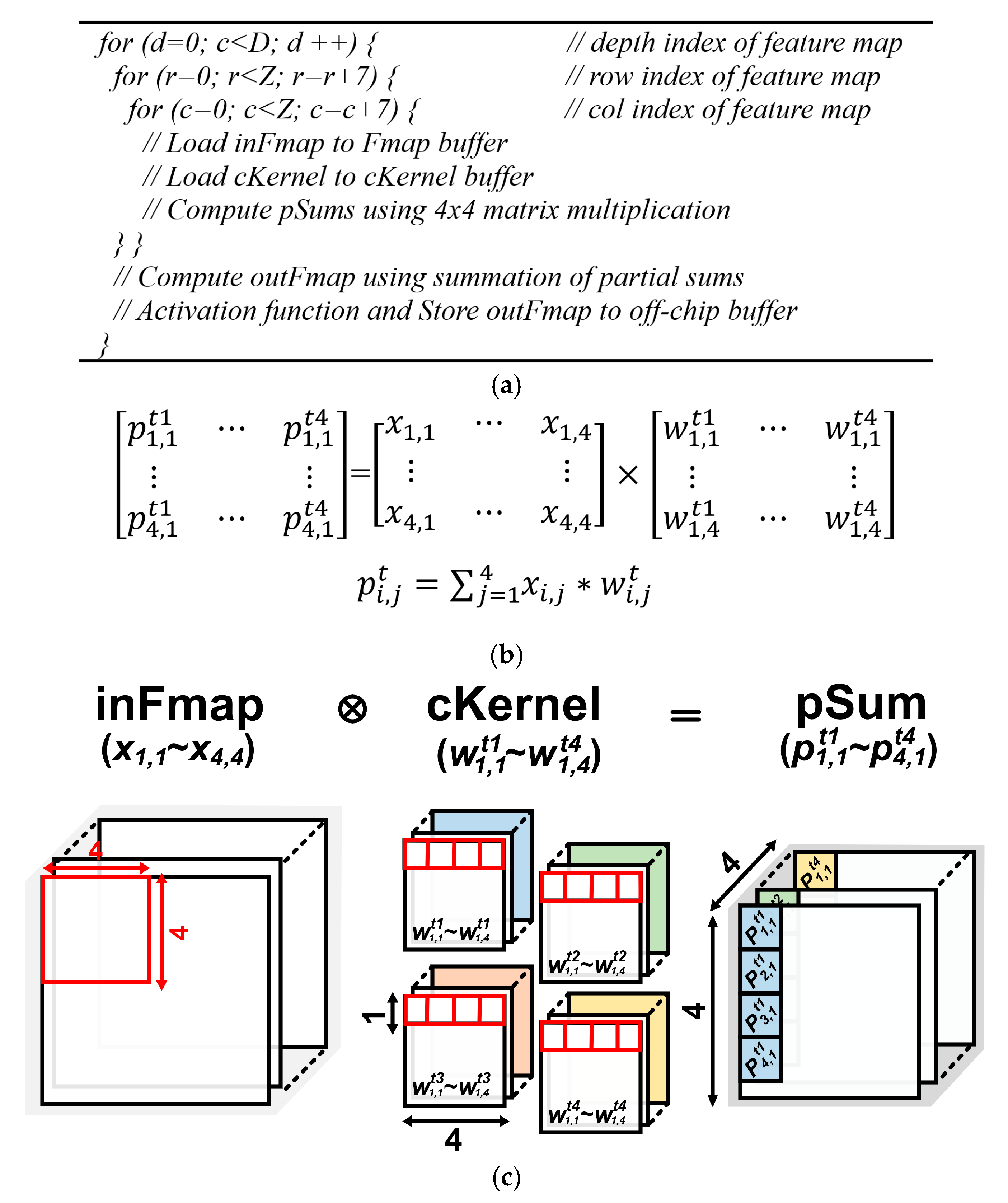
3.3. Convolution Operation in CENNA
3.4. Convolution Operation Using Matrix Mulitplication
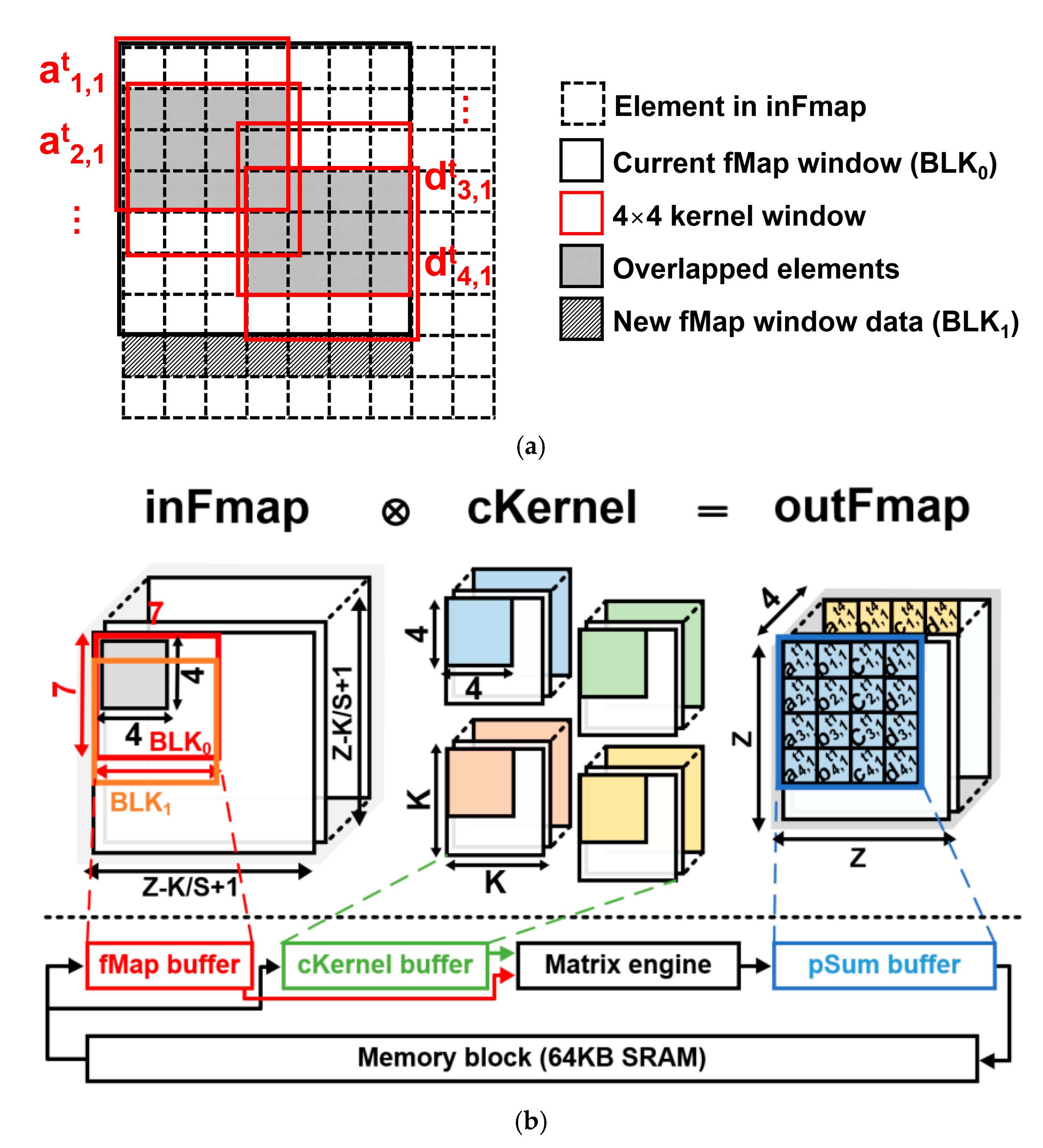
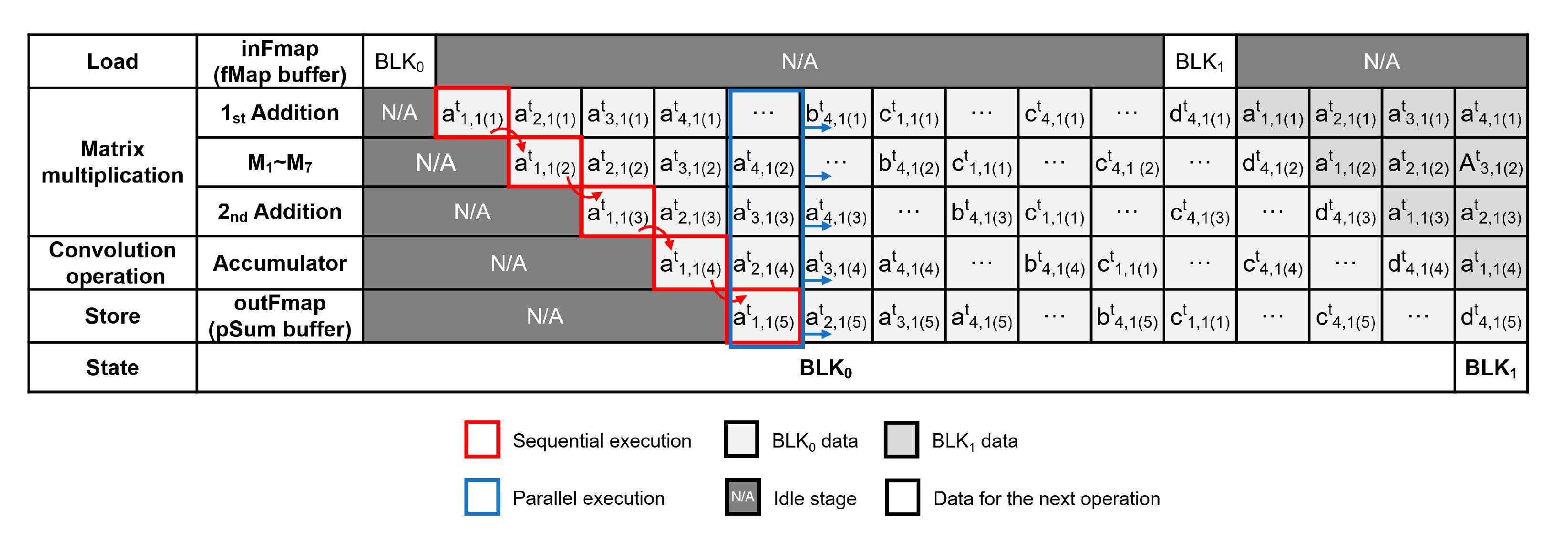
3.5. Tiling-Based Data Reorganization
4. Hardware Implementation
5. Evaluation
5.1. Latency and Throughput of CENNA
5.2. Performance Comparison with the State-of-the-Art Accelerators
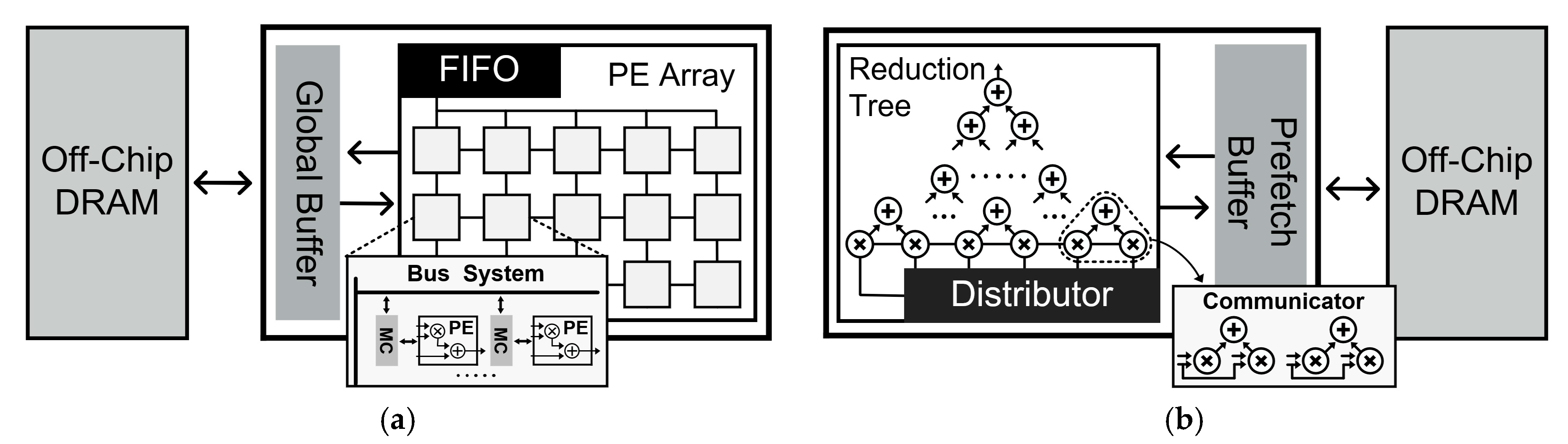
5.2.1. Processing Elements (PE) Array-Based Accelerators
5.2.2. Reduction Tree-Based Accelerators
5.3. Efficiency Comparison with the State-of-the-Art Accelerators
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2012; pp. 1097–1105. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2015; pp. 91–99. [Google Scholar]
- Hershey, S.; Chaudhuri, S.; Ellis, D.P.; Gemmeke, J.F.; Jansen, A.; Moore, R.C.; Plakal, M.; Platt, D.; Saurous, R.A.; Seybold, B. CNN architectures for large-scale audio classification. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 131–135. [Google Scholar]
- Abdel-Hamid, O.; Mohamed, A.-R.; Jiang, H.; Deng, L.; Penn, G.; Yu, D. Convolutional neural networks for speech recognition. IEEE/ACM Trans. Audio Speech Lang. Process. 2014, 22, 1533–1545. [Google Scholar] [CrossRef]
- Lee, G.; Jeong, J.; Seo, S.; Kim, C.; Kang, P. Sentiment Classification with Word Attention based on Weakly Supervised Learning with a Convolutional Neural Network. arXiv 2017, arXiv:1709.09885. [Google Scholar]
- Cong, J.; Xiao, B. Minimizing computation in convolutional neural networks. In International Conference on Artificial Neural Networks; Springer: Berlin/Heidelberg, Germany, 2014; pp. 281–290. [Google Scholar]
- Motamedi, M.; Fong, D.; Ghiasi, S. Fast and energy-efficient cnn inference on iot devices. arXiv 2016, arXiv:1611.07151. [Google Scholar]
- Chen, Y.-H.; Emer, J.; Sze, V. Eyeriss: A spatial architecture for energy-efficient dataflow for convolutional neural networks. In ACM SIGARCH Computer Architecture News; Association for Computing Machinery: New York, NY, USA, 2016; pp. 367–379. [Google Scholar]
- Moons, B.; Verhelst, M. An energy-efficient precision-scalable ConvNet processor in 40-nm CMOS. IEEE J. Solid State Circuits 2016, 52, 903–914. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, D.; Han, X.; Yoshimura, T. Chain-NN: An energy-efficient 1D chain architecture for accelerating deep convolutional neural networks. arXiv 2017, arXiv:1703.01457. [Google Scholar]
- Kwon, H.; Samajdar, A.; Krishna, T. Maeri: Enabling flexible dataflow mapping over dnn accelerators via reconfigurable interconnects. In ACM SIGPLAN Notices; Association for Computing Machinery: New York, NY, USA, 2018; pp. 461–475. [Google Scholar]
- Cavigelli, L.; Benini, L. Origami: A 803-gop/s/w convolutional network accelerator. IEEE Trans. Circuits Syst. Video Technol. 2016, 27, 2461–2475. [Google Scholar] [CrossRef]
- Kyrkou, C.; Plastiras, G.; Theocharides, T.; Venieris, S.I.; Bouganis, C.-S. DroNet: Efficient convolutional neural network detector for real-time UAV applications. arXiv 2018, arXiv:1807.06789v1. [Google Scholar]
- Guo, T. Cloud-based or on-device: An empirical study of mobile deep inference. In Proceedings of the 2018 IEEE International Conference on Cloud Engineering (IC2E), Orlando, FL, USA, 17–20 April 2018; pp. 184–190. [Google Scholar]
- Tang, J.; Liu, S.; Yu, B.; Shi, W. PI-Edge: A Low-Power Edge Computing System for Real-Time Autonomous Driving Services. arXiv 2018, arXiv:1901.04978. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. arXiv 2016, arXiv:1608.06993. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Canziani, A.; Paszke, A.; Culurciello, E. An analysis of deep neural network models for practical applications. arXiv 2016, arXiv:1605.07678. [Google Scholar]
- Wu, S.; Li, G.; Chen, F.; Shi, L. Training and inference with integers in deep neural networks. arXiv 2018, arXiv:1802.04680. [Google Scholar]
- Horowitz, M. Energy table for 45 nm process. Stanford VLSI Wiki. 2014. Available online: https://en.wikipedia.org/wiki/VLSI_Project (accessed on 1 December 2019).
- Lavin, A.; Gray, S. Fast algorithms for convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4013–4021. [Google Scholar]
- Merchant, F.; Vatwani, T.; Chattopadhyay, A.; Raha, S.; Nandy, S.; Narayan, R. Accelerating BLAS on custom architecture through algorithm-architecture co-design. arXiv 2016, arXiv:1610.06385. [Google Scholar]
- Hamilton, K.C. Optimization of energy and throughput for pipelined VLSI interconnect. In UC San Diego; California Digital Library: Oakland, CA, USA, 2010. [Google Scholar]
- Zyuban, V.; Brooks, D.; Srinivasan, V.; Gschwind, M.; Bose, P.; Strenski, P.N.; Emma, P.G. Integrated analysis of power and performance for pipelined microprocessors. IEEE Trans. Comput. 2004, 53, 1004–1016. [Google Scholar] [CrossRef]
- Sartori, J.; Ahrens, B.; Kumar, R. Power balanced pipelines. In Proceedings of the IEEE International Symposium on High-Performance Comp Architecture, New Orleans, LA, USA, 25–29 February 2012; pp. 1–12. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Mackey, L.W.; Jordan, M.I.; Talwalkar, A. Divide-and-conquer matrix factorization. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2011; pp. 1134–1142. [Google Scholar]
- Balasubramonian, R.; Kahng, A.B.; Muralimanohar, N.; Shafiee, A.; Srinivas, V. CACTI 7: New tools for interconnect exploration in innovative off-chip memories. ACM Trans. Archit. Code Optim. 2017, 14, 14. [Google Scholar] [CrossRef]
- Wu, S.; Wang, G.; Tang, P.; Chen, F.; Shi, L. Convolution with even-sized kernels and symmetric padding. arXiv 2019, arXiv:1903.08385. [Google Scholar]
- Yao, S.; Han, S.; Guo, K.; Wangni, J.; Wang, Y. Hardware-frendly convolutional neural network with even-number filter size. Comput. Sci. 2016. Available online: https://pdfs.semanticscholar.org/10b9/92e86ee96cd4c5d73f3d667059beb4749ce3.pdf (accessed on 1 December 2019).
- Cucchiara, R.; Piccardi, M. DARPA benchmark image processing on SIMD parallel machines. In Proceedings of the 1996 IEEE Second International Conference on Algorithms and Architectures for Parallel Processing, Singapore, 11–13 June 1996; pp. 171–178. [Google Scholar]
- Kim, K.; Choi, K. SoC architecture for automobile vision system. In Algorithm & SoC Design for Automotive Vision Systems; Springer: Berlin/Heidelberg, Germany, 2014; pp. 163–195. [Google Scholar]
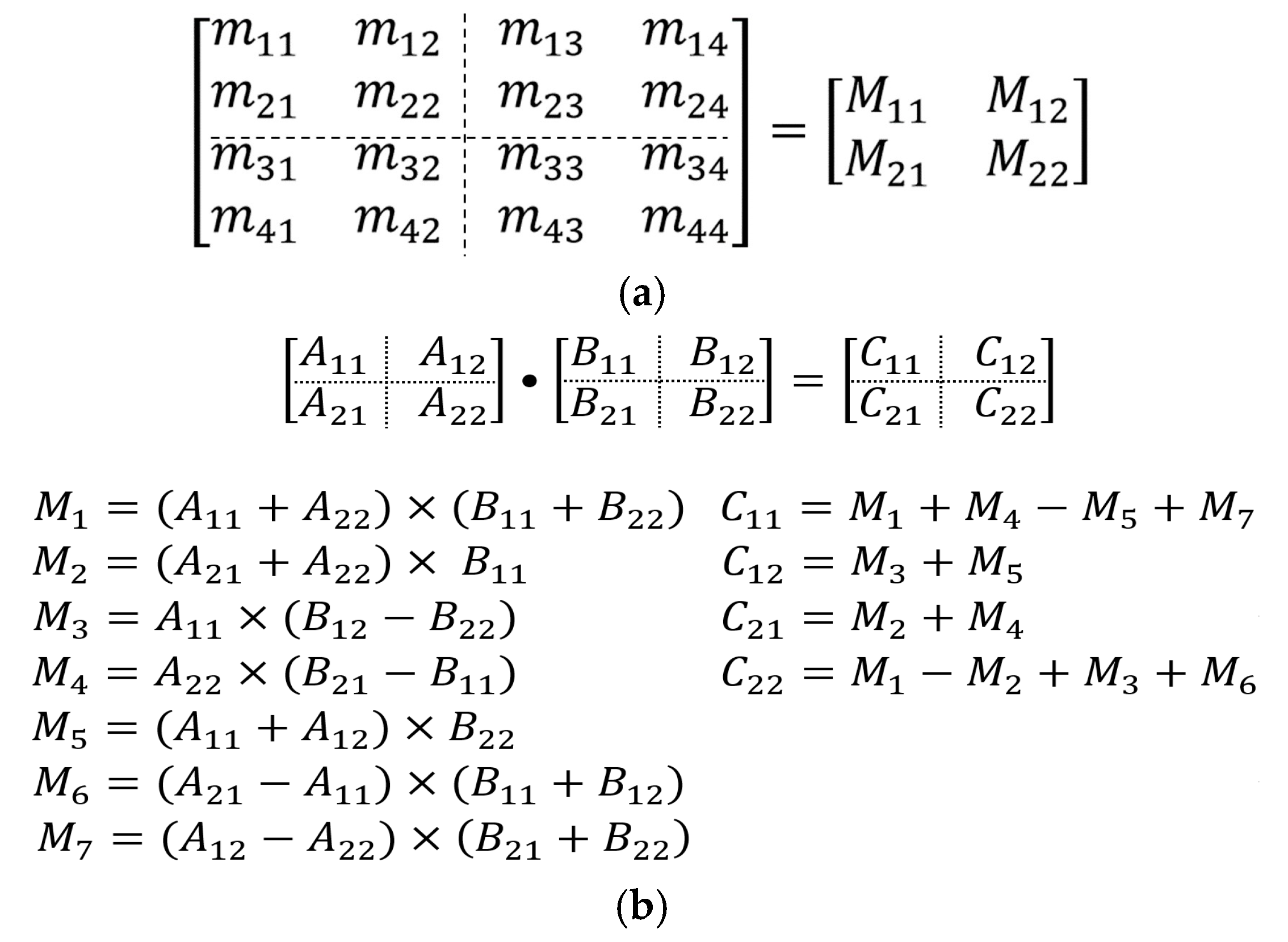

| CNN Model | AlexNet * | VGG-16 ** | GoogLeNet *** | ResNet-152 **** |
|---|---|---|---|---|
| Operation (MAC) 1 | 0.73 M | 16 G | 2 G | 11 G |
| Parameter Mem (Byte) 2 | 233 M | 528 M | 51 M | 220 M |
| Operation | Energy (pJ) | Area (µm2) | ||
|---|---|---|---|---|
| Multiplier | Adder | Multiplier | Adder | |
| 8-bit INT 1 | 0.2 pJ | 0.03 pJ | 282 µm2 | 36 µm2 |
| 16-bit FP 2 | 1.1 pJ | 0.4 pJ | 1640 µm2 | 1360 µm2 |
| 32-bit FP 2 | 3.7 pJ | 0.9 pJ | 7700 µm2 | 4184 µm2 |
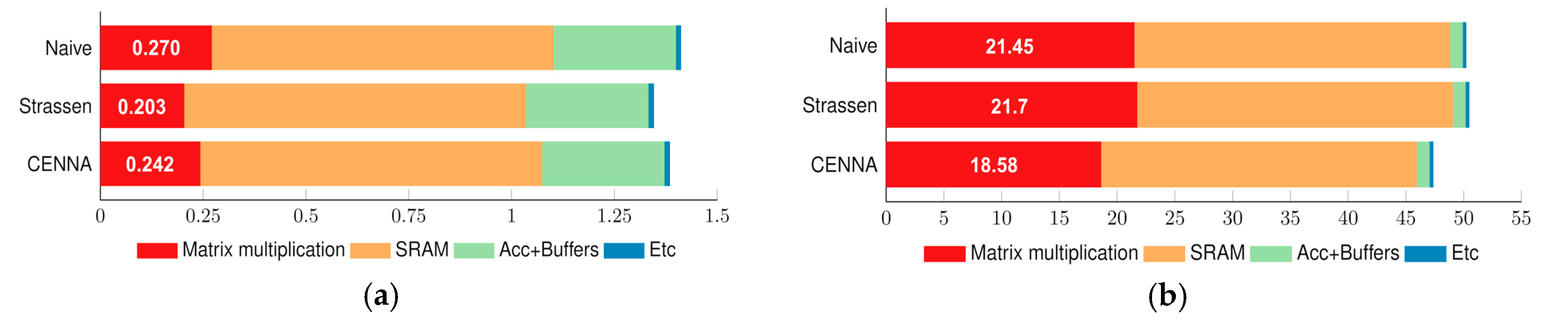
| Cycle/Time (s) (109 4 × 4 Matrices) | Maximum Frequency | # of MUL/ADD | Area | Power | |
|---|---|---|---|---|---|
| Naïve 1 | (109 + 2)/2.00 | 500 MHz | 64/48 | 0.270 mm2 | 21.45 mW |
| Strassen 2 | (109 + 3)/3.16 | 370 MHz | 49/198 | 0.203 mm2 | 21.70 mW |
| Cost-Centric 3 | (109 + 2)/2.00 | 500 MHz | 56/100 | 0.242 mm2 | 18.58 mW |
| Design | Naïve | Strassen | CENNA |
|---|---|---|---|
| # of MUL/ADD | 64/108 | 49/258 | 56/160 |
| Frequency | 500 MHz | 370 MHz | 500 MHz |
| Local Buffer 1 | 448 B | 544 B | 400 B |
| SRAM | 64 KB | 64 KB | 64 KB |
| Area | 1.411 mm2 | 1.345 mm2 | 1.384 mm2 |
| Power | 50.191 mW | 50.462 mW | 47.344 mW |
| Layer | Input (W/H/C) 1 | Output (W/H/C) | # of MAC (Giga) | Total Time (ms) 2 | Memory Access Time (ms) |
|---|---|---|---|---|---|
| Conv1-1 | 224 × 224 × 3 | 224 × 224 × 64 | 0.16 | 4.86 | 0.29 |
| Conv1-2 | 224 × 224 × 64 | 224 × 224 × 64 | 2.62 | 103.61 | 6.09 |
| Conv2-1 | 112 × 112 × 64 | 112 × 112 × 128 | 1.26 | 47.85 | 1.44 |
| Conv2-2 | 112 × 112 × 128 | 112 × 112 × 128 | 2.2 | 95.71 | 2.88 |
| Conv3-1 | 56 × 56 × 128 | 56 × 56 × 256 | 1.42 | 43.16 | 0.66 |
| Conv3-2 | 56 × 56 × 256 | 56 × 56 × 256 | 2.84 | 86.35 | 1.31 |
| Conv3-3 | 56 × 56 × 256 | 56 × 56 × 256 | 2.84 | 86.36 | 1.31 |
| Conv4-1 | 28 × 28 × 256 | 28 × 28 × 512 | 1.21 | 38.26 | 0.31 |
| Conv4-2 | 28 × 28 × 512 | 28 × 28 × 512 | 2.42 | 76.52 | 0.63 |
| Conv4-3 | 28 × 28 × 512 | 28 × 28 × 512 | 2.42 | 76.52 | 0.63 |
| Conv5-1 | 14 × 14 × 512 | 14 × 14 × 512 | 0.42 | 21.05 | 0.63 |
| Conv5-2 | 14 × 14 × 512 | 14 × 14 × 512 | 0.42 | 21.05 | 0.20 |
| Conv5-3 | 14 × 14 × 512 | 14 × 14 × 512 | 0.42 | 21.05 | 0.20 |
| Total | 20.65 | 722.35 | 16.58 | ||
| Design | Naïve | Strassen | CENNA |
|---|---|---|---|
| Total Time | 4.86 ms | 7.68 ms | 4.86 ms |
| Real Throughput 1 | 65.84 GOPS | 41.67 GOPS | 65.84 GOPS |
| Peak Throughput 2 | 86 GOPS | 63.64 GOPS | 86 GOPS |
| Efficiency 3 | 1.31 TOPS/W | 0.83 TOPS/W | 1.39 TOPS/W |
| Metrics | Eyeriss [9] | ConvNet [10] | Chain-NN [11] | CENNA |
|---|---|---|---|---|
| Precision (bit) | 16 | 1–16 | 16 | 16 |
| Process Technology (nm) | 65 | 40 | 28 | 65 |
| Area (mm2) 1 | 12.25 | 2.4 | 10.69 | 1.38 |
| Frequency (MHz) | 200 | 204 | 700 | 500 |
| # of operators 2 | 336 | 204 | 1152 | 232 |
| SRAM (KB) | 192 | 144 | 352 | 64 |
| Peak Throughput (GOPS) | 84 | 102 | 806.4 | 86 |
| Real Throughput (GOPS) 3 | 24.6 | 63.38 | 668.16 | 57.17 |
| Frame Rate (Frame/s) 3 | 0.6 | 1.54 | 16.8 | 1.38 |
| Power (mW) 4 | 236 | 220 | 567.5 | 47.34 |
| Metrics | MAERI [12] | Origami [13] | CENNA |
|---|---|---|---|
| Precision (bit) | 16 | 12 | 16 |
| Process Technology (nm) | 28 | 65 | 65 |
| Area (mm2) | 3.84 | 3.09 | 1.38 |
| Freq (MHz) | 200 | 189 | 500 |
| # of operators | 336 | 388 | 232 |
| SRAM (KB) | 80 | 43 | 64 |
| Peak Throughput (GOPS) | 67.2 | 74 | 86 |
| Real Throughput (GOPS) 1 | 58.27 | 55 | 57.17 |
| Frame Rate (Frame/s) 1 | 1.4 | 7.26 | 1.38 |
| Power (mW) | 370 | 93 | 47.34 |
| Metric | Eyeriss [9] | ConvNet [10] | Chain-NN [11] | MAERI [12] | Origami [13] | CENNA |
|---|---|---|---|---|---|---|
| Power (TOPS/W) | 0.10 | 0.29 * | 1.18 * | 0.16 * | 0.59 | 1.21 |
| Area (GOPS/mm2) | 2.01 | 26.41 ** | 62.5 ** | 15.17 ** | 17.80 | 41.43 |
| Overall (TOPS/W/mm2) | 0.01 | 0.12 *** | 0.11 *** | 0.04 *** | 0.19 | 0.88 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.-S.; Chung, K.-S. CENNA: Cost-Effective Neural Network Accelerator. Electronics 2020, 9, 134. https://doi.org/10.3390/electronics9010134
Park S-S, Chung K-S. CENNA: Cost-Effective Neural Network Accelerator. Electronics. 2020; 9(1):134. https://doi.org/10.3390/electronics9010134
Chicago/Turabian StylePark, Sang-Soo, and Ki-Seok Chung. 2020. "CENNA: Cost-Effective Neural Network Accelerator" Electronics 9, no. 1: 134. https://doi.org/10.3390/electronics9010134
APA StylePark, S.-S., & Chung, K.-S. (2020). CENNA: Cost-Effective Neural Network Accelerator. Electronics, 9(1), 134. https://doi.org/10.3390/electronics9010134





