Abstract
Neural-network computing has revolutionized the field of machine learning. The systolic-array architecture is a widely used architecture for neural-network computing acceleration that was adopted by Google in its Tensor Processing Unit (TPU). To ensure the correct operation of the neural network, the reliability of the systolic-array architecture should be guaranteed. This paper proposes an efficient systolic-array redundancy architecture that is based on systolic-array partitioning and rearranging connections of the systolic-array elements. The proposed architecture allows both offline and online repair with an extended redundancy architecture and programmable fuses and can ensure reliability even in an online situation, for which the previous fault-tolerant schemes have not been considered.
1. Introduction
In the past few years, convolutional neural networks (CNNs) have outperformed traditional machine-learning algorithms. Thus, CNNs are considered state-of-the-art for a wide range of applications, such as image and video recognition [1], text classification [2], and language translation [3]. These neural networks are traditionally operated on central processing units (CPUs), graphics processing units (GPUs), and field-programmable gate arrays (FPGAs) [4], which can be easily adapted to new network architectures. However, to train and execute a CNN, millions of parameters must be taken into consideration, making the construction of neural networks expensive. Several hardware techniques have been developed for accelerating such machine-learning algorithms. In recent years, neural-network accelerator design has been a topic of enormous interest in the computer architecture industry.
A systolic-array is a homogeneous grid of processing elements (PEs), which are small processors, with each element connected only to its neighbors [5]. During its operation, a PE reads data from its neighbors, computes a simple multiplication function, and stores the result in its local memory. Recently, Google developed a Tensor Processing Unit (TPU) that uses a 256 × 256 systolic-array of multiply and accumulate (MAC) units at its core and provides 30–80 times higher performance than CPU- or GPU-based servers [6].
However, if faults occur in some PEs, such as manufacturing problems, this computing architecture in the form of a systolic-array can yield erroneous results. Although neural-network application has a fault-tolerance capability, reliability issues still exist, because a single hardware fault affects all operations of the neural-network application. Besides, post-manufacturing failures may cause the additional erroneous results during the normal operation. Therefore, there is a need for an architecture that can guarantee the reliability of the systolic-array architecture. In this point of view, the proposed idea is the best fit for the CNN applications for high reliability. For example, machine learning solutions in the automotive vehicle industry needs high reliability in sensor fusion, mapping, and path planning [7,8,9].
In general, if a single core has faults, it can be replaced by a redundant core. However, in the conventional multicore CPU architecture, designing a redundancy core is considered inefficient, because each redundant CPU has a very large area overhead. However, application-specific accelerator processors, such as neural-network accelerators, are composed of at least several hundreds to tens of thousands of cores. Owing to this structural characteristic, it can be expected that design of the redundancy of the systolic MAC array incurs a reasonable area overhead compared with the design of the redundancy of the multicore CPU architecture.
The redundancy architecture of the systolic MAC array is configured differently from general redundancy structures, such as through-silicon via (TSV) redundancy and input/output (IO) redundancy structures. In the case of TSV and IO redundancy, rerouting to the redundancy is relatively easy because the signal is connected between only one input and one output. However, in the systolic-array architecture, as there are a large number of connections from one MAC core to other adjacent MAC cores, various routing possibilities should be considered for obtaining the correct calculation results after repair.
In this research, an efficient redundancy architecture for a systolic MAC array is proposed. The proposed method involves offline repair, which is conducted during a manufacturing test by using the additional redundant MACs. Online repair is also performed by using the remaining redundant MACs that are not used in the offline repair. In order to utilize the repair information in the offline repair process, programmable fuses, which are widely used in the memory repair, are adopted in the proposed method. Unlike the previous works, the offline repair process focuses not only the reparability, but also the fault tolerance for online repair. By doing so, the proposed method improves the reliability in the offline and online statuses and requires a small area overhead since the additional redundancies can be used for both repairs. The proposed method provides not only the improved yield and reliability but also the cost-effective design while requiring no drastic change in the IC manufacturing stage.
The remainder of this paper is organized as follows. In Section 2, we review the previous work related to the systolic MAC array and its redundancy architecture. Section 3 presents the proposed redundancy architecture and the basic concept of the proposed repair mechanism. Section 4 presents the experimental results indicating the performance of the proposed architecture with regard to the repair rate and hardware overhead. Finally, Section 5 concludes the paper.
2. Previous Works
In this section, the systolic-array architecture and its fault-tolerance schemes, which were previously proposed, are described.
2.1. Systolic-Array Architecture
Because matrix multiplication and convolution operations are independent for each piece of data, the calculations are optimized using parallel processing with as many processors as possible. However, if the number of processors exceeds several thousand, interconnection problems that transfer data from the memory increase rapidly. To solve these problems, a systolic-array structure was introduced in [5], as shown in Figure 1a.
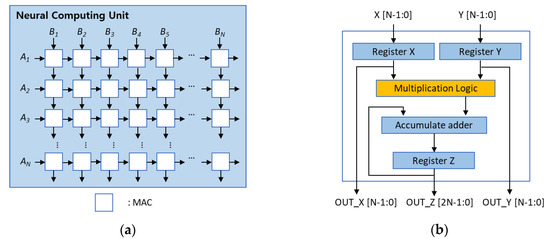
Figure 1.
Neural computing unit structure for calculating matrix multiplication: (a) Systolic-array neural computing unit; (b) Conventional MAC architecture.
In the systolic-array architecture, a MAC unit, which enables MAC functions, is used [10]. The MAC unit performs multiplication and accumulation processes repeatedly to perform continuous and complex operations in digital signal processing. A basic MAC architecture is illustrated in Figure 1b. In neural-network calculations, the convolution-layer operation accounts for most of the computation time. Therefore, by adopting this systolic-array structure, matrix multiplication and convolution calculations can be accelerated.
2.2. Previous Fault Repair Systolic-Array Designs
Fault-tolerant systolic-array designs were proposed by Kung et al. [11] and were later improved [12]. The basic concept of these schemes is considering the array as a small systolic-array when faulty MACs are detected in the array.
Figure 2a shows the redundant MAC architecture for repairing a faulty MAC processor. MAC processors are arranged in a 4 × 4 systolic-array, and redundant MAC processors are placed at the end of each row. These redundant MAC processors can serve as substitutes when a fault occurs in each row. Furthermore, to replace the faulty MAC with the redundant MAC, the signal should be rerouted so that several MUXs are used.
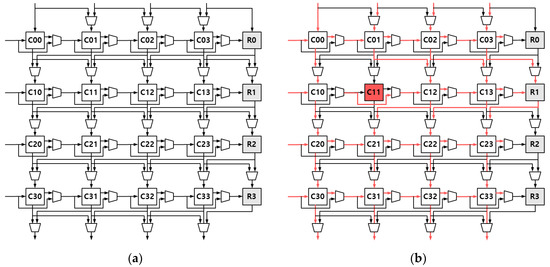
Figure 2.
Previous systolic-array redundant architecture [12]: (a) Overview; (b) Repair example.
An example of a repair process in this redundancy architecture is presented in Figure 2b. According to the characteristics of the systolic-array, if MAC unit C11 has a defect, for normal operation, the role of the faulty core is performed by C12, and the role of C12 is performed by C13. Finally, a redundant core R1 performs the role of C13. Through this process, the repair process is completed in such a manner that the signals to be transmitted to the faulty MAC are shifted to the neighboring MAC and transmitted. Thus, the repair process is completed. Another repair process is proposed in [13]. In this study, the role of the faulty MAC is replaced by the neighboring core which is placed on a diagonal. Basically, switches are located at the intersection point among every four neighboring cores. By utilizing switches, the faulty MAC can be bypassed in either horizontal or vertical ways and shifted by its neighboring core.
Recently, Zhang et al. proposed a fault-tolerant systolic-array design considering the impact of hardware faults in the application domain [14]. The method reduced the effect of the faulty MAC by calculating the weight in the CNN corresponding to the faulty MAC as zero. Although this method reduces the effect of hardware faults without additional redundant MACs, reliability issues still exist, because the systolic-array is comprised of the faulty MACs.
3. Proposed Redundancy Architecture
In this section, the proposed systolic-array redundancy architecture is described. The proposed method has two main features: the “redundancy architecture” and “online error repair.”
3.1. Systolic-Array Redundancy Architecture
The previous redundancy architecture can repair all faulty MACs when only one faulty MAC occurs in each row. This means that faulty MACs cannot be repaired when two or more faulty MACs are exist in a row. Therefore, an extended redundancy architecture is considered in which configuring redundancies at the end of the row and column of the array as shown in Figure 3a. This redundancy architecture can repair faults for various patterns when a large number of MACs fail. The proposed method repairs faulty MACs by using the shift-based repair mechanism which is commonly used for its simple implementation. Figure 3b shows an example in which three faulty MACs are concentrated in an area. In this example, there are two faulty MACs in the 2nd row and the 3rd column. Nevertheless, the redundant MAC architecture structure can repair this faulty pattern with more additional hardware overhead.
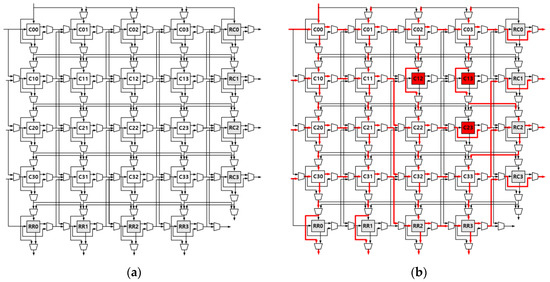
Figure 3.
Redundancies in both rows and columns: (a) Overall architecture; (b) Repair example.
3.2. Redundancy Configuration by Partitioning the Entire Array
In the event of MAC failure, to repair the fault, the signals that should be assigned to the faulty MAC are rerouted to the adjacent MAC, and the signals that should be conveyed to the last MAC in the rows or columns are assigned to the redundant MAC. However, when the number of faulty MACs is high, the redundancy architecture cannot repair the specific faulty MAC patterns. For example, if two or more faults occur in a systolic-array row, one redundant MAC at the end of the row can only repair one faulty MAC. In this case, the remaining unrepaired faulty MACs can be repaired by the redundant MAC located at the end of the column, but if there are other faults in this column, the fault pattern means that the faults cannot be repaired. Therefore, to reduce the probability of these fault patterns occurring, an architecture of configuring redundancies by partitioning a large size systolic-array can be considered. This partitioning architecture, which is called “array partitioning,” is more efficient in terms of repair rate because it can repair more faulty MAC patterns. Increasing the partitioning level means partitioning the entire array into multiple small arrays. For example, if the entire systolic-array size is 128 × 128, setting the partitioning level to 4 will partition the entire array into four 64 × 64 arrays. Similarly, when the partitioning level is set to 16, an entire 128 × 128 array will be partitioned into 16 arrays with a size of 32 × 32. In this paper, the parameter PL (partitioning level) which indicates the number of parts the entire array will be partitioned into is used. Let NROW and NCOL are the number of rows and columns of the systolic-array, respectively. Then, if the PL is set to 4, it means that the entire NROW × NCOL size array is divided into four NROW/2 × NCOL/2 size arrays.
An advantage of the “array partitioning” feature of the proposed method is that it increases the repair rate by increasing PL; however, excessive partitioning of the entire array can increase the redundancies and possibly cause a timing problem due to the redundancy configuration. Therefore, it is important to determine the appropriate PL.
3.3. One Redundancy per Multiple Rows and Columns
A straightforward redundancy architecture for repairing faults in systolic-array partitions involves placing redundancies at the end of every row and column. However, this architecture is inefficient in terms of area overhead unless the probability of a fault occurring in the systolic-array is high. Therefore, to design a more efficient redundancy architecture in terms of area overhead, an architecture whereby a redundancy is placed per two or more rows and columns can be considered. We set the parameters “One redundancy per multiple Rows Level (ORL)” and “One redundancy per multiple Columns Level (OCL)”. If the ORL is set to 2 and the OCL is set to 4, it means one redundancy is placed in two rows and four columns. In addition, when applying the same value to ORL and OCL, use the parameter OL. For example, if OL is set to 4, ORL and OCL have the same value 4.
Figure 4a shows the proposed architecture with OL 2. Redundancy MAC RC0 can repair any one faulty MAC occurring in the first row and the second row. That is, if a faulty core is detected in the first systolic-array row, RC0 should act as the last core of the first row, and if a faulty core is detected in the second systolic row, RC0 should act as the last core in the second row. This extension architecture can reduce the total additional hardware overhead because it can reduce the number of redundant MACs. Similarly, Figure 4b shows the case where OL is 4.
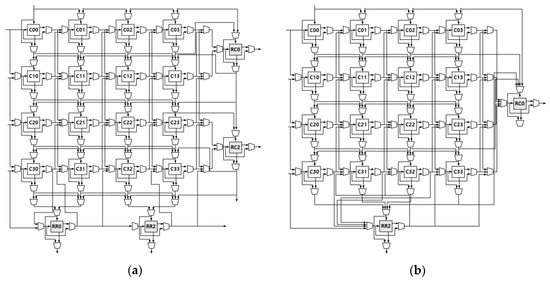
Figure 4.
Proposed redundancy architecture: (a) OL 2; (b) OL 4.
Based on this extension, it is also possible to extend the architecture of one redundant core per three or more rows and columns. However, if three or more rows and columns have only one redundant MAC, this redundancy architecture can be configured with less hardware overhead, but the repair rate will decrease; furthermore, a timing problem may occur because the distance between the redundancy and MAC will increase.
3.4. Repair Strategy for Offline/Online Repair
Typically, redundancies that are not used in offline repair are wasted. However, in the proposed method, the remaining redundancies are used to repair faults during normal operation. If at least one redundant MAC remains unused, the online repair process can be performed. Typically, programmable fuses are used to repair faulty memory cells by programming the address fuses of the spare decoder [15]. In order to utilize the unused redundant MACs, programmable fuses are adopted to enable the online repair process to repair additional erroneous MACs during the normal operation.
Basically, the online repair process is progressed with unused redundant MACs after the offline repair process. It means that if an error occurs in the MAC which cannot be covered by the remaining redundancies, it is impossible to repair the erroneous MAC with the proposed method. Therefore, it is best to leave unused redundant MACs as efficiently as possible during the offline repair process. This does not mean that the number of unused redundant MACs should be maximized because the area of repairable MACs in the online repair process is not fully determined by the quantity of unused redundant MACs. Besides, more unused redundant MACs means redundancies are over-assigned in the first place.
Unlike the previous redundancy architecture, the proposed method assigns redundancies to both the end of the row and column of the array. As mentioned in Section 2.2, each redundant MAC is specialized to repair the faulty MAC at the same line. So, several MACs share the same redundant resources depending on the redundancy architecture. Let’s say that those several MACs belong to the same group. Then, each group has the same number of available redundant MACs to use before the offline repair process. As the repair process is progressed, the number of available redundancies of each group is decreased. The basic concept of the proposed repair strategy is spending redundancies first in the group which has the higher number of available redundant MACs. This prevents the specific group from having no available redundancy even though there is another option to utilize resources of other groups.
The example of the proposed repair strategy is depicted in Figure 5. In this example, there are two faulty MACs, C13 and C33, into a 4 × 4 MAC array as shown in Figure 5a. There are four groups in the MAC array and each group has two available redundant MACs. For example, Group 1 consists of MAC C00, C01, C10, and C11. If a fault occurs in Group 1, redundant MACs, RC0 and RR0, can be utilized. Therefore Group 1 has one available row redundant MAC and one column redundant MAC. Figure 5b depicts the number of available redundant MACs of each group. In this example, C13 and C33 can be repaired by utilizing {RC0, RC2} or {RC0, RR2}. However, choosing {RC0, RR2} as a solution makes Group 2 has no available redundancy in the online repair process. On the other hand, choosing {RC0, RC2} as a solution makes all groups have at least one available redundant MAC in the online repair process as shown in Figure 5d. This repair strategy secures more flexibility in the online repair process.
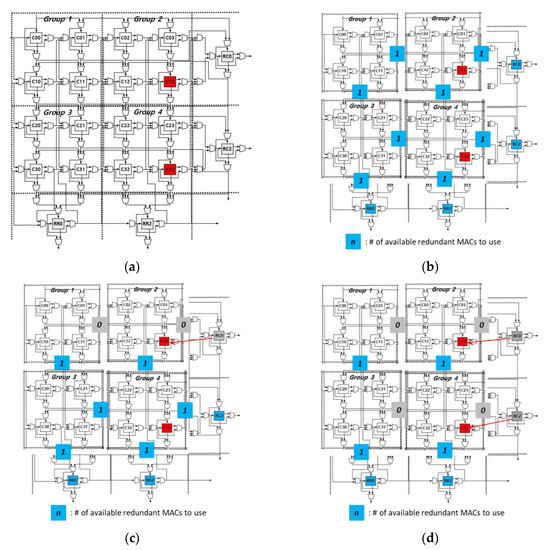
Figure 5.
Example of the proposed repair strategy: (a) Faulty systolic-array example; (b) Visualization of the number of available redundant MACs of each group; (c) Repair decision of C13; (d) Repair decision of C33.
The overall flowchart of the proposed method is shown in Figure 6. First, redundant MACs should be tested before testing normal MACs because only healthy redundant MACs can be utilized in the repair process. And then, the offline test for normal MACs is progressed. When faults are detected in the offline test process, faulty information is collected in the fault list. As get the proper repair solution, the repair decision of the offline repair starts after all the faulty information is collected. Then, the proposed method investigates the number of available redundancies of each group and sorts the numbers in descending order. If there are available redundancies to use, the offline repair process is performed based on the repair strategy. The redundancy list is updated whenever the repair decision is making. If all faulty MACs are repaired, the offline test phase ends. Once the online test phase starts, the first process is to check the available resources through programmable fuses. In the online test phase, repairable MACs are determined by the information of remaining redundant MACs in the redundancy list. Therefore, if an error is detected during the normal operation, the proposed method can instantly find out whether the erroneous MAC is repairable or not. If the group which has the erroneous MAC can utilize two or more redundant MACs, the proposed method seeks the way to avoid the number of available redundant MACs of each group being 0. This decision making process can be easily performed with the simple binary search tree. Then, online repair step is repeatedly performed until there is no remaining redundancy left.
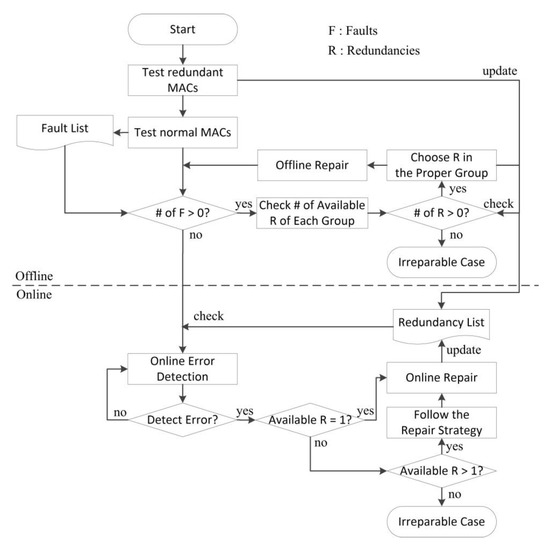
Figure 6.
Flowchart of the proposed method.
3.5. Efficient Redundancy Configuration
To efficiently perform the convolution operation, it is effective to set the systolic-array to 128 × 128 or more. Therefore, a strategy for a systolic-array with a size of 128 × 128 or more should also be configured to construct redundancy. While it is possible to simply place redundancies all the way to the right and to the bottom side of the entire array, this is not an efficient solution in terms of repair rate and hardware overhead.
As mentioned in Section 3.2 and Section 3.3, the proposed architecture can reduce the hardware overhead and can increase the repair rate when multiple faulty MACs are detected. Therefore, the redundancy architecture that can be applied as efficiently as possible in terms of hardware overhead and repair rate with a systolic-array size, can be effectively applied in real neural network operations.
4. Simulation Results
4.1. Simulation Environment
To evaluate the performance of the proposed architecture, hardware overheads, and repair rates induced by the redundancy configuration were calculated and compared with those obtained by changing the parameter of the proposed architecture. For example, Figure 7 shows the redundancy architecture with PL 4 and OL 2. We experimented with large size of systolic-arrays such as 128 × 128, 256 × 256, and 512 × 512. Then, experiments were performed while varying the parameters, PL and OL, for each array size. These experiments were performed in a 3 GHz Linux environment with 256 GB memory.
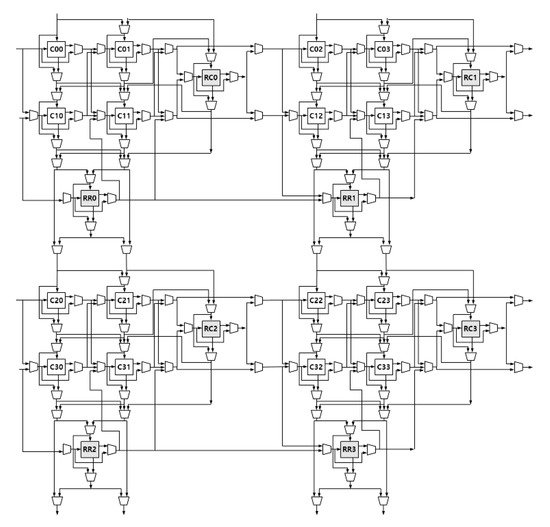
Figure 7.
Proposed redundancy architecture with PL: 4 and OL: 2.
4.2. Repair Rates
To evaluate the repair performance of the redundancy architectures, numerous random fault patterns were introduced into the NROW × NCOL systolic-array MAC architectures. These faulty MACs can be repaired using the redundant MACs that are located at the right and bottom sides. If all faulty MACs are repaired successfully after the repair process, this fault pattern is classified as a “repairable case.” On the other hand, if one or more faulty MACs cannot be repaired, this case is classified as an “irreparable case.” The repair rates are represented as follows:
To investigate the effect of the PL and OL on repair rate, repair rates were measured while increasing PL and OL. In this experiment, the number of fault patterns was randomly generated 100,000 times.
First, the repair rate was measured while PL was increased when OL was fixed to 1. In this case, increasing PL while maintaining OL increases the number of redundancies and also the number of repairable faults. Therefore, as the PL increases, a higher repair rate can be achieved as shown in Figure 8a. In contrast, when the PL was fixed, the repair rate was measured while increasing the OL. The result is shown in Figure 8b. Increasing OL means decrease of the number of redundancies and the repair rate drops. As shown in Figure 8, the increase of PL means the increase in redundancy, which means an improvement in the repair rate. Similarly, the increase of OL causes the decrease of the repair rate because it reduces the number of redundancies. Changing PL and OL is related to changing the number of redundancies and thus a change in the repair rate can be expected. Therefore, to proceed with the experiments with the same number of redundant MACs, experiments were conducted under a given number of PL and OL conditions to equalize the number of redundant MACs. For example, assuming a systolic-array of N × N, the number of redundancies when the proposed architecture is not applied is 2N, where N is placed on the right side and N is placed on the bottom side. Under these conditions, a fourfold increase in the PL will double the number of redundancies, and a doubling of the OL reduces the number of redundancies by half. Therefore, to have the same number of redundancies, which is 2N, when an N × N systolic-array is set, the repair rate was measured with the PL and OL as (1,1), (4,2), (16,4), (64,8), and (256,16), respectively. The results are shown in Figure 9. As can be seen from the results of this experiment, the repair rate is the highest in OL 2 condition. When OL is increased to 2 or more, the effect of reducing repair rate due to the increase of OL, becomes more dominant than the effect of increasing repair rate due to the increase of PL. There is one more important thing in these results. As mentioned in Section 3, the number of used redundant MACs in the offline repair process and the number of the faulty MACs are the same if the faulty systolic-array is repairable. Before the offline repair process, there are 256 redundant MACs in Figure 9a and 512 redundant MACs in Figure 9b. As can be seen from the graphs, the number of unused redundant MACs is much larger than the number of used redundant MACs even in the situations which have low repair rate. These results prove the need for the online repair process with unused redundant MACs.
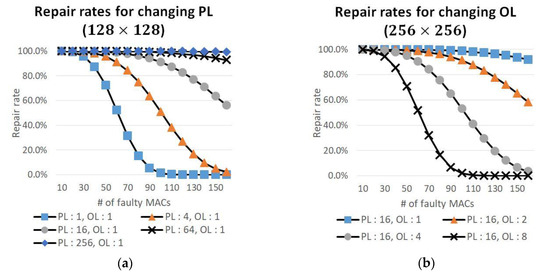
Figure 8.
Repair rate comparison with various PLs and OLs: (a) Fix OL, change PL; (b) Fix PL, change OL.
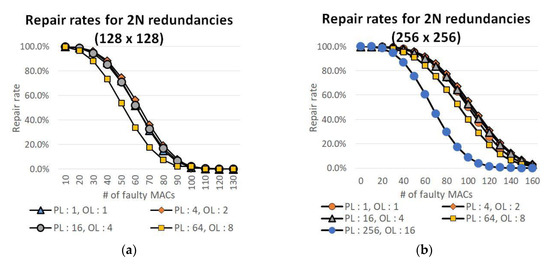
Figure 9.
Repair rate comparison with 2N redundancies: (a) 128 × 128; (b) 256 × 256.
For comparison with the previous architecture [12], the experiments with the number of redundancies is set to N are conducted. Since the previous architecture places redundancy only on its right side, the number of redundancies in this architecture of N × N is determined as N. As can be seen in Table 1, even with the same number of redundancies, the redundancy architecture where redundancies on the right and bottom side has a much higher repair rate than that of the previous architecture under the condition that N is 128, 256, and 512. In addition, it can be seen that, even in this case, as PL and OL increase, the repair rate decreases slightly even if the number of redundancies is the same.

Table 1.
Repair rates comparison with the previous architecture (unit: %).
Finally, repair rates of the online repair process with various redundancy architectures are shown in Figure 10. In this experiment, the data from Figure 9b is utilized. It is assumed that 40 faulty MACs are already repaired in the offline repair process. In order to evaluate the performance of the online repair process, the concept of the error rate is defined as follows. An error rate of a single MAC is the probability that an error occurs in a MAC during the normal operation. Similar to the results of the offline repair process, redundancy architectures, which have high repair rates in the offline repair process, also show good results in the online repair process. In conclusion, the proposed method shows much more improved repair rates compared to the previous work. However, it is necessary to assign the proper value of PL and OL considering the number of faults, the error rate, and overall hardware overhead.
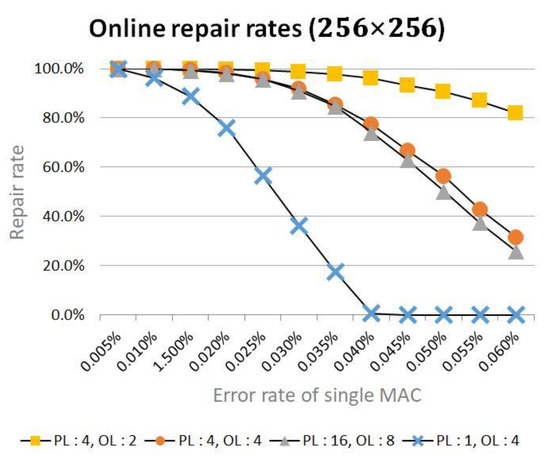
Figure 10.
Online repair rate comparison with various PLs and OLs.
4.3. Hardware Overhead
To calculate the hardware overhead of the redundancy architectures, we employed the synthesis tool Synopsys Design Vision [16] and the Synopsys Armenia Educational Department (SAED) 32/28 nm Open Cell Library [17] technology parameters. The additional hardware consists of MUXs that allow signals to be sent to adjacent MACs to reroute the signal and redundant MACs. In this experiment, the additional area overheads were measured by changing PL and OL in a systolic-array having a large size of 128 × 128 or more.
Figure 11 shows the ratio of the additional hardware size caused by the redundant configuration for the systolic-array compared to the structure without the redundancy. Increasing OL to 1, 2, 4, and 8 in the same PL condition will inevitably lead to hardware reduction because the number of redundant MACs is reduced. Conversely, when OL is fixed and PL is increased, as shown in Figure 12, the area overhead becomes larger because the redundancies are further allocated for each divided systolic-array partition. In addition, we measured the area overhead while adjusting OL and PL for the area comparison under the conditions of the same number of redundancies. As shown in Figure 13, when the number of redundancies is the same, it can be seen that even if PL and OL change, the overall area overhead is similar. However, owing to an increase in OL, the overall area overhead slightly increased because of the addition of a large size MUX for routing in multiple rows and columns. Although 8.9%, 5.8%, and 3.0% hardware overheads are consumed in 8-bit, 16-bit, and 32-bit, respectively, compared to the previous architecture, high repair rates can be achieved through the proposed architecture.
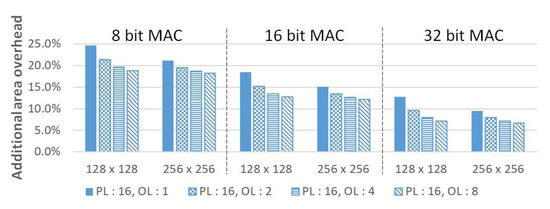
Figure 11.
Hardware overhead comparison for various OLs.
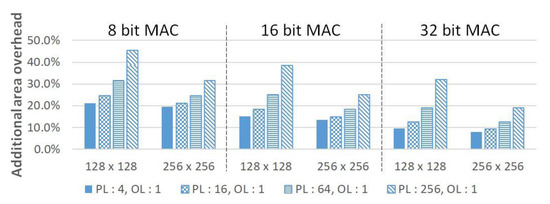
Figure 12.
Hardware overhead comparison for various PLs.
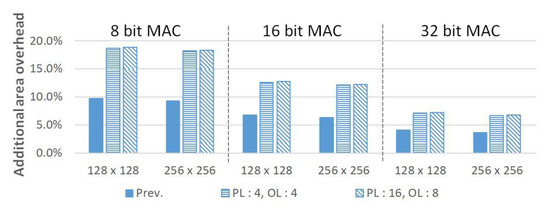
Figure 13.
Hardware overhead comparison under the same number of redundancies condition.
5. Conclusions
To ensure the reliability of the systolic-array architecture, which is widely used in neural-network computing, a new efficient redundancy architecture is proposed. The proposed architecture can repair a larger number of faults than the previous redundancy architecture, with reasonable hardware overhead. Moreover, unused redundant MACs are utilized in the online repair process through programmable fuses. For maximizing the efficiency of the online repair process, group-based repair strategy is adopted in the entire repair process. This provides maximum redundancies utilization by minimizing hardware overhead waste.
Author Contributions
Conceptualization, K.C. and I.L.; methodology, K.C. and I.L.; software, K.C. and I.L.; validation, K.C., I.L., and H.L.; formal analysis, I.L.; investigation, K.C. and H.L.; resources, K.C.; data curation, K.C.; writing—original draft preparation, K.C. and I.L.; writing—review and editing, K.C. and S.K.; visualization, K.C. and I.L.; supervision, S.K.; project administration, S.K.; funding acquisition, S.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Samsung Electronics Company, Ltd., Hwaseong, Korea.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Stateline, NV, USA, 3–8 December 2012; pp. 1097–1105. [Google Scholar]
- Karpathy, A.; Toderici, G.; Shetty, S.; Leung, T.; Sukthankar, R.; Fei, L.F. Large-scale video classification with convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 24–27 June 2014; pp. 1725–1732. [Google Scholar]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 8–13 December 2014; pp. 3104–3112. [Google Scholar]
- Ma, Y.; Suda, N.; Cao, Y.; Seo, J.S.; Vrudhula, S. Scalable and modularized rtl compilation of convolutional neural networks onto fpga. In Proceedings of the Field Programmable Logic and Applications (FPL) 26th International Conference, Lausanne, Switzerland, 29 August–2 September 2016; pp. 1–8. [Google Scholar]
- Kung, H.T. Why systolic architectures? IEEE Comput. 1982, 15, 37–46. [Google Scholar] [CrossRef]
- Jouppi, N.P.; Young, C.; Patil, N.; Patterson, D.; Agrawal, G.; Bajwa, R.; Bates, S.; Bhatia, S.; Boden, N.; Borchers, A.; et al. In-datacenter performance analysis of a tensor processing unit. In Proceedings of the 44th Annual International Symposium on Computer Architecture, ISCA ’17, Toronto, ON, Canada, 26 June 2017; pp. 1–12. [Google Scholar]
- Paine, S.W.; Fienup, J.R. Machine learning for improved image-based wavefront sensing. Opt. Lett. 2018, 43, 1235–1238. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Ko, J.; Davis, C.C. Lossy wavefront sensing and correction of distorted laser beams. Appl. Opt. 2020, 59, 817–824. [Google Scholar] [CrossRef]
- Liu, S.; Tang, J.; Wang, C.; Wang, Q.; Gaudiot, J.L. A unified cloud platform for autonomous driving. Computer 2017, 50, 42–49. [Google Scholar] [CrossRef]
- Hoang, T.T.; Själander, M.; Edefors, P.L. A High-Speed, Energy-Efficient Two-Cycle Multiply-Accumulate (MAC) Architecture and Its Application to a Double-Throughput MAC Unit. Circuits Syst. I Regul. Pap. IEEE Trans. 2010, 57, 3073–3081. [Google Scholar] [CrossRef]
- Kung, H.T.; Lam, M.S. Fault-tolerance and two-level pipelining in vlsi systolic arrays. Tech. Rep. Carnegie Mellon UNIV 1983. [Google Scholar] [CrossRef]
- Kim, J.H.; Reddy, S.M. On the design of fault-tolerant two-dimensional systolic arrays for yield enhancement. IEEE Trans. Comput. 1989, 38, 515–525. [Google Scholar] [CrossRef]
- Takanami, I.; Horita, T.; Akiba, M.; Terauchi, M.; Kanno, T. A built-in self-repair circuit for restructuring mesh-connected processor arrays by direct spare replacement. In Transactions on Computational Science XXVII, LNCS 9570; Springer: Berlin/Heidelberg, Germany, 2016; pp. 97–119. [Google Scholar]
- Zhang, J.; Gu, T.; Basu, K.; Garg, S. Analyzing and mitigating the impact of permanent faults on a systolic array based neural network accelerator. In Proceedings of the IEEE VLSI Test Symposium, San Francisco, CA, USA, 22–25 April 2018; pp. 1–6. [Google Scholar]
- Lee, C.; Kang, W.; Cho, D.; Kang, S. A new fuse architecture and a new post-share redundancy scheme for yield enhancement in 3-d-stacked memories. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2014, 33, 786–797. [Google Scholar]
- Synopsys Design Vision, Synopsys, Mountain View, CA, USA. Available online: https://www.synopsys.com/content/dam/synopsys/implementation&signoff/datasheets/design-compiler-nxt-ds.pdf (accessed on 14 February 2020).
- The Synopsys Armenia Educational Department (SAED) 32/28nm Open Cell Library, Synopsys, Mountain View, CA, USA. Available online: https://www.synopsys.com/community/university-program/teaching-resources.html (accessed on 14 February 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).