Analytical Current-Voltage Model for Gate-All-Around Transistor with Poly-Crystalline Silicon Channel
Abstract
:1. Introduction
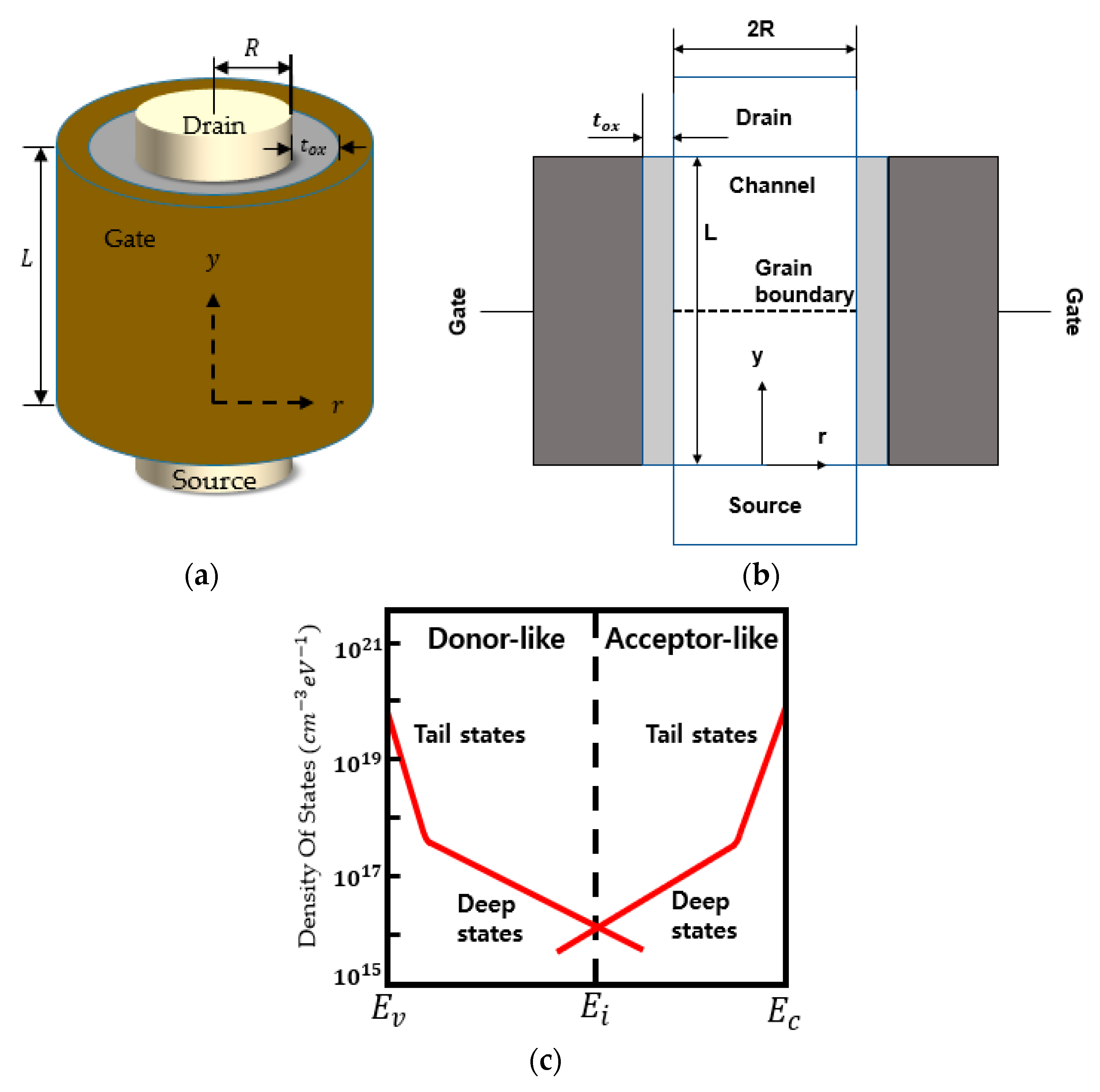
2. Analytical Drain Current Model for GAA Transistor with Poly-Crystalline Silicon Channel
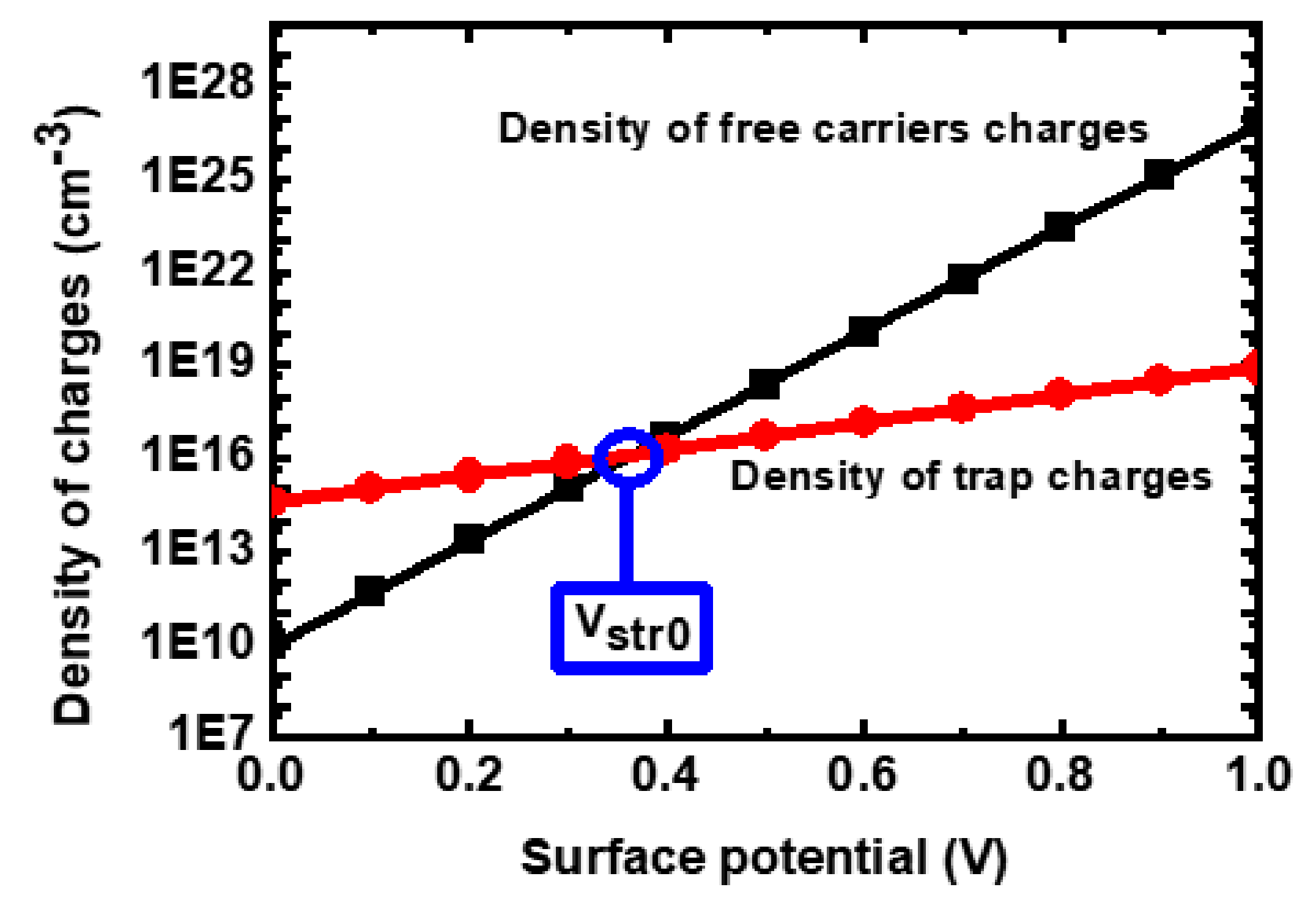
2.1. Electrostatic Potential Modeling
2.2. Drain Current Modeling
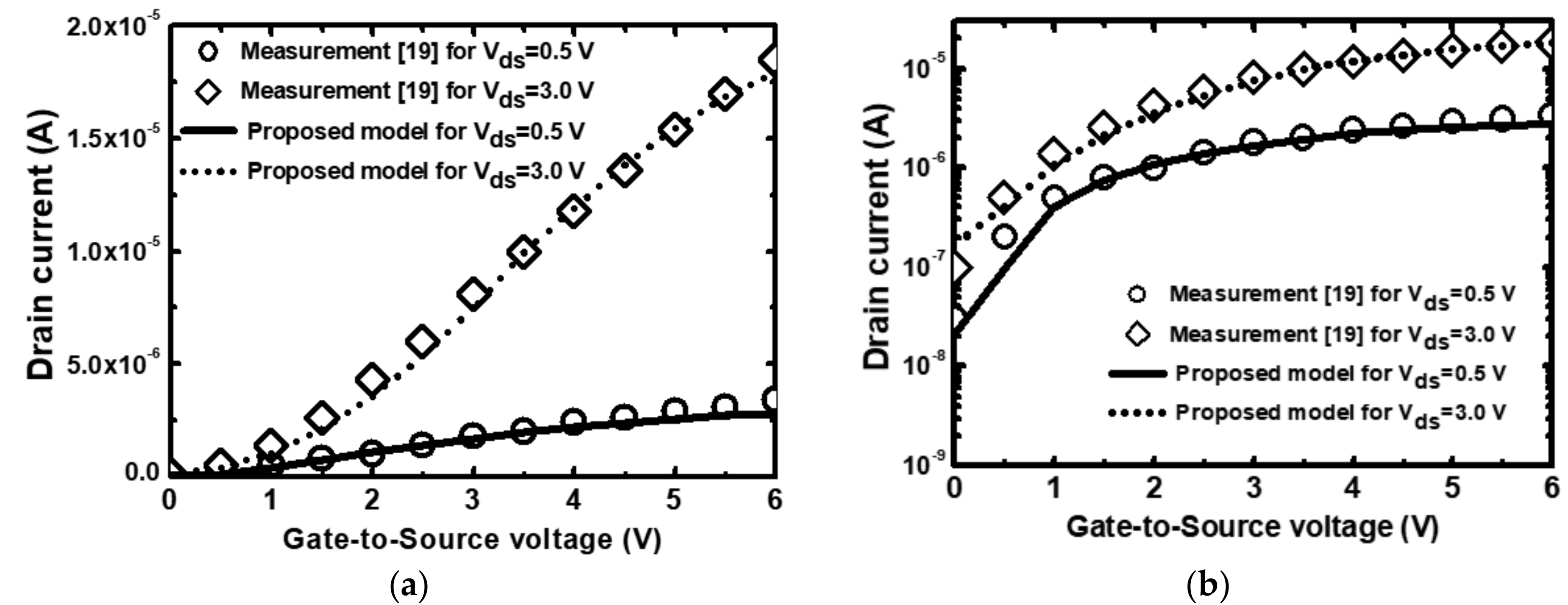
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- El Hamid, H.A.; Iñíguez, B.; Guitart, J.R. Analytical model of the threshold voltage and subthreshold swing of undoped cylindrical gate-all-around-based MOSFETs. IEEE Trans. Electron Devices 2007, 54, 572–579. [Google Scholar] [CrossRef]
- Chen, Y.; Luo, J. A comparative study of double-gate and surrounding gate MOSFETs in strong inversion and accumulation using an analytical model. Integration 2001, 1, 6. [Google Scholar]
- Fortunato, G. Polycrystalline silicon thin-film transistors: A continuous evolving technology. Thin Solid Film. 1997, 296, 82–90. [Google Scholar] [CrossRef]
- Nowak, E.; Kim, J.H.; Kwon, H.; Sim, J.S.; Lim, S.H.; Lee, K.H.; Park, Y.K.; Choi, J.H.; Chung, C. Intrinsic fluctuations in vertical NAND flash memories. In Proceedings of the 2012 Symposium on VLSI Technology (VLSIT), Honolulu, HI, USA, 12–14 June 2012; pp. 21–22. [Google Scholar]
- Yu, B.; Lu, H.; Liu, M.; Taur, Y. Explicit continuous models for double-gate and surrounding-gate MOSFETs. IEEE Trans. Electron Devices 2007, 54, 2715–2722. [Google Scholar]
- Yu, B.; Lu, W.Y.; Lu, H.; Taur, Y. Analytic charge model for surrounding-gate MOSFETs. IEEE Trans. Electron Devices 2007, 54, 492–496. [Google Scholar] [CrossRef]
- Lu, H.; Yu, B.; Taur, Y. A unified charge model for symmetric double-gate and surrounding-gate MOSFETs. Solid State Electron. 2008, 52, 67–72. [Google Scholar] [CrossRef]
- Li, X.; Deng, W.; Huang, J. A physical surface-potential-based drain current model for polysilicon thin-film transistors. J. Semicond. 2012, 33, 034005. [Google Scholar] [CrossRef]
- Deng, W.; Zheng, X.; Chen, R.; Liu, Y. Subthreshold characteristics of polysilicon TFTs. Solid State Electron. 2008, 52, 695–703. [Google Scholar] [CrossRef]
- Chen, S.S.; Shone, F.C.; Kuo, J.B. A closed-form inversion-type polysilicon thin-film transistor dc/ac model considering the kink effect. J. Appl. Phys. 1995, 77, 1776–1784. [Google Scholar] [CrossRef]
- Yu, F.; Deng, W.; Huang, J.; Ma, X.; Chen, S. An Explicit Physics-Based I-V Model for Surrounding-Gate Polysilicon Transistors. IEEE Trans. Electron Devices 2016, 63, 1059–1065. [Google Scholar] [CrossRef]
- Jiménez, D.; Iniguez, B.; Suñe, J.; Marsal, L.F.; Pallares, J.; Roig, J.; Flores, D. Continuous analytic IV model for surrounding-gate MOSFETs. IEEE Electron Device Lett. 2004, 25, 571–573. [Google Scholar] [CrossRef]
- Shur, M.; Hack, M. Physics of amorphous silicon based alloy field-effect transistors. J. Appl. Phys. 1984, 55, 3831–3842. [Google Scholar] [CrossRef]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.; Jeffrey, D.J.; Knuth, D.E. On the Lambert W function. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
- Deng, W.; Huang, J. A physics-based approximation for the polysilicon thin-film transistor surface potential. IEEE Electron Device Lett. 2011, 32, 647–649. [Google Scholar] [CrossRef]
- Wang, M.; Wong, M.; Shi, X.; Zhang, D. Effective channel mobility of poly-silicon thin film transistors. In Proceedings of the 2006 8th International Conference on Solid-State and Integrated Circuit Technology Proceedings, Shanghai, China, 23–26 October 2006; pp. 1395–1397. [Google Scholar]
- Chern, H.N.; Lee, C.L.; Lei, T.F. An analytical model for the above-threshold characteristics of polysilicon thin-film transistors. IEEE Trans. Electron Devices 1995, 42, 1240–1246. [Google Scholar] [CrossRef]
- Xi, X. BSIM 4.5. 0 MOSFET Model User Manual. 2004; University of California: Berkeley, CA, USA, 2004. [Google Scholar]
- Sheu, J.T.; Huang, P.C.; Sheu, T.S.; Chen, C.C.; Chen, L.A. Characteristics of gate-all-around twin poly-Si nanowire thin-film transistors. IEEE Electron Device Lett. 2008, 30, 139–141. [Google Scholar] [CrossRef]


| Symbol (units) | Value | Symbol (units) | Value |
|---|---|---|---|
| 0.002 | |||
| 2 | |||
| 0.1 | 0.01 | ||
| 1 | |||
| 0.001 | |||
| 3 | |||
| 0 | 0.01 | ||
| 50 | 1 | ||
| 0.5 | 20 | ||
| 3 | 10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seon, Y.; Kim, J.; Kim, S.; Jeon, J. Analytical Current-Voltage Model for Gate-All-Around Transistor with Poly-Crystalline Silicon Channel. Electronics 2019, 8, 988. https://doi.org/10.3390/electronics8090988
Seon Y, Kim J, Kim S, Jeon J. Analytical Current-Voltage Model for Gate-All-Around Transistor with Poly-Crystalline Silicon Channel. Electronics. 2019; 8(9):988. https://doi.org/10.3390/electronics8090988
Chicago/Turabian StyleSeon, Yoongeun, Jongmin Kim, Soowon Kim, and Jongwook Jeon. 2019. "Analytical Current-Voltage Model for Gate-All-Around Transistor with Poly-Crystalline Silicon Channel" Electronics 8, no. 9: 988. https://doi.org/10.3390/electronics8090988
APA StyleSeon, Y., Kim, J., Kim, S., & Jeon, J. (2019). Analytical Current-Voltage Model for Gate-All-Around Transistor with Poly-Crystalline Silicon Channel. Electronics, 8(9), 988. https://doi.org/10.3390/electronics8090988




