Abstract
An important issue in cloud computing is the balanced flow of big data centers, which usually transfer huge amounts of data. Thus, it is crucial to achieve dynamic, load-balanced data flow distributions that can take into account the possible change of states in the network. A number of scheduling techniques for achieving load balancing have therefore been proposed. To the best of my knowledge, there is no tool that can be used independently for different algorithms, in order to model the proposed system (network topology, linking and scheduling algorithm) and use its own probability-based parameters to test it for good balancing and scheduling performance. In this paper, a new, Probabilistic Model (ProMo) for data flows is proposed, which can be used independently with a number of techniques to test the most important parameters that determine good load balancing and scheduling performance in the network. In this work, ProMo is only used for testing with two well-known dynamic data flow scheduling schemes, and the experimental results verify the fact that it is indeed suitable for testing the performance of load-balanced scheduling algorithms.
1. Introduction
One of the main challenges in today’s networking is the efficient data flow scheduling among the numerous servers that constitute a data center. The synchronous big data networks [1,2,3] typically transfer vast data amounts from machine to machine, so a load-balanced transferring scheme is necessary to implement these transfers as efficiently as possible [4,5,6,7]. Dynamic load-balanced scheduling is the task of distributing as evenly as possible the traffic within a network (or among its links), while keeping in mind the overall network state at a time, or, at least, at specified time intervals. Recently, the trend in scheduling load-balanced data flows is to use software-defined networking schemes, and OpenFlow is such an example [8,9,10], where the load-balanced flow control is programmable.
While scheduling the flows, it is important to take into consideration the dynamic network changes; in other words, it is important to consider the state of the network. This is due to the fact that while new data flows keep arriving at different (or even similar) rates between data servers, some links may collapse and become unavailable for some time [11], meaning that some data flows may need to be re-transmitted to a different server or servers, thus changing the amount of load being stored and processed by each machine. Thus, the workload distributed fluctuates, and this necessitates a time- or period-based scheduling [12]. In this regard, the static flow scheduling approaches become rather unsuitable for big data flows. During each period, the current workload and the link state are considered, and new scheduling decisions may or may not be taken.
The problem of scheduling big data flows on a distributed-resource environment is an NP hard problem, and heuristics are employed. Most of the strategies developed aim at: (1) maximizing the network throughput while keeping the scheduling overheads reduced and (2) balancing the data loads communicated through the network. In this work, a probabilistic model of dynamic load-balanced data flows is developed. The main contributions of this work are the following:
- The proposed model can be used independently with existing scheduling strategies for testing;
- The proposed model is simple, so its use does not add any overheads to a scheduling scheme;
- The model can be the basis for the development of a complete simulator of data flow scheduling algorithms, which will be used for testing different algorithms, topologies, and network parameters;
- The model can also become the basis for the development of a new scheduling strategy;
- It is a time interval-based model, so it is particularly useful in testing dynamic scheduling algorithms.
The remainder of this work is organized as follows: Section 2 presents the most important of the related papers, focusing on dynamic algorithms. Section 3 initially presents some preliminaries for the dynamic load-balanced scheduling of data flows in cloud systems, and then, it describes in detail the probabilistic model. In Section 4, experimental results are presented, to show that the model indeed fits existing scheduling algorithms. Section 5 concludes the paper and offers aspects for future work.
2. Related Work
Recently, the problem of flow scheduling has attracted considerable attention. The techniques available are mainly classified as static and dynamic. Unlike the dynamic approaches, the static ones schedule the flows based on their known characteristics, but scheduling cannot adapt to any change that may occur in the network. In this section, we will mainly focus our attention on dynamic strategies.
An interesting static approach was presented by Rodriguez et al. [13], who developed the Particle Swarm Optimization (PSO). This technique aims to minimize the overall flow execution cost while meeting deadline constraints (deadline based). It was inspired by the social behavior of bird flocks, and it is based on a swarm of communicating particles through space, to find an optimal search direction. A particle is an individual that moves through the defined problem space and represents a candidate solution to the optimization problem. Modeling is performed in two steps: (a) define how the problem is encoded, that is the solution representation, and (b) define the fitness function, that is how good a possible solution is. This function represents the objectives of the scheduling problem. The fitness function is minimized, so that its value represents the total cost of execution. The results obtained have shown improved performance compared to other strategies and, most importantly, that this technique meets the deadlines met by dynamic algorithms, like Scaling-Consolidation-Scheduling (SCS) (a dynamic algorithm designed to schedule groups of flows, not just single ones).
In [9], the authors developed joint static and dynamic traffic scheduling approaches for data center networks. The authors used the observation that traffic in a data center is a mixture of static and rapidly-changing elements (dynamics), so the scheduler combines both of these elements. Network dynamics has been used for solving other important problems like virus spreading and network attacks [14,15]. Another combination of static and dynamic algorithms was presented by Malawski et al. [16]. The authors aimed at maximizing the amount of work completed. This is defined as the number of executed data flows. Furthermore, their schemes try to meet QoS constraints like deadline and budget. The task execution time may vary based on a uniform distribution, and they employed a cost safety margin to avoid generating a schedule that goes over budget. This shows some type of robustness, which the scheme indeed has.
As already stated from the Introduction, the static approaches are not an ideal solution in the big data era. A good number of researchers have developed dynamic strategies. These strategies can be further categorized into two approaches: the ones that use the traditional networking schemes and the ones that use software-defined networking schemes, where the overall network configuration and flow control is programmable. In the remainder of this section, strategies from both categories are presented. In the experimental results, ProMo was used to test two strategies, one from each category. The criteria behind this choice are explained in the Simulation Analysis section.
2.1. Traditional Networking Schemes
A number of interesting heuristics for dynamic data flow scheduling on traditional networks have been developed. Tsai et al. [17] presented a heuristic scheme called the Hyper-Heuristic Scheduling Algorithm (HHSA), which implements scheduling solutions for cloud computing systems. The proposed algorithm uses certain operators for diversity detection and improvement, to determine the appropriate heuristic dynamically in the search for better candidate solutions. By experimenting on CloudSim and Hadoop, the authors showed that the HHSA scheme reduces significantly the makespan of scheduling. Neely et al. [18] considered the problem where multiple devices make repeated decisions based on the events they observe. The strategy is time interval based, and the events observed determine the values of a utility function and a set of penalty functions. The proposed strategy aims at making decisions at time intervals, such that the utility function is maximized subject to the time constraints imposed by the penalties. Another interesting dynamic approach is the Dynamic Randomized load-Balancing (DRB), suggested by Wang et al. [19]. The aim was to achieve network-wide low levels of path collisions through local-link adjustment, which is free of communications and cooperations between switches. First, a path selection scheme was used to allocate default paths to all source-destination pairs in a fat-tree network, and then, a Threshold-based Two-Choice (TTC) randomized technique was proposed to balance the traffic. Their simulation results showed that DRB in cooperation with the TTC technique achieved significant improvement against other randomized routing schemes scheduled for fat-tree networks. A fat-tree is a network topology where branches near the top of the hierarchy are “fatter” (or thicker) compared to the branches further down the hierarchy. The branches represent the data links, and the thickness (bandwidth) of the data links is determined based on the technology-specific use of the network.
2.2. Software-Defined Networking Schemes
A number of researchers have focused on software-oriented data flow scheduling approaches, and the main example is OpenFlow. In OpenFlow, the control plane (decision, dissemination) is separated from the data plane (discovery, data), and this simplifies to a large extent the network management. All the management and control functions (routing, flow identification, QoS, etc.) are taken over by the OpenFlow controller, which has a global view of the network and configures the switches to forward packets on the basis of a specified flow definition [20,21]. With OpenFlow, load-balancing scheduling techniques are programmable and have received considerable attention. In the remainder of this paragraph, some of the important OpenFlow-based works are presented. Tang et al. [8] proposed a Dynamical Load-Balanced Scheduling (DLBS) approach for maximizing the network throughput and balancing the network load. They developed a set of efficient heuristic scheduling algorithms for the two typical OpenFlow network models, which balance data flows at regular time intervals (specifically, on a time-slot basis). Their experiments showed improvement over typical load-balanced scheduling algorithms like round-robin-based schemes, especially when the data flows are characterized by a large imbalance degree.
In [22], the authors addressed the inter-coflow scheduling problem with two different objectives: (a) to decrease the communication time of data-intensive jobs and (b) to achieve guaranteed predictable communication time. They introduced a system named Varys, which enables data-intensive frameworks to use co-flows with the proposed algorithms while the network is highly utilized and starvation is avoided. The simulations showed that the communication stages complete about three times faster. Furthermore, about twice as many co-flows manage to meet their deadlines when Varys is used, compared to other known co-flow management systems. SlickFlow [23] is another approach implemented with OpenFlow, which allows fast failure recovery by combining the source routing with alternative routing information carried in the packet header. The information (primary and alternative) regarding routing is encoded and placed in the packet header. When failures occur, the packets are rerouted towards the alternative routes by the switches, and the controller itself plays no role in this procedure.
Bolla et al. [24] proposed another OpenFlow system called OpenFlow in the Small (OFiS), scheduled to provide a hardware abstraction layer for heterogeneous multi-core systems, in order to meet application-specific requirements. The experimental results showed that OFiS manages to exploit hardware parallelism to a high degree. A more specialized application of OpenFlow was presented by Egilmez et al. [25], who developed a framework for dynamic rerouting of data flows, to enable dynamic QoS in stream scalable coded videos. An OpenFlow v1.1 hardware-based forwarding plane was implemented, and under cooperation with a performance model, it helped choose a suitable mapping with no need to consider implementation.
This work presents ProMo, a probabilistic mathematical model, which can be employed for testing existing schemes, but also, it can become a basis for the development of the network simulator and a new flow-scheduling strategy. Because of its timing characteristics, it can be used in accordance with dynamic flow-scheduling schemes.
3. The ProMo Model for Dynamic Flow-Scheduling
This section describes the details of ProMo. First, some details regarding the three-layer fully populated network are presented, and then, the details of the model are described.
3.1. Three-Layer Fully-Populated Network
A Fully-Populated Network (FPN) topology has a number of switch-layers and a host layer. The switches at the topmost layer are called the core switches; the switches at the second layer are the intermediate switches; and the switches at the third level are the TOR (Top-Of-Rack) switches. An FPN example is shown in Figure 1a. Each TOR switch is directly connected to 4 end hosts. The switch ports can be divided into two classes [19]: up-ports and down-ports. The up-ports are used to connect to switches at a higher layer, while the down-ports are for connections to switches or hosts at a lower layer. This means that the core switches have only down-ports. The up- and down-ports are shown in Figure 1b.
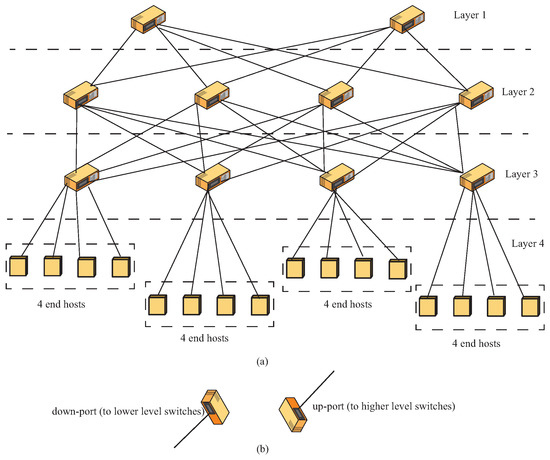
Figure 1.
(a) A three layer fully-populated network, (b) Up and down ports.
3.2. The ProMo Model
The ProMo model is based on the construction of a queuing system. Let represent the three switch layers and represent the end host layer. For the sake of simplicity, let each layer have a single queue of infinite size (or at least, large enough queue). Another assumption necessary for the model is that each layer accepts data flows, and the service times at each layer (the time required to do some processing and forward the flow) are independent and follow the exponential distribution. This independence assumption is necessary, since clouds are most of the time heterogeneous and integrate components from different vendors at different layers. The users are assumed to be an infinite source that produces large data flows that follow the Poisson distribution with rate . In this model, the somehow abstract notion of “data flow” is expressed as the number of jobs, N, submitted by the users over the network [26], and in this sense, can be considered as a function of N (in the following, the terms “jobs” and “data flow” will be used interchangeably). Each layer is considered to have its own service rate (which includes all the necessary processing before forwarding the data). This service rate can be considered as a function of the number of jobs, , being serviced by layer . To link the reader to a broader area of interest, one can conceptually consider this model as related to multiplex opinion networks and the multiplex opinion dynamics model that is probability based [27].
The interconnections between the four layers of the model reflect the actual structure of the FPN. As can be seen from Figure 2, a job enters the system after requests from the users’ community. The job arrival rate is . The jobs enter the first queue and spend some time in the switches of Layer 1. The average service time from Layer 1 is and includes the time required from the time this layer accepts the data flows until these flows are ready for transmission to the next layer. Then, the jobs enter the next layer’s queue, , with probability , which means that there is probability that there is no link collapse and no data corruption, so there is no need for re-transmission. In a similar manner, the communication between Layers 2 and 3 is modeled. Finally, the data arrive to the end hosts. Table 1 summarizes the main parameters required by the ProMo model. Two observations are necessary:

Figure 2.
The interconnections of the Fully-Populated Network (FPN) of Figure 1, as depicted from the Probabilistic Model (ProMo) point of view.

Table 1.
List of parameters required by the Probabilistic Model (ProMo).
- The probability values can be obtained after collecting information regarding the system’s behavior. For example, to obtain the probability of no link collapse, information regarding the total time within a period (for example, one day or some hours) that links work properly is required. Furthermore, to have a probability of data corruption, it is necessary to keep track of how many times the links have received or sent corrupted data out of the total transmission it has taken over.
- The probability values used in the model are the sum of two probabilities per layer (that is, for all the layer links) mentioned in the first observation divided by two (average of the two probabilities).
The state of a network can be modeled using the values of . If a linear vector is used, then the state is described by , where is the sum of all the user jobs at a time. Assume that the system is in state at time t, where . The probabilities (conditional probabilities) that the system transitions to state after time are denoted as:
where is the time required for one change of the system to take place. In the simulation terminology, these small changes are called “events”, and this is the term that will be used from now on. In other words, in the interval , only one event takes place. To determine this event, there are two basic cases:
- A new job arrives, with probability
- A layer completes processing of a job to forward it to another layer, with probability
The two basic cases (C) can by mathematically expressed as follows:
- (C.i)
- No event occurs, that is, :
- (C.ii)
- One new job arrival:
- (C.iii)
- One job completed and transferred from to , or from to , or from to the end nodes:
- (C.iv)
- One job was interrupted due to link collapse or data corruption:
We know that the probability of state at a time is the sum of the products of the probabilities that the system is in state at time t and the probabilities that the system transitions to as a result of an event occurring during the interval , for all the possible states (by , we denote the end node layer):
Now, if the sums of Equation (6) are expanded using Equations (2)–(5):
Equation (7) has eight terms, related to the four cases described in the previous page (C.i–C.iv). The first term of the form corresponds to the case where no events occur (C.i); the second term of the form corresponds to the case of new job arrival (C.ii); the next three terms correspond to the case of a completed job transferred to the next lower layer (C.iii); and the last term corresponds to the case of a job interruption (C.iv). In this last case, one job is subtracted from the lower layer (in case it has been partially transferred or in a corrupted form), and it is added back to the upper layer. The index in every term indicates the time t.
Equation (7) expresses the probability of a transition from a given state at time t to a new state at time , as a function of the mean job arrival rate , of the independent average service times of each layer , of the probabilities of data transfers between layers , that is , and of the probabilities of transfer interruptions between layers , that is . Although Equation (7) has timely characteristics, it has been proven (see Jackson [28]) that there exists a unique and time-independent solution to such an equation. The solution proposed by Jackson is the equilibrium state probability distribution, and it exists if the average arrival rate to each queue in the network is less than the average service rate of that queue. The equilibrium state probability distribution has some very important properties:
Property 1.
Under equilibrium conditions, the average flow leaving the queue will equal the average flow entering the queue. This can be considered as a “per-layer” load balance.
Property 2.
The equilibrium state probability distribution at each layer i is independent of those at the other layers. This means that each layer can be examined independently as an M/M/1 queue with mean arrival rate and mean service rate .
Property 3.
Given the external arrival rates (from the users) to each layer of the FPN network and the routing probabilities from each queue to another (probabilities of normal or interrupted transmission), the job arrival rate to each layer (at equilibrium) can be found by solving the flow balance equations for the network.
Before the solution proposed by Jackson is described for ProMo, it is necessary to define mathematically the relationship between the mean arrival rates per layer and the transition probabilities. According to the model of Figure 2, to find the mean arrival rate per layer, the following considerations are required:
- λ1:
- The mean arrival rate of Layer 1 is determined by ; the arrival rate of the users’ jobs multiplied by a probability equal to one (assuming that the users always generate jobs) plus the mean arrival rate of the next Layer 2, multiplied by the probability of interrupted transmissions from Layer 1 to Layer 2 (due to corrupted data or collapsed links), .
- λ2:
- The mean arrival rate of Layer 2 is determined by the mean arrival rate of Layer 1, , multiplied by the probability of uninterrupted transmissions between Layers 1 and 2, , plus the mean arrival rate of the next Layer 3, multiplied by the probability of interrupted transmissions from Layer 2 to Layer 3 (due to corrupted data or collapsed links), .
- λ3:
- The mean arrival rate of Layer 3 is determined by the mean arrival rate of Layer 2, , multiplied by the probability of uninterrupted transmissions between Layers 2 and 3, , plus the mean arrival rate of the next Layer 4, multiplied by the probability of interrupted transmissions from Layer 4 to Layer 3 (due to corrupted data or collapsed links), .
- λ4:
- The mean arrival rate of Layer 4 is the product of the mean arrival rate of the upper layer multiplied by the probability of uninterrupted transmission from Layer 3 to Layer 4, .
The above considerations are expressed mathematically as follows:
According to Jackson, the solution to the equilibrium state probability distribution:
is given by the product of probabilities:
where:
with the ’s denoting the utilization of an entire layer i given by:
Finally, the mean number of jobs for layer i can be computed as:
3.3. An Illustrative Example
Suppose that, for the network of Figure 1, the users generate jobs with a mean arrival rate of , and the mean service rates of the three layers are ms, 8 ms, while the mean service rate of the end nodes is ms. The probabilities of uninterrupted transfers are . For this example, the values were chosen in random, but for a simulation set, they were obtained based on the network characteristics (the service time values) and through observation and statistics (the mean job generation rate by the users and the probabilities of uninterrupted transfers), as described in the Simulation Analysis section. Then, the mean arrival rates at the network’s layers are found from the system of Equation (8), and they are jobs/s, jobs/s, jobs/s, jobs/s (these values have been rounded to one decimal place). The utilization values for each layer are found from Equation (12). For example: (recall that the values are expressed in ms, while the values are expressed in seconds, hence the division by 1000). Similarly, , , . The mean number of jobs per layer is computed by Equation (13); thus, . The equilibrium state probability for , or is found using Equations (10) and (11):
and finally:
This value means that the probability of changing the state with time is a very small one, 0.001044, which virtually means that the system’s state does not change with time. In other words, if the users generate 70 jobs/s for a period of time, given the mean service times and the probability of uninterrupted transfers per layer, then we can estimate the number of jobs per layer to keep the system at a steady (or equilibrium) state, in which the average flow leaving one layer will equal the average flow entering that layer. This can be considered a “per layer” load-balance. In the next section, the probabilistic model described is used to test parameters that reflect load balancing over the network.
4. Simulation Analysis
In this section, the proposed model is compared with existing strategies to test its validity and accuracy. It is important to note that no scheduling was implemented based on the ProMo model. Instead, existing scheduling algorithms were used, and the metrics, which are indicators of good balancing and performance, were computed using the strategy-defined parameters and the ProMo-defined probabilistic parameters. To determine if the ProMo model is indeed suitable to model existing dynamic data flow schedulers in the cloud, it was necessary to compare the results obtained by its probabilistic parameters against the results obtained by the corresponding strategy-defined parameters. This is the approach taken in this section.
For the analysis that follows, two scheduling scheme were selected: (1) Dynamic Load Balancing Scheduling for FPNs (DLBS-FPN) [8] and (2) the Dynamic Randomized load-Balancing (DRB) [19]. The reason behind this choice is two-fold: first, the schemes are quite simple to implement in a simulator, and second, they are designed for FPN or similar network topologies, so the model can better fit to them. A description of how the aforementioned strategies operate was given in the Related Work section. For the simulation environment, an Intel Core i7-8559U Processor system was used, with a clock speed of 2.7 GHz. In the following subsections, the use of the ProMo to test these two schemes is described in detail.
4.1. Application of ProMo to the DLBS-FPN Scheduling Scheme
In the first set of experiments, the link bandwidth was set to 1 Mbps, and the value of was set to 12.5 user jobs/s. Each job was assumed to have an average size of 1 Mb, and the data flows were assumed to have the same size of 500 MB (average of 500 jobs). Furthermore, the FPN network had 200 core switches, 400 aggregation switches, and 400 ToR switches, to comply with the settings used in [8].
Using the ProMo Model to Study the System’s Throughput
The DLBS-FPN strategy uses a parameter called the scheduling trigger to study the system’s throughput. This parameter tests the network load balancing on different links, and the throughput was examined in accordance to . The scheduling trigger depends on the flow balance degree and network topology of data centers. It can be decided by experiments under a fixed network topology [19]. Under this policy, the flow that occupies the largest amount of bandwidth on the most congested link moves to another available link, whenever , where is the variance between the network bandwidth utilization ratio and the real-time link bandwidth utilization ratio. Because is a threshold value, it is determined by executing the algorithm under a variety of values and, then, according to the relationship between throughput and . Then, is chosen as the value that corresponds to the highest throughput.
In ProMo, a different parameter is introduced to examine the throughput, expressed as a relationship between the Mean Response Time (MRT) and the mean arrival rate of the jobs generated by the users, . For reference, this parameter is called MRT/.
To determine MRT/, it can be observed that the maximum arrival rate of user jobs is the one that can saturate the first level (meaning that ), and it is found by the following equation:
This means that a maximum arrival rate is achieved when is increased by a factor of . Then, the maximum throughput rate will be:
In other words, the throughput reaches a local maximum when is multiplied by a factor f. Clearly, the average throughput is:
The MRT was determined by the well-known Little’s formula, and it is:
From Equations (16) and (17), it is clear that there is a relationship between the MRT, the mean throughput rate , and the mean arrival rate . To study the mean throughput behavior, the DLBS was simulated, and the MRT and values were recorded for a variety values, with mean equal to 12.5 jobs/s. The values were assumed to be equal to 1/50 ms, while the probabilities of uninterrupted transfer between layers were reported to be and . Table 2 shows the values obtained, and Figure 3 shows the relationship between the MRT and the mean throughput .

Table 2.
Results recorded when executing the Dynamical Load-Balanced Scheduling (DLBS) scheme to examine the system throughput. MRT, Mean Response Time.
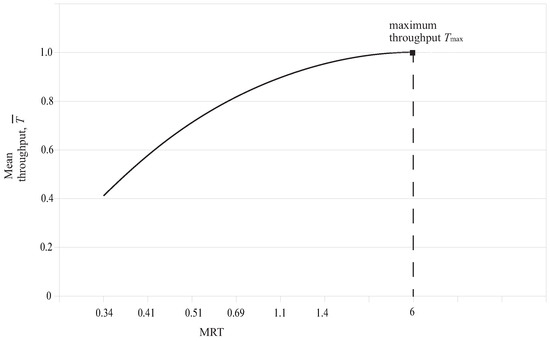
Figure 3.
Relationship between MRT and mean throughput.
A similar behavior has been reported in DLBS, when examining the relationship between the parameter and the throughput achieved (see Figure 6 in [8]). The throughput line had a similar form when plotted against , and it reached its maximum for an value. Beyond this point, there was no further improvement for the DLBS throughput. When applying the ProMo during the DLBS simulation, the model recorded a maximum throughput for MRT close to six. This corresponded to an arrival rate of user jobs/s, and the corresponding f value that saturated the first level was ≈1.31. These values can be verified by applying the values of Table 2 to Equations (14)–(17). The mean throughput curve computed in [8] had an identical slope to the one computed by ProMo, and this was repetitive for different sets of and probabilistic values recorded.
Three observations are necessary here:
- The ProMo model was scheduled to work on network layers, not on single links, so the values obtained were average link values. For example, an average of 10% interrupted transfers was recorded in total for all the links connecting Layers 2 and 3 or 3 and 4. Thus, .
- Continuing the previous observation, the mean throughput values were average layer throughput values. To change these values to bytes/s, it was necessary to consider the average job size, record the number of bytes/s per link, and get the average. This approach will also lead to similar curves.
- The maximum point was the Layer 1 saturation point, beyond which the throughput will be dramatically reduced. In ProMo, this was shown by the fact that for f values beyond 1.31, the value of exceeded one, making negative (see Equation (13)). This is the reason that the curve was not plotted beyond the value of , in Figure 3.
From the above analysis, it can be concluded that the proposed probabilistic model can be used to examine the mean throughput of a scheduling approach, in this case the DLBS.
Using the ProMo Model to Study the Bandwidth Utilization
In DLBS, the authors computed the network bandwidth utilization ratio of all the links of the network. A high and stable value of the network bandwidth is an indication of a good scheduling scheme. In this set of simulations, a uniform transfer pattern was assumed, where the flows are symmetrically distributed among all the hosts and the data are transmitted with equal probability among the links. For ProMo, the average bandwidth utilization was computed as the ratio of the data-in and data-out rates per layer, divided by the number of layers, that is:
In this set of experiments, the parameter values used were similar to the previous set, when examining the system mean throughput. Some values that were recorded during time intervals are given in Table 3.

Table 3.
Results recorded when executing the DLBS scheme to examine the bandwidth utilization.
The average bandwidth utilization rate computed by ProMo is plotted in Figure 4. Again, the line derived from the simulation observations was similar to the one presented in [8] (see Figure 8a of this work). Some points that need to be mentioned here are the following:
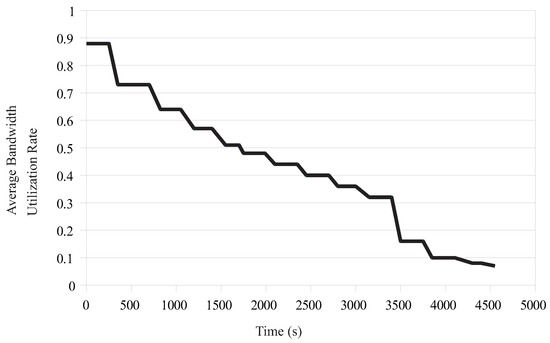
Figure 4.
Average bandwidth utilization rate, as computed by ProMo.
- The bandwidth utilization line presented in [8] was somehow smoother compared to the one of Figure 4. The reason is because the results here were obtained on a per layer basis and not as the average values from the total number of links. Looking at the corresponding graph in [8], one can observe longer periods of stable bandwidth values compared to the line derived by the ProMo tester.
- The bandwidth utilization fell off as the load transmitted kept increasing with time, as also described for the DLBS scheme. This case was modeled by ProMo by an ever-decreased value of to avoid possible congestions in the links. In its turn, this caused a reduction of values, and thus, the average bandwidth utilization was reduced.
4.2. Application of ProMo to the DRB Scheduling Scheme
The DRB is another interesting scheme that is scheduled for fat-tree networks that have a similar topology as the one used in ProMo. The DRB uses another metric to test a scheduling algorithm’s performance, which is the average latency, that is the longest delay of data sent into the network at the same time [19]. In DRB, the hosts were assumed to send data flows continuously into the network. Each host had a packet to send into the network with probability p, and one packet was transmitted over each link at a time. In this set of simulations, a DRB routine was implemented and simulated, using the basic parameters mentioned at the beginning of Section 4.1. The aim here is to verify that the MRT parameter of ProMo displays a similar behavior as the average latency over different traffic scenarios. It is interesting that the average latency in DRB is also related to a probability function, just like the MRT parameter of ProMo. During the simulation, the ProMo model was used to record average MRT values at time intervals. Table 4 shows a set of values recorded for different loads .

Table 4.
Results recorded when executing the DRB scheme to examine the average latency.
It was shown that the MRT increased as the load becomes heavier. Specifically, as seen in Figure 5, the MRT increased very smoothly, until it approached values that saturated the initial layer; these values were close to 16. Above this threshold, the MRT increase was explosive. A similar behavior was described in DRB (see Figure 6 in [19]). A few observations are necessary here:
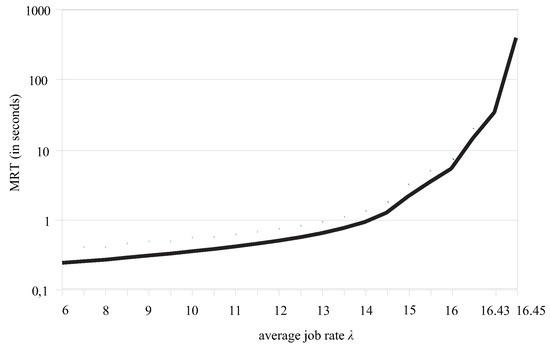
Figure 5.
MRT for different flows, as computed by ProMo.
- The MRT values were on a “per user job basis”. To find the MRT values on a byte basis, it is necessary to use the average job size, but the behavior will be identical.
- The authors in [19] proposed a DRB probability-based threshold, which is used to improve the average latency. In correspondence with this, the value factored by at most f is an analogous parameter in the sense that, above this traffic value, there is not much to be done to prevent the MRT from falling-off.
Again, one can observe that the ProMo model can be used with satisfactory accuracy to test an algorithm’s average latency, in this case the average latency of DRB.
5. Conclusions and Future Work
In this paper, the main goal was to use the ProMo model to test the accuracy of the results found by some state-of-the-art dynamic data flow scheduling algorithms in cloud environments. In this regard, the model was used with two quite simple schemes, the DLBS and the DRB. The ProMo model was basically built to work for FPN networks, and since the aforementioned schemes also operate on similar structures, they were chosen for testing. The results showed that the parameters computed by the ProMo model present similar or identical behavior to those used by DLBS and DRB, in order to verify their load-balancing and good performance. This suggests that ProMo can be used for testing with a satisfactory accuracy.
Much research is now ahead, and many efforts need to be made. First, more schemes have to be tested to guarantee this accuracy. Then, the model itself can be used as the basis for a new scheduler. Finally, it can be the basis of a cloud simulator, in cooperation with the CPN (Colored Petri Nets) tool, which is necessary since each layer, link, and user job will be treated as a token with its own features. This will increase the accuracy of the simulator.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lu, J.; Li, D. Bias Correction in Small Sample from Big Data. IEEE Trans. Knowl. Data Eng. 2013, 25, 2658–2663. [Google Scholar] [CrossRef]
- Han, X.; Li, J.; Yang, D.; Wang, J. Efficient Skyline Computation on Big Data. IEEE Trans. Knowl. Data Eng. 2013, 25, 2521–2535. [Google Scholar] [CrossRef]
- Tantalaki, N.; Souravlas, S.; Roumeliotis, M. A review on Big Data real-time stream processing and its scheduling techniques. Int. J. Parallel Emerg. Distrib. Syst. 2019. [Google Scholar] [CrossRef]
- Souravlas, S.; Roumeliotis, M. Dynamic Load Balancing on All-to-All Personalized Communications Using the NNLB Principal. In Proceedings of the 2014 Sixth International Conference on Computational Intelligence, Communication Systems and Networks, Tetova, Macedonia, 27–29 May 2014; pp. 107–112. [Google Scholar]
- Souravlas, S.I.; Sifaleras, A. Network Load Balancing Using Modular Arithmetic Computations. In GeNeDis 2016; Springer: Berlin, Germany, 2017; Volume 988, pp. 271–280. [Google Scholar]
- Zhang, Q.; Zhani, M.F.; Yang, Y.; Boutaba, R.; Wong, B. PRISM: Fine-Grained Resource-Aware Scheduling for MapReduce. IEEE Trans. Cloud Comput. 2015, 99, 182–194. [Google Scholar] [CrossRef]
- Yuan, Y.; Wang, D.; Liu, J. Joint scheduling of MapReduce jobs with servers: Performance bounds and experiments. In Proceedings of the IEEE Conference on Computer Communications (IEEE INFOCOM 2014), Toronto, ON, Canada, 27 April–2 May 2014; pp. 2175–2183. [Google Scholar]
- Tang, F.; Yang, L.T.; Tang, C.; Li, J., Sr.; Guo, M. A Dynamical and Load-Balanced Flow Scheduling Approach for Big Data Centers in Clouds. IEEE Trans. Cloud Comput. 2018, 6, 915–928. [Google Scholar] [CrossRef]
- Cao, Z.Z.; Kodialam, M.; Lakshman, T.V. Joint Static and Dynamic Traffic Scheduling in Data Center Networks. In Proceedings of the IEEE Conference on Computer Communications 2014 (IEEE INFOCOM 2014), Toronto, ON, Canada, 27 April–2 May 2014; pp. 2445–2553. [Google Scholar]
- Congdon, P.T.; Mohapatra, P.; Farrens, M.; Akella, V. Simultaneously Reducing Latency and Power Consumption in OpenFlow Switches. IEEE/ACM Trans. Netw. 2014, 22, 1007–1020. [Google Scholar] [CrossRef]
- Misra, S.; Das, S.; Khatua, M.; Obaidat, M.S. QoS-Guaranteed Bandwidth Shifting and Redistribution in Mobile Cloud Environment. IEEE Trans. Cloud Comput. 2014, 2, 181–193. [Google Scholar] [CrossRef]
- Zhang, F.; Cao, J.; Hwang, K.; Li, K.; Khan, S.U. Adaptive Workflow Scheduling on Cloud Computing Platforms with Iterative Ordinal Optimization. IEEE Trans. Cloud Comput. 2014, 3, 156–168. [Google Scholar] [CrossRef]
- Rodriguez, M.A.; Buyya, R. Deadline Based Resource Provisioning and Scheduling Algorithm for Scientific Workflows on Clouds. IEEE Trans. Cloud Comput. 2014, 2, 222–235. [Google Scholar] [CrossRef]
- Shang, Y. Optimal Control Strategies for Virus Spreading in Inhomogeneous Epidemic Dynamics. Can. Math. Bull. 2012, 56, 621–629. [Google Scholar] [CrossRef]
- Shang, Y. Optimal Attack Strategies in a Dynamic Botnet Defense Model. Appl. Math. Inf. Sci. 2012, 6, 29–33. [Google Scholar]
- Malawski, M.; Juve, G.; Deelman, E.; Nabrzyski, J. Cost-and deadline-constrained provisioning for scientific workflow ensembles in iaas clouds. In Proceedings of the International Conference on High Performance Computing, Networking, Storage and Analysis, Salt Lake City, UT, USA, 10–16 November 2012; p. 22. [Google Scholar]
- Tsai, C.W.; Huang, W.C.; Chiang, M.H.; Chiang, M.C.; Yang, C.S. A Hyper-Heuristic Scheduling Algorithm for Cloud. IEEE Trans. Cloud Comput. 2014, 2, 236–249. [Google Scholar] [CrossRef]
- Neely, M.J. Distributed stochastic optimization via correlated scheduling. In Proceedings of the IEEE Conference on Computer Communications (IEEE INFOCOM 2014), Toronto, ON, Canada, 27 April–2 May 2014; pp. 2418–2426. [Google Scholar]
- Wang, S.; Luo, J.; Tong, B.K.B.; Wong, W.S. Randomized load-balanced routing for fat-tree networks. arXiv 2017, arXiv:1708.09135v1. [Google Scholar]
- Bianco, A.; Krishnamoorthi, V.; Li, N.; Giraudo, L. OpenFlow driven ethernet traffic analysis. In Proceedings of the 2014 IEEE International Conference on Communications (ICC), Sydney, Australia, 10–14 June 2014; pp. 3001–3006. [Google Scholar]
- Jin, H.; Pan, D.; Liu, J.; Pissinou, N. OpenFlow-Based Flow-Level Bandwidth Provisioning for CICQ Switches. IEEE Trans. Comput. 2013, 62, 1799–1812. [Google Scholar] [CrossRef]
- Chowdhury, M.; Zhong, Y.; Stoica, I. Efficient co-flow scheduling with Varys. In Proceedings of the 2014 ACM conference on SIGCOMM, Chicago, IL, USA, 17–22 August 2014; Volume 44, pp. 443–454. [Google Scholar]
- Ramos, R.M.; Martinello, M.; Rothenberg, E.C. SlickFlow: Resilient source routing in Data Center Networks unlocked by OpenFlow. In Proceedings of the 38th annual IEEE Conference on Local Computer Networks, Sydney, Australia, 21–24 October 2013; pp. 606–613. [Google Scholar]
- Bolla, R.; Bruschi, R.; Lombardo, C.; Podda, F. OpenFlow in the Small: A Flexible and Efficient Network Acceleration Framework for Multi-Core Systems. IEEE Trans. Netw. Serv. Manag. 2014, 11, 390–404. [Google Scholar] [CrossRef]
- Egilmez, H.E.; Civanlar, S.; Tekalp, A.M. An Optimization Framework for QoS-Enabled Adaptive Video Streaming Over OpenFlow Networks. IEEE Trans. Multimed. 2013, 15, 710–715. [Google Scholar] [CrossRef]
- Souravlas, S.; Sifaleras, A. Binary-tree based estimation of file requests for efficient data replication. IEEE Trans. Parallel Distrib. Syst. 2017, 28, 1839–1852. [Google Scholar] [CrossRef]
- Shang, Y. Deffuant model of opinion formation in one-dimensional multiplex networks. J. Phys. Math. Theor. 2015, 48, 395101. [Google Scholar] [CrossRef]
- Jackson, J.R. Jobshop-like Queueing Systems. Manag. Sci. 1963, 10, 131–142. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).