1. Introduction
Presently, mobile robots are becoming more intelligent and can move autonomously in unknown environments. Mapping, localization, path-planning, and path-following aspects have to be implemented in order to solve this inconvenience. Jin et al. [
1] remarked that the smart movement of the robot is associated with the intelligence that has been implemented. Hence, these intelligences are improved by using a combination of sensors and information processing algorithms, as Ortigoza et al. [
2] explained.
Local path-planning or path-following algorithms autonomously move automated guided vehicles (AGVs) to their goal position. Thus, this problem can be described as the process of determining a suitable and safe path, avoiding collisions with the obstacles [
3]. There are many well-known methods to implement this task, such as the dynamic window approach (DWA), which calculates a potential path considering speed restrictions, as Fox et al. [
4] explained. A vector field histogram was developed with the aim of being computationally efficient and robust. In practice, the algorithm became fast and reliable in populated obstacle scenarios, as Borenstein et al. [
5] related. The TangentBug and PointsBug algorithms are really popular, and were compared by Buniyamin et al. [
6]. The TangentBug algorithm depends on the range of the sensor, which is mounted on the robot. Hence, the action plan to reach to the goal uses the sensor information and the knowledge of the robot current position and goal position. However, PointsBug depends on the sensor range, the sudden point, and the trigonometric function. Thus, the algorithm calculates where the next point is to move from the starting point to the goal.
Apart from these classic functions for motion planning, there are some more modern algorithms, for example, swarm optimization (SO), as Ever [
7] has shown. This method is based on a population of candidate solutions that are moving around the search space. The movement of these particles is influenced by the best local particle position. These aspects move the swarm toward the best solutions, which is the goal position. Dynamic movement primitives (DMP), as Mei et al. [
8] analyzed, are another solution, which were motivated by the desire to find a way to represent complex motor actions that can be flexibly adjusted without manual parameter tuning or having to worry about instability. On the end, this intelligence tries to simplify complex movements on a set of primitive actions. Apart from DMP, there is also moving to a point with obstacle avoidance, which uses simple mathematical equations to avoid obstacles, and is proposed by Teso-Fz-Betoño et al. [
9]. Furthermore, it is important to consider Garcia et al. [
10], who proposed a method for industrial mobile robots, which it improve the trajectory in dynamic environments, applying an elastic-band-based method in combination with a model predictive trajectory planner. Apart from this, Pfeiffer et al. [
11] described another investigation, which uses a supervised model to learn complex mapping, and processes the steering commands to arrive at the goal position. Moreover, a model predictive control (MPC), as Yu et al. [
12] proposed, is another intelligence for the vehicles, which provides vehicle control to track the path. With the same technique, Qingjia et al. [
13] improved the results by adopting multi-constraints model predictive control (MMPC). Genetic algorithms are also implemented in mobile robots. Sathiya et al. [
14] explained a novel concept by adopting two techniques, namely multi-objective differential evolution and non-dominated sorting genetic algorithm (NSGA-II), in order to obtain a safer path by optimizing travel time and actuators effort. The ant algorithm is implemented in navigation problematics, such as Xiaoping et al. [
15] explained. However, the recent investigation has been improved by adopting different techniques. For example, Dai et al. [
16] implemented the A* characteristics into an ant algorithm and Yang et al. [
17] presented an efficient double layer ant colony, which is called DL-ACO. This novel concept uses two ant colony running independently and successively. First one controls a collision free path and then the second one optimizes the results of the first ant colony trajectory.
As Bellotto et al. [
18] and Truong et al. [
19] analyzed, there are some situations where the AGV has to interact with humans. This is the reason algorithms must change their behavior, performing harmless maneuvering depending on the scenario conditions.
In the end, the motion planning algorithms have to adapt their behavior with dynamic surroundings. Thus, it is essential to implement an intelligence that changes these parameters from motion planning algorithms. Some investigations apply new solutions to modify DWA constants, depending on the area conditions. In the past, Hong et al. [
20] adapted DWA using a fuzzy logic controller, achieving new suitable weights. These weights are modified considering the goal position and obstacles position information. Abubakr et al. [
21] adopted the same controller; however, the weights were adjusted with obstacle distribution information.
Nevertheless, another alternative for the dynamic window approach is reduced-DWA, which requires much less processing power, as proposed by Arras et al. [
22]. Abubakr et al. [
21] analyzed a novel concept of reduce-DWA, applying a reduced cascaded fuzzy logic controller. The cascade uses two reduced fuzzy logic controllers. Hence, both controllers update three weights of DWA according to the environmental situation. The first controller inspects the surrounds of the robot and identifies the position of the obstacle for determining the obstacle distribution type. The second controller adopts the obstacle distribution type and assigns the best constant for a particular period time.
Overall, the DWA behavior can be adapted to the scenario conditions with fuzzy logic rules. In recent decades, however, fuzzy logic has been improved in learning capabilities, and is known as neuro-fuzzy, as Salleh [
23] mentioned. In 1993, an adaptive neuro-fuzzy inference system (ANFIS) was introduced by Jang [
24]. ANFIS has some limitations, such as the problem of dimensionality and training complexity, which restricts some applications with large datasets. Apart from that, Zamani et al. [
25] explained that ANFIS has a huge generalization capability compared with other neural networks or machine learning techniques. Furthermore, Badde et al. [
26] compared the difference between fuzzy logic and ANFIS, concluding that ANFIS has better performance solving complex problems than the fuzzy controller.
Today, in mobile robots, ANFIS calculates the difference of angular velocity, adopting the smallest distance to the obstacles and the target angle, as Lu et al. [
27] has shown. Singh et al. [
28] investigated a solution for real-time navigation, in which ANFIS has to decide the optimal time for a collision free path in an unknown and dynamic environment. Imen et al. [
29] presented a cascade controller. The first controller uses fuzzy logic, which identifies the curvature of the path and generates the input for the second controller, which is ANFIS. The second controller determines the path for the mobile robot. Pandey et al. [
30] analyzed how ANFIS works as a controller for navigation and obstacle avoidance in unknown static environments.
There are different alternatives for path planning technique. The recent investigations try to develop classic algorithms to improve their performance. DWA algorithm that is a classic function, could be adopted another technique to improve the optimization of the path selection. DWA depends on the AGV model to solve a safe path, such as MPC. It seems logical to modify the optimization function, in order to analyze the future by adopting a prediction window like MPC does. Furthermore, this classic algorithm adopts different weights depending on the human criterion, hence, ANFIS, neural networks or fuzzy logic techniques can be adopted to optimize the fixed parameters. In
Table 1 an overview of presented algorithms is made.
The main goal of the present study is to improve the DWA algorithm, not only by adapting each weight depending on the scenario circumstance, but also by implementing a prediction step to improve the optimization of the path selection. For the and parameter calculations, despite using a classical fuzzy logic controller, ANFIS will be implemented. To make that possible, data collection will be made executing classical DWA with different weight configurations. The AGV speed, heading to the target and the distance to the obstacle will be evaluated in the data collection, so as to change the behavior of ANFIS to DWA by modifying these controller parameters to the scenario conditions.
2. Materials and Methods
DWA is a classical motion planning solution, as Fox et al. [
4] analyzed. This algorithm is divided into two sections in order to predict the best trajectory. The first one is the search space, where different possible
and
are considered. Moreover, this first section is divided into three subsections so as to filter these admissible variables, depending on the actual state. The first subsection is known as the circular trajectories, where the two-dimensional velocity
is calculated based on space. The second one takes all of the calculated velocities and selects only those admissible velocities that have a safe trajectory. The last subsection only contemplates these velocities that can be reached in a short time interval, considering the robot acceleration limitations.
In the second section, however, optimization is made by applying the target heading, distance to the obstacles, and actual velocity. This optimization just selects the best trajectory, rejecting other trajectories. This optimization, however, can be improved by adopting more than one path, as Kim et al. presented, such as in a confidence random tree-based algorithm [
31]. In this article, this problem will be solved, applying a prediction step to the DWA algorithm, known as a predictive dynamic window approach (P-DWA).
Hence, to develop the P-DWA, it is important to place the basic aspect of the DWA optimization function, as Equation (1) represents and in
Table 2 the DWA parameter and variable definition is represented.
The heading is given by 180°—
, where
is the angle of the target point relative to the AGV heading direction as
Figure 1 shown.
Moreover,
,
, and
are the constants that will be adapted using ANFIS. DWA does not always have the capability to avoid the obstacle, as Hong et al. [
20] reviewed. In
Figure 2, there are two different scenarios, in which AGV has to calculate the path using the DWA algorithm. For both scenarios, different weight values will be applied to analyze the consequence of unacceptable configuration. The cases in
Figure 2a,c used the same parameters for different scenarios. The same logic is implemented in the cases in
Figure 2b,d.
Hence, the ANFIS system will choose these parameters depending on the scenario conditions. For each parameter, an adaptive neuro-fuzzy inference system is proposed. The train will be made individually so as to obtain a better resolution, adopting specific inputs. In the fuzzy DWA, however, the rules are designed manually. This tune is not optimized for the scenario, and depends on human criterion.
With the aim of training ANFIS and simplifying the fuzzy logic controller adjustment, DWA will be executed several times in order to collect data. With these data, ANFIS develops a fuzzy inference system (FIS) using a back-propagation algorithm. Thus, FIS will change the DWA parameters to solve a particular scenario.
This functionality is similar to that of a neural network, in which the inputs go through the membership function and associated parameters. Then, the information will propagate to the output membership function and associated parameters in order to obtain a specific output. Moreover, the associated parameters adapt their values depending on the learning process.
3. DWA Improvement
This research will implement two novel concepts for the DWA algorithm. The first one comes from Equation (1), where the classic DWA optimizes the trajectory, just considering the next sample time or step. In this article, however, the DWA algorithm will be executed twice per sample time. In the first execution, DWA analyzed more than one possible path, and in the second one, the DWA analyzed different paths and predicted which one had a better resolution.
The second implementation comes from the DWA constant parameters. As shown in
Figure 3, the importance of selecting the correct weights for each situation is essential. To solve this problem, despite using classic fuzzy inference, ANFIS will be implemented.
3.1. Predictive DWA
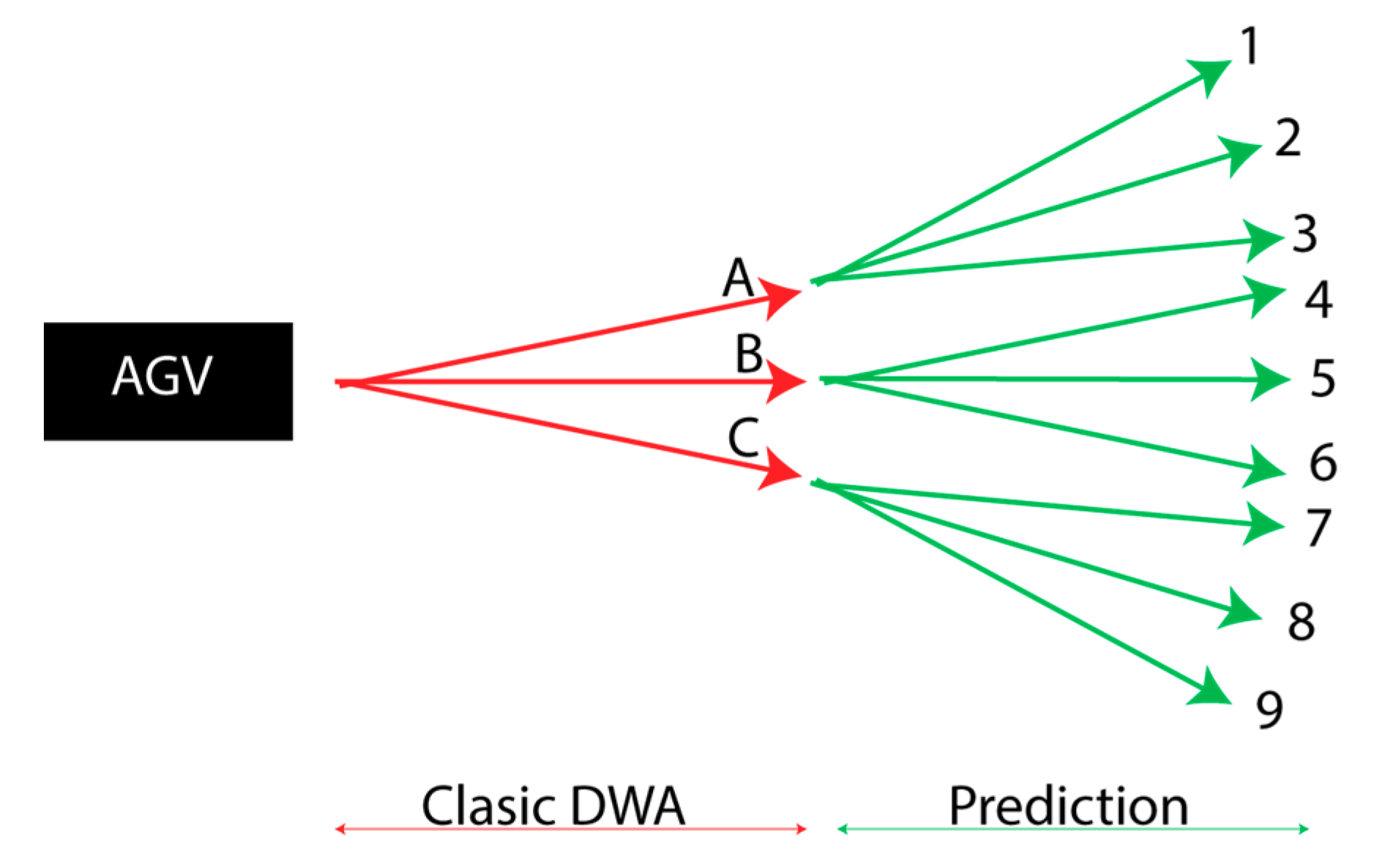
The classic DWA optimization step will be modified to introduce a prediction step. The optimization function, which it is represented in Equation (1), selects the best path, considering the admissible trajectories. On a predictive DWA (P-DWA), however, it is essential to select more than one path. Otherwise, it cannot implement the prediction step. Hence, for this particular case, DWA calculates the three best trajectories (A, B, and C). These trajectories are considered to be the new possible position for the AGV.
After calculating these three new possible positions, it is time to foresee the future. This step is known as the prediction step, where the DWA will be executed for each best trajectory (A, B, and C), so as to obtain another three paths. Thanks to that, the AGV analyzes nine different positions to arrive. These nine positions are theoretical and are used to make an optimization. Thus, the AGV should select the best path to arrive at one of these nine optimum positions. Nevertheless, the vehicle is just going to move to the A, B, or C position. For example, if the prediction estimated that the fifth position was the best one, the AGV would move to the B position. To have a general idea of this, an example is shown in
Figure 3.
Overall, with the normal DWA, the AGV is going to select the best path considering the A, B, or C trajectories. Predictive DWA (P-DWA) gives the chance to analyze the next sample time so as to make a better optimization, as a result of analyzing a large period of time and using more information from the scenario. It is remarkable that it has no sense of how to use a huge prediction time. By using an extensive sample time, the computational cost will be increased considerably. Moreover, by adopting a large period of time, the environment condition could change. Thus, this optimization will not be the best one.
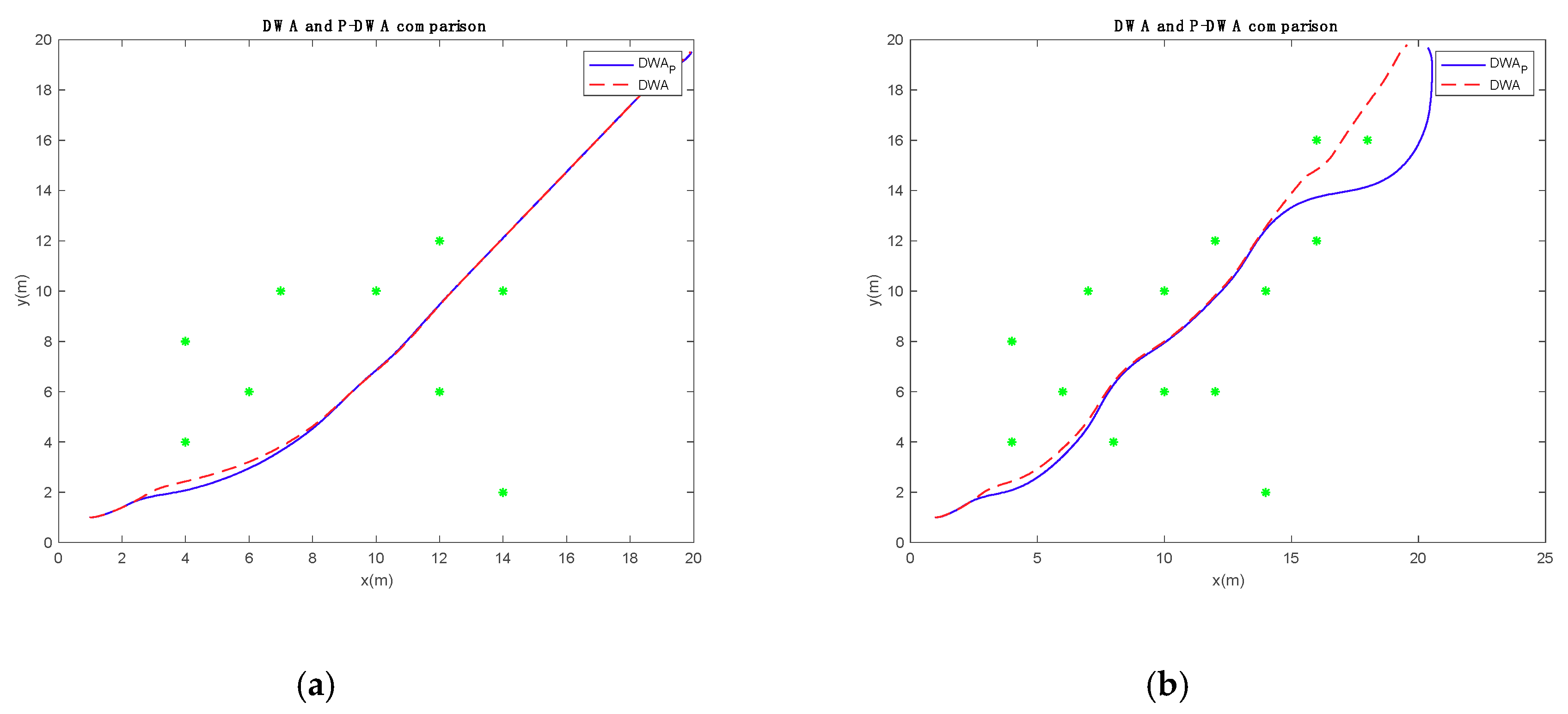
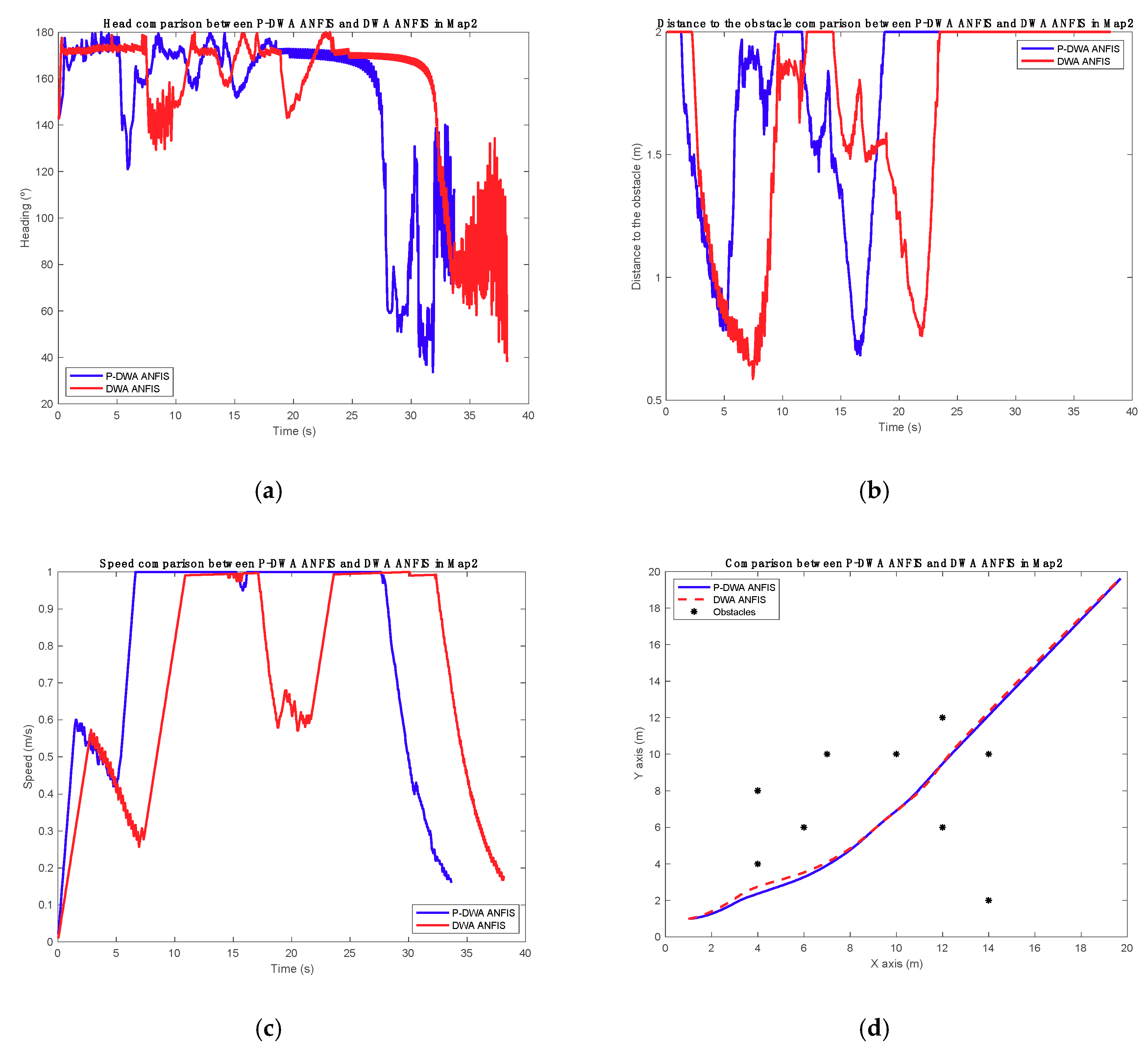
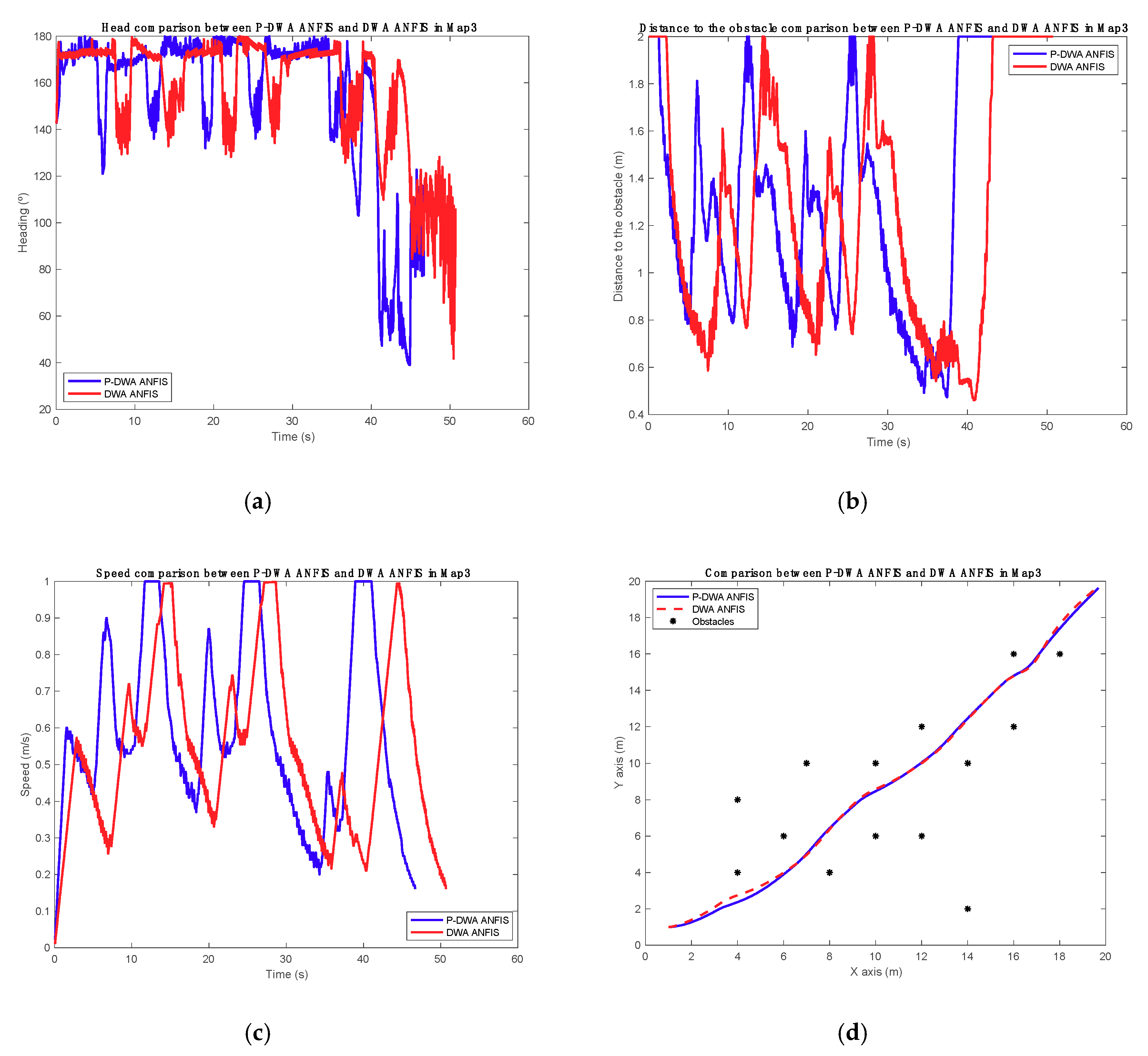
Despite stopping the explanation here, DWA and P-DWA will be compared so as to understand which application has better performance, using the scenarios in
Figure 4b,c. The trajectory results are shown in
Figure 3, and the analytical results are shown in
Table 3 and
Table 4.
In the first execution, for which the trajectory is shown in
Figure 4a and the analytics values are represented in
Table 3, P-DWA has a better performance, arriving at the goal position in less time. Thus, AGV is faster than the normal DWA. The time difference is about 1.25 s, and the speed value variation is 0.03 m/s.
For this particular case, the P-DWA algorithm is executed every 0.05 s, and it calculates three best paths (A, B, and C), and the prediction window is working with 0.5 s sample time to calculate another three trajectories for each best path.
P-DWA analyzes the future by executing the AGV model, and tries to guess the future by foreseeing what will be happen if it moves to a new point, like whether a model predictive control (MPC) [
32] works. Thanks to the prediction window, the algorithm has a better performance and arrives faster at the goal position.
Comparing the paths, both are really similar. P-DWA tries to search an ideal path, giving more space between the AGV and obstacles. With this action, the vehicle can go faster because the calculation has less influence.
The last affirmation can be confirmed with
Table 4. For the second comparison, P-DWA diverts more from the last obstacles so as to maintain a top speed. Hence, AGV diverts more from the ideal path, which is a straight line from the start position to goal position. Nevertheless, P-DWA has the capacity to arrive at the goal point faster than DWA, because the classic algorithm has to cross between two obstacles, thus reducing the speed.
Overall, these comparisons give a general idea about how the DWA path calculation can be optimized, introducing a predictive window. The most relevant parameter is the speed incrementation, where AGV arrives at the goal position in less time. Therefore, there is a path variation between DWA and P-DWA. Depending on the predictive window, the answer will change. Huge predictive windows require a high computational cost. Moreover, if the obstacles change their position, the optimization of the path will not be the best one. Small predictive windows, however, do not affect the path optimization. Thus, P-DWA and DWA will have almost identical paths.
3.2. ANFIS Development
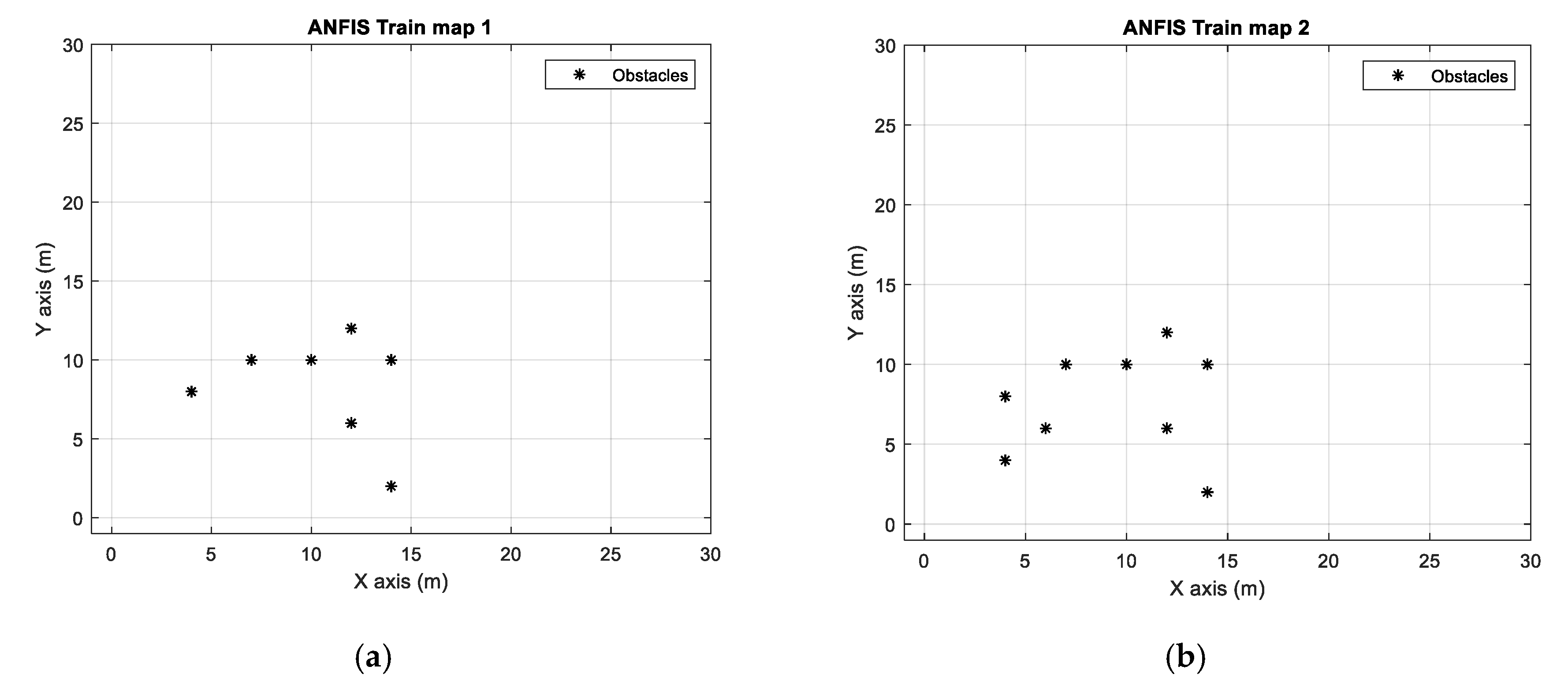
After developing the P-DWA, it is time to evaluate how to adapt the weights using an adaptive neuro-fuzzy inference system. ANFIS, as with the other neural network, depends on the train-data to adjust the fuzzy inference. Therefore, the first action is to develop different scenarios for data acquisition, as shown in
Figure 5. In these scenarios, the AGV will move using a classical DWA algorithm, adopting different
,
, and
parameters per execution. It is true that P-DWA has a better performance, as shown in
Section 3.1. The purpose of this section; however, it is to obtain the speed, distance to the obstacles, and direction for the target information to train ANFIS.
It has to be considered that when P-DWA uses ANFIS, this fuzzy inference will be executed twice. One for the first step, as with a normal DWA, and another for the prediction step, in order to recalculate the , , and parameters so as to have a better optimization for the trajectory.
The scenarios are built thinking that the AGV starts in pose x = 1, y = 1, and σ = 1, and the goal is in x = 20 and y = 20. Hence, the obstacles are around the y = x line, so as to interrupt the AGV best path, which is a straight line between the start point and goal.
The data acquisition is built with 600 samples for each map. In each sample, random , , and values are employed. The random function uses a uniform distribution and the values are from zero to one.
As shown in
Figure 2, the DWA behavior depends on the weight values, because these values, for AGV, in some cases, cannot arrive at the goal position. To reject these invalid parameters, a timer will be used. This timer controls how much time the AGV needs to arrive at the goal. Hence, if the AGV does not arrive at the goal position after 250 s, these parameters would be discarded from the data acquisition. Apart from this, in this research, the
,
, and
parameters will use individual ANFIS to optimize the fuzzy inference.
The data acquisition will be transformed to train the data, in order to achieve the ANFIS. Thus, the values have to be prepared using some functions. In
Table 5, there are some term definitions that are used in the equations.
To develop the
fuzzy inference, which is heading to the target correction, ANFIS will be trained using only the headings means, as shown by Equation (2). Apart from this, for this particular case, the n-maximum value will be 2400, considering that there are 600 for each map, and there are four maps. Moreover, the i-maximum value must be 5000, as a result of the multiplication of the DWA sample time, which is 0,05 s, and the time limit, which is 250 s.
For
, which is the object detection parameter, the trained-data will have the AGV mean speed and the mean distance to the obstacle, as in Equation (3) and Equation (4), respectively. In an obstacle avoidance maneuver, it is important to consider the AGV speed, and how far away the obstacle is from the AGV. Nevertheless, if the trained-data only considers the distance to the obstacle, the AGV could avoid some objects with a high speed. In other words, the AGV is going to make an unsafety avoidance.
Finally, there is , which controls the speed. The trained data will analyze the mean speed, as shown in Equation (3). The parameter will have a high value when the AGV is far away from the goal. Nevertheless, when AGV has a top speed, this value has to be low, in order to not influence the obstacle detection and avoidance.
As a future work, the ANFIS trained-data preparation could be optimized. Instead of applying the means of the direction, speed, or distance, the variance of the obstacle to determine a moving obstacle, the divergence from the ideal path for heading parameter, and so on could be adopted. The aim of this research, however, it is to introduce a novel concept of intelligence, which can simplify the fuzzy inference adjustment.
ANFIS, as with other fuzzy inference systems, needs to define the fuzzy type. For this, a Sugeno model was used, as represented in
Table 6. Hence, it was used as the default configuration for ANFIS, because the aim of this research is to ensure that this algorithm has the capability to adapt the P-DWA and DWA parameters.
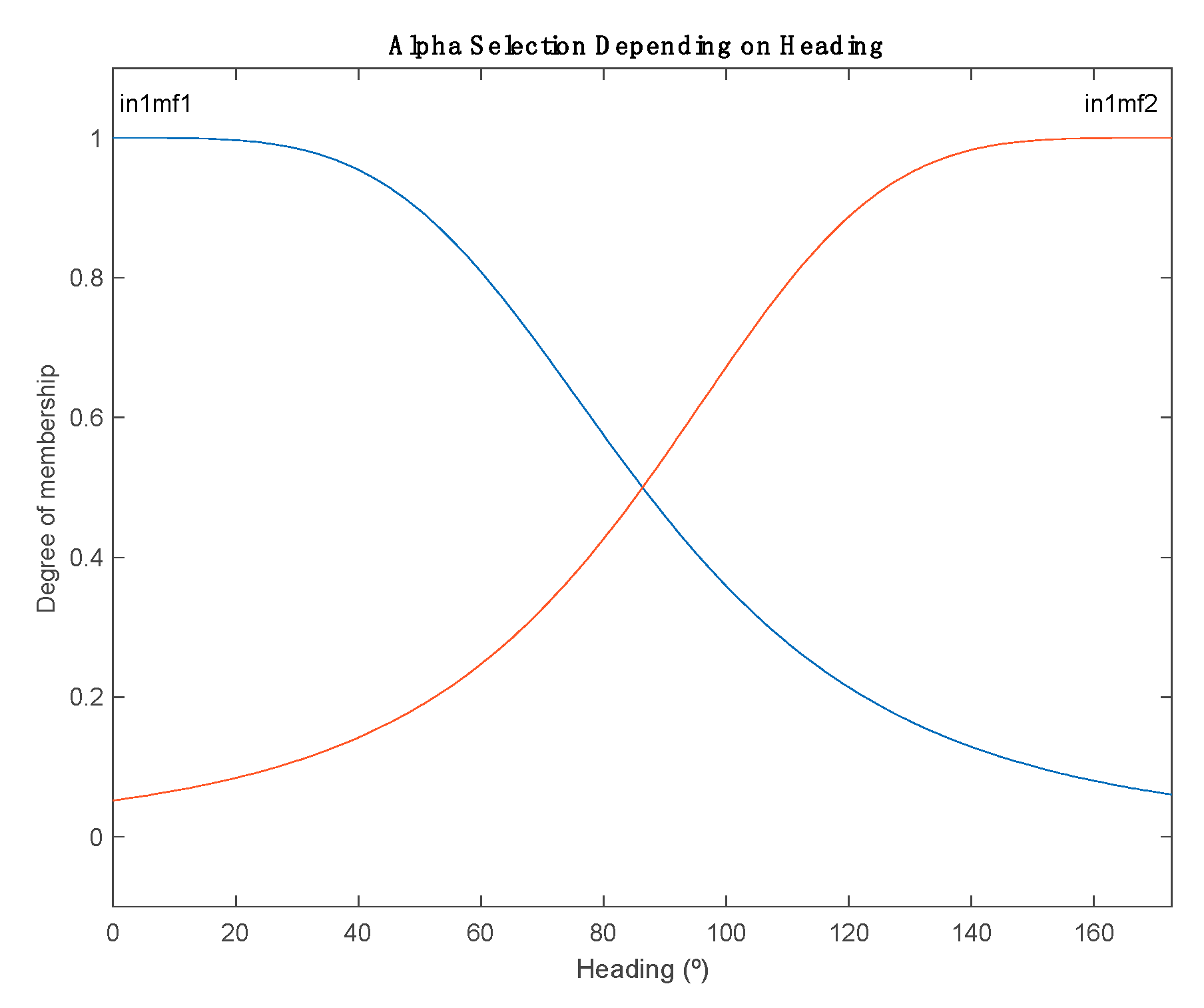
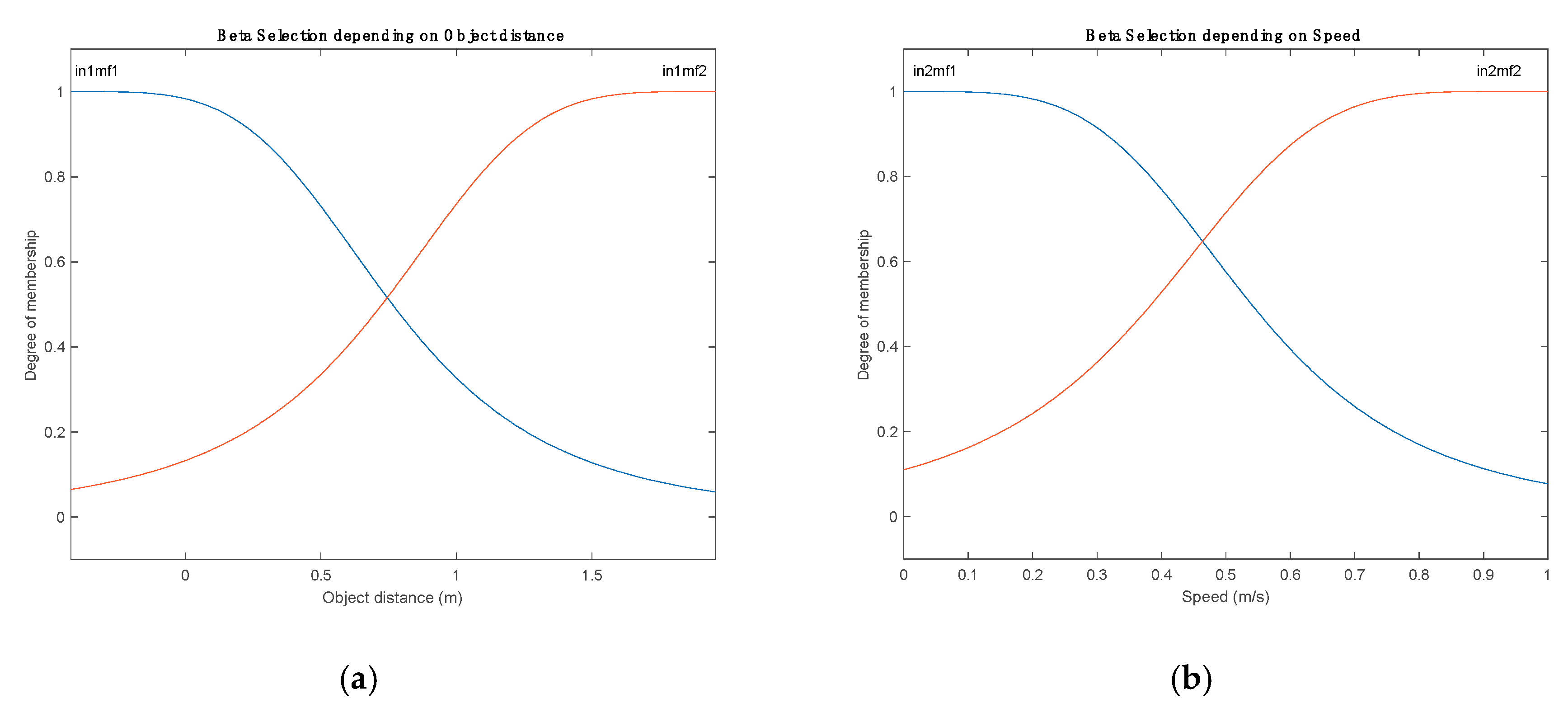
The
parameter inference is analyzed in
Figure 6. As a consequence of the default configuration, the
membership function has two fuzzy rules, which are optimized to solve four train maps, thanks to the backpropagation algorithm.
has two inputs, which depend on the obstacle distances and AGV speed. Both inputs are represented in
Figure 7. As a result, of adopting two inputs,
has two membership functions. Like the other parameter, each membership has two rules.
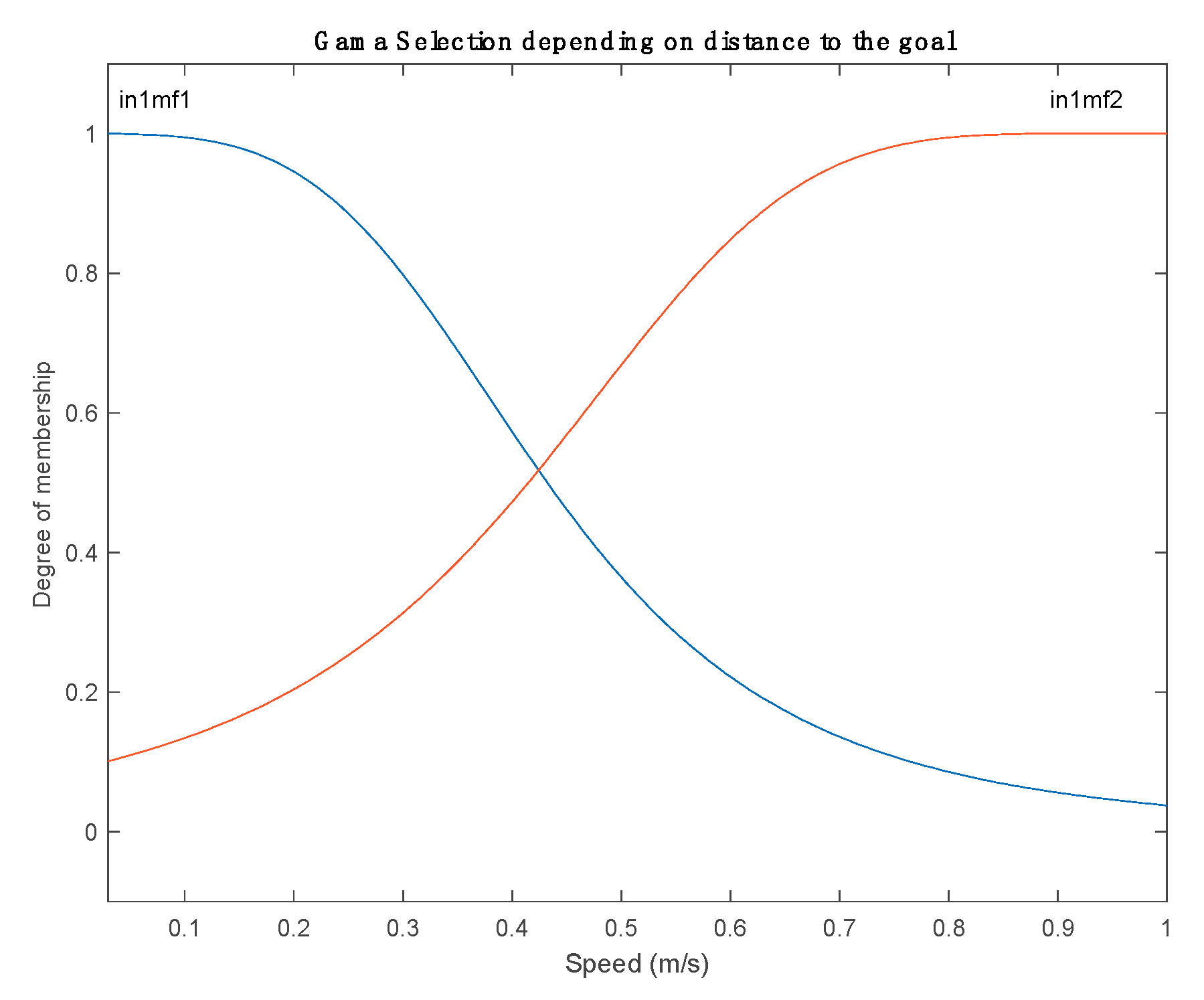
For the last parameter, which is
, the configuration is similar to the first one. It has a single membership function with two rules, as represented in
Figure 8. For this time, the membership degree is determined by the mean speeds.
5. Conclusions
The prediction step and ANFIS technique improvements were proposed in this research work. The development of a P-DWA increases the path mean speed, because the prediction step has better optimization than the DWA. In other words, the prediction step can analyze what will be happen in the next steps, and it can anticipate some situations. Thus, it could be possible to obtain a better performance for the path.
In comparison, P-DWA is faster than DWA, adopting an alternative trajectory to maintain the top speed, despite reducing speed and crossing between two obstacles. Thus, P-DWA maintains more distance between the AGV and obstacle, doing a safety avoidance maneuver.
Furthermore, the prediction sample time has a fixed value, which is 0.5 s. It could be interesting to analyze the behavior of the P-DWA algorithm with different values. Obviously, the low or high values can alter the improvement of the prediction step. With large prediction values, the dynamic obstacles can change the position, hence, the prediction would be wrong. With low values, the algorithm does not have enough information to find an optimum path to avoid an obstacle. Therefore, DWA and P-DWA would have the same behavior.
Apart from P-DWA, the ANFIS algorithm is introduced to optimize the fuzzy inferences. The results show that ANFIS can improve the P-DWA and DWA behavior, changing the parameters depending on the scenario conditions. This configuration is optimized to solve four maps. To improve the ANFIS performance, this algorithm should have a particular training for each map.
Moreover, it is remarkable that the trained-data selection is not the best one to easily solve all of the maps. Nevertheless, adopting different restrictions, such us not crossing obstacles, if the gap is less than a particular distance; speed restriction; and time restriction, the ANFIS behavior can be improved significantly. The aim of this research is not to obtain the best fuzzy inference to solve these four maps. It is to introduce a novel system to develop a classic motion controller, which uses static parameters.
For future work, it could be interesting to analyze the obstacles variance to determinate if there is any moving obstacle. Considering this parameter, AGV has to change speed and direction in order to solve this particular case. Furthermore, it could be interesting to adopt different restrictions to improve the ANFIS resolution, like implementing a more restrictive rejection time.