Network-Wide Throughput Optimization for Highway Vehicle-To-Vehicle Communications
Abstract
1. Introduction
2. Related Work
3. System Model
4. Analysis
Throughput Optimization
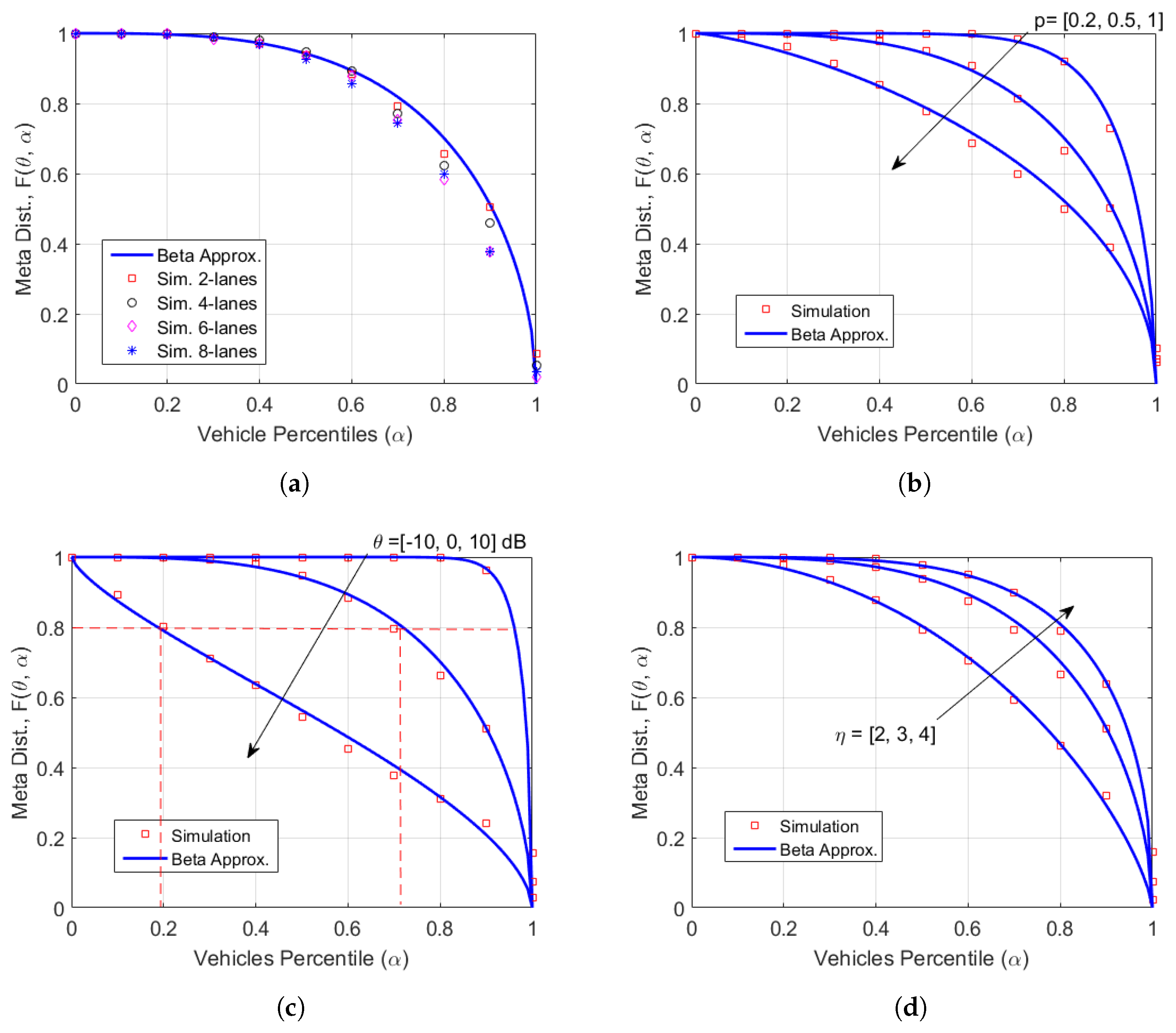
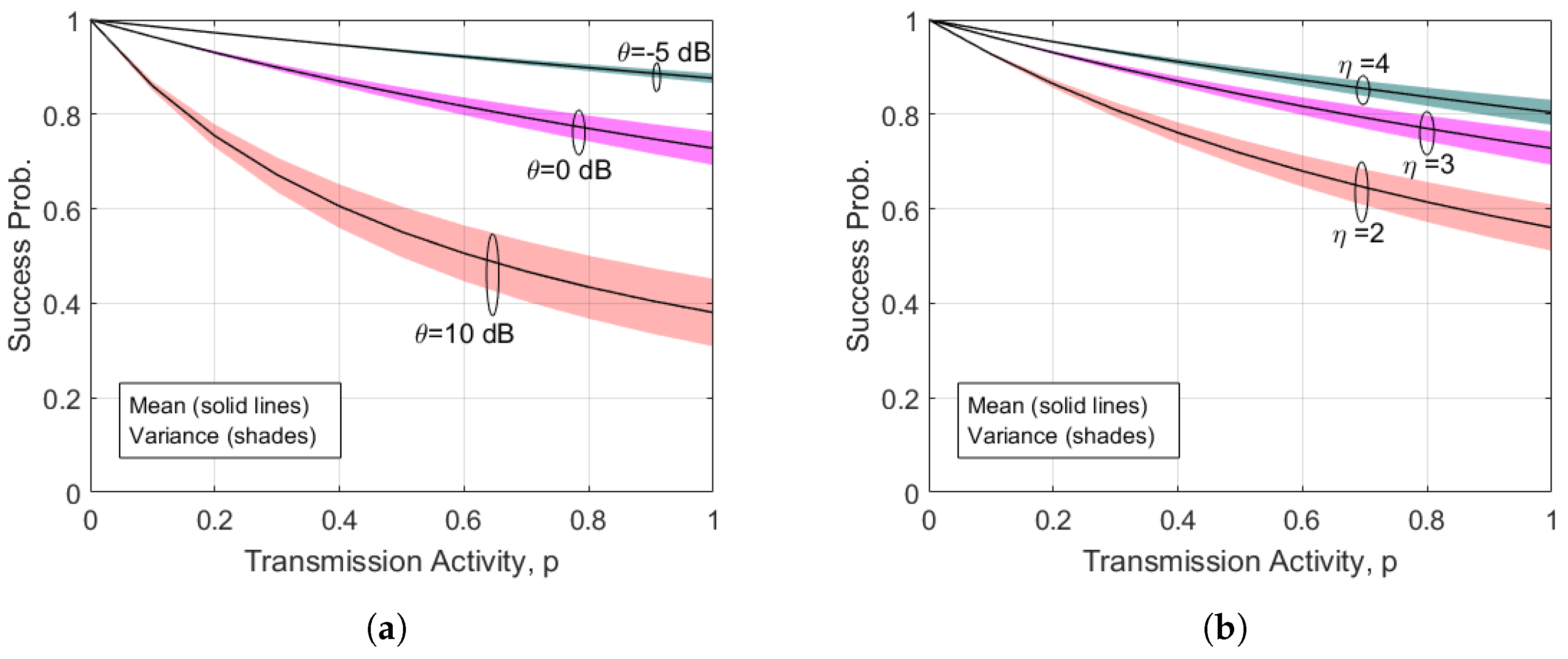
5. Numerical Results
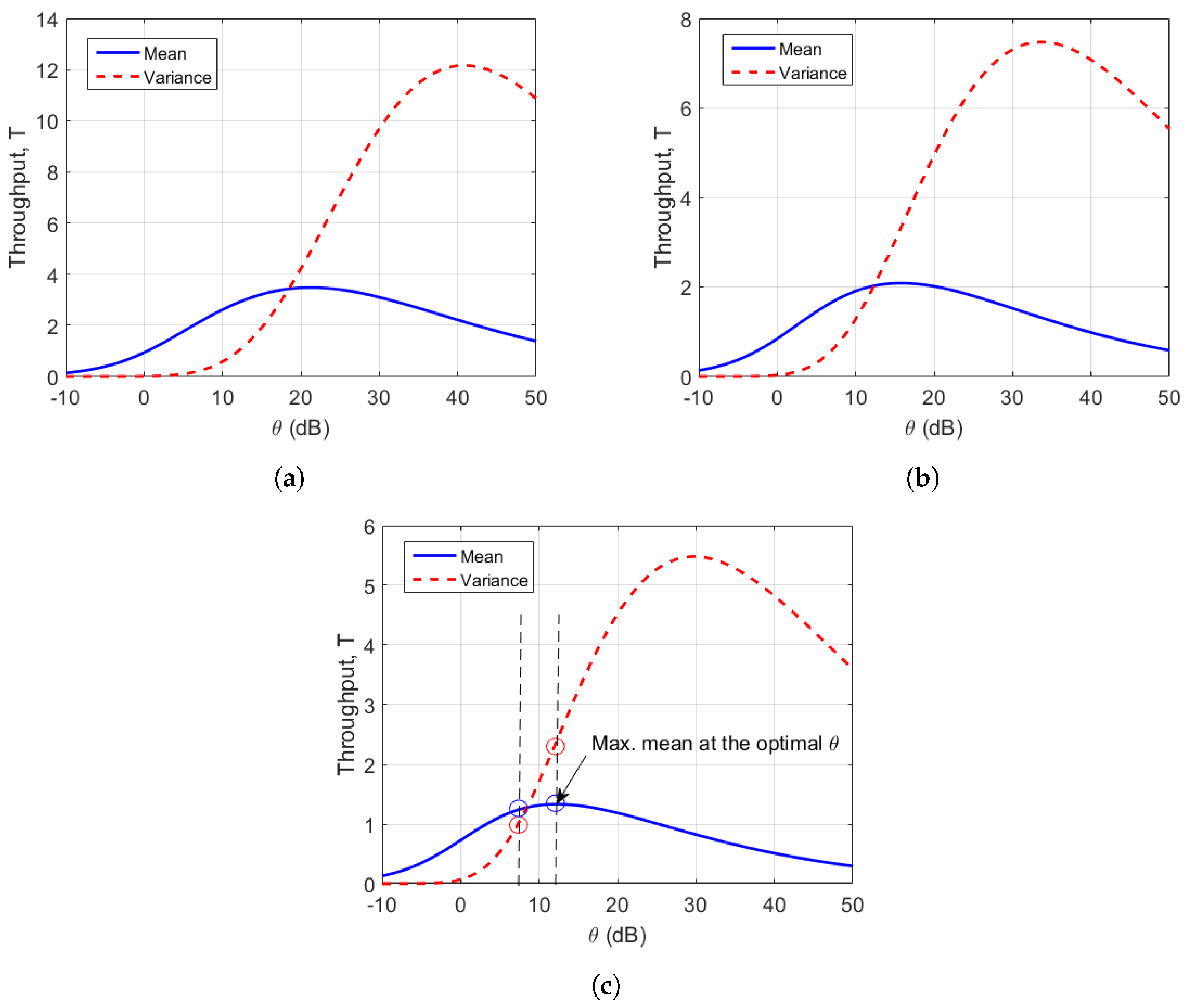
Throughput Evaluation
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- The World Health Report 2015—Reducing Risks, Promoting Healthy Life. Available online: http://www.who.int/whr/2002/chapter4/en/index7.html (accessed on 30 June 2017).
- Review of NHTSA Proposal to Mandate V2V Communication for Safety. Available online: https://www.cargroup.org/publication/review-nhtsa-proposal-mandate-v2v-communication-safety/ (accessed on 5 February 2017).
- Kenney, J.B. Dedicated Short-Range Communications (DSRC) Standards in the United States. Proc. IEEE 2011, 99, 1162–1182. [Google Scholar] [CrossRef]
- Dedicated Short Range Communications (DSRC) Message Set Dictionary. Available online: http://standards.sae.org/j2735_201603/ (accessed on 20 October 2018).
- Hadded, M.; Muhlethaler, P.; Laouiti, A.; Zagrouba, R.; Saidane, L.A. TDMA-Based MAC Protocols for Vehicular Ad Hoc Networks: A Survey, Qualitative Analysis, and Open Research Issues. IEEE Commun. Surv. Tutor. 2015, 17, 2461–2492. [Google Scholar] [CrossRef]
- Abd El-Gawad, M.A.; Elsharief, M.; Kim, H. A cooperative V2X MAC protocol for vehicular networks. EURASIP J. Wirel. Commun. Netw. 2019, 2019, 65. [Google Scholar] [CrossRef]
- Luong, H.P.; Panda, M.; Vu, H.L.; Vo, B.Q. Beacon Rate Optimization for Vehicular Safety Applications in Highway Scenarios. IEEE Trans. Veh. Technol. 2018, 67, 524–536. [Google Scholar] [CrossRef]
- Sommer, C.; Joerer, S.; Segata, M.; Tonguz, O.K.; Cigno, R.L.; Dressler, F. How Shadowing Hurts Vehicular Communications and How Dynamic Beaconing Can Help. IEEE Trans. Mob. Comput. 2015, 14, 1411–1421. [Google Scholar] [CrossRef]
- Lyamin, N.; Vinel, A.; Smely, D.; Bellalta, B. ETSI DCC: Decentralized Congestion Control in C-ITS. IEEE Commun. Mag. 2018, 56, 112–118. [Google Scholar] [CrossRef]
- Bansal, G.; Kenney, J.B.; Rohrs, C.E. LIMERIC: A Linear Adaptive Message Rate Algorithm for DSRC Congestion Control. IEEE Trans. Veh. Technol. 2013, 62, 4182–4197. [Google Scholar] [CrossRef]
- ElSawy, H.; Sultan-Salem, A.; Alouini, M.S.; Win, M.Z. Modeling and analysis of cellular networks using stochastic geometry: A tutorial. IEEE Commun. Surv. Tutor. 2017, 19, 167–203. [Google Scholar] [CrossRef]
- ElSawy, H.; Hossain, E.; Haenggi, M. Stochastic Geometry for Modeling, Analysis, and Design of Multi-Tier and Cognitive Cellular Wireless Networks: A Survey. IEEE Commun. Surv. Tutor. 2013, 15, 996–1019. [Google Scholar] [CrossRef]
- Nguyen, T.V.; Baccelli, F.; Zhu, K.; Subramanian, S.; Wu, X. A performance analysis of CSMA based broadcast protocol in VANETs. In Proceedings of the 2013 Proceedings IEEE INFOCOM, Turin, Italy, 14–19 April 2013; pp. 2805–2813. [Google Scholar] [CrossRef]
- Blaszczyszyn, B.; Mühlethaler, P.; Toor, Y. Maximizing throughput of linear vehicular Ad-hoc NETworks (VANETs)—A stochastic approach. In Proceedings of the 2009 European Wireless Conference, Aalborg, Denmark, 17–20 May 2009; pp. 32–36. [Google Scholar] [CrossRef]
- Zanella, A.; Bazzi, A.; Pasolini, G.; Masini, B.M. On the Impact of Routing Strategies on the Interference of Ad Hoc Wireless Networks. IEEE Trans. Commun. 2013, 61, 4322–4333. [Google Scholar] [CrossRef]
- Farooq, M.J.; ElSawy, H.; Alouini, M.S. A Stochastic Geometry Model for Multi-Hop Highway Vehicular Communication. IEEE Trans. Wirel. Commun. 2016, 15, 2276–2291. [Google Scholar] [CrossRef]
- Steinmetz, E.; Wildemeersch, M.; Quek, T.Q.; Wymeersch, H. A Stochastic Geometry Model for Vehicular Communication near Intersections. In Proceedings of the 2015 IEEE Globecom Workshops (GC Wkshps), San Diego, CA, USA, 6–10 December 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Tong, Z.; Lu, H.; Haenggi, M.; Poellabauer, C. A Stochastic Geometry Approach to the Modeling of DSRC for Vehicular Safety Communication. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1448–1458. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, Y.; Yang, Y.; Wang, X.; Zhang, Y.; Hong, X.; Mao, G. Multi-Hop Connectivity Probability in Infrastructure-Based Vehicular Networks. IEEE J. Sel. Areas Commun. 2012, 30, 740–747. [Google Scholar] [CrossRef]
- Chetlur, V.V.; Dhillon, H.S. Coverage Analysis of a Vehicular Network Modeled as Cox Process Driven by Poisson Line Process. IEEE Trans. Wirel. Commun. 2018, 17, 4401–4416. [Google Scholar] [CrossRef]
- Bazzi, A.; Zanella, A.; Cecchini, G.; Masini, B.M. Analytical Investigation of Two Benchmark Resource Allocation Algorithms for LTE-V2V. IEEE Trans. Veh. Technol. 2019, 68, 5904–5916. [Google Scholar] [CrossRef]
- Choi, C.; Baccelli, F. An Analytical Framework for Coverage in Cellular Networks Leveraging Vehicles. IEEE Trans. Commun. 2018, 66, 4950–4964. [Google Scholar] [CrossRef]
- Martín-Vega, F.J.; Soret, B.; Aguayo-Torres, M.C.; Kovács, I.Z.; Gómez, G. Geolocation-Based Access for Vehicular Communications: Analysis and Optimization via Stochastic Geometry. IEEE Trans. Veh. Technol. 2018, 67, 3069–3084. [Google Scholar] [CrossRef]
- Wang, Y.; Venugopal, K.; Molisch, A.F.; Heath, R.W. MmWave Vehicle-to-Infrastructure Communication: Analysis of Urban Microcellular Networks. IEEE Trans. Veh. Technol. 2018, 67, 7086–7100. [Google Scholar] [CrossRef]
- Haenggi, M. The meta-distribution of the SIR in Poisson bipolar and cellular networks. IEEE Trans. Wirel. Commun. 2016, 15, 2577–2589. [Google Scholar] [CrossRef]
- Giang, A.T.; Busson, A.; Di Renzo, M. Modeling and optimization of CSMA/CA in VANET. Ann. Oper. Res. 2016, 239, 553–568. [Google Scholar] [CrossRef][Green Version]
- Eichler, S. Performance Evaluation of the IEEE 802.11p WAVE Communication Standard. In Proceedings of the 2007 IEEE 66th Vehicular Technology Conference, Baltimore, MD, USA, 30 September–3 October 2007; pp. 2199–2203. [Google Scholar] [CrossRef]
- Gil-Pelaez, J. Note on the inversion theorem. Biometrika 1951, 38, 481–482. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abd El-Gawad, M.A.; ElSawy, H.; Sakr, A.H.; Kim, H. Network-Wide Throughput Optimization for Highway Vehicle-To-Vehicle Communications. Electronics 2019, 8, 830. https://doi.org/10.3390/electronics8080830
Abd El-Gawad MA, ElSawy H, Sakr AH, Kim H. Network-Wide Throughput Optimization for Highway Vehicle-To-Vehicle Communications. Electronics. 2019; 8(8):830. https://doi.org/10.3390/electronics8080830
Chicago/Turabian StyleAbd El-Gawad, Mohamed A., Hesham ElSawy, Ahmed Hamdi Sakr, and HyungWon Kim. 2019. "Network-Wide Throughput Optimization for Highway Vehicle-To-Vehicle Communications" Electronics 8, no. 8: 830. https://doi.org/10.3390/electronics8080830
APA StyleAbd El-Gawad, M. A., ElSawy, H., Sakr, A. H., & Kim, H. (2019). Network-Wide Throughput Optimization for Highway Vehicle-To-Vehicle Communications. Electronics, 8(8), 830. https://doi.org/10.3390/electronics8080830





