Machine Learning Interpretability: A Survey on Methods and Metrics

Abstract

Machine learning systems are becoming increasingly ubiquitous. These systems’s adoption has been expanding, accelerating the shift towards a more algorithmic society, meaning that algorithmically informed decisions have greater potential for significant social impact. However, most of these accurate decision support systems remain complex black boxes, meaning their internal logic and inner workings are hidden to the user and even experts cannot fully understand the rationale behind their predictions. Moreover, new regulations and highly regulated domains have made the audit and verifiability of decisions mandatory, increasing the demand for the ability to question, understand, and trust machine learning systems, for which interpretability is indispensable. The research community has recognized this interpretability problem and focused on developing both interpretable models and explanation methods over the past few years. However, the emergence of these methods shows there is no consensus on how to assess the explanation quality. Which are the most suitable metrics to assess the quality of an explanation? The aim of this article is to provide a review of the current state of the research field on machine learning interpretability while focusing on the societal impact and on the developed methods and metrics. Furthermore, a complete literature review is presented in order to identify future directions of work on this field.

1. Introduction

The ubiquity of machine learning systems is unquestionable: These are becoming increasingly present in different domains and becoming increasingly capable of different tasks. Regarding the presence of machine learning in the contemporary society, this evolution has accentuated the need and importance of machine learning interpretability, which only in the last half-decade has started gaining some traction as a research field. Nevertheless, when in comparison with the focus on developing machine learning techniques and models themselves as well as the focus on achieving better performance metrics, interpretable machine learning research is still a relatively small subset of the whole machine learning research.

Given the importance of interpretability in machine learning, this means there is a clear need to increase the focus on this research field in order to increase progress and converge scientific knowledge. This article aims to be a step forward in that direction by gathering all the relevant details on the research field of machine learning interpretability. Despite being a survey, this article takes a stand on how important interpretability is for our society and our future and on the importance of the sciences involved coming together and producing further and sustained knowledge on this field. The aim is to thoroughly describe the relevance of the field as well as to piece together the existing scientific literature in order to encourage and facilitate future research on this field while encapsulating the pertinent concepts that belong to interpretable machine learning. This review differs from others in that it focuses on the societal impact that interpretable machine learning can have as well as on the methods and metrics that were developed within this research field.

The article is structured as follows. In Section 2, it is given the full context of interpretability in machine learning, going through its emergence while stating its current awareness in today’s society. Afterwards, Section 3 details and explains the motivation and challenges of the field, including high-stakes decisions, societal concerns, and regulation. Following that, Section 4 consists of a thorough literature review where the relevant concepts are explained, as well as how they connect with each other, functioning as a basis for new knowledge. Section 5 describes existing approaches on interpretability assessment. Lastly, conclusions are drawn in Section 6.

2. Context

This section gives a full picture of the context of interpretable machine learning. From the field emergence to its current awareness, this section shows the evolution of the field in the last years and its relevance in our society.

2.1. Relevance

Due to the exponential increase of heterogeneous data collection and massive amount of computational power, machine learning (ML) systems have been reaching greater predictive performance and, for most of them, greater complexity. For example, introduced in 2016, deep residual networks (ResNets) [1] are over 200-layers deep and have been shown to beat human-level performance on object recognition tasks.

Along with the performance improvements, ML systems are increasingly present in diverse domains, products, and services. Whether the presence is in our daily life, with examples ranging from movie recommendation systems to personal voice assistants, or in highly regulated domains involving decisions of great impact, such as mortgage approval models or healthcare decision support systems, the democratization of Artificial Intelligence (AI) in our society is undeniable [2].

To translate this situation into numbers, International Data Corporation (IDC) estimates that worldwide investment on AI will grow from 24 billion U.S. dollars in 2018 to 77.7 billion U.S. dollars in 2022, being the compound annual growth rate (CAGR) for the 2017–2022 forecast period of 37.3% [3]. Moreover, the market intelligence firm Tractica forecasts that global revenue from AI software implementations will increase from $8.1 billion U.S. dollars in 2018 to $105.8 billion U.S. dollars by 2025 [4]. Additionally, according to Gartner, a renowned research and advisory company, AI is the essential foundation for the top 3 strategic technology trends for 2019: autonomous things, augmented analytics, and AI-driven development [5]. Consequently, the widespread use of AI implies an increasingly significant impact on society [2].

2.2. Field Emergence

Though ML algorithms appear powerful in terms of results and predictions, they have their own limitations and pitfalls. The most significant one is the opaqueness or the lack of transparency [6], which inherently characterizes black box ML models. This means that these models’ internal logic and inner workings are hidden to the user, which is a serious disadvantage as it prevents a human, expert, or nonexpert from being able to verify, interpret, and understand the reasoning of the system and how particular decisions are made [7]. In other words, any sufficiently complex system acts as a black box when it becomes easier to experiment with than to understand [8]. Many ML models, including top performing models in various domains, belong to this group of black box models [9], such as ensembles or Deep Neural Networks (DNN).

There has been an increasing trend in healthcare, criminal justice, and other regulated domains to leverage ML for high-stakes prediction applications, which deeply impact human lives [9]. Regarding high-stakes decisions, the stated problem is further compounded because entrusting important decisions to a system that cannot explain itself and cannot be explained by humans presents evident dangers [2].

In an attempt to address this issue (which is of great relevance for our society, the industry, and especially the ML community), Explainable Artificial Intelligence (XAI) emerged as a field of study which focuses research on machine learning interpretability and aims to make a shift towards a more transparent AI. The main goal is to create a suite of interpretable models and methods that produce more explainable models whilst preserving high predictive performance levels [2].

2.3. Historical Context

The term XAI was coined by Lent et al. in order to describe the ability of their system to explain the behavior of AI-controlled entities in simulation game applications [10]. With respect to interpretability itself, historically speaking, there has been sporadic interest in explanations of intelligent systems since the 1970s, beginning with attention on expert systems [11,12,13]; to, a decade after, neural networks [14]; and then to recommendation systems in the 2000s [15,16]. Notwithstanding, the pace of progress towards resolving such problems has slowed down around a decade ago, since the priority of AI research has shifted towards implementing algorithms and models that are focused on predictive power, while the ability to explain decision processes has taken a back seat. Recently, the achievements of ML systems for many domains of high interest, as well as the use of increasingly complex and nontransparent algorithms, such as deep learning, calls for another wave of interest in the need to have a greater understanding of the aforementioned systems’ outputs [17].

2.4. Awareness

2.4.1. Public Awareness

One of the most notable entities in this research field is the Defense Advanced Research Projects Agency (DARPA), which, while funded by the U.S. Department of Defense, created the XAI program for funding academic and military research and resulted in funding for 11 U.S. research laboratories [18]. Regarding the program information, David Gunning, program manager in the Information Innovation Office (I2O) at the time of writing, states that the program aims to produce more explainable models while maintaining high predictive performance levels, enabling appropriate human trust and understanding for better management of the emerging generation of artificially intelligent partners [19].

Nevertheless, this is not the only example of public focus on AI interpretability. With regard to the United States, in 2016, the White House Office of Science and Technology Policy (OSTP) released the U.S. report on AI titled “Preparing for the Future of Artificial Intelligence”, in which it is stated that it should be ensured that AI systems are open, transparent, and understandable so that people can interrogate the assumptions and decisions behind the models’ decisions [20].

Also, the Association for Computing Machinery US Public Policy Council (USACM) released a “Statement on algorithmic transparency and accountability” in 2017, in which it is stated that explainability is one of the seven principles for algorithmic transparency and accountability and the it is particularly important in public policy contexts [21].

Other countries have also made public the demand for AI interpretability. One example is the draft version of the Dutch AI Manifesto (created by IPN SIG AI in 2018), which is utterly focused on explainable AI, stating the the utmost importance of AI systems is being not only accurate but also able to explain how the system came to its decision [22].

Another example is the French Strategy for Artificial Intelligence, presented in 2018 by the President of the French Republic, containing a set of proposals in which the first one is to develop algorithm transparency and audits, which entails producing more explainable models and interpretable user interfaces and understanding the mechanisms in order to produce satisfactory explanations [23].

The Royal Society, which is the United Kingdom’s (UK) Academy of Sciences, published in April 2017 a report on their machine learning project [24]. The report recognizes the importance of interpretability and transparency as well as responsibility and accountability as social issues associated with machine learning applications. Further, interpretability and transparency are considered one of the key areas belonging to the new wave of ML research, noting that support for research in these areas can help ensure continued public confidence in the deployment of ML systems.

Portugal, through its National Initiative on Digital Skills, has published a draft version of the document AI Portugal 2030, outlining an innovation and growth strategy to foster Artificial Intelligence in Portugal in the European context [25]. The document, which represents the current version of the Portuguese national AI strategy, presents transparent AI as one of the fundamental research lines in the future of AI. Additionally, it states that AI will bring ethics and safety as societal challenges, meaning that society will demand transparency and accountability, for which AI-made decision explainability is needed.

Regarding Europe, in April 2018, the European Commission published a communication to many official European bodies, such as the European Parliament and the European Council, on Artificial Intelligence for Europe. In the communication, it is stressed the importance of research into the explainability of AI systems (and of supporting it) to further strengthen people’s trust in AI. Moreover, it is stated that “AI systems should be developed in a manner which allows humans to understand (the basis of) their actions” in order to increase transparency and to minimize the risk of bias error [26]. Within the context of supporting research in the development of explainable AI, the European Commission implemented in March 2018 a 16-month pilot project, proposed by the European Parliament, called Algorithmic Awareness Building [27]. The project, of which the topic is algorithm transparency, consists of an in-depth analysis of the challenges and opportunities emerging in algorithmic decision-making.

The European Union Commission, in a report from July 2018 on Responsible AI and National AI Strategies, also identifies the risk of opaqueness (or black box risk) and the risk of explainability as two performance risks for AI [28].

In April 2019, the High-Level Expert Group on Artificial Intelligence (AI HLEG), which is an independent expert group set up by the European Commission in June 2018 as part of its AI strategy, published the document Ethics Guidelines for Trustworthy AI [29]. This document lists seven key requirements that AI systems should meet in order to be trustworthy, transparency and accountability being two of those key requirements, and presents an assessment list that offers guidance on each requirement’s practical implementation. In this document, the principle of explicability is listed as one of the ethical principles in the context of AI systems. Also, when transparency is presented as one of the seven key requirements for trustworthy AI, the document shows how traceability, explainability, and communication are all important and required to reach AI transparency. Regarding explanation methods, which are stated as one of the technical methods for trustworthy AI, the document notes that “For a system to be trustworthy, we must be able to understand why it behaved a certain way and why it provided a given interpretation.”, while stressing the importance of the XAI research field.

2.4.2. Industry Awareness

Concerning AI-driven companies, Google has made public their recommended and responsible practices in different AI-related areas, one of which is entirely focused on interpretability. Some of the advocated interpretability practices include planning for interpretability, treating interpretability as a core part of the user experience, designing the model to be interpretable, understanding the trained model, and communicating explanations to model users [30].

Apart from strategies and recommended practices, interpretability is also one of the main focuses in currently commercialized ML solutions and products. H2O Driverless AI, an automated machine learning platform offered by H2O.ai, provides interpretability as one of its distinguished features [31]. DataRobot (by DataRobot), which is another commercialized ML solution, “includes several components that result in highly human-interpretable models” [32]. IBM also provides a business AI platform product called IBM Watson AI OpenScale, for which one of the highlighted features is “Trust, transparency, and explainability” [33]. Furthermore, Kyndi provides an XAI platform for government, financial services, and healthcare. Since this product is targeted at regulated business domains, the main feature of this product is, in fact, explainability [34].

In addition to focusing on interpretability for commercialized AI products, there are also companies that invest in research on ML interpretability. One such example is FICO, an analytics software company famous for using AI for credit scores, that has published a white paper “xAI Toolkit: Practical, Explainable Machine Learning” [35], which resulted in including the xAI Toolkit in their Analytics Workbench product [36]. More recently, FICO’s research team explored this topic in the paper “Developing Transparent Credit Risk Scorecards More Effectively: An Explainable Artificial Intelligence Approach” [37], which won the Best Paper Award at the Data Analytics 2018 event organized by IARIA/Think Mind [38].

There are other examples of companies of great dimension that actively invest in this research field. For instance, Google has long recognized the need for interpretability, as previously mentioned, and has developed important research that results in new tools, such as Google Vizier, a service for optimizing black box models [8]. Facebook, in collaboration with Georgia Tech, published a paper where it shows a visual exploration tool of industry-scale DNN models [39]. Uber recently announced Manifold, a model-agnostic visual debugging tool for ML. The tool is not production ready at the time of writing, but a prototype has been developed in one of the most recently published papers by their research team [40].

2.5. Science and Research Emergence

By contemplating ML interpretability as a two-way communication between two entities, the human as the user and the computer as the performer of ML models, one can consider that this research field belongs to three general research areas of science:

• Data Science—ML algorithms are data hungry, as their predictive performance is directly proportional to the quality and quantity of data they train on. More accurate predictions can lead to more accurate explanations. Moreover, one can argue the backward path that starts in the prediction results and that aims to produce better explanations is data dependent. Therefore, Dat Science, which encompasses Machine Learning, is a key component in the interpretability process.
• Human Science—In order to reach human interpretability, one should first study and model how humans produce and understand explanations between each other and which properties make explanations perceivable to humans.
• Human Computer Interaction (HCI)—the user comprehension and trust in the system is dependent on the process of interaction between the aforementioned entities. Taking into account that HCI’s fundamental interest is to empower the user and to prioritize the user’s perception [17], knowledge from this field can help in developing interpretable systems, especially in aiming for more interpretable visualizations. With the help of cognitive science and psychology, it would be even better.

This means that ML interpretability can have contributions from different areas: Advances from one of the areas can improve the research of the other areas. Hence, research communities of these areas should coordinate with each other in order to push ML interpretability further and to provide new findings together. Moreover, it is argued that impactful, widely adopted solutions to the ML interpretability problem will only be possible by truly interdisciplinary research, bridging data science with human sciences, including philosophy and cognitive psychology.

Besides the rapid growth of the volume of research on interpretability [41], the growing interest in ML interpretability has also been reflected in numerous scientific events. Some examples of sessions and workshops on the topic in major conferences are presented in

Table 1. Scientific events with focuses on interpretability.

Name	Year
Fairness, Accountability, and Transparency in Machine Learning (FAT/ML) (NIPS, ICML, DTL, KDD) [42]	2014–2018
ICML Workshop on Human Interpretability in Machine Learning (WHI) [43,44,45]	2016–2018
NIPS Workshop on Interpretable Machine Learning for Complex Systems [46]	2016
NIPS Symposium on Interpretable Machine Learning [47]	2017
XCI: Explainable Computational Intelligence Workshop [48]	2017
IJCNN Explainability of Learning Machines [49]	2017
IJCAI Workshop on Explainable Artificial Intelligence (XAI) [50,51]	2017–2018
“Understanding and Interpreting Machine Learning in Medical Image Computing Applications” (MLCN, DLF, and iMIMIC) workshops [52]	2018
IPMU 2018—Advances on Explainable Artificial Intelligence [53]	2018
CD-MAKE Workshop on explainable Artificial Intelligence [54,55]	2018–2019
Workshop on Explainable Smart Systems (ExSS) [56,57]	2018–2019
ICAPS—Workshop on Explainable AI Planning (XAIP) [58,59]	2018–2019
AAAI-19 Workshop on Network Interpretability for Deep Learning [60]	2019
CVPR—Workshop on Explainable AI [61]	2019

.

It is clear that interpretability is increasingly concerning to the research community. Scientific events definitely play an important role in promoting and encouraging interpretability research.

Furthermore, interpretability competitions have also started to show up. For example, in a collaboration between Google; FICO; and academics at renowned universities, such as Oxford and MIT, the first edition of the Explainable Machine Learning Challenge appeared at NIPS 2018, where teams were challenged to create ML models with both high accuracy and explainability [62]. The goal is to generate new research in the area of algorithmic explainability.

As such, such events and competitions are shown to be a key piece in boosting the growth of the ML interpretability field.

Additionally, there are research centers that focus in ethical AI. As expected, one of the focuses of ethical AI is ML transparency. A key example is the Institute for Ethical AI & Machine Learning, which is a UK-based research centre that carries out highly technical research into responsible machine learning systems; one of their eight principles for responsible development of ML systems is “explainability by justification” [63].

2.6. Terminology

Regarding terminology, there is some ambiguity in this field. Lipton gives a good outline of how some expressions are used in an unclear way when he notes that “the term interpretability holds no agreed upon meaning, and yet machine learning conferences frequently publish papers which wield the term in a quasi-mathematical way” [64].

Practically speaking, interpretability and explainability are tied concepts, often used interchangeably [65]. As stated by Adadi and Berrada, explainability is closely related to the concept of interpretability: Interpretable systems are explainable if their operations can be understood by humans. Nevertheless, they also note that, in the ML community, the term interpretable is more used than explainable [2], which is confirmed by the Google Trends comparison between both terms in Figure 1.

Despite the interchangeability concerning the use of both terms by many authors, there are others that develop some distinguishability between them [9,66,67].

In 2017, a UK Government House of Lords review of AI received substantial expert evidence and noted, “the terminology used by our witnesses varied widely. Many used the term transparency, while others used interpretability or ‘explainability’, sometimes interchangeably”. Intelligibility ended up being their choice [68]. Others have also used the term legibility [69]. In this work, both interpretability and explainability terms will be used interchangeably in the broad general sense of understandability in human terms.

3. Motivation and Challenges

This section explains the reasons why interpretability is of high need to our society. Furthermore, this section also details the challenges this research field is facing.

3.1. Interpretability Requirement

If a machine learning model performs well enough and has an acceptable predictive performance, why do we not just trust the model and disregard why it made a certain decision? Doshi-Velez and Kim answer this question by stating that “the problem is that a single metric, such as classification accuracy, is an incomplete description of most real-world tasks” [41].

Nevertheless, it is worth taking into account that, although the relevance and importance of interpretability has clearly been explained, not all ML systems require interpretability, as there are situations where being able to provide high predictive performance is enough [41], with no need for explaining decisions.

For that reason, according to Doshi-Velez and Kim, there are two kinds of situations where interpretability and, thus, explanations are not necessary [41]: (1) when there is no significant impact or severe consequences for incorrect results and (2) when the problem is well-studied enough and validated in real applications that we trust the system’s decisions, even if the system is not perfect.

The former situation refers to low-risk systems, such as product recommenders and advertisement systems, where a mistake has no severe or even fatal consequences [70]. The latter refers to well-studied systems that have been used for a while, including postal code sorting and aircraft collision systems [71], which compute their output without human intervention.

3.2. High-Stakes Decisions Impact

In the abovementioned circumstances, it is only required to know what was predicted. However, in the majority of cases, it is also very important to know why a certain prediction was made because a correct prediction only partially solves the original problem (this idea is better developed in Section 3.5). As stated in Section 2.2, there has been an increasing trend in healthcare and financial services as well as in other strictly regulated domains to leverage ML systems for high-stakes decisions that deeply impact human lives and society [9], which pushes the demand for interpretability even further.

Nonetheless, the fact that ML is already supporting high-stakes decisions does not mean that it is not prone to errors as various situations where the lack of transparency and accountability of predictive models had severe consequences in different domains has already occurred. These include cases of people incorrectly denied parole [72], incorrect bail decisions leading to the release of potentially dangerous criminals, pollution models stating that dangerous situations are safe [73], and more incidents in other domains, such as healthcare and finance [74]. On top of that, there is evidence that incorrect modeling assumptions were, at least, partially responsible for the recent mortgage crisis [75].

The worst part of such situations is that wronged people remain with little recourse to argue, and on top of that, most of the entities behind these decision support systems cannot explicitly determine how these decisions were made due to the lack of transparency of the same systems.

3.3. Societal Concerns and Machine Learning Desiderata

Going more into detail on wrong algorithmic decisions in sensitive contexts, there is already clear evidence on biased decisions being made with significant impact. One such example is the Correctional Offender Management Profiling for Alternative Sanctions (COMPAS), a widely used criminal risk assessment algorithmic tool which was shown to perform unreliable and biased decisions, harming minority groups [76,77].

When it comes to proprietary, closed source software, such as COMPAS, it is expected that companies try their best to avoid auditing and revealing intellectual propriety. Indeed, the biased decisions made by COMPAS were more difficult to audit because of this [76]. However, it is important to mitigate concerns around trade secrets: Interpretability is a reasonable solution for this problem because explanations can be provided without revealing the internal logic of the system [78].

The importance of handling and understanding wrong decisions comes from the reality that wrong decisions will not cease to exist: Decision systems are not 100% perfect, and it is expected that real-world issues will also exist in ML systems. This does not mean that an ML model is inherently bad. Nevertheless, it is only as good as the information that it is trained with. This means that when real-world data (which potentially contains biased distributions) is fed to a model, then it learns these patterns and returns predictions that are oriented towards such behaviour. Consequently, through biased decisions with significant impact, this can lead to the discrimination of several minority groups [79].

Moreover, as argued by O’Neil [80], compared to human decision making, which can adapt and thus evolve, machines stay the same until engineers intervene to change them. For example, complementing the argument of the previous paragraph, a hypothetical ML model for processing college applications that was trained with data from the 1960s would be expect to be largely inclined towards men in comparison to women due to the data that it was trained with. In other words, ML systems codify the past while not having the capability to evolve or invent the future [80]. That is why it is so critical to conduct algorithmic audits to detect discrimination and bias as well as to embed ethical values into these systems in order to prevent this type of issue.

Therefore, explanations are of uttermost importance to ensure algorithmic fairness, to identify potential bias/problems in the training data, and to ensure that algorithms are performing as expected [66]. Using knowledge from the psychology literature, Keil et al. [81] state that “explanations may highlight an incompleteness”. As the example from this subsection confirms, it is thus very relevant to state that interpretability can and should be used to confirm important desiderata of ML systems, and these desiderata can be some auxiliary criteria that one may wish to optimize. Doshi-Velez and Kim [41] specified the desiderata that can be optimized through interpretability:

• Fairness—Ensure that predictions are unbiased and do not implicitly or explicitly discriminate against protected groups. Explanations help humans to judge whether the decision is based on a learned demographic (e.g., racial) bias.
• Privacy—Ensure that sensitive information in the data is protected.
• Reliability/Robustness—Ensure that small changes in the input do not cause large changes in the prediction.
• Causality—Ensure that only causal relationships are picked up. Deeming causality as the measurement of mapping technical explainability with human understanding, it plays an utterly important role to ensure effective interactions between humans and ML systems. Furthermore, Holzinger et al. [82] propose the notion of causability as the degree to which an explanation to a human expert achieves a specified level of causal understanding with effectiveness, efficiency, and satisfaction in a specified context of use. In other words, causability is the property of the human to understand the system explanations [83]. Consequently, the key to effective human–AI interaction is an efficient mapping of explainability (in the sense of a technical explanation that explain the results of a system) with causability, this being one of the most important end goals of (explainable) ML systems.
• Trust—It is easier for humans to trust a system that explains its decisions rather than a black box that just outputs the decision itself.

Obviously, ML systems may have different end goals: for example, in healthcare the end goal could be to save more patient lives, while in banking, the end goal could be to minimize the number of credit defaults. Notwithstanding, the aforementioned desiderata represent important downstream tasks that one might wish to optimize while still aiming for the end goal of the system. These downstream tasks may also be part of the problem specification, e.g., a bank wants to minimize the number of credit defaults while providing unbiased opportunities to people (fairness) and, thus, should be taken into account when refining the system, which would not be possible without interpretability.

3.4. Regulation

As a consequence of the path towards which our society is progressing, as well as the situations mentioned in the previous Section 3.2 and Section 3.3, new regulations have recently been imposed in order to require verifiability, accountability, and, more importantly, full transparency of algorithmic decisions. A key example is the new European General Data Protection Regulation (GDPR and ISO/IEC 27001) [84], which became enforceable since May 2018, and provides data subjects with the right to an explanation of algorithmic decisions [85]. This does not imply outlawing automatic prediction systems or an obligation to explain everything all the time, but there must be a possibility to make the results re-traceable on demand [86], which may represent a challenging technical task [87]. Additionally, it is necessary to better define when and what kind of explanation might be required [88,89]—what is the most appropriate explanation for each case?

3.5. The Interpretability Problem

As stated in the beginning of Section 3, the need for interpretability arises from an incompleteness in problem formalization [41], which means that, for certain problems or prediction tasks, it is not enough to get the prediction (the what). The model must also explain how it came to the prediction (the why) because a correct prediction only partially solves the original problem.

Moreover, this incompleteness in problem specification can be shown in different scenarios, some of which include the following [41]:

• Safety—because the system is never completely testable, as one cannot create a complete list of scenarios in which the system may fail.
• Ethics—because the human notion of, e.g., fairness can be too abstract to be entirely encoded into the system.
• Mismatched objectives—because the algorithm may be optimizing an incomplete objective, i.e., a proxy definition of the real ultimate goal.
• Multi-objective trade-offs—Two well-defined desiderata in ML systems may compete with each other, such as privacy and prediction quality [90].

One of the reasons behind this unsolved interpretability problem is that interpretability is a very subjective concept and, therefore, hard to formalize [91]. Furthermore, interpretability is a domain-specific notion [91,92], so there cannot be an all-purpose definition [9]. Depending on the context, different types of explanations might be useful. For example, one might want to personally know the main two reasons why a mortgage was declined by the bank, but in a legal scenario, a full explanation with a list of all factors might be required.

Following this example, it is important to take into consideration that, given the number of existing interpretability methods, the need for comparing, validating, quantifying, and thus evaluating these methods arises [2]. Therefore, taking into account the properties of this interpretability problem, it is evident that it is necessary to know what are the methods and explanations which, for a certain problem, including the domain and the use case, provide the greatest satisfaction to a certain audience.

3.6. Towards the Success of AI

A strength of humans is intuition and reasoning [93]. Thus, for the success of AI as an indispensable tool for decision support, it must not only bring forth relevant information for the decision making task but also communicate at an appropriate rate and in a way that allows a human recipient of the information to tap into the strengths of intuition and reasoning [94]. Interpretability is, thus, a necessary milestone for the success of ML and AI themselves. As stated by O’Neil [80], “in the end, mathematical models should be our tools, not our masters”—which is only possible with interpretability.

4. Literature Review

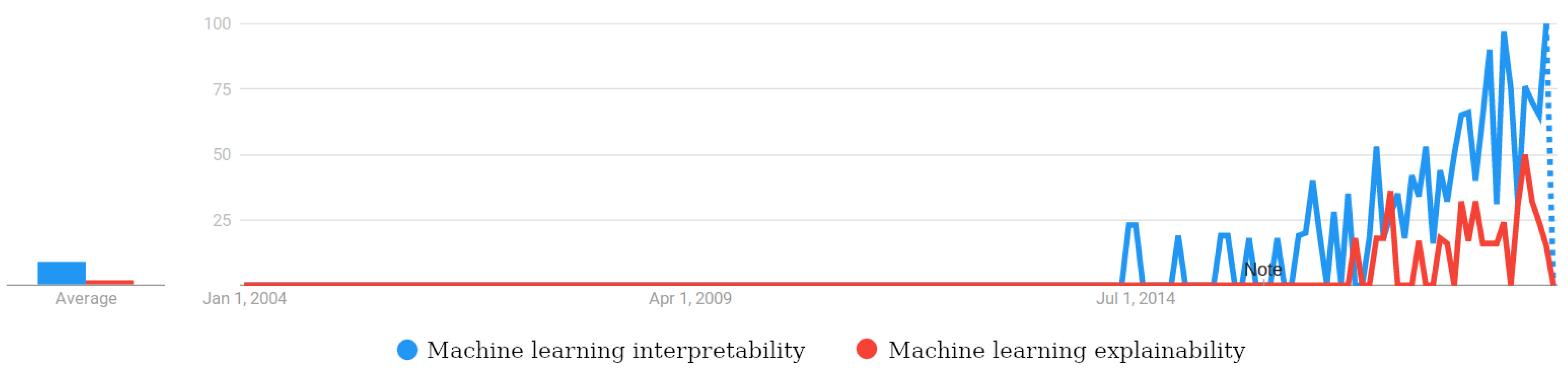
This section results from a detailed literature review, gathering the concepts connected with interpretable machine learning and explaining their details and how they connect with each other.

4.1. Interpretability

There is no mathematical definition of interpretability. A (nonmathematical) definition given by Miller is “Interpretability is the degree to which a human can understand the cause of a decision” [95]. In the context of machine learning (ML) systems, Kim et al. describe interpretability as “the degree to which a human can consistently predict the model’s result” [96]. This means that the interpretability of a model is higher if it is easier for a person to reason and trace back why a prediction was made by the model. Comparatively, a model is more interpretable than another model if the prior’s decisions are easier to understand than the decisions of the latter [95].

More recently, Doshi-Velez and Kim define interpretability as the “ability to explain or to present in understandable terms to a human” [41]. Molnar notes that “interpretable machine learning refers to methods and models that make the behavior and predictions of machine learning systems understandable to humans” [70]. Consequently, interpretability is evidently related to the ability of how well humans grasp some information by looking and reasoning about it.

Roughly speaking, one could argue that there are two different broad paths towards interpretability: creating accurate interpretable-by-nature models, either by imposing constraints or not, and creating explanation methods which are applicable to existing (and future) black box, opaque models.

4.2. Importance of Interpretability in Machine Learning

Many reasons make interpretability a valuable and, sometimes, even indispensable property. Notwithstanding, it is worth to note that, as seen in Section 3.1, not all ML systems need interpretability, since, in some cases, it is sufficient to have an acceptable predictive performance. Otherwise, interpretability can provide added value in different ways.

Firstly, interpretability is a means to satisfy human curiosity and learning [95]. Obviously, humans do not need an explanation for everything they see, e.g., most people do not want or need to know how their computer works. However, the situation is quite different when humans are dealing with unexpected events, as they make humans curious, urging the need to know the reasons why they happened.

Humans have a mental model of their environment that is updated when an unexpected event happens, and this update is performed by finding an explanation for such event. In the same way, explanations and, thus, interpretability are crucial to facilitate learning and to satisfy curiosity as to why certain predictions are performed by algorithms. On top of that, it is important to take into consideration that when opaque machine learning models are used in research, scientific findings remain completely hidden if the model is a black box that only gives predictions without explanations [70].

Another advantage of interpretability is that it helps to find meaning in the world [95]. Decisions based on ML models have increasing impact in peoples’ lives, which means it is of increasing importance for the machine to explain its behavior. If an unexpected event happens, people can only reconcile this inconsistency between expectation and reality with some kind of explanation. for example, if a bank’s ML model rejects a loan application, the applicant will probably want to know, at least, the main causes for such a decision (or what needs to be changed).

However, as seen in Section 3.4, under the new European General Data Protection Regulation (GDPR), the applicant effectively has the so-called right to be informed [89] and a list of all the decision factors might be required. Another example where explanations provide meaningful information is in products or movie recommendations, which usually are accompanied by the motive of recommendation, i.e., a certain movie was recommended because other users who liked the same movies also appreciated the recommended movie [70].

The above example leads towards another benefit of interpretability: social acceptance, which is required for the process of integrating machines and algorithms into our daily lives. A few decades ago, Heider and Simmel [97] have shown that people attribute beliefs and intentions to abstract objects. Therefore, it is intuitive that people will more likely accept ML models if their decisions are interpretable. This is also argued by Ribeiro et al. [98], who state that “if the users do not trust a model or a prediction, they will not use it”. Interpretability is, thus, essential to increase human trust and acceptance on machine learning.

It is also worth noting that explanations are used to manage social interactions. By creating a shared meaning of something, the explainer influences the actions, emotions, and beliefs of the recipient of the explanation. More specifically, for a machine to successfully interact with people, it may need to shape people’s emotions and beliefs through persuasion, so that they can achieve their intended goal [70].

Another crucial value empowered by interpretability is safety [95]. Interpretability enables MLs models to be tested, audited, and debugged, which is a path towards increasing their safety, especially for domains where errors can have severe consequences. For example, in order to avoid self-driving cars running over cyclists, an explanation might show that the most important learned feature to identify bicycles is the two wheels, and this explanation helps to think about edge cases, such as when wheels are covered by side bags [70].

Interpretability also enables detection of faulty model behavior, through debugging and auditing. An interpretation for an erroneous prediction helps to understand the cause of the error. It delivers a direction for how to fix the system and, thereby, increase its safety. For example, in a husky vs. wolf image classifier, interpretability would allow to find out that misclassification occurred because the model learned to use snow as a feature for detecting wolves [70].

According to Doshi-Velez et al. [41], explaining a ML model’s decisions provides a way to check the desiderata of ML systems, as noted in Section 3.3, including fairness, privacy, and trust. In other words, interpretability enables, for example, the detection of bias that ML models learned either from the data or due to wrong parameterization, which arised from the incompleteness of the problem definition. For example, a bank’s ML model main goal is to grant loans only to people who will eventually repay them; however, the bank not only wants to minimize loan defaults but also is obliged not to discriminate on the basis of certain demographics [70].

Finally, it is also noteworthily the goal of science, which is to acquire new knowledge. In spite of that, many problems are solved with big datasets and black box ML models. The model itself becomes the source of knowledge instead of the data. Interpretability makes it possible to extract this additional knowledge captured by the model [70].

4.3. Taxonomy of Interpretability

Explanation methods and techniques for ML interpretability can be classified according to different criteria.

4.3.1. Pre-Model vs. In-Model vs. Post-Model

Interpretability methods can be grouped regarding when these methods are applicable: before (pre-model), during (in-model), or after (post-model) building the ML model [99].

Pre-model interpretability techniques are independent of the model, as they are only applicable to the data itself. Pre-model interpretability usually happens before model selection, as it is also important to explore and have a good understanding of the data before thinking of the model. Meaningful intuitive features and sparsity (low number of features) are some properties that help to achieve data interpretability.

Pre-model interpretability is, thus, closely related to data interpretability, consisting of exploratory data analysis [100] techniques. These techniques range from classic descriptive statistics to data visualization methods, including Principal Component Analysis (PCA) [101] and t-SNE [102] (t-Distributed Stochastic Neighbor Embedding), and clustering methods, such as k-means [103] and MMD-critic [96] (Maximum Mean Discrepancy).

Hence, data visualization is critical for pre-model interpretability, consisting of the graphical representation of information and data with the goal of providing a better understanding of the data. The effort in providing increasingly better visualizations can be noticed, e.g., in two recent tools developed by Google’s group of People + AI Research (PAIR): Facets Overview and Facets Dive [104].

In-model interpretability concerns ML models that have inherent interpretability in it (through constraints or not), being intrinsically interpretable. Post-model interpretability refers to improving interpretability after building a model (post hoc). These two types of interpretability are described more thoroughly in the next section, Section 4.3.2 and Section 4.3.3.

4.3.2. Intrinsic vs. Post Hoc

One of the main criteria is intrinsic vs. post hoc. This criterion is used for distinguishing whether interpretability is achieved through constraints imposed on the complexity of the ML model (intrinsic) or by applying methods that analyze the model after training (post hoc) [70].

Regarding intrinsic interpretability, this refers to models that are interpretable by themselves. This in-model interpretability can be achieved through imposition of constraints on the model, such as sparsity, monotonicity, causality, or physical constraints that come from the domain knowledge [9]. Intrinsic interpretability is also called transparency and answers the question of how the model works [64].

Post hoc (post-model) interpretability refers to explanation methods that are applied after model training. It is noteworthy that there are post hoc methods that can be applied to intrinsically interpretable models, since post hoc methods are usually decoupled from the main model. Lipton [64] argues that post hoc interpretability answers the question what else can the model tell us.

4.3.3. Model-Specific vs. Model-Agnostic

Another important criterion is model-specific vs. model-agnostic. Model-specific interpretation methods are limited to specific model classes because each method is based on some specific model’s internals [70]. For instance, the interpretation of weights in a linear model is a model-specific interpretation, since by definition, the interpretation of intrinsically interpretable models is always model-specific.

On the other hand, model-agnostic methods can be applied to any ML model (black box or not) and are applied after the model has been trained (post hoc; post-model). These methods rely on analyzing pairs of feature input and output. By definition, these methods cannot have access to the model inner workings, such as weights or structural information [70], otherwise they would not be decoupled from the black box model. Another property of these methods is that models are interpreted without sacrificing their predictive power, as they are applied after training [64].

The discussed criteria in the last sections, Section 4.3.1, Section 4.3.2 and Section 4.3.3, are related to each other in some way. This association is presented in

Table 2. Association between interpretability criteria.

Pre-model	N.A.	N.A.
In-model	Intrinsic	Model-specific
Post-model	Post hoc	Model-agnostic

.

In-model interpretability comes from models that are intrinsically interpretable. Although there are some model-specific methods that are post hoc (as seen in Section 4.6.2), most of the model-specific interpretability is achieved through models that are intrinsically interpretable. In an analogous way, post-model interpretability comes from post hoc methods. Since, by definition, post hoc methods are applied after training the model, most of these methods are decoupled from the model and, hence, are model-agnostic.

4.3.4. Results of Explanation Methods

Another criterion that allows to differentiate explanation methods is the result that each method produces [70] or, in other words, the type of explanation that each method provides:

• Feature summary—Some explanation methods provide summary statistics for each feature. This can be, e.g., a single number per feature, such as feature importance.
  Most of the feature summary statistics can be visualized as well. Some of the feature summaries are only meaningful if they are visualized, making no sense to present them in other ways, e.g., partial dependence plots are not intuitive if presented in tabular format.
• Model internals—This is the explanation output of all intrinsically interpretable models. Some methods’ outputs are both model internals and summary statistics, such as the weights in linear models. Interpretability methods that output model internals are, by definition, model-specific.
• Data point—There are methods that return data points (already existent or not) to make a model interpretable. These are example-based methods. To be useful, explanation methods that output data points require that the data points themselves are meaningful and can be interpreted. This works well for images and texts but is less useful for, e.g., tabular data with hundreds of features.
• Surrogate intrinsically interpretable model—Another solution for interpreting black box models is to approximate them (either globally or locally) with an intrinsically interpretable model. Thus, the interpretation of the surrogate model will provide insights of the original model.

One could argue that there are other ways of providing interpretability, such as rule sets, question-answering, or even explanations in natural language. In spite of this, the abovementioned results account for the vast majority of existent interpretability methods.

It is noteworthy that there is also the criterion global vs. local interpretability, but this is related to the scope of interpretability, which is better detailed in the next section, Section 4.4.

4.4. Scope of Interpretability

Interpretability tools can be classified regarding their scope, which refers to the portion of the prediction process they aim to explain.

4.4.1. Algorithm Transparency

Algorithm transparency is about how the algorithm learns a model from the data and what kind of relationships it can learn from it. This refers to how the algorithm (which generates the model itself) works but not to the specific model that is learned in the end and not to how individual predictions are made.

In other words, algorithm transparency only requires knowledge of the algorithm and not of the data or learned model as it answers the question how does the algorithm create the model [70]. One such example is the ordinary least squares method. However, the focus of ML interpretability is on the authors of the predictions: the models themselves and not on the algorithms that produce them.

4.4.2. Global Model Interpretability

On a Holistic Level

Lipton [64] designates this notion as simulatability and defines it by stating that a model can be described as interpretable if you can comprehend the entire model at once. In order to explain the global model output, it needs the trained model, knowledge of the algorithm, and the data.

This level of interpretability refers to comprehending how the model makes decisions, grounded on a holistic view of the data features and each of the learned components, e.g., weights, parameters. In other words, global model interpretability means understanding the distribution of the prediction output based on the features, answering the question how does the trained model make predictions. For this reason, it is very difficult to achieve in practice [70].

Any model that has more than 5 parameters or weights is unlikely to fit into the short-term memory of the average human, especially taking into account that humans can handle at most around 7 cognitive entities at once [105]. Moreover, the fact that people can only visualize 3 dimensions at once makes this type of interpretability even more difficult to reach. Honegger [79] argues that, for a model to fulfill this condition, it must be simple enough.

On a Modular Level

While global, holistic model interpretability is usually out of reach, there is room for comprehending at least some models on a modular level. For example, for linear models, the interpretable parts are the weights; for decision trees, the interpretable parts are the splits (features and cut-off values) and leaf node predictions. This answers the question how do parts of the model affect predictions [70]. Therefore, models that use highly engineered, anonymous, or opaque features do not fulfill this condition [79]. It is also worth noting that, e.g., interpreting a single weight in a linear model is interlocked with all other weights, meaning that this type of interpretability usually does not account for, e.g., feature interaction.

Lipton [64] designates this notion as decomposability, stating that it implies that the inputs that are used to train a model must be interpretable themselves.

Lou et al. [106] describes this as intelligibility, arguing that a Generative Additive Model (GAM) fulfills it.

4.4.3. Local Model Interpretability

For a Single Prediction

Aiming to explain a single prediction, the general idea is to zoom in on a single instance and to try to understand how the model arrived at its prediction. This can be done by approximating a small region of interest in a black box model using a simpler interpretable model. This surrogate model, while not providing an optimal solution, is a reasonably good approximation while maintaining interpretability [91]. The reasoning behind this is that locally, the prediction might only depend linearly or monotonously on some features rather than having a complex dependence on them. This means that local explanations can be more accurate than global explanations [70].

For a Group of Predictions

In order to explain a group of predictions, there are essentially two possibilities: apply global methods and treat the group of predictions of interest as if it was the whole dataset or apply local methods on each prediction individually, aggregating and joining these explanations afterwards [64,70].

4.5. Explanations

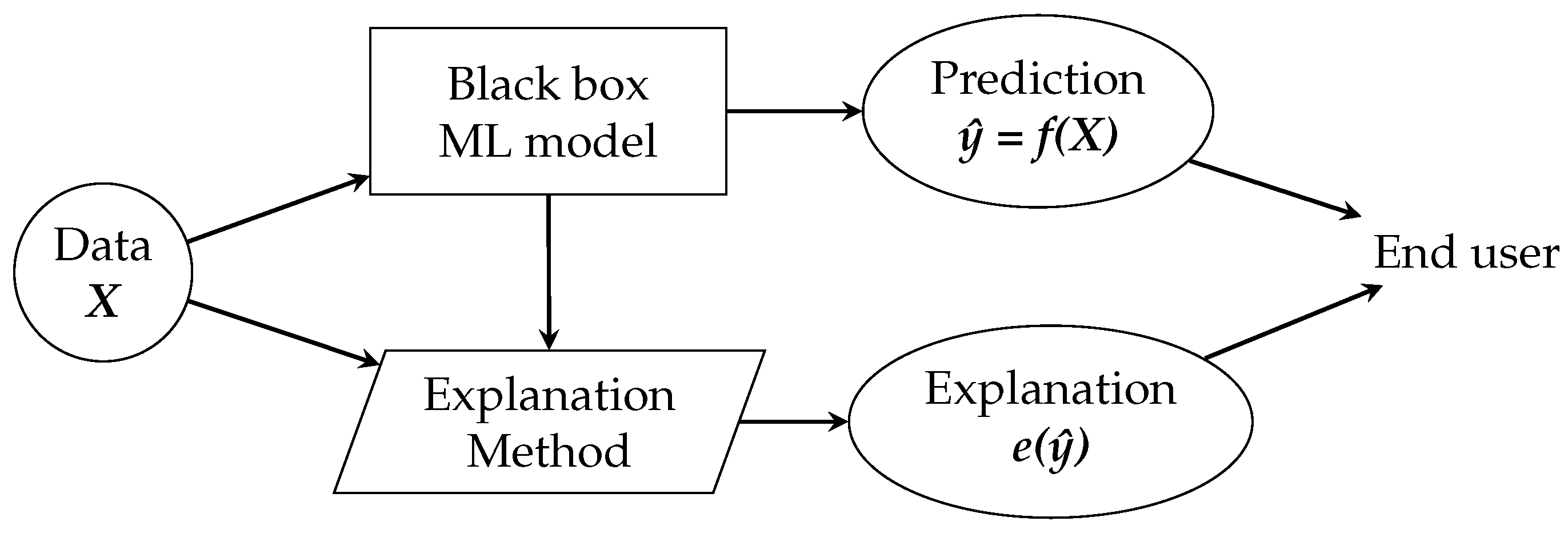
The goal is to make the user understand the predictions of ML models, which is achieved through explanations. For this, we make use of an explanation method, which is nothing more than an algorithm that generates explanations. The role of the explanation methods and generated explanations within the ML pipeline is shown in Figure 2.

What is an explanation? There have been various attempts to define the concept of an explanation across different disciplines, including philosophy and mathematics. An appropriate definition for the term is, thereby, dependent on the application domain and should be formulated regarding the context of use [79]. Miller gives a simple, goal-oriented definition [95], stating that “an explanation is the answer to a why-question”. Indeed, generally speaking, the goal of an explanation is to make something clear, understandable, transparent, and interpretable.

Taking into consideration the abovementioned, explanations can be considered as the means by which ML model decisions are explained. Therefore, interpretability is the end-goal that we want to achieve and explanations are the tools to reach interpretability [79]. An explanation usually relates the feature values of an instance to its respective prediction in a humanly understandable way [70] and, thus, increasing interpretability.

When it comes to explanations, it is important to distinguish whether the aim is the correct explanation or the best explanation, which usually are not the same. Kim states that theories of explanation can be distinguished into two kinds [107] and that these can be generically expressed as the following:

• Non-pragmatic theory of explanation: The explanation should be the correct answer to the why-question.
• Pragmatic theory of explanation: The explanation should be a good answer for an explainer to give when answering the why-question to an audience.

The most significant difference between the two types of theories is that there is no space for the audience in non-pragmatic theories. Non-pragmatic theories typically, but not always, follow a position where it is assumed there is only one true explanation. This means that the correctness of the answer has nothing to do with whether the audience is capable of understanding it or not. Pragmatic theories, in turn, argue that the definition of an explanation should necessarily have a place for the listener.

Since different listeners have different knowledge bases, pragmatic theories are naturally allied with a position where it is assumed that a phenomenon can have multiple explanations—which is a phenomenon called “Rashomon Effect” [108]. Therefore, it is argued that, when it comes to XAI, pragmatic theories of explanation are more appropriate than non-pragmatic ones [107]. The practical, legal, and ethical demands for companies and researchers to develop XAI largely come from the expectations that human users legitimately have. This means that the goal is not to achieve the most correct answer—it is to make the audience understand the reasoning behind a decision or prediction that was made by a ML model.

Miller emphasizes that an explanation is not only a product but also a process that involves a cognitive dimension and a social dimension [95]:

• The cognitive dimension is related to knowledge acquisition and involves deriving the actual explanation by a process of abductive inference, meaning that, first, the causes of an event are identified and, then, a subset of these causes are selected as the explanation.
• The social dimension concerns the social interaction, in which knowledge is transferred from the explainer to the explainee (the person for which the explanation is intended and produced). The primary goal is that the explainee receives enough information from the explainer in order to understand the causes of some event or decision. The explainer can be either a human or a machine.

These dimensions emphasize the subjectivity of explanations, highlighting the need to adapt the explanation to the audience. In other words, there is no such thing as a single explanation that solves all the interpretability problems. For each situation, it needs to take into account the problem domain, the use case, and the audience for which the explanation is aimed to.

4.5.1. Properties of Explanation Methods

Robnik-Sikonja et al. [109] defined some properties of explanation methods, which are stated below. These properties can be used to assess and make a comparison between different explanation methods.

• Expressive power—It is the language or structure of the explanations the method is able to generate. These could be, e.g., rules, decision trees, and natural language.
• Translucency—It represents how much the explanation method relies on looking into the inner workings of the ML model, such as the model’s parameters. For example, model-specific explanation methods are highly translucent. Accordingly, model-agnostic methods have zero translucency.
• Portability—It describes the range of ML models to which the explanation method can be applied. It is inversely proportional to translucency, meaning that highly translucent methods have low portability and vice-versa. Hence, model-agnostic methods are highly portable.
• Algorithmic complexity—It is related to computational complexity of the explanation method. This property is very important to consider regarding feasibility, especially when computation time is a bottleneck in generating explanations.

Additionally, there are other properties that might be useful to assess in certain situations. For instance, regarding randomness, some explanation methods have non-deterministic components, resulting in low stability of explanations. For example, LIME (Local Interpretable Model-agnostic Explanations) includes a random data sampling process, meaning that the explanation results will not be stable, i.e., repeating the explanation generation for the same instance and model with the same configuration arguments will result in different explanations. There are other methods in which the explanation results depend on some choices, such as the number of intervals (e.g., accumulated local effects), data sampling (e.g., Shapley values estimation) and shuffling (e.g., feature importance).

4.5.2. Properties of Individual Explanations

Robnik-Sikonja et al. [109] have also defined some properties for the explanations (i.e., the result generated by the explanation methods). Nevertheless, it is neither clear for all these properties how to measure them correctly nor how useful they are to specific use cases, so one of the challenges is to formalize how they could be calculated.

• Accuracy—It is related to the predictive accuracy of the explanation regarding unseen data. In some cases where the goal is to explain what the black box model does, low accuracy might be fine if the accuracy of the machine learning model is also low.
• Fidelity—It is associated with how well the explanation approximates the prediction of the black box model. High fidelity is one of the most important properties of an explanation because an explanation with low fidelity is essentially useless.
  Accuracy and fidelity are closely related: if the black box model has high accuracy and the explanation has high fidelity, the explanation consequently has high accuracy. Moreover, some explanations only provide local fidelity, meaning that the explanation only approximates well to the model prediction for a group or a single instance.
• Consistency—Regarding two different models that have been trained on the same task and that output similar predictions, this property is related to how different are the explanations between them. If the explanations are very similar, the explanations are highly consistent.
  However, it is noteworthy that this property is somewhat tricky [70], since the two models could use different features but could get similar predictions, which is described by the “Rashomon Effect” [108]. In this specific case, high consistency is not desirable because the explanations should be very different, as the models use different relationships for their predictions. High consistency is desirable only if the models really rely on similar relationships; otherwise, explanations should reflect the different aspects of the data that the models rely on.
• Stability—It represents how similar are the explanations for similar instances. While consistency compares explanations between different models, stability compares explanations between similar instances for a fixed model. High stability means that slight variations in the feature values of an instance do not substantially change the explanation, unless these slight variations also strongly change the prediction.
  Nonetheless, a lack of stability can also be created by non-deterministic components of the explanation method, such as a data sampling step (as noted in the end of the previous Section 4.5.1). Regardless of that, high stability is always desirable.
• Comprehensibility—This property is one of the most important but also one of the most difficult to define and measure. It is related to how well humans understand the explanations. Interpretability being a mainly subjective concept, this property depends on the audience and the context.
  The comprehensibility of the features used in the explanation should also be considered, since a complex transformation of features might be less comprehensible than the original features [70].
• Certainty—It reflects the certainty of the ML model. Many ML models only provide prediction values, not including statement about the model’s confidence on the correctness of the prediction.
• Importance—It is associated with how well the explanation reflects the importance of features or of parts of the explanation. For example, if a decision rule is generated as an explanation, is it clear which of the conditions of the rule was the most important?
• Novelty—It describes if the explanation reflects whether an instance, of which the prediction is to be explained, comes from a region in the feature space that is far away from the distribution of the training data. In such cases, the model may be inaccurate and the explanation may be useless. One way of providing this information is to locate the data instance to be explained in the distribution of the training data.
  Furthermore, the concept of novelty is related to the concept of certainty: the higher the novelty, the more likely it is that the model will have low certainty due to lack of data.
• Representativeness—It describes how many instances are covered by the explanation. Explanations can cover the entire model (e.g., interpretation of weights in a linear regression model) or represent only an individual prediction.

There might be other properties that could be taken into consideration, such as the basic units of the explanation and the number of basic units that each explanation is composed of. These can be seen as qualitative interpretability indicators and are better explored and defined in Section 5.1.

4.5.3. Human-Friendly Explanations

Taking into account that, regarding ML interpretability, the recipient of the explanations are humans; it is of evident importance to analyze what makes an explanation human-friendly because explanations, as correct as they might be, are not necessarily presented in a way that is easily understandable, in other words, checking which attributes are necessary to produce explanations that are more preferable and comprehensible to humans.

With reference to humanities research, Miller [95] conducted a huge survey of publications on explanations. He claimed that most of the existing work in ML interpretability uses solely the researchers’ intuition of what constitutes an appropriated explanation for humans. From his survey, the following human-friendly characteristics of explanations are provided:

• Contrastiveness [110]—Humans usually do not ask why a certain prediction was made but rather why this prediction was made instead of another prediction. In other words, there is a tendency for people to think in counterfactual cases. This means that people are not specifically interested in all the factors that led to the prediction but instead in the factors that need to change (in the input) so that the ML prediction/decision (output) would also change, implying a reference point, which is an hypothetical instance with the needed changes in the input and, consequently, with a different prediction (output).
  Explanations that present some contrast between the instance to explain and a reference point are preferable. However, this makes the explanation application-dependent because of the requirement of a reference object [70]. This concept is also designated as counterfactual faithfulness [78,87].
• Selectivity—People do not expect explanations that cover the actual and complete list of causes of an event. Instead, they prefer selecting one or two main causes from a variety of possible causes as the explanation. As a result, explanation methods should be able to provide selected explanations or, at least, make explicit which ones are the main causes for a prediction.
  The “Rashomon Effect” describes this situation, in which different causes can explain an event [108]—since humans prefer to select some of the causes, the selected causes may vary from person to person.
• Social—Explanations are part of a social interaction between the explainer and the explainee. As seen in the beginning of Section 4.5, this means that the social context determines the content, the communication, and the nature of the explanations.
  Regarding ML interpretability, this implies that, when assessing the most appropriate explanation, one should take into consideration the social environment of the ML system and the target audience. This means that the best explanation varies according to the application domain and use case.
• Focus on the abnormal—People focus more on abnormal causes to explain events [111]. These are causes that had a small probability but, despite everything, happened. The elimination of these abnormal causes would have greatly changed the outcome (counterfactual faithfulness).
  In terms of ML interpretability, if one of the input feature values for a prediction was abnormal in any sense (e.g., a rare category) and the feature influenced the prediction outcome, it should be included in the explanation, even if other more frequent feature values have the same influence on the prediction as the abnormal one [70].
• Truthful—Good explanations are proven to be true in the real world. This does not mean that the whole truth must be in the explanation, as it would interfere with the explanation being selected or not and selectivity is a more important characteristic than truthfulness. With respect to ML interpretability, this means that an explanation must make sense (plausible) and be suitable to predictions of other instances.
• Consistent with prior beliefs of the explainee—People have a tendency to ignore information that is inconsistent with their prior beliefs. This effect is called confirmation bias [112]. The set of beliefs varies subjectively from person to person, but there are also group-based prior beliefs, which are mainly of a cultural nature, such as political worldviews.
  Notwithstanding, it is a trade-off with truthfulness, as prior knowledge is often not generally applicable and only valid in a specific knowledge domain. Honegger [79] argues that it would be counterproductive for an explanation to be simultaneously truthful and consistent with prior beliefs.
• General and probable—A cause that can explain a good number of events is very general and could, thus, be considered a good explanation. This seems to contradict the claim that abnormal causes make good explanations. However, abnormal causes are, by definition, rare in the given scenario, which means that, in the absence of an abnormal cause, a general explanation can be considered a good explanation.
  Regarding ML interpretability, generality can easily be measured by the feature’s support, which is the ratio between the number of instances to which the explanation applies and the total number of instances [70].

These properties are fundamental to enable the importance of interpretability in machine learning (Section 4.2), although some might be more relevant than others depending on the context. No matter how correct an explanation is, if it is not reasonable and appealing for humans (human-friendly), the value of ML interpretability vanishes.

4.6. Interpretable Models and Explanation Methods

4.6.1. Interpretable Models

The easiest way to achieve interpretability is to use only a subset of algorithms that create interpretable models [70], including linear regression, logistic regression, and decision trees. These are global interpretable models on a modular level (Section 4.4.2), meaning that they have meaningful parameters (and features) from which useful information can be extracted in order to explain predictions.

Having different possibilities of choice, it is important to have some kind of assessment on which thw interpretable model is better suited for the problem at hand. Molnar [70] considered the following properties:

• Linearity—A model is linear if the association between feature values and target values is modelled linearly.
• Monotonicity—Enforcing monotonicity constraints on the model guarantees that the relationship between a specific input feature and the target outcome always goes in the same direction over the entire feature domain, i.e., when the feature value increases, it always leads to an increase or always leads to a decrease in the target outcome. Monotonicity is useful for the interpretation because it makes it easier to understand the relationship between some features and the target.
• Interaction—Some ML models have the ability to naturally include interactions between features to predict the target outcome. These interactions can be incorporated in any type of model by manually creating interaction features through feature engineering. Interactions can improve predictive performance, but too many or too complex interactions will decrease interpretability.

Not going into detail on how each interpretable model might be interpreted or what is the meaning of each of the models’ parameters regarding the performed predictions, this analysis will not go further than a general overview. As so,

Table 3. Interpretable models comparison.

Algorithm	Linear	Monotone	Interaction	Task
Linear regression	Yes	Yes	No	Regression
Logistic regression	No	Yes	No	Classification
Decision Trees	No	Some	Yes	Classification, Regression
RuleFit	Yes	No	Yes	Classification, Regression
Naive Bayes	No	Yes	No	Classification

presents an overview between intrinsically interpretable models regarding their properties, with information gathered by Molnar [70].

This table shows the prediction task for which each interpretable model is suited as well as which of the aforementioned properties each model has. Some models may be more fit for certain tasks than others, as they may have different predictive accuracies for different prediction tasks.

Additionally, although not as popular as the previously mentioned models, there are other classes of intrinsically interpretable models, which are considered to have greater simplicity. These include decision sets [113], rule-based classifiers [114,115,116,117], and scorecards [37,118]. The latter is typically used in regulated domains, such as credit score systems.

In addition to existent intrinsically interpretable models, there has also been some research on creating interpretable models by imposing some kind of interpretability constraint. These include, for example, classifiers that are comprised of a small number of short rules [119], Bayesian case-based reasoning models [120], and neural networks with L1 penalties to their input gradients for sparse local explanations [121]. Lage et al. [122] have gone even further by optimizing for interpretability by directly including human feedback in the model optimization loop.

It is also worth mentioning existing works that make use of tensor product representation to perform knowledge encoding and logical reasoning based on common-sense inference [123], which is useful for increasing interpretability through question-answering with the model [124].

4.6.2. Model-Specific Explanation Methods

Although it is not the focus of this work, there has been some research in creating (post hoc) explanation methods that leverage intrinsic properties of specific types of models in order to generate explanations. The drawback is that using this type of methods limits the model choice to specific model classes.

Many model-specific methods are designed for Deep Neural Networks (DNN), which is a class of models that is widely used because of its predictive performance in spite of being very opaque in terms of interpretability, a typical example of black box model. There are many notorious examples of such DNN explanation methods [7], most of which are used in computer vision [125], including guided backpropagation [126], integrated gradients [127], SmoothGrad saliency maps [128], Grad-CAM [129], and more recently, testing with Concept Activation Vectors (TCAV) [130].

One type of post hoc model-specific explanation methods is knowledge distillation, which is about extracting knowledge from a complex model to a simpler model (which can be from a completely different class of models). This can be achieved, for example, through model compression [131] or tree regularization [132] or even by combining model compression with dimension reduction [133]. Research in this type of methods exists for some years [134] but recently increased along with the ML interpretability field [135,136,137].

Moreover, the increasing interest in model-specific explanation methods that focus on specific applications can be seen, for example, in the recent 2019 Conference on Computer Vision and Pattern Recognition (CVPR), which featured an workshop on explainable AI [61]. There are CVPR 2019 papers with a great focus on interpretability and explainability for computer vision, such as explainability methods for graph CNNs [138], interpretable and fine-grained visual explanations for CNNs [139], interpreting CNNs via Decision Trees [140], and learning to explain with complemental examples [141].

4.6.3. Model-Agnostic Explanation Methods

Model-agnostic explanation methods are not dependent on the model. Although, for a specific model, in particular cases, some model-specific explanation methods might be more useful than model-agnostic explanation methods; the latter have the advantage of being completely independent from the original model class, persisting the possibility to reuse these methods in completely different use cases where the predictive model is also different.

It is worth asserting that method-agnostic explanation methods are also post hoc, since they are mostly decoupled from the black box model, as seen in Section 4.3. Some of the explanation methods are example-based, which means they return a (new or existent) data point.

Table 4. Model-agnostic explanation methods comparison.

Explanation Method	Scope	Result
Partial Dependence Plot [142]	Global	Feature summary
Individual Condition Expectation [143]	Global/Local	Feature summary
Accumulated Local Effects Plot [144]	Global	Feature summary
Feature Interaction [145]	Global	Feature summary
Feature Importance [146]	Global/Local	Feature summary
Local Surrogate Model [98]	Local	Surrogate interpretable model
Shapley Values [147]	Local	Feature summary
BreakDown [148]	Local	Feature summary
Anchors [149]	Local	Feature summary
Counterfactual Explanations [87]	Local	(new) Data point
Prototypes and Criticisms [96]	Global	(existent) Data point
Influence Functions [150]	Global/Local	(existent) Data point

presents an overview of the existing model-agnostic (post hoc) explanation methods, regarding the scope and the result criteria (explained in Section 4.3).

As a side note, some of these methods might be referred to by other names. Feature importance is the same as feature attribution. LIME stands for Local Interpretable Model-agnostic Explanations. Shapley Values is sometimes called by SHAP. Prototypes and Criticisms might be referred to as MMD-Critic, which is the name of the main algorithm behind this explanation method.

Many of the considered explanation methods return feature summary statistics which can be visualized, as stated in Section 4.3.4. Only with proper visualization and compositionality are some of these explanations considered interpretable, e.g., the relationship between a feature and the target outcome is better grasped with a plot and the feature importance values are more meaningful if features are ordered from the most important to the least important. It is also worth noting that some explanation methods have both global and local scopes, depending on if they are applied to explain the whole model or a specific prediction, e.g., the most influential instances for the whole model might be different than the most influential instances for a specific prediction.

Although these model-agnostic explanation methods provide the impactful advantage of being theoretically applicable to any model, most of them do not leverage intrinsic properties of specific types of models in order to generate explanations, meaning that, regarding some models, they may be more limited when compared to model-specific explanation methods.

4.7. Evaluation of Interpretability

As seen in Section 4.1, there is no single definition that suits what interpretability is regarding ML. This ambiguity also applies to the interpretability measurement, being unclear which way is the most appropriate one [70,151]. Nevertheless, existing research has shown attempts to formulate some approaches for interpretability assessments, as described in this Section 4.7 and in Section 5.

Doshi-Velez and Kim [41] propose three main levels of experiments for the evaluation of interpretability. These levels are ordered by descending order regarding cost of application and validity of results:

• Application-grounded evaluation (end task)—Requires conducting end-user experiments within a real application. This experiment is performed by using the explanation in a real-world application and having it tested and evaluated by the end user, who is also a domain expert. A good baseline for this is how good a human would be at explaining the same decision [70].
• Human-grounded evaluation (simple task)—Refers to conducting simpler human–subject experiments that maintain the essence of the target application. The difference is that these experiments are not carried out with the domain experts but with laypersons. Since no domain experts are required, experiments are cheaper and it is easier to find more testers.
• Functionally grounded evaluation (proxy task)—Requires no human experiments. In this type of evaluation, some formal definition of interpretability serves as a proxy to evaluate the explanation quality, e.g., the depth of a decision tree. Other proxies might be model sparsity or uncertainty [70]. This works best when the class of model being used has already been evaluated by someone else in a human-level evaluation.

Application-grounded evaluation is definitely the most appropriate evaluation, since it assesses interpretability in the end goal with the end users. In spite of this, it is very costly and it is difficult to compare results in different domains. Functionally grounded evaluation appears on the other end of the spectrum, since it requires no human subjects and the defined proxies for this evaluation are usually comparable in different domains. Nevertheless, the results that come from functionally grounded evaluation have low validity, since the proxies that might be defined are not real measures of interpretability and there is no human feedback. Human-grounded evaluation comes as an intermediate solution, having lower cost than application-grounded evaluation but higher validity than functionally grounded evaluation—the results come from human feedback but disregard the domain in which the assessed interpretability would be applied.

4.7.1. Goals of Interpretability

Although there is no consensus on how to exactly measure interpretability [70,151], there is still room to define what are the goals for which interpretability aims. Rüping et al. [91] argued that interpretability is composed of three goals, which are connected and often competing:

• Accuracy—Refers to the actual connection between the given explanation by the explanation method and the prediction from the ML model [151]. Not achieving this goal would render the explanation useless, as it would not be faithful to the prediction it aims to explain. This goal is a similar concept to the fidelity property mentioned in Section 4.5.2.
• Understandability—Is related to the easiness of how an explanation is comprehended by the observer. This goal is crucial because, as accurate as an explanation can be, it is useless if it is not understandable [151]. This is similar to the comprehensibility property mentioned in Section 4.5.2.
• Efficiency—Reflects the time necessary for a user to grasp the explanation. Evidently, without this condition, it could be argued that almost any model is interpretable, given an infinite amount of time [151]. Thereby, an explanation should be understandable in a finite and preferably short amount of time. This goal is related to the previous one, understandability: in general, the more understandable is an explanation, the more efficiently it is grasped.

This means that high interpretability would, thus, be scored by an explanation that is accurate to the data and to the model, understandable by the average observer, and graspable in a short amount of time [79]. Nonetheless, as stated by Rüping et al. [91], there is usually a trade-off between these goals, e.g., the more accurate an explanation is, the less understandable it becomes.

4.8. Literature Review Summary

In order to provide a more clear view of the contents of this literature review section (Section 4),

Table 5. Literature review summary.

Section	Content
Interpretability importance	Satisfy human curiosity
	Scientific findings
	Find meaning
	Regulation requirements
	Social acceptance and trust
	Safety
	Acquire new knowledge
Taxonomy of interpretability	Pre-model vs. In-model vs. Post-model
	Intrinsic vs. Post-hoc
	Model-specific vs. Model-agnostic
	Results of explanation methods
Scope of interpretability	Algorithm transparency
	Global model interpretability (holistic vs. modular)
	Local model interpretability (single prediction vs. group of predictions)
Properties of explanation methods	Expressive power; Translucency; Portability; Algorithmic complexity
Properties of explanations	Accuracy; Fidelity; Consistency; Stability; Comprehensibility; Certainty; Importance; Novelty; Representativeness
Human-friendly explanations	Contrastiveness; Selectivity; Social; Focus on the abnormal; Truthful; Consistent with prior beliefs; General and probable
Interpretability evaluation	Application-level
	Human-level
	Functional-level
Interpretability goals	Accuracy
	Understandability
	Efficiency

presents a summary of the literature review.

The next section focuses on the existing approaches on interpretability assessment methods and metrics.

5. Approaches on Interpretability Assessment

In spite of the clearly stated need for interpretability in various different aspects, the question of interpretability measurement and assessment remains unanswered, which should be expected after reviewing the motivations and challenges for this issue in Section 3.

Doshi-Velez and Kim [41] question, “Are all models in all defined-to-be-interpretable model classes equally interpretable? [...] Moreover, do all applications have the same interpretability needs? If we are to move this field forward—to compare methods and understand when methods may generalize—we need to formalize these notions and make them evidence-based.’. This question is equally applicable to both interpretable models and explanation methods, as each provides progress towards interpretability in its own way.

However, most of the work in the ML interpretability research field has focused on creating new methods and techniques that aim to improve interpretability in prediction tasks while trying to minimize the decrease in the predictive accuracy. Indeed, despite the growing body of research that produces methods for improving ML interpretability, there seems to be very little research on developing measures and approaches for ML interpretability assessment. While there has been some advances in terms of new interpretable models and explanation methods, ML interpretability research has not focused on comparing and assessing the interpretability properties (and thus the quality) of explanation methods, meaning there has been few work on developing means of assessing and choosing the most appropriate explanation as well as metrics to quantify the interpretability of explanation methods [79]. According to Adadi and Berrada, only 5% of the papers they have studied for their XAI survey focus on this particular issue of assessing interpretability methods [2].

It is worth noting that the (little) existing research on ML interpretability assessment is mainly concerned about indicators (or metrics) that attempt to measure interpretability properties, enabling the characterization and distinguishability of different explanation methods. Therefore, this section will focus on this type of work.

Research shows that there are two types of indicators for assessment and comparison of explanations: qualitative and quantitative indicators, the latter of which is used as numerical proxies for explanation quality.

5.1. Qualitative Interpretability Indicators

With regard to qualitative indicators of interpretability, Doshi-Velez and Kim [41,152] mention five factors related to explanations (note that the term cognitive chunks refers to the basic units of explanation):

• Form of cognitive chunks—This relates to the basic units of explanation, i.e., what are the explanations composed of? These could be, e.g., feature importance values, examples from the training set, or even rule lists. In certain domains, there are other possibilities, such as groups of pixels for the specific case of image recognition.
• Number of cognitive chunks that the explanation contains. How does the quantity interact with the form? In other words, taking into consideration that an example could contain a lot more information than a feature, can we handle both in similar quantities, in terms of ease of comprehension? If the explanation is composed of features, does it contain all features or only a few (selectivity)?
• Compositionality—This is related to the organization and structure of the cognitive chunks. Rules, hierarchies, and other abstractions may influence the human processing capacity. For example, an explanation may define a new unit (cognitive chunk) that is a function of raw units and provide an explanation in terms of that new unit. Other simple examples of compositionality are, e.g., the ordering of feature importance values or any threshold used to constrain the explanation.
• Monotonicity and other interactions between units. These interactions could be, e.g., linear, nonlinear, or monotone. Which type of relation between units is more intuitive for humans? Some relations may seem more natural for some than for others.
• Uncertainty and stochasticity refer to the explanation returning some comprehensible uncertainty measure and if any random processes are part of the explanation generation, e.g., sampling and random perturbation.

All of the aforementioned factors mostly impact the interpretability goals of understandability and efficiency [91] mentioned in Section 4.7.1. For example, if an explanation makes use of a small number of basic explanation units, the explanation is clearly more understandable by humans (selectivity) and, in addition, more rapidly processed, thereby increasing the efficiency of the explanation.

5.2. Quantitative Interpretability Indicators

Moving on to quantitative indicators for explanation assessment, this type of indicator is preferable due to its nature. Quantifying explanation quality in numbers (proxy metrics) provides an intuitive way for comparing different explanations.

Sundararajan et al. created an axiom-based approach in order to attribute Deep Neural Network (DNN) predictions to the original input features [127]. Although their goal was to develop a model-specific explanation method for neural networks, which was called integrated gradients, the axioms they have defined can also be seen as qualitative indicators, which are proxies for explanation quality (or interpretability) assessment.

They proposed two axioms that explanations for DNNs should fulfill:

• The sensitivity axiom is related to individual feature importance values and is composed of two parts:

  -

  Firstly, if there are two different predictions for two inputs that only differ in a single feature value, then this feature should have a nonzero attribution (or importance, which in this case refers to the same). This seems intuitive because the difference in the prediction should have been caused by the difference in the feature value, meaning that this feature should have a nonzero importance.

  -

  Secondly, if the DNN never depends on some feature value for its predictions (which would mean that the feature is noise for the specified prediction task), then the importance value for that feature should always be zero. This follows the same intuitive logic presented above.

• The implementation invariance axiom argues that if two DNNs are equal, i.e., they were trained on the same prediction task and they return identical predictions for the same inputs, then the corresponding attributions for these networks must also be identical, even if these have different implementations. This means that if an explanation method does not satisfy this axiom, then the method is potentially sensitive to irrelevant properties of the models, e.g., the architecture they have, which is clearly undesirable.
  It can be argued that the two DNNs could be looking to different parts of the data; however, if that would be the case, then they probably would not return identical predictions for the same inputs.

These axioms seem to mainly impact the interpretability goals of accuracy and understandability [91]. For example, the second axiom, implementation invariance, refers to the accuracy of the explanation, i.e., there will be higher explanation accuracy if the explanation is taking into account the features that the model used and not the model itself. Consequently, the explanation consistency achieved by better accuracy will contribute to better understandability by humans.

Still in respect of quantitative indicators, Honegger stated [79] that the aforementioned axioms are the foundation for the Axiomatic Explanation Consistency Framework he developed in his research with the purpose of providing a model-agnostic framework for assessing and comparing the explanation consistency across different explanation methods in both regression and classification cases. This framework can be considered as functionally grounded evaluation method, earlier defined by Reference [41], as it consists of three proxies (axioms) for measuring the consistency of explanation methods. In other words, the framework measures if and how much an explanation method fulfills the objective of attaining explanation consistency [79]. This goal is reinforced by Lundberg and Lee, as they state that model prediction explanations should be consistent with human explanations [147], which means that they should be aligned with and based on human intuition.

The below mentioned axioms, which Honneger argues are grounded on human intuition [79], consist of relating an object to its corresponding explanation. For clarification purposes, the term object is used to mention the set of an instance and its corresponding prediction and the term explanation refers only to feature importance values, which already indicates a clear limitation of this framework because it is only applicable to explanation methods that output feature importance values as explanations [79]. The three axioms are as follows:

• Identity—Identical objects must have identical explanations. This makes sense because two equal instances should have equal predictions and, consequently, equal feature importance values. If an explanation method is prompted several times to explain the same object, it is expected to always generate the same explanation. If the explanation varied inconsistently, it would be confusing for a human trying to understand it. Furthermore, if an explanation method does not always return the same explanation for the same object, the method is not accurate due to its random nature.
• Separability—Nonidentical objects cannot have identical explanations. This follows the same logic as the previous axiom. Two different objects have different feature values and, thus, should have different feature importance values. Even if a model predicts the same outcome for different instances, the explanation should be different due to the different feature values that generated the prediction. However, it is worth noting that this axiom only holds if the model does not have more degrees of freedom than needed to represent the prediction function [127].
• Stability—Similar objects must have similar explanations. This axiom was inspired in the concept of algorithmic stability: a prediction algorithm is said to be stable if slight perturbations in the input data only result in small changes in the predictions [153]. Similarly, Honneger defines an explanation method as stable if it returns similar explanations for slightly different (similar) objects, implying a directly proportional relationship between the similarity among objects and the similarity among the respective explanations. Notwithstanding, the implementation of this axiom in Honneger’s research lacks some useful information, namely the distance metric used in the pairwise distance matrices for the regression case.

Continuing the review of quantitative indicators, Wilson et al. defined, in their recent work [65], three proxy metrics used in binary classification with the objective of summarizing explanation quality under certain assumptions. This work was validated in healthcare applications. The considered explanations in this work are rule-based and example-based. They consider an explanation as a simple model that can be applied to a local context of the data and state that a good explanation should maximize the following properties, which they call “the three Cs of interpretability” [65]:

• Completeness—This is related to the audience verifying the validity of the explanation, i.e., the coverage of the explanation in terms of the number of instances which are comprised by the explanation,
• Correctness—The explanation should generate trust. In other words, it should be correct. This property is related to the label coherence of the instances covered by explanation, i.e., the instances covered by a correct explanation should have the same label.
• Compactness—The explanation should be succinct, which can be verified by the number of conditions in the decision rule and the feature dimensionality of a neighbor-based explanation. This proxy is related to the number qualitative indicator [152] and, therefore, to the selectivity of the explanation (Section 4.5.3).

Having reviewed the indicators defined in the existing approaches, of which the objective is to assess interpretability, it is possible to make an association between the quantitative indicators proposed by the mentioned work in this Section 5 and the explanation properties mentioned in Section 4.5.2. This association is presented in

Table 6. Association between explanation properties and quantitative interpretability indicators.

Property (Section 4.5.2) [109]	Sundararajan et al. [127]	Honegger [79]	Wilson et al. [65]
Accuracy	N.A.	N.A.	Correctness
Fidelity	Sensitivity	Identity, Separability	Correctness
Consistency	Implementation invariance	N.A.	Yes
Stability	N.A.	Stability	N.A.
Comprehensibility	N.A.	N.A.	Compactness
Certainty	N.A.	N.A.	N.A.
Importance	Sensitivity	N.A.	N.A.
Novelty	N.A.	N.A.	N.A.
Representativeness	N.A.	N.A.	Completeness

.

6. Final Remarks

As seen in Section 3.5, the main cause for the interpretability problem to remain unsolved is that interpretability is a very subjective concept and, thus, hard to formalize [91]. Despite some of the presented work having been done for general purposes, interpretability is a domain-specific notion [91,92], so there cannot be an all-purpose definition [9]. This means that, when it comes to ML interpretability, it is necessary to take into consideration the application domain and use case for each specific problem.

Section 5 shows that, although there has been useful work in interpretability assessments, the ML interpretability research field needs to focus more on the comparison of existing explanation methods instead of just creating new ones: only with interpretability assessment, including metrics that help to measure interpretability and context definitions that assist in comparing different use cases, can we know in which direction the explanation methods should aim. Moreover, interpretability assessment should be a contextualized process: one should take into account the application domain and the use case of the problem in hand, as well as the type of audience that is asking questions about the model’s decisions. These are requirements for providing interpretability in a proper way.

Ultimately, the long-term solution would be a model-agnostic framework (which, at the time of writing, was not developed yet to our knowledge) that is capable of recommending the best explanation among the available ones while considering the problem domain, use case, and type of user.