Efficient Implementation of 2D and 3D Sparse Deconvolutional Neural Networks with a Uniform Architecture on FPGAs
Abstract
:1. Introduction
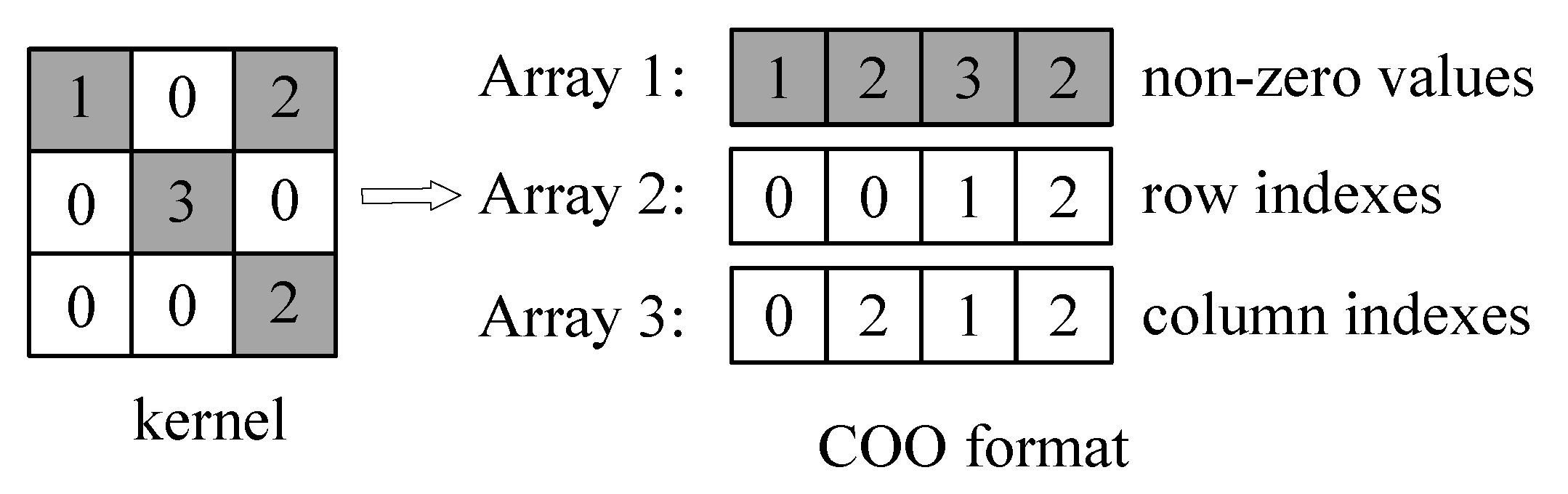
- A pruning algorithm [12] is creatively applied on DCNNs to remove low-weight connections and the remaining non-zero weights are encoded in coordinate (COO) format, which can significantly reduce the size of DCNNs.
- We propose an efficient mapping scheme of 2D and 3D sparse DCNNs on the uniform architecture, which can efficiently improve the parallel computational ability and computational efficiency of the accelerator.
2. Related Work
3. Background
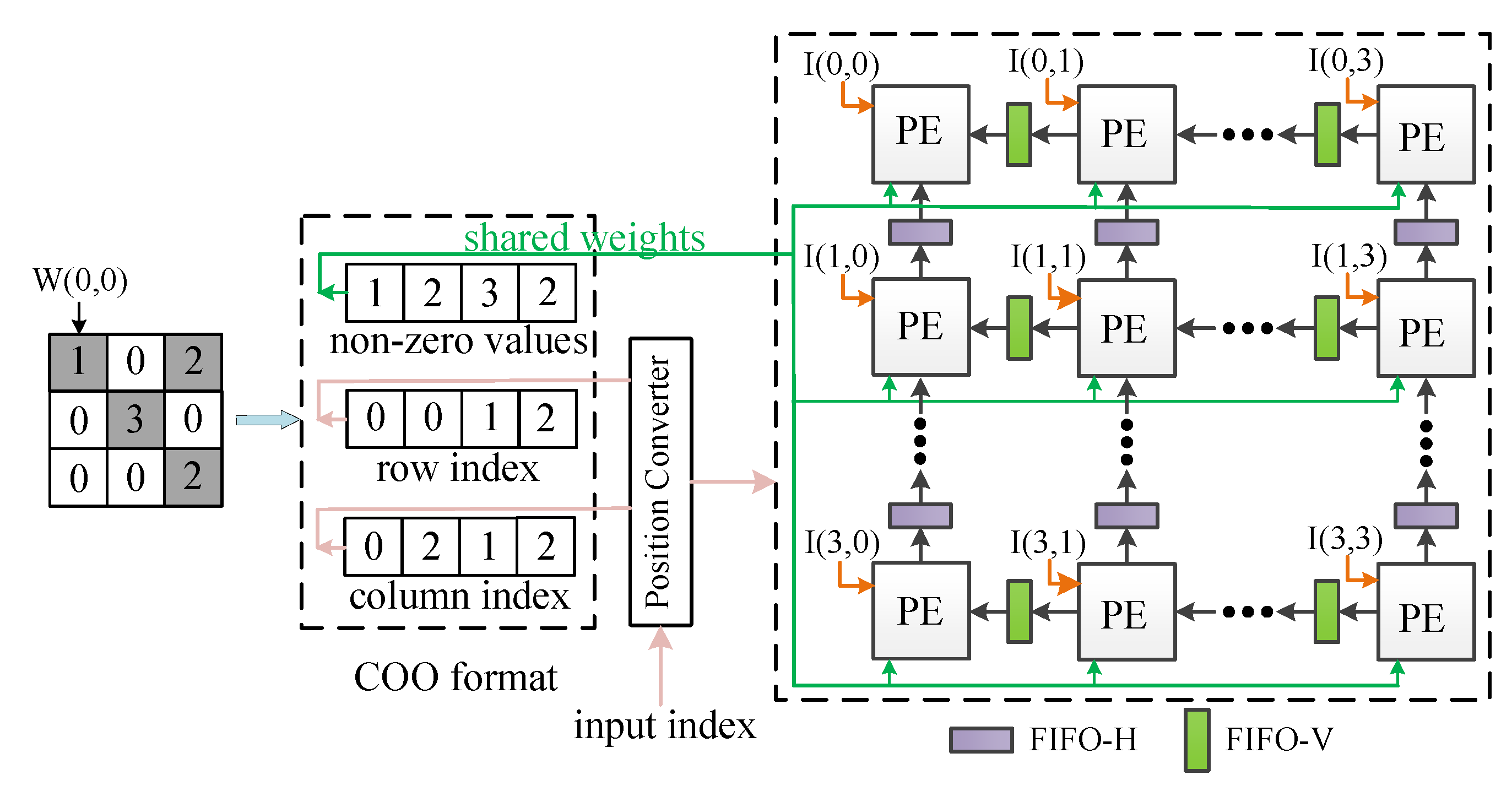
3.1. Pruning and Encoding
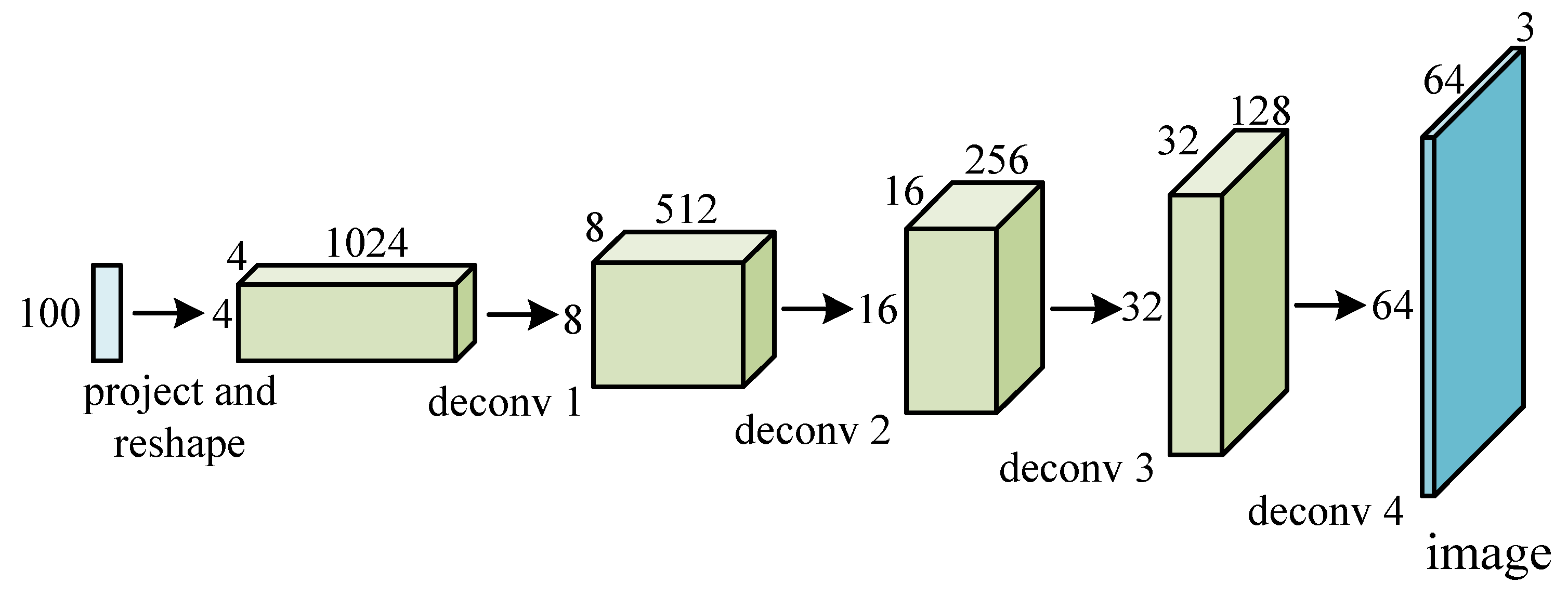
3.2. Deconvolution
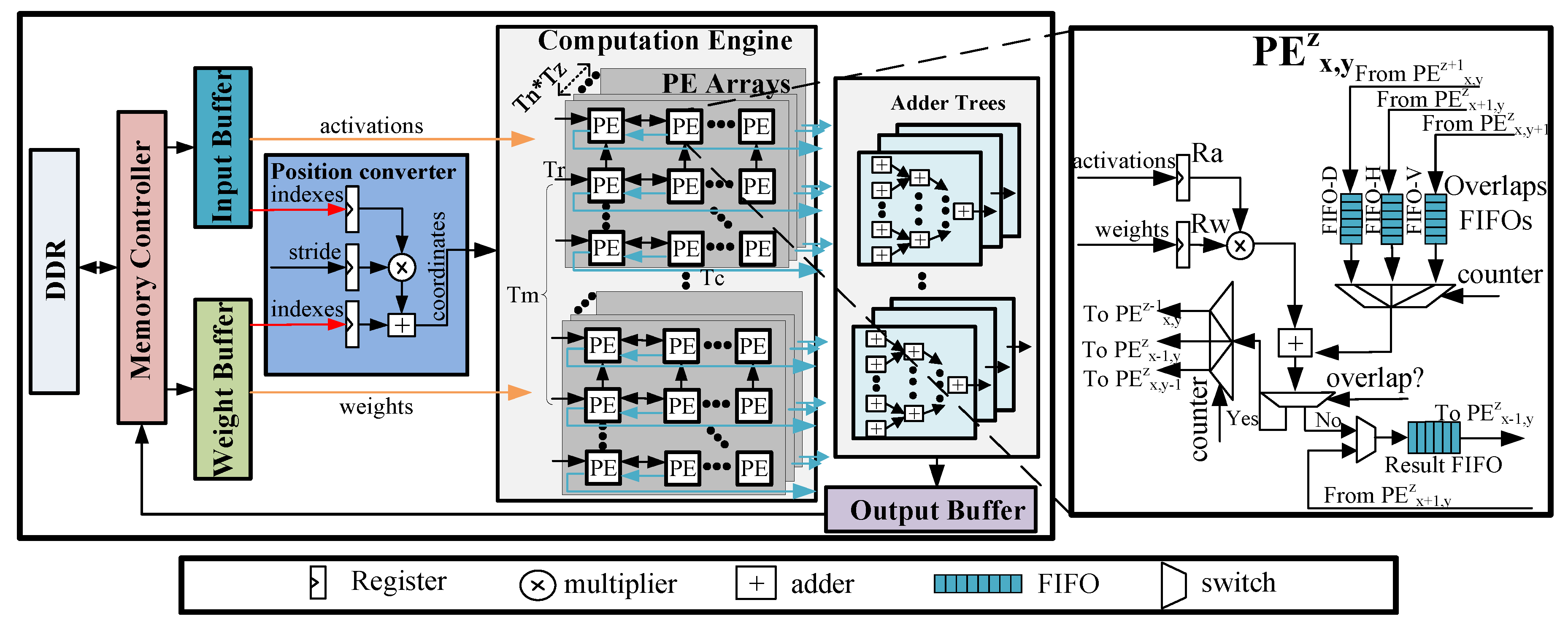
4. The Proposed Architecture
4.1. Architecture Overview
4.2. Support for Sparse Weights
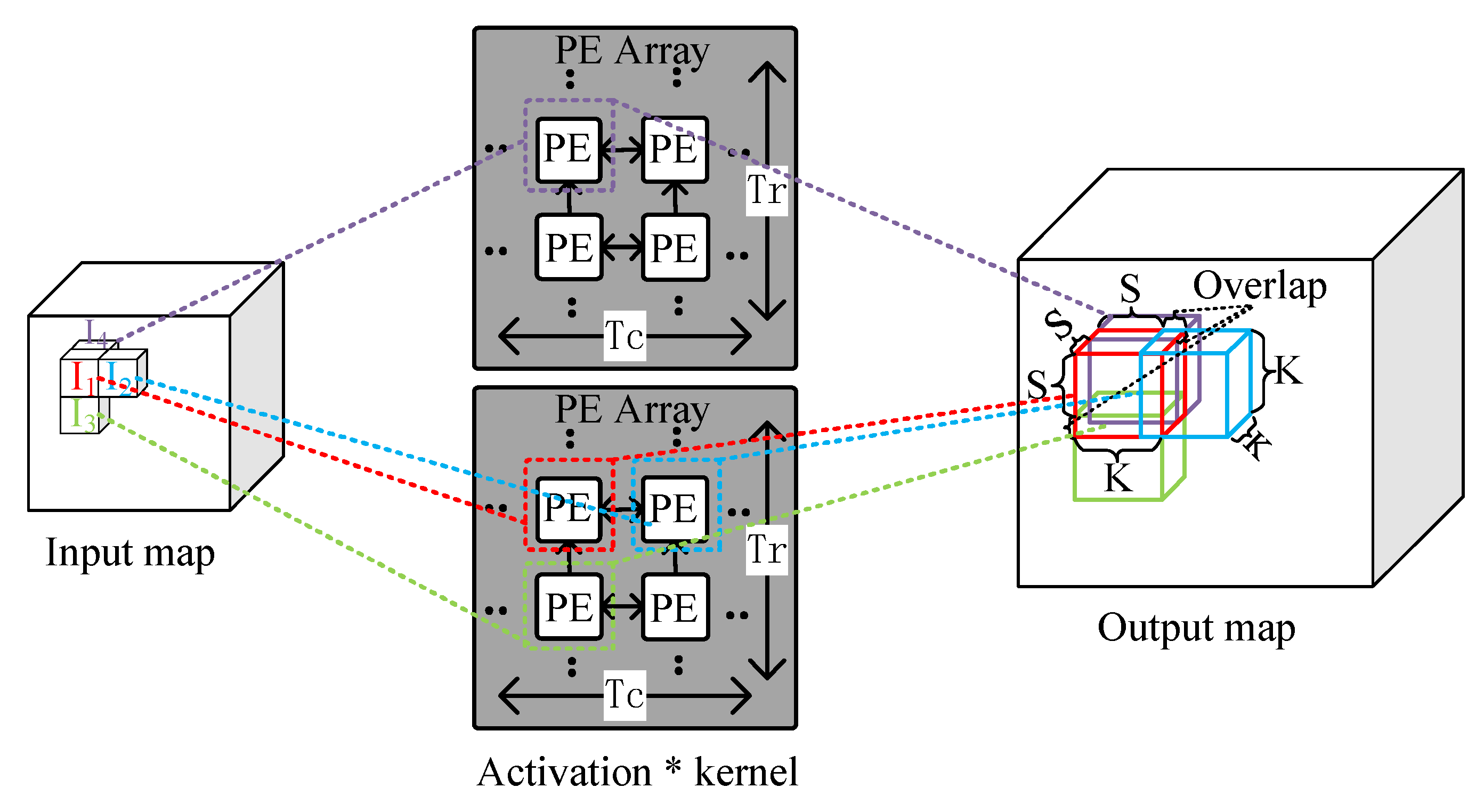
4.3. 3D IOM Method
| Algorithm 1 Pseudo code for 3D deconvolution. |
|
4.4. Support for the Acceleration of 2D and 3D DCNNs
5. Experimental Results
5.1. Experiment Setup
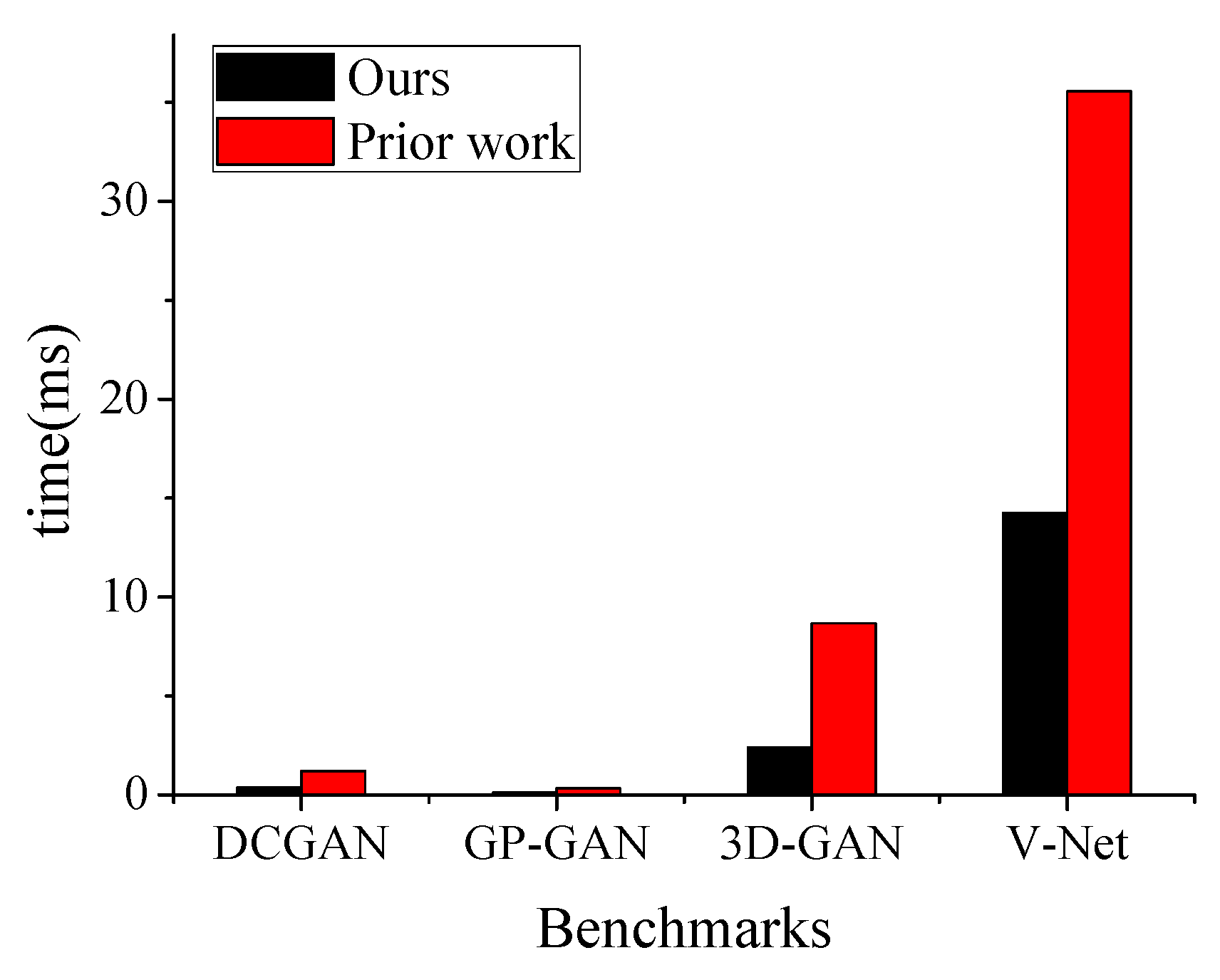
5.2. Performance Analysis
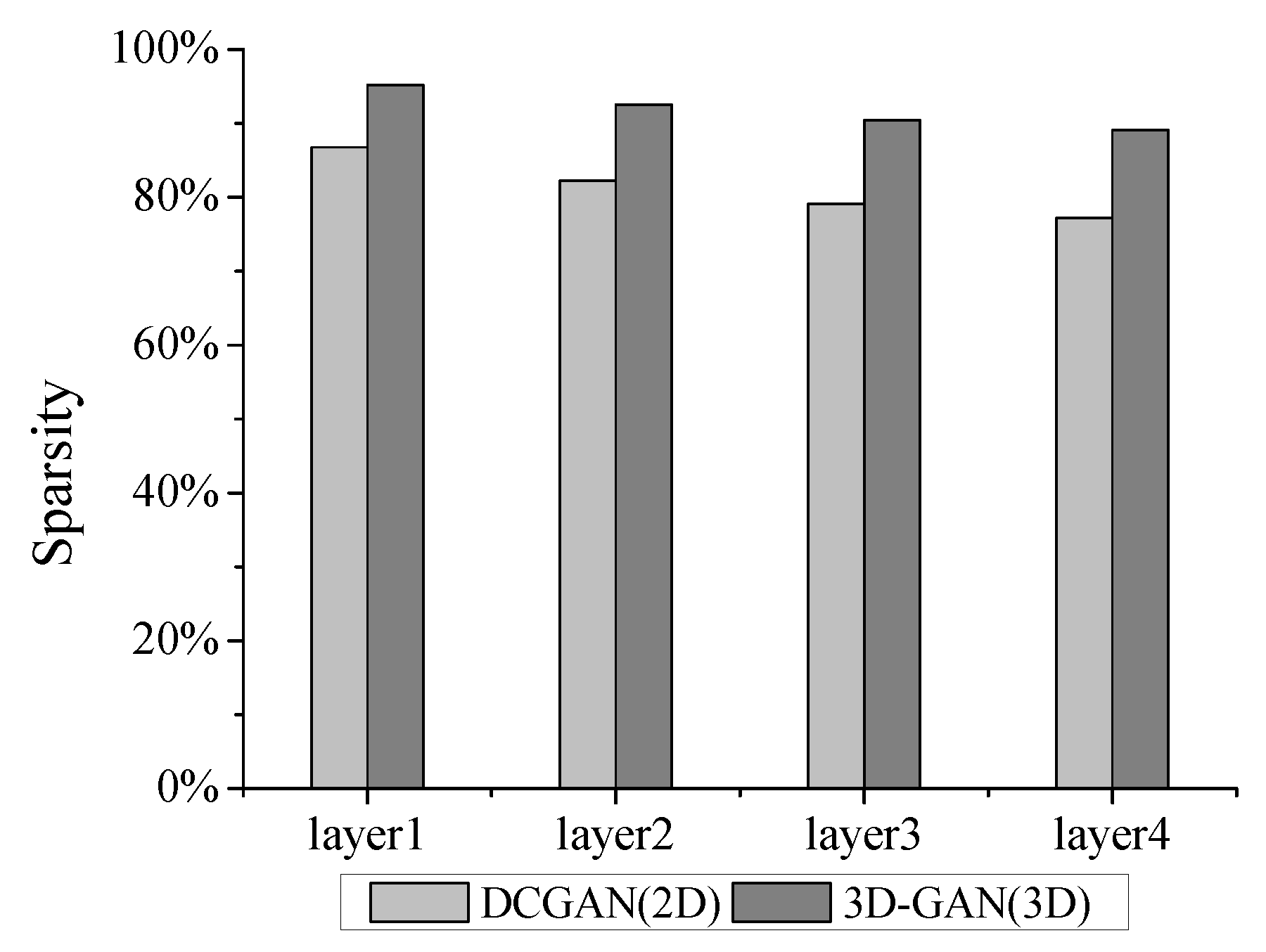
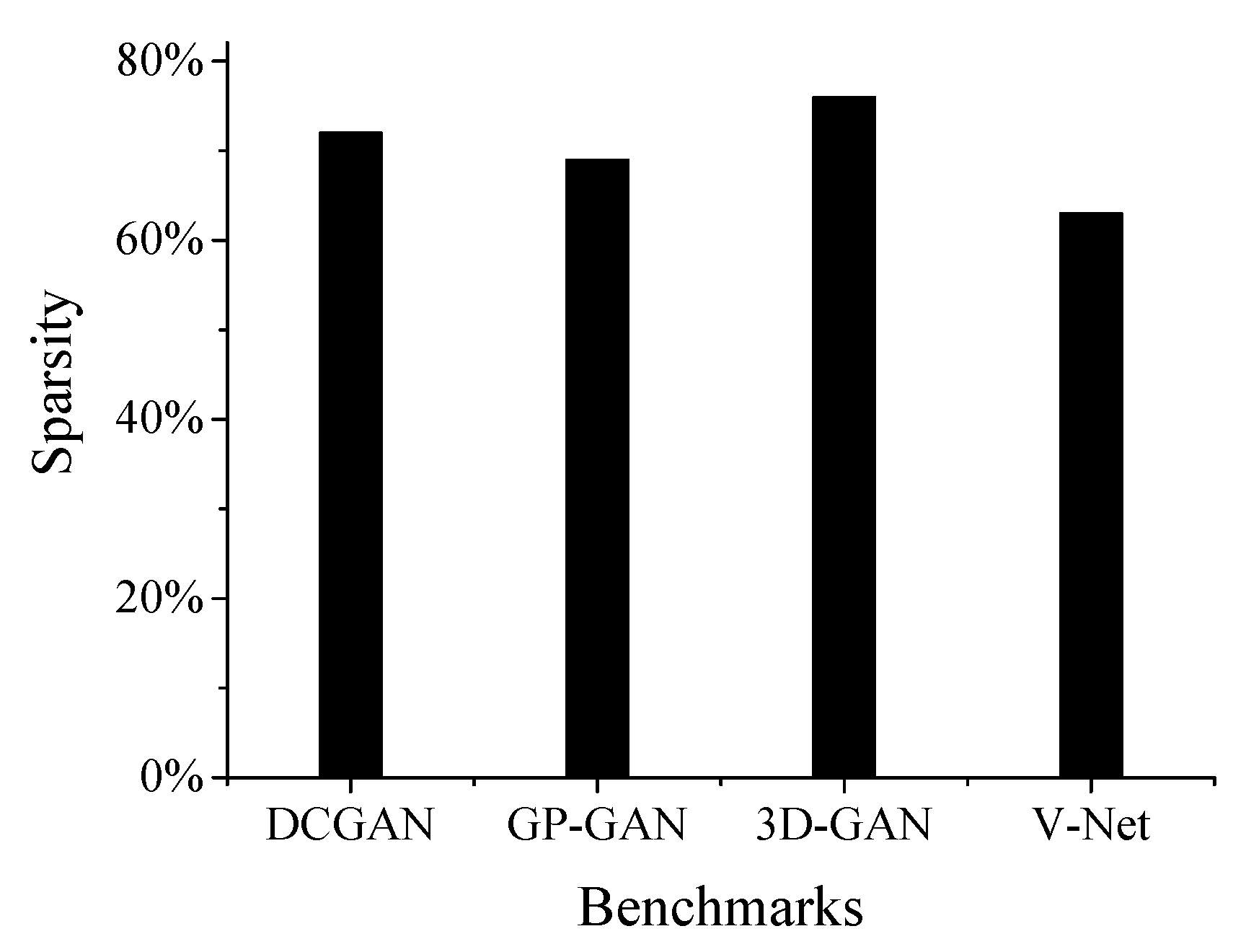
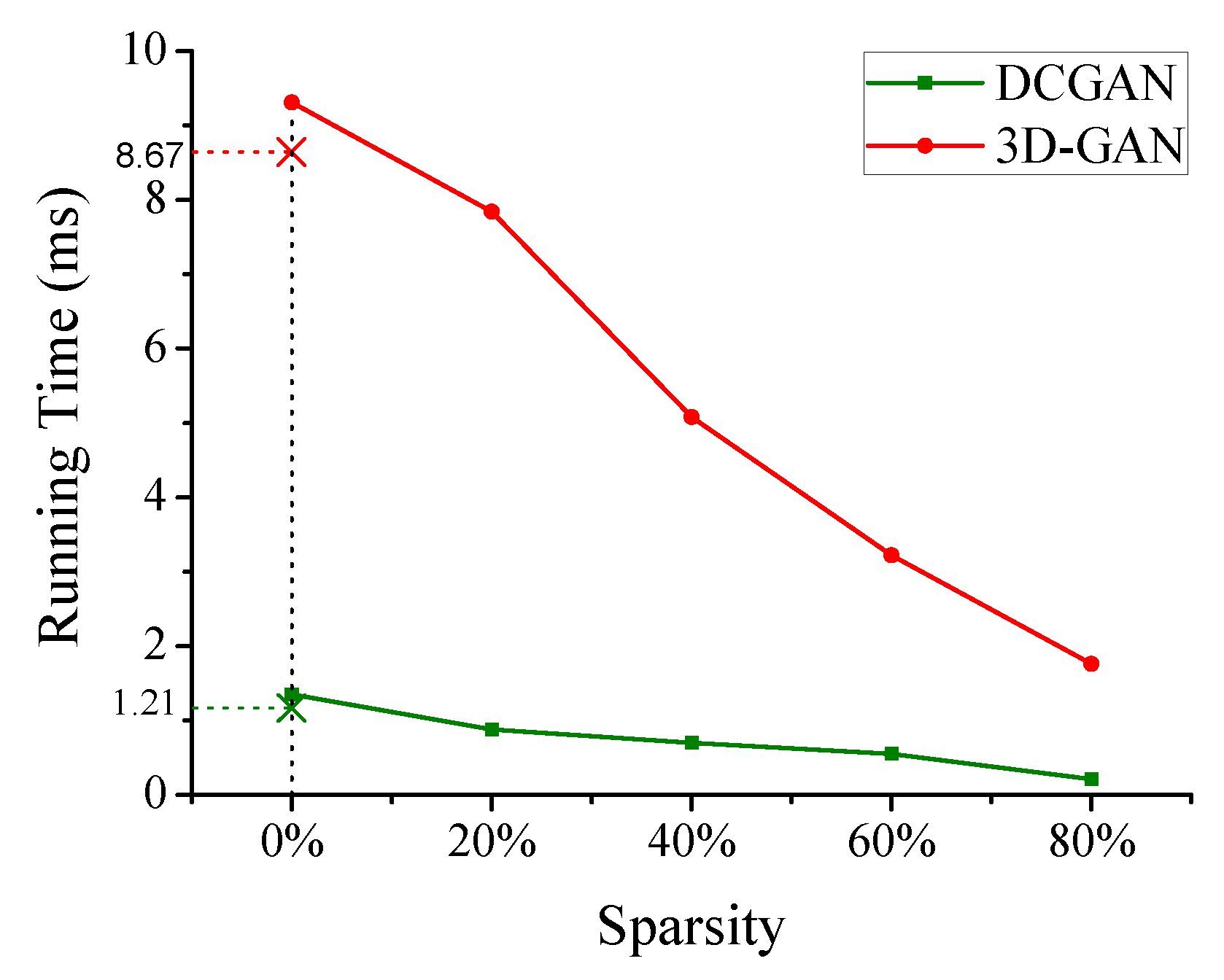
5.3. Sensitive to Weights Sparsity
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Radford, A.; Metz, L.; Chintala, S. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv 2015, arXiv:1511.06434. [Google Scholar]
- Dong, C.; Loy, C.C.; Tang, X. Accelerating the super-resolution convolutional neural network. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 391–407. [Google Scholar]
- Milletari, F.; Navab, N.; Ahmadi, S.A. V-net: Fully convolutional neural networks for volumetric medical image segmentation. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 565–571. [Google Scholar]
- Wu, J.; Zhang, C.; Xue, T.; Freeman, B.; Tenenbaum, J. Learning a probabilistic latent space of object shapes via 3d generative-adversarial modeling. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2016; pp. 82–90. [Google Scholar]
- Han, S.; Mao, H.; Dally, W.J. Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding. arXiv 2015, arXiv:1510.00149. [Google Scholar]
- Yan, J.; Yin, S.; Tu, F.; Liu, L.; Wei, S. GNA: Reconfigurable and Efficient Architecture for Generative Network Acceleration. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2018, 37, 2519–2529. [Google Scholar] [CrossRef]
- Zhang, C.; Li, P.; Sun, G.; Guan, Y.; Xiao, B.; Cong, J. Optimizing fpga-based accelerator design for deep convolutional neural networks. In Proceedings of the 2015 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 22–24 February 2015; ACM: New York, NY, USA, 2015; pp. 161–170. [Google Scholar]
- Qiu, J.; Wang, J.; Yao, S.; Guo, K.; Li, B.; Zhou, E.; Yu, J.; Tang, T.; Xu, N.; Song, S.; et al. Going deeper with embedded fpga platform for convolutional neural network. In Proceedings of the 2016 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 21–23 February 2016; ACM: New York, NY, USA, 2016; pp. 26–35. [Google Scholar]
- Liu, Z.; Dou, Y.; Jiang, J.; Xu, J.; Li, S.; Zhou, Y.; Xu, Y. Throughput-Optimized FPGA Accelerator for Deep Convolutional Neural Networks. ACM Trans. Reconfig. Technol. Syst. TRETS 2017, 10, 17. [Google Scholar] [CrossRef]
- Wang, D.; Shen, J.; Wen, M.; Zhang, C. Towards a Uniform Architecture for the Efficient Implementation of 2D and 3D Deconvolutional Neural Networks on FPGAs. In Proceedings of the 2019 IEEE International Symposium on Circuits and Systems (ISCAS), Sapporo, Japan, 26–29 May 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Han, S.; Pool, J.; Tran, J.; Dally, W. Learning both weights and connections for efficient neural network. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2015; pp. 1135–1143. [Google Scholar]
- Wu, H.; Zheng, S.; Zhang, J.; Huang, K. Gp-gan: Towards realistic high-resolution image blending. arXiv 2017, arXiv:1703.07195. [Google Scholar]
- Hardieck, M.; Kumm, M.; Möller, K.; Zipf, P. Reconfigurable Convolutional Kernels for Neural Networks on FPGAs. In Proceedings of the 2019 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Seaside, CA, USA, 24–26 February 2019; ACM: New York, NY, USA, 2019; pp. 43–52. [Google Scholar]
- DiCecco, R.; Lacey, G.; Vasiljevic, J.; Chow, P.; Taylor, G.; Areibi, S. Caffeinated FPGAs: FPGA framework for convolutional neural networks. In Proceedings of the 2016 International Conference on Field-Programmable Technology (FPT), Xi’an, China, 7–9 December 2016; pp. 265–268. [Google Scholar]
- Han, X.; Zhou, D.; Wang, S.; Kimura, S. CNN-MERP: An FPGA-based memory-efficient reconfigurable processor for forward and backward propagation of convolutional neural networks. In Proceedings of the 2016 IEEE 34th International Conference on Computer Design (ICCD), Phoenix, AZ, USA, 3–5 October 2016; pp. 320–327. [Google Scholar]
- Bettoni, M.; Urgese, G.; Kobayashi, Y.; Macii, E.; Acquaviva, A. A convolutional neural network fully implemented on fpga for embedded platforms. In Proceedings of the 2017 New Generation of CAS (NGCAS), Genova, Italy, 6–9 September 2017; pp. 49–52. [Google Scholar]
- Mousouliotis, P.G.; Panayiotou, K.L.; Tsardoulias, E.G.; Petrou, L.P.; Symeonidis, A.L. Expanding a robot’s life: Low power object recognition via FPGA-based DCNN deployment. In Proceedings of the 2018 7th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 7–9 May 2018; pp. 1–4. [Google Scholar]
- Yazdanbakhsh, A.; Falahati, H.; Wolfe, P.J.; Samadi, K.; Kim, N.S.; Esmaeilzadeh, H. GANAX: A Unified MIMD-SIMD Acceleration for Generative Adversarial Networks. arXiv 2018, arXiv:1806.01107. [Google Scholar]
- Yazdanbakhsh, A.; Brzozowski, M.; Khaleghi, B.; Ghodrati, S.; Samadi, K.; Kim, N.S.; Esmaeilzadeh, H. FlexiGAN: An End-to-End Solution for FPGA Acceleration of Generative Adversarial Networks. In Proceedings of the 2018 IEEE 26th Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), Boulder, CO, USA, 29 April–1 May 2018; pp. 65–72. [Google Scholar]


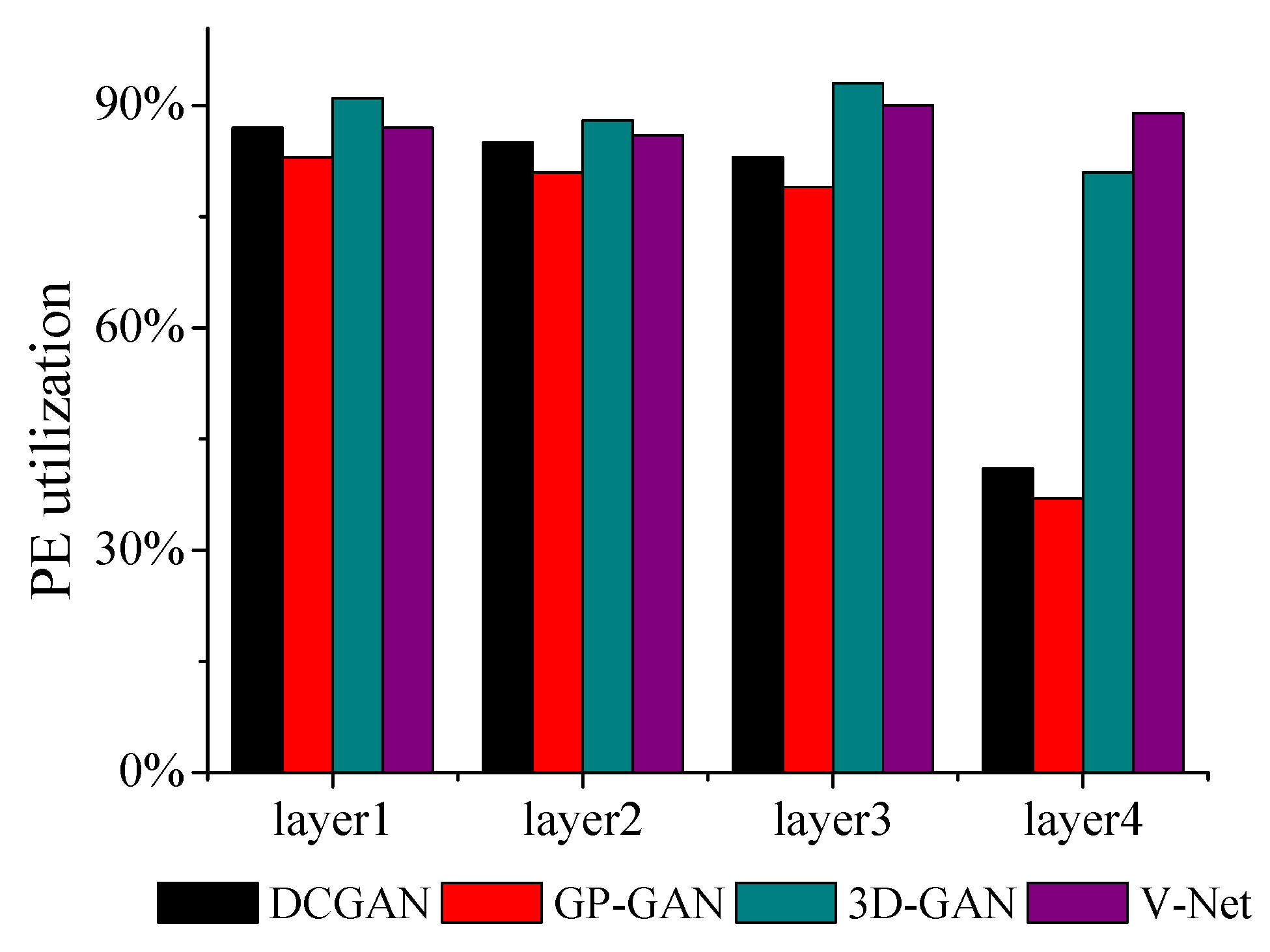
| DCGAN | 3D-GAN | |||
|---|---|---|---|---|
| Layer | Weights | Non-Zero Ratio | Weights | Non-Zero Ratio |
| deconv1 | 4.5 M | 28% | 2.0 M | 25% |
| deconv2 | 1.1 M | 33% | 0.5 M | 29% |
| deconv3 | 288.0 K | 35% | 128.0 K | 23% |
| deconv4 | 3.4 K | 38% | 1.0 K | 30% |
| Total | 5.9 M | 29% (1.7 M) | 2.6 M | 26% (0.7 M) |
| Parameter | Description |
|---|---|
| I (, ) | element of input feature maps |
| W (, ) | element of kernels |
| Benchmarks | |||||
|---|---|---|---|---|---|
| 2D DCNNs | 2 | 64 | 1 | 4 | 4 |
| 3D DCNNs | 2 | 16 | 4 | 4 | 4 |
| Resource | DSP48Es | Block RAMs | FFs | LUTs |
|---|---|---|---|---|
| Available | 3600 | 1470 | 866,500 | 433,200 |
| Utilization | 2304 | 712 | 602,749 | 304,247 |
| Percentage (%) | 64.00 | 48.44 | 69.56 | 70.24 |
| Works | [7] | Ours |
|---|---|---|
| Platform | ASIC 28nm | VX690t |
| Frequency (MHz) | 200 | 200 |
| Data precision | 16-bit fixed | 16-bit fixed |
| Model | SR | DCGAN |
| Throughput (GOPS) | 72.8 | 1578 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Shen, J.; Wen, M.; Zhang, C. Efficient Implementation of 2D and 3D Sparse Deconvolutional Neural Networks with a Uniform Architecture on FPGAs. Electronics 2019, 8, 803. https://doi.org/10.3390/electronics8070803
Wang D, Shen J, Wen M, Zhang C. Efficient Implementation of 2D and 3D Sparse Deconvolutional Neural Networks with a Uniform Architecture on FPGAs. Electronics. 2019; 8(7):803. https://doi.org/10.3390/electronics8070803
Chicago/Turabian StyleWang, Deguang, Junzhong Shen, Mei Wen, and Chunyuan Zhang. 2019. "Efficient Implementation of 2D and 3D Sparse Deconvolutional Neural Networks with a Uniform Architecture on FPGAs" Electronics 8, no. 7: 803. https://doi.org/10.3390/electronics8070803
APA StyleWang, D., Shen, J., Wen, M., & Zhang, C. (2019). Efficient Implementation of 2D and 3D Sparse Deconvolutional Neural Networks with a Uniform Architecture on FPGAs. Electronics, 8(7), 803. https://doi.org/10.3390/electronics8070803





