1. Introduction
The straightforward structure of frequency modulated continuous wave (FMCW) radar contributes to its broad application [
1,
2,
3]. The electronic scanning radar sees a decreasing cost as time division multiplexing (TDM) switch antenna array (SAA) is applied [
4,
5,
6]. However, considering the application of the SAA FMCW radar in moving scenarios, such as unmanned aerial vehicle (UAV) motion sensing and vehicle collision avoidance, the motion-induced phase will result in a direction estimation error [
7,
8]. On that account, with the purpose to make an accurate estimation on target direction, researchers put forward phase compensation methods [
9,
10,
11]. However, some of these methods are only applicable to TDM multiple-input-multiple-output (MIMO) FMCW radar. For example, an improved Doppler processing method was proposed in [
12] and a phase compensation method based on sparse reconstruction was also developed in [
13]. Additionally, Guetlein [
14] found that the phase difference introduced by the target motion can be ignored when the transmit antenna was quickly switched at a single frequency.
The phase compensation method aiming at SAA FMCW radar is less published. L. Yang [
15] successfully estimated direction and velocity using two-dimensional MUSIC signal processing. M.-S. Lee [
16] introduced the ‘time-invariant steering vector (TISV)’ to modify the conventional digital beam forming (DBF) algorithm and finally achieves multi-parameter (i.e., range, velocity, and direction) estimation. However, these methods are confronted with the ambiguous velocity estimation problem. Z. Dominik [
17] estimated the velocity of the moving target to make compensation on its phase response. Similarly, it is impossible to implement compensation correctly at an ambiguous velocity. A valuable random switching method was developed in a previous study [
18] which realizes the focusing of moving tanks through timing optimization and FOCUSS algorithm but has several notable disadvantages. The target azimuth focus cannot be achieved through conventional DBF algorithms. Also, the switching timing must be re-optimized for different target characteristics. Similar drawbacks exist in the switching sequence optimization method [
19]. A phase recovery method was proposed to image the moving tank [
20]. However, experimental verification has not been conducted.
To solve the problems above, this paper proposes a computationally simple method to eliminate motion-induced phase for SAA FMCW radar, where a double-time switching scheme (DTSS) instead of a conventional switching scheme (CSS) is used for echo signals receiving. Elementary signal processing techniques are sufficient for eliminating the motion-induced phase. Furthermore, the proposed method does not require an optimization algorithm or velocity estimation.
The rest of this paper is organized as follows. Firstly, the signal model based on CSS is established in
Section 2. Then, the phase elimination method based on DTSS is proposed, and its signal processing flow is shown in
Section 3. Finally, simulation and experimental testing are conducted to validate the proposed method in
Section 4.
2. Signal Model Based on CSS
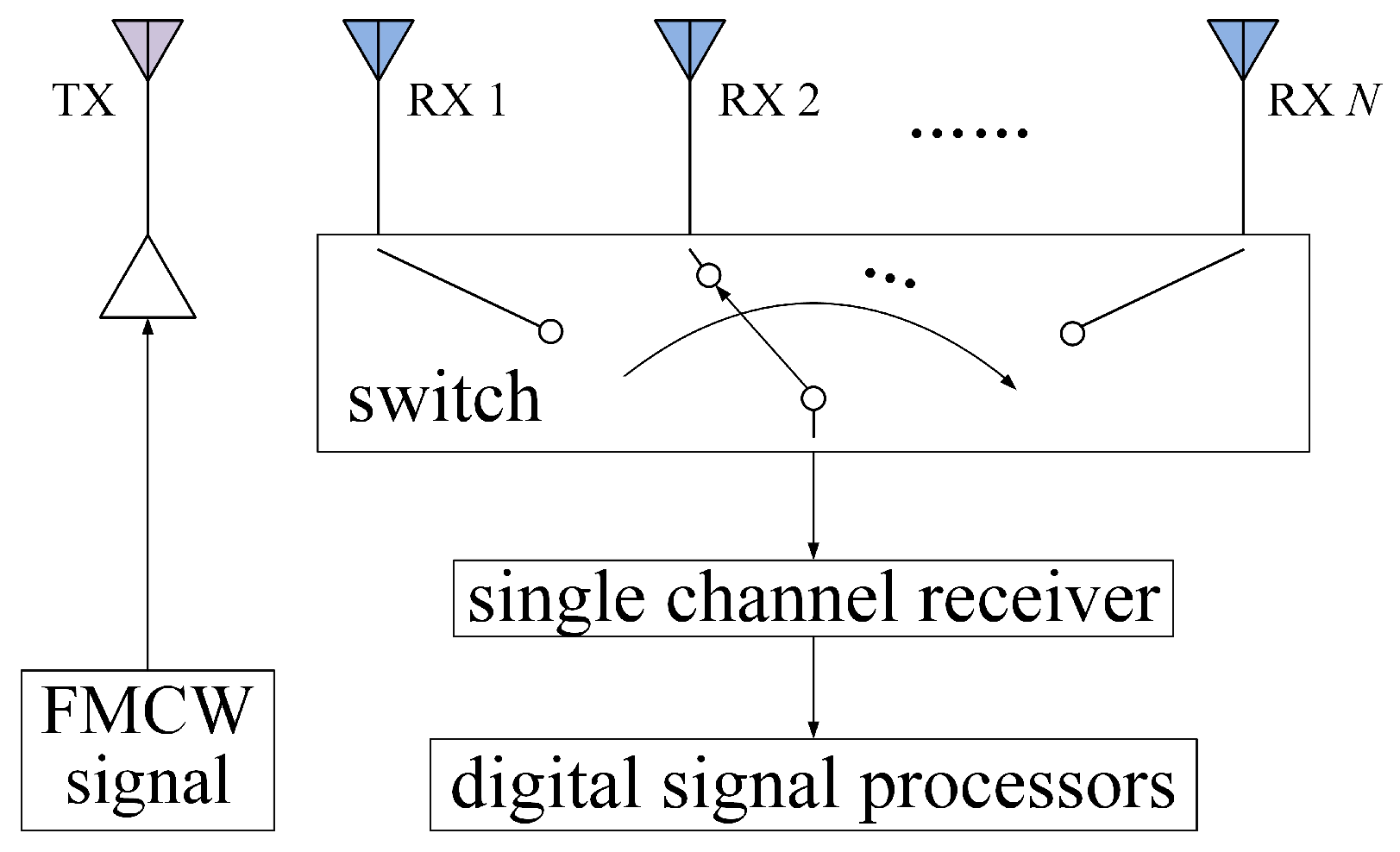
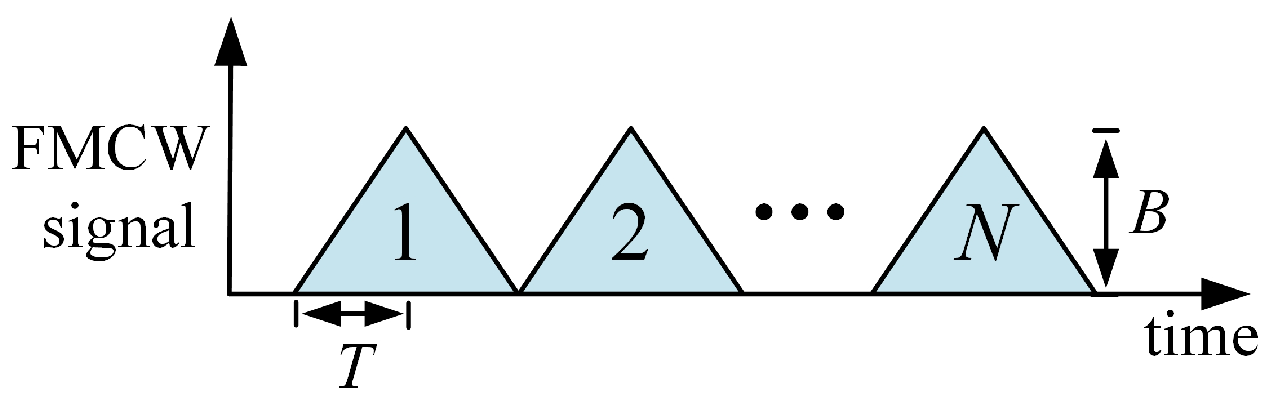
Figure 1 illustrates a traditional SAA FMCW radar system. The antenna is comprised of a transmitting antenna and a receiving uniform linear SAA with
N elements. SAA shares one single receiver channel. The waveform used in this paper is triangle FMCW which is composed by up-chirp and down-chirp. The frequency modulation period of the single chirp is
T, and the sweep bandwidth is
B. In CSS as shown in
Figure 2,
N elements are switched in sequence. The switching interval is
, which is equivalent to repetition interval of the transmitted FMCW signal.
The transmit FMCW signal is written as
where
is the carrier frequency, and
k is the chirp rate defined as
The positive
k represents up-chirp and negative
k stands for down-chirp. Since the signal model of up-chirp is similar to that of down-chirp, the signal model of down-chirp is omitted. The echo signal received by the
n-th antenna element using CSS is
where subscript
i indicates the
i-th target (
),
c is the speed of light.
and
are the range and azimuth, respectively.
is the relative radial velocity between the target and the radar.
is the spacing between adjacent elements of SAA.
is the amplitude of the signal received by the
n-th receiving element.
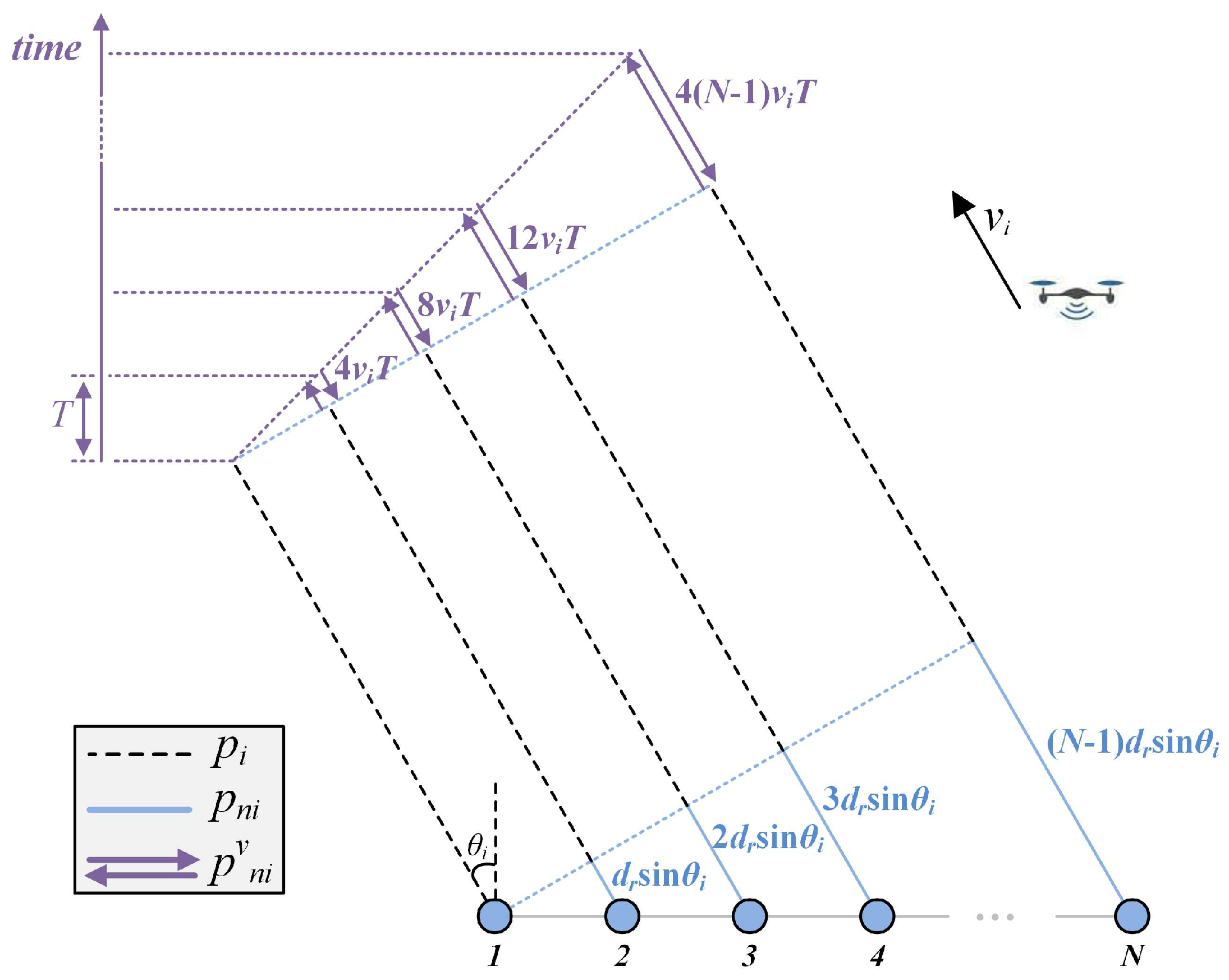
is the two-way wave propagation time of the echo signal, it is determined by the two-way wave propagation path which is composed of three terms. The schematic diagram of the wave propagation path is shown in
Figure 3 for clear description. The first term
is the wave propagation path of the echo signal received by the 1st element. The second term
is the wave propagation delay of the echo signal between the 1st element and the
n-th element. The third term
is the motion-induced path.
The received echo signal is then processed using a deramp technique, in which the echo signal
is mixed with the complex conjugate transmitted signal
. We obtain a down-converted signal
and, assuming the amplitude of the signal received by
N elements is consistent, namely
. Additionally,
,
are considered, Equation (
4) can be simplified to the following form [
15]
where
is the deramped signal received by the first element.
and
are the frequency and phase information, respectively.
After the range processing with zero-padding fast Fourier transform (FFT), the target will be distributed in its range unit. The
n-th element’s complex signal of the range unit where the target is located is expressed as
where
is the estimated range of the
i-th target,
is the signal of the 1st element.
and
are the amplitude and phase information, respectively. The parameter
is the motion-induced phase and it depends on
,
and
T. In the case of stationary targets, namely
, the direction estimation is independent with this phase. However, in the case of moving targets, namely
, it will lead to an inaccurate direction estimation.
3. Phase Elimination Method Based on DTSS
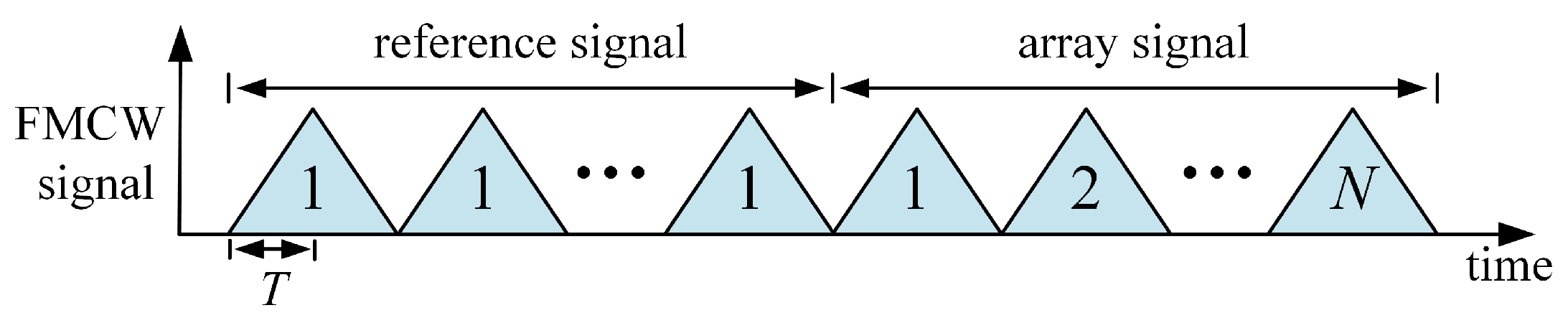
In order to eliminate the motion-induced phase term
in Equation (
6), we propose the switching scheme as shown in
Figure 4. Since its signal acquisition time required for one round of switching is twice that of CSS, it is named as double-time switching scheme (DTSS). By DTSS, one component of the received signal is the reference signal, where the 1st element is switched
N times to receive
N chirps. After the range processing, the
q-th chirp’s complex signal of the range unit where the target is located is expressed as
Another component of the received signal is the array signal, where the array element is switched in sequence from 1 to
N. After the range processing, the
n-th element’s complex signal of the range unit where the target is located is expressed as
The motion-induced phase
can be eliminated using below formula
where
represents the
n-th element’s complex signal after the motion-induced phase is eliminated. We can find that the phase difference between adjacent elements changes from
to
, which has no connection with the target’s velocity. Additionally,
is a constant term which has no impact on the direction estimation.
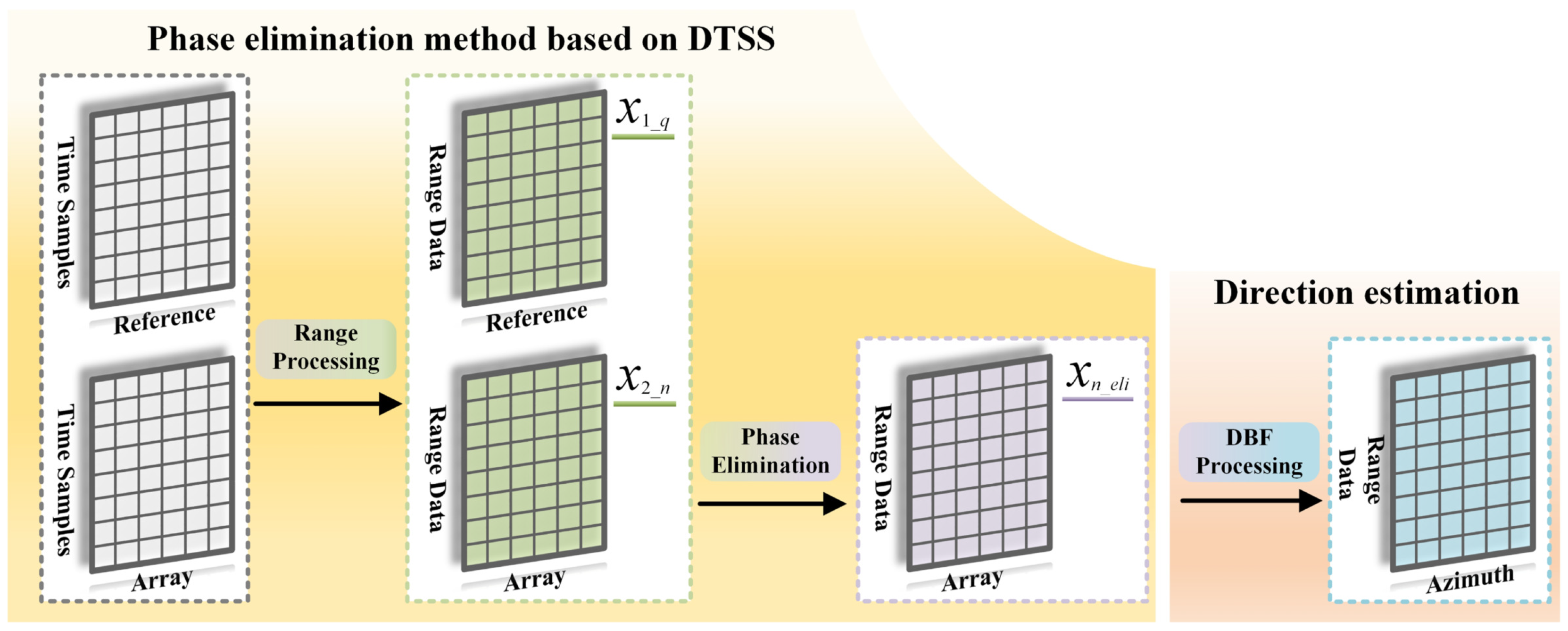
Figure 5 shows the signal processing flow chart of the proposed phase elimination method based on DTSS. At first, the signal is received in accordance with DTSS shown in
Figure 4. Then, the zero-padding Fast Fourier Transformation (FFT) is conducted on the received signal to operate the range processing and get the range complex signals. At this stage, the Hamming window is used to suppress the side-lobe. At last, the motion-induced phase is eliminated via (
9), and the array signal with phase elimination is obtained. This signal can then be used for further processing. For example, the direction estimation can be implemented by applying the conventional algorithm, including conventional beam-former (CBF), Capon beam-former and MUSIC.
It should be noted that the key problem we address is the phase elimination of motion-induced phase to achieve accurate angle estimation. As for the accurate estimations of range and velocity, the approaches in [
21,
22,
23] can be considered, in which the range offset caused by Doppler shift needs to be corrected using the estimated velocity.
4. Simulation and Measurement
In this section, the results of the phase response using CSS and DTSS are given to verify the effectiveness of the phase elimination method based on DTSS. Then, the DBF processing results and imaging results further demonstrate the feasibility of the proposed method for accurate direction estimation. Besides, imaging results of the TISV-based multi-parameter (i.e., range, velocity, and azimuth) estimation method [
16] are also given for comparison. Of course, the signal acquisition time of this method was set to be identical with the proposed method to ensure comparability of results. The DBF processing method adopted here was the conventional beam-former (CBF) with 30 dB Chebyshev side-lobe attenuation. Additionally, Capon beam-former and MUSIC were applied to get spatial spectrum with high angular resolution. Note that the signal processing results of up-chirp were consistent with those of down-chirp, only the results of up-chirp are given.
4.1. Simulation Results
The simulated SAA FMCW radar operates at 10 GHz. Frequency modulation period was T = 0.1 ms and sweep bandwidth was B = 100 MHz. We use an antenna with a cosine pattern as the transmitting antenna and SAA element. The SAA consisted of N = 32 elements with = 15 mm spacing. Three scatterers at different locations served as moving targets. Their ranges, velocities and azimuths were {, , } = {60 m, −5 m/s, }, {, , } = {100 m, −10 m/s, } and {, , } = {130 m, 5 m/s, }, respectively. The relative amplitudes of these targets were :::1:1.
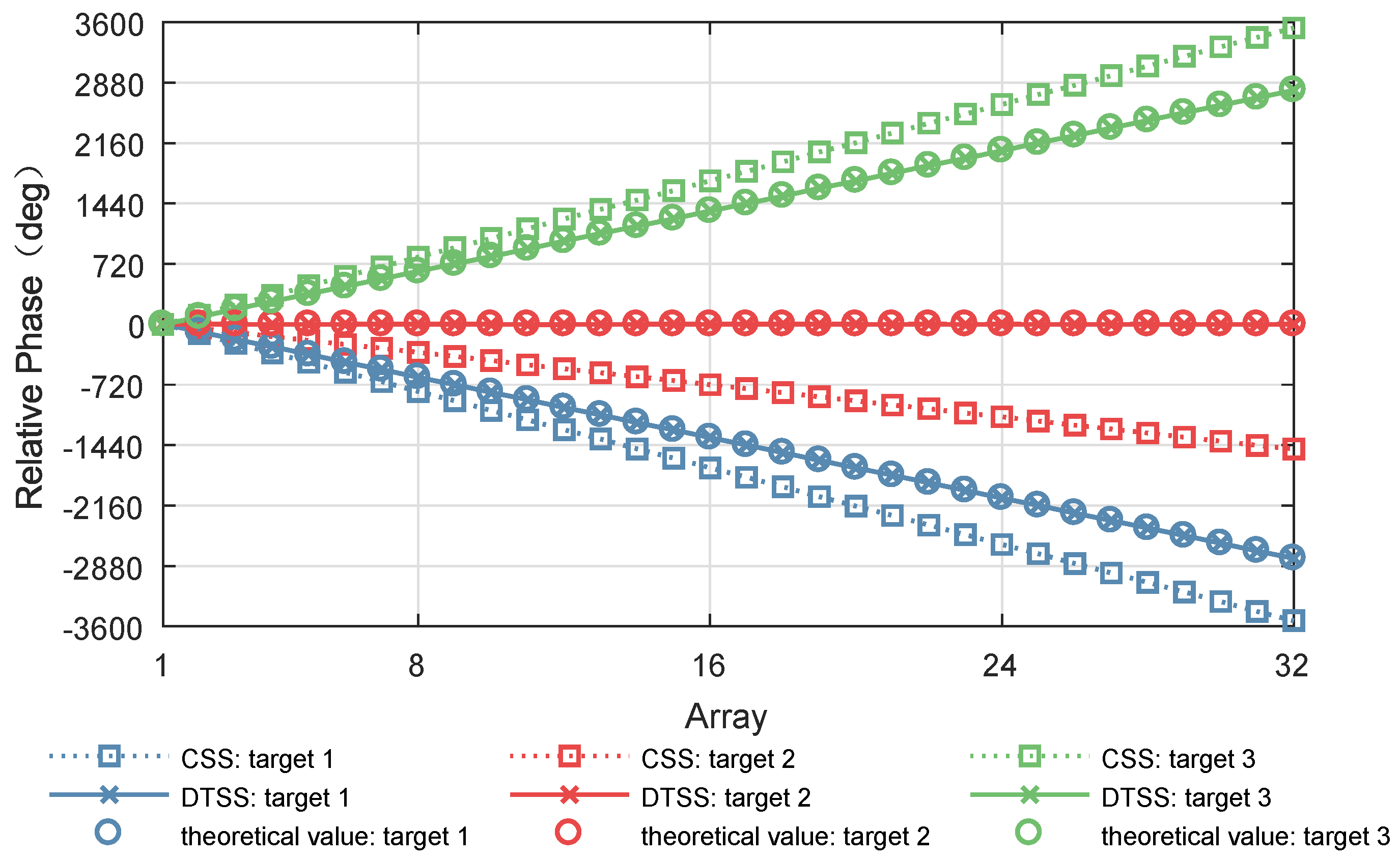
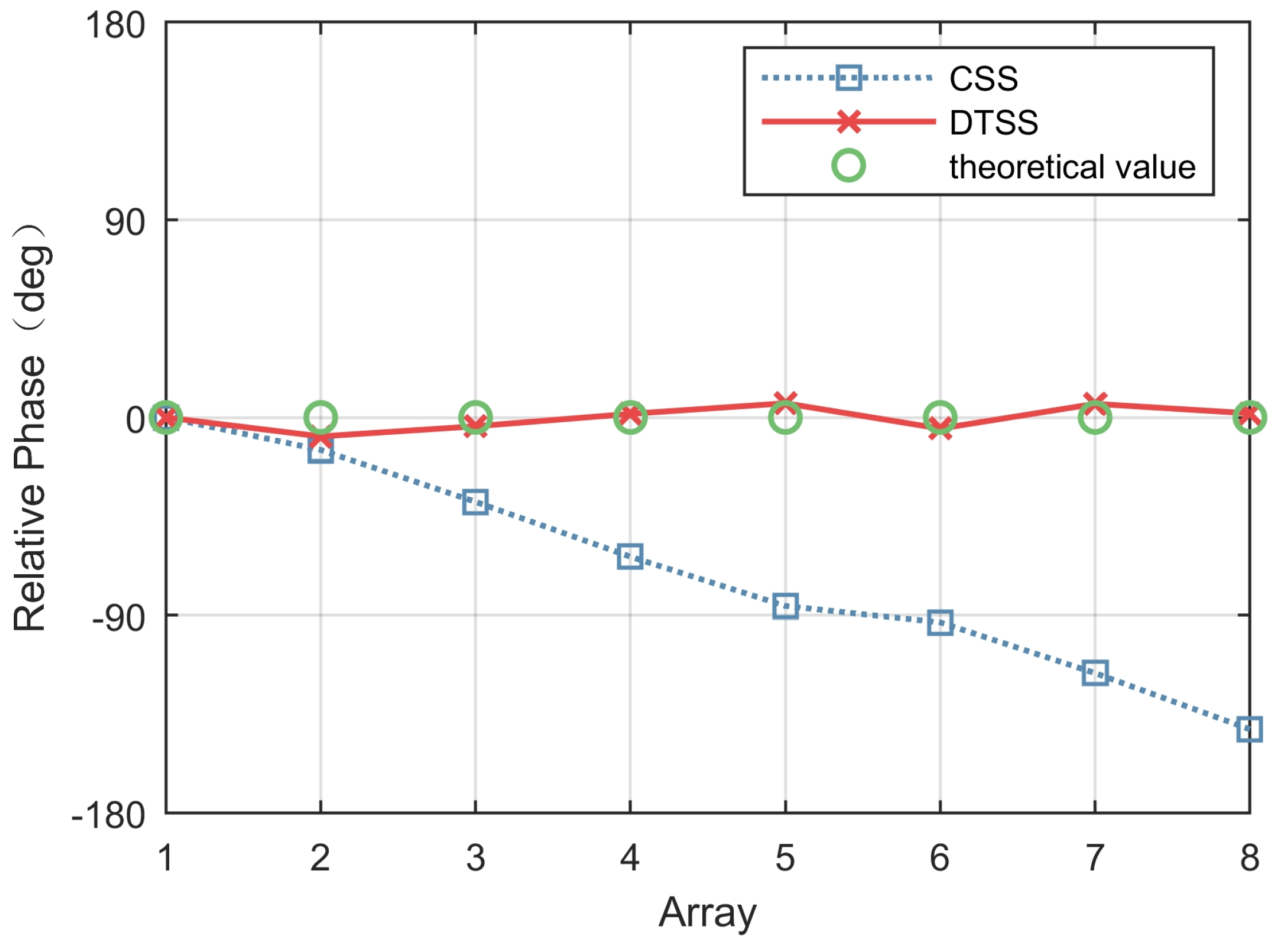
Figure 6 shows the phase response of SAA. The phase response using CSS had motion-induced phase distortion. By contrast, the phase response using DTSS with phase elimination processing was in good agreement with the theoretical value which represents the phase response of the multi-channel antenna array. The DBF processing results are shown in
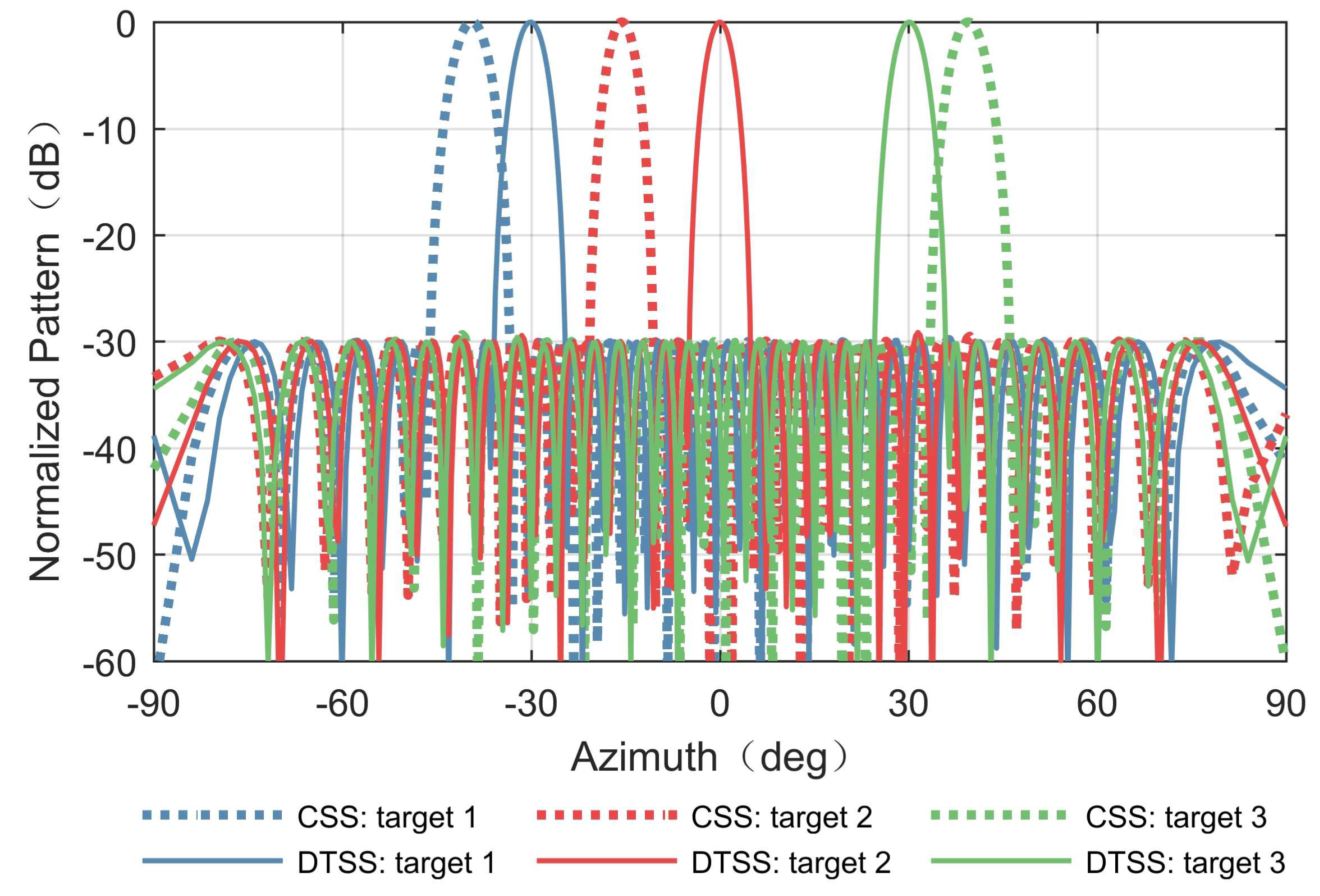
Figure 7. It was observed that the estimated azimuths of the targets using CSS were
,
, and
, respectively, which deviated greatly from their true values. By contrast, when DTSS with phase elimination processing was adopted, the azimuths can be estimated correctly, which were exactly the true values (i.e.,
,
, and
). The imaging result using DTSS with phase elimination processing is shown in
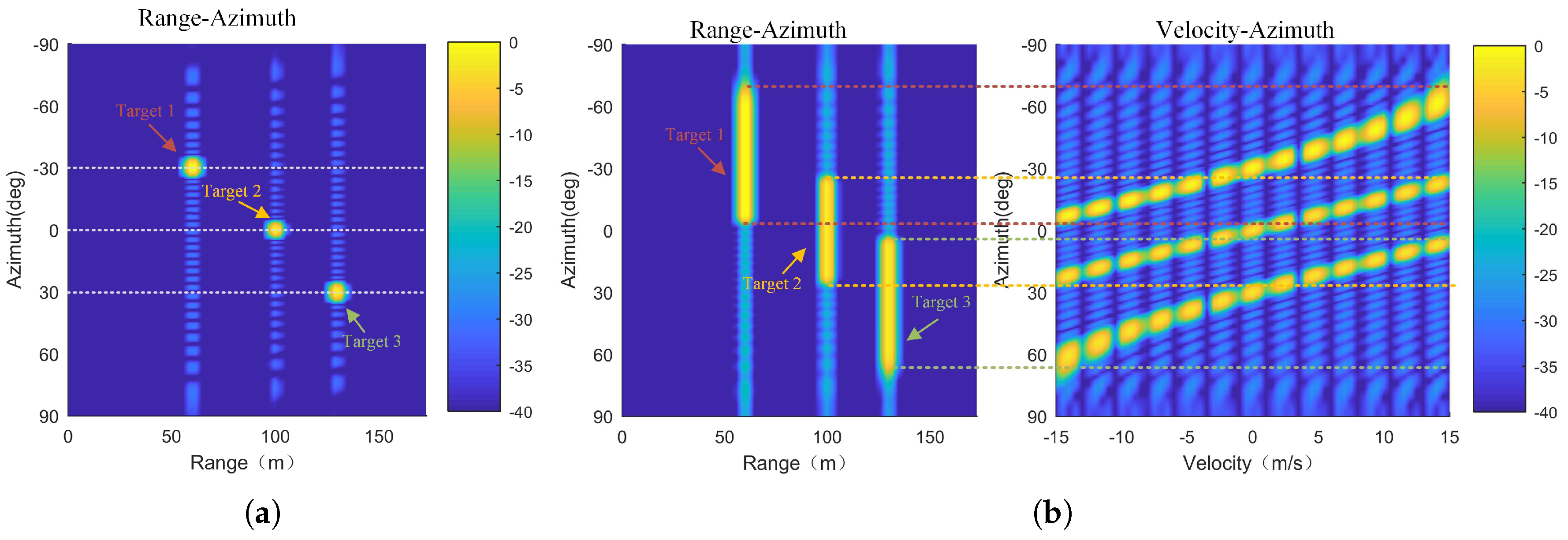
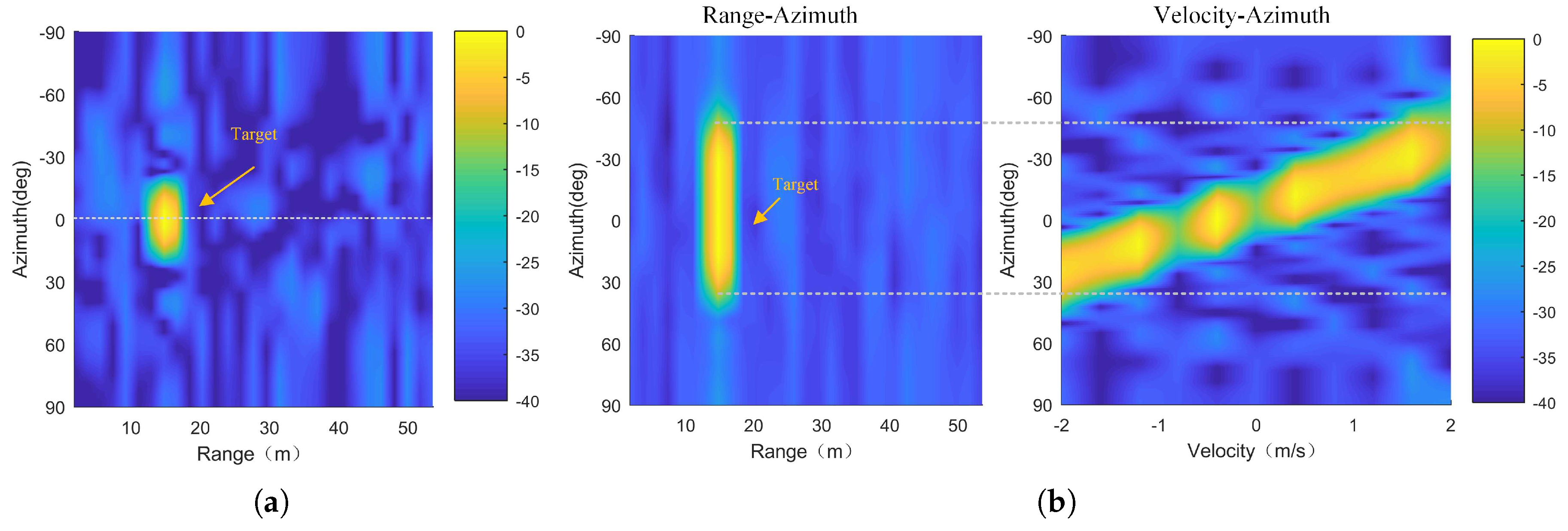
Figure 8a, and from which we could see that the three targets were well focused as a point on the preset positions. As a comparison, the imaging results of the TISV-based multi-parameter estimation method are shown in
Figure 8b. We found that the estimated velocity in the velocity-azimuth image was blurred, eventually resulting in a defocusing of the targets in the azimuth. This was exactly the ambiguous velocity estimation problem that the TISV-based multi-parameter estimation method faces.
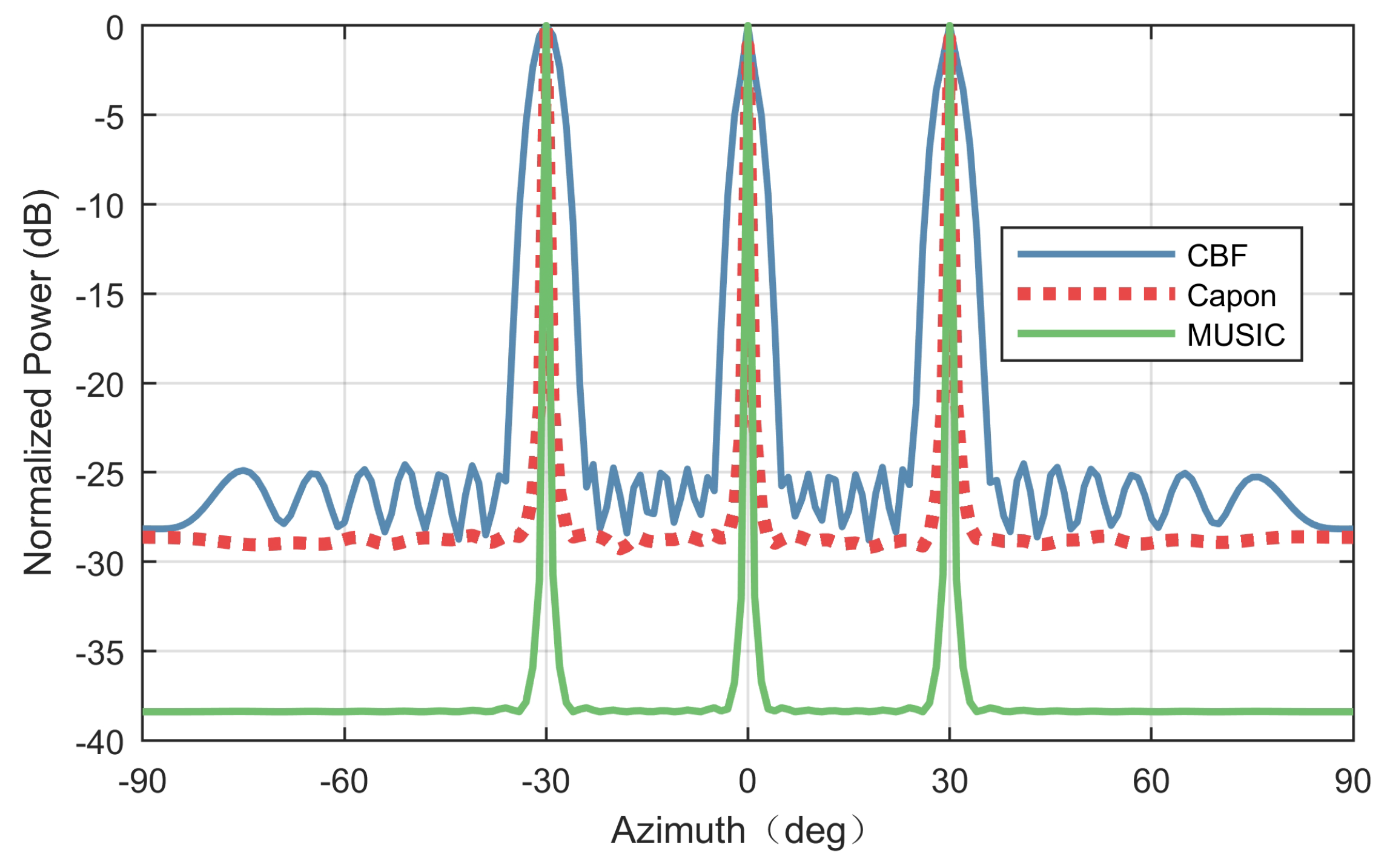
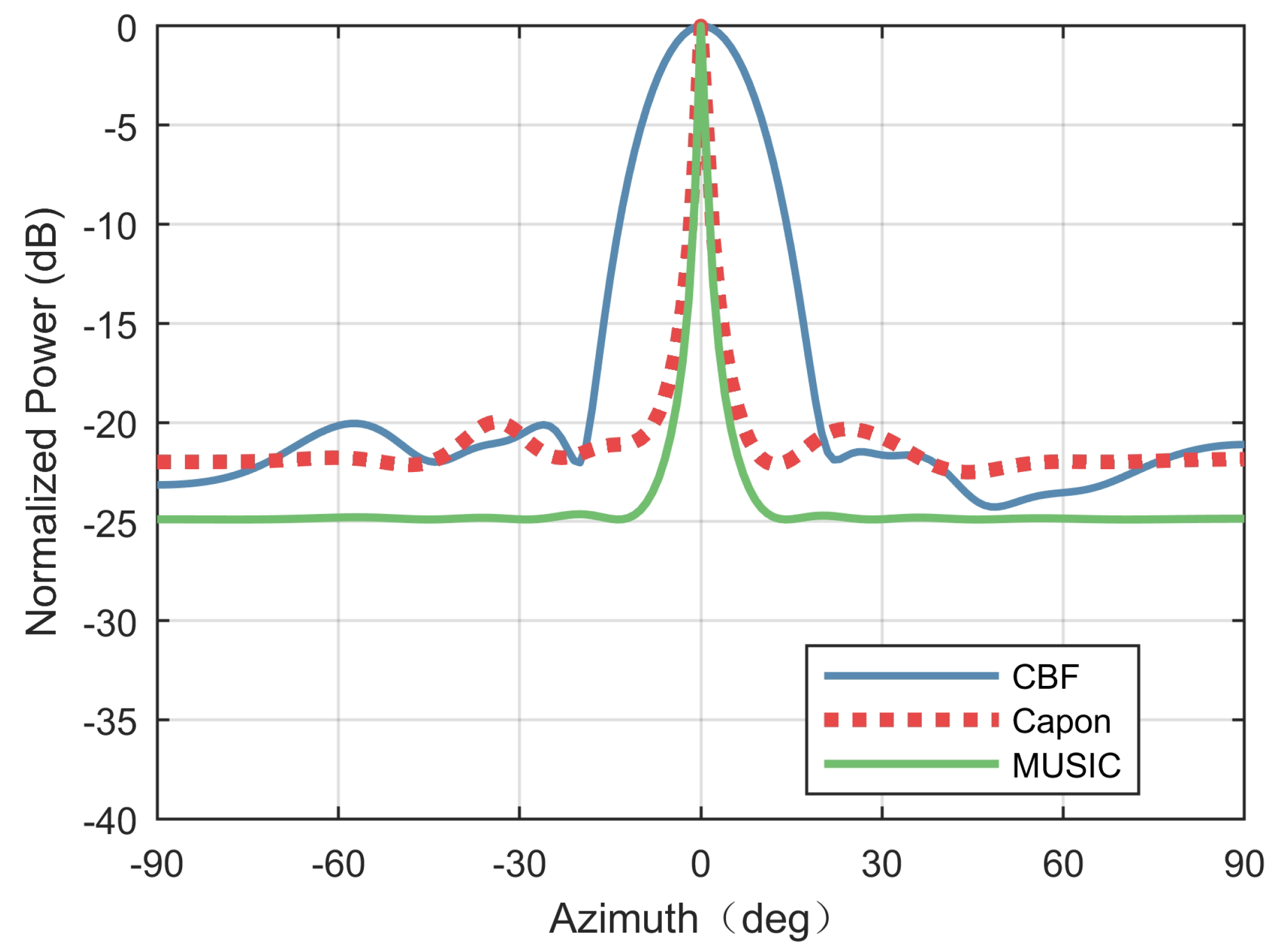
Figure 9 shows the spatial spectrum obtained by CBF, Capon beam-former and MUSIC. Three targets were estimated at
, respectively. Compared with CBF, Capon beam-former and MUSIC achieved higher angular resolution.
Another simulation test was concerned with accuracy analysis of direction-of-arrival (DOA) estimation with various signal-to-noise ratios (SNRs). The SAA consisted of
N = 8 elements with
= 15 mm spacing. A scattering point with
r = 50 m,
v = 8 m/s,
=
served as the moving target. The SNR increase from −30 dB to 20 dB.
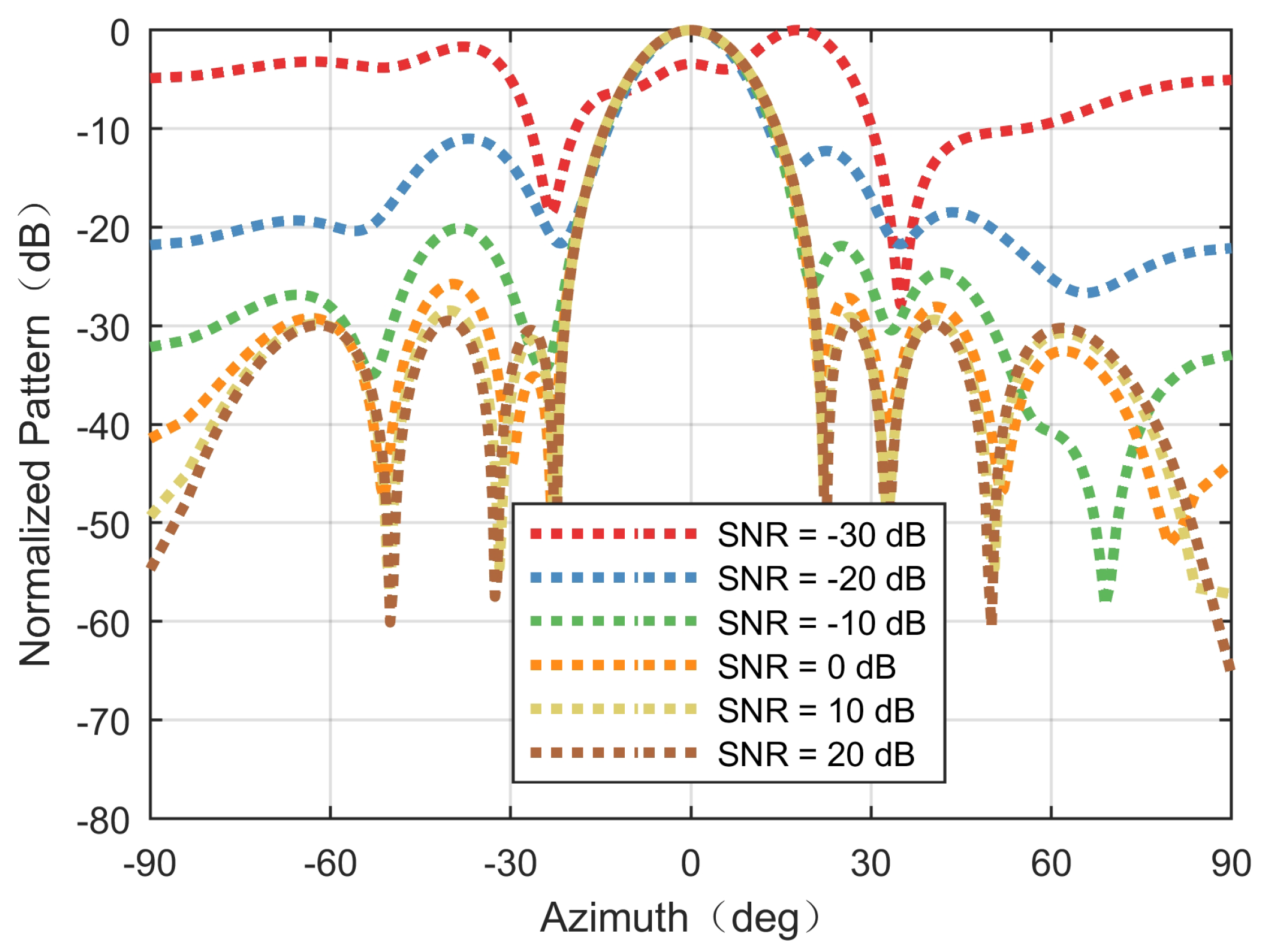
Figure 10 shows the DBF processing results with various SNRs. When SNR = −30 dB, the pattern was severely distorted, and the main beam and side-lobe could not be resolved. When SNR = −20 dB, the main beam and side-lobe were easily resolved, and the side-lobe level is less than −10 dB. As the SNR increased, the side-lobe level gradually decreased and approached the preset value, i.e., −30 dB. In addition, we conducted 100 independent Monte Carlo simulation tests, and
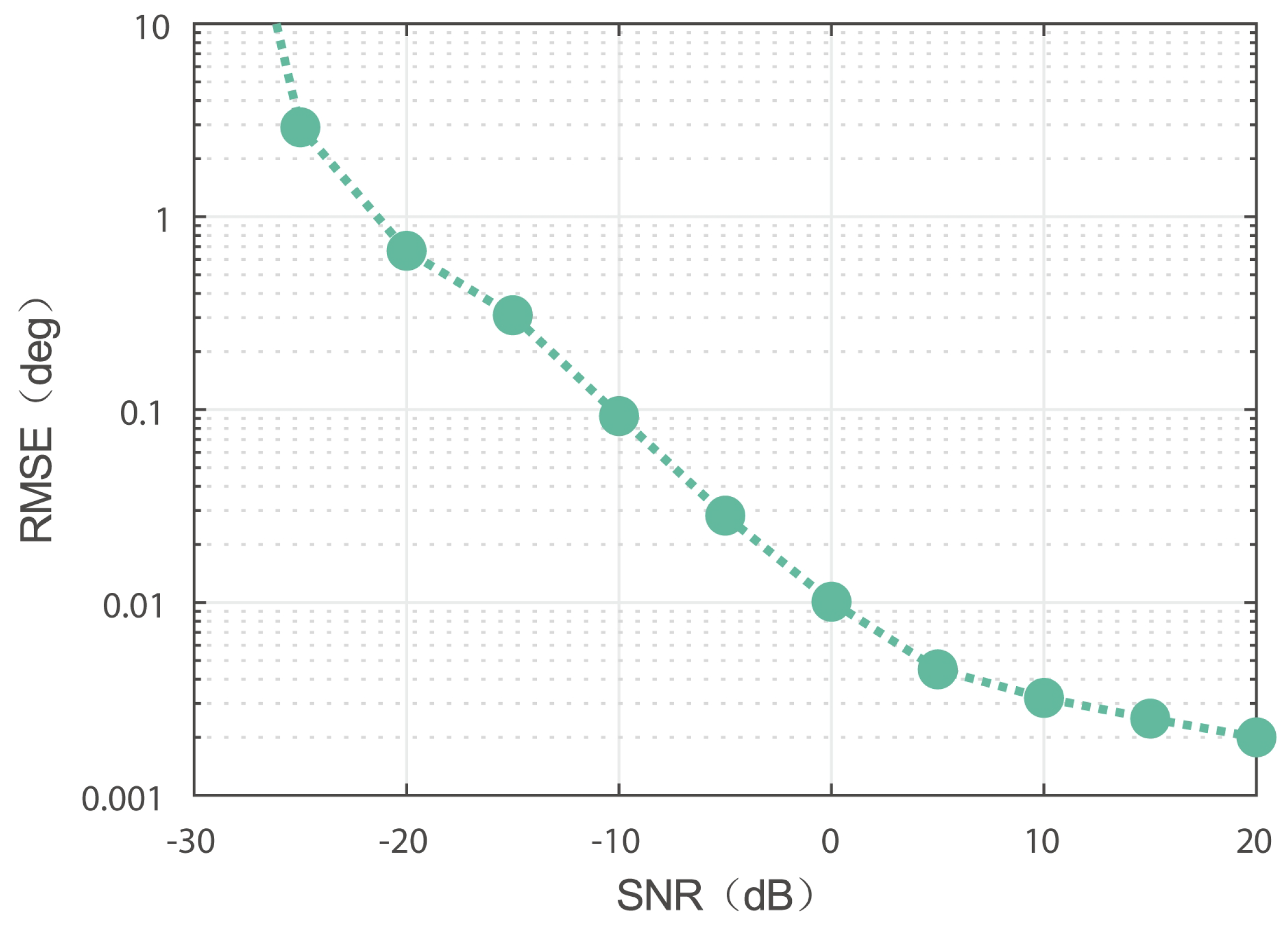
Figure 11 shows the computed root-mean-square errors (RMSEs) of DOA estimation as a function of SNR. When SNR < −22 dB, the RMSE was greater than 1. As the SNR increased, the RMSE gradually decreased. When SNR > 0 dB, the RMSE was less than 0.01.
4.2. Experimental Results
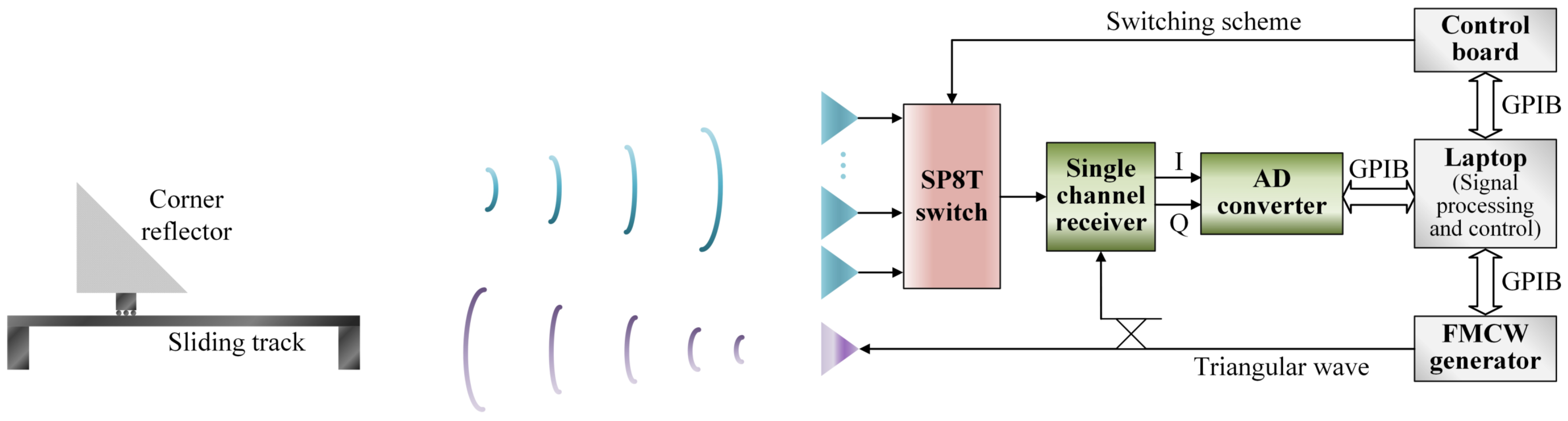
A test bed, as shown in
Figure 12, was set up to evaluate the algorithm performance. A single-pole-eight-throw (SP8T) switch was used for antenna switching. A single channel receiver was used for signal reception and dechirp. A two-channel A/D converter was used to sample beat I and Q signals. A laptop was used for signal processing and control. The sampled data were transferred to the laptop through a general purpose interface bus (GPIB) card. The control board was used to implement the switching scheme. An FMCW generator, which generates the triangular wave, was controlled by the laptop. Timing synchronization between modules was also regulated by the laptop. A corner reflector fixed on a sliding track was used as the moving target.
Figure 13 shows the measurement scenario, with the radar operating frequency of 10.25–10.35 GHz, frequency modulation period of
T = 1 ms. We used a substrate integrated waveguide (SIW) slot array antenna as the transmitting antenna and SAA element in this experiment. The SAA consists of
N = 8 elements with
= 15.4 mm spacing. The target refers to a corner reflector located at (15 m,
). Being fixed on a sliding track, the corner reflector was controlled to move away from the radar at 0.4 m/s.
Figure 14 shows the phase response of SAA. The linear phase distortion was observed when the CSS was adopted. By contrast, the phase response using DTSS with phase elimination processing was coincident with the theoretical value. The DBF processing results are shown in
Figure 15. It was observed that the azimuth of the target was misestimated in
when CSS was applied. However, when DTSS with phase elimination processing was adopted, the azimuth of the target was estimated correctly in
. The imaging results are shown in
Figure 16, from which a phenomenon similar to the simulation results could be observed. The targets were well focused as a point on its real position in the azimuth when the proposed method was used. However, when it came to the TISV-based multi-parameter estimation method, the targets could not be focused because of the ambiguous velocity estimation problem.
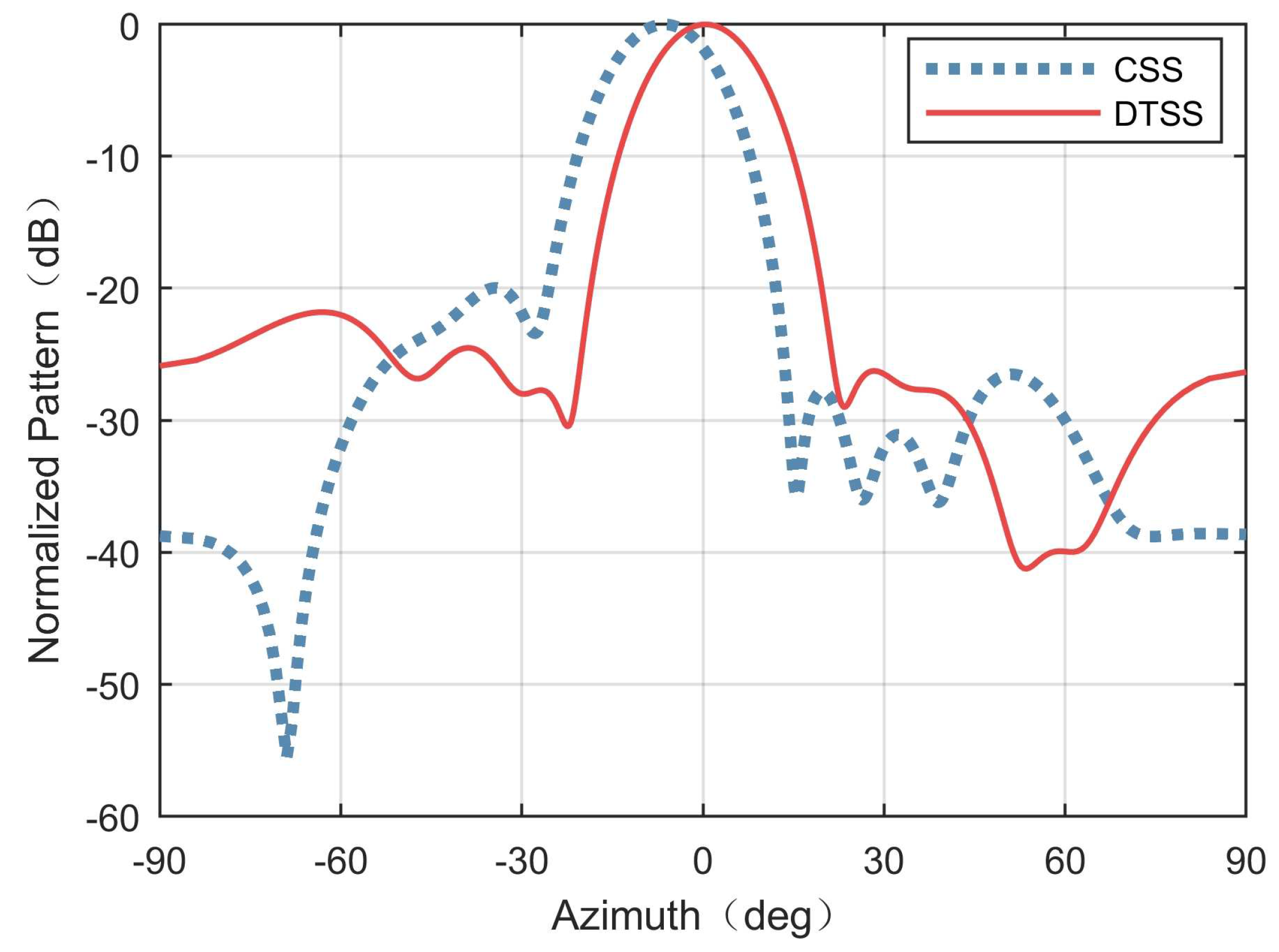
Figure 17 shows the spatial spectrum. The target was estimated at
. The higher angular resolution was obtained by Capon beam-former and MUSIC.
In summary, in the proposed method, velocity estimation is not required, which avoids the problem of ambiguous velocity estimation. This is exactly the main benefit of the proposed method.