Ultrasonic Health Monitoring of Lithium-Ion Batteries
Abstract
1. Introduction
2. Ultrasonic Sensing for Lithium-Ion Batteries
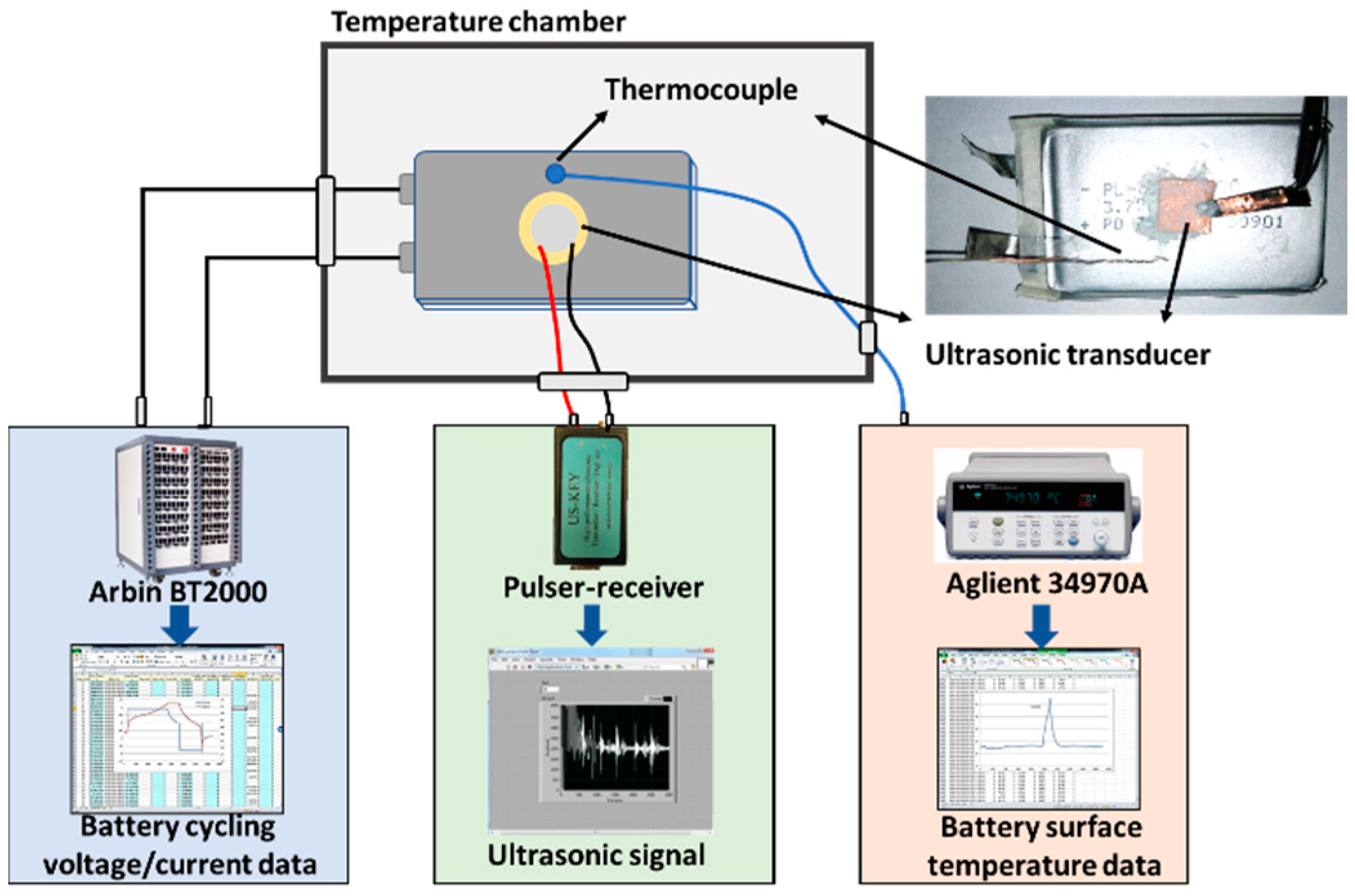
3. Experimental Setup
4. Ultrasonic Results for Lithium-Ion Batteries
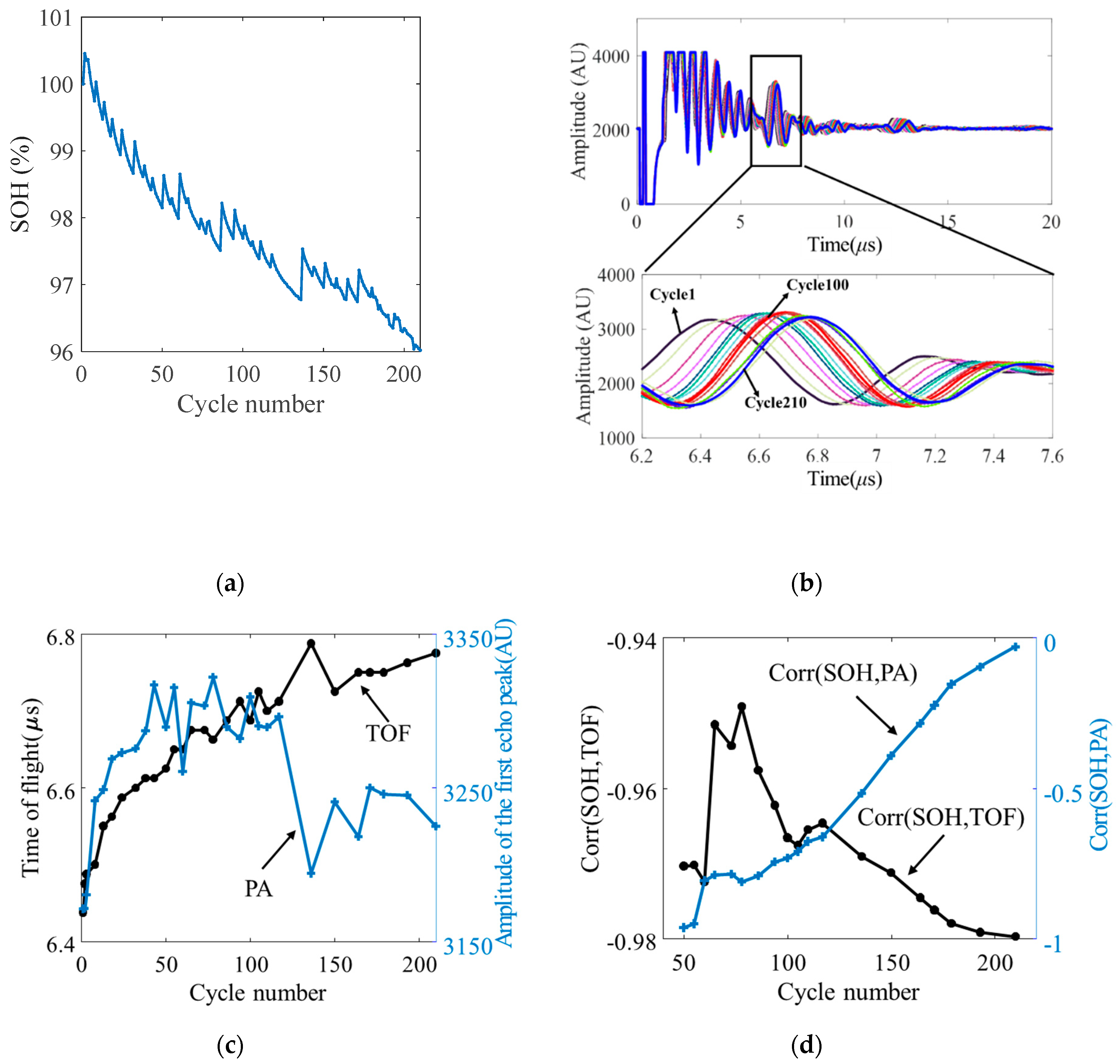
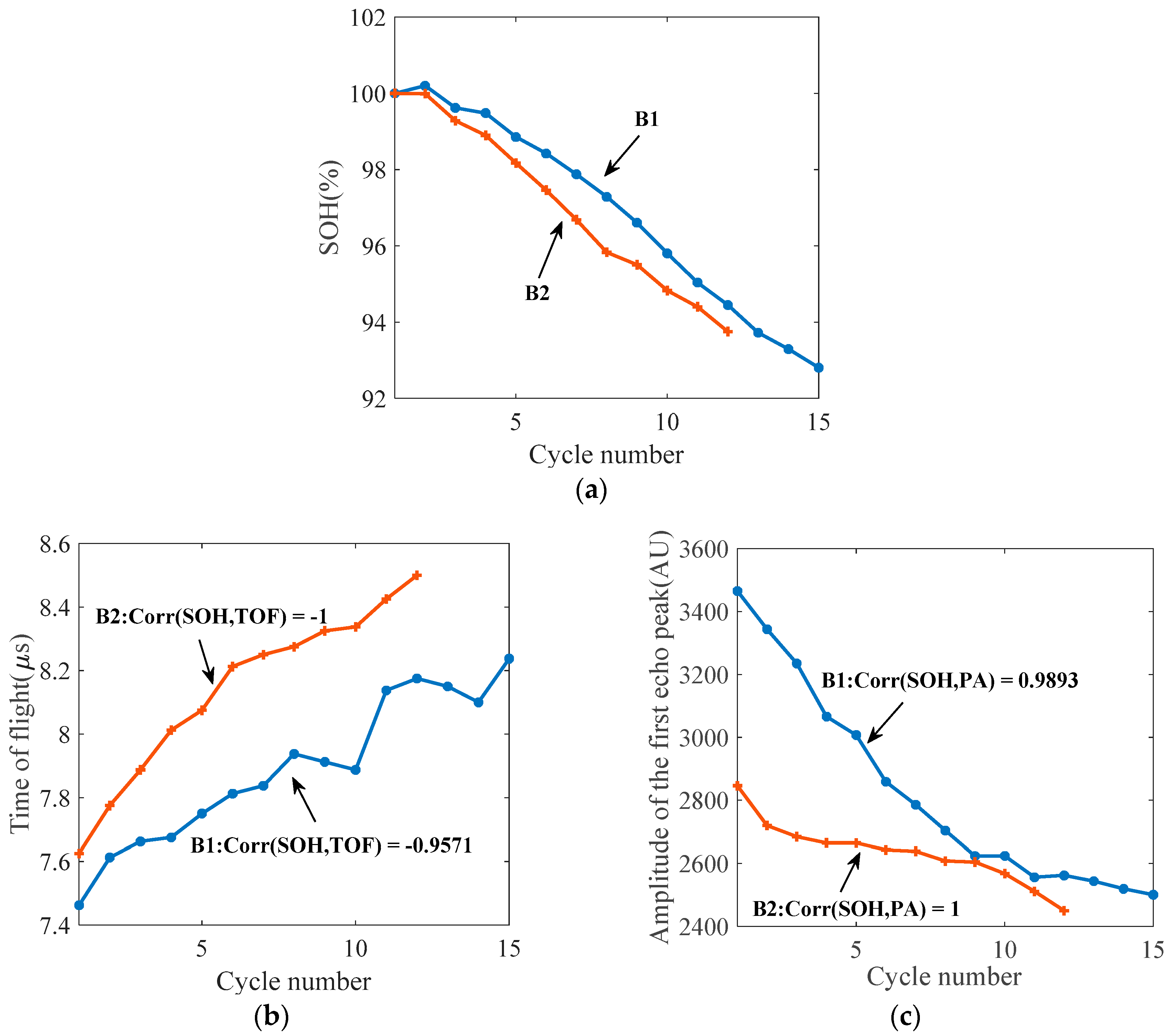
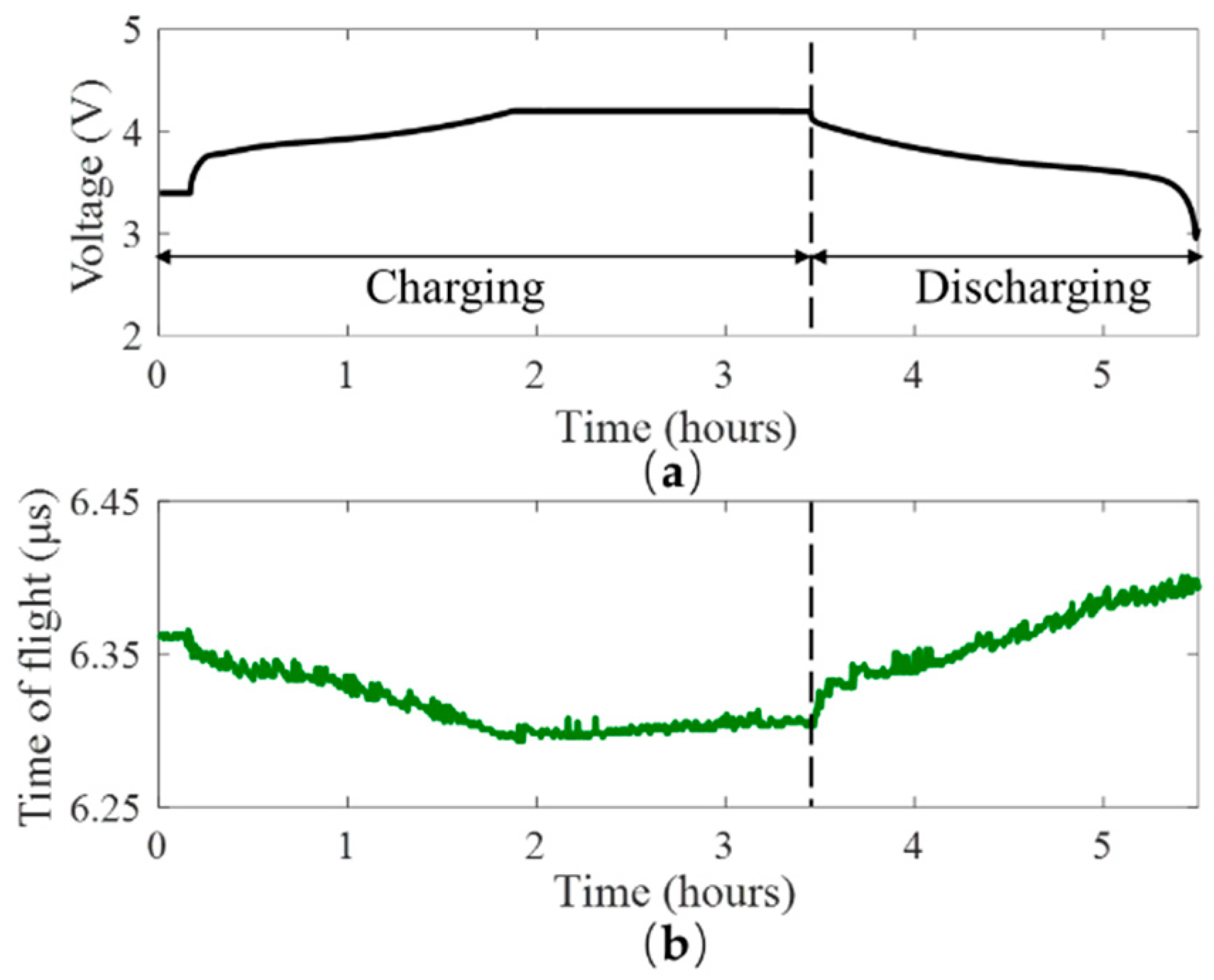
4.1. Ultrasonic Results for the Cycling Tests
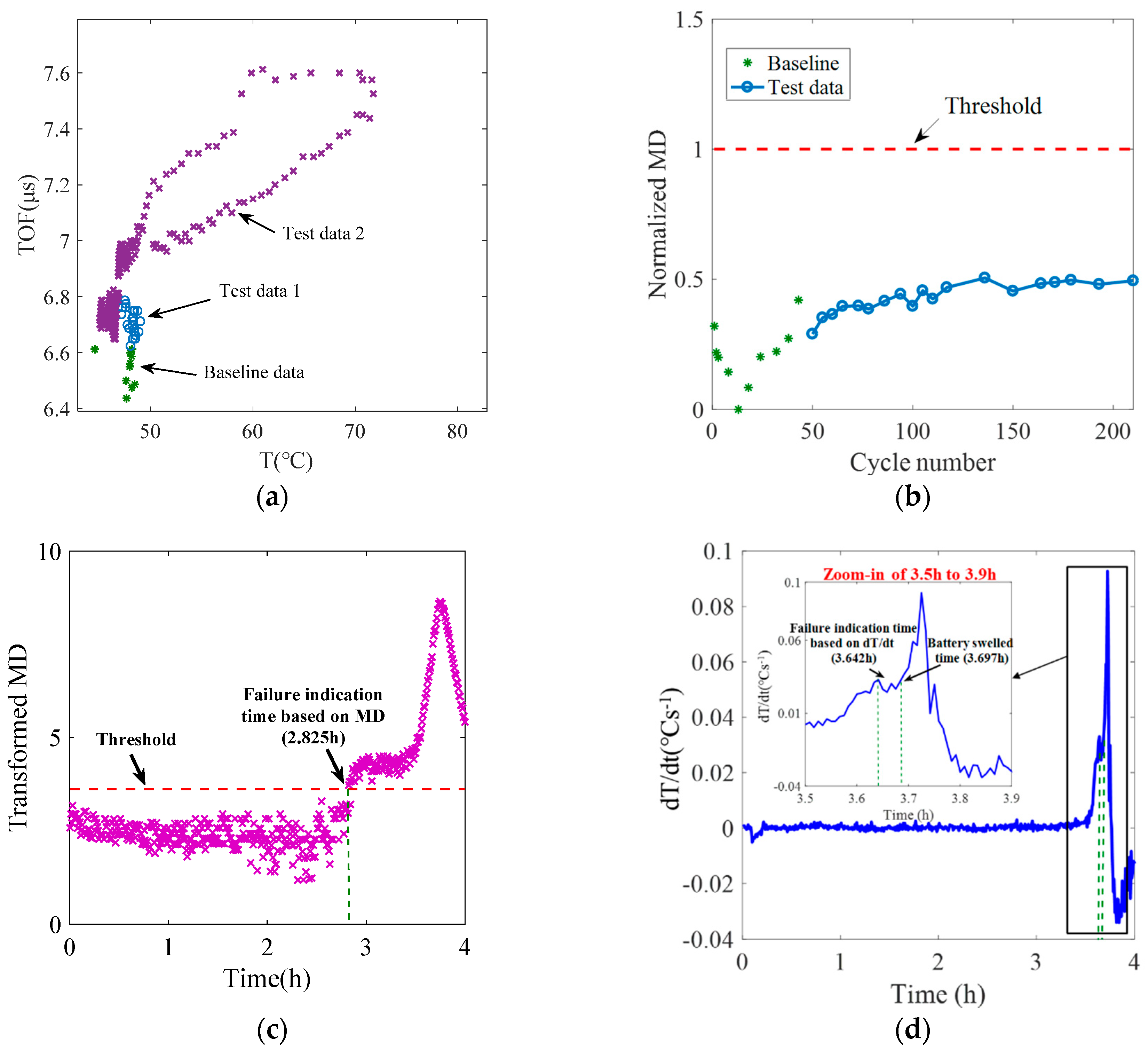
4.2. Ultrasonic Results for the Abusive Test
5. Ultrasonic Health Monitoring for Lithium-Ion Batteries
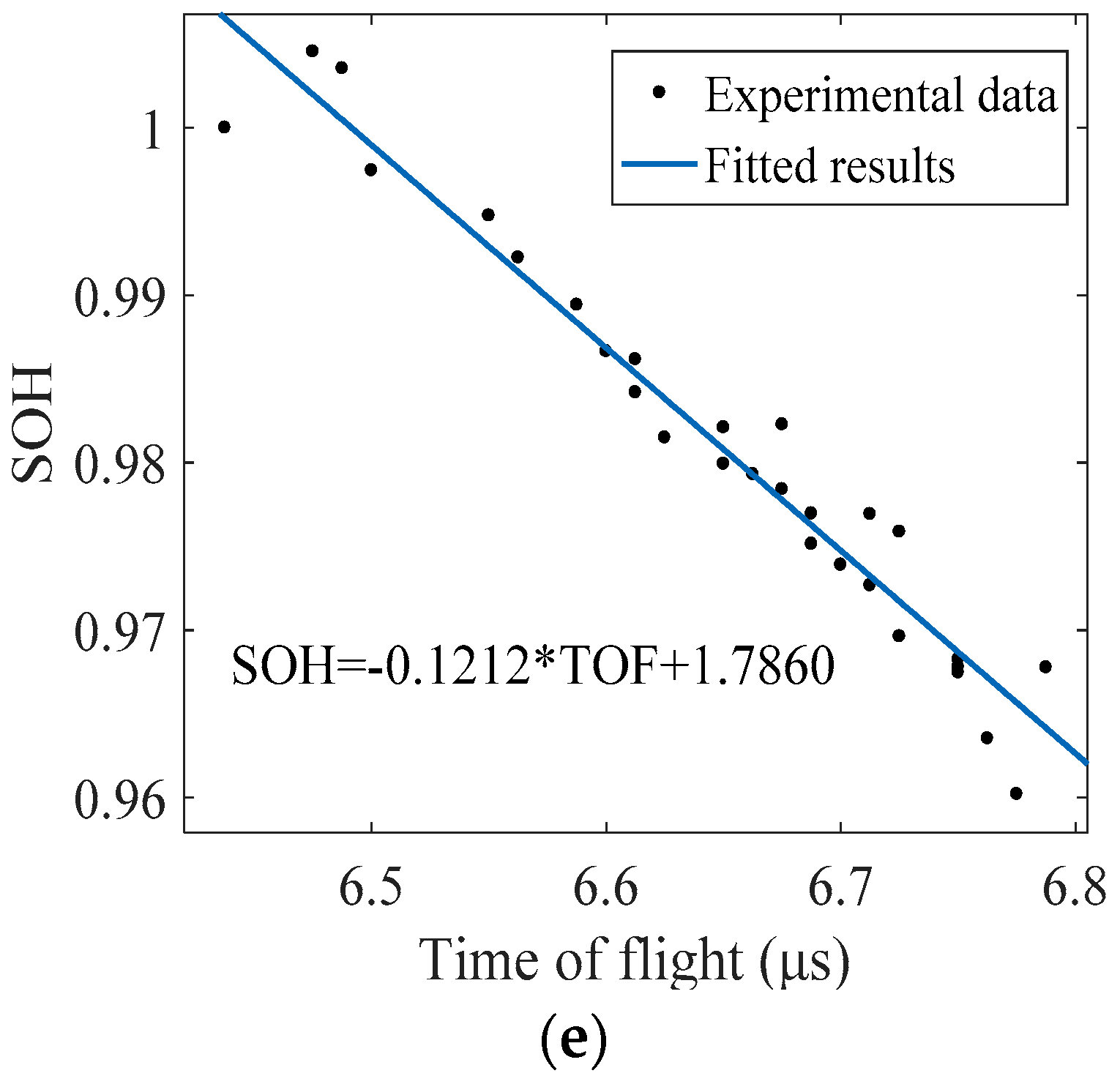
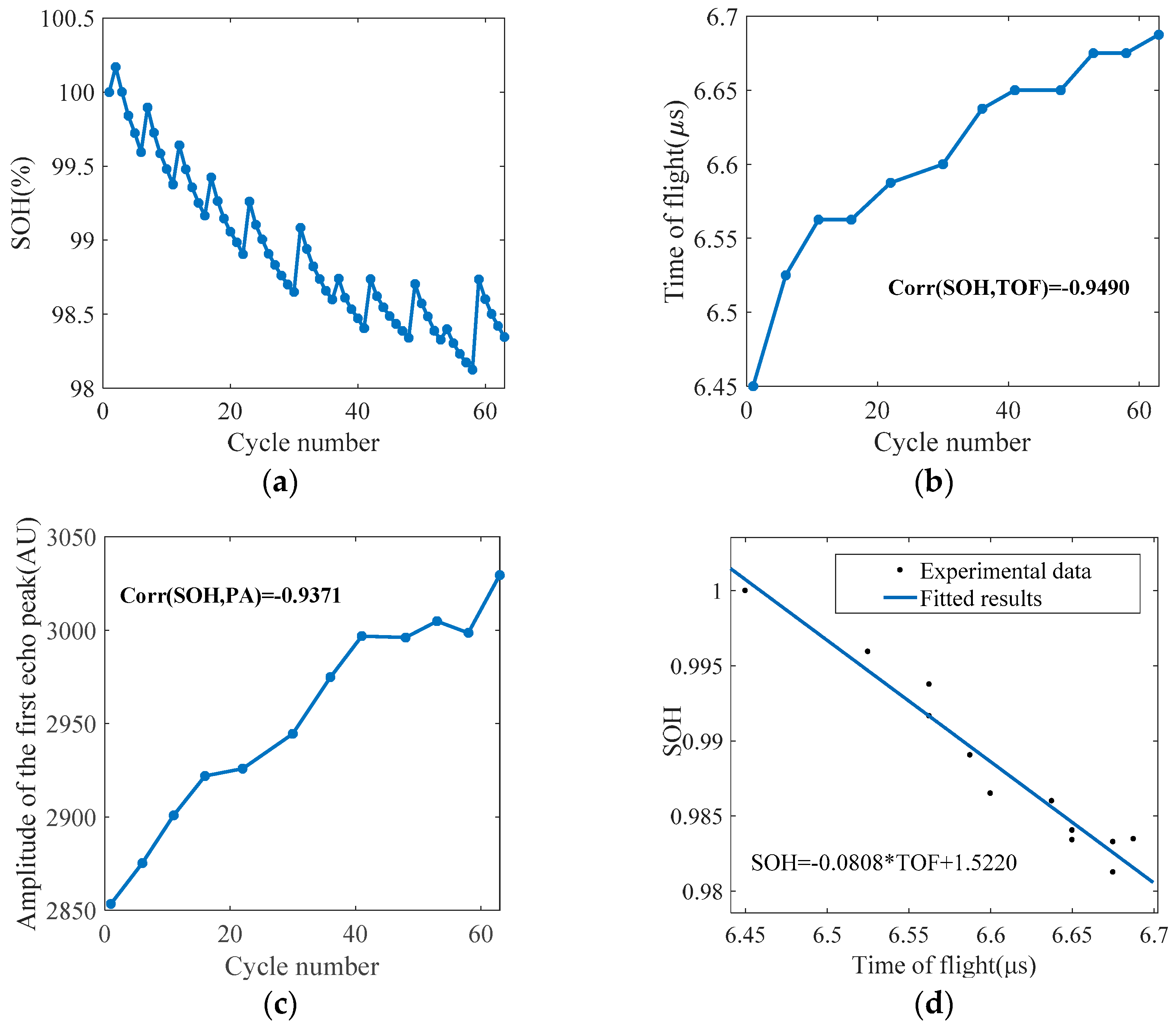
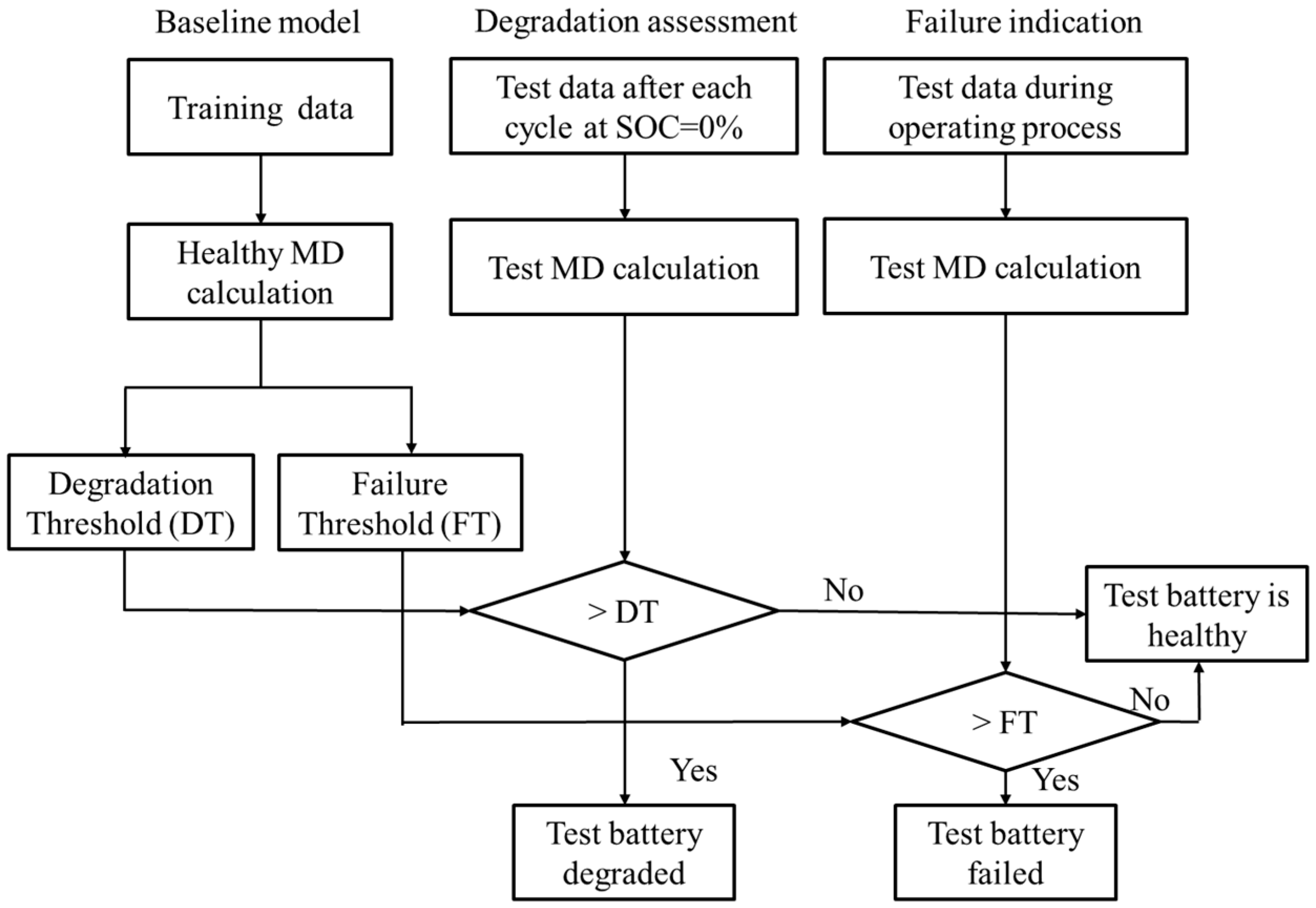
5.1. Methodology
5.2. Battery Health Monitoring Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Arora, P. Capacity fade mechanisms and side reactions in lithium-ion batteries. J. Electrochem. Soc. 1998, 145, 3647. [Google Scholar] [CrossRef]
- Kim, G.H.; Smith, K.; Ireland, J.; Pesaran, A. Fail-safe design for large capacity lithium-ion battery systems. J. Power Sources 2012, 210, 243–253. [Google Scholar] [CrossRef]
- Wu, Y.; Saxena, S.; Xing, Y.; Wang, Y.; Li, C.; Yung, W.K.C.; Pecht, M. Analysis of manufacturing-induced defects and structural deformations in lithium-ion batteries using computed tomography. Energies 2018, 11, 925. [Google Scholar] [CrossRef]
- Williard, N.; He, W.; Hendricks, C.; Pecht, M. Lessons learned from the 787 Dreamliner issue on lithium-ion battery reliability. Energies 2013, 6, 4682–4695. [Google Scholar] [CrossRef]
- Hendricks, C.; Williard, N.; Mathew, S.; Pecht, M. A failure modes, mechanisms, and effects analysis (FMMEA) of lithium-ion batteries. J. Power Sources 2015, 297, 113–120. [Google Scholar] [CrossRef]
- Abada, S.; Marlair, G.; Lecocq, A.; Petit, M.; Sauvant-Moynot, V.; Huet, F. Safety focused modeling of lithium-ion batteries: A review. J. Power Sources 2016, 306, 178–192. [Google Scholar] [CrossRef]
- El Mejdoubi, A.; Oukaour, A.; Chaoui, H.; Gualous, H.; Sabor, J.; Slamani, Y. State-of-charge and state-of-health lithium-ion batteries’ diagnosis according to surface temperature variation. IEEE Trans. Ind. Electron. 2016, 63, 2391–2402. [Google Scholar] [CrossRef]
- Berecibar, M.; Gandiaga, I.; Villarreal, I.; Omar, N.; Van Mierlo, J.; Van den Bossche, P. Critical review of state of health estimation methods of Li-ion batteries for real applications. Renew. Sustain. Energy Rev. 2016, 56, 572–587. [Google Scholar] [CrossRef]
- Lipu, M.S.H.; Hannan, M.A.; Hussain, A.; Hoque, M.M.; Ker, P.J.; Saad, M.H.M.; Ayob, A. A review of state of health and remaining useful life estimation methods for lithium-ion battery in electric vehicles: Challenges and recommendations. J. Clean. Prod. 2018, 205, 115–133. [Google Scholar] [CrossRef]
- Ahwiadi, M.; Wang, W. An enhanced mutated particle filter technique for system state estimation and battery life prediction. IEEE Trans. Instrum. Meas. 2019, 68, 923–935. [Google Scholar] [CrossRef]
- Liu, Z.; Sun, G.; Bu, S.; Han, J.; Tang, X.; Pecht, M. Particle learning framework for estimating the remaining useful life of lithium-ion batteries. IEEE Trans. Instrum. Meas. 2017, 66, 280–293. [Google Scholar] [CrossRef]
- Liu, D.; Song, Y.; Li, L.; Liao, H.; Peng, Y. On-line life cycle health assessment for lithium-ion battery in electric vehicles. J. Clean. Prod. 2018, 199, 1050–1065. [Google Scholar] [CrossRef]
- Xing, Y.; Ma, E.W.M.; Tsui, K.; Pecht, M. An ensemble model for predicting the remaining useful performance of lithium-ion batteries. Microelectron. Reliab. 2013, 53, 811–820. [Google Scholar] [CrossRef]
- Novais, S.; Nascimento, M.; Grande, L.; Domingues, M.F.; Antunes, P.; Alberto, N.; Leitão, C.; Oliveira, R.; Koch, S.; Kim, G.T.; et al. Internal and external temperature monitoring of a Li-ion battery with fiber Bragg grating sensors. Sensors 2016, 16, 1394. [Google Scholar] [CrossRef] [PubMed]
- Raghavan, A.; Kiesel, P.; Sommer, L.W.; Schwartz, J.; Lochbaum, A.; Hegyi, A.; Schuh, A.; Arakaki, K.; Saha, B.; Ganguli, A.; et al. Embedded fiber-optic sensing for accurate internal monitoring of cell state in advanced battery management systems part 1: Cell embedding method and performance. J. Power Sources 2017, 341, 466–473. [Google Scholar] [CrossRef]
- Ganguli, A.; Saha, B.; Raghavan, A.; Kiesel, P.; Arakaki, K.; Schuh, A.; Schwartz, J.; Hegyi, A.; Sommer, L.W.; Lochbaum, A.; et al. Embedded fiber-optic sensing for accurate internal monitoring of cell state in advanced battery management systems part 2: Internal cell signals and utility for state estimation. J. Power Sources 2017, 341, 474–482. [Google Scholar] [CrossRef]
- Lee, C.-Y.; Lee, S.-J.; Hung, Y.-M.; Hsieh, C.-T.; Chang, Y.-M.; Huang, Y.-T.; Lin, J.-T. Integrated microsensor for real-time microscopic monitoring of local temperature, voltage and current inside lithium ion battery. Sens. Actuators A Phys. 2017, 253, 59–68. [Google Scholar] [CrossRef]
- Giurgiutiu, V. Structural Health Monitoring: With Piezoelectric Wafer Active Sensors; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Schmerr, L.W. Fundamentals of Ultrasonic Nondestructive Evaluation; Springer: New York, NY, USA, 2016. [Google Scholar]
- Inspection of Prismatic Lithium Ion Batteries for Consumer Electronics. Available online: http://ultrangroup.com/applications/inspection-of-prismatic-lithium-ion-batteries-for-consumer-electronics/ (accessed on 12 March 2019).
- Sood, B.; Osterman, M.; Pecht, M. Health monitoring of lithium-ion batteries. In Proceedings of the 2013 IEEE Symposium on Product Compliance Engineering (ISPCE), Austin, TX, USA, 7–9 October 2013; pp. 1–6. [Google Scholar]
- Li, H.; Zhou, Z.; Li, H.; Zhou, Z. Numerical simulation and experimental study of fluid-solid coupling-based air-coupled ultrasonic detection of stomata defect of lithium-ion battery. Sensors 2019, 19, 2391. [Google Scholar] [CrossRef] [PubMed]
- Ladpli, P.; Nardari, R.; Kopsaftopoulos, F.; Wang, Y.; Chang, F.K. Design of multifunctional structural batteries with health monitoring capabilities. In Proceedings of the 8th European Workshop on Structural Health Monitoring, Bilbao, Spain, 5–8 July 2016; pp. 1–13. [Google Scholar]
- Ladpli, P.; Kopsaftopoulos, F.; Nardari, R.; Chang, F.K. Battery charge and health state monitoring via ultrasonic guided-wave-based methods using built-in piezoelectric transducers. In Proceedings of the Smart Materials and Nondestructive Evaluation for Energy Systems, Portland, OR, USA, 25–29 March 2017; p. 1017108. [Google Scholar]
- Ladpli, P.; Kopsaftopoulos, F.; Chang, F.-K. Estimating state of charge and health of lithium-ion batteries with guided waves using built-in piezoelectric sensors/actuators. J. Power Sources 2018, 384, 342–354. [Google Scholar] [CrossRef]
- Hsieh, A.G.; Bhadra, S.; Hertzberg, B.; Gjeltema, P.J.; Goy, A.; Fleischer, J.W.; Steingart, D. Electrochemical-acoustic time of flight: In operando correlation of physical dynamics with battery charge and health. Energy Environ. Sci. 2015, 8, 1569–1577. [Google Scholar] [CrossRef]
- Gold, L.; Bach, T.; Virsik, W.; Schmitt, A.; Müller, J.; Staab, T.E.M.; Sextl, G. Probing lithium-ion batteries’ state-of-charge using ultrasonic transmission—Concept and laboratory testing. J. Power Sources 2017, 343, 536–544. [Google Scholar] [CrossRef]
- Davies, G.; Knehr, K.W.; Van Tassell, B.; Hodson, T.; Biswas, S.; Hsieh, A.G.; Steingart, D.A. State of charge and state of health estimation using electrochemical acoustic time of flight analysis. J. Electrochem. Soc. 2017, 164, A2746–A2755. [Google Scholar] [CrossRef]
- Choi, J.W.; Aurbach, D. Promise and reality of post-lithium-ion batteries with high energy densities. Nat. Rev. Mater. 2016, 1, 16013. [Google Scholar] [CrossRef]
- Olivares, B.E.; Cerda Munoz, M.A.; Orchard, M.E.; Silva, J.F. Particle-filtering-based prognosis framework for energy storage devices with a statistical characterization of state-of-health regeneration phenomena. IEEE Trans. Instrum. Meas. 2013, 62, 364–376. [Google Scholar] [CrossRef]
- Swallow, J.G.; Woodford, W.H.; McGrogan, F.P.; Ferralis, N.; Chiang, Y.-M.; Van Vliet, K.J. Effect of electrochemical charging on elastoplastic properties and fracture toughness of LiXCoO2. J. Electrochem. Soc. 2014, 161, F3084–F3090. [Google Scholar] [CrossRef]
- Jameson, N.J.; Azarian, M.H.; Pecht, M. Impedance-based condition monitoring for insulation systems used in low-voltage electromagnetic coils. IEEE Trans. Ind. Electron. 2017, 64, 3748–3757. [Google Scholar] [CrossRef]
- Ohsaki, T.; Kishi, T.; Kuboki, T.; Takami, N.; Shimura, N.; Sato, Y.; Sekino, M.; Satoh, A. Overcharge reaction of lithium-ion batteries. J. Power Sources 2005, 146, 97–100. [Google Scholar] [CrossRef]
- Wang, Y.; Miao, Q.; Ma, E.W.M.; Tsui, K.L.; Pecht, M.G. Online anomaly detection for hard disk drives based on Mahalanobis distance. IEEE Trans. Reliab. 2013, 62, 136–145. [Google Scholar] [CrossRef]
- Patil, N.; Das, D.; Pecht, M. Anomaly detection for IGBTs using Mahalanobis distance. Microelectron. Reliab. 2015, 55, 1054–1059. [Google Scholar] [CrossRef]
- Berecibar, M.; Garmendia, M.; Gandiaga, I.; Crego, J.; Villarreal, I. State of health estimation algorithm of LiFePO4 battery packs based on differential voltage curves for battery management system application. Energy 2016, 103, 784–796. [Google Scholar] [CrossRef]
- Kumar, S.; Chow, T.W.S.; Pecht, M. Approach to fault identification for electronic products using Mahalanobis distance. IEEE Trans. Instrum. Meas. 2010, 59, 2055–2064. [Google Scholar] [CrossRef]
- Jin, X.; Wang, Y.; Chow, T.W.S.; Sun, Y. MD-based approaches for system health monitoring: A review. IET Sci. Meas. Technol. 2017, 11, 371–379. [Google Scholar] [CrossRef]
- Box, G.E.P.; Box, G.E.P.; Cox, D.R. An analysis of transformations. J. R. Stat. Soc. Ser. B 1964, 26, 211–252. [Google Scholar] [CrossRef]


| Test Type | Test Method | Test Description |
|---|---|---|
| Cycling test | Normal cycling | CC charge at 0.5C until 4.2 V, then CV charge until current <0.05C Rest 10 min Discharge at 1C to 2.75 V Rest 10 min |
| Overcharge cycling | CC charge at 0.5C until 4.5 V, then CV charge until current <0.05C Rest 10 min Discharge at 1C to 2.75 V Rest 10 min | |
| Abusive test | Overcharge | CC charge at 0.5C until 5 V CV charge until the battery swells |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Wang, Y.; Yung, W.K.C.; Pecht, M. Ultrasonic Health Monitoring of Lithium-Ion Batteries. Electronics 2019, 8, 751. https://doi.org/10.3390/electronics8070751
Wu Y, Wang Y, Yung WKC, Pecht M. Ultrasonic Health Monitoring of Lithium-Ion Batteries. Electronics. 2019; 8(7):751. https://doi.org/10.3390/electronics8070751
Chicago/Turabian StyleWu, Yi, Youren Wang, Winco K. C. Yung, and Michael Pecht. 2019. "Ultrasonic Health Monitoring of Lithium-Ion Batteries" Electronics 8, no. 7: 751. https://doi.org/10.3390/electronics8070751
APA StyleWu, Y., Wang, Y., Yung, W. K. C., & Pecht, M. (2019). Ultrasonic Health Monitoring of Lithium-Ion Batteries. Electronics, 8(7), 751. https://doi.org/10.3390/electronics8070751





