Abstract
Accurate battery models are integral to the battery management system and safe operation of electric vehicles. Few investigations have been conducted on the influence of current rate (C-rate) on the available capacity of the battery, for example, the kinetic battery model (KiBaM). However, the nonlinear characteristics of lithium-ion batteries (LIBs) are closer to a fractional-order dynamic system because of their electrochemical materials and properties. The application of fractional-order models to represent physical systems is timely and interesting. In this paper, a novel fractional-order KiBaM (FO-KiBaM) is proposed. The available capacity of a ternary LIB module is tested at different C-rates, and its parameter identifications are achieved by the experimental data. The results showed that the estimated errors of available capacity in the proposed FO-KiBaM were low over a wide applied current range, specifically, the mean absolute error was only 1.91%.
1. Introduction
Electric vehicles have the advantages of high fuel economy and zero exhaust emissions [1,2]. As clean and efficient energy sources, power batteries are core components and are critical to the comprehensive performance of vehicles. Lithium-ion batteries (LIBs) show strong overall advantages in the field of power batteries because of their high energy density, long life, and excellent cycle performance [2,3].
Battery states mainly include the state of charge (SOC), state of health (SOH), state of power (SOP), state of energy (SOE), and state of function (SOF) [4,5,6]. However, they cannot be measured directly; they can only be estimated by testing battery voltage, current, and temperature, among other factors. Battery state estimation is extremely important in battery management systems (BMSs) to guarantee the safe and reliable operation of batteries, and a multitude of research has investigated the methods of state estimation of LIBs based on an accurate model [7,8,9,10,11,12,13,14]. Commonly used battery models include electrochemical models (EchMs) [11,14], analytical models (AMs) [7,12,13,14], stochastic models (SMs) [7,12,14], neural network models (NNMs) [14], and equivalent circuit models (ECMs) [8,9,10,11,14]. EchMs are accurate in describing the internal electrochemical reaction using complex, nonlinear differential equations, but they are difficult to understand. AMs model the major properties of the battery using only a few equations, and are much easier to use than EchMs. SMs mainly concern the battery recovery characteristics as a Markov process, in which the pulse discharge characteristics of the battery can be described, but they are not applicable for variable current. NNMs have fast parallel processing capabilities as well as strong self-learning and self-organizing abilities, but they require a large amount of training data, and errors can arise from the training data and training methods. ECMs are widely used for electrical design and modelling simulations [9,10] because they can accurately describe the battery voltage-current (U-I) performance. Many improved models have been proposed by scholars that not only describe U-I performance (external characteristics) but also the capacity performance (internal characteristics). For instance, an ECM with a variable effective capacity for LIBs is proposed in [15], and the model is further optimized using computational intelligence techniques [16].
However, an accurate and concise battery model is not readily achievable because the models are highly nonlinear and complex. Few investigations have been conducted on the influence of the current rate (C-rate) on the available capacity of batteries because the characteristics of LIBs will change significantly under different conditions in view of its sensitivity to C-rate, temperature, cycle life, etc. As described in detail in Figure 1, the battery capacity is not similar to water in a bucket. It is mainly manifested as “capacity nonlinear effect” and “recovery effect” [7,11,12]. The capacity nonlinear effect is that the available capacity will decline nonlinearly with C-rates; the greater the discharge current, the less the available capacity. The recovery effect is that the battery’s available capacity will rise up when discharge is stopped. For instance, a released capacity of 50 A will be much less than that at 5 A, and the capacity will be restored if the battery rests for a while.
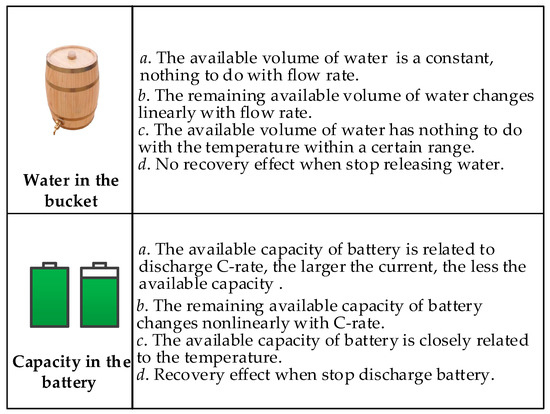
Figure 1.
Battery capacity is not similar to water in a bucket.
The remaining available battery capacity is critical in electric vehicles, similar to the role of the remaining fuel in internal combustion vehicles. Thus, the available capacity estimation of a battery considering C-rate is very important. Overall, commonly used models for available capacity estimation of the battery mainly include two classic analytical models: Peukert’s law and the kinetic battery model (KiBaM). Proposed by Wilhelm Peukert, Peukert’s law was used to estimate nonlinear delivered capacity and predict the battery run time of a rechargeable lead–acid battery at different constant discharge C-rates from the fully charged state [17]. The nonlinear properties between the available capacity and the C-rate are considered, and the battery’s run time can be approximated. The model itself is relatively simple compared to KiBaM. However, it does not consider the recovery effect of the battery when discharge stops. Fortunately, Manwell and McGowan proposed a kinetic battery model (KiBaM) to model lead–acid storage batteries in 1993 [13]. It is intuitionistic and easy to understand based on perceptual knowledge. Moreover, it can be used in modelling and simulation [7,12,13,14]. In [14], a widely-used KiBaM was used to capture nonlinear capacity effects for accurate SOC tracking and runtime predictions of the battery. In [18], KiBaM was extended to consider the temperature effect on battery capacity. The proposed temperature-dependent KiBaM (T-KiBaM) can handle operating temperatures, and it can provide better estimates for battery lifetimes and voltage behaviors. However, the classic KiBaM is described by regular calculus. A precise and concise battery model at various conditions has always been challenging for researchers to create. Using fractional calculus with impedance models is quite common in the modelling of energy storage and generation elements, including capacitors/super capacitors [19,20,21] and batteries [19,22,23]; what is more, the fractional calculus has also been used in the state estimation and prediction of batteries [21,23,24]. Actually, the nonlinear characteristics of lithium-ion batteries are closer to a fractional-order dynamic system, because the material diffusion and electrochemical properties have been successfully described using fractional calculus. The application of fractional-order models to represent physical systems is timely and interesting.
In this paper, a novel fractional-order KiBaM (FO-KiBaM) is proposed to describe the nonlinear capacity characteristics of LIBs. The research ideas and arrangement of the rest of the paper are as follows. Firstly, the capacity nonlinear effect and recovery effect of KiBaM are analyzed in Section 2. The basic principle of fractional calculus and its application in the proposed FO-KiBaM are introduced in Section 3. In Section 4 the charge and discharge experiments of a LIB module are designed and conducted under different C-rates. Finally, the results and model error analyses are compared and illustrated in Section 5, followed by the conclusion in Section 6.
2. Kinetic Battery Model (KiBaM)
As shown in Figure 2, KiBaM uses two wells of different sizes to describe the dynamic changes in battery capacity. Thus, it is also called a “two-well” model. The two wells represent the “directly available capacity” and the “temporary capacity” of the battery, respectively [13,14]. The directly available capacity can be obtained directly at discharge, denoted as y1, and its height is denoted as h1. The “temporary capacity” cannot be directly obtained at discharge, denoted as y2, and its height is denoted as h2. It is easy to understand that the sum of y1 and y2 is the total capacity of the battery, and the sum of y1 and a part of y2 is the available capacity of the battery. The letter k represents the rate that the charge flow from y2 into y1; and the letter c represents the capacity proportion of the two wells. The k and c variables affect the nonlinear battery capacity characteristics; notably, they are closely related to the materials and composition of the battery.
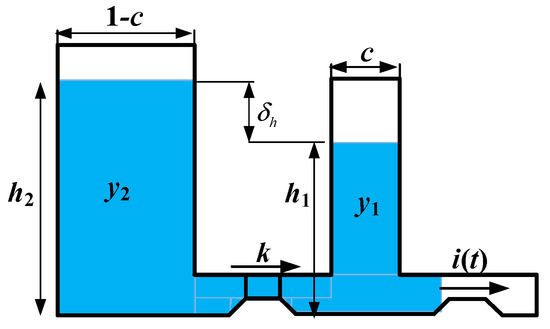
Figure 2.
Kinetic battery model (KiBaM).
It is clear that the directly available capacity y1, the temporary capacity y2, and the heights h1 and h2 in the KiBaM are satisfied by the following:
where represents the height difference between the two wells.
The principle of the KiBaM is as follows. When the battery is discharged, the charge of y1 flows out, simultaneously, the charge of y2 flows into y1 slowly with k. The charge flowing out of y1 is faster than flowing in, so the height difference between y1 and y2 will increase. The larger the discharge current, the less capacity that is released, which reflects the nonlinear effect of the battery’s capacity. Additionally, the unavailable capacity of the battery is the capacity represented by the height differences of y1 and y2. Once discharging is stopped, the charge of y2 will flow into y1 slowly until the heights of y1 and y2 are equal, and the charge of y1 will pick up, which reflects the battery’s recovery effect. From the above intuitive graphical description of KiBaM, the changes of the charges y1 and y2 in the two wells can be expressed as follows:
From here, the capacity variance of the battery with time can be expressed as follows:
where Crem, Cunav, and Cav represent the remaining capacity of battery, the unavailable capacity of battery, and the available capacity of battery, respectively.
Take the constant-current discharge for example. As shown in Figure 3, the time course can be described as follows:
where represents the initial time, the discharge end time, and the recovery end time, respectively.
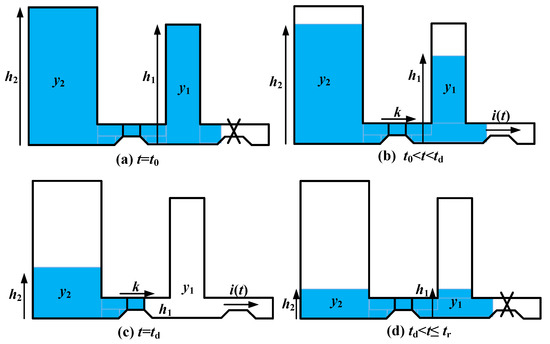
Figure 3.
Battery capacity changes with the discharge time in the discharge process.
Actually, when the battery is discharged in a time-varying current, the entire process can be divided into multiple discharge segments in accordance with the time interval. In each segment, the battery can be considered discharged with a constant current and then set aside for a while.
By the Laplace transform and inverse Laplace transform of (2), the following expression can be obtained:
where .
The unavailable capacity of battery in (3) can be derived as follows:
It can be further expressed as follows:
As can be seen from (7), in the discharge period , the battery’s unavailable capacity is impacted nonlinearly by the discharge time; the longer the time and the larger the current, the larger the unavailable capacity. In the stationary period , the unavailable capacity decreases with time, because the charge of y2 flows into y1, which reflects the recovery effect of the battery in an open circuit state.
It can be seen that when y1 = 0 (or h1 = 0), the battery is discharged completely. At this point, all the remaining capacity is unavailable. Therefore, judging whether the battery is fully discharged is shown as follows:
The remaining available capacity of the battery can be expressed as follows:
If the initial conditions , and the battery is discharged at a constant current I, the initial state of y1 and y2 of the battery are shown as below:
where C0 is the initial total capacity of battery. Then, Formula (3) can be simplified as follows:
3. The Proposed Fractional-Order KiBaM (FO-KiBaM)
3.1. Fractional Calculus Theory
Fractional calculus is not a new concept, in fact, it can be traced back to the discussion of Leibniz and Hospital’s research work in 1695, but due to a variety of calculation difficulties in practical applications, it was only a purely theoretical exploration in the early days. However, fractional calculus attracts great attention in complex engineering applications because of the continuous developments in natural science and computer technology. In recent decades, theoretical and mathematical tools have been used in research in a multitude of disciplines, and they are especially successful in high-energy physics, fluid mechanics, viscoelastic material mechanics, anomalous diffusion, electronic components analysis, and system control [20,25]. Fractional calculus has been a research hotspot for its unique and irreplaceable advantages.
Fractional derivative definitions (FDD) are defined in different ways; the most commonly used include the Grunwald–Letnikov definition (GL-FDD), the Riemann–Liouville definition (RL-FDD), and the Caputo definition (Caputo-FDD) [20,25]. The GL-FDD is expressed as:
where represents the GL-FDD type; f(t) is an arbitrary integrable function; α is an arbitrary real number; n = represents the integer part; and represents the coefficient of recursive function.
In fact, the RL-FDD is obtained on the basis of GL-FDD by simplifying the calculation process. RL-FDD can be expressed as follows:
where represents the RL-FDD type; n is an integer; and Γ(·) is the Gamma function, a commonly used basic functions in fractional calculus, defined as follows:
The function Γ(·) has the following properties:
And the Laplace transform will be established by:
where H(x) denotes the unit step function, which implies that it only needs . The formula and its inverse transformation are often used in fractional calculus.
The Caputo-FDD is expressed as follows:
where represents the Caputo-FDD type.
The Laplace transform of the Caputo-FDD is expressed as follows:
Thus, the Laplace transform of the Caputo-FDD under the zero initial conditions is:
The derivation of constants in the Caputo-FDD is bounded, while the derivation of constants in the RL-FDD is unbounded. The RL-FDD needs to solve an initial value problem that it is theoretically feasible but lacks physical meaning. Therefore, the Caputo-FDD is more suitable for solving the initial value problem of fractional calculus. Thus, it was adopted in this paper.
3.2. Fractional-Order KiBaM
The internal electrochemical reaction of a power battery is extremely complex. The strong nonlinear characteristics of LIBs shows a fractional-order dynamic behavior [21,22,23]. Therefore, fractional calculus can be used to model a novel fractional-order KiBaM (FO-KiBaM) with a higher accuracy [26]. Fractional derivatives can be replaced to describe the battery capacity change process in (2).
where is the order of fractional derivative equations, and .
In the case when the initial time , and the battery is discharged at a constant current I, the Laplace transform of (20) will be expressed as:
Similarly, assuming that the initial state of y1 and y2 are the same as in (10), the following will be obtained:
The above inverse Laplace transform of the fractional calculus transfer function can be obtained using the Mittag-Leffler function, a commonly used basic function in fractional calculus [27,28,29,30]. The Mittag-Leffler function has two different definition forms: the single-parameter form and the two-parameter form. The two-parameter form of the Mittag-Leffler function is defined as shown below:
If , the single-parameter form of the Mittag-Leffler function will be obtained:
The exponential function is critical in calculus. Similarly, the Mittag-Leffler function equally plays an important role, and it appears frequently in solutions of fractional differential equations. Sometimes the Mittag-Leffler function with two parameters is also called a generalized exponential function. In fact, can be seen as a special case of the Mittag-Leffler function, because they are equal if .
To facilitate the inverse Laplace transform, we defined a new function as shown below:
Its Laplace transform can be obtained as follows:
According to the above properties of (22), it is clear that in the transfer function (27), and its inverse Laplace transform will be obtained as shown below:
Similarly, the height difference of two wells can be obtained:
Therefore, the capacity of the battery with fractional calculus can be expressed as follows:
The SOC of the battery is similar to the fuel gauge of conventional internal combustion vehicles, which can be used to estimate the distance the vehicle can travel. The definition of SOC is:
where , represents the remaining capacity and the maximum available capacity of battery.
The unavailable capacity of the battery is not considered in this definition. Thus, it cannot tell the driver the actual available battery capacity at different C-rates. To predict the remaining mileage of electric vehicles more accurately, it is necessary to improve the SOC definition. An improved SOC definition is shown as below:
This definition of SOC takes into account the unavailable capacity of battery. Thus, it is useful in estimating the run time of the battery, and it can predict the remaining mileage of electric vehicles more accurately to relieve the “range anxiety” for the drivers. At the same time, by a more accurate definition of SOC, it can help to determine effective management strategies to avoid overcharging and over discharging the battery.
Further, we found that the height of y1 in the proposed FO-KiBaM can be expressed as follows:
As can be seen from (32) and (33), the height h1 of the left “well” reflects the change in the battery’s remaining available capacity, and it also explains why the height h1 is an intuitive representation of the battery SOC.
4. Parameter Identification and Experiment Verification
4.1. Experimental Platform and Test Results
As shown in Figure 4, the platform of the battery test system consisted of a battery charging and discharging cycler MKLtech MCT8-100-05Z, a programmable temperature chamber, a LiNiMnCoO ternary LIB module, and a computer with control software. The voltage and the current range of the battery cycler was 0–5 V and ±100 A, respectively. The temperature of the chamber was maintained at 30 °C. The sampling rate of voltage and current was set at 1 Hz. The tested ternary LIB module had a capacity of 32.50 Ah, which consisted of 13 battery cells connected in parallel, as shown in Figure 5. Table 1 shows the specifications of the ternary LIB cells. The available capacity tests at different C-rates of 0.2, 0.67, 1, 1.5, 2, and 3 C were carried out. Here, 1 C indicated that the rechargeable battery was continuously discharged for 1 h at a current equal to the battery’s nominal capacity.

Figure 4.
The battery test experimental platform.

Figure 5.
Battery module with 13 cells connected in parallel.

Table 1.
Specification of the ternary lithium-ion battery (LIB) cell.
In the test, first the ternary battery module was fully charged by the constant current, constant voltage (CCCV) charging strategy. The constant current (CC) was 10 A, and the constant voltage (CV) was 4.2 V. The cutoff point for the CV charging stage was when the charging current was less than 1/50 C, or the CV charging time had reached 1 h. Then, the battery was left standing in the open-circuit state. In the discharging procedure, the battery was fully discharged to the cutoff voltage (3.0 V) at 0.2 C. Then, the above test process was repeated to complete the available capacity tests at different C-rates. Throughout the testing, the discharge time, voltage, current, released capacity, and energy were monitored and recorded simultaneously. The current of the battery module in the charge and discharge processes at 2 C is shown in Figure 6.
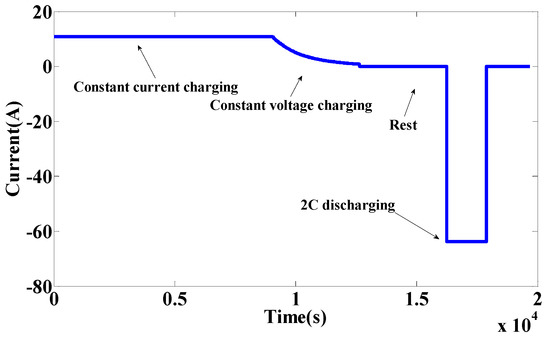
Figure 6.
The battery testing currents.
The available capacity of the tested LIB module at different C-rates is shown in Table 2. It can be seen that the battery released 96.12% of the maximum capacity at 0.2 C; while the battery released 94.52% of the maximum capacity at 1 C. When the current was further increased to 3 C, the battery only released 84.89%. The result was consistent with the “capacity nonlinear effect”, and the relationship of the available capacity and current was nonlinear.

Table 2.
Available capacity and discharge time at different C-rates.
4.2. Parameter Identification
The identification parameters of KiBaM, including capacity distribution ratio c, rate coefficient k, and fractional order α, were the key in achieving satisfactory accuracy based on the experimental data [31,32,33]. The identification parameters were mainly arranged as follows.
Distribution ratio (c): The battery was charged until full, SOC = 1, as the initial state; and then the battery was discharged at a large constant current, here it was 95.69 A (3 C). The released capacity was denoted as C1, and as shown in Table 2, C1 = 27.59 Ah. The maximum available capacity of the battery was 32.50 Ah, denoted as Cmax; then, c = C1/Cmax = 0.849.
Rate coefficient (k): The available capacity of the battery was tested at different C-rates. For the classic KiBaM, we only needed one set of experimental data, and k′ could be obtained. The data measured at 1 C were selected here, and the data at other C-rates were used to verify the model’s accuracy later.
A new function can be defined and modified as follows:
The change of the function F(k′) with is depicted in Figure 7, and the solution, = 0.000836, could be confirmed when F(k′) is 0. Thus, the unavailable capacity of the tested battery in KiBaM was obtained as follows:
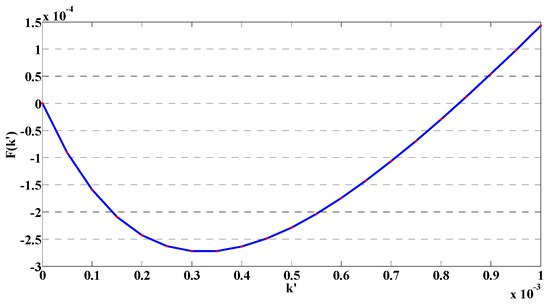
Figure 7.
The function curve that changes as k′ changes.
As for the FO-KiBaM, k′ and α of the tested battery module could also be identified by using one set of experimental data at 1 C.
And a new function could be defined and modified as follows:
The change of the function with and α is shown in Figure 8, where α changed from 0.1 to 0.9. We can see that it tended towards 0 when α was 0.9. Further, its trend was depicted in Figure 9 when α changed from 0.91 to 0.99. It was revealed that the numerical solution of was not unique. The values of and α could be a combination within a suitable range. Here, the parameters = 0.000689 and were selected for the FO-KiBaM. Thus, the unavailable capacity of the tested battery in FO-KiBaM was obtained.
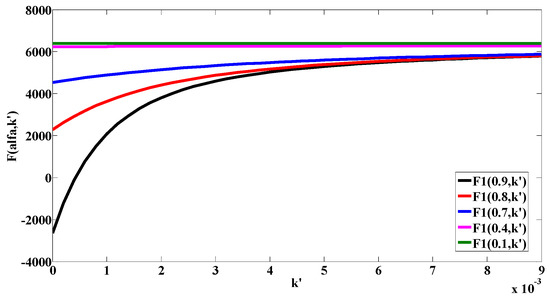
Figure 8.
Trend of the function as k′ and α (0.1 to 0.9) changes.
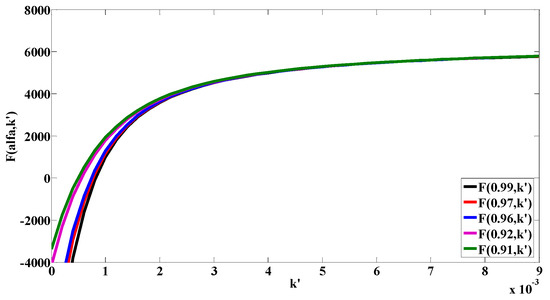
Figure 9.
Trend of the function as k′ and α (0.91 to 0.99) changes.
4.3. Experiment Verification
The effect of the C-rate on the available capacity of the battery was verified by experiment. The variation of the total capacity and unavailable capacity of the battery at different C-rates are depicted in Figure 10 and Figure 11, in which the discharge was finished when the total capacity of the battery (black line) intercepted the unavailable capacity (red/blue lines). At this point, all the remaining capacity of the battery was the unavailable capacity, so the discharge process was over. The prediction results of the available capacity of the battery are listed in Table 3. It can be seen that compared with the classic KiBaM, the errors of available capacity in the proposed FO-KiBaM were less, and it performed well over a wid applied current range. Specifically, its mean absolute error (MAE) was only 1.91%, with an improvement of 0.44%. Although the accuracy of KiBaM was already high, the proposed FO-KiBaM still had a smaller fitting error over a wide applied current range. Further study on the state estimations of LIBs and the high-precision optimization control of energy management will be useful, especially with the FO-KiBaM.
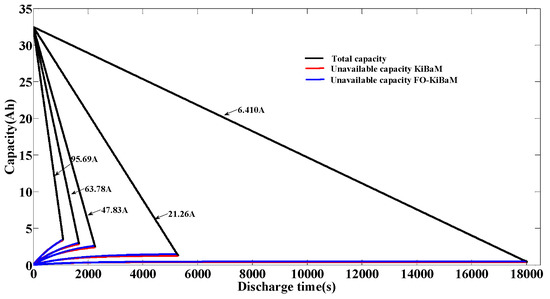
Figure 10.
Battery capacity variance at different C-rates.
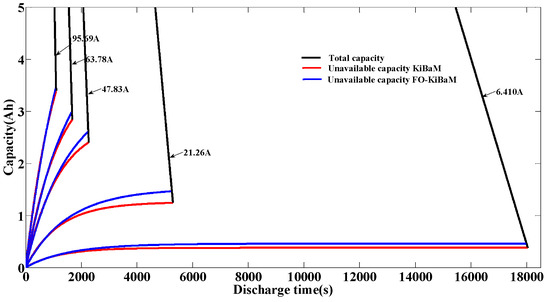
Figure 11.
Battery capacity variance at different C-rates (local magnification).

Table 3.
Prediction results of the battery’s available capacity at different C-rates.
It should be pointed out that if the estimation accuracy was higher in some applications, we could achieve parameter identification according to current interval (segmentation) by using several sets of the tested data instead of just one set, so that the accuracy of the model could be improved. If we thought the parameters of the model were related to the current, we could even identify the parameters under different currents. Thus, that the accuracy of the model can be further improved, but the amount of calculation would also increase. The whole process of parameter identification is the same, whether it is how to select the data or how many sets of data will be weighed. However, if the accuracy of the model identified by only one set of data met the application requirements, it would significantly reduce the amount of calculation. For a fair comparison and reduction in the number of calculations, we only selected one set of data to identify the parameters of both the KiBaM and the FO-KiBaM.
5. Conclusions
In recent years, various families of fractional-order systems have been found to be remarkably important and fruitful. Fractional calculus plays an important role in complex systems and, therefore, allows us to better describe real-world phenomena. By obtaining more parameters and degrees of freedom, fractional-order models can describe nonlinear performances of complex systems more accurately. Due to specific material and chemical properties of batteries, fractional calculus is more reasonable to describe the nonlinear performance of a battery’s capacity. The proposed FO-KiBaM can describe the battery’s nonlinear characteristics more accurately, with greater flexibility and novelty compared to the classic KiBaM. The proposed model can be applied in engineering. The estimation of the available capacity of LIBs is meaningful with a wide applicable current range, and only a set of data at one C-rate is needed to accurately estimate the available capacity at different rates, which greatly reduces the number of calculations. What is more, the proposed FO-KiBaM provides a basic battery model for further research on SOC estimation methods.
6. Patents
A patent, termed fractional order KiBaM (kinetic battery model) that considers nonlinear capacity characteristics and parameter identification methods, resulted from the work reported in this manuscript, which can be seen on academic websites such as Google Patents. The progress status of this patent is as follows. Application filed by Shandong University and priority to CN201710093350.0A on 21 February 2017, publication of CN106855612A on 16 June 2017, and Notice of First Review on 16 November 2018. PCT/CN2017/106912 application filed by Shandong University on 19 October 2017, and publication of WO2018153116A1 on 30 August 2018.
Author Contributions
Conceptualization, Q.Z. and Y.S.; methodology, Q.Z. and Y.S.; software, Q.Z. and Y.L.; validation, Q.Z.; formal analysis, Q.Z. and Y.L.; writing—original draft preparation, Q.Z.; writing—review and editing, N.C. and B.D.; project administration, N.C., B.D., and C.Z.; funding acquisition, N.C., B.D., and C.Z.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No.61527809, U1864205, U1764258, and 61633015) in part, and the National Key Research and Design program of China (Grant No. 2018YFB0104000) in part, which are gratefully acknowledged. Most importantly, the authors would also like to thank the anonymous reviewers for their valuable comments and suggestions.
Acknowledgments
The English writing of this manuscript has been carefully edited by a native English speaker. The authors would like to thank him for the proofreading and editing. Special thanks to Professor Igor Podlubny for sharing the Matlab routine for evaluating the Mittag-Leffler function with two parameters in Matlab Central at https://www.mathworks.com/matlabcentral/fileexchange/8738-mittag-leffler-function.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| LIB | lithium-ion battery |
| EchM | electrochemical model |
| AM | analytical model |
| SM | stochastic model |
| NNM | neural network model |
| ECM | equivalent circuit model |
| U-I | voltage-current |
| KiBaM | kinetic battery model |
| T-KiBaM | temperature-dependent kinetic battery model |
| FO-KiBaM | fractional-order kinetic battery model |
| BMS | battery management system |
| Ah | ampere hours |
| SOC | state of charge |
| SOH | state of health |
| SOP | state of peak power |
| SOF | state of function |
| SOE | state of energy |
| C-rate | current rate |
| CCCV | constant-current and constant-voltage |
| CC | constant current |
| CV | constant voltage |
| FDD | fractional derivative definition |
| GL-FDD | Grunwald-Letnikov fractional derivative definitions |
| RL-FDD | Riemann-Liouville fractional derivative definitions |
| MAE | mean absolute error |
| Nomenclature | |
| y1 | directly available capacity |
| h1 | height of directly available capacity |
| y2 | temporary capacity |
| h2 | height of temporary capacity well |
| the height difference of two wells | |
| k | rate that the charge flows from y2 into y1 |
| c | capacity proportion of two wells |
| i | discharge current |
| I | the constant discharge current |
| the initial time | |
| the discharge end time | |
| the recovery end time | |
| Cav | available capacity of battery |
| Cunav | unavailable capacity of battery |
| Crem | remaining available capacity of battery |
| Cmax | the maximum available capacity of battery |
| Ct0 | initial capacity of battery |
References
- Lievre, A.; Sari, A.; Venet, P.; Hijazi, A.; Ouattarabrigaudet, M.; Pelissier, S. Practical online estimation of lithium-ion battery apparent series resistance for mild hybrid vehicles. IEEE Trans. Veh. Technol. 2016, 65, 4505–4511. [Google Scholar] [CrossRef]
- Xia, B.; Nguyen, T.; Mi, C. A correlation-based fault detection method for short circuits in battery packs. J. Power Sources 2017, 337, 1–10. [Google Scholar] [CrossRef]
- Shang, Y.; Zhang, Q.; Cui, N.; Zhang, C. A cell-to-cell equalizer based on three-resonant-state switched-capacitor converters for series-connected battery strings. Energies 2017, 10, 206. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Mohamed, A. A review of lithium-ion battery state of charge estimation and management system in electric vehicle applications: Challenges and recommendations. Renew. Sustain. Energy Rev. 2017, 78, 834–854. [Google Scholar] [CrossRef]
- Rivera-Barrera, J.P.; Muñoz-Galeano, N.; Sarmiento-Maldonado, H.O. SoC Estimation for Lithium-ion Batteries: Review and Future Challenges. Electronics 2017, 6, 102. [Google Scholar] [CrossRef]
- Lai, X.; Yi, W.; Zheng, Y.; Zhou, L. An All-Region State-of-Charge Estimator Based on Global Particle Swarm Optimization and Improved Extended Kalman Filter for Lithium-Ion Batteries. Electronics 2018, 7, 321. [Google Scholar] [CrossRef]
- Jongerden, M.R.; Haverkort, B.R. Which battery model to use? IET Softw. 2009, 3, 445–457. [Google Scholar] [CrossRef]
- Ko, S.T.; Ahn, J.H.; Lee, B.K. Enhanced Equivalent Circuit Modeling for Li-ion Battery Using Recursive Parameter Correction. J. Electr. Eng. Technol. 2018, 13, 1147–1155. [Google Scholar]
- He, H.; Xiong, R.; Guo, H.; Li, S. Comparison study on the battery models used for the energy management of batteries in electric vehicles. Energy Convers. Manag. 2012, 64, 113–121. [Google Scholar] [CrossRef]
- Shang, Y.; Zhang, Q.; Zhang, C.; Cui, N. Research on variable-order RC equivalent circuit model for lithium-ion battery based on the AIC criterion. Trans. China Electrotech. Soc. 2015, 30, 55–62. [Google Scholar]
- Zhou, Y.; Huang, M. On-board Capacity Estimation of Lithium-ion Batteries Based on Charge Phase. J. Electr. Eng. Technol. 2018, 13, 733–741. [Google Scholar]
- Cloth, L.; Jongerden, M.R.; Haverkort, B.R. Computing battery lifetime distributions. In Proceedings of the 37th Annual IEEE/IFIP International Conference on Dependable Systems and Networks (DSN’07), Edinburgh, UK, 25–28 June 2007; pp. 780–789. [Google Scholar]
- Manwell, J.; McGowan, J. Lead acid battery storage model for hybrid energy systems. Sol. Energy 1993, 50, 399–405. [Google Scholar] [CrossRef]
- Kim, T.; Qiao, W. A hybrid battery model capable of capturing dynamic circuit characteristics and nonlinear capacity effects. IEEE Trans. Energy Convers. 2011, 26, 1172–1180. [Google Scholar] [CrossRef]
- Blanco, C.; Sánchez, L.; González, M.; Antón, J.C.; García, V.; Viera, J.C. An equivalent circuit model with variable effective capacity for lifepo4 batteries. IEEE Trans. Veh. Technol. 2014, 63, 3592–3599. [Google Scholar] [CrossRef]
- Sánchez, L.; Blanco, C.; Antón, J.C.; García, V.; González, M.; Viera, J.C. A variable effective capacity model for LiFePO4 traction batteries using computational intelligence techniques. IEEE Trans. Ind. Electron. 2015, 62, 555–563. [Google Scholar] [CrossRef]
- Baert, D.; Vervaet, A. Lead-acid battery model for the derivation of Peukert’s law. Electrochim. Acta 1999, 44, 3491–3504. [Google Scholar] [CrossRef]
- Rodrigues, L.M.; Montez, C.; Moraes, R.; Portugal, P.; Vasques, F. A Temperature-Dependent Battery Model for Wireless Sensor Networks. Sensors 2017, 17, 422. [Google Scholar] [CrossRef]
- Freeborn, T.J.; Maundy, B.; Elwakil, A.S. Fractional-order models of supercapacitors, batteries and fuel cells: A survey. Mater. Renew. Sustain. Energy 2015, 4, 9. [Google Scholar] [CrossRef]
- Wang, W.G.; Li, Y.; Chen, Y.Q. Ubiquitous fractional order capacitors. In Proceedings of the International Conference on Fractional Dierentiation and Its Applications, Novi Sad, Serbia, 18–20 July 2016. [Google Scholar]
- Malek, H.; Dadras, S.; Chen, Y. Fractional order equivalent series resistance modelling of electrolytic capacitor and fractional order failure prediction with application to predictive maintenance. IET Power Electron. 2016, 9, 1608–1613. [Google Scholar] [CrossRef]
- Sabatier, J.; Merveillaut, M.; Francisco, J.; Guillemard, F.; Porcelatto, D. Fractional models for lithium-ion batteries. In Proceedings of the 2013 European Control Conference, Zürich, Switzerland, 17–19 July 2013; pp. 3458–3463. [Google Scholar]
- Sabatier, J.; Cugnet, M.; Laruelle, S.; Grugeon, S.; Sahut, B.; Oustaloupa, A.; Tarasconb, J.M. A fractional order model for lead-acid battery crankability estimation. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1308–1317. [Google Scholar] [CrossRef]
- Sun, Y.; Wu, X.; Cao, J.; Wei, Z.; Sun, G. Fractional extended Kalman filtering for nonlinear fractional system with Lévy noises. IET Control Theory Appl. 2017, 11, 349–358. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, Y.; Wei, S.; Zhu, J.; Chen, W. A space fractional constitutive equation model for non-Newtonian fluid flow. Commun. Nonlinear Sci. Numer. Simul. 2018, 62, 409–417. [Google Scholar] [CrossRef]
- Zhang, Q.; Shang, Y.; Cui, N.; Li, Y.; Zhang, C. A fractional-order KiBaM of lithium-ion batteries with capacity nonlinearity. In Proceedings of the 2017 Chinese Automation Congress, Jinan, China, 20–22 October 2017; pp. 4995–5000. [Google Scholar]
- Li, Y.; Chen, Y.Q.; Podlubny, I. Mittag-Leffler stability of fractional order nonlinear dynamic systems. Automatica 2009, 45, 1965–1969. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.Q.; Podlubny, I. Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag-Leffler stability. Comput. Math. Appl. 2010, 59, 1810–1821. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, J.; Ding, D.; Qi, D. Adaptive Mittag-Leffler stabilization of a class of fractional order uncertain nonlinear systems. Asian J. Control 2016, 18, 2343–2351. [Google Scholar] [CrossRef]
- Khurram, A.; Rehman, H.; Mukhopadhyay, S.; Ali, D. Comparative Analysis of Integer-order and Fractional-order Proportional Integral Speed Controllers for Induction Motor Drive Systems. J. Power Electron. 2018, 18, 723–735. [Google Scholar]
- Yang, J.; Xia, B.; Shang, Y.L.; Huang, W.; Mi, C. Improved battery parameter estimation method considering operating scenarios for HEV/EV applications. Energies 2016, 10, 5. [Google Scholar] [CrossRef]
- Feng, F.; Lu, R.; Wei, G.; Zhu, C. Identification and analysis of model parameters used for LiFePO4 cells series battery pack at various ambient temperature. IET Electr. Syst. Transp. 2016, 6, 50–55. [Google Scholar] [CrossRef]
- Hua, C.C.; Fang, Y.H.; Chen, Y.L. Modified rectifications for improving the charge equalisation performance of series-connected battery stack. IET Power Electron. 2016, 6, 1924–1932. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).