Adaptive Algorithm on Block-Compressive Sensing and Noisy Data Estimation

Abstract

In this paper, an altered adaptive algorithm on block-compressive sensing (BCS) is developed by using saliency and error analysis. A phenomenon has been observed that the performance of BCS can be improved by means of rational block and uneven sampling ratio as well as adopting error analysis in the process of reconstruction. The weighted mean information entropy is adopted as the basis for partitioning of BCS which results in a flexible block group. Furthermore, the synthetic feature (SF) based on local saliency and variance is introduced to step-less adaptive sampling that works well in distinguishing and sampling between smooth blocks and detail blocks. The error analysis method is used to estimate the optimal number of iterations in sparse reconstruction. Based on the above points, an altered adaptive block-compressive sensing algorithm with flexible partitioning and error analysis is proposed in the article. On the one hand, it provides a feasible solution for the partitioning and sampling of an image, on the other hand, it also changes the iteration stop condition of reconstruction, and then improves the quality of the reconstructed image. The experimental results verify the effectiveness of the proposed algorithm and illustrate a good improvement in the indexes of the Peak Signal to Noise Ratio (PSNR), Structural Similarity (SSIM), Gradient Magnitude Similarity Deviation (GMSD), and Block Effect Index (BEI).

1. Introduction

The traditional Nyquist sampling theorem states that the sampling frequency of a signal must be more than twice its highest frequency to ensure that the original signal is completely reconstructed from the sampled value, while the compressive sensing (CS) theory breaks through the traditional limitation of the Nyquist sampling theorem in signal acquisition and can achieve reconstructing a high-dimensional sparse signal or compressible signal from the lower-dimensional measurement [1]. As an alternative to the Nyquist sampling theorem, CS theory is being widely studied, especially in the current image processing. The research of CS theory mainly focuses on several important aspects such as sparse representation, measurement matrix construction, and the reconstruction algorithm [2,3]. The main research hotspot of sparse representation is how to construct a sparse dictionary of the orthogonal system and an over-complete dictionary for suboptimal approximation [4,5]. The construction of the measurement matrix mainly includes the universal random measurement matrix and the improved deterministic measurement matrix [6]. The research of the reconstruction algorithm mainly focuses on the suboptimal solution problem and a training algorithm based on self-learning [7,8]. With the advancement of research and application about CS theory, especially in 2D or 3D image processing, the CS technology faces several challenges, including computational dimensional disaster and the spatial storage problem with the increase of the images geometric scale. To solve these challenges, the researchers proposed many fast-compressive sensing algorithms to solve the computation cost and the block-compressive sensing (BCS) algorithm to solve the space storage problem [9,10,11,12]. This article is based on the analysis of the above two points.

The CS recovery algorithm of images can mainly be divided into convex optimization recovery algorithms, non-convex recovery algorithms, and hybrid algorithms. The convex optimization algorithms include basis pursuit (BP), greedy basis pursuit (GBP), iterative hard threshold (IHT), etc. Non-convex algorithms include orthogonal matching pursuit (OMP), subspace matching basis pursuit (SP), and iteratively reweighted least square (IRLS), etc. The hybrid algorithms include sparse Fourier description (SF), chain pursuit (CP), and heavy hitters on steroids pursuit (HHSP) and other mixed algorithms [13,14,15]. The convex optimization algorithms based on l₁ minimization have benefits on the reconstruction effect, but with large computational complexity and high time complexity. Compared with convex optimization algorithms, the non-convex algorithms, such as the greedy pursuit algorithm, operate quickly, with a slightly poor accuracy based on l₀ minimization, and can also meet the general requirements of practical applications. In addition, the iterative threshold method has also been widely used in both of them with excellent performance. However, the iterative threshold method is sensitive to the selection of the threshold and the initial value of the iteration that affects the efficiency and accuracy of the algorithm [16,17]. The selection of thresholds in this process often uses simple error values (including absolute or relative values) or quantitative iterations as stopping criterion of the algorithm, which does not guarantee algorithm optimization [18,19].

The focus of this paper is on three aspects, namely, the block partitioning under weighted information entropy, the adaptive sampling based on synthetic features, and the iterative reconstruction through error analysis. The mean information entropy (MIE) and texture saliency (TS) are introduced in the block partitioning to provide a basis for promoting the algorithm. This part of adaptive sampling mainly improves the overall image quality through designing the block sampling rate by means of variance and local saliency (LS). The iterative reconstruction part mainly uses the relationship of three errors to provide the number of iterations required for the best reconstructed image in different noise backgrounds. Based on the above points, this paper proposes an altered adaptive block-compression sensing algorithm with flexible partitioning and error analysis, which is called FE-ABCS.

The remainder of this paper is organized as follows. In Section 2, we focus on the preliminaries of BCS. Section 3 includes the problem formulation and important factors. Then, the structure of the proposed FE-ABCS algorithm is presented in Section 4. In Section 5, the experiments and results analysis are listed to show the benefit of the FE-ABCS. The paper concludes with Section 6.

2. Preliminaries

2.1. Compressive Sensing

The algorithm theory of compressive sensing is derived from the sparse characteristic of natural signals that can be sparsely represented under a certain sparse transform basis, enabling direct sampling of sparse signals (sampling and compressing simultaneously). Set the sparse representation $s$ of an original digital signal $x$ which can be obtained by the transformation of sparse basis $\Psi$ with K sparse coefficients and the signal $x$ is observed by a measurement matrix $\Phi$, then the observation signal $y$ can be expressed as:

$$y=\Phi x=\Phi \Psi s=\Omega s$$

(1)

where, $x\in R^N$, $s\in R^N$, and $y\in R^M$. Consequently, $\Omega \in R^{M\times N}$ is the product of the matrix $\Phi \in R^{M\times N}$ and $\Psi \in R^{N\times N}$, named the sensing matrix, and the value of M is much less than N because of the compressive sensing theory.

The reconstruction process is an NP-hard problem which restores the N-dimensional original signal from the M-dimensional measurement value through nonlinear projection and cannot be solved directly. Candès et al. pointed out that, the number M must meet the condition $M=O\left(K\log \left(N\right)\right)$ in order to reconstruct the N-dimensional signal $x$ accurately, and the sensing matrix $\Omega$ must satisfy the Restricted Isometry Property (RIP) [20]. Furthermore, the former theories proved that the original signal $x$ can be accurately reconstructed from the measured value $y$ by solving the $l_0$ norm optimization problem:

$$\widehat{x}=\Psi \widehat{s},\widehat{s}=\arg \min {\Vert s\Vert }_{0}s.t.y=\Phi x=\Phi \Psi s$$

(2)

In the above formula, ${\Vert \ast \Vert }_0$ is the $l_0$ norm of a vector, which represents the number of non-zero elements in the vector.

With the wide application of CS technology, especially for 2D/3D image signal processing, it inevitably leads to a dimensional computing disaster problem (because the amount of calculation increases with the square/cube of dimensions), which is not directly overcome by CS technology itself. Here, it is necessary to introduce block partitioning and parallel processing to improve the algorithm, that is, the BCS algorithm improves its universality.

2.2. Block-Compressive Sensing (BCS)

The traditional method of BCS used in image signal processing is to segment the image and process the sub-images in parallel for reducing the cost of storage and calculation. Suppose the original image ($I_W\times I_H$) with $N=W\times H$ pixels in total, the observation with M-dimension and the definition of total sampling rate (TSR = M/N), in the normal processing of BCS, the image is divided into small blocks with a size of $B\times B$, each of which is sampled with the same operator. Let $x_i$ represent the vectorized signal of the i-th block through raster scanning, and the output vector $y_i$ of BCS measurement can be written as:

$$y_i={\Phi }_B{x}_i$$

(3)

where, ${\Phi }_B$ is an $m\times n$ matrix with $n=B^2$ and $m=\lfloor n·TSR\rfloor$. The matrix ${\Phi }_B$ is usually taken as an orthonormalized i.i.d Gaussian matrix. For the whole image, the equivalent sampling operator $\Phi$ in (1) is thus a block diagonal matrix taking the following form:

$$\Phi =\left[\begin{array}{ccc}{\Phi }_B& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\Phi }_B\end{array}\right]$$

(4)

2.3. Problems of BCS

The mentioned BCS algorithm for solving the storage space, dividing image into multiple sub-images, reduces the scale of the measurement matrix on the one hand, and on the other hand could be conducive to the parallel processing of the sub-images. However, BCS still has the following problems that need to be investigated and solved:

• Most existing research papers of BCS do not perform useful analysis on image partitioning and then segment according to the analysis result [21,22]. The common partitioning method (n = B × B) of BCS only considers reducing the computational complexity and storage space problem without considering the integrity of the algorithm and other potential effects, such as providing a better foundation for subsequent sampling and reconstructing by combining the structural features and the information entropy of the image.
• The basic sampling method used in BCS is to sample each sub-block uniformly according to the total sampling rate (TSR), while the adaptive sampling method selects different sampling rates according to the sampling feature of each sub-block [23]. Specifically, the detail block allocates a larger sampling rate, and the smooth block matches a smaller sampling rate, thereby improving the overall quality of the reconstructed image at the same TSR. But the crux is that the studies of criteria (feature) used to assign adaptive sampling rates are rarely seen in recent articles.
• Although there are many studies on the improvement of the BCS iterative construction algorithm [24], few articles focus on optimizing the performance of the algorithm from the aspect of iteration stop criterion in the image reconstruction process, especially in the noise background.

In addition, the improvement on BCS also includes blockiness elimination and engineering implementation of the algorithm. Finally, although BCS technology still has some aspects to be solved, due to its advantages, the technology has been widely applied to optical/remote sensing imaging, medical imaging, wireless sensor networks, and so on [25].

3. Problem Formulation and Important Factors

3.1. Flexible Partitioning by Mean Information Entropy (MIE) and Texture Structure (TS)

Reasonable block partitioning reduces the information entropy (IE) of each sub-block to improve the performance of the BCS algorithm at the same total sampling rate (TSR), and ultimately improves the quality of the entire reconstructed image. In our paper, we adopt flexible partitioning with image sub-block shape $n=row\times column=l\times h$ to remove the blindness of image partitioning with the help of texture structure (TS) and mean information entropy (MIE) instead of the primary shape $n=B\times B$. The expression of TS is based on the gray-tone spatial-dependence matrices and the angular second moment (ASM) [26,27]. The value of TS is defined as follows using ASM:

$$\begin{array}{l}{g}_{TS}={{\displaystyle \sum _{i=0}^{255}{\displaystyle \sum _{j=0}^{255}\left\{p(i,j,d,a)\right\}}}}^2\\ p(i,j,d,a)=P(i,j,d,a)/R\end{array}$$

(5)

where, $P(i,j,d,a)$ is the (i,j)-th entry in a gray-tone spatial-dependence matrix, $p(i,j,d,a)$ is the normalized form of $P(i,j,d,a)$, $(i,j,d,a)$ is the neighboring pixel pair with distance $d$, orientation $a$, and gray value $(i,j)$ in the image, and $R$ denotes the number of neighboring resolution cell pairs. The definition of MIE of the whole image is as follows:

$$g_{MIE}=\frac{1}{N/n}{\displaystyle \sum _{i=1}^{N/n}(-{\displaystyle \sum _{j=0}^{255}{e}_{i,j}{\log }_2{e}_{i,j}}})=\frac{1}{T_1}{\displaystyle \sum _{i=1}^{T_1}(-{\displaystyle \sum _{j=0}^{255}{e}_{i,j}{\log }_2{e}_{i,j}}})$$

(6)

where, $e_{i,j}$ is the proportion of pixels with gray value $j$ in the i-th sub-image, and $T_1$ is the number of sub-images.

Suppose the flexible partitioning of BCS is reasonable, increasing the similarity between pixels in each sub-block and reducing the MIE of the whole image sub-blocks will inevitably bring about a decrease in the difficulty of image sampling and recovery, which means that the flexible partitioning itself is a process of reducing order and rank. Figure 1 shows the effect on the MIE of four 256 × 256-pixel-testing gray images with 256 gray levels by different partitioning methods when the number of pixels per sub-image is limited to 256. The abscissa represents different 2-base partitioning modes, the ordinate represents the MIE of the whole image in different partitioning modes. Figure 1 indicates that images with different structures reach minimum MIE on different partitioning points which will be used in flexible partitioning to provide a basis for block segmentation.

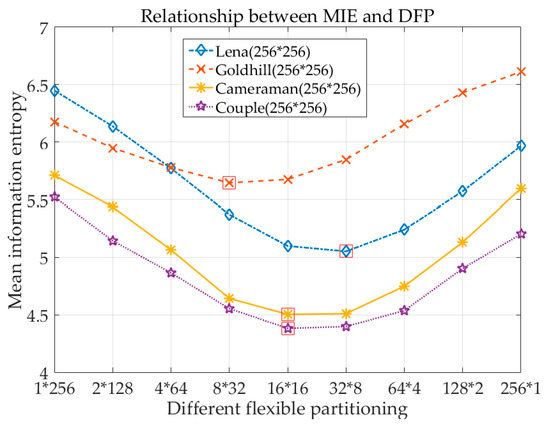
Figure 1. Effect of different partitioning methods on mean information entropy (MIE) of images (the abscissa represents flexible partitioning with shape $n=l\times h=2^{i-1}\times 2^{9-i}=256$).

Furthermore, the MIE guiding the partitioning of the image only considers the pixel level of the image, i.e., gray scale distribution, without considering the image optimization of the spatial level, i.e., texture structure. In fact, TS information is also very important for image restoration algorithms. Therefore, this paper uses the method of $g_{MIE}$ combined with $g_{TS}$ to provide the basis for flexible partitioning, that is, weighted MIE (WM) which is defined as follows:

$$g_{FB}=c_{TS}\times g_{MIE}=f(g_{TS})\times g_{MIE}$$

(7)

where, $c_{TS}$ is the weighting coefficient, $f(\ast )$ is the weighting coefficient function, and its value is related to the TS information $g_{TS}$.

3.2. Adaptive Sampling with Variance and Local Salient Factor

The feature selection for distinguishing the detail block and the smooth block is very important on the process of adaptive sampling. Information entropy, variance, and local standard deviation are often used as criteria for features, respectively. The shortcomings are found in using the above features individually as criteria for adaptive sampling, such as information entropy only reflects the probability of gray distribution, the variance is also only related to the degree of dispersion of the pixels, and the local standard deviation only focuses on the spatial distribution of the pixels. Secondly, the adaptive sampling rate is mostly set using segment adaptive sampling instead of step-less adaptive sampling in the previous literature [28], which leads to the discontinuity of sampling rate and the inadequacy utilization of the distinguishing feature.

In order to overcome the shortcomings of individual features, this paper uses the synthetic feature to distinguish between smooth blocks and detail blocks. The synthetic feature for adaptive sampling is defined as:

$$J(x_i)=L{(x_i)}^{{\lambda }_1}\times D{(x_i)}^{{\lambda }_2}$$

(8)

where, $D(x_i)$ and $L(x_i)$ denote the variance and local salient factor in the i-th sub-image, and ${\lambda }_1$ and ${\lambda }_2$ are the corresponding weighting coefficients. The expressions of variance and local salient factor for the sub-block are as follows:

$$\begin{array}{l}D(x_i)=\frac{1}{n}{\displaystyle \sum _{j=1}^n{(x_{ij}-{\mu }_i)}^2}\\ L(x_i)=\frac{1}{n}{\displaystyle \sum _{j=1}^n\frac{{\displaystyle \sum _{k=1}^q\left|x_{{}_{ij}}^k-x_{ij}\right|}}{x_{ij}}}\end{array}$$

(9)

where, $x_{ij}$ is the gray value of the j-th pixel in the i-th sub-image, ${\mu }_i$ is the gray mean of the i-th sub-block image, $x_{ij}^k$ is the gray value of the k-th pixel in the salient operator domain around the center pixel $x_{ij}$, and $q$ represents the number of pixels in the salient operator domain. The synthetic feature $J(x_i)$ can not only reflect the degree of dispersion and relative difference of sub-image pixels, but also combines the relationship between sensory amount and physical quantity of Weber’s Law [29].

In order to avoid the disadvantage of segmented adaptive sampling, step-less adaptive sampling is adopted in this literature [30,31,32]. The key point of step-less adaptive sampling is how to select a continuous sampling rate accurately based on the synthetic feature. The selection of continuous sampling rates is achieved by setting the sampling rate factor (${\eta }_{SR}$) based on the relationship between the sensory amount and the physical quantity in Weber’s Law. The sampling rate factor (${\eta }_{SR}$) and the step-less adaptive sampling rate ($c_{SR}$) are defined as follows:

$${\eta }_{SR}(x_i)=\frac{{\log }_{2}J(x_i)}{\frac{1}{T_1}{\displaystyle \sum _{j=1}^{T_1}{\log }_{2}J(x_j)}}$$

(10)

$$c_{SR}(x_i)={\eta }_{SR}(x_i)\times TSR$$

(11)

where, TSR is the total sampling rate of the whole image.

3.3. Error Estimation and Iterative Stop Criterion in Reconstruction Process

The goal of the reconstruction process is to provide a good representative of the original signal:

$$x^{\ast }={\left[x_1^{\ast },x_2^{\ast },\cdots ,x_N^{\ast }\right]}^T,x^{\ast }\in R^N.$$

(12)

Given the noisy observed output ($\tilde{y}$) and finite-length sparsity (K), the performance of reconstruction is usually measured by the similarity or the error function between $x^{*}$ and $x$. In addition, the reconstruction method, whether it is a convex optimization algorithm or a non-convex optimization algorithm, needs to solve the NP-hard problem by linear programming (LP), wherein the number of the correlation vectors is crucial. Therefore, the error estimation and the selection of the number of correlation vectors are two important factors of reconstruction. Especially in some non-convex optimization restoration algorithms, such as the OMP algorithm, the selection of the number of correlation vectors is linearly related to the number ($v$) of iterations of the algorithm. So, the two points (error estimation and optimal iteration) need to be discussed below.

3.3.1. Reconstruction Error Estimation in Noisy Background

In the second section, Equation (1) was used to describe the relationship model between the original signal and the noiseless observed signal, but the actual observation is always in the noise background, so the observed signal in this noisy environment is as shown in the following equation:

$$\tilde{y}=\Phi x+w=\Phi \Psi s+w=\Omega s+w$$

(13)

where, $\tilde{y}$ is the observed output in the noisy environment, and $w$ is an additive white Gaussian noise (AWGN) with zero-mean and standard deviation ${\sigma }_w$. The M-dimension AWGN $w$ is independent of the signal $x$. Here, we discuss the reconstruction error in two steps, the first step confirms the entire reconstruction model, and the second step derives the relevant reconstruction error.

Since the original signal ($x$) itself is not sparse, it is K-sparse under sparse basis ($\Psi$), so we have:

$$s={\Psi }^{-1}x,s={[s_1,s_2,\cdots ,s_k,\cdots ,s_N]}^T$$

(14)

where, ${[s_1,s_2,\cdots ,s_k,\cdots ,s_N]}^T$ is a vector of length N which only has K non-zero elements, i.e., the remaining N-K micro elements are zero or much smaller than any of the K non-zero elements. Assuming that the first K elements of the sparse representation s are just non-zero elements without loss of generality, we can have:

$$s=\left[\begin{array}{c}{s}_K\\ s_{N-K}\end{array}\right]$$

(15)

where, $s_K$ is a K dimensional vector and $s_{N-K}$ is a vector of length N-K. The actual observed signal obtained by Equations (13) and (15) can be described as follows:

$$\tilde{y}=y+w=\Omega s+w=\left[\begin{array}{cc}{\Omega }_K& {\Omega }_{N-K}\end{array}\right]\left[\begin{array}{c}{s}_K\\ s_{N-K}\end{array}\right]+w={\Omega }_K{s}_K+{\Omega }_{N-K}{s}_{N-K}+w$$

(16)

where, $\Omega =\left[\begin{array}{cccccc}{\omega }_1& \cdots & {\omega }_K& {\omega }_{K+1}& \cdots & {\omega }_N\end{array}\right]$ is an M × N matrix generated of N vectors with M-dimension.

In order to estimate the error of the recovery algorithm accurately, we define three error functions using the $l_2$ norm:

$$\mathrm{Original}\mathrm{data}\mathrm{error}:e_x=\frac{1}{N}{\Vert x-x^{\ast }\Vert }_2^2$$

(17)

$$\mathrm{Observed}\mathrm{data}\mathrm{error}:e_y=\frac{1}{M}{\Vert y-y^{*}\Vert }_2^2$$

(18)

$$\mathrm{Sparse}\mathrm{data}\mathrm{error}:e_s=\frac{1}{N}{\Vert s-s^{\ast }\Vert }_2^2$$

(19)

where, $x^{\ast },y^{\ast },s^{\ast }$ represent the reconstructed values of $x,y,s$, respectively. The three reconstructed values are obtained by maximum likelihood (ML) estimation using $l_0$ minimization. The number of iterations in the restoration algorithm is $v$ times, that is, the number of correlation vectors. In addition, in the process of solving $s^{\ast }$ by using pseudo-inverse, which is based on the least-squares algorithm, the value of $v$ is smaller than M. Using Equations (13) and (15), the expressions of $x^{\ast },y^{\ast },s^{\ast }$ are listed as follows:

$$s^{*}=\left[\begin{array}{l}{s}_v^{*}\\ s_{N-v}^{*}\end{array}\right]=\left[\begin{array}{l}{s}_v^{*}\\ 0_{N-v}^{*}\end{array}\right]=\left[\begin{array}{l}{\Omega }_v^{+}\tilde{y}\\ 0_{N-v}^{*}\end{array}\right]=\left[\begin{array}{l}{\Omega }_v^{+}\left({\Omega }_v{s}_v+{\Omega }_{N-v}{s}_{N-v}+w\right)\\ 0_{N-v}^{*}\end{array}\right]=\left[\begin{array}{l}{s}_v+{\Omega }_v^{+}\left({\Omega }_{N-v}{s}_{N-v}+w\right)\\ 0_{N-v}^{*}\end{array}\right]$$

(20)

$$x^{*}=\Psi s^{*}$$

(21)

$$y^{\ast }=\Omega s^{\ast }$$

(22)

where, ${\Omega }_v^{+}$ is the pseudo inverse of ${\Omega }_v$, and its expression is ${\Omega }_v^{+}={\left({\Omega }_v^T{\Omega }_v\right)}^{-1}{\Omega }_v^T$.

Using Equations (20–22), the three error functions are rewritten as follows:

$$e_x=\frac{1}{N}{\Vert \left[-{\Psi }_v{\Omega }_v^{+}\left({\Omega }_{N-v}{s}_{N-v}+w\right)+{\Psi }_{N-v}{s}_{N-v}\right]\Vert }_2^2$$

(23)

$$e_y=\frac{1}{M}{\Vert \left[-{\Omega }_v{\Omega }_v^{+}\left({\Omega }_{N-v}{s}_{N-v}+w\right)+{\Omega }_{N-v}{s}_{N-v}\right]\Vert }_2^2$$

(24)

$$e_s=\frac{1}{N}{\Vert \left[\begin{array}{c}-{\Omega }_v^{+}\left({\Omega }_{N-v}{s}_{N-v}+w\right)\\ s_{N-v}\end{array}\right]\Vert }_2^2.$$

(25)

According to the definition of $\Psi ,\Omega$ and the RIP, we know:

$$e_s=e_x$$

(26)

$$\left(1-{\delta }_K\right)e_s\le e_y\le \left(1+{\delta }_K\right)e_s$$

(27)

where, ${\delta }_K\in (0,1)$ represents a coefficient associated with $\Omega$ and K. According to Gershgorin circle theorem [33], ${\delta }_K=\left(K-1\right)\mu (\Omega )$ for all $K<\mu {(\Omega )}^{-1}$, where $\mu (\Omega )$ denotes the coherency of $\Omega$:

$$\mu (\Omega )=\underset{1\le i<j\le N}{\max }\frac{\left|⟨{\omega }_i,{\omega }_j⟩\right|}{{\Vert {\omega }_i\Vert }_2{\Vert {\omega }_j\Vert }_2}.$$

(28)

Using Equations (26) and (27), the boundaries of the original data error are as follows:

$$\frac{1}{(1+{\delta }_K)}{e}_y\le e_x\le \frac{1}{(1-{\delta }_K)}{e}_y.$$

(29)

Therefore, from the above analysis, we can conclude that the three errors are consistent, and the minimizing of the three errors is equivalent. Due to the complexity and reliability of the calculation ($e_x$-too complicated, $e_s$-insufficient dimensions), $e_y$ is used as the target in the optimization function of the recovery algorithm.

3.3.2. Optimal Iterative Recovery of Image in Noisy Background

The optimal iterative recovery of image discussed in this paper refers to the case where the error function of the image is the smallest, as can be seen from the minimization of $e_y$ in the form of $l_2$ norm:

$$v_{opt}=\left\{v|\arg \underset{v}{\min }{e}_y\right\}$$

(30)

$$\arg \min e_y=\arg \min \frac{1}{M}{\Vert G_v{\Omega }_{N-v}{s}_{N-v}-C_{v}w\Vert }_2^2$$

(31)

$$\{\begin{array}{l}{G}_v=I-{\Omega }_v{\Omega }_v^{+}\\ C_v={\Omega }_v{\Omega }_v^{+}\end{array}$$

(32)

while $G_v$ is a projection matrix of rank $M-v$, $C_v$ is a projection matrix of rank $v$. Since the projection matrices $G_v$ and $C_v$ in Equation (30) are orthogonal, the inner product of the two vectors $G_v{\Omega }_{N-v}{s}_{N-v}$ and $C_{v}w$ is zero and therefore:

$$e_y=\frac{1}{M}{\Vert C_{v}w\Vert }_2^2+\frac{1}{M}{\Vert G_v{\Omega }_{N-v}{s}_{N-v}\Vert }_2^2=e_y^w+e_{\mathrm{y}}^s$$

(33)

According to [34], the observed data error $e_y$ is a Chi-square random variable with degree of freedom $v$, and the expected value and the variance of $e_y$ are as follows:

$$\frac{M}{{\sigma }_w^2}{e}_y\sim {\chi }_v^2$$

(34)

$$E\left(e_y\right)=\frac{v}{M}{\sigma }_w^2+\frac{1}{M}{\Vert G_v{\Omega }_{N-v}{s}_{N-v}\Vert }_2^2$$

(35)

$$\mathrm{var}\left(e_y\right)=\frac{2v}{M^2}{\left({\sigma }_w^2\right)}^2$$

(36)

The expected value of $e_y$ has two parts. The first part $\frac{v}{M}{\sigma }_w^2$ is the noise-related part, which is a function that is positively related to the number $v$. The second part $\frac{1}{M}{\Vert G_v{\Omega }_{N-v}{s}_{N-v}\Vert }_2^2$ is a function of the unstable micro element $s_{N-v}$, which is decreased as the number $v$ increases. Therefore, the observed data error $e_y$ is normally called a bias-variance tradeoff.

Due to the existence of the uncertain part $e_y^s$, this results in an impossible-to-seek optimal number of iterations $v_{opt}$ by solving the minimum value of $e_y$ directly. As a result, another bias-variance tradeoff $e_y^{\ast }$ is introduced to provide probabilistic bounds on the $e_y^s$ by using the noisy output $\tilde{y}$ instead of noiseless output $y$:

$$e_{{}_y}^{*}=\frac{1}{M}{\Vert \tilde{y}-y^{*}\Vert }_2^2=\frac{1}{M}{\Vert G_v{\Omega }_{N-v}{s}_{N-v}+G_{v}w\Vert }_2^2.$$

(37)

According to [35], the second observed data error $e_y^{\ast }$ is a Chi-square random variable of order $M-v$, and the expected value and the variance of $e_y^{\ast }$ are as follows:

$$\frac{M}{{\sigma }_w^2}{e}_y^{*}\sim {\chi }_{M-v}^2$$

(38)

$$E\left(e_y^{*}\right)=\frac{M-v}{M}{\sigma }_w^2+\frac{1}{M}{\Vert G_v{\Omega }_{N-v}{s}_{N-v}\Vert }_2^2=\frac{M-v}{M}{\sigma }_w^2+e_{\mathrm{y}}^s$$

(39)

$$\mathrm{var}\left(e_y^{*}\right)=\frac{2(M-v)}{M^2}{\left({\sigma }_w^2\right)}^2+\frac{4{\sigma }_w^2}{M^2}{\Vert G_v{\Omega }_{N-v}{s}_{N-v}\Vert }_2^2$$

(40)

So, we can derive probabilistic bounds for the observed data error $e_y$ using probability distribution of the two Chi-square random variables:

$$\underset{\_}{e_y\left(p_1,p_2\right)}\le e_y\le \overline{e_y\left(p_1,p_2\right)}$$

(41)

where, $p_1$ is the confidence probability on a random variable of the observed data error $e_y$, and $p_2$ is the validation probability on a random variable of the second observed data error $e_y^{\ast }$. As both of the two errors satisfy the Chi-square distribution, Gaussian distribution can be used to estimate them. Therefore, confidence probability $p_1$ and validation probability $p_2$ can be calculated as:

$$p_1=Q(\alpha )={\displaystyle {\int }_{-\alpha }^{\alpha }\frac{1}{\sqrt{2\pi }}}{e}^{\frac{-x^2}{2}}dx$$

(42)

$$p_2=Q(\beta )={\displaystyle {\int }_{-\beta }^{\beta }\frac{1}{\sqrt{2\pi }}}{e}^{\frac{-x^2}{2}}dx$$

(43)

where, $\alpha$ and $\beta$ denote the tuning parameters of confidence and validation probabilities, respectively. Furthermore, the worst case is considered when calculating the minimum value of $e_y$, that is, by calculating the minimum value of the upper bound of $e_y$:

$$\begin{array}{l}{v}_{opt}=\left\{v|\arg \underset{v}{\min }\overline{e_y}\right\}=\left\{v|\arg \underset{v}{\min }\overline{e_y(p_1,p_2)}\right\}=\left\{v|\arg \underset{v}{\min }\overline{e_y(\alpha ,\beta )}\right\}\\ =\left\{v|\arg \underset{v}{\min }(\frac{2v-M}{M}{\sigma }_w^2+e_y^{*}+\alpha \frac{\sqrt{2v}}{M}{\sigma }_w^2+\beta \mathrm{var}\left(e_y^{*}\right))\right\}\end{array}$$

(44)

Normally, based on Akaike information criterion (AIC) or Bayesian information criterion (BIC), the optimum number of iterations can be chosen as follows:

AIC: Set $\alpha =\beta =0$

$$\overline{e_y}=\overline{e_y\left(\alpha =0,\beta =0\right)}=(\frac{2v}{M}-1){\sigma }_w^2+e_y^{*}$$

(45)

BIC: Set $\alpha =\sqrt{v}\log M$ and $\beta =0$.

$$\overline{e_y}=\overline{e_y\left(\alpha =\sqrt{v}\log M,\beta =0\right)}=(\frac{(2+\sqrt{2}\log M)v}{M}-1){\sigma }_w^2+e_y^{*}$$

(46)

where, $e_y^{\ast }$ can be calculated based on the noisy observation data and the reconstruction algorithm.

3.3.3. Application of Error Estimation on BCS

The proposed algorithm (FE-ABCS) is based on block-compressive sensing, so the optimal number of iterations ($v_{opt}$) derived in the above section also requires a variant to be applied to the above algorithm:

$$\begin{array}{l}{v}_{opt}^i=\left\{v^i|\arg \underset{v^i}{\min }\overline{e_{y_i}}\right\}=\left\{v^i|\arg \underset{v^i}{\min }\overline{e_{y_i}(p_1^i,p_2^i)}\right\}=\left\{v^i|\arg \underset{v^i}{\min }\overline{e_{y_i}({\alpha }_i,{\beta }_i)}\right\}\\ =\left\{v^i|\arg \underset{v^i}{\min }(\frac{2v^i-m^i+{\alpha }_i\sqrt{2v^i}}{m^i}{\sigma }_{w^i}^2+{\beta }_i\mathrm{var}\left(e_{y_i}^{*}\right)+e_{y_i}^{*})\right\}\end{array}$$

(47)

where, $i=1,2,\cdots ,T_1$ represents the serial number of all sub-images. Similarly, the values of ${\alpha }_i$ and ${\beta }_i$ can be valued according to the AIC and BIC criteria.

4. The Proposed Algorithm (FE-ABCS)

With the knowledge presented in the previous section, the altered ABCS (FE-ABCS) is proposed for the recovery of block sparse signals in noiseless or noise backgrounds. The workflow of the proposed algorithm is presented in Section 4.1 while the specific parameter settings of the proposed algorithm is introduced in Section 4.2.

4.1. The Workflow and Pseudocode of FE-ABCS

In order to better express the idea of the proposed algorithm, the workflow of the typical BCS algorithm and the FE-ABCS algorithm are presented, as shown in Figure 2.

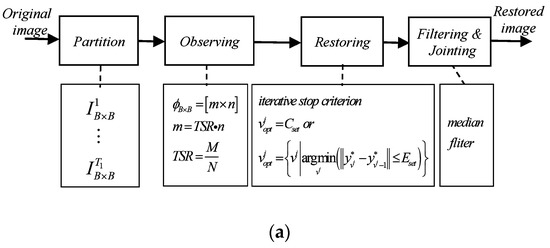
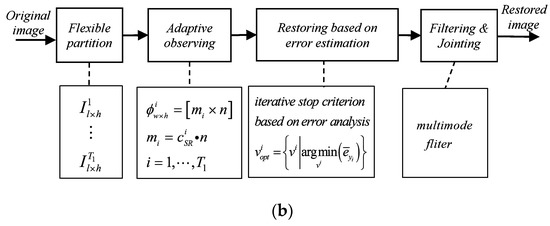
Figure 2. The workflow of two block-compressive sensing (BCS) algorithms. (a) Typical BCS algorithm, (b) FE-ABCS algorithm.

According to Figure 2, compared with the traditional BCS algorithm, the main innovations of this paper can be reflected in the following points:

• Flexible partitioning: using the weighted MIE as the block basis to reduce the average complexity of the sub-images from the pixel domain and the spatial domain;
• Adaptive sampling: adopting synthetic feature and step-less sampling to ensure a reasonable sample rate for each subgraph;
• Optimal number of iterations: using the error estimate method to ensure the minimum error output of the reconstructed image in the noisy background.

Furthermore, since the FE-ABCS algorithm is based on iterative recovery algorithm, especially the non-convex optimization iterative recovery algorithm, this paper uses the OMP algorithm as the basic comparison algorithm without loss of generality. The full pseudocode of the proposed algorithm is presented as follows.

FE-ABCS Algorithm based on OMP (Orthogonal Matching Pursuit)

1: Input: Original image I, total sampling  rate TSR, sub-image dimension n  ($n=2^b,b=2,4,6,\cdots$), sparse matrix $\Psi \in R^{n\times n}$,  initialized measurement matrix $\Phi \in R^{n\times n}$ 2: Initialization: $\left\{x|x\leftarrow Iandx\in R^N\right\}$;  $T_1=\raisebox{1ex}{$N$}\!\left/ \!\raisebox{-1ex}{$n$}\right.$; //$quantityofsubimages$  $T_2=1+{\log }_{2}n$; //$typeofflexiblepartitioning$  step1: flexible partitioning (FP) 3: for j = 1,…,T2 do 4: $l_j\times h_j=2^{j-1}\times 2^{T_2-j};{\left\{I_i,i=1,\cdots ,T_1\right\}}_j\leftarrow I$;  ${\left\{x_i,i=1,\cdots ,T_1\right\}}_j\leftarrow x$; 5: $g_{MIE}^j=MIE\left({\left\{x_i,i=1,\cdots ,T_1\right\}}_j\right)$;  $c_{TS}^j={(f(g_{TS}))}_j={(f([g_{TS}^H,g_{TS}^V]))}_j$; 6: $g_{FB}^j=c_{TS}^j·g_{MIE}^j$;  // Weighted MIE--Base of FP 7: end for 8:$j_{opt}=\arg \underset{j}{\min }\left(\left\{g_{FB}^j,j=1,\cdots ,T_2\right\}\right)$; 9:$l\times h=2^{j_{opt}-1}\times 2^{T_2-j_{opt}}$; $\left\{I_i,i=1,\cdots ,T_1\right\}\leftarrow I$;  $\left\{x_i,i=1,\cdots ,T_1\right\}\leftarrow x$;  step2: adaptive sampling (AS) 10: for i = 1,…,T1 do 11: $D(x_i)\leftarrow x_i$; $L(x_i)\leftarrow I_i$; $J(x_i)=L{(x_i)}^{{\lambda }_1}·D{(x_i)}^{{\lambda }_2}$;   // synthetic feature (J)--Base of AS 12: end for 13: $\eta (\left\{x_i,i=1,\cdots ,T_1\right\})=\frac{{\log }_{2}J(\left\{x_i,i=1,\cdots ,T_1\right\})}{\frac{1}{T_1}{\displaystyle \sum _{i=1}^{T_1}{\log }_{2}J(x_i)}}$; 14: $c_{SR}(\left\{x_i,i=1,\cdots ,T_1\right\})=\eta (\left\{x_i,i=1,\cdots ,T_1\right\})·TSR$;  // $c_{SR}$--AS ratio of sub-images   $\left\{m_i,i=1,\cdots ,T_1\right\}=c_{SR}(\left\{x_i,i=1,\cdots ,T_1\right\})·n$; 15: $\Phi ={\left({\varphi }_1,\cdots ,{\varphi }_n\right)}^T,{\chi }_i=randperm\left(n\right),{\Phi }_{{\chi }_i}=\Phi \left({\chi }_i,:\right)$; 16: $\left\{{\Phi }_i,i=1,\cdots ,T_1\right\}=\left\{{\Phi }_{{\chi }_i}(\left[1,\cdots ,m_i\right],:),i=1,\cdots ,T_1\right\}$; 17: $\left\{y_i,i=1,\cdots ,T_1\right\}=\left\{{\Phi }_i·x_i,i=1,\cdots ,T_1\right\}$;

step3: restoring based on error estimation 18:$\left\{{\tilde{y}}_i,i=1,\cdots ,T_1\right\}=\left\{y_i+w_i,i=1,\cdots ,T_1\right\}$;  // $w_i:m_i-dimensionAWGN,w_i=0:noiseless$ 19: $\left\{{\Omega }_i,i=1,\cdots ,T_1\right\}=\left\{{\Phi }_i·\Psi ,i=1,\cdots ,T_1\right\}$; 20: for i = 1,…,T1 do 21:  ${\Omega }_i=\left\{{\omega }_{i1},\cdots ,{\omega }_{in}\right\},r={\tilde{y}}_i,A=\varnothing ,s^{*}=0^n$;   //$\left\{{\omega }_{ij},j=1,\dots ,n\right\}$-- column vector of ${\Omega }_i$ 22:  $v_{opt}^i=\left\{v^i|\arg \underset{v^i}{\min }\overline{e_{y_i}}\right\}$;   // calculate optimal iterative of sub-images 23:   for $j=1,\cdots ,v_{opt}^i$ do 24:    $\wedge =\arg \underset{j}{\min }\left|⟨r,w_{ij}⟩\right|$; 25:    $A=A\cup \{\wedge \}$; 26:    $r={\tilde{y}}_i-{\Omega }_i(:,A)·{\left[{\Omega }_i(:,A)\right]}^{+}·{\tilde{y}}_i$; 27:   end for 28: $s_i^{\ast }={\left[{\Omega }_i(:,A)\right]}^{+}·{\tilde{y}}_i$;  // $s_i^{\ast }$--reconstructed sparse representation 29: $x_i^{*}=\Psi ·s_i^{\ast }$;  // $x_i^{\ast }$--reconstructed original signal 30: end for 31: $x^{*}=\left\{x_i^{*},i=1,\cdots ,T_1\right\},I_r^{*}=\left\{x^{*},l,h\right\}$;  // $I_r^{\ast }$--reconstructed image without filter  step4: multimode filtering (MF) 32: $if\left(BEI\ge BE{I}^{*}\right)$; //$BE{I}^{*}-Threshodofblockeffect$ 33: $I_r^{*}=deblock(I_r^{*})$; 34: $endif$ 35: $if\left(TSR\ge TS{R}^{*}\right)$; //$TS{R}^{*}-ThreshodofTSR$ 36: $I_F^{*}=wienerfilter(I_r^{*})$; 37: $else{I}_F^{*}=medfilter(I_r^{*})$; 38: $endif$ 39: $I^{*}=I_F^{*}$  // $I^{\ast }$--reconstructed image with M

4.2. Specific Parameter Setting of FE-ABCS

4.2.1. Setting of the Weighting Coefficient $c_{TS}$

The most important step in achieving flexible partitioning is to the minimum of the weighted MIE, where the design of the weighting coefficient function is the most critical point. Therefore, this section focuses on the specific design of the function which ensures optimal partitioning of the image:

$$\begin{array}{l}{c}_{TS}=f(g_{TS})=\left\{{(f(g_{TS}))}_j,1,\cdots ,T_2\right\}=\left\{{(f([g_{TS}^H,g_{TS}^V]))}_j,1,\cdots ,T_2\right\}\\ =\{\begin{array}{l}ones(1,T_2)g_{TS}^H\le G_{TS}\&g_{TS}^V\le G_{TS}\\ [0,1,\cdots ,b]/(b/2)g_{TS}^H\le G_{TS}\&g_{TS}^V>G_{TS}\\ [b,\cdots ,1,0]/(b/2)g_{TS}^H>G_{TS}\&g_{TS}^V\le G_{TS}\\ \frac{[b,{\log }_2^{(n/2+2)},{\log }_2^{(n/4+4)},\cdots ,{\log }_2^{(4+n/4)},{\log }_2^{(2+n/2)},b]}{b/2+1}{g}_{TS}^H>G_{TS}\&g_{TS}^V>G_{TS}\end{array}\end{array}$$

(48)

where, $g_{TS}^H$ and $g_{TS}^V$ represent the value of horizontal and vertical TS by using ASM, and $G_{TS}$ represents the threshold at which the TS feature value reaches a significant degree.

4.2.2. Setting of the Adaptive Sampling Rate $c_{SR}$

In the process of adaptive observation, the most important thing is to design a reasonable random observation matrix, and the dimension of this matrix needs to be constrained by the adaptive sampling rate, so as to assign the different sampling of each sub-image with a different complexity. Therefore, the setting of $c_{SR}=\left\{c_{SR}\left(x_i\right),i=1,\cdots ,T_1\right\}$ is crucial, and its basic form is mainly determined by the synthetic feature ($J=\left\{J\left(x_i\right),i=1,\cdots ,T_1\right\}$) and the sampling rate factor (${\eta }_{SR}=\left\{{\eta }_{SR}\left(x_i\right),i=1,\cdots ,T_1\right\}$).

The definition of $J\left(x_i\right)$ can be implemented by setting the corresponding weighting coefficients ${\lambda }_{1}and{\lambda }_2$. This article obtains the optimization values for ${\lambda }_{1}and{\lambda }_2$ through analysis and partial verification experiments: ${\lambda }_1=1and{\lambda }_2=2$.

The purpose of setting ${\eta }_{SR}(x_i)$ is to establish the mapping function relationship between $J\left(x_i\right)$ and $c_{SR}$ by Equations (10) and (11). However, the mapping relationship established by Equation (10) does not consider the minimum sampling rate. In fact, the minimum sampling rate factor (MSRF) is considered in the proposed algorithm to improve performance, that is, the function between ${\eta }_{SR}(x_i)$ and $J\left(x_i\right)$ should be modified as follows.

• Initial value calculation of ${\eta }_{SR}(x_i)$: get the initial value of the sampling factor by Equation (10).
• Judgment of ${\eta }_{SR}(x_i)$ through MSRF (${\eta }_{\min }$): if the corresponding sampling rate factor of all image sub-blocks meets the minimum threshold requirement (${\eta }_{SR}(x_i)>{\eta }_{\min },i\in \left\{1,2,\cdots ,T_1\right\}$), there is no need for modification, however, if it is not satisfied, modify it.
• Modifying of ${\eta }_{SR}(x_i)$: if ${\eta }_{SR}(x_i)\le {\eta }_{\min }$, then ${\eta }_{SR}(x_i)={\eta }_{\min }$; if ${\eta }_{SR}(x_i)>{\eta }_{\min }$, then use the following equation to modify the value:

  $${\eta }_{SR}(x_i)==(1+(1-{\eta }_{\min })\frac{T_1-T_1{}^{\prime }}{T_1{}^{\prime }})\frac{{\log }_{2}J(x_i)}{\frac{1}{T_1{}^{\prime }}{\displaystyle \sum _{j=1}^{{T^{\prime }}_1}{\log }_{2}J(x_j)}}$$

  (49)

  where, $T_1{}^{\prime }$ is the number of sub-images that can meet the requirement of the minimum threshold.

4.2.3. Setting of the Iteration Stop Condition $v_{opt}$

The focus of the proposed algorithm in the iterative reconstruction part is to make the best effect of the rebuilt image by choosing $v_{opt}$ in the actual noisy background. This paper combines BIC and BCS to propose the calculation formula of the optimal iteration number of the proposed algorithm:

$$v_{opt}=\{v_{opt}^i,i=1,\cdots ,T_1\}=\left\{v^i|\arg \underset{v^i}{\min }(\frac{(2+\sqrt{2}\log m^i)v^i-m^i}{m^i}{\sigma }_{w^i}^2+e_{y_i}^{*}),i=1,\cdots ,T_1\right\}.$$

(50)

5. Experiments and Results Analysis

In order to evaluate the FE-ABCS algorithm, experimental verification is performed in three scenarios. This paper first discusses the performance of the improved algorithm by flexible partitioning and adaptive sampling in the absence of noise, and secondly discusses how to combine the number of optimal iterations to eliminate the noise effect and achieve the best quality (comprehensive indicator) under noisy conditions. Finally, the differences between this proposed algorithm and other non-CS image compression algorithms is analyzed. The experiments were carried out in the matlab2016b software environment, and 20 typical grayscale images with 256 × 256 resolution were used for testing, which were selected from the LIVE Image Quality Assessment Database, the SIPI Image Database, the BSDS500 Database, and other digital image processing standard test Databases. The performance indicators mainly adopt Peak Signal to Noise Ratio (PSNR), Structural Similarity (SSIM), Gradient Magnitude Similarity Deviation (GMSD), Block Effect Index (BEI), and Computational Cost (CC). The above five performance indicators are defined as follows:

The PSNR indicator is an index that shows the amplitude error between the reconstructed image and the original image, which is the most common and widely used objective measure of image quality:

$$PSNR=20\times {\log }_{10}(\frac{255}{\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^N{(x_i-x_i^{\ast })}^2}}})$$

(51)

where, $x_i$ and $x_i^{\ast }$ are the gray value of i-th sub-image of the reconstructed image and the original image.

The SSIM indicator is adopted to indicate similarity between the reconstructed image and the original image:

$$SSIM=\frac{(2{\mu }_x{\mu }_{x^{\ast }}+c_1)(2{\sigma }_x{}_{x^{\ast }}+c_2)}{({\mu }_x^2+{\mu }_{x^{\ast }}^2+c_1)({\sigma }_x^2+{\sigma }_{x^{\ast }}^2+c_2)}$$

(52)

where, ${\mu }_x$ and ${\mu }_{x^{\ast }}$ are the mean of x and x^*, ${\sigma }_x$ and ${\sigma }_{x^{\ast }}$ are the standard deviation of x and x^*, ${\sigma }_{x{x}^{\ast }}$ represents the covariance of x and x^*, constant $c_1={(0.01L)}^2$ and $c_2={(0.03L)}^2$, and L is the range of pixel values.

The GMSD indicator is mainly used to characterize the degree of distortion of the reconstructed image. The larger the value, the worse the quality of the reconstructed image:

$$GMSD=std(\left\{GMS(i)|i=1,\cdots ,N\right\})=std(\left\{\frac{2m_x(i)m_{x^{\ast }}(i)+c_3}{m_x^2(i)+m_{x^{\ast }}^2(i)+c_3}|i=1,\cdots ,N\right\})$$

(53)

where, $std(\ast )$ is the standard deviation operator, GMS is the gradient magnitude similarity between x and x^*, $m_x(i)=\sqrt{{(h_H\otimes x(i))}^2+{(h_V\otimes x(i))}^2}$ and $m_y\left(\mathrm{i}\right)=\sqrt{{(h_H\otimes x^{\ast }(i))}^2+{(h_V\otimes x^{\ast }(i))}^2}$ are the gradient magnitude of x(i) and x^*(i), $h_H$ and $h_V$ represent the Prewitt operator of horizontal and vertical direction, and $c_3$ is an adjustment constant.

The main purpose of introducing BEI is to evaluate the blockiness of the algorithm in a noisy condition, which means that the larger the value, the more obvious the block effect:

$$BEI={\log }_2\left[\frac{sum(edge(x^{*}))-sum(edge(x))+sum(\left|edge(x^{*})-edge(x)\right|)}{2}\right]$$

(54)

where, $edge(\ast )$ denotes the edge acquisition function of the image, $sum(\ast )$ represents the function of finding the number of all edge points of the image, and $|\ast |$ is an absolute value operator.

The Computational Cost is introduced to measure the efficiency of the algorithm, which is usually represented by Computation Time (CT). The smaller the value of CT, the higher the efficiency of the algorithm:

$$CT=t_{end}-t_{start}$$

(55)

where, $t_{start}$ and $t_{end}$ indicate the start time and end time, respectively.

In addition, the sparse basis and the random measurement matrices use discrete cosine orthogonal basis and orthogonal symmetric Toeplitz matrices [36,37], respectively.

5.1. Experiment and Analysis without Noise

5.1.1. Performance Comparison of Various Algorithms

In order to verify the superiority of the proposed ABCS algorithm, this paper mainly uses the OMP algorithm as the basic reconstruction algorithm. Based on the OMP reconstruction algorithm, eight BCS algorithms (including the proposed algorithm with the idea of flexible partitioning and adaptive sampling) are listed, and the performance of these algorithms under different overall sampling rates is compared, which is shown in Table 1. In this experiment, four normal grayscale standard images are used for performance testing, the dimension of the subgraph and the iterative number of reconstructions are limited to 256 and one quarter of the measurement’s dimension, respectively.

Table 1. The Peak Signal to Noise Ratio (PSNR) and Structural Similarity (SSIM) of reconstructed images with eight BCS algorithms based on OMP. (TSR = total sampling rate).

Images	Algorithms	TSR = 0.2	TSR = 0.3	TSR = 0.4	TSR = 0.5	TSR = 0.6
		PSNR/SSIM	PSNR/SSIM	PSNR/SSIM	PSNR/SSIM	PSNR/SSIM
Lena	M-B_C	29.0945/0.7684	29.8095/0.8720	30.6667/0.9281	31.8944/0.9572	32.9854/0.9719
	M-B_S	31.1390/0.8866	31.7478/0.9227	32.4328/0.9480	33.2460/0.9651	34.2614/0.9763
	M-FB_MIE	30.7091/0.8613	31.2850/0.9115	32.0093/0.9413	32.9032/0.9600	33.8147/0.9737
	M-FB_WM	31.1636/0.8880	31.7524/0.9236	32.4623/0.9479	33.2906/0.9645	34.2691/0.9763
	M-B_C-A_I	29.1187/0.7838	29.8433/0.8803	30.8898/0.9305	32.0023/0.9577	33.2193/0.9732
	M-FB_WM-A_I	31.1763/0.8967	31.8872/0.9344	32.7542/0.9584	33.7353/0.9732	34.8647/0.9827
	M-FB_WM-A_V	31.2286/0.9087	32.0579/0.9433	33.0168/0.9643	34.1341/0.9775	35.4341/0.9856
	M-FB_WM-A_S	31.3609/0.9138	32.0943/0.9487	33.1958/0.9681	34.3334/0.9807	35.8423/0.9878
Goldhill	M-B_C	28.4533/0.7747	28.9144/0.8718	29.3894/0.9080	29.7706/0.9315	30.2421/0.9495
	M-B_S	29.5494/0.8785	29.9517/0.9089	30.3330/0.9341	30.8857/0.9514	31.4439/0.9640
	M-FB_MIE	29.7012/0.8882	29.9811/0.9154	30.4465/0.9364	30.9347/0.9516	31.5153/0.9642
	M-FB_WM	29.7029/0.8867	30.0277/0.9151	30.4827/0.9361	30.9555/0.9516	31.5333/0.9649
	M-B_C-A_I	28.4436/0.7809	28.8691/0.8693	29.3048/0.9089	29.7046/0.9321	30.2355/0.9499
	M-FB_WM-A_I	29.6708/0.8918	30.0833/0.9215	30.5120/0.9424	31.0667/0.9574	31.6899/0.9697
	M-FB_WM-A_V	29.5370/0.8957	30.0891/0.9253	30.5379/0.9456	31.0922/0.9607	31.8011/0.9724
	M-FB_WM-A_S	29.7786/0.8975	30.1482/0.9272	30.5689/0.9472	31.1310/0.9622	31.8379/0.9736
Cameraman	M-B_C	28.5347/0.7787	29.0078/0.8559	29.3971/0.9051	29.9417/0.9379	30.6612/0.9592
	M-B_S	31.1796/0.8763	31.4929/0.9121	31.9203/0.9391	32.3009/0.9581	32.7879/0.9704
	M-FB_MIE	31.1487/0.8782	31.5067/0.9123	31.8644/0.9403	32.3170/0.9577	32.7946/0.9703
	M-FB_WM	31.2118/0.8675	31.4645/0.9072	31.8130/0.9365	32.2050/0.9559	32.6811/0.9686
	M-B_C-A_I	28.5669/0.7852	28.8807/0.8612	29.3928/0.9164	29.9924/0.9461	30.6130/0.9639
	M-FB_WM-A_I	31.2554/0.8901	31.5975/0.9296	32.0955/0.9533	32.6859/0.9701	33.4007/0.9802
	M-FB_WM-A_V	31.2869/0.9085	31.8762/0.9550	32.5052/0.9746	33.3531/0.9848	34.4449/0.9904
	M-FB_WM-A_S	31.3916/0.9287	31.9731/0.9621	32.6508/0.9790	33.6779/0.9877	34.8958/0.9918
Couple	M-B_C	28.6592/0.7582	29.0162/0.8557	29.5471/0.9109	30.2260/0.9440	30.9136/0.9640
	M-B_S	30.1529/0.8912	30.6910/0.9289	31.2853/0.9541	31.9693/0.9695	32.7464/0.9796
	M-FB_MIE	30.1920/0.8895	30.7257/0.9282	31.2948/0.9531	31.9509/0.9692	32.7424/0.9794
	M-FB_WM	30.1357/0.8917	30.6890/0.9259	31.3185/0.9539	31.9520/0.9691	32.7622/0.9793
	M-B_C-A_I	28.5694/0.7428	29.0442/0.8589	29.5828/0.9088	30.2127/0.9444	30.9839/0.9642
	M-FB_WM-A_I	30.2105/0.9027	30.7783/0.9413	31.4680/0.9630	32.3143/0.9759	33.2604/0.9840
	M-FB_WM-A_V	30.1896/0.9099	30.8541/0.9454	31.4990/0.9670	32.3769/0.9792	33.3260/0.9864
	M-FB_WM-A_S	30.3340/0.9117	30.9047/0.9475	31.5496/0.9686	32.3788/0.9798	33.3561/0.9869

These 8 BCS algorithms are named as M-B_C, M-B_S, M-FB_MIE, M-FB_WM, M-B_C-A_S, M-FB_WM-A_I, M-FB_WM-A_V, and M-FB_WM-A_S respectively, which in turn represent BCS with a fixed column block, BCS with a fixed square block, BCS with flexible partitioning by MIE, BCS with flexible partitioning by WM, BCS with a fixed column block and IE-adaptive sampling, BCS with WM-flexible partitioning and IE-adaptive sampling, BCS with WM-flexible partitioning and variance-adaptive sampling, and BCS with WM-flexible partitioning and SF-adaptive sampling (A form of FE-ABCS algorithm in the absence of noise). Comparing the data in Table 1, there are the following consensuses:

• Analysis of the performance indicators of the first four algorithms shows that for the BCS algorithm, BCS with a fixed column block is inferior to BCS with a fixed square block because square partitioning makes good use of the correlation of intra-block regions. MIE-based partitioning minimizes the average amount of information entropy of the sub-images. However, when the overall image has obvious texture characteristics, simply using MIE as the partitioning basis may not necessarily achieve a good effect, and the BCS algorithm based on weighted MIE combined with the overall texture feature can achieve better performance indicators.
• Comparing the adaptive BCS algorithms under different features in Table 1, variance has obvious superiority to IE among the single features, because the variance not only contains the dispersion of gray distribution but also the relative difference of the individual gray distribution of sub-images. In addition, the synthetic feature (combined local saliency) has a better effect than a single feature. The main reason for this is that the synthetic feature not only considers the overall difference of the subgraphs, but also the inner local-difference of the subgraphs.
• Combining experimental results of the eight BCS algorithms in Table 1 reveals that using adaptive sampling or flexible partitioning alone does not provide the best results, but the proposed algorithm combining the two steps will have a significant effect on both PSNR and SSIM.

Figure 3 shows the reconstructed images of Cameraman using the above eight BCS algorithms and multimode filter at the overall sampling rate of 0.5. Compared with other algorithms, the graph (i) reconstructed by the proposed algorithm has good quality both in performance indicators and subjective vision. Adding multimode filtering has improved the performance of the above eight BCS algorithms. While comparing the corresponding data (SR = 0.5) in Figure 3 and Table 1, it was found that PSNR has a certain improvement after adding multimode filtering, and so as to SSIM under the first six BCS algorithms except the latter two algorithms. The reason is that the adaptive sampling rates of the latter two algorithms are both related to the variance (the more variance, the more sampling rate), and SSIM is related to both the variance and the covariance. In addition, to filter out high-frequency noise, the filtering process will also lose some high-frequency components (a contribution to the improvement of SSIM) of signal itself. Therefore, the latter two algorithms will reduce the value of SSIM for images with a lot of high-frequency components (SSIM value of graph (h) and (i) of Figure 3 is a little smaller than the corresponding value in Table 1), but for most images without lots of high-frequency information, the value of SSIM is improved.

Figure 3. Reconstructed images of Cameraman and performance indicators with different BCS algorithms (TSR = 0.5).

Secondly, in order to evaluate the effectiveness and universality of the proposed algorithm, in addition to the OMP reconstruction algorithm as the basic comparison algorithm, the IRLS and BP reconstruction algorithms were also adopted and combined with the proposed method to generate eight BCS algorithms, respectively. Table 2 shows the experimental data records of the above two types of algorithms tested with the standard image Lena. From the resulting data, the proposed method has a certain improvement for the BCS algorithm based on IRLS and BP, although it will bring a slightly higher cost in computation time due to the increase of the proposed algorithm’s complexity itself.

Table 2. The PSNR and SSIM of reconstructed images with eight BCS algorithms based on iteratively reweighted least square (IRLS) and basis pursuit (BP).

Restoring Method	Algorithms	TSR = 0.4				TSR = 0.6
		PSNR	SSIM	GMSD	CT	PSNR	SSIM	GMSD	CT
IRLS	R-B_C	32.38	0.9361	0.1943	5.729	33.42	0.9790	0.1348	13.97
	R-B_S	32.67	0.9634	0.1468	5.928	35.08	0.9843	0.0987	14.94
	R-FB_MIE	32.14	0.9593	0.1658	5.986	34.44	0.9825	0.1094	13.79
	R-FB_WM	32.46	0.9631	0.1441	6.071	34.80	0.9841	0.0992	14.25
	R-B_C-A_I	30.55	0.9460	0.1882	6.011	34.08	0.9825	0.1238	14.46
	R-FB_WM-A_I	33.05	0.9714	0.1346	6.507	36.01	0.9894	0.0863	14.98
	R-FB_WM-A_V	33.25	0.9751	0.1216	6.994	36.71	0.9914	0.0691	17.34
	R-FB_WM-A_S	33.59	0.9787	0.1188	7.456	37.23	0.9927	0.0661	19.38
BP	P-B_C	30.56	0.9380	0.1984	33.47	33.35	0.9787	0.1378	69.67
	P-B_S	32.72	0.9638	0.1484	34.22	34.61	0.9823	0.1072	71.00
	P-FB_MIE	32.00	0.9531	0.1627	34.04	34.14	0.9810	0.1149	68.78
	P-FB_WM	32.82	0.9635	0.1512	35.08	34.57	0.9832	0.1070	69.48
	P-B_C-A_I	30.72	0.9428	0.1973	33.84	33.57	0.9795	0.1335	70.27
	P-FB_WM-A_I	33.01	0.9705	0.1442	35.63	35.70	0.9884	0.0888	70.73
	P-FB_WM-A_V	33.32	0.9750	0.1277	36.98	36.37	0.9909	0.0742	72.59
	P-FB_WM-A_S	33.49	0.9773	0.1210	37.85	37.45	0.9932	0.0662	74.41

Furthermore, comparative experiments of the proposed algorithm combined with different image reconstruction algorithms (OMP, IRLS, BP, and SP) have also been carried out. Figure 4 is the data record of the above experiments tested with the standard image Lena under the conditions of TSR = 0.4 and TSR = 0.6, respectively. The experimental data shows that the proposal using these four algorithms has little difference between the PSNR and SSIM performance index. However, in terms of the GMSD index, the IRLS and BP algorithms are obviously better than the OMP and SP. In terms of calculation time, BP is based on the $l_1$ norm, its performance is significantly worse than the other three, which is also consistent with the content of Section 1.

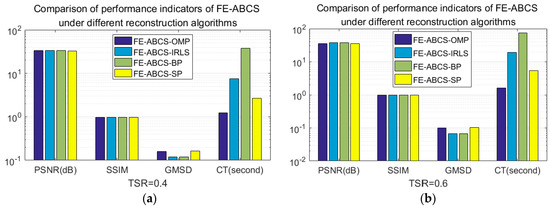
Figure 4. The comparison of the proposed algorithm with 4 reconstruction algorithms (OMP, IRLS, BP, SP): (a) TSR = 0.4, (b) TSR = 0.6.

5.1.2. Parametric Analysis of the Proposed Algorithm

The main points of this proposed algorithm involves the design and verification of weighting coefficients ($c_{TS}$, ${\lambda }_1$, ${\lambda }_2$) and minimum sampling rate factor (${\eta }_{\min }$). The design of the three weighting coefficients of the algorithm in this paper was introduced in Section 4.2, and its effect on performance was reflected in the comparison of the eight algorithms in Section 5.1.1. Here, only the selection and effect of ${\eta }_{\min }$ need to be researched, and the influence of ${\eta }_{\min }$ on the PSNR under different TSR is analyzed.

Figure 5 shows the analysis results of the test image Lena on the correlation between PSNR, TSR, and MSRF (${\eta }_{\min }$). It can be seen from Figure 5 that the optimal value (maximizing the PSNR of Lena’s recovery image) of minimum sampling rate factor (OMSRF) decreases as the TSR increases. In addition, the gray value in Figure 5 means the revised PSNR of the recovery image (${\mathrm{PSNR}}^{*}=\mathrm{PSNR}-\overline{\mathrm{PSNR}}$).

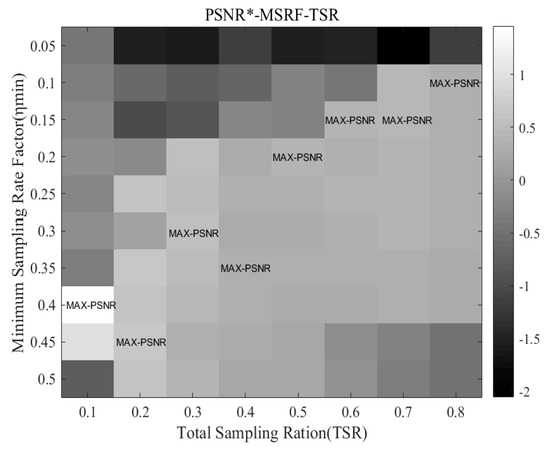
Figure 5. Correlation between PSNR^*, MSRF, and TSR of test image Lena.

Then, many other test images were analyzed in this paper to verify the relationship between TSR and OMSRF (${\eta }_{opt}=\left\{{\eta }_{\min }|\underset{{\eta }_{\min }}{\arg \max }(PSNR(x,{\eta }_{\min }))\right\}$), and the experimental results of eight typical test images are shown in Figure 6. According to the data, the reasonable setting of MSRF (${\eta }_{opt}$) in the algorithm can be obtained by the curve fitting method. The baseline fitting method (a simple curve method) is used in the proposed algorithm of this article (${\eta }_{opt}=0.1+6\times (0.8-TSR)/7$).

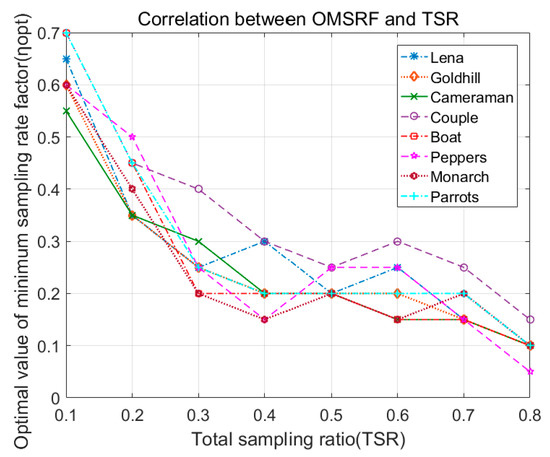
Figure 6. Correlation between OMSRF (${\eta }_{opt}$) and TSR.

5.2. Experiment and Analysis Under Noisy Conditions

5.2.1. Effect Analysis of Different Iteration Stop Conditions on Performance

In the case of noiseless, the larger the iterative number ($v$) of the reconstruction algorithm, the better the effect of the reconstructed image. But in the noisy condition, the quality of the reconstructed image does not become monotonous with the increase of $v$, which has been carefully analyzed in Section 3.3. The usual iteration stop conditions are: (1) using the sparsity ($\varsigma$) of signal as the stopping condition, i.e., fixed number of iterations ($v_{stop1}=\varsigma ·m$), and (2) using the certain differential threshold ($\gamma$) of the recovery value as the stopping condition, i.e., the difference between the adjacent two results of the iterative output less than the threshold ($v_{\mathrm{s}top2}==\left\{v|\arg \underset{v}{\min }(\Vert y_{{}_{v-1}}^{*}-y_{{}_v}^{*}\Vert \le \gamma )\right\}$). Since the above two methods could not guarantee the optimal recovery of the original signal in the noisy background, the innovation of the FE-ABCS algorithm is to make up for the above deficiency and propose a constraint ($v_{opt}$) based on error analysis to ensure the best iterative reconstruction. Then the rationality of the proposed scheme would be verified through experiments in this section, and without loss of generality, OMP is used as the basic reconstruction algorithm, just like what was done in Section 5.1.

The specific experimental results of test image Lena for selecting different iteration stop conditions under different noise backgrounds are recorded in Table 3. The value of Noise-std represents the standard deviation of additional Gaussian noise signal. From the overall trend of Table 3, selecting $v_{opt}$ has better performance than selecting $v_{stop1}$ as the stop condition for iterative reconstruction. This advantage is especially pronounced as the Noise-std increases.

Table 3. The experimental results of Lena at different stop conditions and noise background (TSR = 0.4).

	Sparsity	${\mathit{v}}_{\mathit{\varsigma }=0.1}$	${\mathit{v}}_{\mathit{\varsigma }=0.2}$	${\mathit{v}}_{\mathit{\varsigma }=0.3}$	${\mathit{v}}_{\mathit{\varsigma }=0.4}$	${\mathit{v}}_{\mathit{\varsigma }=0.5}$	${\mathit{v}}_{\mathit{o}\mathit{p}\mathit{t}}$
Noise-std		PSNR and SSIM and GMSD and BEI and CT
5		32.95	32.71	32.39	32.12	31.96	32.48
		0.961	0.965	0.961	0.957	0.955	0.960
		0.165	0.160	0.169	0.173	0.178	0.171
		10.63	10.25	10.04	9.92	9.98	10.09
		0.741	0.949	1.166	1.567	1.911	1.481
10		32.40	31.81	31.30	31.07	30.92	32.23
		0.957	0.955	0.949	0.941	0.937	0.956
		0.169	0.179	0.190	0.194	0.200	0.177
		10.29	10.04	10.14	10.15	10.20	10.21
		0.741	0.922	1.233	1.637	1.961	0.926
15		31.63	30.87	30.46	30.27	30.12	31.81
		0.948	0.937	0.926	0.917	0.912	0.949
		0.180	0.202	0.213	0.220	0.223	0.185
		10.32	10.25	10.32	10.38	10.39	10.25
		0.727	0.933	1.154	1.550	2.063	0.798
20		30.97	30.08	29.83	29.66	29.61	31.48
		0.936	0.916	0.898	0.887	0.879	0.941
		0.197	0.219	0.236	0.244	0.247	0.191
		10.45	10.34	10.39	10.43	10.43	10.50
		0.720	0.914	1.203	1.476	2.348	0.739
30		30.03	29.34	29.04	28.94	28.89	30.75
		0.901	0.862	0.832	0.816	0.803	0.920
		0.227	0.257	0.266	0.272	0.275	0.204
		10.59	10.52	10.54	10.55	10.67	10.62
		0.901	0.947	1.237	1.500	1.996	0.690
40		29.38	28.77	28.57	28.50	28.45	30.14
		0.856	0.795	0.756	0.734	0.717	0.899
		0.252	0.277	0.286	0.290	0.291	0.221
		10.79	10.57	10.71	10.68	10.67	10.72
		0.736	0.791	1.169	1.534	2.047	0.678

In addition, in order to comprehensively evaluate the impact of different iteration stop conditions on the performance of reconstructed images, this paper combined the above three indicators to form a composite index PSB (PSB = PSNR × SSIM/BEI) for evaluating the quality of reconstructed images. The relationship between PSB and Noise-std of the reconstructed image under different iterations was researched in this article, so as to explore the relationship between PSB and TSR. Figure 7 shows the corresponding relationship between the PSB, Noise-std, and TSR under the above six different iteration stop conditions of Lena. It can be seen from Figure 7a that compared with the other five sparsity-based ($\varsigma$) reconstruction algorithms, the $v_{opt}$-based error analysis reconstruction algorithm generally has relatively good performance under different noise backgrounds. Similarly, Figure 7b shows that the $v_{opt}$-based error analysis reconstruction algorithm has advantages over other algorithms at different total sampling rates.

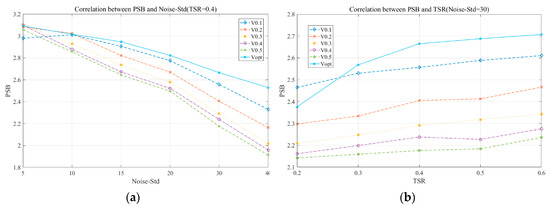
Figure 7. The correlation between the PSB, Noise-std, and TSR under the six different iteration stop conditions of Lena: (a) PSB changes with Noise-std, (b) PSB changes with TSR.

Furthermore, the differential threshold (γ)-based reconstruction algorithm and the $v_{opt}$-based error analysis reconstruction algorithm were compared in this article. Two standard test images and two real-nowadays images are adopted for the comparative experiment at the condition of Noise-std = 20 and TSR = 0.5. Experimental results show that the $v_{opt}$-based error analysis reconstruction algorithm has a significant advantage over the γ-based reconstruction algorithm in both PSNR and PSGBC (another composite index: PSGBC = PSNR × SSIM/GMSD/BEI/CT), which can be seen from Table 4, although there is a slight loss in BEI. Figure 8 shows the reconstruction images of these four images with differential threshold (γ) and error analysis ($v_{opt}$) as the iterative stop condition.

Table 4. The performance indexes of test images under different iterative stop condition.

	Images	Lena	Baboon	Flowers	Oriental Gate	Index
Stop Condition
γ = 300		32.17	29.84	31.40	33.05	PSNR
		0.9562	0.8703	0.9744	0.9698	SSIM
		0.1661	0.2095	0.1812	0.1636	GMSD
		10.16	10.72	9.866	8.845	BEI
		0.8310	0.855 0	0.844 0	1.050	CT
		21.93	13.52	20.28	21.09	PSGBC
γ =1		31.99	29.75	31.50	32.66	PSNR
		0.9574	0.8731	0.9768	0.9693	SSIM
		0.1638	0.1738	0.1571	0.1459	GMSD
		10.01	10.58	9.583	8.745	BEI
		2.905	2.704	2.823	3.578	CT
		6.429	5.224	7.240	6.934	PSGBC
$v_{opt}$		32.75	30.03	31.78	33.15	PSNR
		0.9603	0.8729	0.9771	0.9637	SSIM
		0.1471	0.1956	0.1538	0.1471	GMSD
		9.898	10.68	9.693	9.025	BEI
		0.7630	0.8900	0.8500	0.8740	CT
		28.31	14.10	24.50	27.53	PSGBC

Figure 8. Iterative reconstruction images based on $\gamma$ and $v_{opt}$ at the condition of Noise-std = 20 and TSR = 0.5.

5.2.2. Impact of Noise-Std and TSR on $v_{opt}$

Since $v_{opt}$ is important to the proposed algorithm in this paper, it is necessary to analyze its influencing factors. According to Equation (44), $v_{opt}$ is mainly determined by the measurement dimension of the signal and the added noise intensity under the BIC condition. In this section, the test image Lena is divided into 256 sub-images, and the relationship between the optimal iterative recovery stop condition ($v_{opt}^i$) of each sub-image, the TSR and the Noise-std is analyzed, and the experimental results are recorded in Figure 9. It can be seen from Figure 9a that the correlation between $v_{opt}$ and TSR is small, but it can be seen from Figure 9b that $v_{opt}$ has a strong correlation with Noise-std, that is, the larger the Noise-std, the smaller the $v_{opt}$.

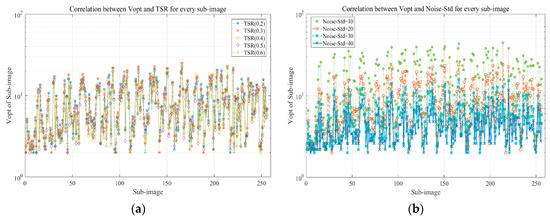
Figure 9. Correlation between $v_{opt}$, TSR, and Noise-std of sub-images: (a) Noise-std = 20, (b) TSR = 0.4.

5.3. Application and Comparison Experiment of FE-ABCS Algorithm in Image Compression

5.3.1. Application of FE-ABCS Algorithm in Image Compression

Although the FE-ABCS algorithm belongs to the CS theory which is mainly used for reconstruction of sparse images at low sampling rates, the algorithm can also be used for image compression after modification. The purpose of conventional image compression algorithms (such as JPEG, JPEG2000, TIFF, and PNG) is to reduce the amount of data and maintain a certain image quality through quantization and encoding. Therefore, the quantization and encoding module are added to the FE-ABCS in Figure 2b to form a new algorithm for image compression, which is shown in Figure 10 and named FE-ABCS-QC.

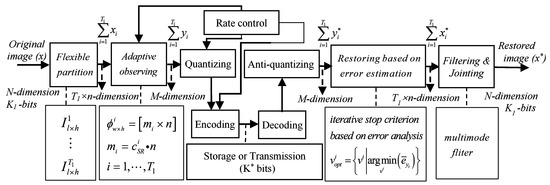
Figure 10. The workflow of the FE-ABCS-QC algorithm.

In order to demonstrate the difference between the proposed algorithm and the traditional image compression, without loss of generality, the JPEG2000 algorithm is selected as the comparison algorithm and is shown in Figure 11. Comparing Figure 10 and Figure 11, it is found that the modules of FDWT and IDWT in the JPEG2000 algorithm are replaced by the observing module and the restoring module in the proposal respectively, and the dimensions of the input and output signals are both different in the observing and restoring module (M < T₁ × n = N), that is different from the modules of FDWT and IDWT in which dimensions of the input and output signals are the same (both T₁ × n = N). These differences make the proposed algorithm have a larger compression ratio (CR) and smaller bits per pixel (bpp) than JPEG2000 under the same quantization and encoding conditions.

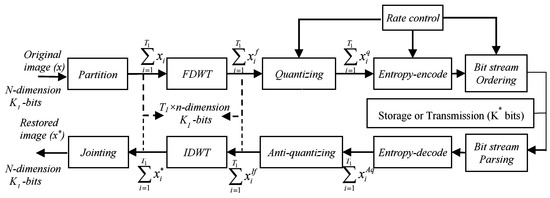
Figure 11. The workflow of the JPEG2000 algorithm.

5.3.2. Comparison Experiment between the Proposed Algorithm and the JPEG2000 Algorithm

In general, the evaluation of image compression algorithms is performed by rate-distortion performance. For the comparing of the FE-ABCS-QC and JPEG2000 algorithms, the indicators of PSNR, SSIM, and GMSD are adopted in this section. In addition, the definition of Rate (bpp) in the above two algorithms is as follows:

$$Rate=\frac{K^{\ast }}{N}$$

(56)

where, K* is the number of bits in the code stream after encoding, and N is the number of pixels in the original image.

In order to compare the performance of the above two algorithms, multiple standard images are tested, and Table 5 records the complete experimental data for the two algorithms at various rates when using Lena and Monarch as test images. At the same time, the relationship between PSNR (used as the main distortion evaluation index) and the Rate of the two test images is illustrated in Figure 12. Based on the objective data of Table 5 and Figure 12, it can be seen that, compared with the JPEG2000 algorithm, the advantage of the FE-ABCS-QC algorithm becomes stronger with the increase of the rate, that is, at the small rate, the JPEG2000 algorithm is superior to the FE-ABCS-QC algorithm, while at medium and slightly larger rates, the JPEG2000 algorithm is not as good as the FE-ABCS-QC algorithm.

Table 5. The comparison results of different test-images under the various conditions (bits per pixel (bpp)) based on the JPEG2000 algorithm and the FE-ABCS-QC algorithm.

	Method	JPEG2000 (PSNR/SSIM/GMSD)	FE-ABCS-QC (PSNR/SSIM/GMSD)	∆P/∆S/∆G
Test Image
Lena	bpp = 0.0625	31.64/0.9387/0.1842	30.58/0.7341/0.2478	−1.06/−0.2046/0.0636
	bpp = 0.125	33.38/0.9697/0.1399	32.79/0.9413/0.1702	−0.59/−0.0284/0.0303
	bpp = 0.2	34.59/0.9807/0.1161	34.20/0.9710/0.1339	−0.39/−0.0097/0.0178
	bpp = 0.25	35.25/0.9850/0.0996	37.80/0.9932/0.0612	2.55/0.0082/−0.0384
	bpp = 0.3	35.73/0.9875/0.0917	38.28/0.9941/0.0554	2.55/0.0066/−0.0363
Monarch	bpp = 0.0625	30.56/0.8184/0.2335	27.52/0.3615/0.2726	−3.04/−0.4569/0.0391
	bpp = 0.125	31.31/0.9074/0.1881	29.12/0.6388/0.2568	−2.19/−0.2686/0.0687
	bpp = 0.2	32.49/0.9466/0.1554	32.91/0.9473/0.1507	0.42/0.0007/−0.0047
	bpp = 0.25	32.81/0.9572/0.1476	35.77/0.9886/0.0682	2.96/0.0314/−0.0794
	bpp = 0.3	33.40/0.9679/0.1305	36.17/0.9896/0.0664	2.77/0.0217/−0.0641

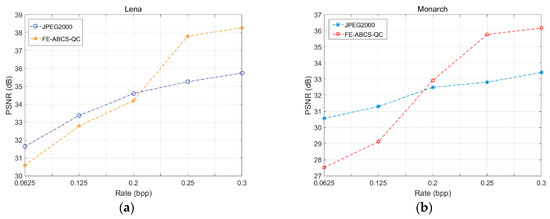
Figure 12. Rate-distortion performance for JPEG2000 and FE-ABCS-QC: (a) Lena, (b) Monarch.

Furthermore, the experiment results are recorded in the form of images in addition to the objective data comparison. Figure 13 shows the two algorithms’ comparison of the compressed image restoration effects in the case of bpp = 0.25 when using Bikes as the test image. Comparing (b) and (c) of Figure 13, the image generated by the FE-ABCS-QC algorithm is slightly better than the one of the JPEG2000 algorithm, either from the perception of objective data or subjective sense.

Figure 13. The two algorithms’ comparison of test image Bikes at the condition of bpp = 0.25: (a) original image, (b) JPEG2000 image (PSNR = 29.80, SSIM = 0.9069, GMSD = 0.1964), (c) image by the FE-ABCS-QC algorithm (PSNR = 30.50, SSIM = 0.9366, GMSD = 0.1574).

Finally, the following conclusions could be gained by observing experimental data and theoretical analysis.

• Small Rate (bpp): the reason why the performance of the FE-ABCS-QC algorithm is worse than the JPEG2000 algorithm at this condition is that the small value of M which changes with Rate causes the observing process to fail to cover the overall information of the image.
• Medium or slightly larger Rate (bpp): the explanation for the phenomenon that the performance of the FE-ABCS-QC algorithm is better than the JPEG2000 algorithm in this situation is that the appropriate M can ensure the complete acquisition of image information and can also provide a certain image compression ratio to generate a better basis for quantization and encoding.
• Large Rate (bpp): this case of the FE-ABCS-QC algorithm is not considered because the algorithm belongs to the CS algorithm and requires M << N itself.

6. Conclusions

Based on the traditional block-compression sensing theory model, an improved algorithm (FE-ABCS) was proposed in this paper, and its overall workflow and key points were specified. Compared with the traditional BCS algorithm, firstly, a flexible partition was adopted in order to improve the rationality of partitioning in the proposed algorithm, secondly the synthetic feature was used to provide a more reasonable adaptive sampling basis for each sub-image block, and finally error analysis was added in the iterative reconstruction process to achieve minimum error between the reconstructed signal and the original signal in the noisy background. The experimental results show that the proposed algorithm can improve the image quality in both noiseless and noisy backgrounds, especially in the improvement of a reconstructed image’s composite index under a noisy background, and will be beneficial to the practical application of the BCS algorithm, and the application of the FE-ABCS algorithm in image compression.