Abstract
In this article, a computationally-efficient approach is presented for Bit Error Rate (BER) calculations in multi-user Multiple Input Multiple Output (MIMO) frequency selective fading environments, operating in spatial multiplexing transmission mode. To this end, theoretical expressions for the equivalent Signal to Interference plus Noise Ratio (SINR) per active user and transmission mode, as well as mean BER, are derived. The key idea is that all parameters related to BER calculations can be expressed as sums of identically distributed random variables (RVs). Hence, computational burden can be reduced, since summation formulas take into account the parameters of a standalone RV along with the correlation of an arbitrary pair of RVs. As results indicate, the proposed approach can accurately estimate mean BER in multiuser MIMO orientations with increased reception diversity order, for arbitrary number of transmit/receive antennas, a modulation scheme, and a number of resolvable multi-path components.
1. Introduction
A challenging task in the design and implementation of next generation broadband wireless networks is data rate maximization for all active users, under limited bandwidth constraints. To this end, several approaches in literature have been proposed, such as the deployment of multiple input multiple output (MIMO) architecture at both ends of the wireless orientation [1]. In this case, two operational modes can be supported: diversity combining (DC), where the same information is sent and received from all antennas of the MIMO orientation, as well as spatial multiplexing (SM), where individual data streams are sent and received from the various modes of the MIMO link [2]. In DC, the mean bit error rate (BER) is improved, as outage probability is minimized, since information is sent and received from all the antennas of the MIMO configuration. In SM, transmission rates can be maximized, at the cost of increased reception complexity, since the diversity order of the system is reduced.
However, in realistic wireless orientations, actual performance improvement from the deployment of MIMO architecture may be significantly different from the theoretically expected one, due to multiple access interference (MAI) [3]. In this context, various studies in recent literature have focused on estimating performance metrics in MIMO orientations. In Reference [3], the authors have derived the outage probability and capacity of cellular MIMO systems with SM and linear receivers, using the code division multiple access (CDMA) physical layer protocol. As results indicate, capacity can be severely affected in the presence of multiple interferences.
In Reference [4], a CDMA network is taken into account as in Reference [3], where BER is evaluated in a Nakagami-m fading channel, considering multiple antennas at the receiver side. In Reference [5], performance metrics are presented comparing the outage probability and transmission rate of DC and SM, including a use case with the Orthogonal Frequency Division Multiplexing (OFDM) protocol. According to the presented results, the increase in the available degrees of freedom offered by SM schemes can be beneficial for the overall performance of the wireless orientation, provided that channel coding and other key features are adequately modelled. In Reference [6], an interference scenario of a heterogeneous network has been considered, where SM interferes with spatial modulation. As results indicate, in strong SM interference scenarios, significant performance degradation may occur. In Reference [7], BER is derived for massive MIMO systems, using the orthogonal frequency division multiplexing (OFDM) physical layer protocol. In this context, a reduced complexity approximation is introduced, using Newton’s interpolation with different polynomial orders for log-likelihood ratio calculations. In Reference [8], the probability of error for a space-time spreading scheme in the CDMA system operating in Nakagami-m fast-fading channels using a decorrelator detector and BPSK modulation has been derived, for MIMO systems with two transmit and L receive antennas. In Reference [9], BER of MIMO-OFDM due to the frequency offset and channel estimation errors has been analyzed. The BER expressions for no combining, equal gain combining (EGC) and maximal ratio combining (MRC) were derived. Intercarrier interference (ICI) and interantenna interference (IAI) due to the residual frequency offsets were analyzed, and the average signal-to-interference-and-noise ratio (SINR) was derived. In Reference [10], BER calculations for downlink multi-user MIMO systems with imperfect channel state information (CSI) are presented, considering MIMO-OFDMA and space time block coding (STBC) scenarios. Performance evaluation of massive MIMO (M-MIMO) systems (e.g., codebook design [11], implementation issues [12], etc.) is a recent challenging research field for next generation networks [13,14]. In this context, in Reference [15], the performance evaluation of BER for an M-MIMO system with M-ary PSK (phase shift keying) scheme over a three-dimensional (3-D) correlated fading model is presented, which involves correlation phenomena between angles of arrival and departure. In Reference [16], the effects of spatial correlation are highlighted in BER calculations in M-MIMO systems.
In all the previously mentioned studies, however, either a limited number of antennas/active users or non-frequency selective fading environments were considered. In this article, a computationally efficient BER calculation method is proposed and evaluated, for various MIMO orientations. To this end, BER can be calculated for a varying number of transmit/receive antennas, as well as resolvable multi-path components. Therefore, the maximum number of active users for a specific quality of service (equivalently express via the maximum BER) can be directly calculated. Although the CDMA physical layer protocol has been considered, the same formula can be applied in OFDMA networks as well.
The rest of this article is organized as follows. The MIMO SM transceiver model is described in Section 2, while BER calculations along with the proposed approach for SINR estimation are presented in Section 3. Results are presented and discussed in Section 4, while concluding remarks along with proposals for future work are described in Section 5.
2. MIMO Spatial Multiplexing Transceiver Model
Considering the downlink of an arbitrary MIMO-CDMA orientation with Nt antennas at the transmitter and Nr antennas at the receiver (Nt × Nr) then the transmitted signal for the kth (1 ≤ k ≤ K) user will be given by the equation below [17].
By defining dim = min (Nt, Nr) as the dimension of the MIMO channel, then xk(t) is the dim × 1 transmission signal matrix, Pk is a diagonal dim × dim matrix indicating the transmission power per data stream, bk(t) is the dim × 1 symbol matrix, ck is the Gold coding sequence [17], and tk is the dim × dim precoding matrix. The various data streams in the bk matrix will also be referred to as modes throughout the rest of this article. The received signal per active user can be described as a superposition of the L multipath components from all active users.
where τl/Hk,l are the delay and channel coefficient of the lth multipath component (1 ≤ l ≤ L) and nk is the corresponding Gaussian dim × 1 noise. The real and complex parts of each element of the channel matrix are assumed to be normally distributed with zero mean value and a variance equal to 0.5.
This signal is processed by a bank of L 2-D RAKE receivers, where the time of arrival of each multipath component along with the corresponding channel coefficient are estimated [18]. The output dim × 1 signal of the lth RAKE finger after correlation with the desired spreading sequence and MRC will be given by the Equation below.
where and the corresponding conjugate are the partial cross correlations [4], is the MRC multiplying matrix (AH is the conjugate transpose of matrix A), bk,0 is the symbol matrix at the current symbol period, and bk,−1 is the corresponding matrix at the previous symbol period. Assuming independent symbol matrices among the various users of the MIMO, CDMA network, the signal power of the desired user, the Intersymbol Interference (ISI), MAI power, and the total noise power will be given by Equations (4)–(7), respectively.
where No is the noise level and Re(x) is the real part of x.
All output expressions from Equations (4)–(7) are dim × dim matrices. In order to avoid interstream interference, appropriate transmission matrices should be selected, so as to provide diagonal expressions for each Ps,k matrix.
3. BER Calculation in Frequency Selective Fading MIMO Orientations
Each diagonal element of Ps,k can be equivalently written using the Equation below.
where
In Equation (9), Pk,d is the power allocated to the dth transmission mode. In the remainder of this article, the ith entry of matrix X will be denoted as Xi. In this context, in Equations (8) and (9), Hk,l,q,v represents the channel coefficient from the vth transmit antenna (1 ≤ v ≤ Nt) to the qth receiver antenna (1 ≤ q ≤ Mr) for the lth multipath and tk,v,d the (v,d) element of the precoding matrix tk.
The summation of a large number of random variables (RVs) is normally distributed, where mean and standard deviation values are given by the equation below.
according to the Central Limit Theorem (CLT) [19]. In Equation (10), represents the mean value of . At this point, it is reasonable to assume that all variables have similar probability density function (pdf) curves with the same mean (μd) and standard deviation (σd). Under this assumption, Equation (10) can be written by using the formula below.
where ρo,d is the correlation coefficient for an arbitrary pair . Moreover, MAI from the k′th user can be expressed by Equation (12) below.
where, as before the real and complex part of each, the MAIk′,d variable is normally distributed, according to CLT. The equivalent SINR for the kth user and dth transmission mode will be given by Equation (13) below (Im(x) is the imaginary part of x).
where ISI and noise power can be neglected for increased MAI scenarios. The denominator of SINRk,d is Chi-squared distributed [19], since it represents sum of squares of normal RVs. However, an alternate representation based on Gamma distribution will be considered, in order to include the special case of correlated sums.
Considering two RVs X and Y, then the cumulative distribution function (cdf) of the ratio Z = Y/X can be derived using the formula below [19] (SINRk,d ≥ 0).
The differentiation of FZ(z) leads to the pdf of Z.
Throughout the rest of this manuscript, all variables will be indexed by the corresponding transmission dimension (i.e., d). Therefore, if Yd denotes the square of γk,d, which is normally distributed with mean/standard deviation equal to /, respectively, and Xd is the denominator of Equation (13), then the following is true.
where Γ(x) is the Gamma function and αd/θd denote the shape/scale parameter of the Gamma distribution. If then . Hence, the equation below is found.
For large number of users and minimum correlation, it can be assumed that ad ≈ [ad], where [x] is the integer part of x. Starting from the known integral, Equation (18) is found, which is shown below.
and considering the Taylor series expansion for erf(x), then Equation (19) is uncovered.
Using the adth derivative of Equation (19) with respect to g, can be written as:
For the derivation of the Gamma pdf, the Maximum Likelihood Parameter Estimation (MLPE) method in Reference [20] is taken into account. Lastly, for the BPSK modulation equivalent, BER can be expressed as Reference [21] (Q function is considered in the integral).
Note that for the derivation of Equations (17) and (20), it has been assumed that Xd and Yd are uncorrelated. In the opposite case, the following transformation can be applied.
In Equation (22), is the correlation coefficient of Xd and Yd.
In the proposed approach, transmission matrices are iteratively calculated (Table 1), where n is the repetition index, Idim the dim × dim identity matrix, and tr(X) is the trace of matrix X. In this context, singular value decomposition takes place, where the left and right singular matrices (U,V) of the desired signal matrix as well as the corresponding eigenvalues matrix (Σ) are calculated. Note that, even for arbitrary number of interferers, the equivalent parameters of only two users need to be calculated: the desired one and the interferer. Hence, at the nth channel realization, mean and standard deviation (std) values of all related parameters are calculated considering the first n samples, until convergence of the transmission matrices is achieved. Afterward, total MAI power from K-1 users is calculated using squares of samples generated from a normal distribution, by taking into account calculated correlation.

Table 1.
Iterative BER Calculations.
4. Results
Results are presented in Figure 1, Figure 2, and Figure 3, for various MIMO orientations. Note that in all figure legends, the notation (Mt,Mr,L,PG) has been considered. In Figure 1, three MIMO cases are depicted (three group of curves from left to right): (4,4,6,32), (4,4,2,32) and (8,8,6,32). In this particular set of simulations, pdf curves of γk,d from MC simulations considering the first transmission mode are compared with the ones derived using curve fitting with normal distribution. As is evident from Figure 1, for large MIMO orientations, normal distribution can accurately model the desired user signal.
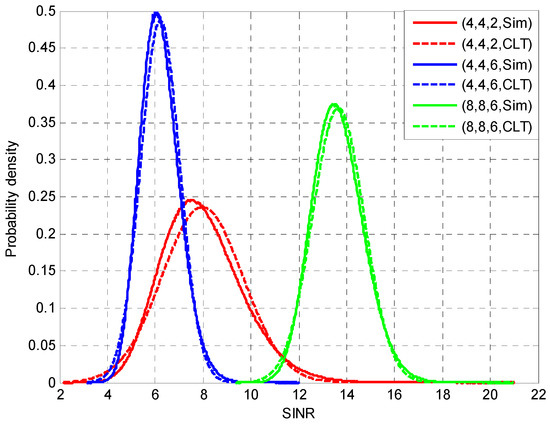
Figure 1.
CLT curve fitting for various MIMO orientations.
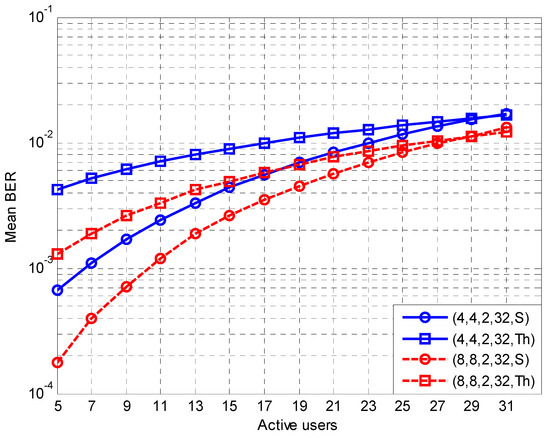
Figure 2.
BER values for reduced diversity order MIMO orientations.
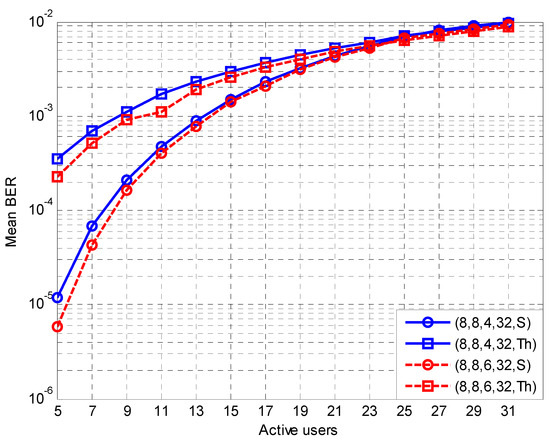
Figure 3.
BER values for increased diversity order MIMO orientations.
In Figure 2 and Figure 3, BER results from MC simulations are compared with the theoretical ones, as derived by Equation (21). For a maximum transmission rate, processing gain (PG) is set to 32 [7]. Hence, the data rate per user is 120 × Mt Kbps. Mean BER simulation values for the BPSK modulation were calculated for two MIMO cases (4 × 4, 8 × 8) (denoted as S), and compared to the theoretical ones (denoted as Th). Users may vary from 5 to 31 with a step of 2. Hence, total throughput varies from 2.4 Mbps to 14.88 Mbps in the 4 × 4 orientation and from 4.8 Mbps to 29.76 Mbps in the 8 × 8 orientation. In Figure 2, results are depicted considering reduced diversity order MIMO cases (i.e., L × Mr). In particular, in each group of curves, two resolvable multi-path components are taken into account. Hence, the diversity order can be either 8 (4 × 4 system) or 16 (8 × 8 system). As can be observed, significant variations may occur among the calculated BER values with the proposed approach and the ones derived from simulations. However, in both groups of curves, convergence is improved for an increased number of interfering users, since, in this case, CLT is more accurate for the MAI estimation.
In Figure 3, the number of resolvable multipath components in an 8 × 8 MIMO orientation can be either 4 or 6, which improves diversity order (i.e., 32 or 48). As can be observed, there is good agreement per group of curves for a reduced number of users compared to the previous case. In particular, for 25 users, simulation and theoretical BER values are 6.9 × 10−3/7.1 × 10−3 for four multipath components, respectively. Hence, the calculation error is 3%. For six multi-paths and 23 users, corresponding values are 5.3 × 10−3/5.4 × 10−3. Therefore, the calculation error is further reduced to 2%.
5. Conclusions
The performance of MIMO SM orientations was analyzed, in terms of achievable BERs. In this context, desired user signal and total interference were expressed in terms of summation of identically distributed random variables, which reduces computational complexity. As the results indicate, the calculation error is minimized for high diversity multi-user MIMO orientations. Knowledge of uncoded BER is particularly important for the design of next generation broadband wireless networks, since it allows capacity estimations when advanced encoding techniques are employed.
Future work includes, among others, the extension of the presented results in multicellular orientations, as well as BER calculations in Non Orthogonal Multiple Access (NOMA) networks.
Author Contributions
Conceptualization, P.K.G. and D.I.K.; methodology, P.K.G. and D.I.K.; software, P.K.G.; validation, P.K.G. and D.I.K.; formal analysis, P.K.G. and D.I.K.; writing—original draft preparation, P.K.G. and D.I.K.; writing—review and editing, P.K.G. and D.I.K.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Paulraj, A.J.; Gore, D.A.; Nabar, R.U.; Bölcskei, H. An overview of MIMO communications—A key to gigabit wireless. Proc. IEEE 2004, 92, 198–218. [Google Scholar] [CrossRef]
- Stuber, G.L.; Barry, J.R.; McLaughlin, S.W.; Li, Y.; Ingram, M.A.; Pratt, T.G. Broadband MlMO-OFDM wireless communications. Proc. IEEE 2004, 92, 271–294. [Google Scholar] [CrossRef]
- Choi, W.; Andrews, J. Spatial multiplexing in cellular MIMO-CDMA systems with linear receivers: Outage probability and capacity. IEEE Trans. Wirel. Commun. 2007, 6, 2612–2621. [Google Scholar] [CrossRef]
- Efthymoglou, G.P.; Piboongungon, T.; Aalo, V.A. Performance of DS-CDMA receivers with MRC in Nakagami-m fading channels with arbitrary fading parameters. IEEE Trans. Veh. Tech. 2006, 55, 104–114. [Google Scholar] [CrossRef]
- Lozano, A.; Jindal, N. Transmit diversity vs. spatial multiplexing in modern MIMO systems. IEEE Trans. Wirel. Commun. 2010, 9, 186–197. [Google Scholar] [CrossRef]
- Basnayaka, D.A.; Haas, H. MIMO interference channel between spatial multiplexing and spatial modulation. IEEE Trans. Commun. 2016, 6, 3369–3381. [Google Scholar] [CrossRef]
- Al-Askery, A.J.; Tsimenidis, C.C.; Boussakta, S.; Chambers, J.A. Performance analysis of coded massive MIMO-OFDM systems using effective matrix inversion. IEEE Trans. Commun. 2017, 65, 5244–5256. [Google Scholar] [CrossRef]
- Sacramento, A.L.; Hamouda, W. Multiuser decorrelator detectors in MIMO CDMA systems over Nakagami fading channels. IEEE Trans. Wirel. Commun. 2009, 8, 1944–1952. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, L.; You, M.; Lei, M. Bit error rate approximation of MIMO-OFDM systems with carrier frequency offset and channel estimation errors. EURASIP J. Wirel. Commun. Netw. 2010, 176083. [Google Scholar] [CrossRef][Green Version]
- Pattanayak, P.; Trivedi, V.K.; Chakraborty, S.; Kumar, P. BER performance of multi user scheduling for MIMO-STBC and MIMO-OFDM broadcast network with imperfect CSI. In Proceedings of the 4th International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 2–3 February 2017. [Google Scholar]
- Li, H.; Gao, Q.; Chen, R.; Tamrakar, R.; Sun, S.; Chen, W. Codebook design for massive MIMO systems in LTE. In Proceedings of the IEEE 83rd VTC, Nanjing, China, 15–18 May 2016. [Google Scholar]
- Ji, H.; Kim, Y.; Lee, J.; Onggosanusi, E.; Nam, Y.; Zhang, J.; Lee, B.; Shim, B. Overview of full-dimension MIMO in LTE-Advanced Pro. IEEE Commun. Mag. 2016, 55, 176–184. [Google Scholar] [CrossRef]
- Andrews, J.G.; Buzzi, S.; Choi, W.; Hanly, S.V.; Lozano, A.; Soong, A.C.K.; Zhang, C.J.Z. What Will 5G Be? IEEE J. Sel. Areas Commun. 2014, 32, 1065–1082. [Google Scholar] [CrossRef]
- Huo, Y.; Dong, X.; Xu, W.; Yuen, M. Cellular and WiFi Co-design for 5G User Equipment. In Proceedings of the IEEE 5G World Forum (5GWF), Silicon Valley, CA, USA, 30 September–2 October 2018; pp. 256–261. [Google Scholar]
- Chen, J.; Lee, B.H.; Wu, W.B. Performance evaluation of BER for an massive-MIMO with M-ary PSK scheme over three-dimension correlated channel. Comput. Electr. Eng. (Elsevier) 2018, 65, 196–206. [Google Scholar] [CrossRef]
- Eduru, S.; Rangaswamy, N. BER analysis of massive MIMO systems under correlated Rayleigh fading channel. In Proceedings of the 9th International Conference on Computing, Communication and Networking Technologies (ICCCNT), Bangalore, India, 10–12 July 2018. [Google Scholar]
- Holma, H.; Toskala, A. WCDMA for UMTS. Radio Access for Third Generation Mobile Communications; Wiley: Chichester, West Sussex, UK, 2004. [Google Scholar]
- Khalaj, B.H.; Paulraj, A.; Kailath, T. 2D RAKE receivers for CDMA cellular systems. In Proceedings of the IEEE Globecom, San Francisco, CA, USA, 28 November–2 December 1994. [Google Scholar]
- Papoulis, A.; Pillai, S. Probability, Random Variables and Stochastic Processes, 4th ed.; McGraw Hill: New York, NY, USA, 2002. [Google Scholar]
- Kazeminia, M.; Mehrjoo, M. A new method for maximum likelihood parameter estimation of Gamma-Gamma distribution. J. Lightwave Technol. 2013, 31, 1347–1353. [Google Scholar] [CrossRef]
- Goldsmith, A. Wireless Communications; Camb. University Press: Cambridge, UK, 2005. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).