Reduced Complexity BER Calculations in Large Scale Spatial Multiplexing Multi-User MIMO Orientations in Frequency Selective Fading Environments
Abstract
1. Introduction
2. MIMO Spatial Multiplexing Transceiver Model
3. BER Calculation in Frequency Selective Fading MIMO Orientations
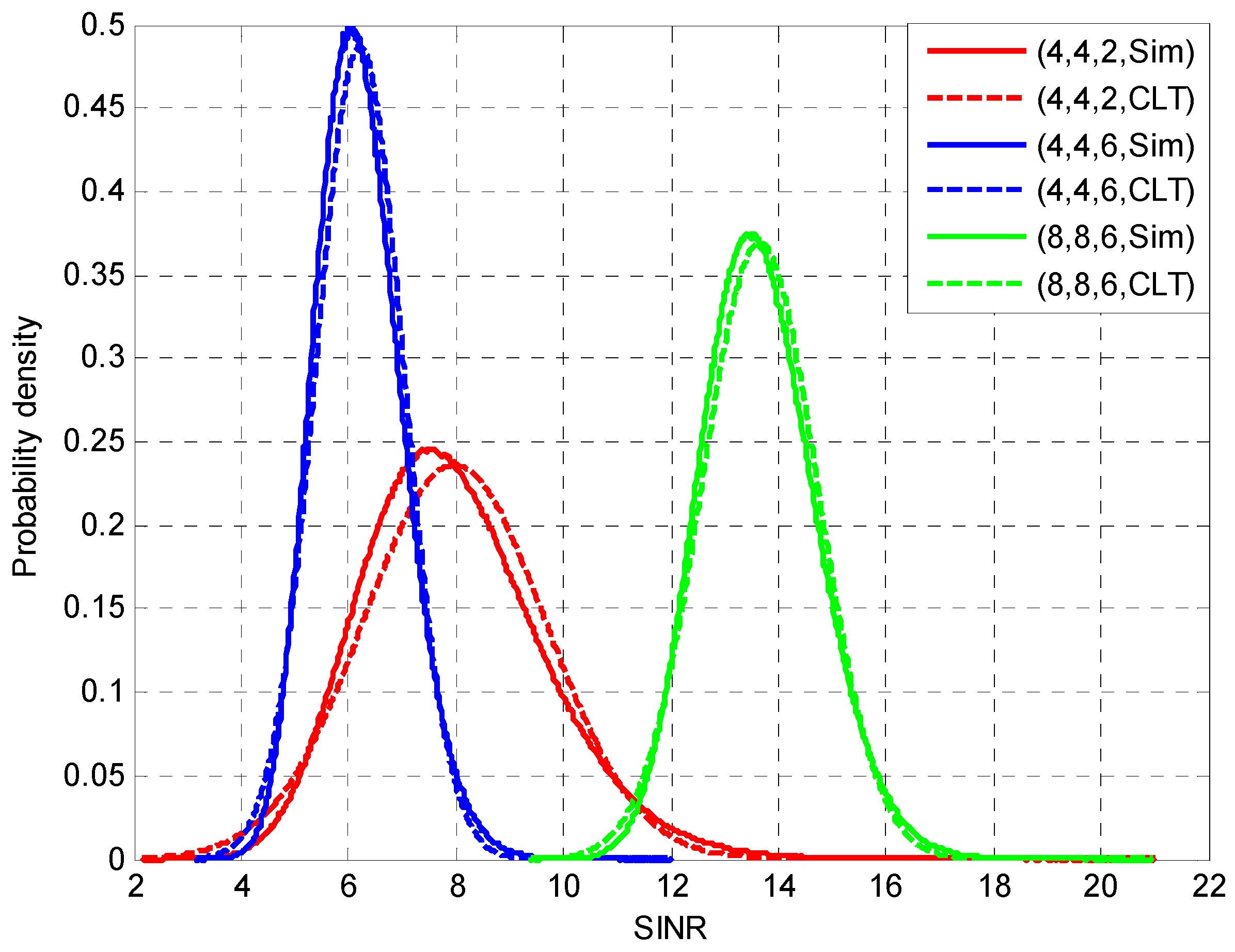
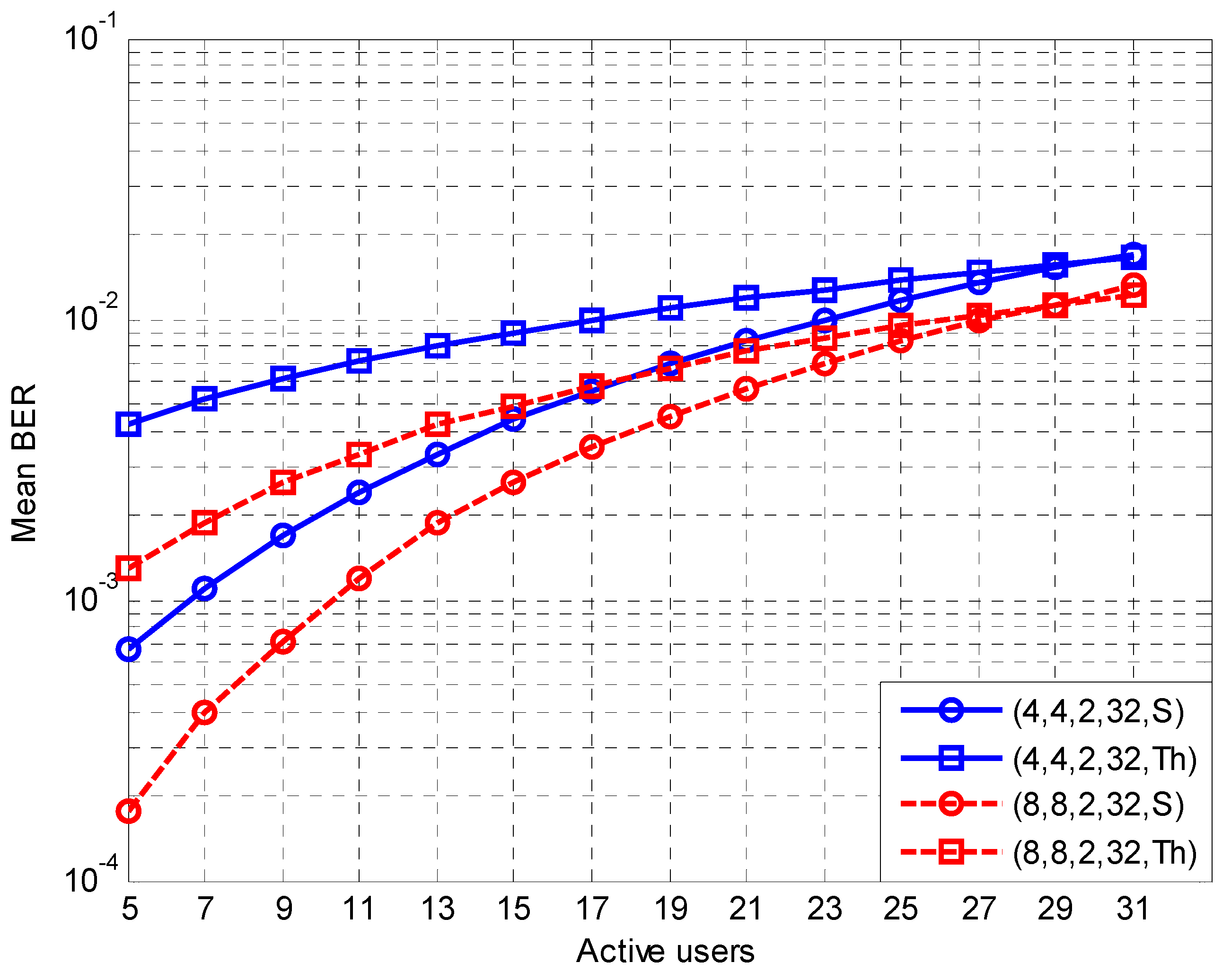
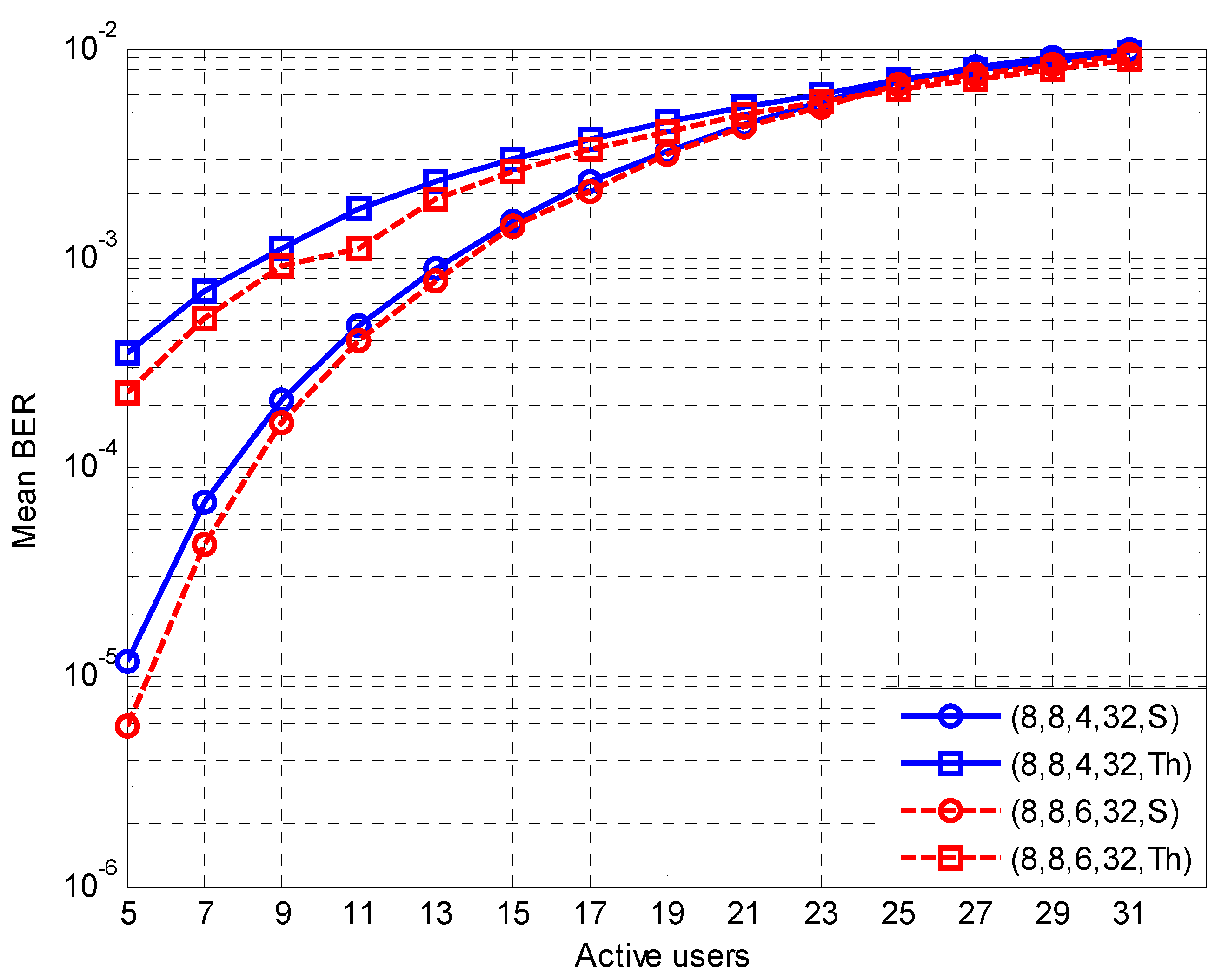
4. Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Paulraj, A.J.; Gore, D.A.; Nabar, R.U.; Bölcskei, H. An overview of MIMO communications—A key to gigabit wireless. Proc. IEEE 2004, 92, 198–218. [Google Scholar] [CrossRef]
- Stuber, G.L.; Barry, J.R.; McLaughlin, S.W.; Li, Y.; Ingram, M.A.; Pratt, T.G. Broadband MlMO-OFDM wireless communications. Proc. IEEE 2004, 92, 271–294. [Google Scholar] [CrossRef]
- Choi, W.; Andrews, J. Spatial multiplexing in cellular MIMO-CDMA systems with linear receivers: Outage probability and capacity. IEEE Trans. Wirel. Commun. 2007, 6, 2612–2621. [Google Scholar] [CrossRef]
- Efthymoglou, G.P.; Piboongungon, T.; Aalo, V.A. Performance of DS-CDMA receivers with MRC in Nakagami-m fading channels with arbitrary fading parameters. IEEE Trans. Veh. Tech. 2006, 55, 104–114. [Google Scholar] [CrossRef]
- Lozano, A.; Jindal, N. Transmit diversity vs. spatial multiplexing in modern MIMO systems. IEEE Trans. Wirel. Commun. 2010, 9, 186–197. [Google Scholar] [CrossRef]
- Basnayaka, D.A.; Haas, H. MIMO interference channel between spatial multiplexing and spatial modulation. IEEE Trans. Commun. 2016, 6, 3369–3381. [Google Scholar] [CrossRef]
- Al-Askery, A.J.; Tsimenidis, C.C.; Boussakta, S.; Chambers, J.A. Performance analysis of coded massive MIMO-OFDM systems using effective matrix inversion. IEEE Trans. Commun. 2017, 65, 5244–5256. [Google Scholar] [CrossRef]
- Sacramento, A.L.; Hamouda, W. Multiuser decorrelator detectors in MIMO CDMA systems over Nakagami fading channels. IEEE Trans. Wirel. Commun. 2009, 8, 1944–1952. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, L.; You, M.; Lei, M. Bit error rate approximation of MIMO-OFDM systems with carrier frequency offset and channel estimation errors. EURASIP J. Wirel. Commun. Netw. 2010, 176083. [Google Scholar] [CrossRef][Green Version]
- Pattanayak, P.; Trivedi, V.K.; Chakraborty, S.; Kumar, P. BER performance of multi user scheduling for MIMO-STBC and MIMO-OFDM broadcast network with imperfect CSI. In Proceedings of the 4th International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 2–3 February 2017. [Google Scholar]
- Li, H.; Gao, Q.; Chen, R.; Tamrakar, R.; Sun, S.; Chen, W. Codebook design for massive MIMO systems in LTE. In Proceedings of the IEEE 83rd VTC, Nanjing, China, 15–18 May 2016. [Google Scholar]
- Ji, H.; Kim, Y.; Lee, J.; Onggosanusi, E.; Nam, Y.; Zhang, J.; Lee, B.; Shim, B. Overview of full-dimension MIMO in LTE-Advanced Pro. IEEE Commun. Mag. 2016, 55, 176–184. [Google Scholar] [CrossRef]
- Andrews, J.G.; Buzzi, S.; Choi, W.; Hanly, S.V.; Lozano, A.; Soong, A.C.K.; Zhang, C.J.Z. What Will 5G Be? IEEE J. Sel. Areas Commun. 2014, 32, 1065–1082. [Google Scholar] [CrossRef]
- Huo, Y.; Dong, X.; Xu, W.; Yuen, M. Cellular and WiFi Co-design for 5G User Equipment. In Proceedings of the IEEE 5G World Forum (5GWF), Silicon Valley, CA, USA, 30 September–2 October 2018; pp. 256–261. [Google Scholar]
- Chen, J.; Lee, B.H.; Wu, W.B. Performance evaluation of BER for an massive-MIMO with M-ary PSK scheme over three-dimension correlated channel. Comput. Electr. Eng. (Elsevier) 2018, 65, 196–206. [Google Scholar] [CrossRef]
- Eduru, S.; Rangaswamy, N. BER analysis of massive MIMO systems under correlated Rayleigh fading channel. In Proceedings of the 9th International Conference on Computing, Communication and Networking Technologies (ICCCNT), Bangalore, India, 10–12 July 2018. [Google Scholar]
- Holma, H.; Toskala, A. WCDMA for UMTS. Radio Access for Third Generation Mobile Communications; Wiley: Chichester, West Sussex, UK, 2004. [Google Scholar]
- Khalaj, B.H.; Paulraj, A.; Kailath, T. 2D RAKE receivers for CDMA cellular systems. In Proceedings of the IEEE Globecom, San Francisco, CA, USA, 28 November–2 December 1994. [Google Scholar]
- Papoulis, A.; Pillai, S. Probability, Random Variables and Stochastic Processes, 4th ed.; McGraw Hill: New York, NY, USA, 2002. [Google Scholar]
- Kazeminia, M.; Mehrjoo, M. A new method for maximum likelihood parameter estimation of Gamma-Gamma distribution. J. Lightwave Technol. 2013, 31, 1347–1353. [Google Scholar] [CrossRef]
- Goldsmith, A. Wireless Communications; Camb. University Press: Cambridge, UK, 2005. [Google Scholar]
| Step 1: n ← 0. Set du ← 1, iu ← 2, U← duiu, ε = 10−3. For every kU: tk,n ←, Pk,n ← Step 2: n ← n + 1, and Step 3: Step 4: For arbitrary values of l, q, l′, q′ calculate: , For the real and complex part of calculate: , ← If go to Step 2 Step 5: Calculate αd, θd from the generated samples of Xd Calculate BER from Equation (21) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gkonis, P.K.; Kaklamani, D.I. Reduced Complexity BER Calculations in Large Scale Spatial Multiplexing Multi-User MIMO Orientations in Frequency Selective Fading Environments. Electronics 2019, 8, 727. https://doi.org/10.3390/electronics8070727
Gkonis PK, Kaklamani DI. Reduced Complexity BER Calculations in Large Scale Spatial Multiplexing Multi-User MIMO Orientations in Frequency Selective Fading Environments. Electronics. 2019; 8(7):727. https://doi.org/10.3390/electronics8070727
Chicago/Turabian StyleGkonis, Panagiotis K., and Dimitra I. Kaklamani. 2019. "Reduced Complexity BER Calculations in Large Scale Spatial Multiplexing Multi-User MIMO Orientations in Frequency Selective Fading Environments" Electronics 8, no. 7: 727. https://doi.org/10.3390/electronics8070727
APA StyleGkonis, P. K., & Kaklamani, D. I. (2019). Reduced Complexity BER Calculations in Large Scale Spatial Multiplexing Multi-User MIMO Orientations in Frequency Selective Fading Environments. Electronics, 8(7), 727. https://doi.org/10.3390/electronics8070727






