3D Multi-Beam and Null Synthesis by Phase-Only Control for 5G Antenna Arrays
Abstract
1. Introduction
2. Problem Formulation
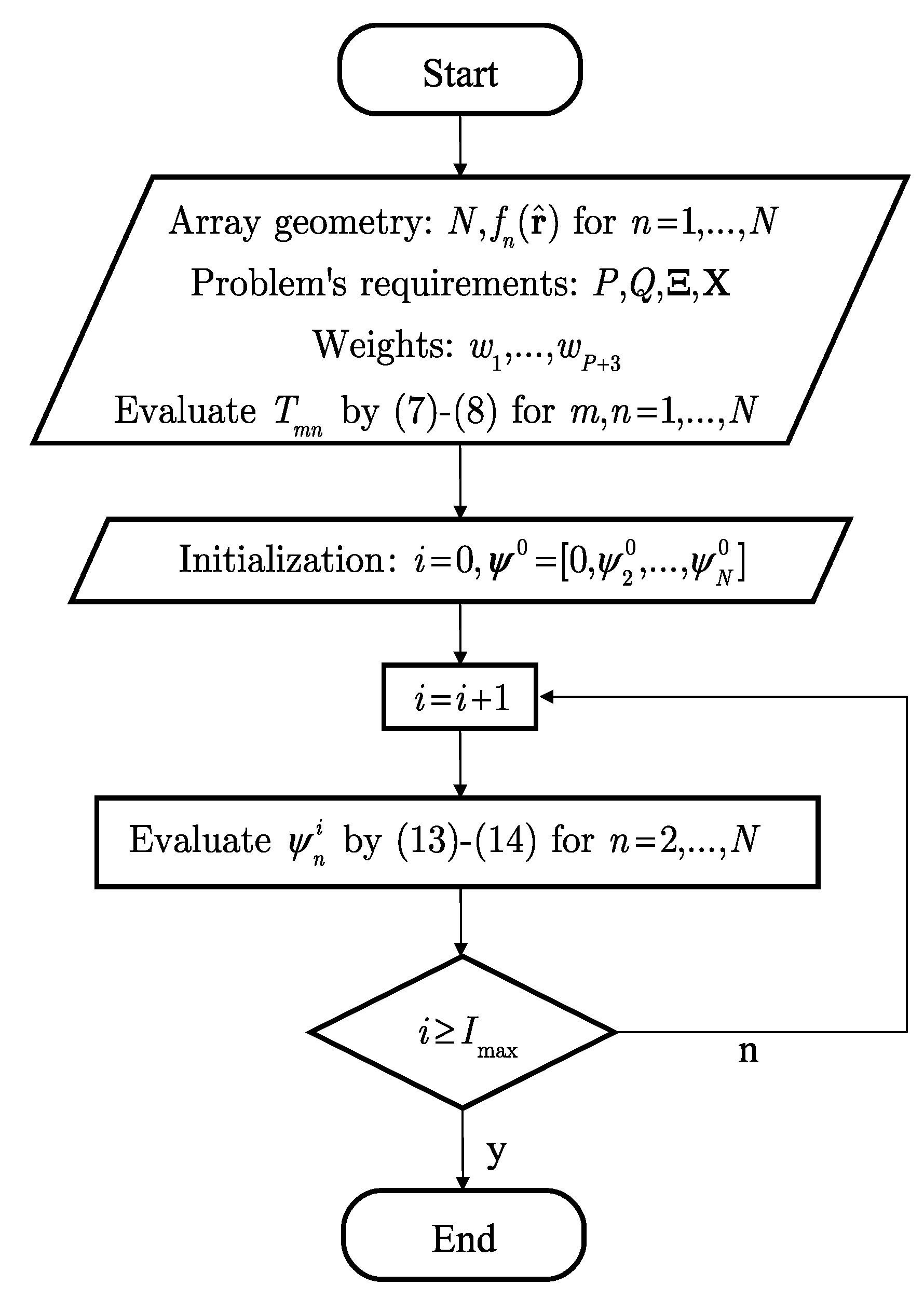
3. Algorithm
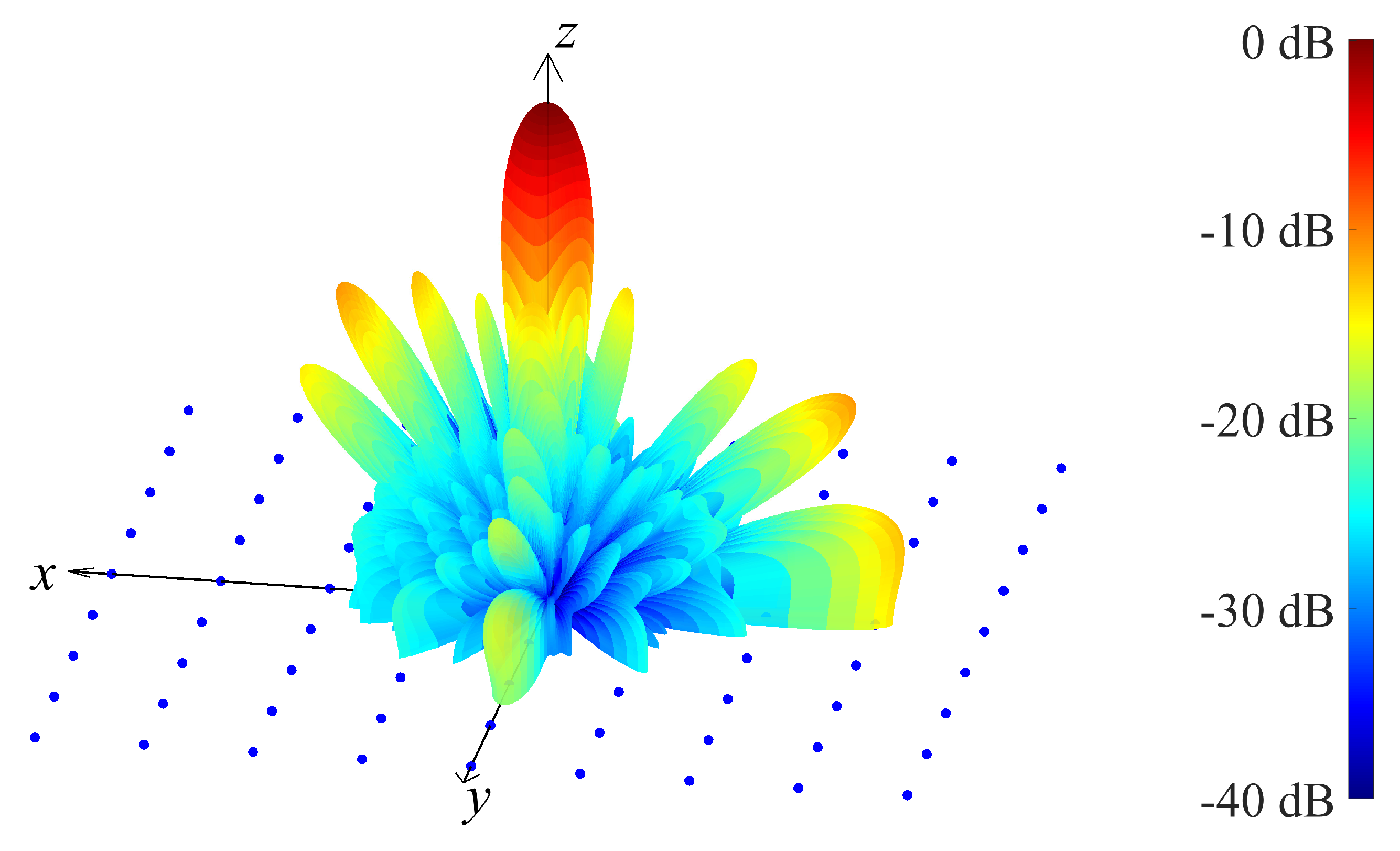
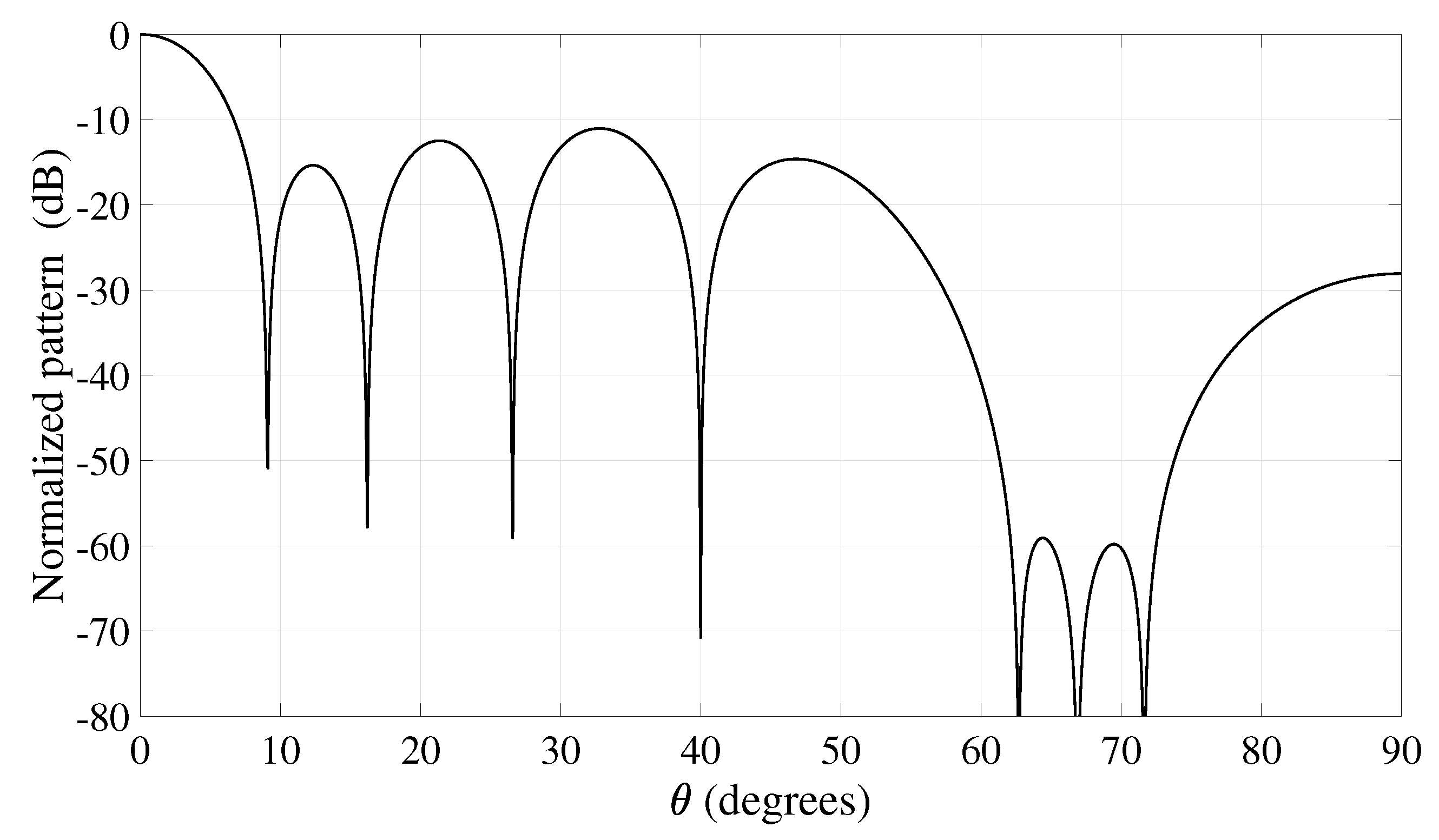
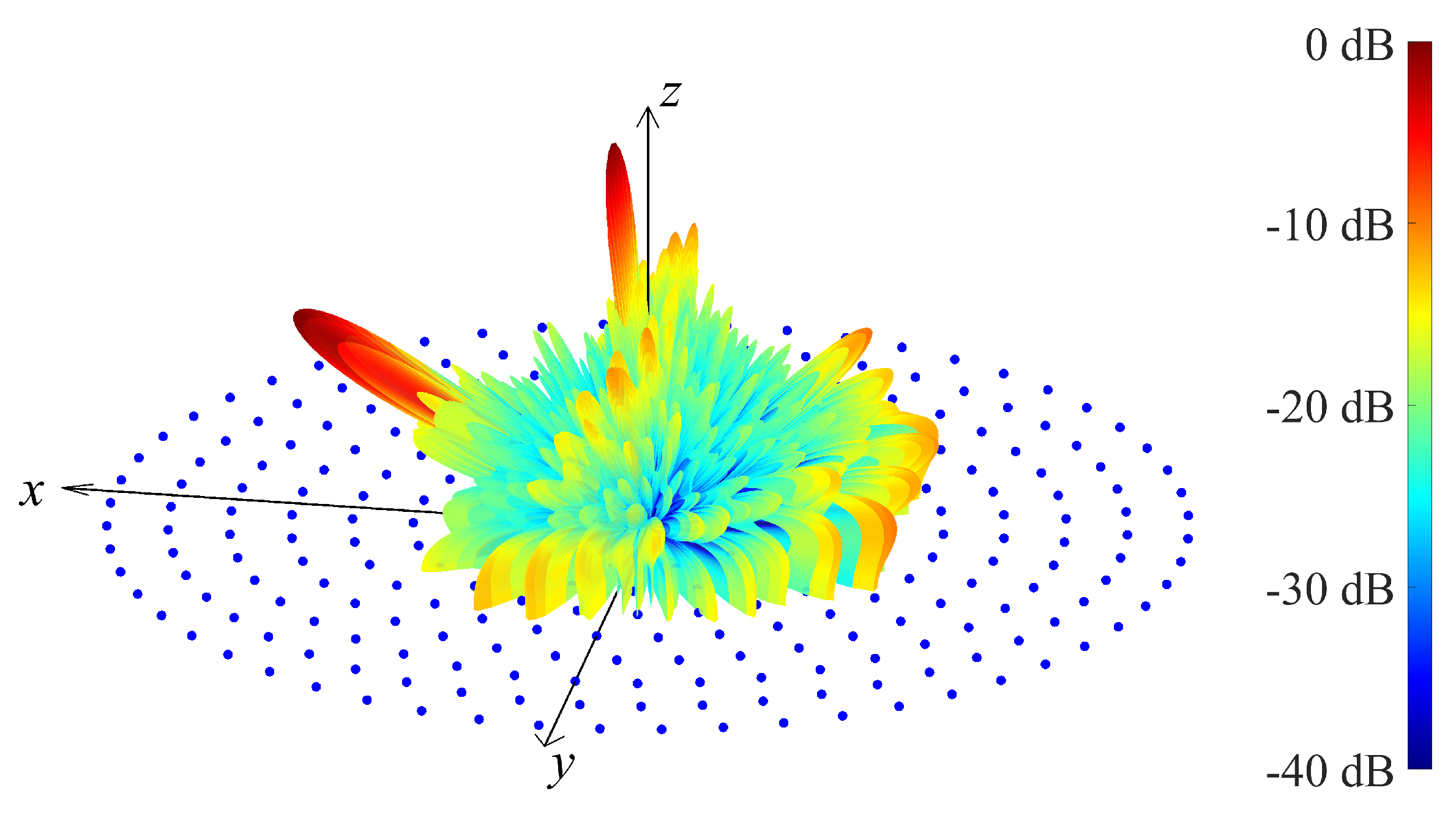
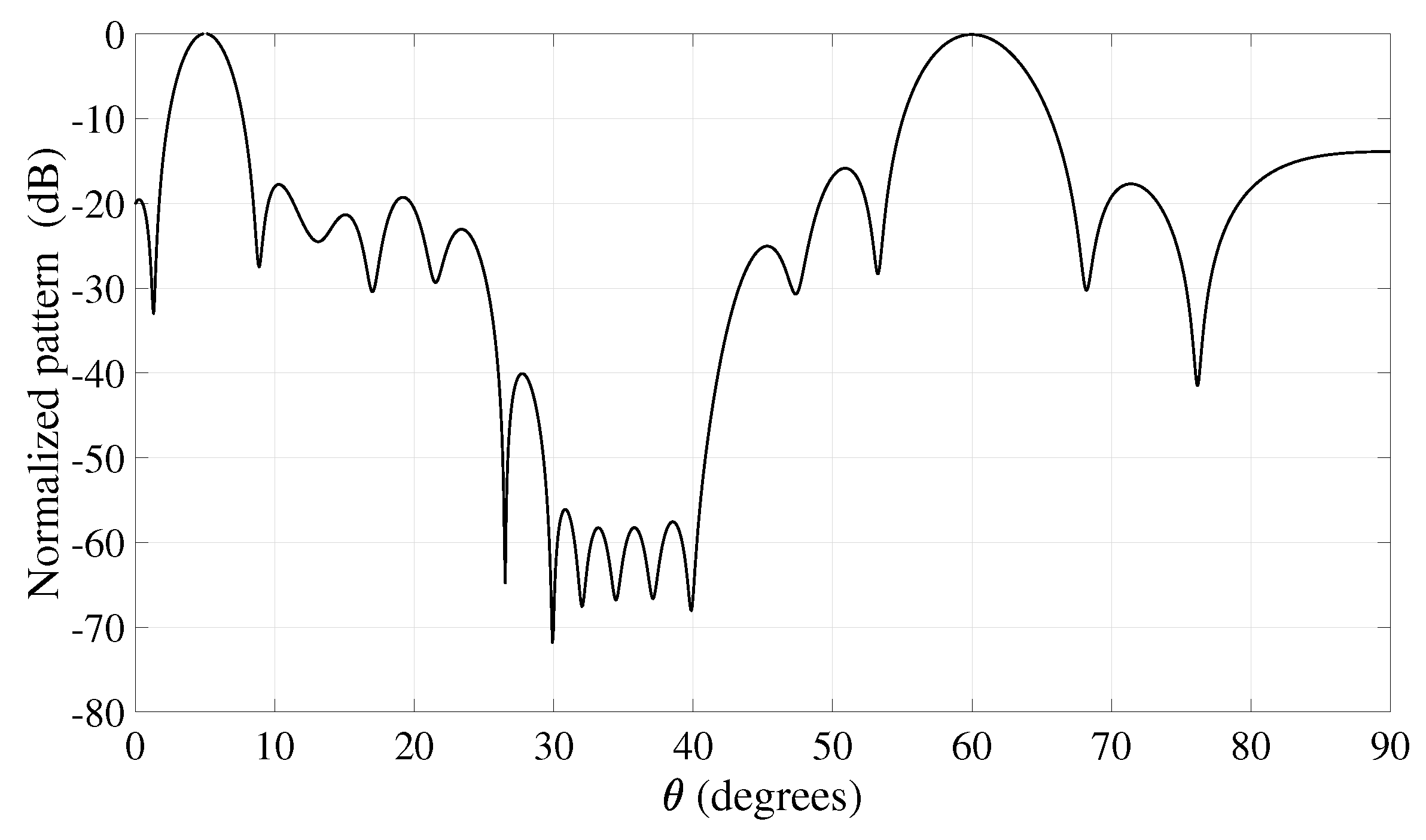
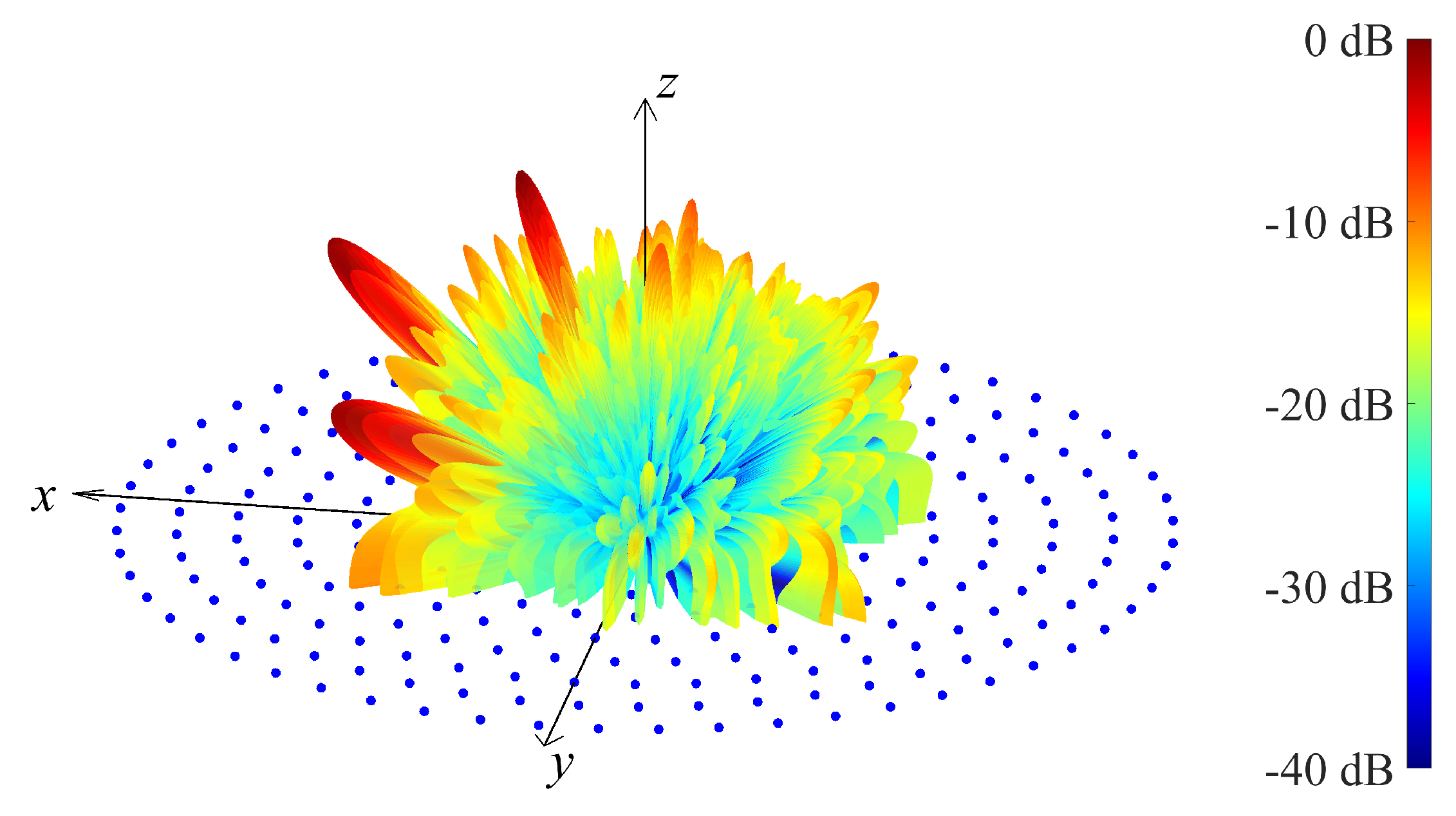
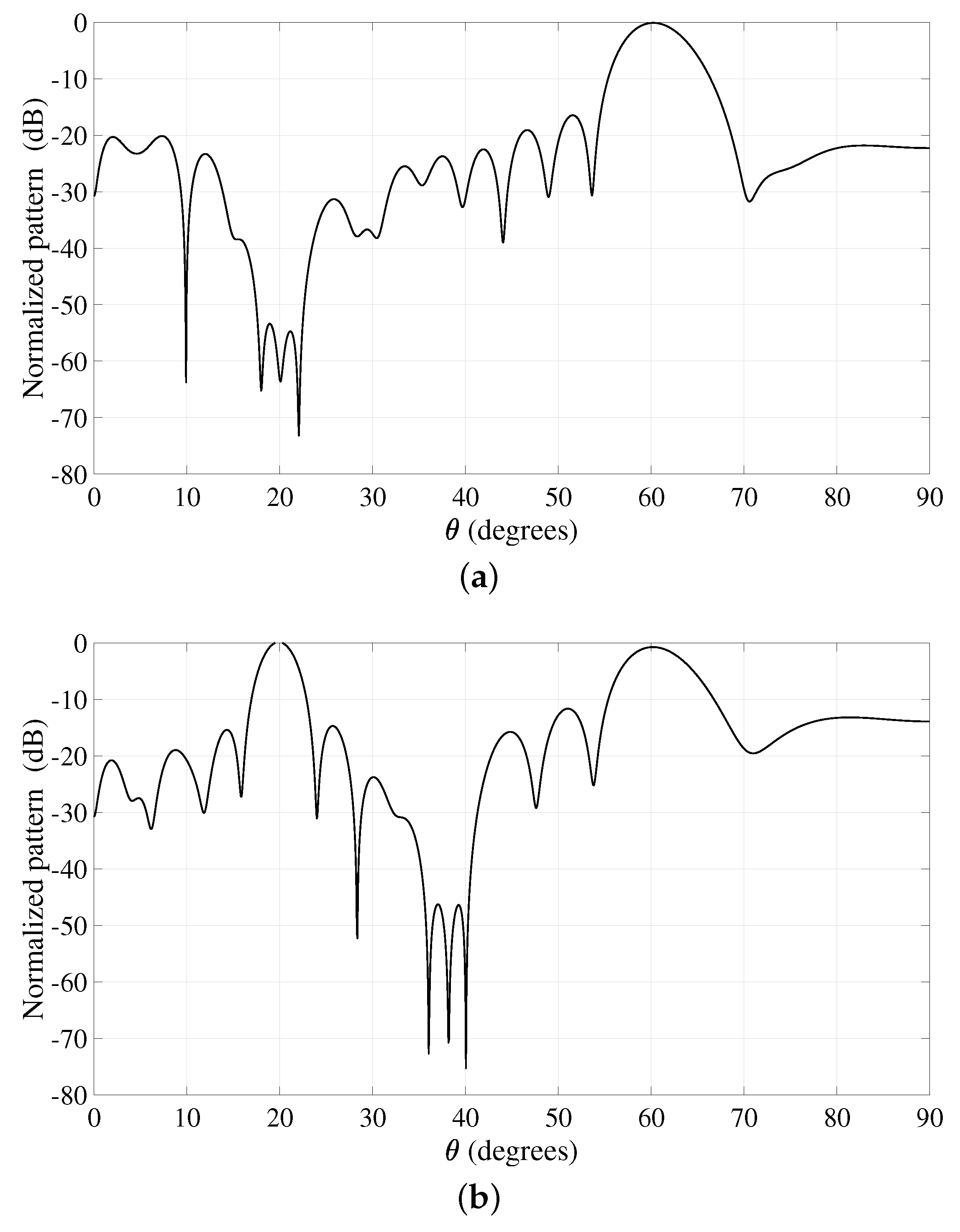
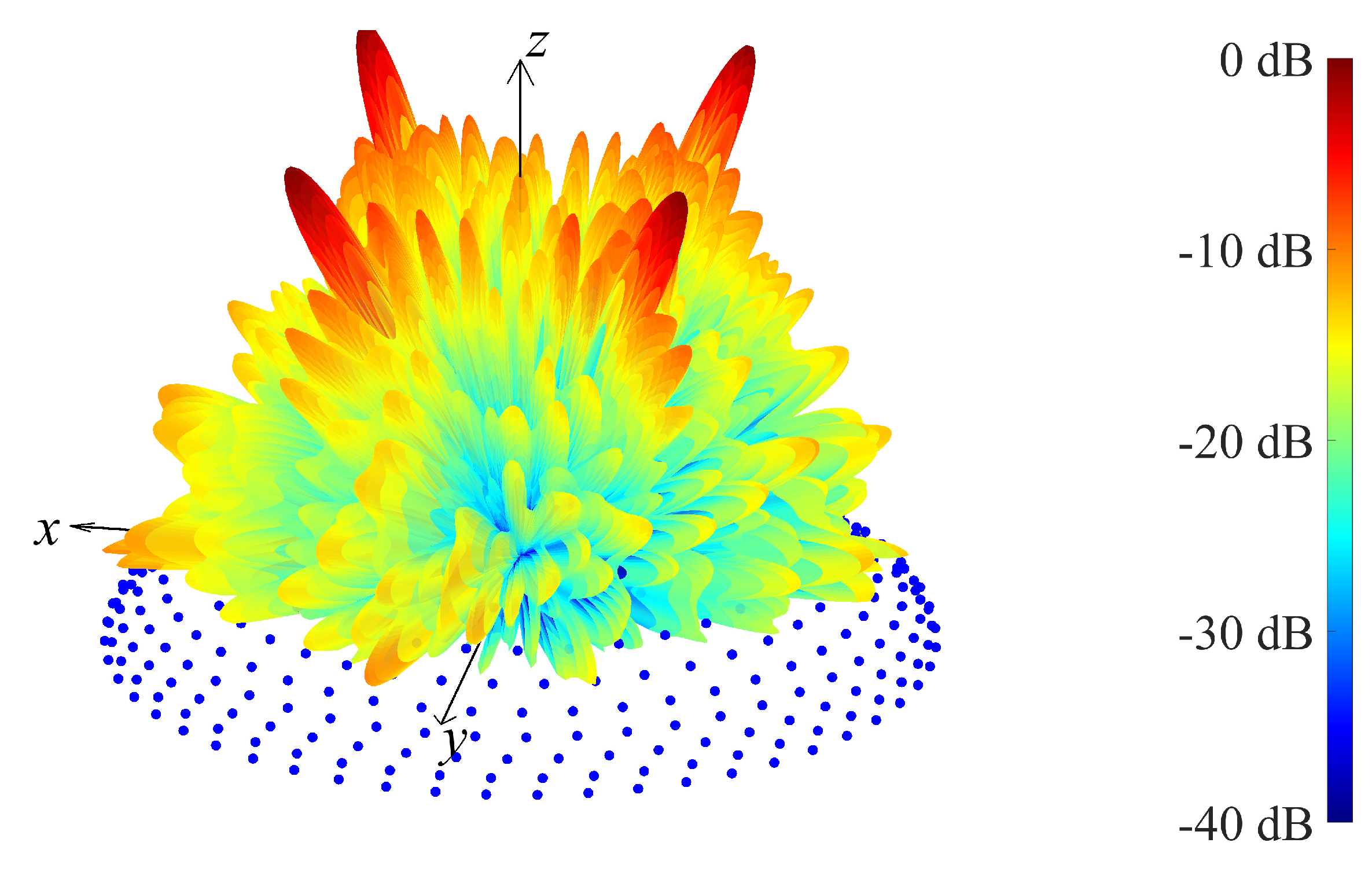
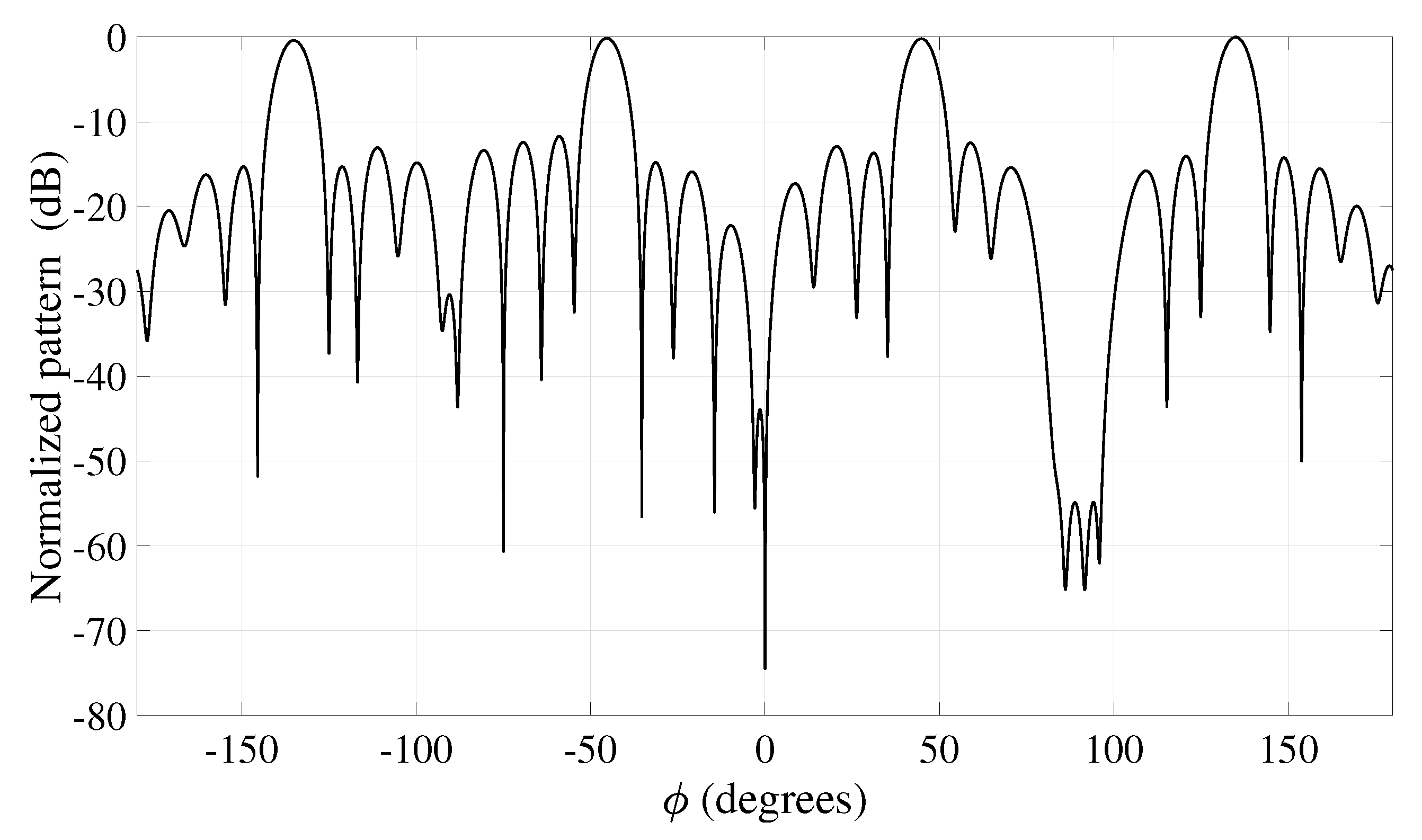
4. Results
Observations and Suggestions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Haupt, R.L.; Rahmat-Samii, Y. Antenna array developments: A perspective on the past, present and future. IEEE Antennas Propag. Mag. 2015, 57, 86–96. [Google Scholar] [CrossRef]
- Liu, M.; Ma, L.; Wang, N.; Zhang, Y.; Yang, Y.; Wang, H. Passive multiple target indoor localization based on joint interference cancellation in an RFID system. Electronics 2019, 8, 426. [Google Scholar] [CrossRef]
- Hunter, A.M.; Andrews, J.G.; Weber, S. Transmission capacity of ad hoc networks with spatial diversity. IEEE Trans. Wirel. Commun. 2008, 7, 5058–5071. [Google Scholar] [CrossRef]
- Hu, W.; Wen, G.; Inserra, D.; Huang, Y.; Li, J.; Chen, Z. A circularly polarized antenna array with gain enhancement for long-range UHF RFID systems. Electronics 2019, 8, 400. [Google Scholar] [CrossRef]
- Comisso, M.; Buttazzoni, G.; Vescovo, R. Reconfigurable antenna arrays with multiple requirements: A versatile 3D approach. Int. J. Antennas Propag. 2017, 2017, 1–9. [Google Scholar] [CrossRef]
- Godara, L.C. Application of antenna arrays to mobile communications, Part II: Beam forming and direction-of-arrival considerations. Proc. IEEE 1997, 85, 1193–1245. [Google Scholar]
- Zhang, J.; Zhang, S.; Lin, X.; Fan, Y.; Pedersen, G.F. 3D radiation pattern reconfigurable phased array for transmission angle sensing in 5G mobile communication. Sensors 2018, 18, 4204. [Google Scholar] [CrossRef]
- Babich, F.; Comisso, M. Including the angular domain in the analysis of finite multi-packet peer-to-peer networks with uniformly distributed sources. IEEE Trans. Commun. 2016, 64, 2494–2510. [Google Scholar] [CrossRef]
- Pinchera, D.; Migliore, M.D.; Schettino, F.; Panariello, G. Antenna arrays for line-of-sight massive MIMO: Half wavelength is not enough. Electronics 2017, 6, 57. [Google Scholar] [CrossRef]
- Parchin, N.O.; Alibakhshikenari, M.; Basherlou, H.J.; Abd-Alhameed, R.A.; Rodriguez, J.; Limiti, E. MM-wave phased array quasi-Yagi antenna for the upcoming 5G cellular communications. Appl. Sci. 2019, 9, 978. [Google Scholar] [CrossRef]
- Kummer, W.H. Basic array theory. Proc. IEEE 1992, 80, 127–140. [Google Scholar] [CrossRef]
- Fuchs, B.; Fuchs, J.J. Optimal polarization synthesis of arbitrary arrays with focused power pattern. IEEE Trans. Antennas Propag. 2011, 59, 4512–4519. [Google Scholar] [CrossRef]
- Choni, Y.I. Synthesis of an antenna according to a given amplitude radiation pattern. AIEE Radio Eng. Electron. Phys. 1971, 16, 770–778. [Google Scholar]
- Mautz, J.R.; Harrington, R.F. Computational methods for antenna pattern synthesis. IEEE Trans. Antennas Propag. 1975, 23, 507–512. [Google Scholar] [CrossRef]
- Rodríguez, J.A.; Landesa, L.; Rodíguez, J.L.; Obelleiro, F.; Ares, F.; García-Pino, A. Pattern synthesis of array antennas with arbitrary elements by simulated annealing and adaptive array theory. Microw. Opt. Tech. Lett. 1999, 20, 48–50. [Google Scholar] [CrossRef]
- Akdeniz, M.R.; Liu, Y.; Samimi, M.K.; Sun, S.; Rangan, S.; Rappaport, T.S.; Erkip, E. Millimeter wave channel modeling and cellular capacity evaluation. IEEE J. Sel. Areas Commun. 2014, 32, 1164–1179. [Google Scholar] [CrossRef]
- Vaskelainen, L.I. Constrained least-squares optimization in conformal array antenna synthesis. IEEE Trans. Antennas Propag. 2007, 55, 859–867. [Google Scholar] [CrossRef]
- Han, Y.; Wan, C. Scalable alternating projection and proximal splitting for array pattern synthesis. Int. J. Antennas Propag. 2015, 2015, 1–13. [Google Scholar] [CrossRef]
- Mao, C.; Gao, S.; Wang, Y. Broadband high-gain beam-scanning antenna array for millimeter-wave applications. IEEE Trans. Antennas Propag. 2017, 65, 4864–48687. [Google Scholar] [CrossRef]
- Gao, X.; Dai, L.; Han, S.; Chih-Lin, I.; Heath, R.W., Jr. Energy-efficient hybrid analog and digital precoding for mmWave MIMO systems with large antenna arrays. IEEE J. Sel. Areas Commun. 2016, 34, 998–1009. [Google Scholar] [CrossRef]
- Khzmalyan, A.D.; Kondrat’yev, A.S. Fast iterative methods for phase-only synthesis of antenna array pattern nulls. Electron. Lett. 1995, 31, 601–602. [Google Scholar] [CrossRef]
- van Luyen, T.; Giang, T.V.B. Interference suppression of ULA antennas by phase-only control using bat algorithm. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 3038–3042. [Google Scholar] [CrossRef]
- Buttazzoni, G.; Comisso, M.; Ruzzier, F.; Vescovo, R. Phase-only antenna array reconfigurability with Gaussian-shaped nulls for 5G applications. Int. J. Antennas Propag. 2019, 2019, 1–8. [Google Scholar] [CrossRef]
- Mouhamadou, M.; Vaudon, P.; Rammal, M. Smart antenna array patterns synthesis: Null steering and multi-user beamforming by phase control. Progr. Electromag. Res. PIER 2006, 60, 95–106. [Google Scholar] [CrossRef]
- Ghayoula, R.; Fadlallah, N.; Gharsallah, A.; Rammal, M. Phase-only adaptive nulling with neural networks for antenna array synthesis. IET Microw. Antennas Propag. 2007, 3, 154–163. [Google Scholar] [CrossRef]
- Comisso, M.; Vescovo, R. Multi-beam synthesis with null constraints by phase control for antenna arrays of arbitrary geometry. Electron. Lett. 2007, 43, 374–375. [Google Scholar] [CrossRef]
- Yu, B.; Yang, K.; Sim, C.; Yang, G. A novel 28 GHz beam steering array for 5G mobile device with metallic casing application. IEEE Trans. Antennas Propag. 2018, 66, 462–466. [Google Scholar] [CrossRef]
- Oliveri, G.; Gottardi, G.; Robol, F.; Polo, A.; Poli, L.; Salucci, M.; Chuan, M.; Massagrande, C.; Vinetti, P.; Mattivi, M.; et al. Co-design of unconventional array architectures and antenna elements for 5G base station. IEEE Trans. Antennas Propag. 2017, 65, 6752–6767. [Google Scholar] [CrossRef]
- Ismail, T.H.; Mismar, M.J.; Dawoud, M.M. Linear array pattern synthesis for wide band sector nulling. Progr. Electromag. Res. PIER 1999, 21, 91–101. [Google Scholar] [CrossRef]
- Güney, K.; Akdağli, A. Null steering of linear antenna arrays using a modified tabu search algorithm. Progr. Electromag. Res. PIER 2001, 33, 167–182. [Google Scholar]
- Andrews, J.G.; Buzzi, S.; Choi, W.; Hanly, S.V.; Lozano, A.; Soong, A.C.K.; Zhang, J.C. What will 5G be? IEEE J. Sel. Areas Commun. 2014, 32, 1065–1082. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Comisso, M.; Palese, G.; Babich, F.; Vatta, F.; Buttazzoni, G. 3D Multi-Beam and Null Synthesis by Phase-Only Control for 5G Antenna Arrays. Electronics 2019, 8, 656. https://doi.org/10.3390/electronics8060656
Comisso M, Palese G, Babich F, Vatta F, Buttazzoni G. 3D Multi-Beam and Null Synthesis by Phase-Only Control for 5G Antenna Arrays. Electronics. 2019; 8(6):656. https://doi.org/10.3390/electronics8060656
Chicago/Turabian StyleComisso, Massimiliano, Gabriele Palese, Fulvio Babich, Francesca Vatta, and Giulia Buttazzoni. 2019. "3D Multi-Beam and Null Synthesis by Phase-Only Control for 5G Antenna Arrays" Electronics 8, no. 6: 656. https://doi.org/10.3390/electronics8060656
APA StyleComisso, M., Palese, G., Babich, F., Vatta, F., & Buttazzoni, G. (2019). 3D Multi-Beam and Null Synthesis by Phase-Only Control for 5G Antenna Arrays. Electronics, 8(6), 656. https://doi.org/10.3390/electronics8060656





