Abstract
Due to the non-linear and non-stationary characteristics of ship radiated noise (SR-N) signal, the traditional linear and frequency-domain denoising methods cannot be used for such signals. In this paper, an SR-N signal denoising method based on modified complete ensemble empirical mode decomposition (EMD) with adaptive noise (CEEMDAN), dispersion entropy (DE), and interval thresholding is proposed. The proposed denoising method has the following advantages: (1) as an improved version of CEEMDAN, modified CEEMDAN (MCEEMDAN) combines the advantages of EMD and CEEMDAN, and it is more reliable than CEEMDAN and has less consuming time; (2) as a fast complexity measurement technology, DE can effectively identify the type of intrinsic mode function (IMF); and (3) interval thresholding is used for SR-N signal denoising, which avoids loss of amplitude information compared with traditional denoising methods. Firstly, the original signal is decomposed into a series of IMFs using MCEEMDAN. According to the DE value of IMF, the modes are divided into three types: noise IMF, noise-dominated IMF and pure IMF. After noise IMFs are removed, the noise-dominated IMFs are denoised using interval thresholding. Finally, the pure IMF and the processed noise-dominated IMFs are reconstructed to obtain the final denoised signal. The denoising experiments with the Chen’s chaotic system show that the proposed method has a higher signal-to-noise ratio (SNR) than the other three methods. Applying the proposed method to denoise the real SR-N signal, the topological structure of chaotic attractor can be recovered clearly. It is proved that the proposed method can effectively suppress the high-frequency noise of SR-N signal.
1. Introduction
Ship radiated noise (SR-N) signals are caused by various vibrations and sound sources from a ship, including mechanical noise, propeller noise, and hydrodynamic noise [1]. SR-N signals contain many types of information about ship characteristics, such as the type of ship, speed, tonnage, etc. [2,3]. The navy collects SR-N signals using underwater acoustic detection equipment, torpedoes, etc., and uses the SR-N signal as a source of target information [4]. At the same time, SR-N signals are the basis for the development, testing and use of these naval equipment. Due to the marine environmental noise and the time-varying characteristics of the underwater acoustic channel, the measured SR-N signal is a nonlinear and non-stationary chaotic signal [5,6]. Noise reduction of SR-N signal is beneficial to further feature extraction, classification and detection [7]. However, traditional linear and frequency-domain denoising methods cannot be directly applied to SR-N signal. It is necessary to find a denoising method suitable for SR-N signal. At present, a data-driven adaptive signal decomposition method provides a new idea for underwater acoustic signal processing.
Empirical mode decomposition (EMD) [8] is an adaptive signal decomposition method, which can decompose the signal into a series of intrinsic mode functions (IMFs). Therefore, EMD provides a new idea for nonlinear and non-stationary signal processing, but EMD has problems such as the mode mixing and residual noise. In order to alleviate the above problems, some noise-assisted versions have been proposed, such as ensemble EMD (EEMD) [9], complementary EEMD (CEEMD) [10] and complete EEMD with adaptive noise (CEEMDAN) [11]. These optimized EMD algorithms are widely used in various fields, especially in medicine [12,13], fault diagnosis [14,15], chaotic signal processing [16], wind power prediction [17] and so on.
CEEMDAN can overcome the mode mixing of EMD and reduce the reconstruction error of EEMD. However, each time an IMF is extracted, white Gaussian noise is added multiple times in the signal, which increases the algorithm complexity. In fact, in the decomposition process, the high-frequency intermittent components and noises that cause the mode mixing are usually decomposed first [18]. After separating these components, the extreme values of the remaining signal are evenly distributed [19]. Therefore, there is no need to use white Gaussian noise as an auxiliary for residual signal, the EMD decomposition can be directly performed. In order to solve the above problems, we introduce the new permutation entropy (NPE) [20] to detect the complexity of signal, and propose a modified CEEMDAN (MCEEMDAN) algorithm.
A growing number of scholars are focusing on developing Shannon entropy algorithms, and these algorithms are employed in underwater acoustic processing, such as permutation entropy (PE) [5,21], sample entropy (SE) [22], and differential symbolic entropy (DSE) [23], etc. Although SE is robust to noise, its computational efficiency is low. PE is a widely used entropy, but it ignores the magnitude of time series and it is sensitive to noise [24]. Dispersion entropy (DE) [25], a novel Shannon entropy, has higher computational efficiency and can accurately measure the complexity of time series.
Recently, Kopsinis et al. [26] proposed a denoising algorithm, the EMD interval thresholding (EMD-IT) method, which overcomes the problem that the WT method needs to select the wavelet basis. EMD-IT was applied to chaotic signal noise reduction, but this method needs to pre-select the order of the IMF that need to be denoised [27,28]. In this paper, an SR-N signal denoising method is proposed, which applies MCEEMDAN to SR-N signal denoising. The DE value is used to determine the type of IMF. The noise-dominated IMFs are processed using interval thresholding. In order to evaluate the performance of the method, the Chen’s chaotic system and the SR-N signal are used for the simulation experiments, respectively.
The structure of this paper is as follows. In Section 2, the EEMD and CEEMDAN algorithms are reviewed and then MCEEMDAN is proposed; and the basic theory of DE and IT are introduced. Section 3 introduces the denoising method proposed in this paper and gives the evaluation criteria of the denoising method. Section 4 analyzes the performance of MCEEMDAN and DE through two simulation experiments. In Section 5 and Section 6, the proposed denoising method is applied to the Chen’s chaotic signal and the real SR-N signal, respectively. The conclusion is given in the final section.
2. Basic Theory
2.1. CEEMDAN
CEEMDAN, an improved version of EEMD proposed by Torres et al. [11], is a data-driven adaptive signal decomposition algorithm. It reduces the reconstruction error and its decomposition process is complete. As the basis of CEEMDAN, the steps of EEMD can be briefly described as follows [29]:
- Step 1.
- Generate , where is a zero mean unit variance white noise realization;
- Step 2.
- Decompose completely each by EMD getting their modes , where indicates the mode;
- Step 3.
- Assign as the kth mode of x, obtained by averaging the corresponding modes: .
Let be the operator that produces the kth mode obtained by EMD, and be the averaging operator. The CEEMDAN algorithm can be described as follows [29]:
- Step 1.
- For every decompose each by EMD, until its first mode and compute ;
- Step 2.
- At the first stage () compute the first residue ;
- Step 3.
- For every decompose each by EMD and define the second CEEMDAN mode as ;
- Step 4.
- For calculate the kth residue ;
- Step 5.
- For every decompose each by EMD and define the CEEMDAN mode as .
2.2. MCEEMDAN Method
In the decomposition process, NPE is first used to determine whether the signal contains abnormal components, and then to decide whether to add noise for assistance. Therefore, a NPE-based MCEEMDAN algorithm is proposed in this paper.
2.2.1. NPE
The algorithm steps of NPE are as follows [21]:
For a time series , with given embedding dimension m and time delay d, the embedding vectors are represented as:
where . Then each of the vectors is arranged in ascending order:
If , then . Next, an ordinal pattern, which is one of possibilities, can be assigned to each and be denoted as:
where . Compute the probability distribution of each ordinal pattern, then the NPE of time series x can be defined as:
where . Compare with PE, is replaced by , and a constant is added. When , NPE reaches the smallest value 0, this means that the distance to white noise is 0. Li et al. [21] have proved that NPE is more stable than PE, and NPE has strong noise recognition ability.
2.2.2. Steps of MCEEMDAN Method
Use the same , , and operators as CEEMDAN and let be the NPE threshold. The decomposition process of MCEEMDAN is as follows:
- Step 1.
- Set , and ;
- Step 2.
- Set , and generate signal group (). Determine the first IMF by EMD: ; then obtain the first residue . Calculate of and judge whether is greater than . If , go to step 5, otherwise do ;
- Step 3.
- Generate signal group (). Determine the kth IMF by EMD: ; then obtain the kth residue ;
- Step 4.
- Calculate the of . Is larger than ?
- Yes, go to step 5, and save 1st to k−1th IMFs as noise-assisted IMFs;
- No, do , go back to step 3 for next IMF;
- Step 5.
- Decompose by EMD to obtain the remaining IMFs.
Finally, the combination of noise-assisted IMFs and the remaining IMFs decomposed by EMD is the decomposition result of MCEEMDAN. Compared with CEEMDAN, MCEEMDAN further reduces the amount of calculation. Through multiple tests, we set the threshold of NPE to 0.18.
2.3. DE
Given a univariate signal , the DE algorithm is as follows [30]:
- Step 1.
- Mapping of the N elements in the input signal x into c classes. The first part of the mapping applies the normal cumulative distribution function (NCDF) to x in order to obtain a normalized vector y (with values from 0 to 1). Then, y is linearly mapped to a vector z with integers values from 1 to c using the formula , where the rounding can be an increasing or a decreasing to the next digit;
- Step 2.
- Creation of embedding vectors (namely ), where m is the number of embedding dimensions and d the time delay. Each element of the embedding vectors is defined choosing m elements from z at distance d starting from position i (that is, , with i and j ranging from 1 to and from 1 to m respectively). Each embedding vector is mapped to a dispersion pattern , where , ,…, ;
- Step 3.
- Calculation of the probabilities of each of the dispersion patterns (i.e., the number of occurrences of each dispersion pattern out of the number of embedding vectors);
- Step 4.
- Calculation of the normalized dispersion entropy .
There are three parameters for DE, including the embedding dimension m, the time delay d, and number of classes c. This paper uses the same parameters as the literature [25], that is, , , and .
2.4. Interval Thresholding
In the EMD-based SR-N signal denoising method, noise evaluation criteria are often used to divide the modes into noise IMFs and pure IMFs, and then the pure IMFs are reconstructed to obtain denoised signal. However, there may be useful information in the noise IMF, so it is necessary to reduce the loss of useful information. In this paper, the EMD-IT method is introduced into the SR-N signal denoising, and the interval thresholding is used to denoise the noise-dominated IMFs. The main principle of EMD-IT is as follows [26,31]: the first step is to find the interval of each IMF, where and are the mth and m+1th zeros of the ith IMF, and there is only one extreme value in this interval. The second step is to compare the magnitude of the extreme value and the threshold. If the extreme value is greater than the threshold, all amplitudes within the interval are retained, otherwise all amplitudes within the interval are set to zero. The interval thresholding can be expressed as:
where , and is the total number of extreme points of the ith IMF. is the threshold value of the ith IMF, which can be calculated by:
where is the number of sampling points of the original signal. C represents the weight, generally taking 0.6 to 0.8 [32]. represents the noise energy in the ith IMF, which can be estimated by:
where β and are parameters that have be estimated by a large number of independent noise realizations and their IMFs. Flandrin et al. [33] proposed setting the values of these two parameters to 0.719 and 2.01, respectively. is the noise energy of the first IMF, which can be estimated by the noise standard deviation of IMF1, that is:
3. Steps of MCEEMDAN-DE-IT
3.1. The Proposed Method
We propose a denoising method named MCEEMDAN-DE-IT for ship radiated noise signal. The flow chart of the proposed denoising method is shown in Figure 1.
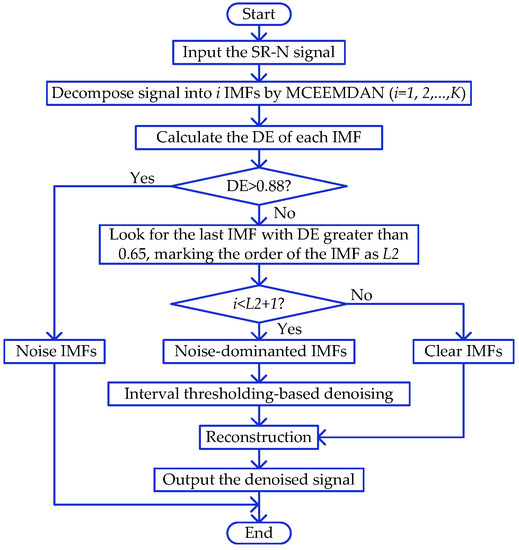
Figure 1.
The flowchart of the proposed method.
- Step 1.
- The SR-N signal is decomposed into a series of IMFs by MCEEMDAN.where is the ith IMF and K is the number of IMFs (the residue from the decomposition is treated as the last IMF);
- Step 2.
- Calculate the DE of each IMF;
- Step 3.
- According to the DE value, IMFs are divided into three types: noise IMFs, noise-dominated IMFs, and pure IMFs. If DE is greater than 0.88, the corresponding IMF is determined to be a noise IMF. Then look for the last IMF with DE greater than 0.65, and determine the IMF and the previous IMFs as noise-dominated IMFs. In addition, the remaining IMFs are pure IMFs;
- Step 4.
- Interval threshold denoising is performed on all noise-dominated IMFs;
- Step 5.
- Finally, the noise IMFs are removed, and the pure IMFs and the processed noise-dominated IMFs are reconstructed to obtain the final denoised signal. Therefore, the denoised signal can be expressed as:where and represent the order of the noise-dominated IMFs. is the thresholded version of the noise-dominated .
3.2. Evaluation Criteria for SR-N Signal Noise Reduction
To quantitatively evaluate the denoising effect of the method on the SR-N signal, it is necessary to calculate some feature parameters before and after noise reduction. These feature parameters include noise intensity (NI) [5], spatial-dependence recurrence sample entropy (sdrSampEn) [34] and DE.
3.2.1. NI
Assuming a time series of N samples in length, that is . Its NI can be approximated by the standard deviation, i.e.,:
where represents the mean of the time series.
3.2.2. SdrSampEn
The traditional sample entropy (SampEn) is a tool to measure the complexity of time series and is widely used in chaotic signal analysis. However, the SampEn does not take sequential information, which is inherently useful, into its calculation of sample similarity. So, Pham et al. proposed a tool that is based on the mathematical principle of the SampEn and enables the capture of sequential information of a time series in the context of spatial dependence provided by the binary-level co-occurrence matrix (BLCM) of a recurrence plot (RP). The sdrSampEn algorithm can be described as follows [33]:
- Step 1.
- Given a time series and model parameters embedding dimension m, and spatial offset δ;
- Step 2.
- Use time series, m, to compute the RP by using the Chebyshev distance;
- Step 3.
- Use offset δ to construct the BLCM of the RP to obtain ;
- Step 4.
- Set , repeat steps 2–3 to obtain ;
- Step 5.
- Finally, .
Pham et al. [34] used SdrSampEn to measure the uncertainty of Lorenz signal. At the same time, it is pointed out that SdrSampEn have a better discriminative ability in measuring the irregularity of chaotic time series. Detailed calculation of SdrSampEn can be seen in [34].
4. Simulation Signal Analysis
4.1. Performance Analysis of MCEEMDAN
In this section, we will use a simulated signal to test the performance of MCEEMDAN and compare the proposed method with EMD, EEMD, CEEMD, and CEEMDAN.
where , , and represent the three components of . The time-domain waveform of simulated signal is shown in Figure 2. For EEMD, CEEMD, CEEMDAN and its modified version, the noise standard deviation and the ensemble size are set to 0.2 and 60, respectively. Figure 3 shows the decomposed results of simulation signals. Since the decomposition results of EEMD and CEEMD are similar, only CEEMD is shown in Figure 3b.
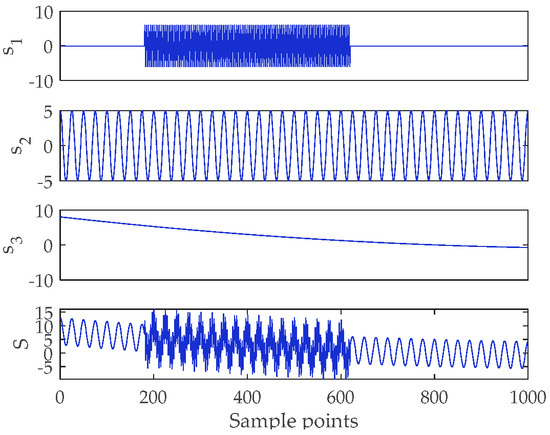
Figure 2.
Time-domain waveform of simulated signal.
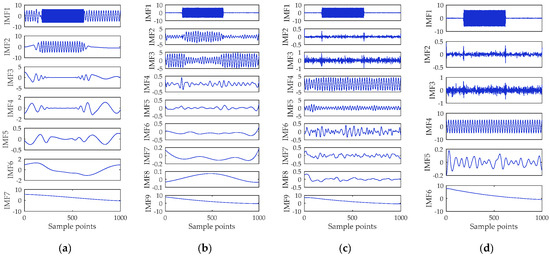
Figure 3.
Decomposition results of simulated signal by (a) empirical mode decomposition (EMD); (b) complementary ensemble EMD (CEEMD); (c) complete ensemble EMD with adaptive noise (CEEMDAN); and (d) modified CEEMDAN (MCEEMDAN).
Figure 3 shows obvious mode mixing of the IMF1 simulated with EMD. Although CEEMD improved the mode mixing, it divided into two IMFs with large amplitude changes. The IMF4 and IMF5 of CEEMDAN method have the same frequency components, and there are some pseudo components that have no physical meaning. Figure 3d shows that the modified CEEMDAN can restore the time-domain waveform of the simulated signal better.
In order to quantitatively evaluate the effect of these decomposition algorithms, index of orthogonality (IO), consuming time (CT), and reconstruction error order of magnitude (REOM) are calculated [18]. Where CT is the running time statistics of each decomposition algorithm. IO can be used to measure the accuracy of decomposition algorithms. If IO is smaller, then the decomposition accuracy is higher. Otherwise, the decomposition accuracy is lower. IO can be defined as [18]:
where represents the original time series and its sample length is L. The original time series is decomposed into K IMFs. and represent the ith and jth IMF, respectively. The decomposition performances of these decomposition algorithms are shown in Table 1.

Table 1.
The decomposition performances of these decomposition algorithms.
Table 1 shows that the CEEMDAN method overcomes the mode mixing problem to a certain extent, but because of the multiple addition of white Gaussian noise, the CT is the largest. The above results show that the MCEEMDAN method has a small IO, and its computational efficiency is higher than that of CEEMDAN.
4.2. Comparison of SE, PE, and DE
To compare the performance of SE, PE and DE, give an example. We added white Gaussian noise with different signal-to-noise ratios (SNRs) to the sinusoidal signal, and then calculated the SE, PE, and DE of the simulation signal separately. The simulation signals can be determined by:
where represents the white Gaussian noise, and the sampling frequency is 100 Hz. is added with −10 dB to 35 dB white Gaussian noise with an interval of 5 dB. The time-domain waveform of the noisy simulation signal is shown in Figure 4. The values of the three types of entropy are shown in Figure 5, and the CT of each entropy algorithm is also listed in Table 2.
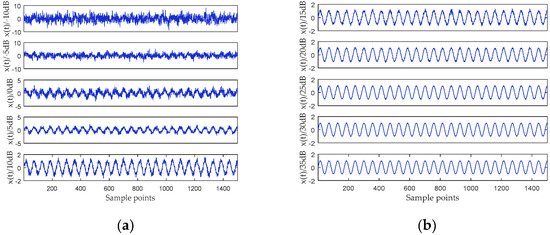
Figure 4.
Time-domain waveforms of simulated signals with different signal-to-noise ratios (SNRs).
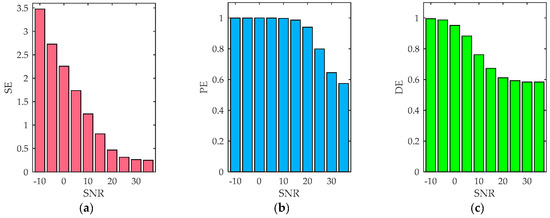
Figure 5.
Entropy values of noisy simulated signals. (a) sample entropy (SE); (b) permutation entropy (PE); and (c) dispersion entropy (DE).

Table 2.
Consuming time of different entropy algorithms.
Figure 4 shows that when the SNR is less than 0 dB, the sinusoidal signal is almost overwhelmed by noise. When the SNR is greater than 5 dB, the influence of noise on the sinusoidal signal is small. Figure 5 shows that when the SNR is less than 0 dB, the DE is greater than 0.88. With the increase of SNR, the DE of simulation signal gradually decreases, and finally approaches 0.6. When SNR is less than 15 dB, the PE of the simulation signal is basically greater than 0.95. Compared to PE, SE and DE are more robust to noise, so they can better describe the complexity of noise sinusoidal signals. However, the value of SE is between 0 and 3.5, which limits its use because it is difficult to normalize the SE. In addition, from the CT of the three algorithms, SE has the lowest computational efficiency. In summary, DE can not only accurately measure the complexity of time series, but also has the highest computational efficiency, so we introduce DE into the denoising of SR-N signals. In the following, if the DE of the IMF is greater than 0.88, it is determined to be a noise IMF.
5. Denoising of Chen’s Chaotic Signal
Chen’s system can be expressed as:
when the parameters , and , the system is in typical chaotic state. The equation is integrated by using a fourth-order Runge–Kutta method with a fixed step size of 0.01, and the initial values of the equation are , , . The y component signal with a length of 2048 points is selected as a chaotic signal, and the signal are added the white Gaussian noise with SNR = 11 dB. The time-domain waveforms of the noisy signal and the noiseless signal are shown in Figure 6.
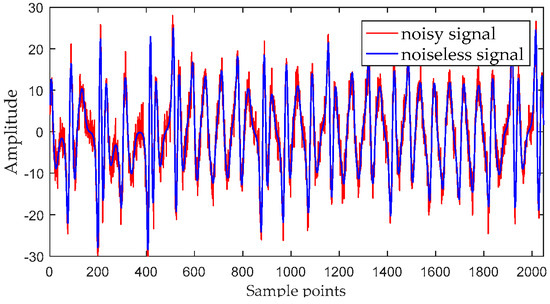
Figure 6.
The noisy signal and the noiseless signal.
First, the noisy Chen’s signal is decomposed by MCEEMDAN. Figure 7 shows that the Chen’s signal is decomposed into 12 IMFs. It can be seen that the frequency decreases with the increase of IMF order. The DE of each IMF is calculated, and DE values are listed in Table 3.
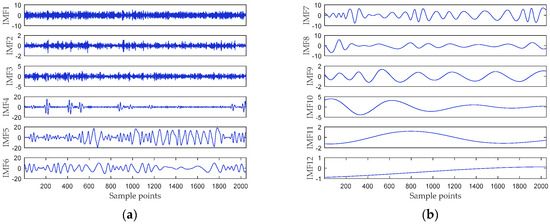
Figure 7.
The decomposition result of MCEEMDAN.

Table 3.
The DEs of intrinsic mode functions (IMFs).
As can be seen from Table 3, since DEs of IMF1 to IMF3 are both greater than 0.88, they are judged as noise IMFs. The last IMF with DE greater than 0.65 is IMF5, so IMF4 and IMF5 are determined to be noise-dominated IMFs. IMF6–IMF12 are pure IMFs. The noise-dominated IMFs are denoised by the interval thresholding method. The time-domain waveforms of IMF4 and IMF5 before and after noise reduction are shown in Figure 8. It can be seen that in IMF4, the lower amplitude intervals are filtered out as noise, while the other intervals are retained. For IMF5, the extreme values in most of the intervals are greater than the threshold, so there is no significant difference before and after noise reduction.
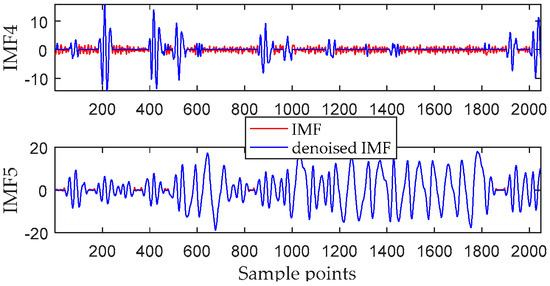
Figure 8.
IMF4 and IMF5 before and after interval thresholding-based denoising.
The pure IMFs and the processed noise-dominated IMFs are restructured to obtain the denoised Chen’s signal. In order to prove the superiority of MCEEMDAN-DE-IT method, this method is compared with EMD-DE-IT, EEMD-DE-IT, and CEEMD-DE-IT. Among them, EMD-DE-IT uses the EMD-IT code provided in [26], and noise evaluation criteria is the same as this paper. For the sake of evaluating the performance of these methods, the SNR and root mean square error (RMSE) are adopted and defined as follows [28]:
where x and are the noiseless signal and the denoised signal; N represents the length of the signal. The time-domain waveform before and after noise reduction for noisy Chen’s signal when SNR = 11 dB are shown in Figure 9.
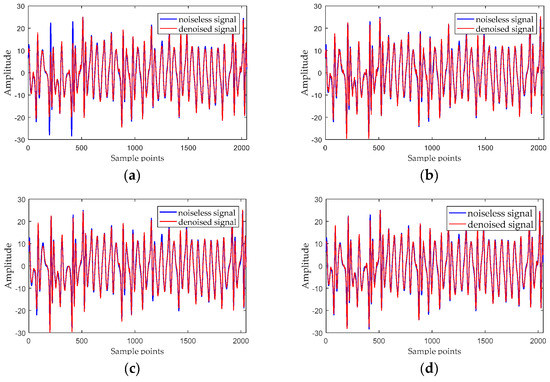
Figure 9.
Time-domain waveforms for (a) the EMD-DE-IT method; (b) the EEMD-DE-IT method; (c) the CEEMD-DE-IT method; and (d) the proposed method.
Figure 9 shows that the EMD-DE-IT method loses some important information of the noiseless signal, and its noise reduction performance is the worst. Both EEMD-DE-IT and CEEMD-DE-IT have good noise reduction effects, and CEEMD-DE-IT is superior to EEMD-DE-IT, but there is still some residual noise in some details. In addition, Table 4 shows that the proposed method has a better noise reduction effect for the Chen’s signal with SNR = 11 dB. As shown in Figure 10, in order to compare noise reduction effects more intuitively, we also display the phase diagrams before and after noise reduction.

Table 4.
Denoising result of the Chen’s signal when SNR is 11 dB.
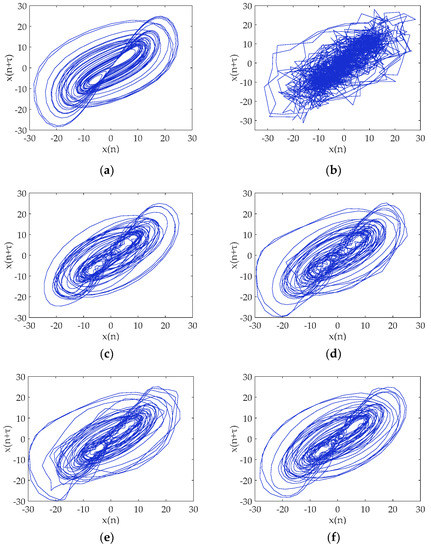
Figure 10.
Phase diagrams for (a) the noiseless Chen’s signal; (b) the noisy Chen’s signal when SNR is 11 dB; (c) the EMD-DE-IT method; (d) the EEMD-DE-IT method; (e) the CEEMD-DE-IT method; and (f) the proposed method.
By comparing the phase diagram in Figure 10, it can be seen that the attractor of the noisy Chen’s signal is annihilated by the noise, and the fractal features are hardly observed. After the noise reduction by the EMD-DE-IT method, the shape of the attractor is quite different from the noiseless signal, indicating that some important information is actually lost. Both EEMD-DE-IT and CEEMD-DE-IT methods roughly restore the phase diagram of the pure attractor, but there are still deformed orbits. Since the intensity of the noise determines the damage degree of the attractor’s self-similar structure, it indicates that the denoised signal still has some noise. Using the proposed method, the geometry of the attractor structure is more regular and the degree of self-similarity is higher. The phase diagram after noise reduction is closer to that of the noiseless signal, which indicates that the proposed method can effectively filter out the noise of the noisy signal. Therefore, Figure 10 objectively shows that the denoising effect of the proposed method is better than the other three methods.
To further compare the noise reduction effect, we added −5 dB, 0 dB, 5 dB, 10 dB, and 15 dB white Gaussian noise in the Chen’s signal, respectively. Figure 11 presents the comparison of the SNR and the RMSE of the above four methods. The results are averaged from 10 random experiments. It can be seen that the performance of EEMD-DE-IT is similar to that of CEEMD-DE-IT, and the performance of EMD-IT method is poor at high SNR. Experiments show that the proposed method has better noise suppression ability for the Chen’s signal with low SNR. From the RMSE point of view, the reconstruction accuracy of this method is better than other methods at low SNR.
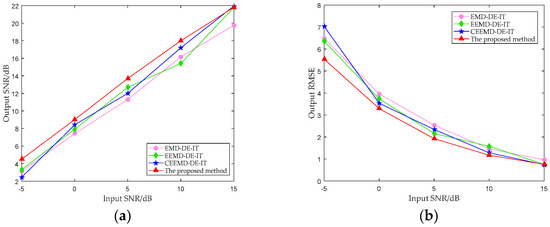
Figure 11.
(a) SNR comparison among different methods; and (b) RMSE comparison among different methods.
6. Denoising of Real Ship Radiated Noise Signal
In this paper, three different types of SR-N signals are selected as sample data, namely the Ship-I, the Ship-II, and the Ship-III. The SR-N signals were measured in the South China Sea. Each type of SR-N signals has 100 sample data. Each sample length is 2048 points and sampling interval is 0.05 ms. Before the noise reduction experiment, the sample data have been filtered, normalized, and sampled. SR-N signals and denoised SR-N signals and their attractor trajectories are shown in Figure 12, Figure 13 and Figure 14.
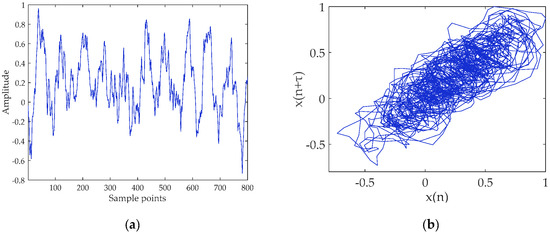
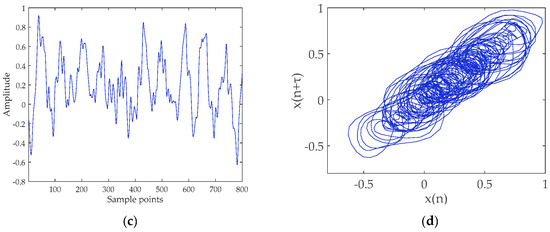
Figure 12.
Ship-I and denoised Ship-I signals and their attractor trajectories. (a) Ship-I (select 800 points); (b) attractor trajectory for Ship-I; (c) denoised Ship-I (select 800 points); and (d) attractor trajectory for denoised Ship-I.
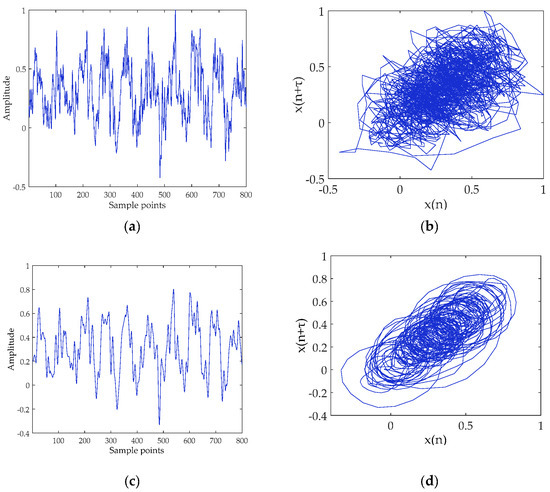
Figure 13.
Ship-II and denoised Ship-II signals and their attractor trajectories. (a) Ship-II (select 800 points); (b) attractor trajectory for Ship-II; (c) denoised Ship-II (select 800 points); and (d) attractor trajectory for denoised Ship-II.
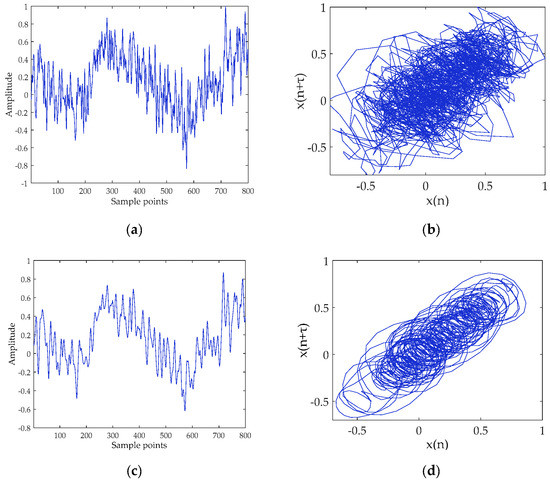
Figure 14.
Ship-III and denoised Ship-III signals and their attractor trajectories. (a) Ship-III (select 800 points); (b) attractor trajectory for Ship-III; (c) denoised Ship-III (select 800 points); and (d) attractor trajectory for denoised Ship-III.
It can be seen from the time-domain waveforms in Figure 12, Figure 13 and Figure 14 that the original SR-N signals contain ocean background noise, and the high-frequency noise is filtered out after noise reduction. The phase diagram shows that the attractor of the original signal appears as a disorderly pseudo-random property. After noise reduction, the orbits of attractors become smooth, clear and regular. The proposed method does reduce the noise, enhances the inherent deterministic component of the SR-N signal, and reveals the inherent dynamic characteristics of chaotic system.
We calculated the feature parameters of the SR-N signal before and after noise reduction. Table 5 shows that the feature parameters after noise reduction have been improved, indicating that the complexity of the SR-N signal has been reduced. In summary, the MCEEMDAN-DE-IT method can be used for noise reduction of real SR-N signals.

Table 5.
Feature parameters before and after noise reduction.
7. Conclusions
An SR-N signal denoising method based on modified CEEMDAN, dispersion entropy, and interval thresholding is proposed. The original signal is decomposed into a series of IMFs by MCEEMDAN. According to DE, the IMFs are divided into three parts: noise IMFs, noise-dominated IMFs and pure IMFs. The noise-dominated IMFs are processed using interval thresholding. Finally, the noise-dominated IMFs and the pure IMFs are reconstructed to obtain the denoised SR-N signal. The experimental results of the simulated signal and the real SR-N signal show that the denoising method has the following advantages:
- (1)
- MCEEMDAN, the modified signal decomposition method proposed in this paper, combines CEEMDAN and traditional EMD through NPE. It not only inherits the advantages of CEEMDAN, but also reduces the consuming time. MCEEMDAN is suitable for nonlinear and non-stationary signal processing, so we introduce it into the denoising of SR-N signal.
- (2)
- Simulation results show that, compared with SE and PE, DE is robust to noise and computationally fast. Therefore, we use DE to measure the complexity of IMF.
- (3)
- The Chen’s chaotic signals with different SNRs are denoised by four methods. The experimental results show that compared with EMD-DE-IT, EEMD-DE-IT and CEEMD-DE-IT, the proposed method has lower RMSE and higher SNR.
- (4)
- For the real SR-N signal, two kinds of evaluated criteria for denoised effect are introduced (NI, and SdrSampEn). The results show that the proposed method can reduce the high-frequency noise of SR-N signal and has advantages in chaotic attractor topological configuration reversion.
A hybrid denoising method for SR-N signal is proposed in this paper. Although this method can effectively reduce the noise of real SR-N signals, it does not consider the real-time performance of signal processing, which will be the direction to be improved. In addition, our further research on the application of MCEEMDAN and Shannon entropy in underwater acoustic signal processing, including detection, feature extraction and classification.
Author Contributions
G.L., Z.Y., and H.Y. conceived the idea and research theme. Z.Y. designed and performed the experiments. G.L., Z.Y., and H.Y. analyzed the experimental results. G.L., Z.Y., and H.Y. wrote and revised the paper.
Funding
This work was supported by the National Natural Science Foundation of China (No. 51709228) and the Innovation Funds of Graduate Programs of Xi’an University of Posts and Telecommunications (No. CXJJ2017022).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tani, G.; Viviani, M.; Hallander, J.; Johansson, T.; Rizzuto, E. Propeller underwater radiated noise: A comparison between model scale measurements in two different facilities and full scale measurements. Appl. Ocean Res. 2016, 56, 48–66. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y.; Li, Y.; Yu, J. PHD and CPHD algorithms based on a novel detection probability applied in an active sonar tracking system. Appl. Sci. 2018, 8, 36. [Google Scholar] [CrossRef]
- Li, D.Q.; Hallander, J.; Johansson, T. Predicting underwater radiated noise of a full scale ship with model testing and numerical methods. Ocean Eng. 2018, 161, 121–135. [Google Scholar] [CrossRef]
- Chen, Z.; Li, Y.; Chen, X. Underwater acoustic weak signal detection based on Hilbert transform and intermittent chaos. Acta Phys. Sin. 2015, 64, 200502. [Google Scholar]
- Li, G.; Yang, Z.; Yang, H. Noise reduction method of underwater acoustic signals based on uniform phase empirical mode decomposition, amplitude-aware permutation entropy, and Pearson correlation coefficient. Entropy 2018, 20, 918. [Google Scholar] [CrossRef]
- Siddagangaiah, S.; Li, Y.; Guo, X.; Chen, X.; Zhang, Q.; Yang, K.; Yang, Y. A complexity-based approach for the detection of weak signals in ocean ambient noise. Entropy 2016, 18, 101. [Google Scholar] [CrossRef]
- Li, Y.; Chen, X.; Yu, J.; Yang, X. A fusion frequency feature extraction method for underwater acoustic signal based on variational mode decomposition, Duffing chaotic oscillator and a kind of permutation entropy. Electronics 2019, 8, 61. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.A.; Yen, N.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Yeh, J.R.; Shieh, J.S.; Huang, N.E. Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method. Adapt. Data Anal. 2010, 2, 135–156. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Satija, U.; Ramkumar, B.; Manikandan, M.S. Automated ECG noise detection and classification system for unsupervised healthcare monitoring. IEEE J. Biomed. Health 2017, 22, 722–732. [Google Scholar] [CrossRef] [PubMed]
- Motin, M.A.; Karmakar, C.K.; Palaniswami, M. Selection of empirical mode decomposition techniques for extracting breathing rate from PPG. IEEE Signal Process. Lett. 2019, 26, 592–596. [Google Scholar] [CrossRef]
- Fu, Q.; Jing, B.; He, P.; Si, S.; Wang, Y. Fault feature selection and diagnosis of rolling bearings based on EEMD and optimized Elman AdaBoost algorithm. IEEE Sens. J. 2018, 18, 5024–5034. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, Z.; Chen, B.; Zhang, W.; Huang, G. An improved complementary ensemble empirical mode decomposition with adaptive noise and its application to rolling element bearing fault diagnosis. ISA Trans. 2019. [Google Scholar] [CrossRef] [PubMed]
- Butusov, D.; Karimov, T.; Voznesenskiy, A.; Kaplun, D.; Andreev, V.; Ostrovskii, V. Filtering techniques for chaotic signal processing. Electronics 2018, 7, 450. [Google Scholar] [CrossRef]
- Safari, N.; Chung, C.Y.; Price, G.C.D. A novel multi-step short-term wind power prediction framework based on chaotic time series analysis and singular spectrum analysis. IEEE Trans. Power Syst. 2018, 33, 590–601. [Google Scholar] [CrossRef]
- Niu, F.; Hui, J.; Zhao, A.B.; Cheng, Y.; Chen, Y. Application of SN-EMD in mode feature extraction of ship radiated noise. Math. Probl. Eng. 2018, 2018, 2184612. [Google Scholar] [CrossRef]
- Zheng, J.D. Rolling bearing fault diagnosis based on partially ensemble empirical mode decomposition and variable predictive model-based class discrimination. Arch. Civ. Mech. Eng. 2016, 16, 784–794. [Google Scholar] [CrossRef]
- Keller, K.; Mangold, T.; Stolz, I.; Werner, J. Permutation entropy: New ideas and challenges. Entropy 2017, 19, 134. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Chen, X.; Yu, J. Denoising and feature extraction algorithms using NPE combined with VMD and their applications in ship-radiated noise. Symmetry 2017, 9, 256. [Google Scholar] [CrossRef]
- Li, Y.; Chen, X.; Yu, J.; Yang, X.; Yang, H. The data-driven optimization method and its application in feature extraction of ship-radiated noise with sample entropy. Energies 2019, 12, 359. [Google Scholar] [CrossRef]
- Li, G.; Yang, Z.; Yang, H. Feature extraction of ship-radiated noise based on regenerated phase-shifted sinusoid-assisted EMD, mutual information, and differential symbolic entropy. Entropy 2019, 21, 176. [Google Scholar] [CrossRef]
- Fadlallah, B.; Chen, B.; Keil, A.; Príncipe, J. Weighted-permutation entropy: A complexity measure for time series incorporating amplitude information. Phys. Rev. E 2013, 87, 022911. [Google Scholar] [CrossRef] [PubMed]
- Rostaghi, M.; Azami, H. Dispersion entropy: A measure for time series analysis. IEEE Signal Process. Lett. 2016, 23, 610–614. [Google Scholar] [CrossRef]
- Kopsinis, Y.; Mclaughlin, S. Development of EMD-based denoising methods inspired by wavelet thresholding. IEEE Trans. Signal Process. 2009, 57, 1351–1362. [Google Scholar] [CrossRef]
- Klionskiy, D.M.; Kaplun, D.I.; Geppener, V.V. Empirical mode decomposition for signal preprocessing and classification of intrinsic mode functions. Pattern Recognit. Image Anal. 2018, 28, 122–132. [Google Scholar] [CrossRef]
- Wang, X.; Qu, J.; Gao, F.; Zhou, Y.; Zhang, X. A chaotic signal denoising method developed on the basis of noise-assisted nonuniformly sampled bivariate empirical mode decomposition. Acta Phys. Sin. 2014, 63, 170203. [Google Scholar]
- Wang, J.; Luo, Y.; Tang, L.; Ge, P. A new weighted CEEMDAN-based prediction model: An experimental investigation of decomposition and non-decomposition approaches. Knowl.-Based Syst. 2018, 160, 188–199. [Google Scholar]
- Baldini, G.; Giuliani, R.; Steri, G.; Neisse, R. Physical layer authentication of Internet of Things wireless devices through permutation and dispersion entropy. In Proceedings of the 2017 Global Internet of Things Summit (GIoTS), Geneva, Switzerland, 6–9 June 2017; pp. 1–6. [Google Scholar]
- Klionskiy, D.; Kupriyanov, M.; Kaplun, D. Signal denoising based on empirical mode decomposition. J. Vibroeng. 2017, 19, 5560–5570. [Google Scholar] [CrossRef]
- Wang, M.J. Research on noise suppression for chaotic signals. Ph.D. Thesis, South China University of Technology, Guangzhou, China, 2015. [Google Scholar]
- Flandrin, P.; Rilling, G.; Gonçalvès, P. EMD Equivalent Filter Banks, from Interpretation to Applications, Hilbert-Huang Transform and Its Applications; World Scientific: Singapore, 2005. [Google Scholar]
- Pham, T.D.; Yan, H. Spatial-dependence recurrence sample entropy. Physica A 2017, 494, 581–590. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).