Abstract
In practical array systems, the gain-phase errors among antennas degrade the performance of direction finding significantly. In this paper, a novel sparse system model for direction of arrival (DOA) estimation in the scenario with gain-phase errors is proposed by exploiting the signal sparsity in the spatial domain. In contrast to the existing sparse-based methods using the grids to construct the dictionary matrix, a novel gridless method based on atomic norm and convex optimization is proposed, where the gain-phase errors are described by a diagonal matrix. With the Schur complement, a semidefinite programming is formulated from the optimization problem, and can be solved efficiently. With the gain-phase errors, the corresponding Cram’er-Rao lower bound (CRLB) of direction finding is derived as an estimation benchmark. Simulation results show that the proposed method performs better than the state-of-the-art methods in the scenario with correlated signals and gain-phase errors.
1. Introduction
Direction of arrival (DOA) estimation, which is of great significance in array signal processing [,], is solved by estimating the spatial spectrum, such as conventional beamforming (CBF) method []. However, the “Rayleigh limit” [] restrains the angular resolution and the targets within one beam cannot be distinguished by the CBF method. Many super-resolution methods such as Pisarenko spectral analysis method [], Capon minimum variance method [] and Burg maximum entropy method [] have been proposed to break through the Rayleigh limit [] and obtain a higher angular resolution. To improve the estimation performance, some subspace-based methods, such as multiple signal classification (MUSIC) [] and estimating signal parameters via rotational invariant techniques (ESPRIT) [] have also been proposed. Additionally, an asymptotically unbiased and efficient method named the least squares-ESPRIT [] is used widely and the maximum likelihood (ML) [,] method achieves a better performance in the scenario with low signal-to-noise ratio (SNR).
By exploiting the signal sparsity, the DOA estimation performance can be improved further. With the knowledge of compressed sensing (CS), unknown signals can be acquired and reconstructed by dealing with underdetermined linear systems. Correspondingly, some CS-based DOA estimation methods are proposed and can obtain a better performance. Focal underdetermined system solver (FOCUSS) method [] converts the problem of DOA estimation into that of sparse recovery firstly. Then, combining the CS theory and subspace algorithm, -SVD method [,,,] obtains the signal subspace using SVD decomposition. A sparse iterative covariance-based estimation (SPICE) method is proposed in [], and the method minimizes a covariance matrix fitting criterion to obtain the DOAs. penalty also provides an approach to solve the DOA estimation problem, and develops many methods. Basis pursuit (BP) method [] and match pursuit (MP) [] are 2 typical -based methods. However, the sparse-based methods cannot deal with the scenario with low SNR.
When correlations exist between signals, the DOA estimation performance degrades seriously [,]. At concerns the cost of losing the array aperture, the forward/backward spatial smoothing (FBSS) method proposed by [,] can solve the problem efficiently. To avoid the aperture loss, non-dimensionality reduction processing [] introduces a toeplitz matrix composed of the received data, which can also achieve decoherence. However, the computational complexity increases. Then, ref. [] proposes an ESPRIT-like method, which is computational efficient and can be applied to any single row of an array output covariance matrix. In the ESPRIT-like method, the number of signals determines the rank of the toeplitz matrix.
Specifically, the spatial frequency of an array is a traditional representation of DOA. As CS theory shown in [], without knowing any locations and gains of grids, the signals can be exactly recovered by using a convex optimization method in the scenario with the frequencies laying on the discretized grids, and convex optimization is firstly introduced in [] as near-optimal way to obtain frequency information. However, in most cases, the sparse signals are continuous and the off-grid errors are introduced by applying the method with discretized grids. When denser grids are used to fit the continuous characteristic and to solve the DOA estimation problem, the correlation between adjacent steering vectors (or atoms) becomes higher which further degrades the performance of sparse signal recovery [,].
Thus, to avoid describing the DOA problem by discretizing the spatial domain, another general framework of converting the DOA estimation problem into a convex optimization method, which appeared in [,], is proposed as the atomic norm-based method. In the problem of sparse signal estimation, the atomic norm and a norm are considered equivalent [], and nuclear norm are generalized to reconstruct the low-rank matrix in []. In [], the atomic norm is applied to solve the problem of a spectrally-sparse signal recovery in case of a small number of consecutive samples from the time domain. Besides, known as the reweighted atomic norm minimization, the nonconvex sparse method is proposed in []. Without the acknowledge of model order, the enhanced matrix completion (EMaC) method based on the structured matrix completion is proposed in []. An enhanced covariance matrix in sparse representation method is used in [] to dealing with the coherent signals for the DOA estimation problem. Ref. [,,] developed a toeplitz matrix constraint for the semidefinite program (SDP) of the atomic norm-based method with single sampled signals. Then, the problem with multiple sampled signals is discussed in ref. [].
Additionally, after establishing a model of atomic norm, ref. [] further defines an infinite atom set, and applies the dual problem to estimate the signal frequency. Without using the toeplitz matrix, a new method is proposed in. [], and the dual problem and SDP method are also used to recover the sparse signal. Based on existing work, with an order of random samples, sparse signals can be recovered with high probability in the case that the spatial frequencies are separated by no more than , where the number of sampled signals is denoted by n, and r denotes the sparsity.
The inconsistence of antennas degrades the DOA estimation performance too []. Some work has been done to deal with the unknown mutual coupling effect [,,]. In this paper, we concentrate on compensating for the effects of the gain and phase errors. Before our study, ref. [] introduced a calibration matrix composed of the unknown gain, phase and mutual-coupling coefficients, the eigen structure [] and eigen decomposition [], consisting of the covariance and conjugate matrices is used to get better estimation performance in the scenario with gain and phase errors. Later, a simultaneous orthogonal matching pursuit (SOMP)-based method has been proposed [], which introduces a diagonal matrix composed of phase errors and estimate the DOAs and phase errors iteratively. However, the computational complexity is so high that the above methods are not applicable to a practical scenario. Some articles work to solve the gain and phase errors disturb at the same time. Ref. [] exploits the structural features of the uniform circular array covariance matrix and ref. [] introduces a universal method for self-calibration based on the minimize cost functionto obtain a better estimation performance.
In this paper, the DOA estimation problem with unknown gain and phase errors among antennas is investigated. With gain-phase errors being described as a diagonal matrix, the CS-based system model is formulated and the corresponding DOA estimation problem is transmitted into sparse reconstruction problem.Then, a novel atomic norm minimization approach is proposed to improve performance of the DOA estimation in the scenario with gain-phase uncertainties and can deal with correlated signals. We focus on the dual problem of the atomic norm and solve the associate convex optimization problem using SDP without calculating the gain and phase errors. In contrast to the traditional atomic norm-based method, a new matrix constraint is proposed in the dual problem instead of the toeplitz matrix in the existing methods. Then, we derive the Cram’er-Rao lower bound (CRLB) [] of the system model. Finally, the proposed method is compared with the classical methods including SOMP, MUSIC, the off-grid sparse Bayesian inference method (OGSBI) and toeplitz-based atomic norm (TAN). To conclude, our contributions in this papers can be summarized as follows:
- The system model with gain-phase uncertainties: The system model is formulated, where the gain-phase uncertainties among antennas is formulated by a diagonal matrix.
- The proposed method for direction finding with gain-phase uncertainties: A novel atomic norm-based gridless method is proposed. In this method, the DOAs are estimated without knowing the gain and phase errors. The proposed method focus on the dual problem of the atomic norm and using SDP method to recover the sparse signals. The proposed method behaves better than the existing methods in the case with correlated signals and gain-phase uncertainties.
- The theoretical expression of SDP: The convex optimization problem is solved using SDP in the proposed method. By analyzing the structure of the dual problem, we theoretically derive the expression of the SDP.
The organization of the paper is as follows. Section 2 introduces the CS-based system model with gain-phase uncertainties. Section 3 describes the proposed gridless method with gain-phase uncertainties. Section 4 derives the CRLB of DOA estimation with correlated signals. Section 5 gives the simulation results. Finally, Section 6 concludes the paper.
Notations: Matrices are denoted by capital letters in boldface, and vectors are denoted by lowercase letters in boldface. , , and denote the Frobenius norm, Atomic norm, norm and Hermitian transpose, respectively. A matrix with complex entries is denoted by . We use to denote the identity matrix. The symbol denotes a diagonal matrix which diagonal entry is the vector , and is the -th entry of the vector . The symbol denotes linearly transmitting the matrix into a column vector, and denotes the trace of . For a complex , denotes the real part c. denotes the mathematical expectation. ⊗ denotes the Kronecker product.
2. Problem Formulation
2.1. Ideal System Model
The ULA system for direction finding shown in Figure 1 has N antennas and K target signals, d denotes the intersensor spaces of receivers. The antenna considered in our article is an omnidirectional antenna. The target signals are reflected by K slowly moving targets. The DOA of the k-th target is described by . We consider the situation with M samples, and the received signal are sampled with a sampling interval . For all antennas, the sampled signals during the sampling time can be expressed as , and the noise vector is defined as , while for all target signals, the signal vector is denoted by . The DOA vectors are given by () for the k-th antenna. In contrast to the independent signals in the traditional methods, we consider the DOA estimation problem for the correlated signals.
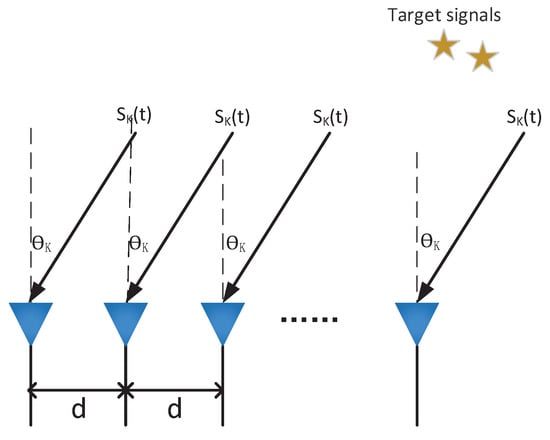
Figure 1.
The direction finding system.
Assuming that our target signals are far-field, the signals received can be written as:
where , and the k-th signal is weighted by corresponding directional vector . The correlated target signal , and the received signal . Besides, describes the additive white Gaussian noise (AWGN).
2.2. System Considering Gain-Phase Uncertainties
In practice, gain-phase uncertainties among antennas affect the ideal steering vector significantly. Thus, a matrix is introduced to modify the ideal system model in Equation (1). is a diagonal matrix, and the element of the diagonal is associated with the gain and phase errors. We define , where , and () and () denote the gain and phase error for the n-th receiving antenna respectively. Accordingly, the received signals considering the effects of gain and phase errors can be described as:
Thus, we express the system model for direction finding with gain-phase uncertainties in Equation (2). DOA vector will be estimated by using the method based on atomic norm with unknown parameters and correlated signals in the next section.
3. Atomic Norm-Based Algorithm for DOA Estimation
We use Equation (2) to describe the system model for direction finding with gain and phase uncertainties among antennas. In this section, a novel gridless DOA estimation approach is proposed. The new method is based on atomic norm and can obtain an estimate of signal . By treating the DOA as a continuous parameter, the method is capable of recovering the sparse signal without requirement of signals falling on the discretized frequency grids. We will give more particulars about the proposed direction finding approach in the scenario with gain-phase uncertainties.
An atomic norm is introduced to solve the direction finding problem with antenna inconsistent. The atomic norm for is defined as
where () with is defined as an atom for representing . We use the diagonal matrix to denote the phase errors among antennas. , and and denote the gain error and phase error of the n-th receiving antenna respectively.
However, it is difficult to solve , which is an NP-hard problem. We convert it into a convex optimization norm
where denotes the convex hull of elements in . We use the atomic norm to enforce sparsity in and solve denoising estimation problem. Ref. [] firstly introduced concept of applying the atomic norm to encourage sparsity for a universal set of atoms. As prescribed in [], the atomic norm minimization method is a solution of line spectrum estimation problem and denoising from noisy observations of multiple spectral-sparse signals. We can convert the DOA estimation problem into an optimization one
where is a properly chosen regularization parameter. With already known noise, an upper bound of mean square error (MSE) is provided.
Next, the framework of the dual problem will be analyzed. We can identify the DOA vector that comprises the optimal using the dual optimal solution.
We construct the dual problem of Equation (5). Firstly, we define dual norm as
where the inner product is .
By introducing the Lagrangian variable , primal variable and , the Lagrangian function of Equation (5) can be expressed as
We minimize the over all and to get the dual function to be the function of , then maximize the to get the result. So we can get the dual problem of the optimization problem
The Lagrangian can be minimized over all and by breaking it up and which can be simplified as
where means that the value is 0 when the condition in the set is satisfied, otherwise the value is ∞. Therefore, the dual problem of (5) can be simplified as
Furthermore, according to (6), can be expressed as
where . Equation (11) accludes the dual atomic norm equals to the upper bound of , which means, the constraint equals to
Semidefinite matrix theorem []: if there exists a semidefinite matrix , the necessary and sufficient condition for is and .
By the above theorem, we can build a semidefinite matrix
where . Then according to Schur complement, we know that
which means for any ), we have
Observing Equation (15), it is easy to find that when , the equation can be rewritten as
Thus, when , we can meet the constraint of Equation (12).
Therefore, with matrix satisfying Equation (17), the constraint of Equation (15) can be met. Then the optimization problem Equation (10) can be expressed as
Here, the three linear inequalities of Equation (19) are equal to the dual norm constraint Equation (17). By solving the SDP optimization problem Equation (19), the variable can be obtained and we can get the DOA vector after substituting into Equation (12).
5. Simulation Results
In this section, we provide some simulation results to demonstrate the capability of the raised method. Table 1 shows the simulation parameters. We use MATLAB R2015b to realize all the simulations on a workstation with 3.40 GHz Intel Core i7-6700 and 32 GB RAM.

Table 1.
Simulation Parameters.
- SOMP: The SOMP method is proposed in []. The SOMP algorithm is also called synchronous OMP algorithm. The main idea is that similar atoms have the same sparse characteristics. Therefore, when the sparse representation of similar atoms is assumed, the sparse atoms are located at the same position, and the selected atoms in the overcomplete dictionary are the same. The OMP algorithm is a special case when the original signal is an atom.
- MUSIC: The MUSIC method was first proposed in []. Based on the feature structure analysis, the MUSIC method is a classical super-resolution spatial spectrum estimation method. In this algorithm, characteristic decomposition is conducted for the covariance matrix of any array output data, which leads to a signal subspace orthogonal with a noise subspace corresponding to the signal components.
- TAN: The TAN method is proposed in []. The TAN method provides an approach to deal with off-grid signals. By converting the atomic norm minimization into a SDP problem and introduces the constraint of toeplitz matrix, the DOA estimation performance is improved significantly.
- OGSBI: appeared in []. The OGSBI can process off-grid signal model. The method can be applies to both single measurement vector (SMV) and multiple measurement vector (MMV) cases, while exploiting the combined sparsity among different measurements through supposing a Laplace prior for any measurements.
The above methods are classical DOA estimation algorithms, so we choose them as a comparison to show the estimation capability of the method raised above. Additionally, many other articles like [] shows that some simulation parameters such as SNRs, the number of antennas and samples will influence the simulation results significantly. In this paper, we also choose these variables to be our simulation parameters.
The range of phase uncertainties are from to 5 °. The gain errors are from 0.9 times to 1.1 times of original value. Both gain and phase errors obey the Gaussion distribution.
In this paper, The numerical results is achieved by much quantities of Monte Carlo trials and the results can be reproduced by using the given parameters. The DOA estimation performance is measured by the root-mean-square error (RMSE)
where we use K to denote the number of signals, and to denote the number of Monte Carlo simulations. and respectively denote the estimated and ground-truth DOA vector in the i-th Monte Carlo simulation.
First, Figure 2 shows the estimated polynomials of proposed method processing narrow-band signals and wide-band signals. Narrow-band signals are generated by wide-band signals passing through low-pass filters. The DOA estimation errors (in deg) of proposed method in processing narrow-band signals and wide-band signals are and , respectively. This figure reveals that performance can be improved by raised method in processing narrow-band signals than wide-band signals, which indicates that the proposed method is more applicable to deal with narrow-band signal recovery problem. Thus, the narrow-band signals are used as our received signals in the following simulation experiments.
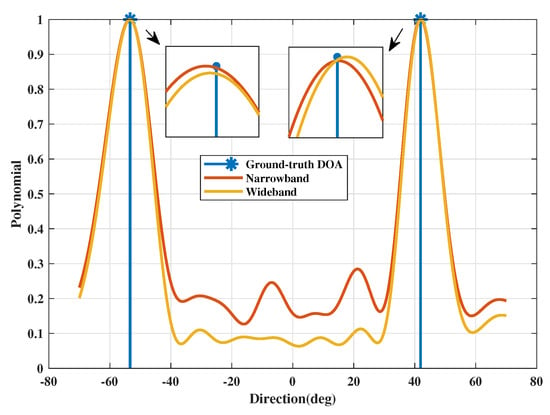
Figure 2.
The polynomials in dual problem for DOA estimation.
Figure 3 shows that the performance of estimating for arrival direction can be influenced by the change of correlation coefficients and an increased value of the correlation coefficient the estimation degradation. Furthermore, the proposed method can performs better compared with existing methods such as MUSIC, SOMP, OGSBI and TAN. The performance of traditional methods deteriorates much faster than proposed methods, as the correlation coefficient increases.
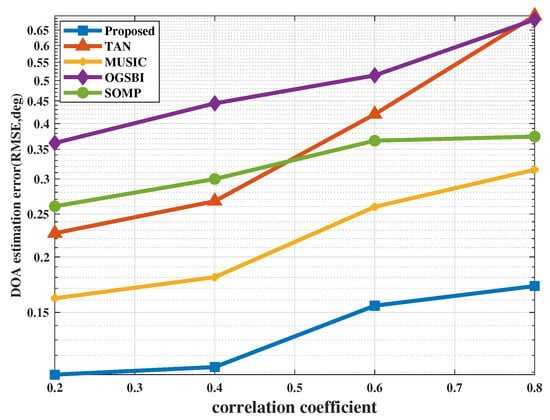
Figure 3.
DOA estimation performance with different correlation coefficients.
In Figure 4, we compare the estimated polynomials of the proposed method and TAN. The DOA estimation errors (in deg) of proposed method and the traditional atomic norm-based method are and , respectively. According to this figure, we can know that the proposed method can reach a much better performance than the traditional method both in gain and phase estimation.Then, estimated spatial spectrum of 2 target signals are shown in Figure 5. In this figure, the raised method is compared with 4 traditional DOA estimation methods including MUSIC, OGSBI, SOMP and TAN. We can see that the signals recovered by the proposed method are more closer to the target signals than the other four methods. Table 2 gives the corresponding estimated directions for 2 signals. The DOA estimation errors (in deg) of proposed method, SOMP, OGSBI, MUSIC and the traditional atomic norm-based method are , , , and and , respectively. Thus, the direction performance is better using the raised method than the traditional method such as SOMP, OGSBI, MUSIC and TAN.
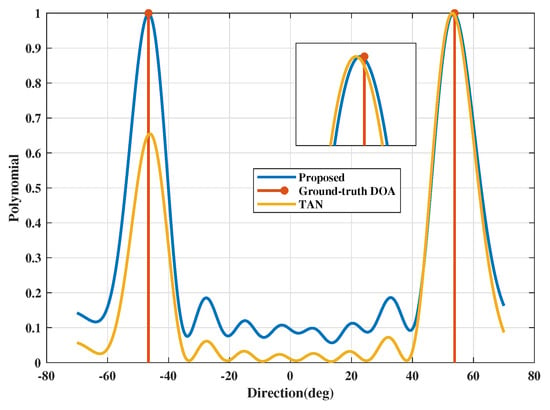
Figure 4.
The polynomials in dual problem for DOA estimation.
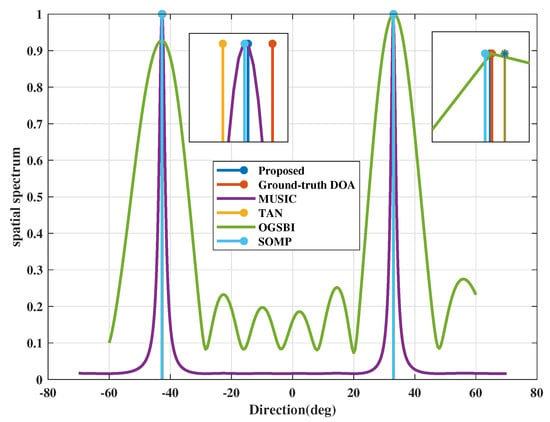
Figure 5.
The spatial spectrum for DOA estimation.

Table 2.
Simulation time.
Moreover, Figure 6 shows the comparison of direction finding capability of raised method with other four traditional methods in with different SNRs, and the SNR falls in the range of 0 dB to 40 dB. The capability of direction finding improves greatly with the increase of SNR in the case that the SNR is smaller than 10 dB. Besides, the direction finding capability almost unchanged in the scenario with the SNR is larger than 10 dB. According to this figure, the proposed method behaves better than the other methods, including SOMP, MUSIC, OGSBI and TAN. The associated CRLB of DOA estimation is also shown in Figure 6. We can conclude that the proposed method is closet to the CRLB among the existing methods including SOMP, MUSIC, OGSBI and TAN.
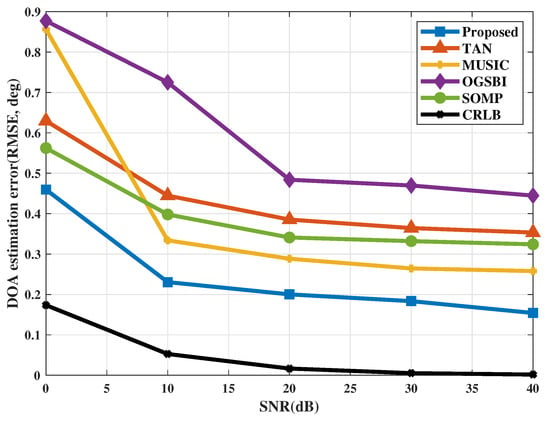
Figure 6.
DOA estimation performance with different SNRs.
As shown in Figure 7, the direction finding performs better with the sample number increases. The better performance can be reached by the proposed method than the existing methods including MUSIC, SOMP, OGSBI and TAN with different sample numbers.
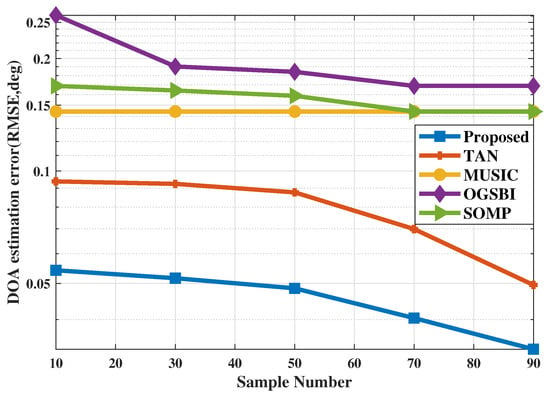
Figure 7.
DOA estimation performance with different sample numbers.
Figure 8 shows the direction finding performances with different quantities of antennas. With the increasing number of antennas, the DOA estimation performance improves. When less than 20 antennas exist in the ULA system, raised method performs similarly to other traditional DOA estimation methods including MUSIC, SOMP and OGSBI and TAN. When the number is larger than 30, the proposed method outperforms the others.
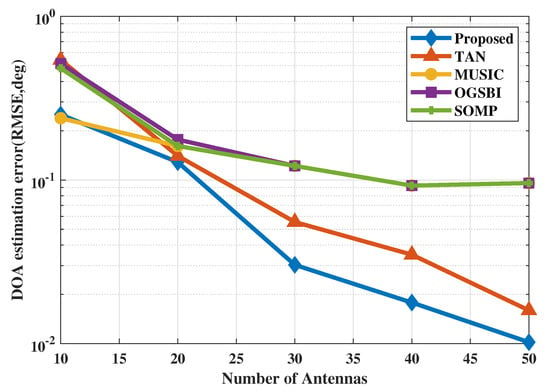
Figure 8.
DOA estimation performance with different antenna numbers.
Finally, Table 3 compares the computational time between raised method and the other 4 state-of-the-art methods. OGSBI has the least computational time, but the performance is much worse. TAN has the longest computational time and the proposed method is the second. Compared to the TAN method, the proposed method has the less computation complexity and better estimation performance.Thus, at an acceptable cost of computation complexity, the off-grid DOA estimation performance with inconsistent antennas and correlated signals are improved using the proposed method.

Table 3.
Simulation time.
6. Conclusions
This paper has investigated a novel gain and phase errors compensation method that is capable of the direction of arrival (DOA) estimation in the ULA system. The system model in the scenario with inconsistent antennas is formulated by introducing a diagonal matrix whose elements are gain-phase uncertainties. Thus, the DOA estimation problem has been transfered to a sparse reconstruction one. Then, the proposed method is developed concentrating on the dual of the atomic norm minimization problem and the corresponding convex optimization problem is addressed using semidefinite programming (SDP). We also derive the CRLB of the system model. According to the simulation results, the cost-efficient method raised in this paper shows better performance than the traditional DOA estimation methods. Processing uncorrelated signals by the raised method will be the focus of our future work.
Author Contributions
Data curation, P.C. and Z.C. (Zhenxin Cao); Funding acquisition, P.C.; Resources, Z.C. (Zhimin Chen); Software, X.Z. and L.L.; Writing—original draft, X.Z. and L.L.; Writing—review & editing, P.C.
Funding
This work was supported in part by the the National Natural Science Foundation of China (Grant No. 61801112, 61601281), the Pre-research fund of Equipments of China (Grant No. JZX7Y20190258056301), the Natural Science Foundation of Jiangsu Province (Grant No. BK20180357), the Open Program of State Key Laboratory of Millimeter Waves (Southeast University, Z201804), Nanjing Overseas Science and Technology Project (Grant No. 1104000384), and the Fundamental Research Funds for the Central Universities (Grant No. 2242019k1G022).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, P.; Qi, C.; Wu, L.; Wang, X. Waveform design for Kalman filter-based target scattering coefficient estimation in adaptive radar system. IEEE Trans. Veh. Technol. 2018, 67, 11805–11817. [Google Scholar] [CrossRef]
- Cao, Z.; Chen, P.; Chen, Z.; He, X. Maximum likelihood-based methods for target velocity estimation with distributed MIMO radar. Electronics 2018, 7, 29. [Google Scholar] [CrossRef]
- Krim, H.; Viberg, M. Two decades of array signal processing research: The parametric approach. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Winters, J. On the Capacity of Radio Communication Systems with Diversity in a Rayleigh Fading Environment. IEEE J. Sel. Areas Commun. 1987, 5, 871–878. [Google Scholar] [CrossRef]
- Kay, S.M.; Marple, S.L. Spectrum analysis-A modern perspective. Proc. IEEE 1981, 69, 1380–1419. [Google Scholar] [CrossRef]
- Ables, J.G. Maximum Entropy Spectral Analysis. Astron. Astrophys. Suppl. Ser. 1974, 15, 383. [Google Scholar]
- Capon, J. High-resolution frequency-wavenumber spectrum analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef]
- Schmidt, R.O. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Roy, R.; Paulraj, A.; Kailath, T. Comparative performance of ESPRIT and MUSIC for direction-of-arrival estimation. In Proceedings of the ICASSP ’87. IEEE International Conference on Acoustics, Speech, and Signal Processing, Dallas, TX, USA, 12 April 1987; pp. 2344–2347. [Google Scholar]
- Roy, R.; Paulraj, A.; Kailath, T. ESPRIT—A Subspace Rotation Approach to Estimation of Parameters of Cisoids in Noise. Trans. Acoust. Speech Signal Process. 1986, 34, 1340–1342. [Google Scholar] [CrossRef]
- Stoica, P.; Arye, N. MUSIC, maximum likelihood, and Cramer-Rao bound. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 720–741. [Google Scholar] [CrossRef]
- Ottersten, B.; Viberg, M.; Stoica, P.; Nehorai, A. Exact and Large Sample Maximum Likelihood Techniques for Parameter Estimation and Detection in Array Processing; Springer: Berlin/Heidelberg, Germany, 1993; pp. 99–151. [Google Scholar]
- Gorodnitsky, I.F.; George, J.S.; Rao, B.D. Neuromagnetic source imaging with focuss: A recursive weighted minimum norm algorithm. Electroencephalogr. Clin. Neurophysiol. 1995, 95, 231–251. [Google Scholar] [CrossRef]
- Malioutov, D.; Cetin, M.; Willsky, A.S. A sparse signal reconstruction perspective for source localization with sensor arrays. IEEE Trans. Signal Process. 2005, 53, 3010–3022. [Google Scholar] [CrossRef]
- Chen, P.; Zheng, L.; Wang, X.; Li, H.; Wu, L. Moving Target Detection Using Colocated MIMO Radar on Multiple Distributed Moving Platforms. IEEE Trans. Signal Process. 2017, 65, 4670–4683. [Google Scholar] [CrossRef]
- Malioutov, D.M.; Cetin, M.; Willsky, A.S. Source localization by enforcing sparsity through a Laplacian prior: An SVD-based approach. In Proceedings of the IEEE Workshop on Statistical Signal Processing, St. Louis, MO, USA, 28 September–1 October 2003; pp. 573–576. [Google Scholar]
- Cetin, M.; Malioutov, D.M.; Willsky, A.S. A variational technique for source localization based on a sparse signal reconstruction perspective. In Proceedings of the 2002 IEEE International Conference on Acoustics, Speech, and Signal Processing, Orlando, FL, USA, 3 May 2002; pp. III:2965–III:2968. [Google Scholar]
- Stoica, P.; Babu, P.; Li, J. Spice: A sparse covariance-based estimation method for array processing. IEEE Trans. Signal Process. 2011, 59, 629–638. [Google Scholar] [CrossRef]
- Chen, S.; Donoho, D.; Saunders, M. Atomic decomposition by basis pursuit. SIAM Rev. 2001, 43, 129–159. [Google Scholar] [CrossRef]
- Candes, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Zhang, W.; Han, Y.; Jin, M.; Qiao, X. Multiple-Toeplitz Matrices Reconstruction Algorithm for DOA Estimation of Coherent Signals. IEEE Access 2019, 7, 49504–49512. [Google Scholar] [CrossRef]
- Shan, T.; Wax, M.; Kailath, T. On spatial smoothing for direction-of-arrival estimation of coherent signals. IEEE Trans. Acoust. Signal Process. 1985, 33, 806–811. [Google Scholar] [CrossRef]
- Pillai, S.U.; Kwon, B.H. Forward/backward spatial smoothing techniques for coherent signal identification. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 8–15. [Google Scholar] [CrossRef]
- Thompson, J.S.; Grant, P.M.; Mulgrew, B. Performance of spatial smoothing algorithms for correlated sources. IEEE Trans. Signal Process. 1996, 44, 1040–1046. [Google Scholar] [CrossRef]
- Chen, H.; Hou, C.; Wang, Q.; Huang, L.; Yan, W. Cumulants-Based Toeplitz Matrices Reconstruction Method for 2-D Coherent DOA Estimation. IEEE Sens. J. 2014, 14, 2824–2832. [Google Scholar] [CrossRef]
- Han, F.; Zhang, X. An ESPRIT-like algorithm for coherent DOA estimation. IEEE Antennas Wirel. Propag. Lett. 2005, 4, 443–446. [Google Scholar]
- Candes, E.J.; Wakin, M.B. An Introduction to Compressive Sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Yang, Z.; Xie, L. On Gridless Sparse Methods for Line Spectral Estimation From Complete and Incomplete Data. IEEE Trans. Signal Process. 2015, 63, 3139–3153. [Google Scholar] [CrossRef]
- Chi, Y.; Scharf, L.L.; Pezeshki, A.; Calderbank, A.R. Sensitivity to Basis Mismatch in Compressed Sensing. IEEE Trans. Signal Process. 2011, 59, 2182–2195. [Google Scholar] [CrossRef]
- Chandrasekaran, V.; Recht, B.; Parrilo, P.A.; Willsky, A.S. The Convex Geometry of Linear Inverse Problems. Found. Comput. 2012, 12, 805–849. [Google Scholar] [CrossRef]
- Semper, S.; Roemer, F.; Hotz, T.; Del Galdo, G. Grid-free direction-of-arrival estimation with compressed sensing and arbitrary antenna arrays. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 3251–3255. [Google Scholar]
- Candes, E.J.; Romberg, J.K.; Tao, T. Stable signal recovery from incomplete and inaccurate measurements. Commun. Pure Appl. Math. 2006, 59, 1207–1223. [Google Scholar] [CrossRef]
- Recht, B.; Fazel, M.; Parrilo, P.A. Guaranteed Minimum-Rank Solutions of Linear Matrix Equations via Nuclear Norm Minimization. Siam Rev. 2010, 52, 471–501. [Google Scholar] [CrossRef]
- Candes, E.J.; Fernandezgranda, C. Towards a mathematical theory of super-resolution. Commun. Pure Appl. Math. 2014, 67, 906–956. [Google Scholar] [CrossRef]
- Yang, Z.; Xie, L. Enhancing sparsity and resolution via reweighted atomic norm minimization. IEEE Trans. Signal Process. 2016, 64, 995–1006. [Google Scholar] [CrossRef]
- Chen, Y.; Chi, Y. Robust spectral compressed sensing via structured matrix completion. IEEE Trans. Inf. Theory 2014, 60, 6576–6601. [Google Scholar] [CrossRef]
- Yang, J.; Liao, G.; Li, J. An efficient off-grid DOA estimation approach for nested array signal processing by using sparse Bayesian learning strategies. Signal Process. 2016, 128, 110–122. [Google Scholar] [CrossRef]
- Tang, G.; Bhaskar, B.N.; Shah, P.; Recht, B. Compressed sensing off the grid. IEEE Trans. Inf. Theory 2013, 59, 7465–7490. [Google Scholar] [CrossRef]
- Chen, P.; Cao, Z.; Chen, Z.; Yu, C. Sparse off-grid DOA estimation method with unknown mutual coupling effect. Digit. Signal Process. 2019, 90, 1–9. [Google Scholar] [CrossRef]
- Bhaskar, B.N.; Recht, B. Atomic norm denoising with applications to line spectral estimation. In Proceedings of the Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, 28–30 September 2011; pp. 261–268. [Google Scholar] [CrossRef]
- Li, Y.; Chi, Y. Off-the-grid line spectrum denoising and estimation with multiple measurement vectors. IEEE Trans. Signal Process. 2016, 64, 1257–1269. [Google Scholar] [CrossRef]
- Runze, D.; Ying, G.; Hongguang, L.; Ping, S.; Yinsong, Y. Parameter estimation of multi frequency-hopping signals based on atomic norm. In Proceedings of the 2018 10th International Conference on Communication Software and Networks (ICCSN), Chengdu, China, 6–9 July 2018; pp. 391–395. [Google Scholar] [CrossRef]
- Ephraim, Y.; Malah, D. Speech enhancement using a minimum-mean square error short-time spectral gain estimator. IEEE Trans. Acoust. Speech Signal Process. 1984, 32, 1109–1121. [Google Scholar] [CrossRef]
- Chen, P.; Cao, Z.; Chen, Z.; Liu, L.; Feng, M. Compressed sensing-based doa estimation with unknown mutual coupling effect. Electronics 2018, 7, 424. [Google Scholar] [CrossRef]
- Chen, P.; Cao, Z.; Chen, Z.; Wang, X. Off-grid DOA estimation using sparse bayesian learning in MIMO radar with unknown mutual coupling. IEEE Trans. Signal Process. 2019, 67, 208–220. [Google Scholar] [CrossRef]
- Ly-Gagnon, D.; Tsukamoto, S.; Katoh, K.; Kikuchi, K. Coherent detection of optical quadrature phase-shift keying signals with carrier phase estimation. J. Lightw. Technol. 2006, 24, 12–21. [Google Scholar] [CrossRef]
- Friedlander, B.; Weiss, A. Eigenstructure methods for direction finding with sensor gain and phase uncertainties. In Proceedings of the ICASSP-88, International Conference on Acoustics, Speech, and Signal Processing, New York, NY, USA, 11–14 April 1988; pp. 2681–2684. [Google Scholar]
- Liu, A.; Liao, G.; Zeng, C.; Yang, Z.; Xu, Q. An Eigenstructure Method for Estimating DOA and Sensor Gain-Phase Errors. IEEE Trans. Signal Process. 2011, 59, 5944–5956. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, X.; Chen, P. Compressed sensing-based doa estimation with antenna phase errors. Electronics 2019, 8, 294. [Google Scholar] [CrossRef]
- Lu, Z.; Jiang, H.; Gao, Y.; Shi, Y. Gain and phase errors self-correcting algorithm based on the uniform circular array. In Proceedings of the 2012 2nd International Conference on Computer Science and Network Technology, Changchun, China, 29–31 December 2012; pp. 136–140. [Google Scholar]
- Wang, J.; Song, Y. Self-calibration algorithm for the gain and phase error of the multiple beam antenna. In Proceedings of the 2009 International Conference on Computational Intelligence and Software Engineering, Wuhan, China, 11–13 December 2009; pp. 1–3. [Google Scholar]
- Stoica, P.; Nehorai, A. MUSIC, maximum likelihood and Cramer-Rao bound: Further results and comparisons. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 2140–2150. [Google Scholar] [CrossRef]
- Cheng, Y. Generalization of the theorems of alternatives in semidefinite programming. In Proceedings of the 2007 IEEE International Conference on Automation and Logistics, Jinan, China, 18–21 August 2007; pp. 634–637. [Google Scholar]
- Tropp, J.A.; Gilbert, A.C.; Strauss, M.J. Algorithms for simultaneous sparse approximation. Part I: Greedy pursuit. Signal Process. 2006, 86, 572–588. [Google Scholar] [CrossRef]
- Chen, J.; Huo, X. Theoretical results on sparse representations of multiple-measurement vectors. IEEE Trans. Signal Process. 2006, 54, 4634–4643. [Google Scholar] [CrossRef]
- Yang, Z.; Xie, L.; Zhang, C. Off-grid direction of arrival estimation using sparse bayesian inference. IEEE Trans. Signal Process. 2013, 61, 38–43. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).