1. Introduction
An inertial navigation system (INS) can provide continuous and real-time navigation information for the carrier, and it is characterized by strong autonomy and good concealment. However, the navigation error of INS will accumulate over time, therefore it is hard to adapt to a long endurance mission. On the other hand, geomagnetic navigation is based on Earth’s geophysical field, which is passive, radiation-free and displays good stealth. Most importantly, the location error of geomagnetic navigation does not accumulate over time [
1,
2,
3,
4]. Therefore, constructing an inertial/ geomagnetic integrated navigation system can not only overcome the disadvantages of INS, such as accumulated navigation errors and poor long-term stability, but also can realize all-weather and all-region navigation.
According to their different combinations, inertial/geomagnetic integrated navigation algorithms can be divided into two categories, namely the loose and tight navigation algorithm. Generally speaking, the loose navigation algorithm mainly consists of the geomagnetic matching algorithm (GMA) and integrated navigation algorithm (INA), in which the locations evaluated by the GMA are used as observations of the integrated filter to estimate INS’s error [
5]. The structure of loose navigation is beneficial for fault diagnosis, and is convenient for adding other navigation subsystems, but its filtering accuracy is largely affected by the location precision of GMA. As for the tight navigation algorithm, the measured magnetic values are directly used as observations of the integrated navigation filter [
6]. As the measurement equation of tight navigation system is always nonlinear [
7,
8], the Extended Kalman Filter (EKF) [
9], Unscented Kalman Filter (UKF) [
10] and Particle Filter (PF) [
11,
12,
13] are most commonly used. A linear approximation of the geomagnetic map is needed in EKF and UKF, but not for PF. Considering the non-linearity of the geomagnetic map, the EKF may easily diverge. Secondly, when other navigation subsystems are added, the loose INA is easier to implement.
It should be noted that the GMA is the core of loose INA, which estimates the carrier’s position by matching the geomagnetic characteristics measured in real time with the geomagnetic map previously stored in the navigation computer. Once the accuracy of the magnetic map is fixed, GMA is mainly affected by the magnetic measurements. Generally, the geomagnetic measurement error includes the instrument error, which is caused by the structure and materials of the magnetometer [
14] and the interference field error, which is caused by the superposition of external interference field. Among them, the external interference field is mainly led by the hard and soft magnetic material of the carrier, and the random magnetic field which is difficult to describe using the magnetic model. In general, the non-random interference field in geomagnetic measurement can be processed by model compensation algorithms, but for the random interference field and other unknown interference factors that may appear in practice, the compensation result is always unsatisfactory. Currently, there are two ways to solve the problem: (1) In order to reduce the influence of interference field, process the magnetic measurements, such as Hilbert-Huang transform (HHT) [
15], wavelet transform [
16] and so on. (2) To study new GMA with good robustness.
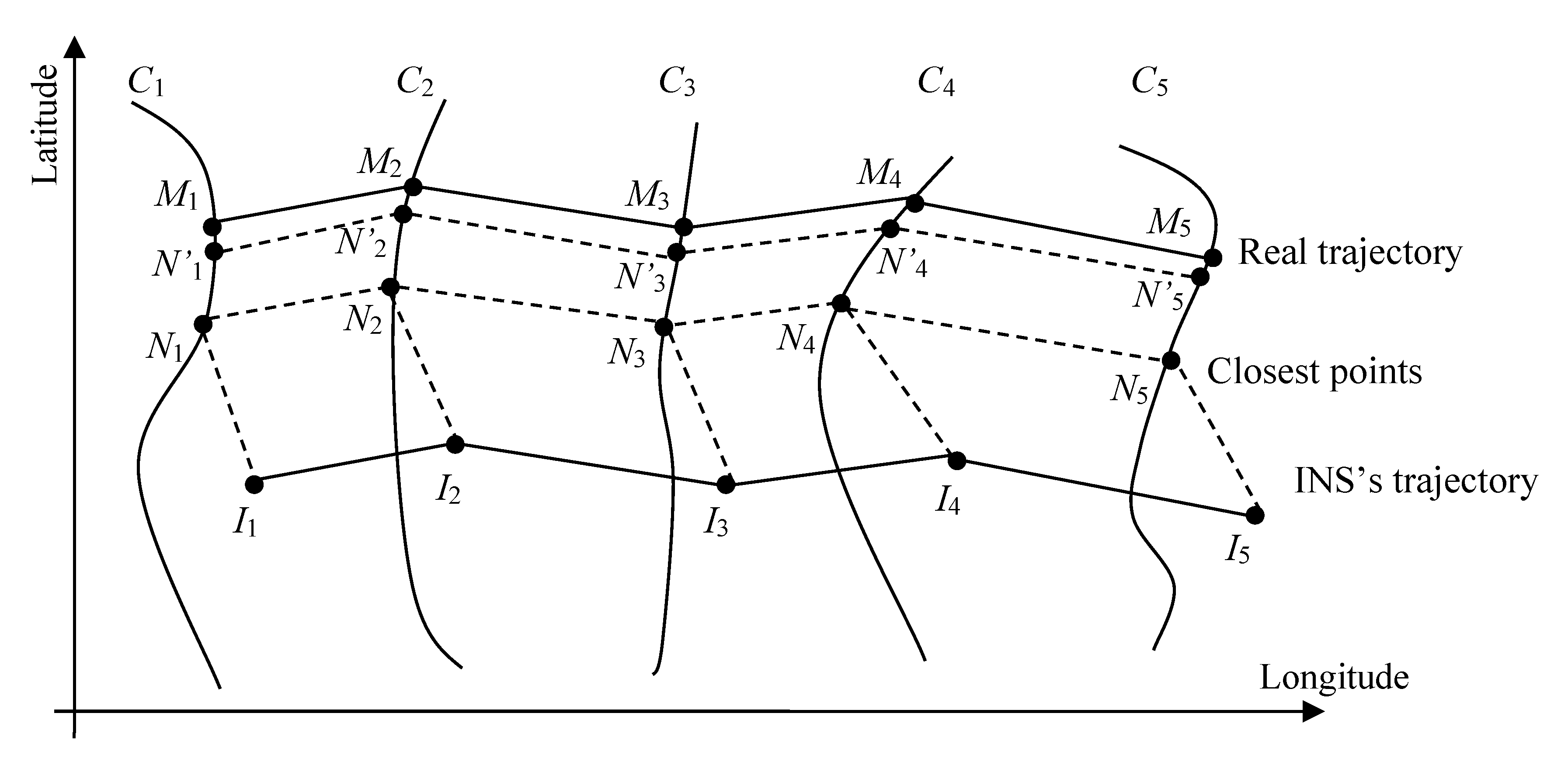
The Iterated Closest Contour Point (ICCP) algorithm is a common method in geomagnetic matching, whose basic principle is shown in
Figure 1. As is illustrated, suppose the matching length of ICCP algorithm is 5;
C1 to
C5 are five geomagnetic contour lines of a navigation area;
M1 to
M5 denote the real trajectory of the carrier; the carrier’s coordinates offered by the reference navigation system (usually the INS) at the sampling points are denoted by
I1 to
I5.
If there is no magnetic interference, point
Mn (
n = 1, 2, …, 5) must be located on a geomagnetic contour line, but on which point of the contour is unknown. At the first step of geomagnetic ICCP algorithm, it finds the points closest to INS’s trajectory on the contour lines. The closest points are represented by
N1 to
N5 in
Figure 1. Then ICCP algorithm will calculate the rigid transformation
T (including rotation and transformation) between
In and
Nn (
n = 1, 2, …, 5). Afterwards, the transformation
T is applied to INS’s trajectory, and the new trajectory is denoted by
N’1 to
N’5. In next interaction, a new transformation will be used to minimize the distance between
N’n (
n = 1, 2, …, 5) and their closest points. The criterion to measure the distance between the points is in Formula (1). The above process will be iterated many times. Finally,
In will continuously approximate the real trajectory of the carrier.
where
d measures the distance of
In and its corresponding contour line
Cn.
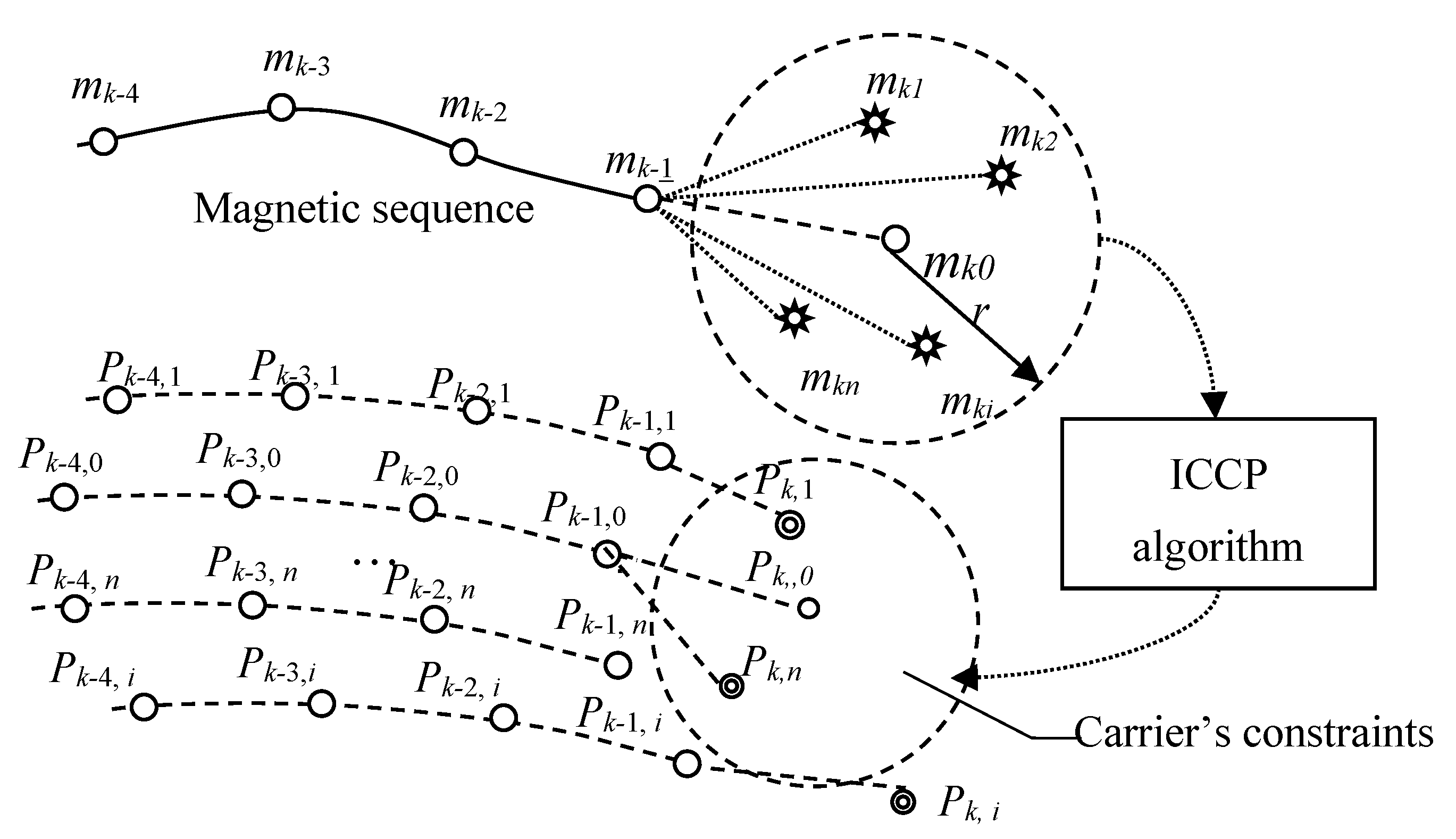
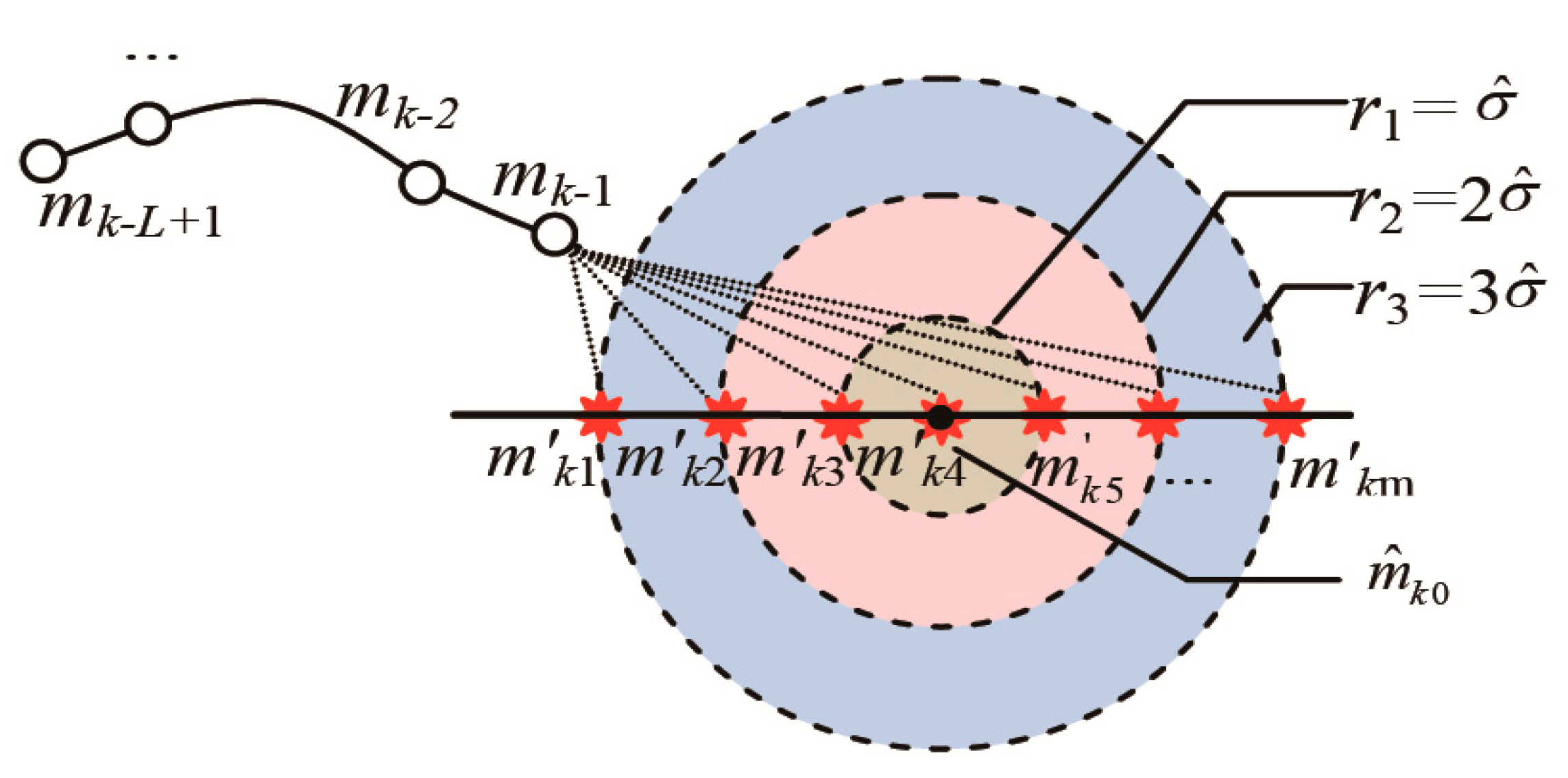
The ICCP algorithm assumes that the magnetic sensor has no measurement error, and the real position of the carrier is located on or very close to the magnetic contour that corresponds to the magnetic measurement [
17]. If the hypothesis is not satisfied, the accuracy of GMA would be hard to guarantee. Wu proposed a GMA based on the tree searching algorithm. It does not need to consider the distribution of measurement errors and has a certain anti-interference ability [
18]. Xiao combined the probability data association (PDA) algorithm with the ICCP algorithm [
19,
20] and proposed a PDA-ICCP algorithm. It regarded all measurements of the magnetometer within a certain confidence range in interference environment as the effective measurements of a position, and finally evaluated the carrier’s location with the PDA fusion algorithm. The algorithm comprehensively considered the effects of measurement error and interference field and improved the GMA’s adaptability to a practical environment.
To guarantee the accuracy of the integrated inertial/geomagnetic navigation under interference environment, the PDA-ICCP algorithm is improved in our study and on basis of it, a new integrated navigation filter is designed. Finally, the feasibility and effectiveness of the proposed algorithm are verified through simulation physical and experiments.
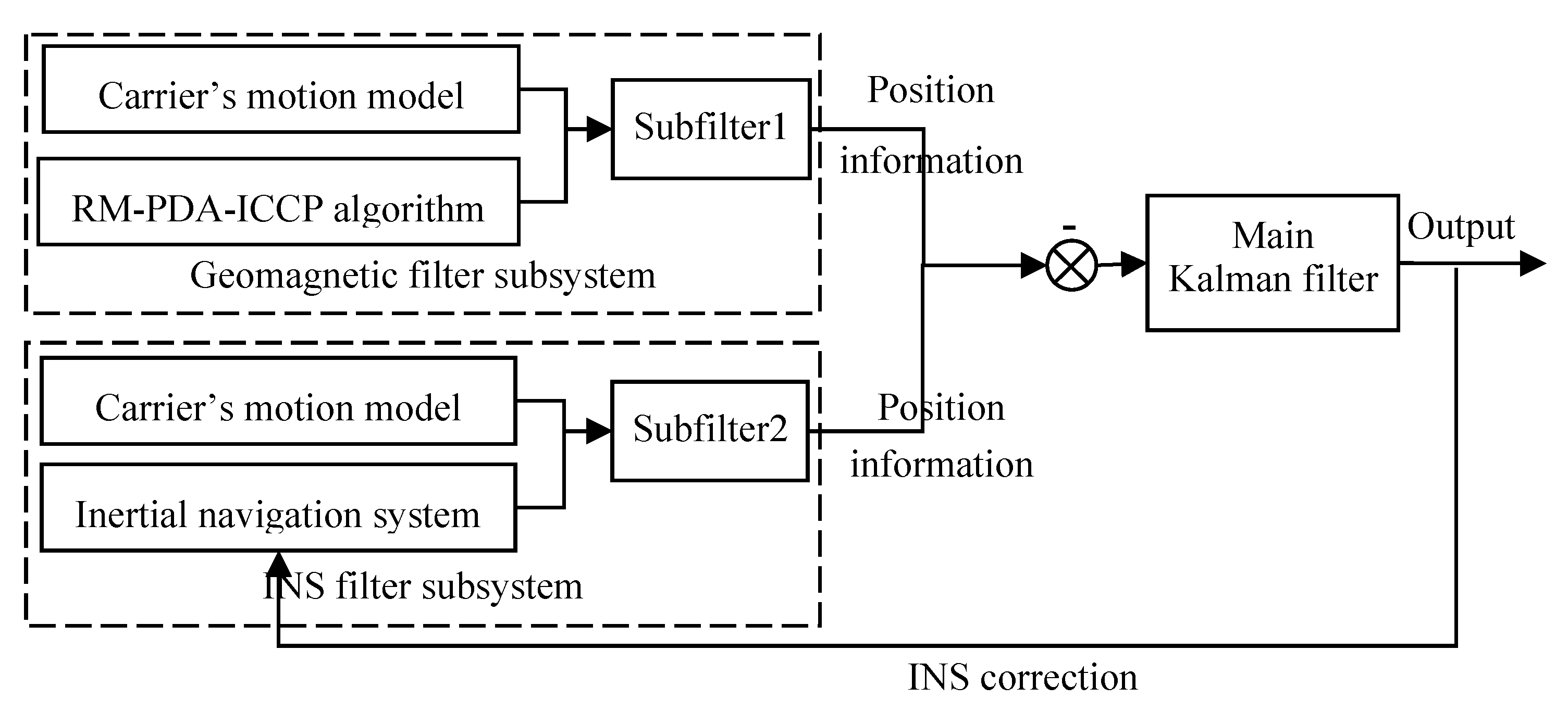
3. Design of the Integrated Navigation System
According to different state variables, the loose integrated navigation algorithm can be divided into two types: the one based on position error [
2] and the one based on location (and speed) [
5]. The former usually takes the error equation of INS as the state equation of the integrated navigation filter, and the position error of GMA as the observations to estimate the attitude error, velocity error and position error of the carrier. While the latter directly takes the motion equation of the carrier as state equation, and updates the position and speed immediately. The above two integrated algorithms have been applied in integrated navigation system that based on geophysical fields such as geomagnetism, gravity and terrain. In our study, a hierarchical filter is put forward. The inertial/geomagnetic integrated navigation system is designed in
Figure 5, which adopts the carrier’s location as the state variable. As is shown, the hierarchical filter is divided into two layers, the first layer consists of two subfilters, and the second one includes a main filter.
The above system consists of two sub-filters and one main filter. First, the geomagnetic and inertial navigation subsystems independently execute the Kalman filtering algorithm and give an estimate of the carrier’s position. Then the main filter integrates the position information of two subsystems to evaluate the position error and velocity error of the carrier. Ultimately, the INS can be corrected. In the following, the state equation, measurement equation and filtering algorithm of the integrated navigation system are described in detail.
3.1. State Equation and Observation Equation of the Subsystem
Assume the carrier is in the uniform rectilinear motion, the matching results of GMA are taken as observations of the filter, and the position and velocity in longitude and latitude are taken as the state, namely
, then the state equation and observation equation of the geomagnetic filter subsystem can be expressed as:
where
,
,
,
T is the time between two sampling points,
Uk is the random disturbance during the movement of the carrier,
Vk is the location estimation noise of GMA.
The RM-PDA-ICCP algorithm executes once a magnetic measurement is obtained. In the regions where the geomagnetic fluctuation is not very obvious, the RM-PDA-ICCP algorithm is prone to mismatching. If the mismatched results are sent to the main filter, the precision of integrated navigation system will greatly reduced. In this sense, the geomagnetic filter subsystem will evaluate a proper result for the main filter. Finally, the accuracy and real-time performance of the integrated navigation algorithm are ensured.
The state and observation equation of the inertial subsystem are the same as the geomagnetic filter subsystem, which are not discussed to keep our study concise.
3.2. State Equation and Observation Equation of the Main Filter
In the main filter, the position difference between two subsystems is taken as the observation. Its state equation and observation equation are:
where
,
wk is the system noise;
λGMNS and
λINS are the matching position of the geomagnetic filter subsystem and inertial subsystem in longitude respectively,
LGMNS and
LINS are the positions in latitude.
nk is the location estimation noise,
,
.
3.3. Integrated Filtering Algorithm
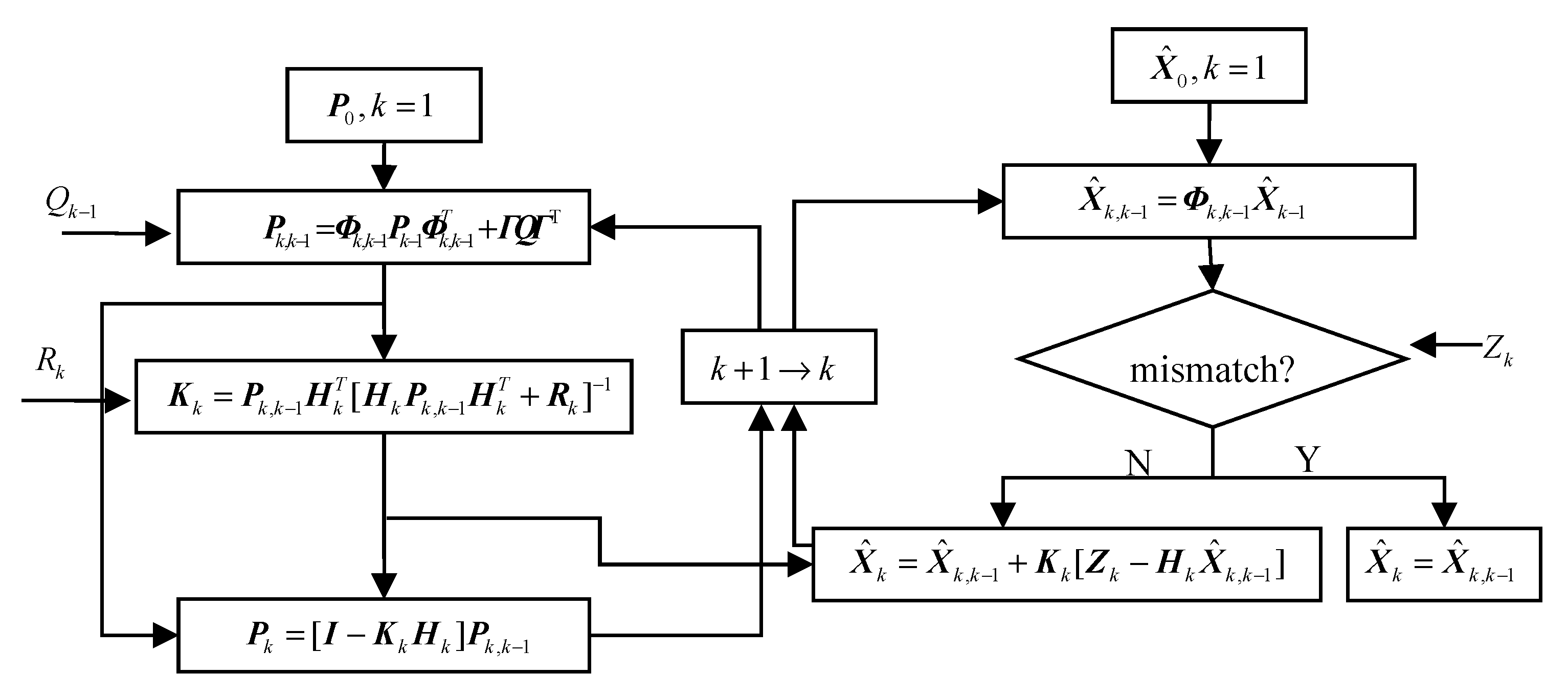
As the state and observation equations of the integrated navigation system are all linear, a standard KF algorithm can be adopted. The difference between the subfilters and main filter is that a threshold is set in the geomagnetic filter subsystem to restrict the matching results whose error is very large. The filtering and updating process of the geomagnetic filter subsystem is shown in
Figure 6, in which
Q and
R stand for the variance of the process noise
Uk and measurement noise
Vk;
Zk is the observation, which is corresponding to the matching results of RM-PDA-ICCP algorithm.
P0 and
are the initial states of filtering;
P is the covariance matrix,
K is the filtering gain matrix, and
is the state estimation of the subsystem. Other variables are the same with that in Formula (9)–(12).
In
Figure 6, the covariance matrix, gain matrix and filtering state are updated during the filtering process. If the observation
Zk exceeds the presupposed threshold, the estimated state
should be taken as current state
, otherwise
should be updated with the KF algorithm. The filtering process of the main filter is a standard KF.
In essence, the algorithm above belongs to the loose integrated navigation algorithm. Furthermore, only minor changes are needed when other auxiliary navigation methods are added to the integrated navigation system. In addition, introducing filtering algorithm to the geomagnetic matching module is beneficial to improve the adaptability to the geomagnetic environment.
In a word, the proposed algorithm can be summarized as follows:
Step 1: To execute the RM-PDA-ICCP algorithm and obtain the estimated position of the carrier;
Step 2: The result in Step 1 is taken as the observation of the geomagnetic filter subsystem;
Step 3: The information offered by the inertial system is used in the INS filter subsystem;
Step 4: The results of Step 2 and Step 3 are fused by the main filter. Finally, the positions of the carrier are continuously calculated.
5. Flight Experiment
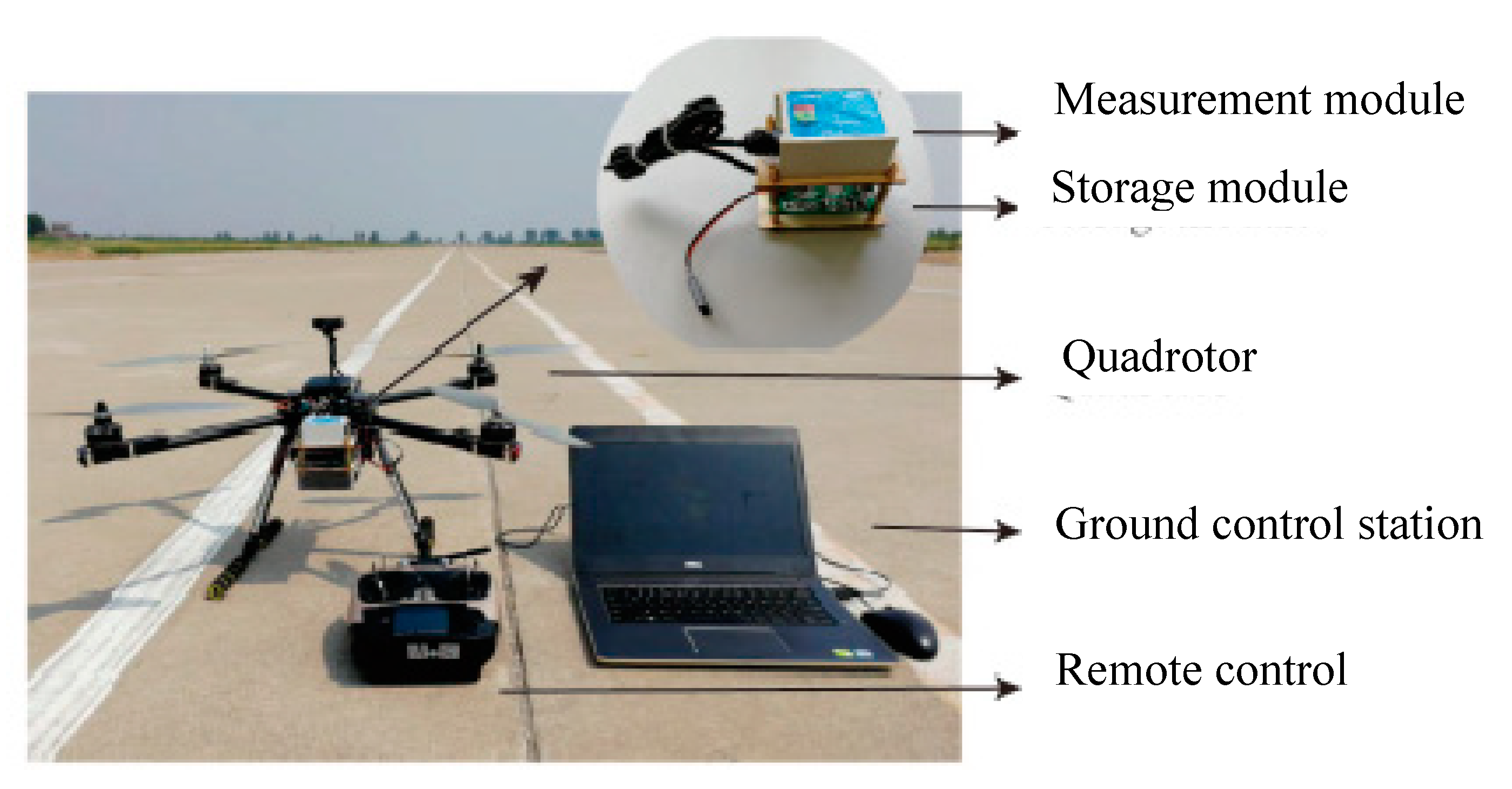
Considering the magnetic field in the air is relatively pure, a quadrotor is used in our study to test the proposed integrated navigation algorithm. The experiment system is shown in
Figure 12.
As is shown, the inertial/geomagnetic integrated navigation system mainly includes the following parts: the measurement and storage module, the quadrotor and the ground control station. Among them, the measurement module is a 10-axis high precision attitude-angle sensor made by Wit Smart Company, which contains the RM3100 geomagnetic sensor, inertial element and GPS module. Its main parameters are listed in
Table 2. The storage module uses a serial port to SD card to storage data. To avoid the influence of carrier’s material on the magnetic measurement, the frame of the quadrotor is made of carbon.
In the system, the real position of the carrier is given by GPS; the ground control station is used to communicate with the quadrotor, to load the planed trajectory and to conduct the integrated navigation algorithm.
The total magnetic values of the sensor are applied in navigation. Finally, a measured geomagnetic field with the size of 1400 m × 600 m is taken as the background, whose grid resolution is 25 m. The quadrotor is in the uniform rectilinear motion at the speed of 5 m/s with the starting point being (199.3 m, 201.5 m) and altitude 40 m. Suppose the baud rate of sensor module is 9600, its output frequency is 10 Hz. Limited by the endurance time of the quadrotor, the INS element has worked for a while before the flight experiment, so its accumulated error is obtained. Assume the original position errors of INS in longitude and latitude are both 40 m, namely the total error of INS is 56.57 m (about 2.26 magnetic grids), bias of the gyro is 1 °/h.
Then the proposed integrated navigation algorithm is executed. In the geomagnetic filter subsystem, the state and observation equation follow Formula (9) and (10), where T = 5 s. The variance matrix of the observation noise , and the process noise .
In the main filter, the process noise
. Other parameters are unchanged.
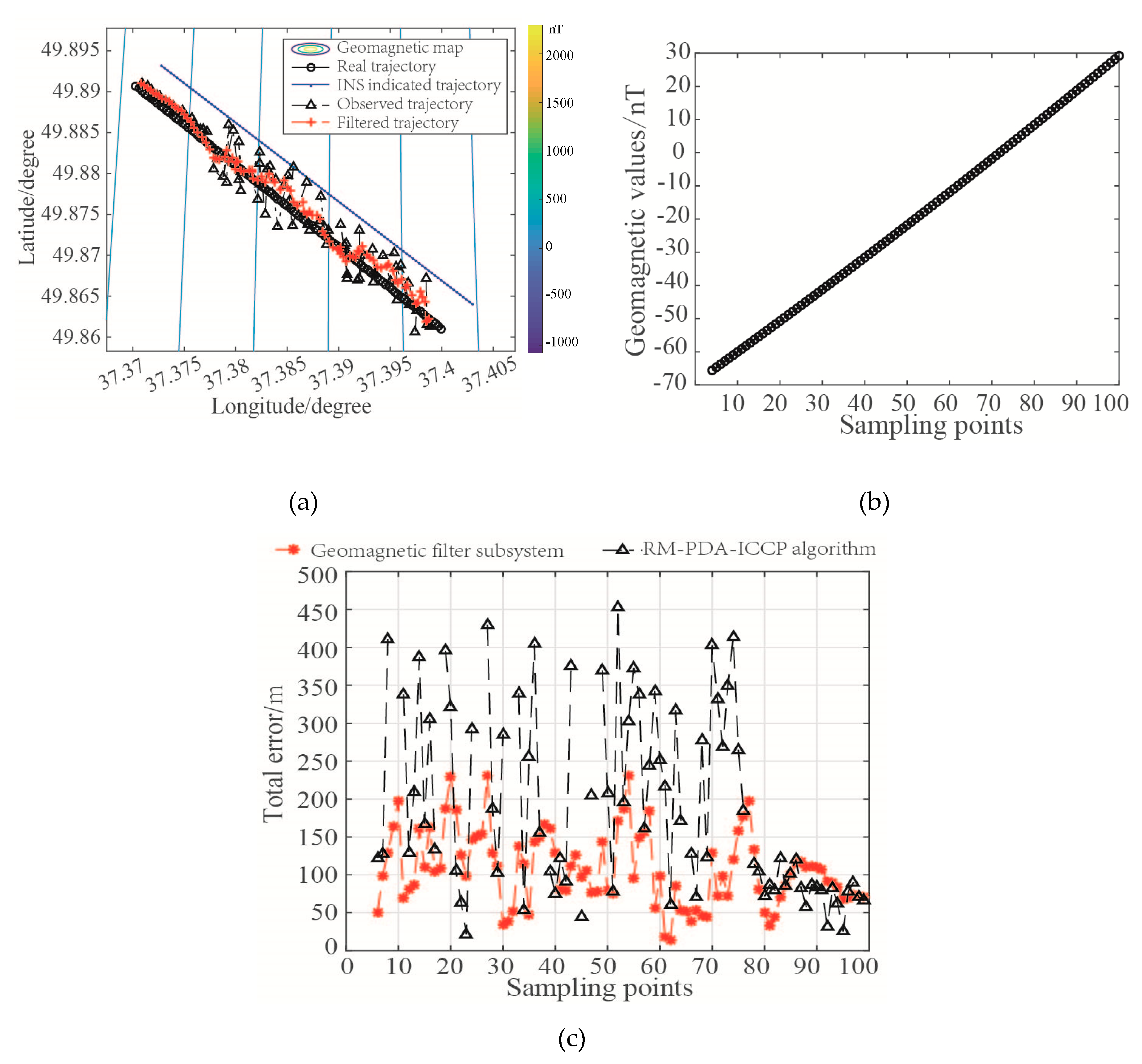
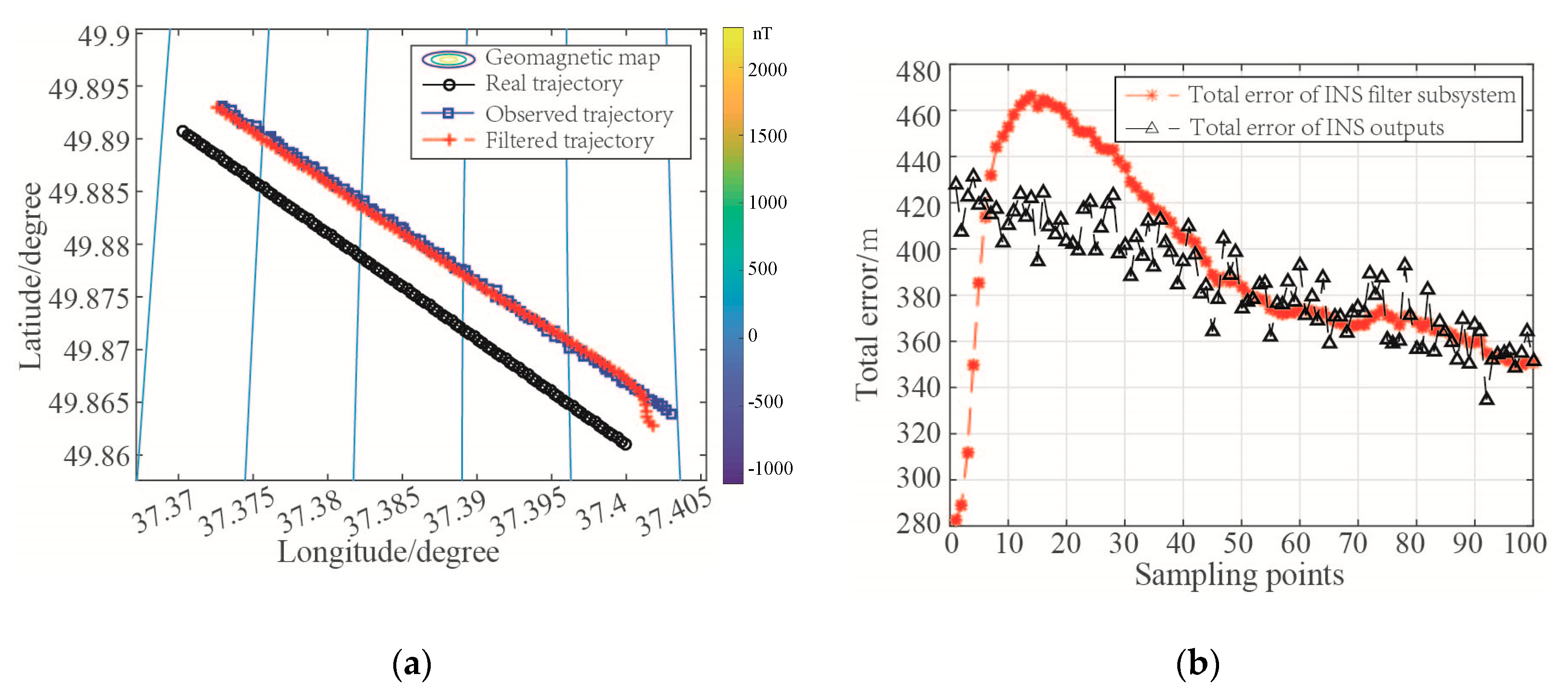
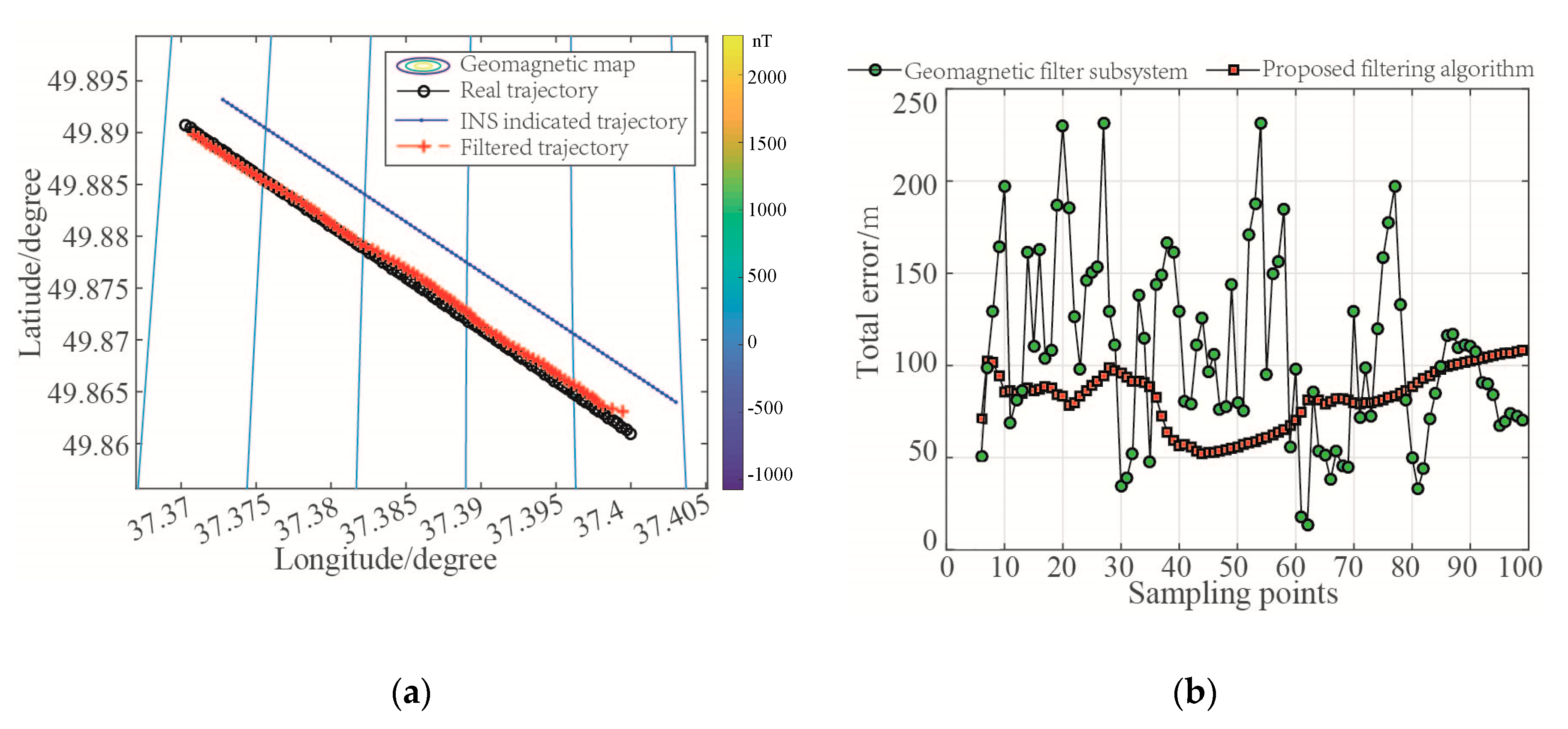
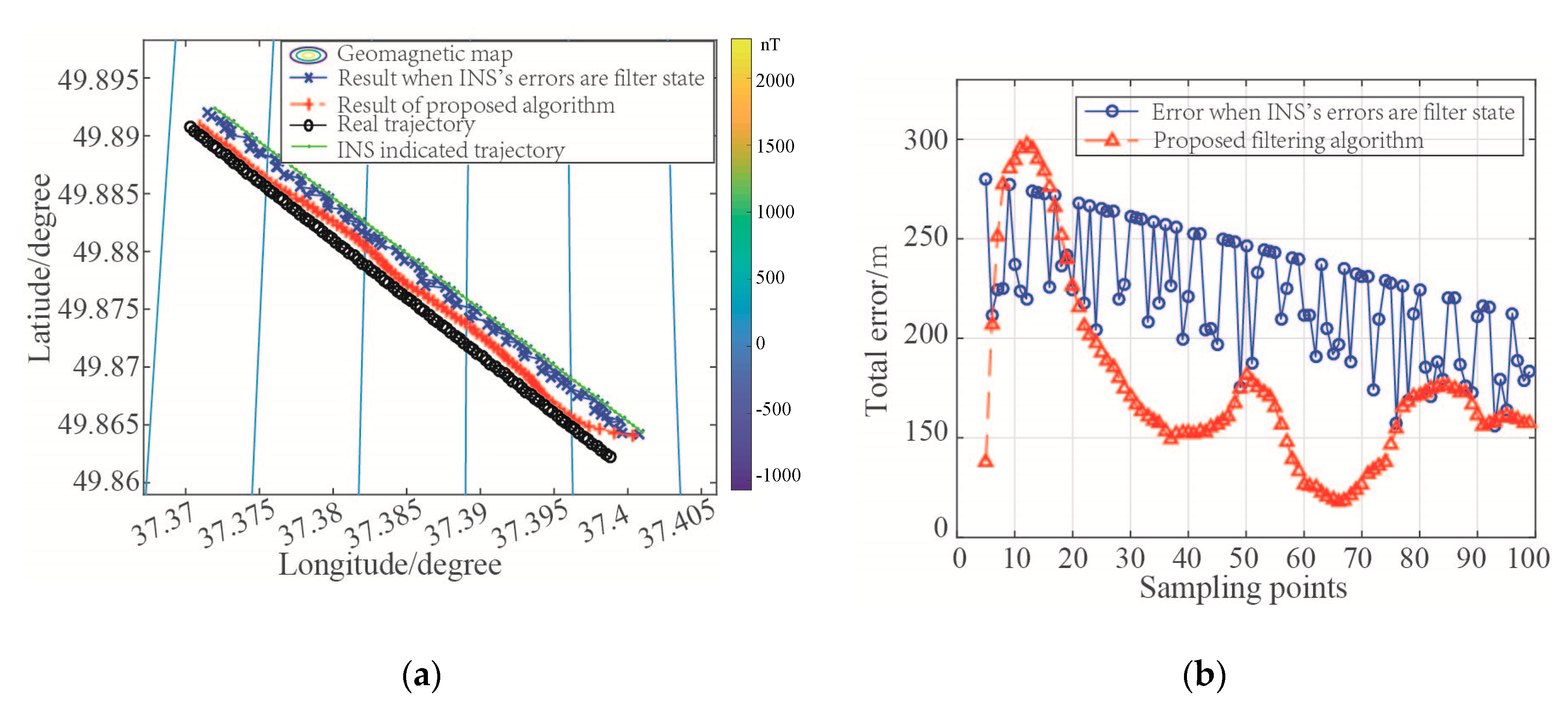
Figure 13,
Figure 14,
Figure 15 and
Figure 16 respectively show the filtering results of the geomagnetic filter subsystem and the integrated navigation system, and
Table 3 lists some statistical characteristics of the location error of each system.
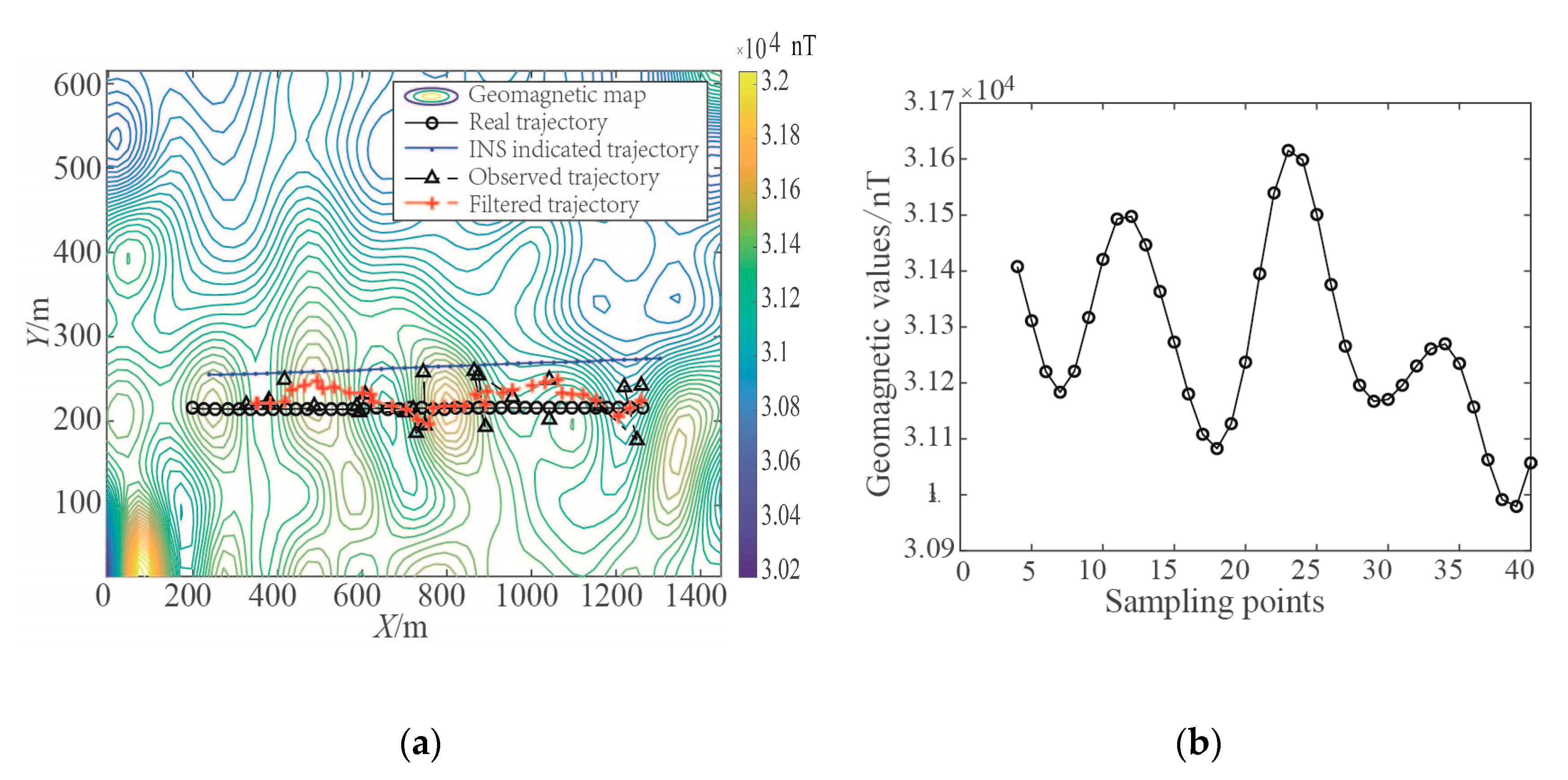
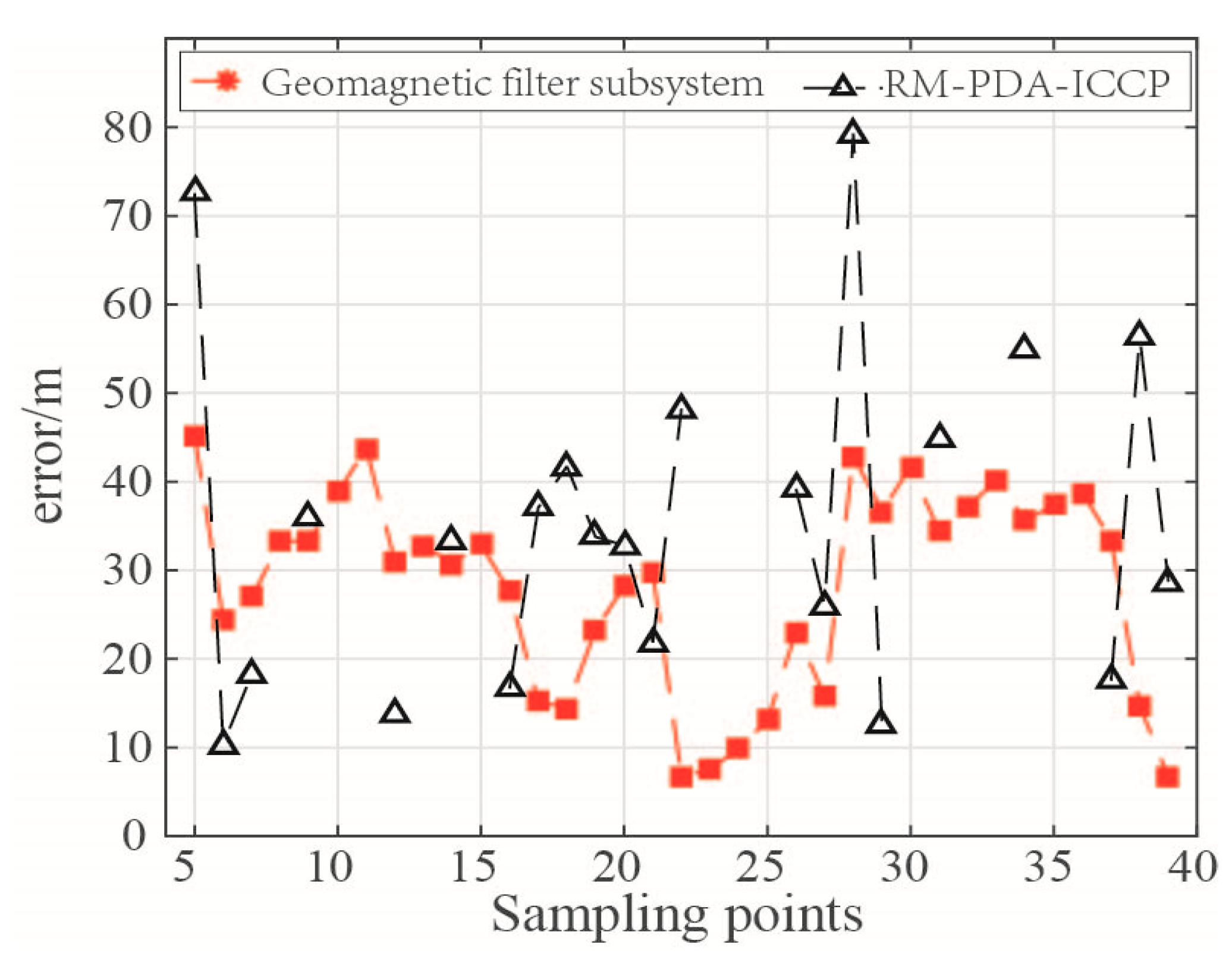
In
Figure 14, as all matching results corresponding to the RMs are beyond the threshold of effective matching, the RM-PDA-ICCP algorithm has no output at some sampling points. Besides, the matching errors at some points are too large, for example the 5th and the 28th sampling points. However, the total location error of the subsystem after filtering is within 50 m (about 2 magnetic grids). As a result, the locations of the carrier could be output continuously by the geomagnetic filter subsystem. Comparing the final filtered trajectory with the carrier’s real trajectory in
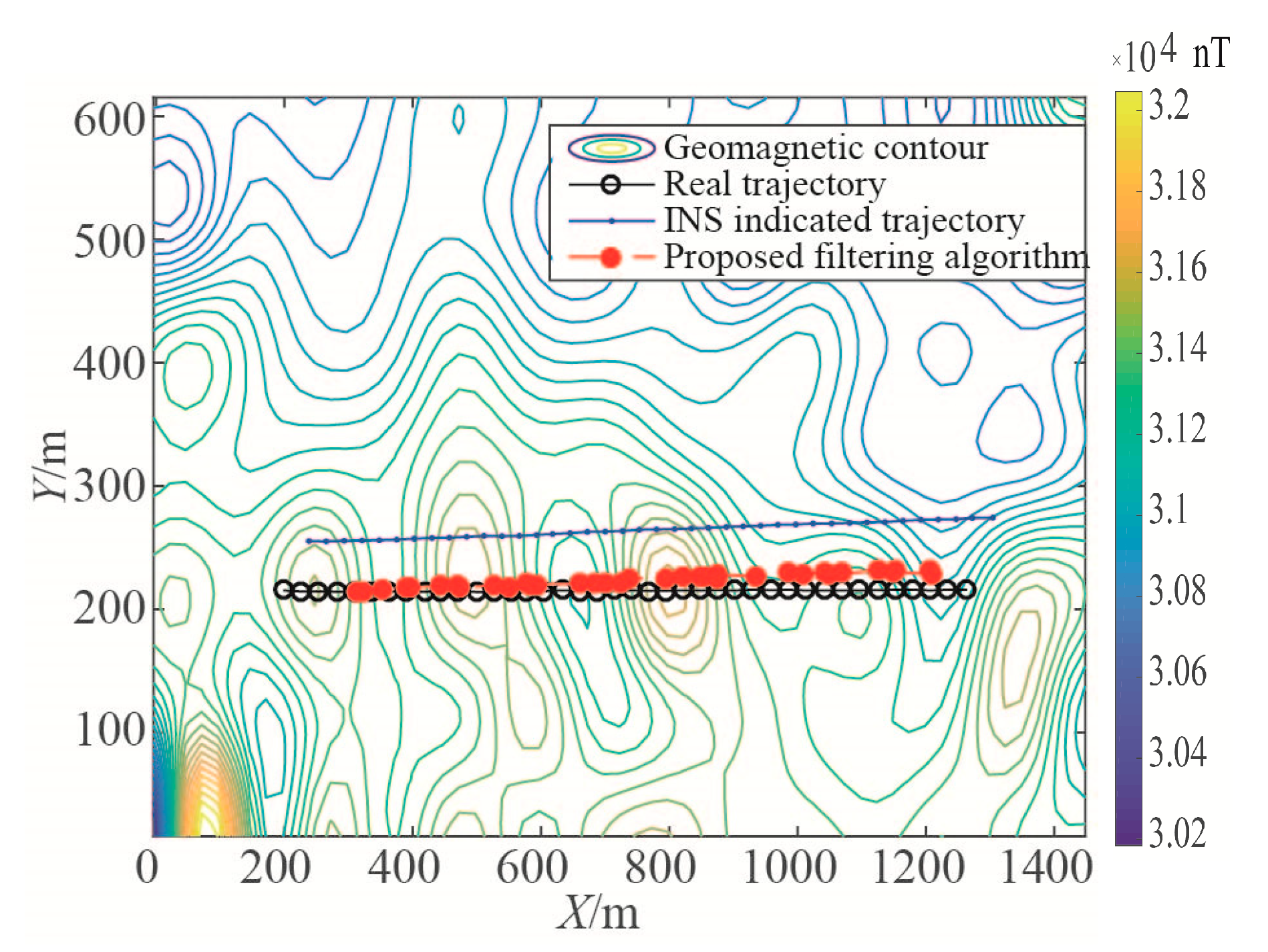
Figure 13a, it is shown that the observations have a great influence on the filtering algorithm.
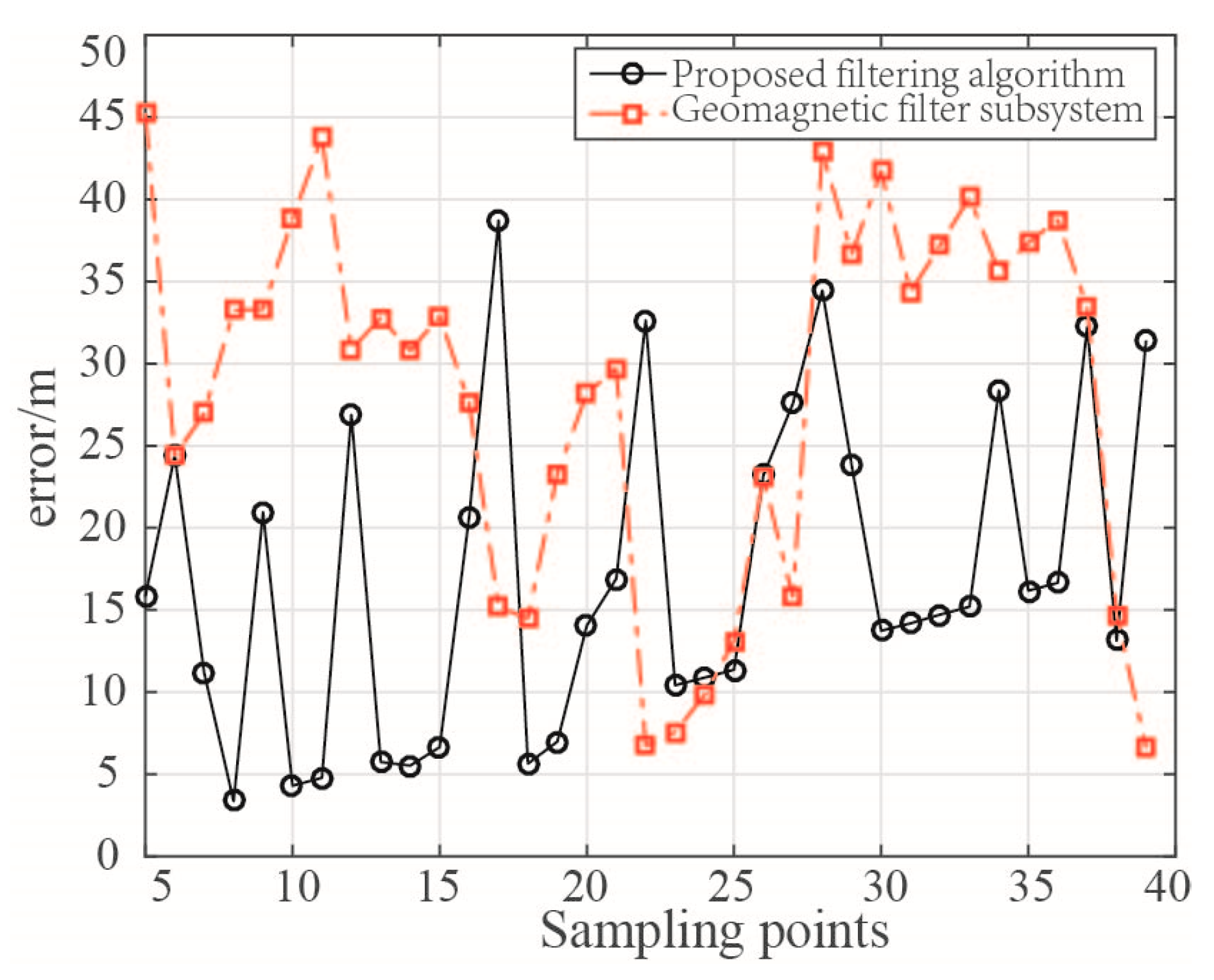
In
Figure 15 and
Figure 16, the filtering trajectory of integrated navigation system is very close to carrier’s real trajectory, and all the total filtering errors are less than 40 m (about 1.6 magnetic grids). Compared with the geomagnetic filter subsystem, the filtering results are obviously improved. This result proves the effectiveness of proposed combined navigation algorithm.