A Simplified Optimal-Switching-Sequence MPC with Finite-Control-Set Moving Horizon Optimization for Grid-Connected Inverter
Abstract
:1. Introduction
2. Conventional OSS-MPC
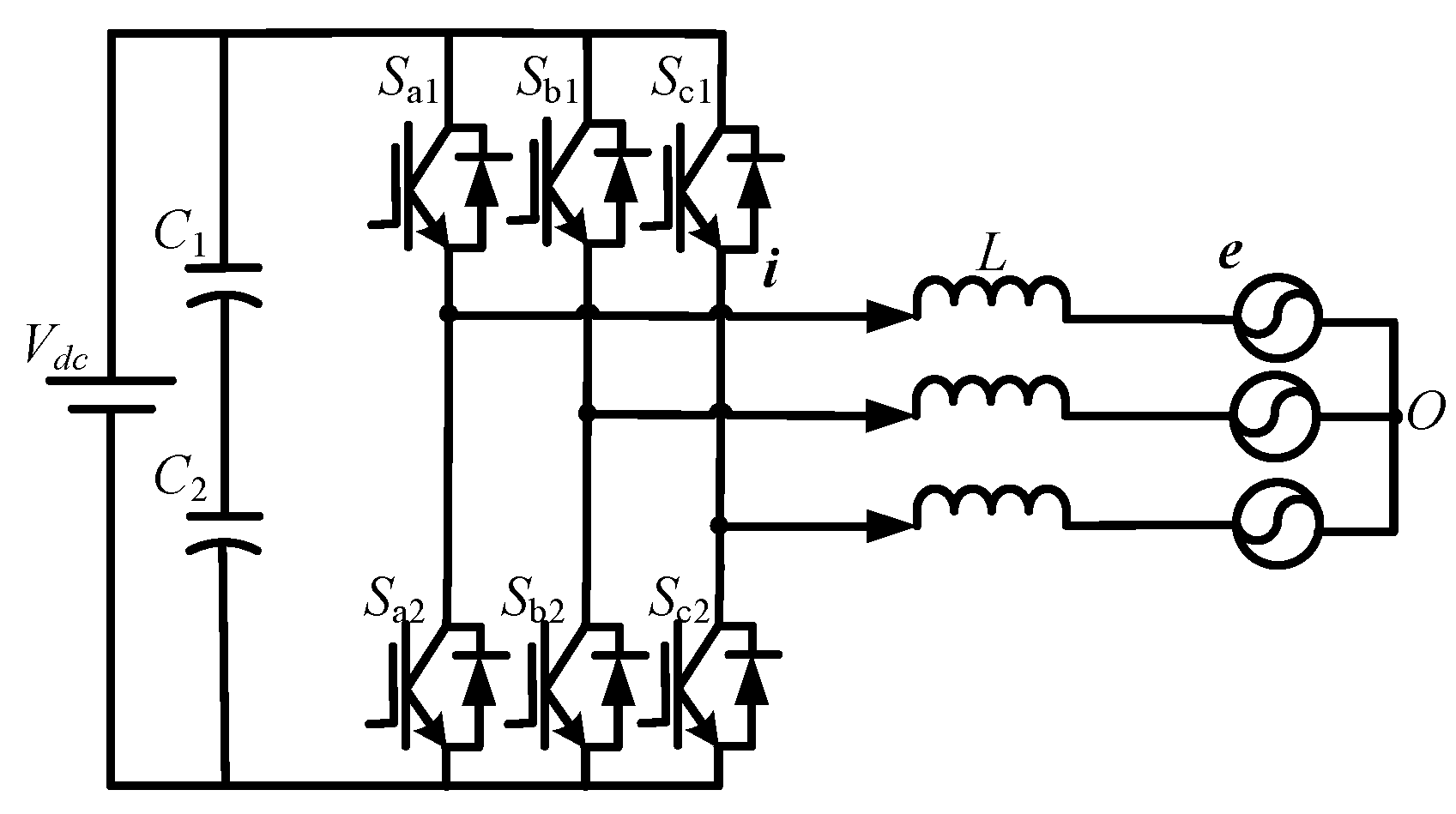
2.1. Model of Two-Level Grid-Connected Inverter
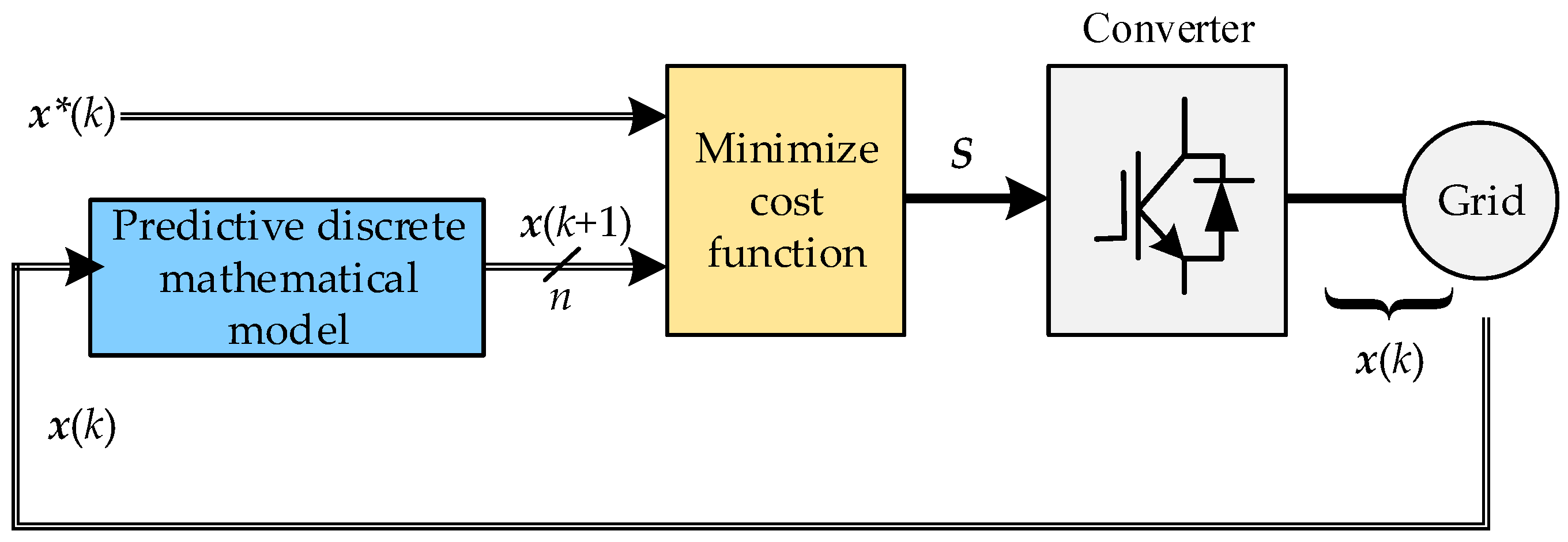
2.2. FCS-MPC
2.3. Conventional OSS-MPC
3. Simplified OSS-MPC
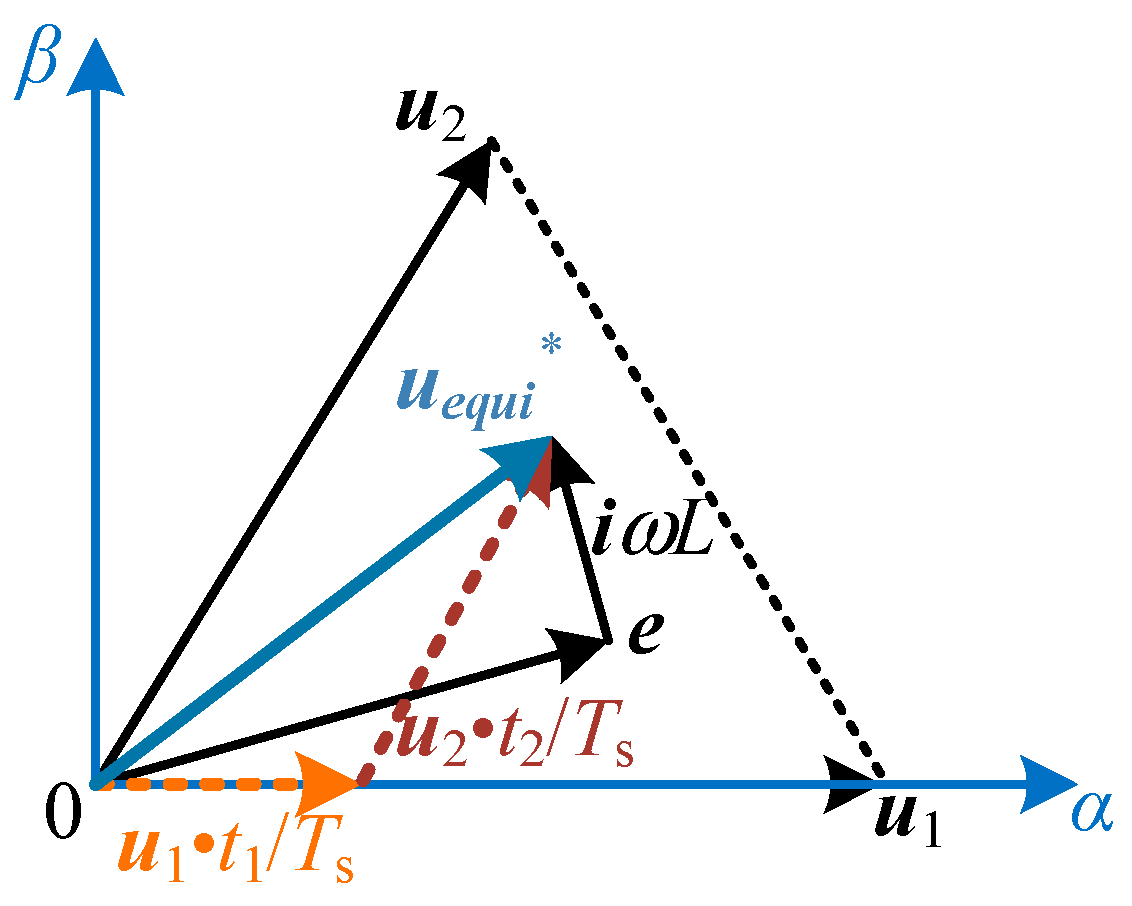
3.1. Equivalent Ideal Voltage Vector of Output Voltage Vector Sequence
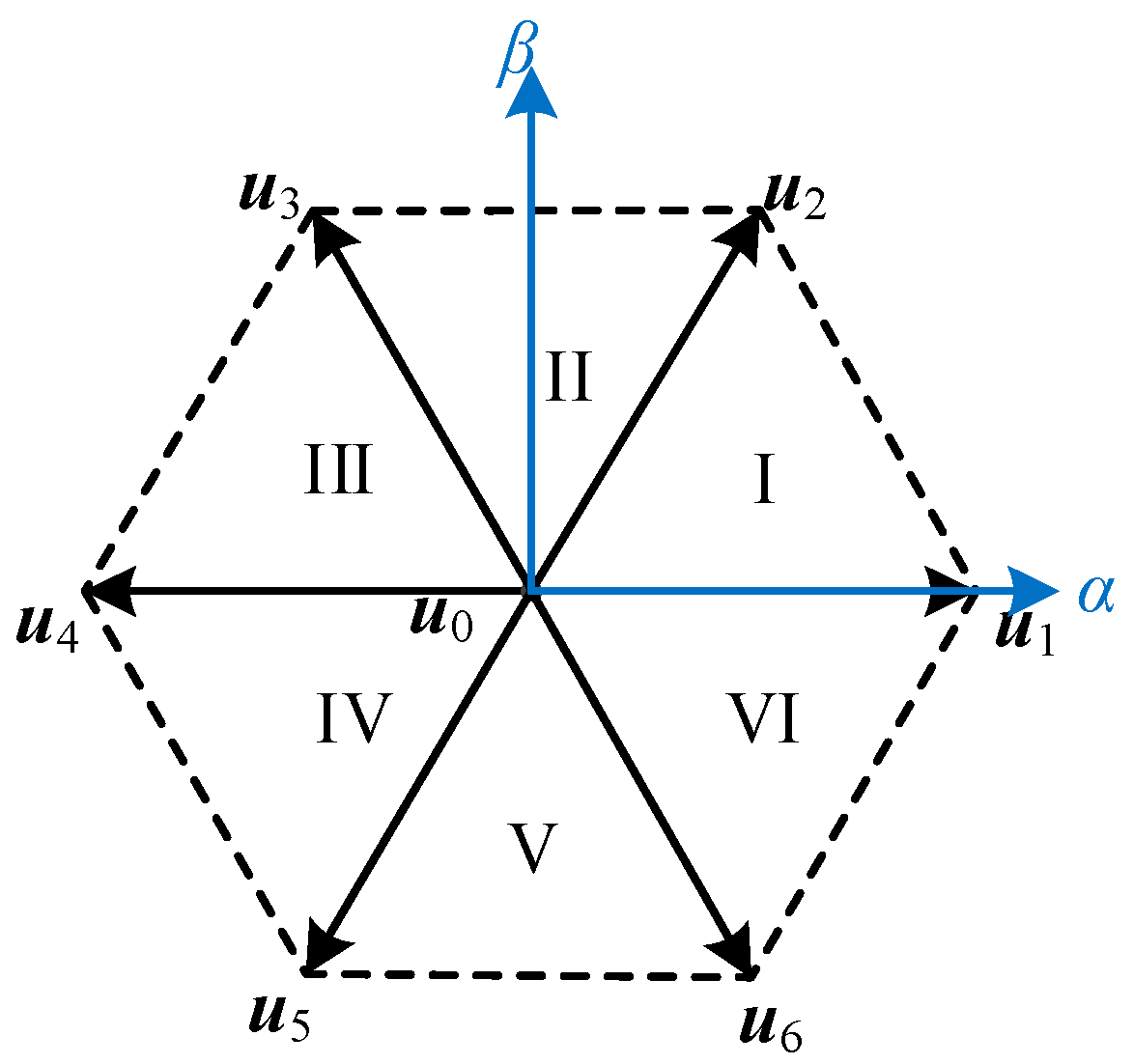
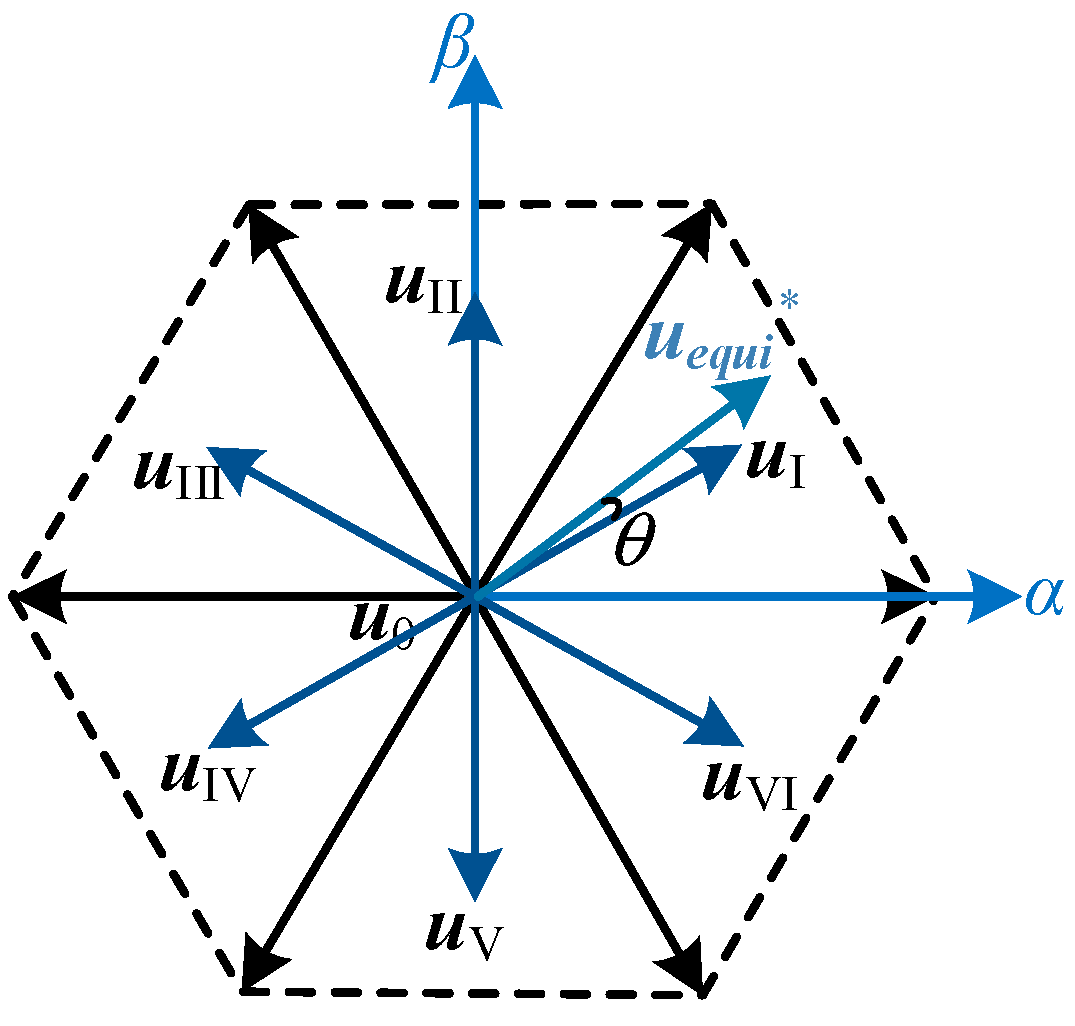
3.2. Center Vectors in Six Sectors
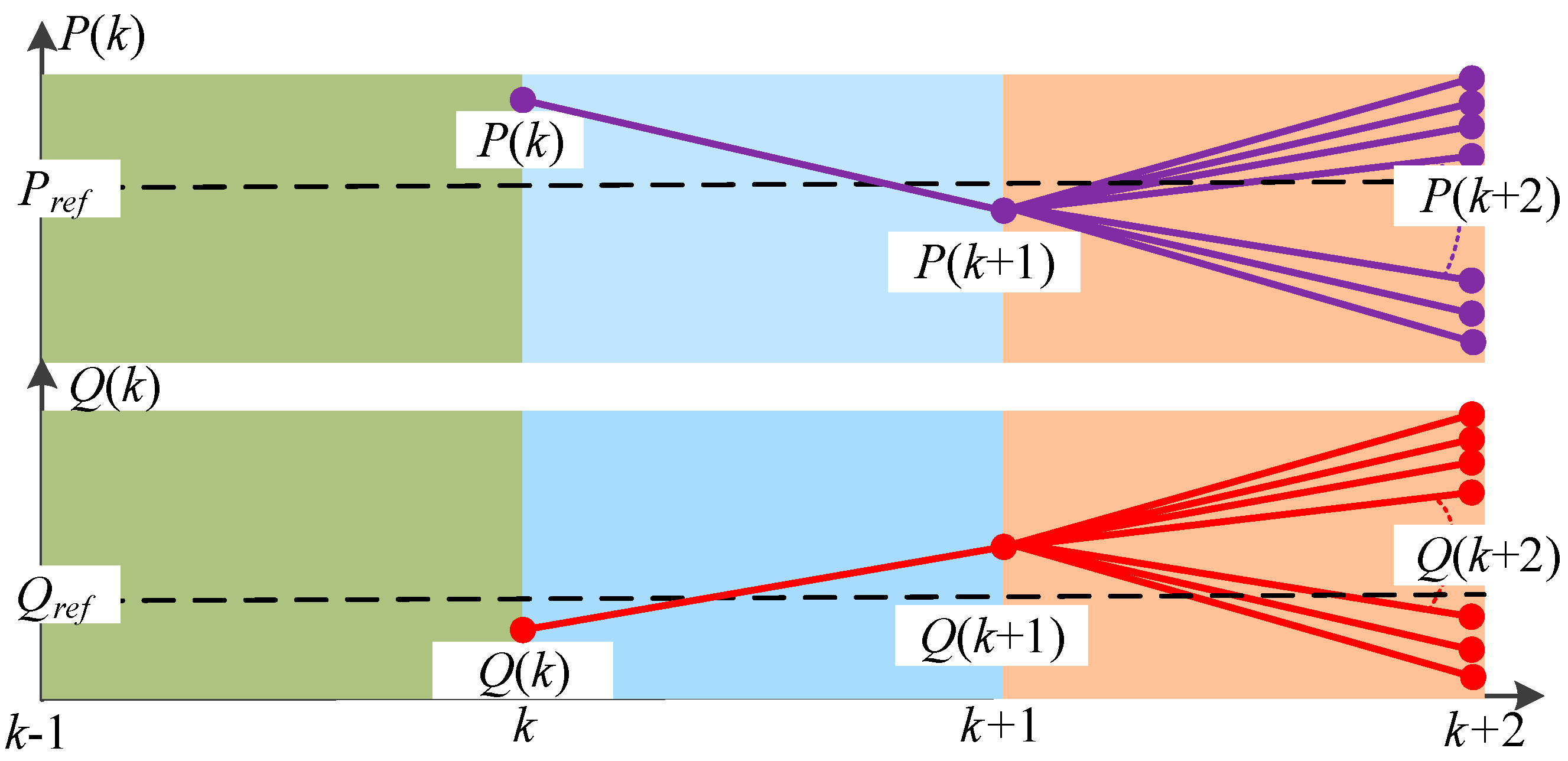
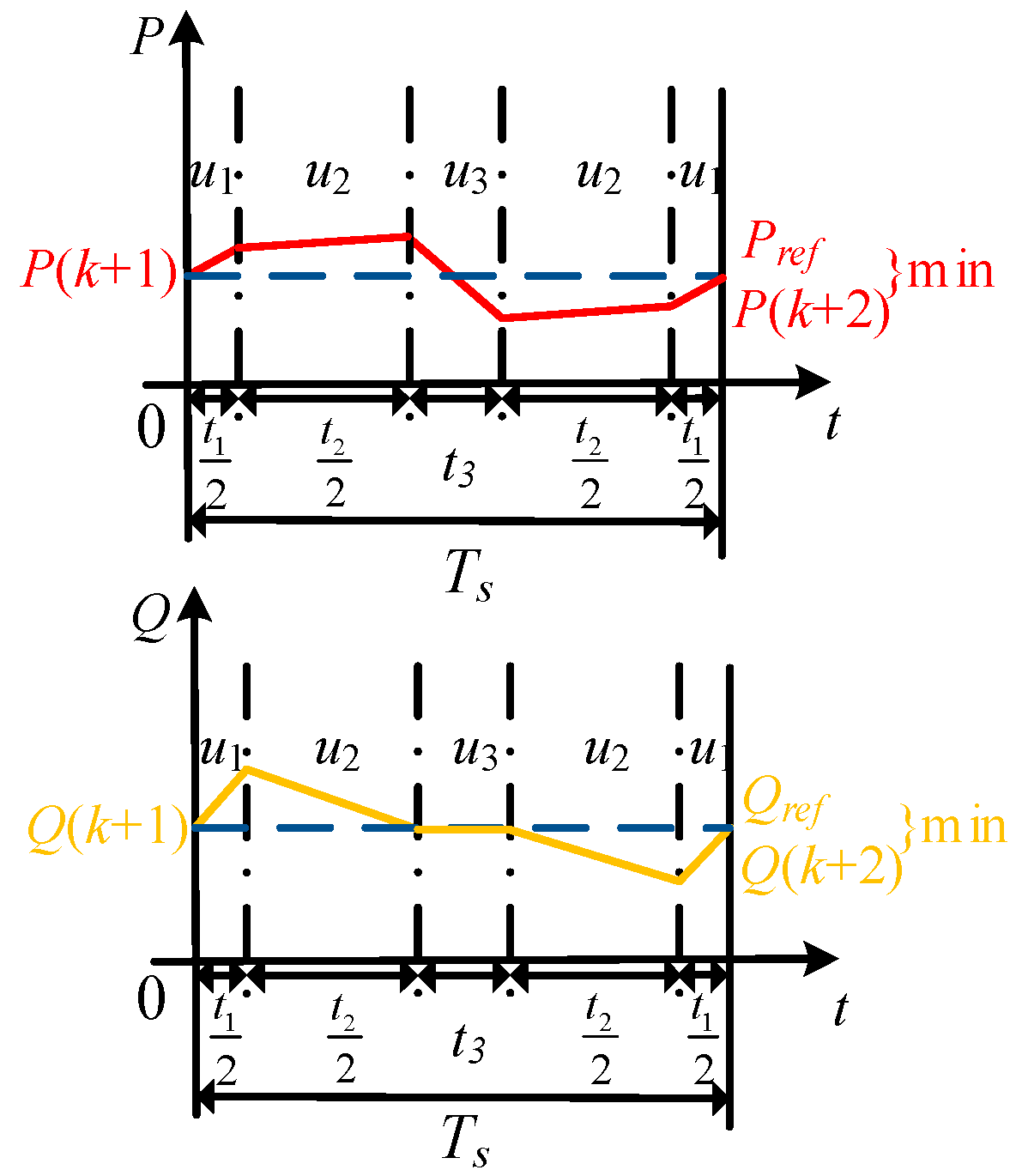
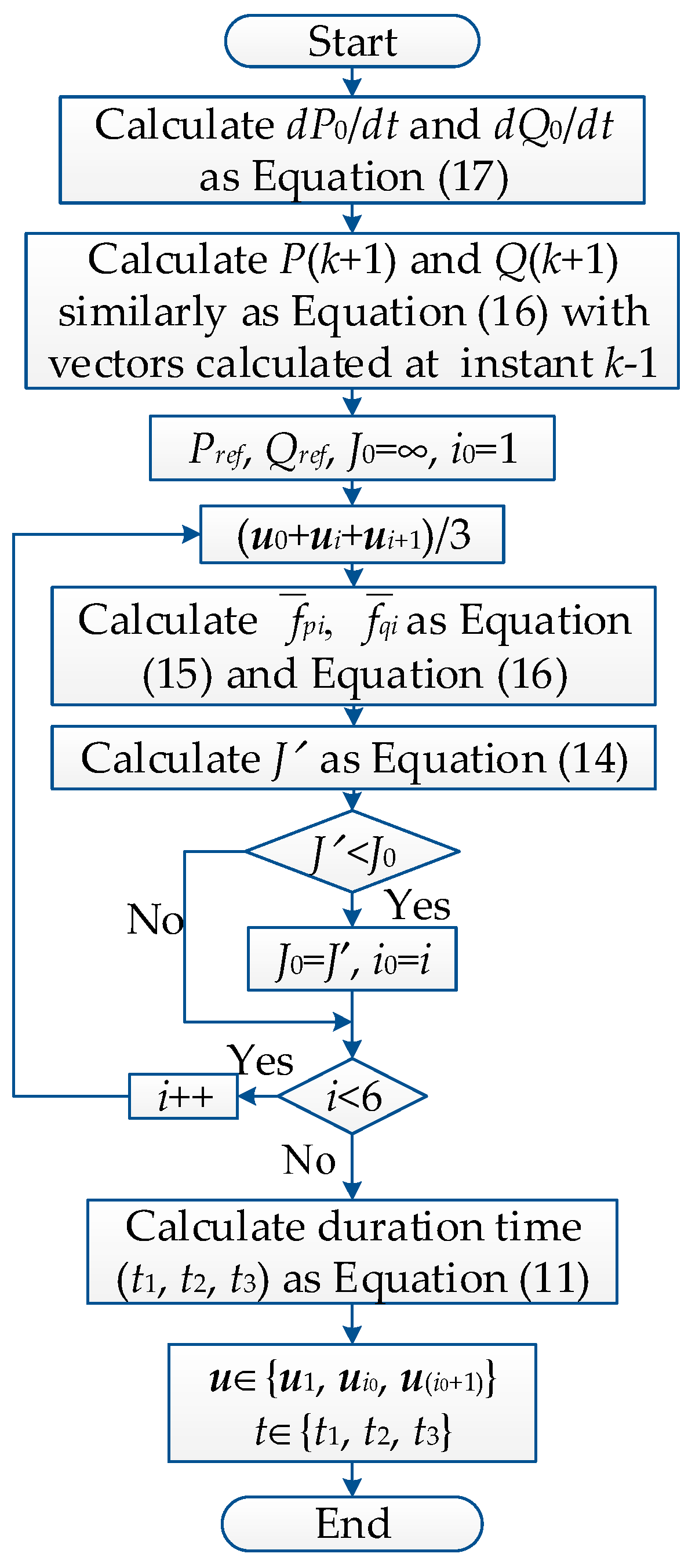
3.3. FCS Moving Horizon Optimization
3.4. Further Reduce the Computational Expense
4. Simulation and Experimental Results
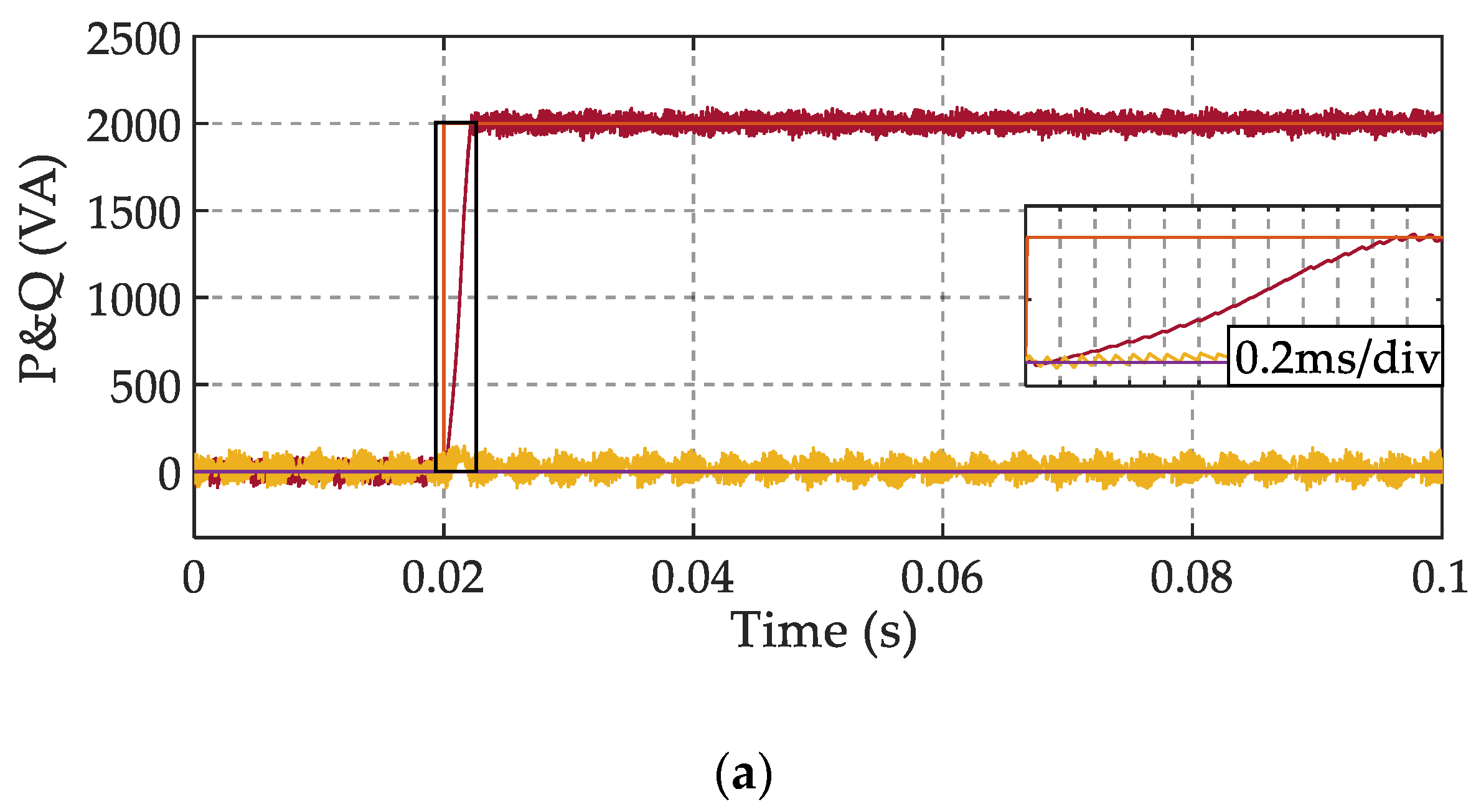
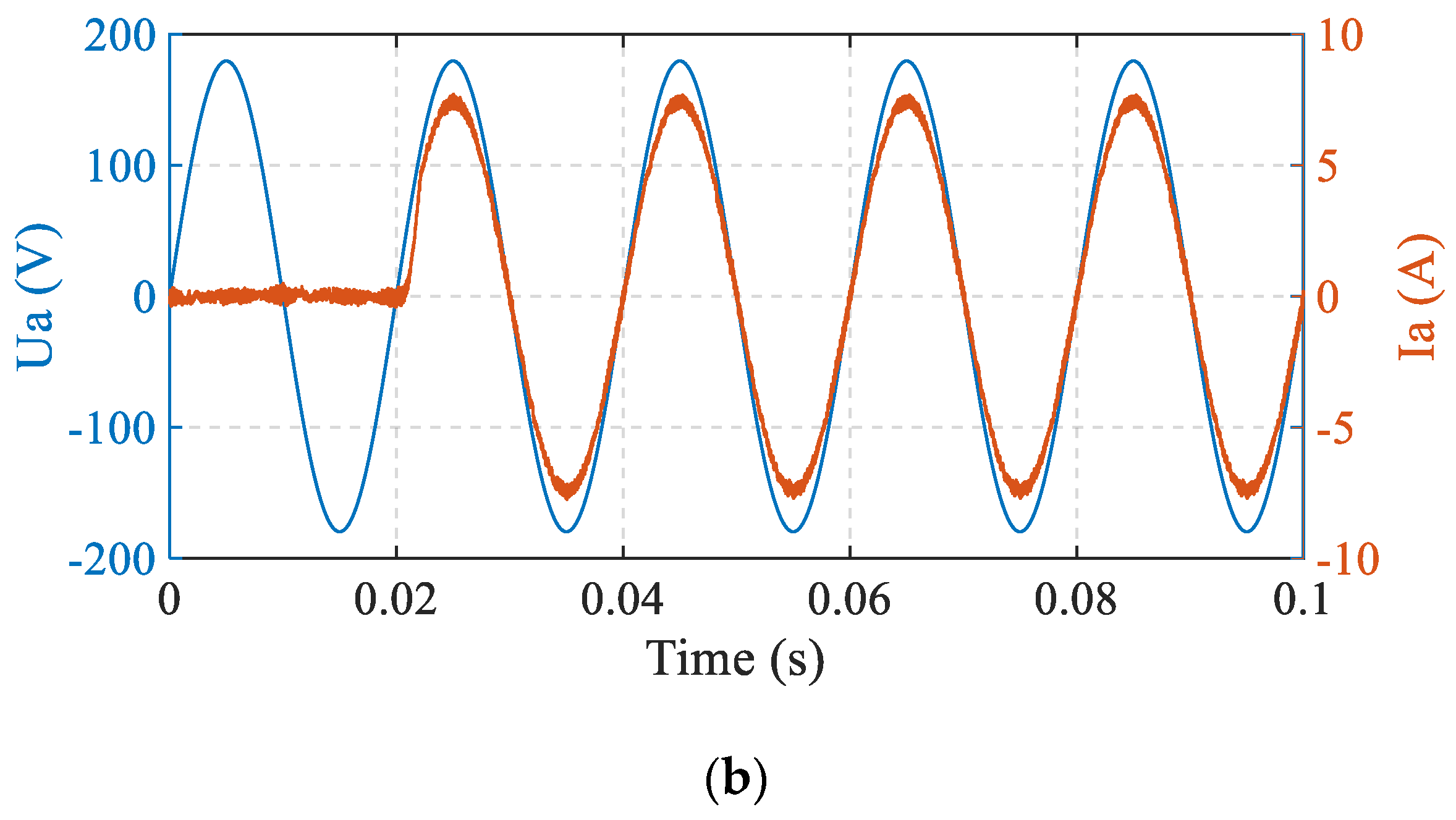
4.1. Simulation Results
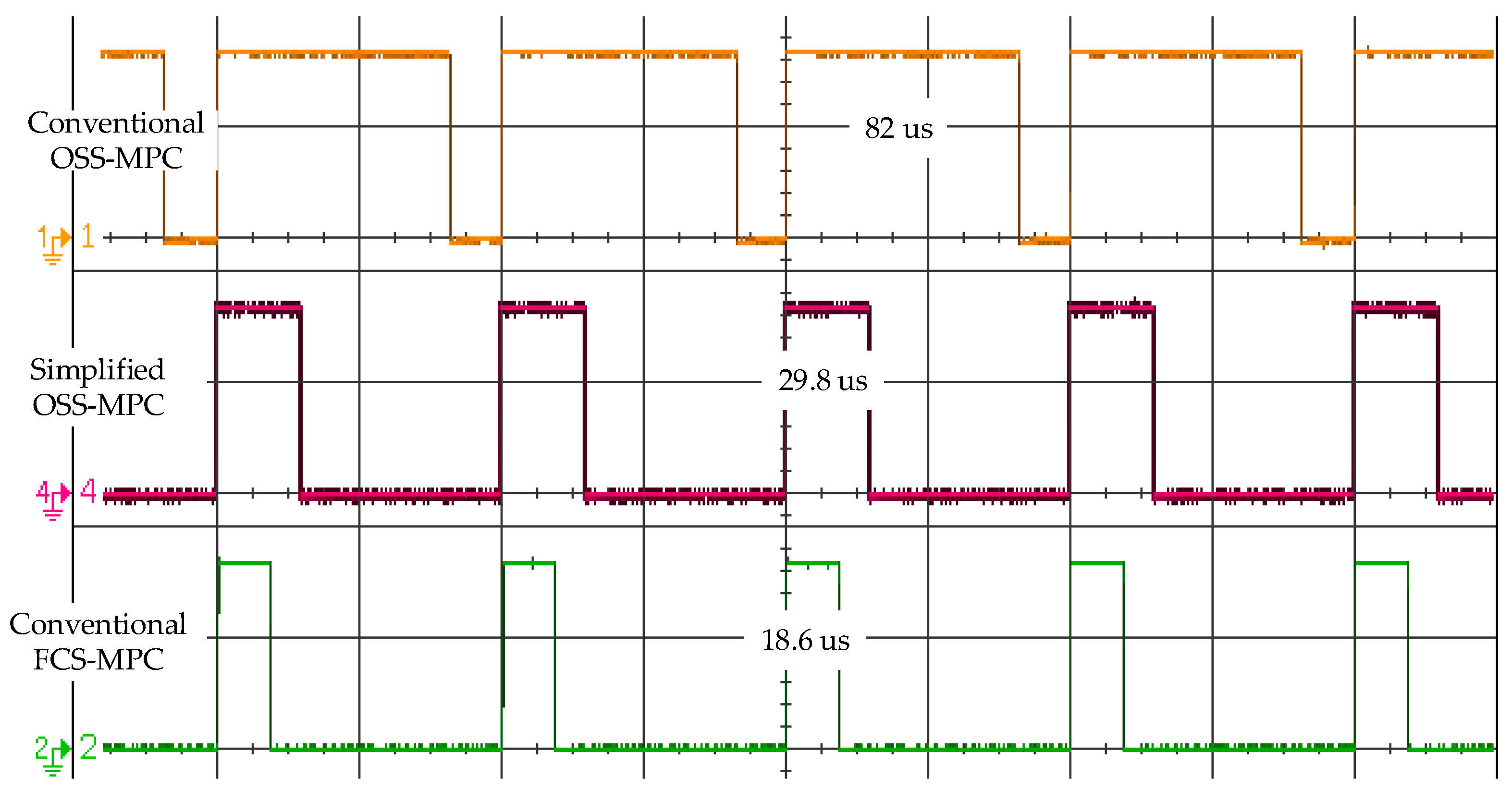
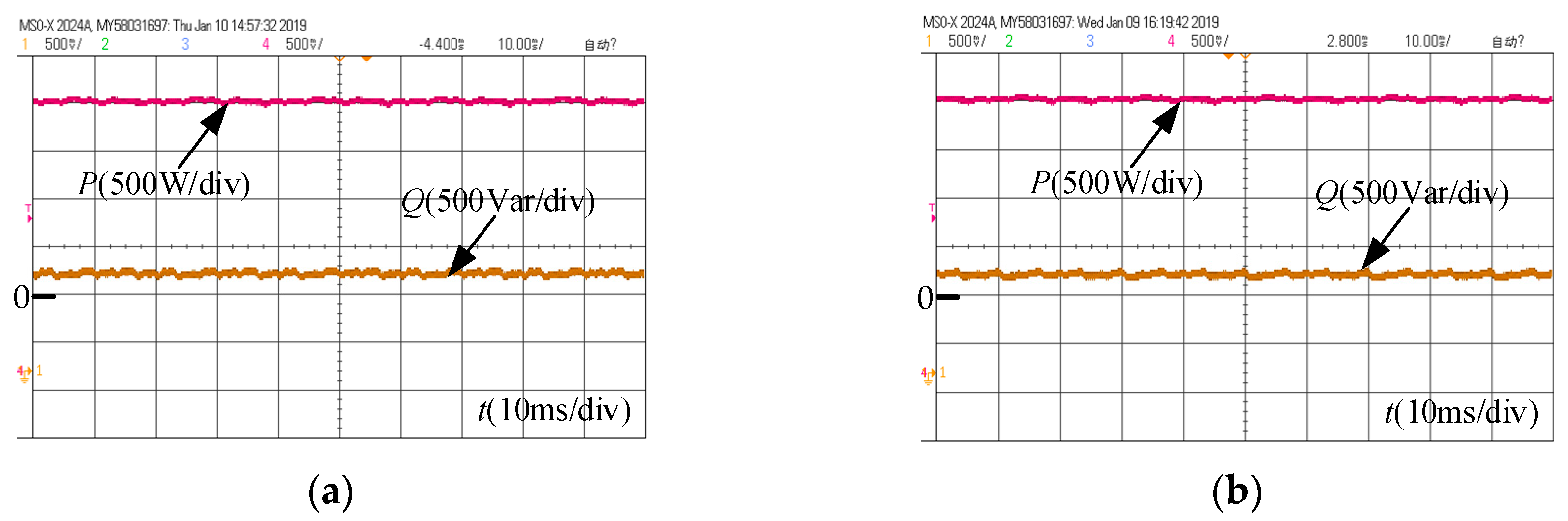
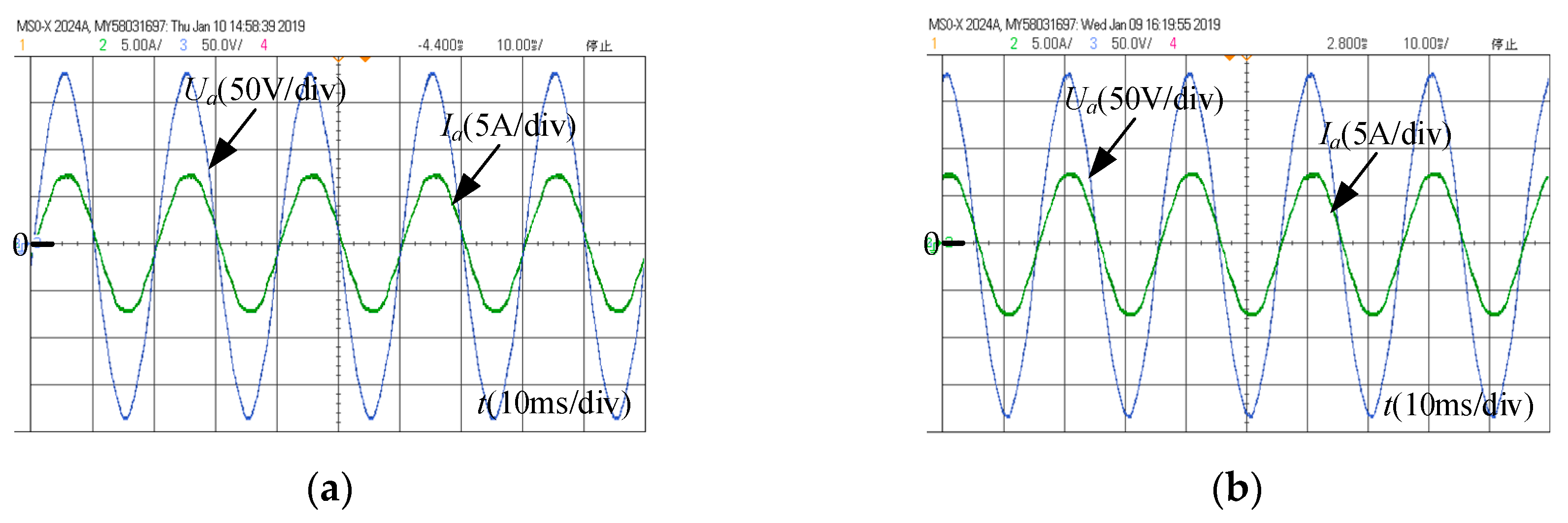
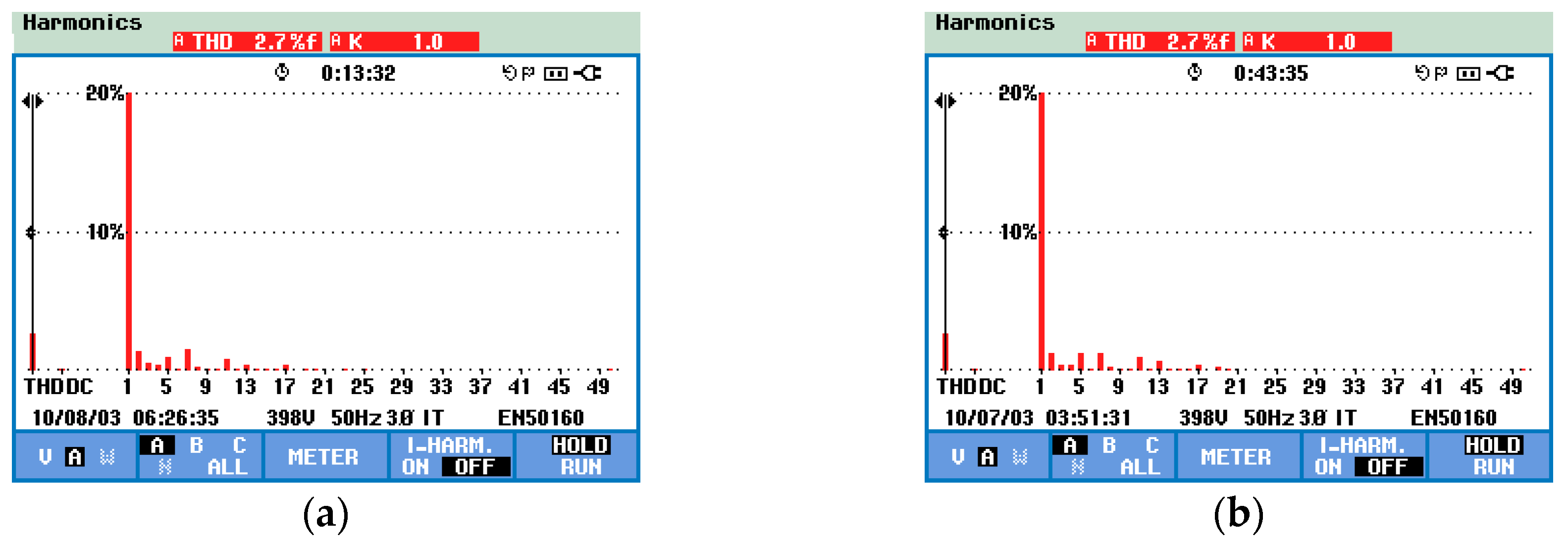
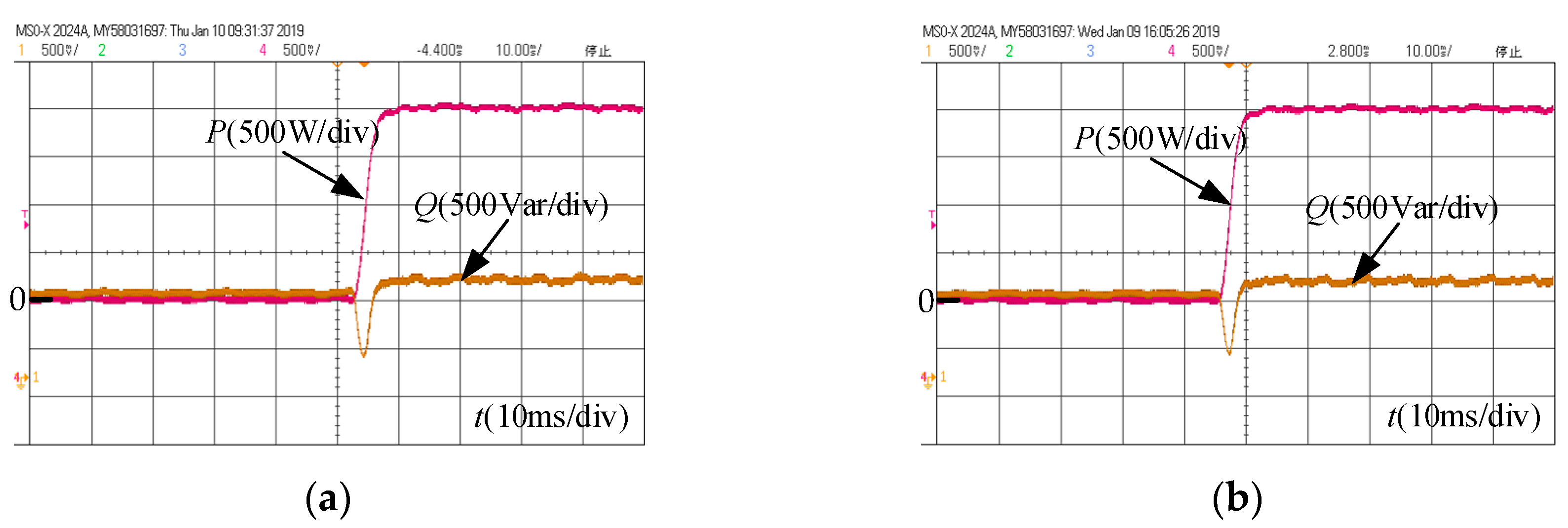
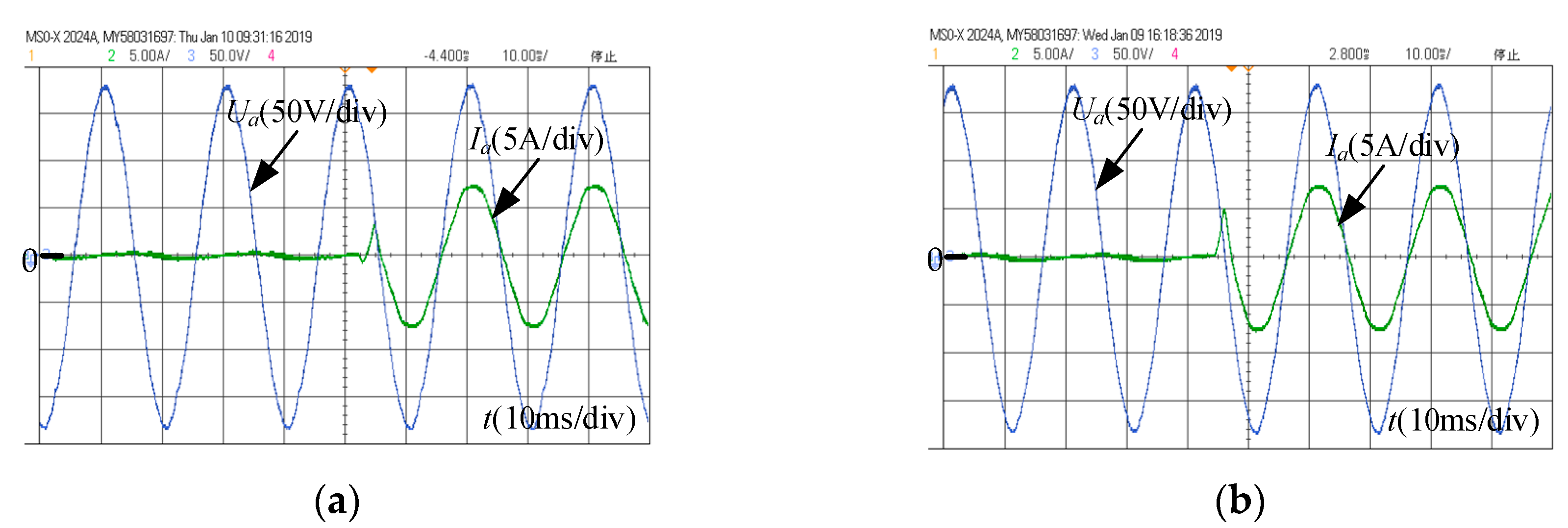
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| MPC | Model predictive control |
| OSS-MPC | Optimal-switching-sequence model-predictive-control |
| CCS-MPC | Continuous-control-set model-predictive-control |
| FCS-MPC | Finite-control-set model-predictive-control |
| DSP | Digital signal processor |
| VOC | Voltage oriented control |
| PI | controller Proportional integral controller |
| DPC | Direct power control |
| DTC | Direct torque control |
| P-DPC | Predictive direct power control |
| SVM | Space vector modulation |
| D-MPC | Dual vector based model-predictive-control |
| ROSS-DPC | Reduced optimal-switching-sequence direct power control |
| IGBT | Insulated gate bipolar transistor |
| e | Grid voltage |
| Vdc | Direct current power supply |
| L | Inductance of AC filter |
| C1, C2 | Dc-link capacitors |
| SX1, SX2 | Upper and lower switching states of each phase |
| ui (u0, u1, u2, u3, u4, u5, u6) | Output voltage vector of switching state |
| i | Grid current vector |
| ^ | Complex conjugate |
| S | Apparent power |
| P | Active power |
| Q | Reactive power |
| MPPC | Model predictive power control |
| MPCC | Model predictive current control |
| ω | Grid angular frequency |
| fpi, fqi | Derivatives of active and reactive power |
| Ts | Sampling period |
| tdelay | Delay time between sampling instant and implementation |
| J | Cost function |
| t1, t2, t3 | Optimal duration time of optimal switching sequence |
| uci (uI, uII, uIII, uIV, uV, uVI) | Center vector |
| u*equi | Ideal voltage vector |
| l | Distance between u*equi and center vector |
| J′ | Cost function to obtain the sector where ideal voltage vector u*equi is located |
| , | Derivatives of active and reactive power of center vector |
| dP0/dt, dQ0/dt | Constant term of derivatives of active and reactive power |
| f | Line voltage frequency |
| fs | Sampling frequency |
| THD | Total harmonic distortion |
References
- Cheng, C.; Nian, H.; Wang, X.; Sun, D. Dead-beat predictive direct power control of voltage source inverters with optimised switching patterns. IET power Electron. 2017, 10, 1438–1451. [Google Scholar] [CrossRef]
- Song, Z.; Tian, Y.; Chen, W.; Zou, Z.; Chen, Z. Predictive Duty Cycle Control of Three-Phase Active-Front-End Rectifiers. IEEE Tran. Power Electron. 2016, 31, 698–710. [Google Scholar] [CrossRef]
- Blasko, V.; Kaura, V. A new mathematical model and control of a three-phase AC-DC voltage source converter. IEEE Trans. Power Electron. 1997, 12, 116–123. [Google Scholar] [CrossRef]
- Malinowski, M.; Kazmierkowski, M.P.; Hansen, S.; Blaabjerg, F.; Marques, G.D. Virtual-Flux-Based Direct Power Control of Three-Phase PWM Rectifiers. IEEE Trans. Ind. Appl. 2001, 37, 1019–1027. [Google Scholar] [CrossRef]
- Noguchi, T.; Tomiki, H.; Kondo, S.; Takahashi, I. Direct power control of PWM converter without power-source voltage sensors. IEEE Trans. Ind. Appl. 1998, 34, 473–479. [Google Scholar] [CrossRef]
- Young, H.A.; Perez, M.A.; Rodriguez, J.; Abu-Rub, H. Assessing Finite-Control-Set Model Predictive Control: A Comparison with a Linear Current Controller in Two-Level Voltage Source Inverters. IEEE Ind. Electron. 2014, 8, 44–52. [Google Scholar] [CrossRef]
- Kouro, S.; Cortes, P.; Vargas, R.; Ammann, U.; Rodriguez, J. Model Predictive Control—A Simple and Powerful Method to Control Power Inverters. IEEE Trans. Ind. Electron. 2009, 56, 1826–1838. [Google Scholar] [CrossRef]
- Dragičević, T. Model Predictive Control of Power Inverters for Robust and Fast Operation of AC Microgrids. IEEE Trans. Power Electron. 2018, 33, 6304–6317. [Google Scholar] [CrossRef]
- Panten, N.; Hoffmann, N.; Fuchs, F.W. Finite Control Set Model Predictive Current Control for Grid-Connected Voltage-Source Inverters with LCL Filters: A Study Based on Different State Feedbacks. IEEE Trans. Power Electron 2016, 31, 5189–5200. [Google Scholar] [CrossRef]
- Zhang, Y.; Peng, Y.; Yang, H. Performance Improvement of Two-Vectors-Based Model Predictive Control of PWM Rectifier. IEEE Trans. Power Electron 2016, 31, 6016–6030. [Google Scholar] [CrossRef]
- Nikhil, P.; Sonam, K.; Monika, M.; Wagh, S. Finite control set model predictive control for two level inverter with fixed switching frequency. In Proceedings of the 2018 SICE International Symposium on Control Systems (SICE ISCS), Tokyo, Japan, 9–11 March 2018; pp. 74–81. [Google Scholar]
- Donoso, F.; Mora, A.; Cardenas, R.; Angulo-Cárdenas, A.; Sáez, D. Finite-Set Model Predictive Control Strategies for a 3L-NPC Inverter Operating with Fixed Switching Frequency. IEEE Trans. Ind. Electron. 2018, 65, 3954–3965. [Google Scholar] [CrossRef]
- Hu, J. Improved Dead-Beat Predictive DPC Strategy of Grid-Connected DC–AC Inverters with Switching Loss Minimization and Delay Compensations. IEEE Trans. Ind. Inf. 2013, 9, 728–738. [Google Scholar] [CrossRef]
- Hu, J.; Zhu, Z.Q. Improved Voltage-Vector Sequences on Dead-Beat Predictive Direct Power Control of Reversible Three-Phase Grid-Connected Voltage-Source Inverters. IEEE Trans. Power Electron. 2013, 28, 254–267. [Google Scholar] [CrossRef]
- Vazquez, S.; Marquez, A.; Aguilera, R.; Quevedo, D. Predictive Optimal Switching Sequence Direct Power Control for Grid-Connected Power Inverters. IEEE Trans. Ind. Electron. 2015, 62, 2010–2020. [Google Scholar] [CrossRef]
- Tarisciotti, L.; Zanchetta, P.; Watson, A.; Bifaretti, S.; Clare, J.C. Modulated Model Predictive Control for a Seven-Level Cascaded H-Bridge Back-to-Back Inverter. IEEE Trans. Ind. Electron. 2014, 61, 5375–5383. [Google Scholar] [CrossRef]
- Tarisciotti, L.; Zanchetta, P.; Watson, A.; Clare, J.C.; Degano, M.; Bifaretti, S. Modulated Model Predictive Control for a Three-Phase Active Rectifier. IEEE Trans. Ind. Appl. 2015, 51, 1610–1620. [Google Scholar] [CrossRef]
- Yang, Y.; Wen, H.; Li, D. A Fast and Fixed Switching Frequency Model Predictive Control with Delay Compensation for Three-phase Inverters. IEEE Access. 2017, 5, 17904–17913. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, W.; Li, Z.; Zhang, Y. Low-Complexity Model Predictive Power Control: Double-Vector-Based Approach. IEEE Trans. Ind. Electron. 2014, 61, 5871–5880. [Google Scholar] [CrossRef]
- Zhang, Z.; Hackl, C.M.; Kennel, R. Computationally Efficient DMPC for Three-Level NPC Back-to-Back Inverters in Wind Turbine Systems with PMSG. IEEE Trans. Power Electron. 2017, 32, 8018–8034. [Google Scholar] [CrossRef]
- Bozorgi, A.M.; Gholami-Khesht, H.; Farasat, M.; Mehraeen, S.; Monfared, M. Model Predictive Direct Power Control of Three-Phase Grid-Connected Inverters with Fuzzy-Based Duty Cycle Modulation. IEEE Trans. Ind. Appl. 2018, 54, 4875–4885. [Google Scholar] [CrossRef]
- Yang, Y.; Wen, H.; Fan, M.; Xie, M.; Chen, R. Fast Finite-Switching-State Model Predictive Control Method Without Weighting Factors for T-Type Three-Level Three-Phase Inverters. IEEE Trans. Ind. Inf. 2019, 15, 1298–1310. [Google Scholar] [CrossRef]
- Mariethoz, S.; Morari, M. Explicit Model-Predictive Control of a PWM Inverter with an LCL Filter. IEEE Trans. Ind. Electron. 2009, 56, 389–399. [Google Scholar] [CrossRef]
- Beccuti, A.G.; Kvasnica, M.; Papafotiou, G.; Morari, M. A Decentralized Explicit Predictive Control Paradigm for Parallelized DC-DC Circuits. IEEE Trans. Control Syst. Technol. 2013, 21, 136–148. [Google Scholar] [CrossRef]
- Xia, C.; Tao, L.; Shi, T.; Song, Z. A Simplified Finite-Control-Set Model-Predictive Control for Power Converters. IEEE Trans. Ind. Inf. 2014, 10, 991–1002. [Google Scholar]
- Liu, X.; Wang, D.; Peng, Z. Improved finite-control-set model predictive control for active front-end rectifiers with simplified computational approach and on-line parameter identification. ISA Trans. 2017, 69, 51–64. [Google Scholar] [CrossRef]
- Kwak, S.; Park, J.C. Switching Strategy Based on Model Predictive Control of VSI to Obtain High Efficiency and Balanced Loss Distribution. IEEE Trans. Power Electron. 2014, 29, 4551–4567. [Google Scholar] [CrossRef]
- Rodriguez, J.; Kazmierkowski, M.P.; Espinoza, J.R.; Zanchetta, P.; Abu-Rub, H.; Young, H.A.; Rojas, C.A. State of the Art of Finite Control Set Model Predictive Control in Power Electronics. IEEE Trans. Ind. Inf. 2013, 9, 1003–1016. [Google Scholar] [CrossRef]
- Hu, B.; Kang, L.; Cheng, J.; Zhang, Z.; Zhang, J.; Luo, X. Double-step model predictive direct power control with delay compensation for three-level converter. IET Power Electron. 2019, 12, 899–906. [Google Scholar] [CrossRef]
- Ngo, V.-Q.-B.; Nguyen, M.-K.; Tran, T.-T.; Choi, J.-H.; Lim, Y.-C. A Modified Model Predictive Power Control for Grid-Connected T-Type Inverter with Reduced Computational Complexity. Electronics 2019, 8, 217. [Google Scholar] [CrossRef]
- Aguilera, R.P.; Quevedo, D.E.; Vazquez, S.; Franquelo, L.G. Generalized Predictive Direct Power Control for AC/DC converters. In Proceedings of the IEEE ECCE Asia Downunder (ECCE Asia), Melbourne, VIC, Australia, 3–6 June 2013; pp. 1215–1220. [Google Scholar]



| System Parameter | Symbol | Value |
|---|---|---|
| Filter inductance | L | 9 mH |
| Line voltage frequency | f | 50 Hz |
| DC-link capacitor | C1, C2 | 1000 μF |
| DC-link voltage | Udc | 350 V |
| Sampling frequency | fs | 10 kHz |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, L.; Cheng, J.; Hu, B.; Luo, X.; Zhang, J. A Simplified Optimal-Switching-Sequence MPC with Finite-Control-Set Moving Horizon Optimization for Grid-Connected Inverter. Electronics 2019, 8, 457. https://doi.org/10.3390/electronics8040457
Kang L, Cheng J, Hu B, Luo X, Zhang J. A Simplified Optimal-Switching-Sequence MPC with Finite-Control-Set Moving Horizon Optimization for Grid-Connected Inverter. Electronics. 2019; 8(4):457. https://doi.org/10.3390/electronics8040457
Chicago/Turabian StyleKang, Longyun, Jiancai Cheng, Bihua Hu, Xuan Luo, and Jianbin Zhang. 2019. "A Simplified Optimal-Switching-Sequence MPC with Finite-Control-Set Moving Horizon Optimization for Grid-Connected Inverter" Electronics 8, no. 4: 457. https://doi.org/10.3390/electronics8040457
APA StyleKang, L., Cheng, J., Hu, B., Luo, X., & Zhang, J. (2019). A Simplified Optimal-Switching-Sequence MPC with Finite-Control-Set Moving Horizon Optimization for Grid-Connected Inverter. Electronics, 8(4), 457. https://doi.org/10.3390/electronics8040457





