A Privacy-Preserving Authentication and Key Agreement Scheme with Deniability for IoT
Abstract
:1. Introduction
- User anonymity. No entity except the trusted gateway nodes can obtain any information about the identity of the users during the authentication phase.
- Deniability. The gateway node can generate another message that is indistinguishable from the received message from the user, such that when the user request a service via the gateway node, any third party cannot tell whether the message is sent by the user or generated by the gateway node. Therefore, the user can deny that he or she has requested the service.
- Unlinkability. Any external entity except the trusted gateway node cannot determine whether two messages from distinguished authentication sessions are sent by the same entity.
- Traceability. If any dispute or misbehavior occurs during the authentication phase, the trusted gateway node can reveal the identity of the user with the exchanged messages.
- High-efficiency. Due to the adoption of low-cost hash functions and ECC(elliptic curve cryptography) operations, the proposed scheme is more efficient than the existing exponential or bilinear pairing-based authentication schemes.
2. Preliminaries
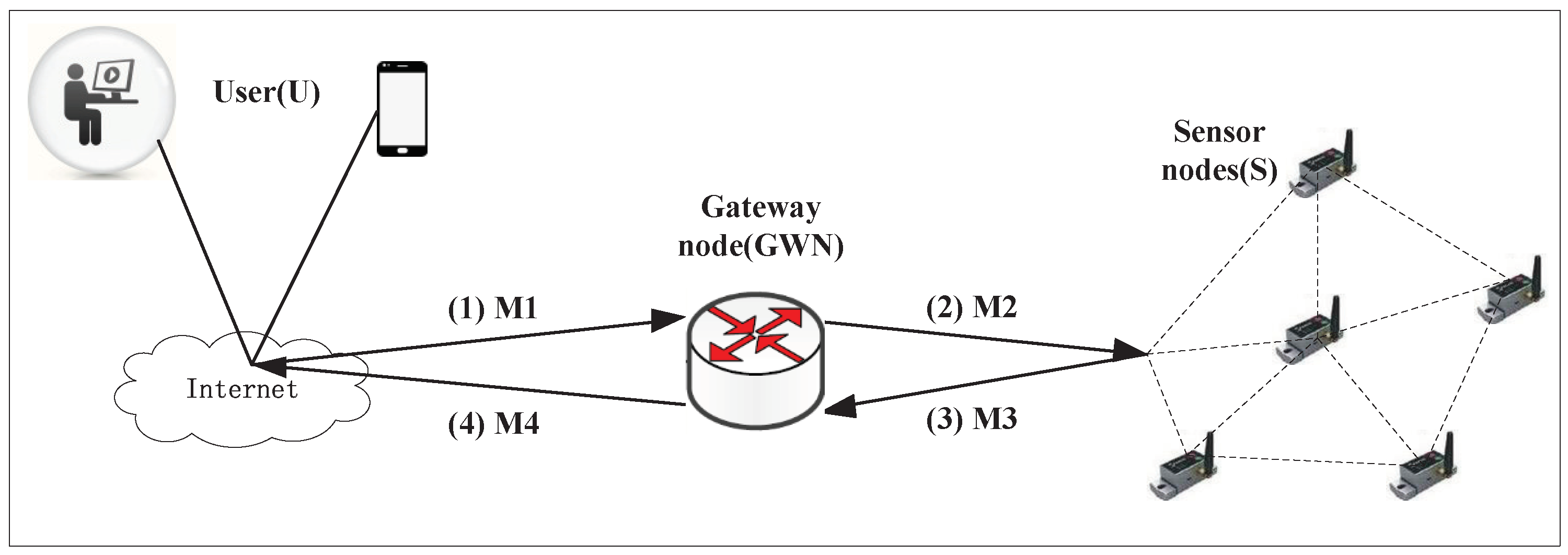
2.1. Communication Model
2.2. Security Definition
- : This query issued by the adversary simulates the eavesdropping attacks on honest executions among the user instance , trusted gateway instance and sensor instance . It outputs a transcript of the exchanged messages during the honest execution of the protocol.
- : This query models the active attacks such as impersonation attack and replay attack. Once has received the messages, returns a corresponding result to .
- : This query is issued by the adversary , it is used to simulate the attack that corrupts an entity from . can get the private key of a participant with this query.Please note that this query does not corrupt the partner’s same internal data and ephemeral values of the instance .
- : The query is designed to simulate known session key attack. If there is a valid session from the instance , returns the shared session key to . Otherwise, returns null.
- : This query is used to model the capability of the adversary to distinguish between a random number and a real session key by flipping an unbiased coin b. If the session key of the instance has been defined, the session key of will be responded to if or a random value will be returned if ; otherwise, ⊥ will be responded.
- : As soon as the adversary makes query adaptively on the message x, it returns the existing if the list exist a tuple , where initially is an empty set; otherwise, it picks a random value , stores the tuple in the list and returns to .
- : Upon receiving the query about y from the adversary , examines whether the tuple is in , where initially is an empty set. If so, it responds to the existing to ; otherwise, it generates a random value , stores the tuple in the list and returns to .
2.3. Elliptic Curve Discrete Logarithm Problem
- Elliptic curve discrete logarithm (ECDL) problem: Given for unknown , to find a.
- Elliptic curve computational Diffie-Hellman (ECCDH) problem: Given P, , for unknown a, , to compute .
3. The Proposed Scheme
3.1. System Setup Phase
- chooses a non-singular elliptic curve over a prime finite , where p is a large prime. Let G be an elliptic curve group. Then, chooses a generator P of order q over . selects its private key and computes the public key in accordance with .
- selects three collision-resistant one-way hash functions .
- Finally, the system parameters is published while the private key is kept secretly by .
3.2. Registration Phase
3.2.1. User Registration Phase
- U selects an identity , a private key and then gets the public key according to . Then, U calculates the registration message , and sends it to via a non-public channel.
- After receiving the registration message from U, calculates and returns it to U via a non-public channel.
- U computes and deletes .
3.2.2. Sensor Node Registration Phase
- S generates its identity , private key and computes the corresponding public key and . Then, S sends to GWN via a non-public channel.
- After receiving the message from S, computes and sent it to S. publish and stores into its database.
- Upon receiving from , S stores it into its memory.
3.3. Authentication and Key Agreement Phase
- U selects a random number , generates the current timestamp and computes , , , , , and . Then, U sends the request message via a public channel to GWN.
- When receives the authentication request message from U at the time , it checks whether the condition holds. If yes, then computes: , . then verifies U by computing the following: , , , and . verifies if the equation holds or not. If the verification does not hold, rejects the user’s authentication request; else, goes to 3.
- generates its current timestamp , selects a random number and calculates: , , , . Then, the gateway node sends the message {, , , , , } to S via a public channel.
- Upon receiving the authentication message from at time , S first checks the validity of the timestamp on the condition . If is invalid, S terminates the session. If it is valid, S then computes: , , and . Next, S verifies . If , the sensor node S accepts and goes to 5; otherwise, it rejects .
- S generates its current timestamp and selects a random number , and computes , , , and . S sends the message to via a public channel. Then, S computes the session key .
- Upon receiving the replied message from S at time , checks the validity of on the condition . If is valid, computes and . Then, checks whether . If yes, generates its current timestamp , computes and sends the message to U.
- After receiving the replied message from at time , U checks the validity of with the condition . If it is valid, U computes and checks whether . If yes, U computes , . Then, U checks whether . If yes, U calculates the secret session key .
4. Analysis of Correctness and Security
4.1. Correctness
- : P believes X.
- : P sees X. i.e., P has received messages containing X.
- : P said X. i.e., P has sent messages containing X.
- : P controls X.
- or : X is a fresh message. X is usually a temporary value.
- : The hashed value of X.
- : K is a shared secret key between P and Q.
- : X is combined with secret Y.
- : X or Y is one part of .
- Message-meaning rule: orIf P believes that K is a shared secret key between P and Q and has received messages containing X, P believes that Q has sent messages containing the message X.
- Nonce-verification rule: orIf P believes that X is a fresh message and Q has sent messages containing the message X, P believes that Q believes the message X.
- Jurisdiction rule: orIf P believes that Q controls the message X and Q believes the message X, P believes the message X.
- Freshness rule: orIf P believes that X is a fresh message, P believes is fresh messages.
- Belief rule: orIf P believes the messages , P believes the message X.
- Goal 1:
- Goal 2:
- Message 1: :
- Message 2: :
- Message 3: :
- Message 4: :
- A1:
- A2:
- A3:
- A4:
- A5:
- A6:
- A7:
- A8: .
- A9: .
- From Message 1, we have:S has received the message encrypted by .
- According to the message-meaning rule, if the Formula (1) and the state assumption A4 hold at the same time, we can infer that:S believes that has sent the messages .
- According to the freshness rule, if the state assumption A1 holds, we then obtain:S believes the message are fresh.
- According to the belief rule, if the Formula (4) holds, we can get:S believes that believes is a shared secret key between and S.
- According to the jurisdiction rule, if the Formula (5) and the state assumption A6 hold at the same time, we can obtain:S believes that is a shared secret key between and S.
- From Message 2, we can have:S has received the message encrypted by .
- According to the freshness rule, if the state assumption A2 holds, we can deduce:S believes the messages are fresh.
- According to the belief rule, if the Formula (10) holds, we can obtain:S believes that believes is a shared secret key between U and S.
- According to the jurisdiction rule, if the Formula (11) and the state assumption A7 hold at the same time, we can have:S believes that is a shared secret key between U and S.
- From Message 3, we can get:U has received the message encrypted by .
- According to the message-meaning rule, if the Formula (14) and the state assumption A5 hold at the same time, we can deduce:U believes that has sent the message .
- According to the freshness rule, if the state assumption A3 holds, we can have:U believes the message are fresh.
- According to the belief rule, if the Formula (17) holds, we can infer:U believes that believes is a shared secret key between U and .
- According to the jurisdiction rule, if the Formula (18) and the state assumption A8 hold at the same time, we can deduce:U believes that is a shared secret key between U and .
- From Message 4, we can get:which means that U has received the message encrypted by .
- According to the freshness rule, if the state assumption A3 holds, we can have:which means that U believes the message are fresh.
- According to the belief rule, if the Formula (23) holds, we can infer:U believes that believes is a shared secret key between U and S.
- According to the jurisdiction rule, if the Formula (24) and the state assumption A9 hold at the same time, we can deduce:U believes that is a shared secret key between U and S.
- According to the belief rule, if the Formula (25) holds, we can have:U believes that is a shared secret key between U and S.
4.2. Security
4.3. Deniable Authentication
- selects a random number , computes and .
- chooses a user pseudo-identity and a public key, computes , and .
4.4. Anonymity
4.5. Mutual Authentication
4.6. Unlinkability
4.7. Traceability
4.8. Resistance to Impersonation Attack
4.9. Resistance to Replay Attack
4.10. Forward Security
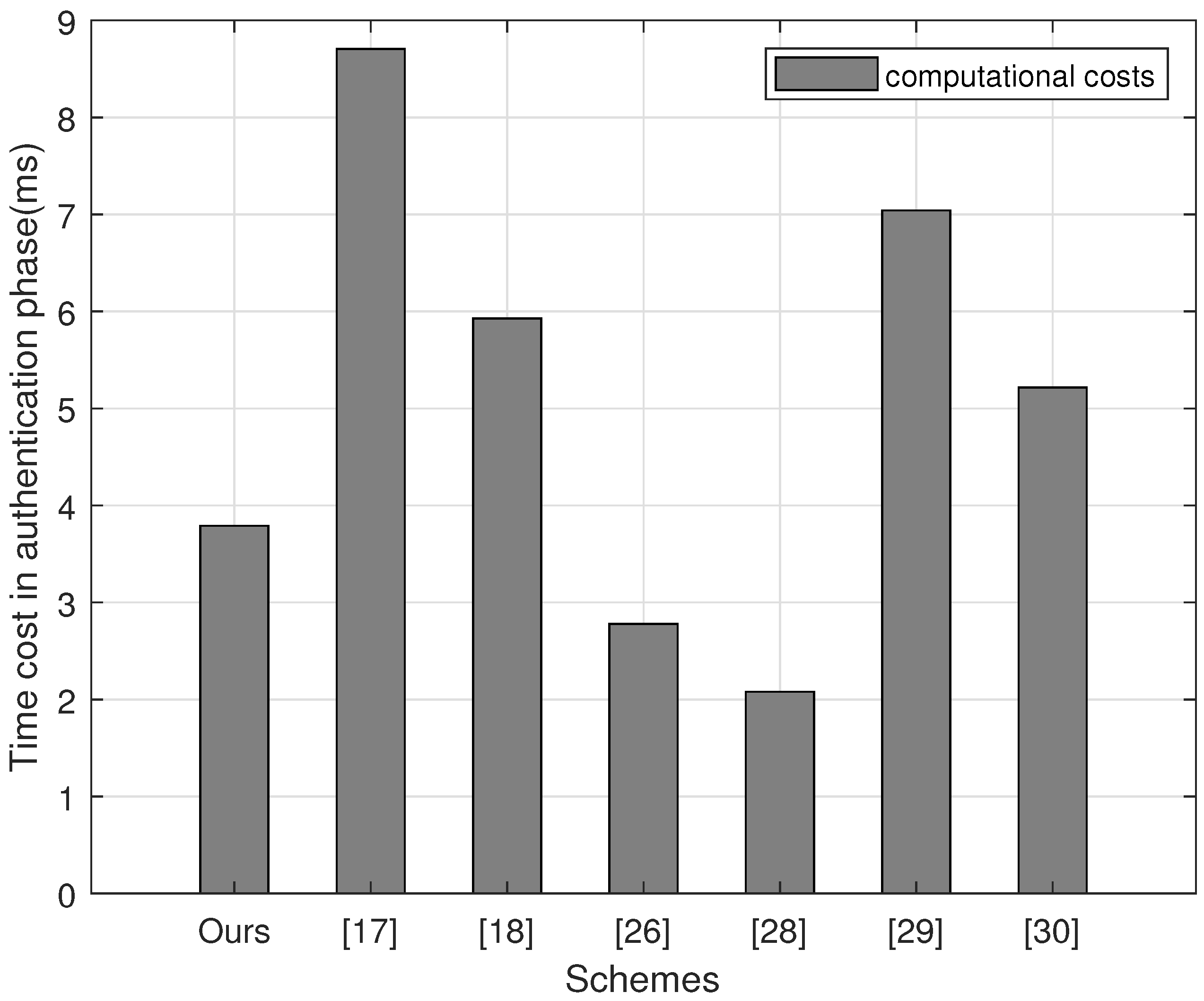
5. Performance Comparison
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Sundmaeker, H.; Guillemin, P.; Friess, P. Vision and challenges for realising the Internet of Things. Clust. Eur. Res. Proj. Internet Things Eur. Commis. 2010, 3, 34–36. [Google Scholar] [CrossRef]
- Lo, N.W.; Tsai, J.L. An efficient conditional privacy-preserving authentication scheme for vehicular sensor networks without pairings. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1319–1328. [Google Scholar] [CrossRef]
- He, D.; Kumar, N.; Chen, J. Robust anonymous authentication protocol for health-care applications using wireless medical sensor networks. Multimed. Syst. 2015, 21, 49–60. [Google Scholar] [CrossRef]
- Li, X.; Niu, J.; Kumari, S.; Liao, J.; Liang, W.; Khan, M.K. A new authentication protocol for healthcare applications using wireless medical sensor networks with user anonymity. Secur. Commun. Netw. 2016, 9, 2643–2655. [Google Scholar] [CrossRef]
- Wu, F.; Xu, L.; Kumari, S. An improved and anonymous two-factor authentication protocol for health-care applications with wireless medical sensor networks. Multimed. Syst. 2017, 23, 195–205. [Google Scholar] [CrossRef]
- He, D.; Kumar, N.; Chilamkurti, N. A secure temporal-credential-based mutual authentication and key agreement scheme for wireless sensor networks. Int. Symp. Wirel. Pervasive Comput. 2013, 36, 316–323. [Google Scholar] [CrossRef]
- Castiglione, A.; Santis, A.D.; Castiglione, A.; Palmieri, F. An Efficient and Transparent One-Time Authentication Protocol with Non-interactive Key Scheduling and Update. In Proceedings of the 2014 IEEE 28th International Conference on Advanced Information Networking and Applications, Gwangju, Korea, 25–27 March 2014; pp. 351–358. [Google Scholar] [CrossRef]
- Gupta, A.; Tripathi, M. A lightweight Mutually Authenticated Key-Agreement scheme for Wireless Body Area Networks in Internet of Things Environment. Radio Freq. Identif. IoT Secur. 2018, 804–806. [Google Scholar] [CrossRef]
- Li, X.; Niu, J.; Kumari, S.; Wu, F.; Sangaiah, A.K.; Choo, K.-K.R. A three-factor anonymous authentication scheme for wireless sensor networks in internet of things environments. J. Netw. Comput. Appl. 2018, 103, 194–204. [Google Scholar] [CrossRef]
- Wong, K.H.M.; Zheng, Y.; Cao, J.; Wang, S. A dynamic user authentication scheme for wireless sensor networks. In Proceedings of the IEEE International Conference on Sensor Networks, Ubiquitous, and Trustworthy Computing (SUTC’06), Taichung, Taiwan, 5–7 June 2006; Volume 1, p. 8. [Google Scholar] [CrossRef]
- Das, M.L. Two-factor user authentication in wireless sensor networks. IEEE Trans. Wirel. Commun. 2009, 17, 1086–1090. [Google Scholar] [CrossRef]
- Khan, M.K.; Alghathbar, K. Cryptanalysis and Security Improvements of ‘Two-Factor User Authentication in Wireless Sensor Networks’. Sensors 2010, 10, 2450–2459. [Google Scholar] [CrossRef]
- Chen, T.-H.; Shih, W.-K. A Robust Mutual Authentication Protocol for Wireless Sensor Networks. ETRI J. 2010, 32, 704–712. [Google Scholar] [CrossRef]
- He, D.; Gao, Y.; Chan, S. An Enhanced Two-factor User Authentication Scheme in Wireless Sensor Networks. Ad Hoc Wirel. Netw. 2010, 10, 361–371. [Google Scholar]
- Holbl, M.; Welzer, T.; Brumen, B. Two proposed identity-based three-party authenticated key agreement protocols from pairings. Comput. Secur. 2010, 29, 244–252. [Google Scholar] [CrossRef]
- Holbl, M.; Welzer, T.; Brumen, B. An improved two-party identity-based authenticated key agreement protocol using pairings. J. Comput. Syst. Sci. 2012, 78, 233–271. [Google Scholar] [CrossRef]
- Jung, J.; Kim, J.; Choi, Y. An Anonymous User Authentication and Key Agreement Scheme Based on a Symmetric Cryptosystem in Wireless Sensor Networks. Sensors 2016, 16, 1299. [Google Scholar] [CrossRef] [PubMed]
- Xue, K.; Ma, C.; Hong, P. A temporal-credential-based mutual authentication and key agreement scheme for wireless sensor networks. J. Netw. Comput. Appl. 2013, 36, 316–323. [Google Scholar] [CrossRef]
- Jiang, Q.; Ma, J.; Lu, X. An efficient two-factor user authentication scheme with unlinkability for wireless sensor networks. Peer-to-Peer Netw. Appl. 2015, 8, 1070–1081. [Google Scholar] [CrossRef]
- Das, A.K. A secure and robust temporal credential-based three-factor user authentication scheme for wireless sensor networks. Peer-to-Peer Netw. Appl. 2016, 9, 223–244. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Y. New Authentication Scheme for Wireless Body Area Networks Using the Bilinear Pairing. J. Med. Syst. 2015, 39, 136. [Google Scholar] [CrossRef] [PubMed]
- Tong, L.; Yuhui, Z.; Ti, Z. Efficient Anonymous Authenticated Key Agreement Scheme for Wireless Body Area Networks. Secur. Commun. Netw. 2017, 2017. [Google Scholar] [CrossRef]
- Porambage, P.; Braeken, A.; Schmitt, C. Group Key Establishment for Enabling Secure Multicast Communication in Wireless Sensor Networks Deployed for IoT Applications. IEEE Access 2015, 3, 1503–1511. [Google Scholar] [CrossRef]
- Xiong, H.; Qin, Z. Revocable and Scalable Certificateless Remote Authentication Protocol with Anonymity for Wireless Body Area Networks. IEEE Trans. Inf. Forensics Secur. 2015, 10, 1442–1455. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Z.; Chen, X.; Kwak, K.S. Certificateless Remote Anonymous Authentication Schemes for WirelessBody Area Networks. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 332–342. [Google Scholar] [CrossRef]
- Abdalla, M.; Fouque, P.-A.; Pointcheval, D. Password-Based Authenticated Key Exchange in the Three-Party Setting; Springer: Berlin/Heidelberg, Germany, 2015; pp. 65–84. [Google Scholar]
- Burrows, M.; Abadi, M.; Needham, R.M. A logic of authentication. R. Soc. 1989, 426, 233–271. [Google Scholar] [CrossRef]

| Symbol | Definition |
|---|---|
| An elliptic curve over a prime finite defined by the equation p | |
| G | An elliptic curve group with the order q, where G is constitutive of all points on E and the point at infinity O |
| P | A generator of the group G |
| Two large prime numbers | |
| U | User |
| S | Sensor node |
| Gateway node | |
| Identity of the user U | |
| Identity of the sensor node S | |
| Three collision-resistant one-way hash functions, where , , | |
| An elliptic curve point in a non-singular elliptic curve , and are x and y coordinates of P respectively | |
| The private key and the corresponding public key of respectively | |
| The private key and the corresponding public key of U respectively | |
| The private key and the corresponding public key of S respectively | |
| r | The random number selected by involved entities |
| The time stamps of respectively | |
| Maximum transmission delay | |
| ⊕ | The XOR operation |
| ‖ | Thet concatenation operation |
| Operation | Description | Computation Time (ms) |
|---|---|---|
| a hash function | ||
| a bilinear pairing | ||
| a ECC-based point multiplication | ||
| a ECC-based point addition |
| Protocol | Computational Cost | Running Time (ms) |
|---|---|---|
| Ours | ≈3.791 | |
| [15] | ≈8.705 | |
| [16] | ≈5.927 | |
| [21] | ≈2.779 | |
| [23] | ≈2.079 | |
| [24] | ≈7.041 | |
| [25] | ≈5.215 |
| Scheme | Ours | [15] | [16] | [21] | [23] | [24] | [25] |
|---|---|---|---|---|---|---|---|
| Anonymity | Yes | No | No | No | No | No | No |
| Mutual authentication | Yes | No | Yes | Yes | Yes | Yes | Yes |
| Session key security | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| Perfect forward secrecy | Yes | Yes | Yes | Yes | No | Yes | Yes |
| Resistance to replay attack | Yes | No | No | Yes | No | No | No |
| Resistance to impersonation attack | Yes | Yes | Yes | No | Yes | No | No |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Liu, T.; Tang, F.; Wang, F.; Tinashe, M. A Privacy-Preserving Authentication and Key Agreement Scheme with Deniability for IoT. Electronics 2019, 8, 450. https://doi.org/10.3390/electronics8040450
Zhou Y, Liu T, Tang F, Wang F, Tinashe M. A Privacy-Preserving Authentication and Key Agreement Scheme with Deniability for IoT. Electronics. 2019; 8(4):450. https://doi.org/10.3390/electronics8040450
Chicago/Turabian StyleZhou, Yousheng, Tong Liu, Fei Tang, Feng Wang, and Magara Tinashe. 2019. "A Privacy-Preserving Authentication and Key Agreement Scheme with Deniability for IoT" Electronics 8, no. 4: 450. https://doi.org/10.3390/electronics8040450
APA StyleZhou, Y., Liu, T., Tang, F., Wang, F., & Tinashe, M. (2019). A Privacy-Preserving Authentication and Key Agreement Scheme with Deniability for IoT. Electronics, 8(4), 450. https://doi.org/10.3390/electronics8040450





