Rolling 3D Laplacian Pyramid Video Fusion

Abstract

In this paper, we present a novel algorithm for video fusion of multi-sensor sequences applicable to real-time night vision systems. We employ the Laplacian pyramid fusion of a block of successive frames to add temporal robustness to the fused result. For the fusion rule, we first group high and low frequency levels of the decomposed frames in the block from both input sensor sequences. Then, we define local space-time energy measure to guide the selection based fusion process in a manner that achieves spatio-temporal stability. We demonstrate our approach on several well-known multi-sensor video fusion examples with varying contents and target appearance and show its advantage over conventional video fusion approaches. Computational complexity of the proposed methods is kept low by the use of simple linear filtering that can be easily parallelised for implementation on general-purpose graphics processing units (GPUs).

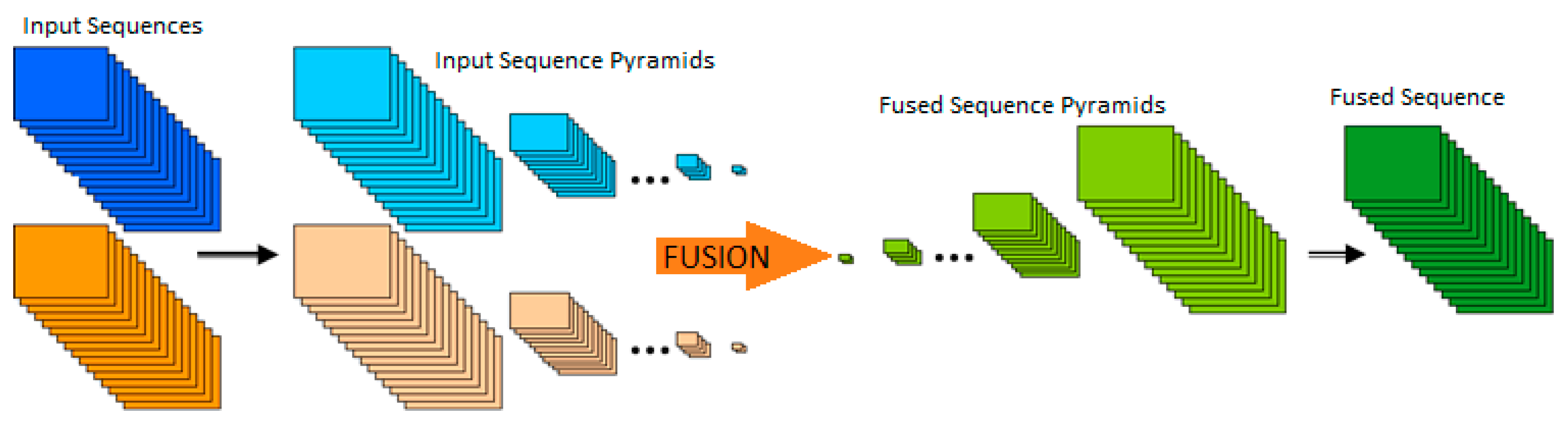
1. Introduction

Multi-sensor night-vision systems use multiple sensors based on different physical phenomena to monitor the same scene. This eliminates reliability deficiencies of individual sensors, and leads to a reliable scene representation in all conditions. For example, combinations of thermal infrared (IR) sensors and visible range cameras can operate in both day and nighttime.

Additional sensors however, mean more data to process as well as display to human observers who cannot effectively monitor multiple video streams simultaneously [1]. Some form of coordination of all data sources is necessary. These problems can be solved by using multi-sensor data fusion methods [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57], which combine multiple image or video signals into a single, fused output signal. These algorithms significantly reduce the amount of raw data with ideally, minimal loss of information, which is a reliable path to follow when dealing with information fusion from several sensors.

Video signal processing used in many fields of vision and algorithms for video fusion that combine two or more video streams into a single fused stream are developing rapidly. The main goal is a better computational efficiency with equivalent or even improved fusion performance. The use of real-time image or video fusion is important in military, civil aviation and medical applications. The requirements for video, also known as dynamic fusion are broadly similar to those of static image fusion. Given that fusion is a significant data reduction process, it is necessary to preserve as much useful information as possible from the input videos while avoiding distortions in the fused signal. An additional requirement, specific to video fusion is the temporal stability of the fused result, which means a temporally consistent fused output despite the dynamically changing scene content. Finally, video fusion algorithms are generally supposed to work in real-time, which means a fusion rate of at least 25 frames per second, or indeed up to 60 for real-time head-up-display applications [6,24].

There are many methods to achieve for image and video fusion, but the field is dominated by multi-resolution and multi-scale methods [1,2,3,4,5,6,7,8,9,10,11]. The multi-resolution analysis decomposes image signals, or frames in case of video, into pyramid representations containing sub-band signals of decreasing resolution, where each sub-band is a part of the original spectrum. Larger structures in the scene are represented in lower frequency sub-bands, while finer details are in high frequency sub-bands. Fusing multi-resolution pyramids rather than complete image signals, provides greater flexibility when choosing relevant information for fused image, allowing the selection of spatially overlapping features from different inputs, if they occupy different scale ranges. The most common multi-resolution techniques are the Laplacian pyramid (LAP) [25,27], ROLP or Contrast pyramid [26,45], Discrete wavelet transform (DWT) [46,47,48], Shift invariant discrete wavelet (SIDWT) [21], bilateral filter [11], guided filter [12,13], Shearlet Transform [3], Nonsubsampled contourlet transform [14] etc.

2. Video Fusion

Video fusion algorithms can be classified into three basic categories [15]. First, are static image fusion algorithms, developed over the last 30 years, where fusion is performed frame by frame to form the fused video sequence. The most popular and widely used algorithms are the Laplacian pyramid fusion [25,27] and Wavelet transform [46,47]. Further to these classic algorithms, new multi-scale techniques have more recently been proposed based on the static fusion using Curvelets [50], Ridgelets [51], Contourlets [14], Shearlet [3] as well as the Dual tree complex wavelet transform (DTCWT) [48]. The static fusion methods for video fusion are generally less computationally demanding, but since they ignore the temporally varying component of the available scene information, they can result in temporally unstable fused sequences exhibiting blinking effect distortions that affect the perceived fused video quality [15,24].

In the second category are fusion algorithms that take the temporal, as well as spatial component of the data into account. Most common techniques use some of the static image methods or modified static image fusion method with additional calculation of temporal factors such as optical flow [22], motion detection or motion compensation [15]. These algorithms compare pixel or pixel block change through frames, forming the selection decisions for fused pixels in sequence. These “real” video fusion methods achieve better results than static fusion applied dynamically, but these methods, depending on the used technique and its complexity, can generally jeopardize real-time operation. The most popular algorithms in this category are Optical flow [22], and Discrete wavelet transform with motion compensation [15]. The algorithm in [53] periodically calculates the background over a specific period T (T = 4 s) by taking the most repetitive pixel value. The background is refreshed every T/4. That way the background image fusion is also executed every T/4, while the moving object fusion is calculated for each frame using the Laplace pyramid fusion [27].

Finally, the third category is made up of so-called 3D algorithms [54,55,56,57,58,59]. These algorithms represent an extension of the conventional static image fusion algorithms into 3D space. The most important aspect of these algorithms is that they cannot be used in real-time applications, even though they provide better results than the algorithms described above. It should also be taken into consideration that video signals are not a simple 3D extension of 2D static images; and motion information needs to be considered very carefully. Computational demands, as well as memory consumption are, in this case, way above the requirements of algorithms from the first two groups. 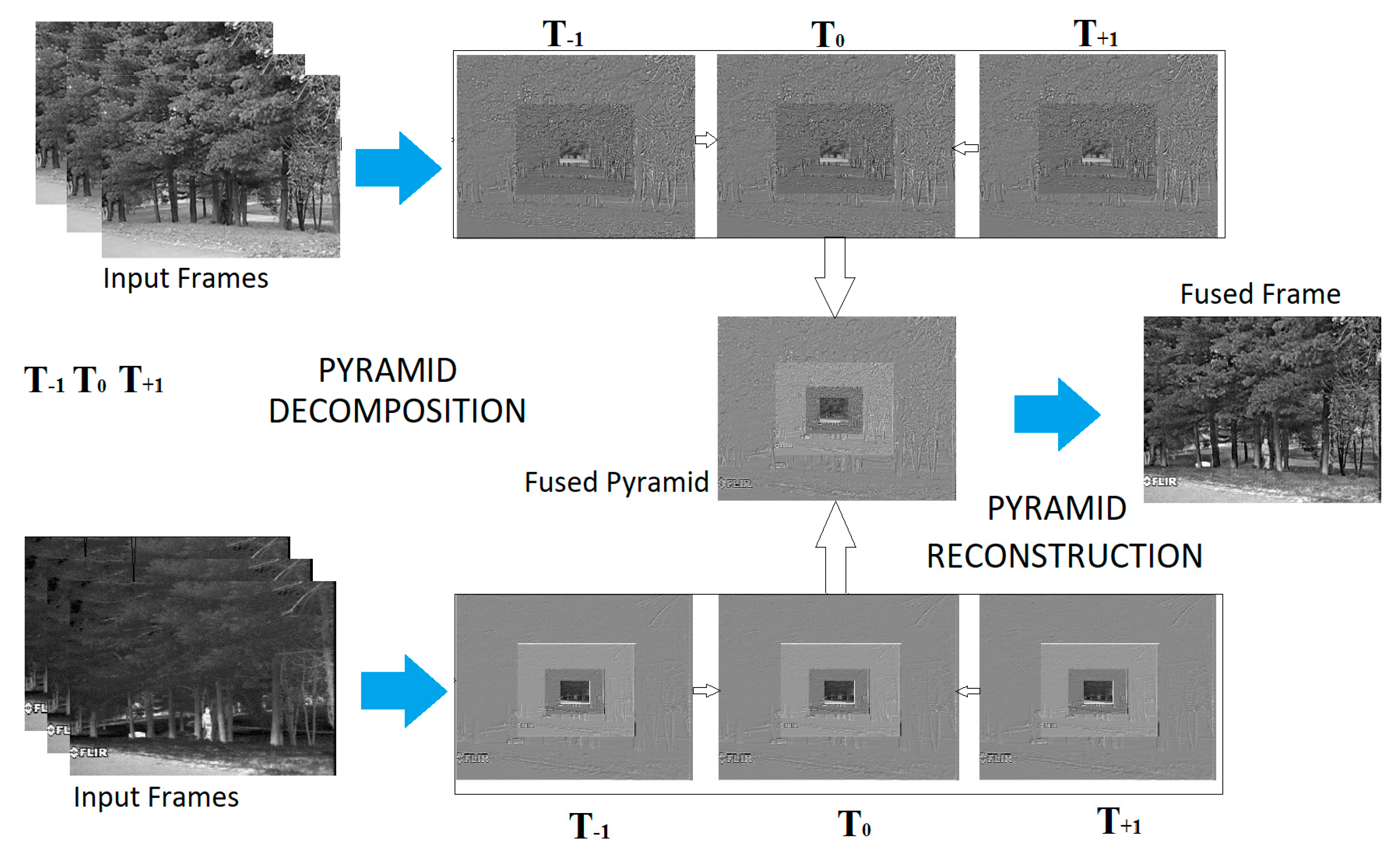In the 3D Laplace pyramid fusion [54], the Gaussian pyramid decomposition is performed in three dimensions using identical 1 × 5 1D Gaussian filter response (with values: [1 4 6 4 1]/16). The condition for this type of pyramid decomposition is that the length of the sequence is greater than 2^N+1, where N is the number of pyramid levels. Similar to the 2D filtering situation, where each next level is obtained by decimation with factor 2, in the 3D case the number of frames is also decreased with factor 2 (Figure 1). The equivalent 3D Laplacian pyramid of a sequence is obtained in the same way as in the 2D case, using the Gaussian pyramid expansion and subtraction. The 3D pyramid fusion can then be performed using the same conventional methods of pyramid fusion used in image fusion. The final fused sequence is formed by reconstructing the 3D Laplace pyramid (Figure 1). Other methods of the static image fusion extended to the 3D fusion in this manner are 3D DWT [54], 3D DT CWT [55,56] and 3D Curvelets [16,17]. A related, advanced 3D fusion approach used to additionally achieve noise reduction is polyfusion [59], which performs the Laplace pyramid fusion of different 2D sections of the 3D pyramid (e.g., spatial only sections or spatio-dynamic sections involving lateral pyramid side (Figure 2). The final fused sequence is obtained by fusing these two fusion results, while taking care of the dynamic value range.

Figure 3 shows a multi-sensor view, in this case IR and TV images, of the same scene. The IR image clearly shows a human figure but not the general structure of the scene [57,58], while it is not immediately detectable in the TV image. Figure 4 shows a fused image using the Laplacian pyramid fusion [27]. Laplacian fusion robustly transfers important objects from the IR image and preserves structures from the TV image.

3. Dynamic Laplacian Rolling-Pyramid Fusion

Video fusion methods mentioned above take into account the temporal data component and give better results than standard frames by frame methods, but they are time-consuming and for higher video resolutions cannot be used in real-time. These methods require the fusion of already existing multi-resolution methods, decomposing more than one frame for calculating the fusion current-frame coefficient and additional temporal parameters (motion detection, temporal filters), which significantly increases their computational complexity.

Therefore, a new approach for video sequence fusion is required that would not only alleviate identified shortcomings of current methods but also introduce spatio-temporal stability into the fusion process. Furthermore, it must be computationally efficient to allow real-time fusion of two multi-sensor streams with a maximum latency of no more than a single frame period. Both subjective tests and objective measures comparisons of still image fusion methods have shown that the Laplacian pyramid fusion provides optimal or near optimal fusion results in terms of both of the subjective impression of the fused results and objective fusion performance as measured with a range of objective fusion metrics. Furthermore, this is achieved with a lower complexity in comparison to algorithms that give similar results [6]. In [6] 18 different fusion methods [10,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43] are compared using nine objective fusion performance metrics and computational complexity evaluations. The analysis concluded that out of the real-time capable fusion algorithms, the Laplacian fusion performs best for the majority of metrics.

For these reasons, the Laplacian pyramid approach could solve existing problems in video fusion while being suitable for real-time operation. In order to reduce processing time and process the temporal information properly, it is necessary to reduce the number of frames to be processed. The approach however must facilitate robust selection input structures from input pyramids, which critically affects the fused result.

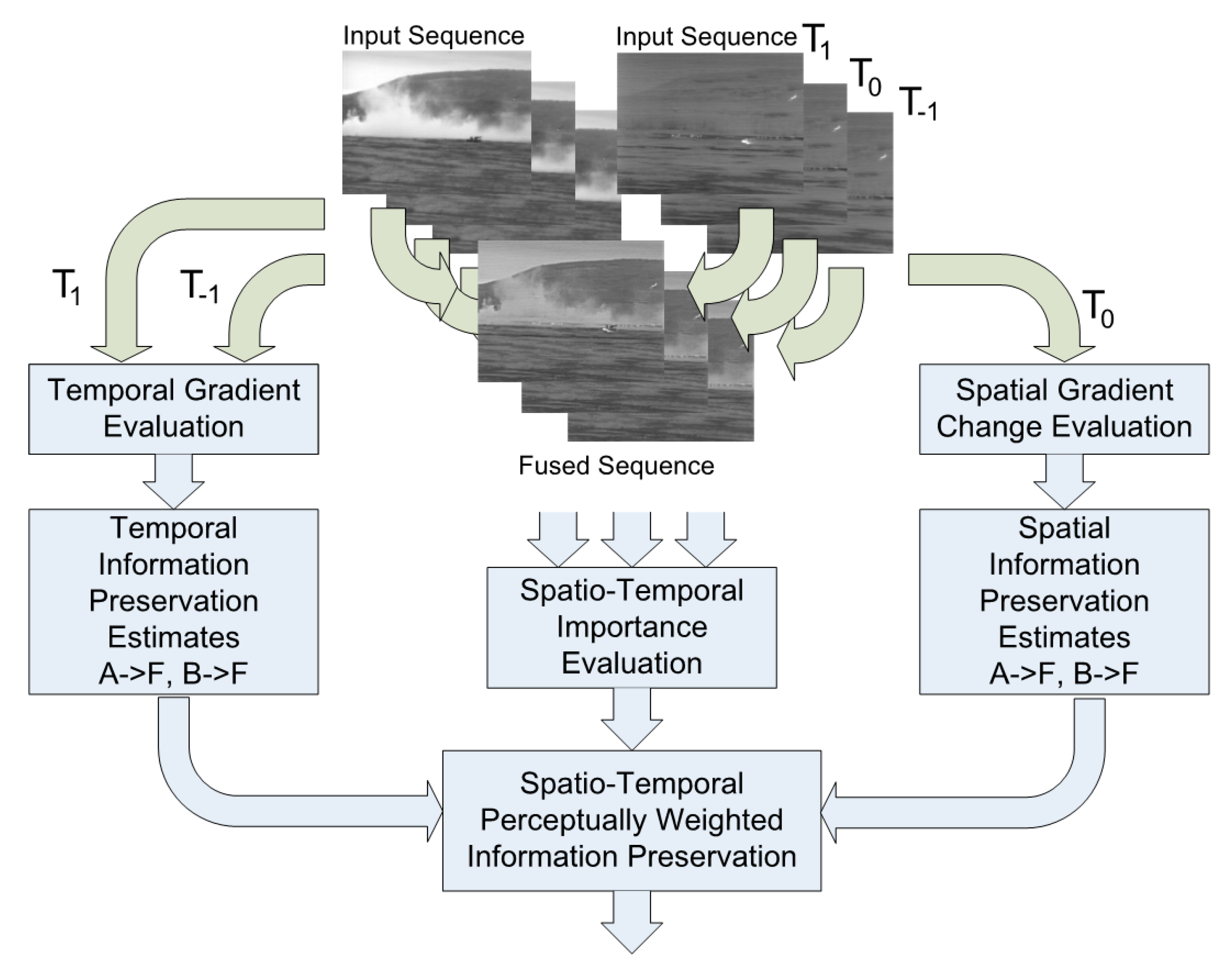
The proposed algorithm broadly follows the conventional strategy of decomposing the input streams into pyramid representations, which are then fused using a spatio-temporal pyramid fusion approach and finally reconstructed into the fused sequence. The adopted approach uses a modified version of the multi-dimensional Laplacian pyramid to decompose the video sequence. Specifically, it maintains a rolling buffer version of the 3D pyramid constructed from the 2D Laplacian pyramids of three successive frames only, current and two previous frames, to fuse each frame. The advantage in complexity of this algorithm in comparison with existing fusion methods is the fact that for the fusion of one frame only one frame needs to be decomposed into its pyramid, while the two other frames used in the 3D pyramid are taken from memory (previous frame pyramids). Furthermore, the pyramid fusion is performed on one 2D frame pyramid only and only one fused frame needs to be reconstructed from a 2D representation. All this results in a significantly faster operation. Additionally, there is no need for further processing such as motion detection or background subtraction.

The dynamic pyramid fusion, as mentioned above, is applied to the whole rolling 3D pyramid but only to fuse the central frame. Specifically, only the central frame of the fused pyramid is constructed from equivalent frames in the rolling input pyramids. For this purpose, only values from these input frames are used to construct the fused value at each location, while previous and next frames serve to determine their respective importance and combination factors (Figure 5).

The first step is to group high and low frequency levels of the pyramid of all three frames from both input sensor sequences. The fusion rule for low frequency details is a spatio-temporal selection rule based on central pixel neighbourhood energy. The neighbourhood evaluation space is thus M × N × T, where M, N are window dimensions, and T is the number of frames in our rolling pyramid (in our case we use simply M = N = T = 3). Even though this neighbourhood seems small both spatially and temporally, it is in fact enough as will be shown to achieve temporal stability.

Low-frequency coefficients of the fused Laplacian pyramid are obtained by:

$$F_{L0}^k\left(m,n\right)={\omega }_{Va}^k\left(m,n\right)L_0^{Va,k}\left(m,n\right)+{\omega }_{Vb}^k\left(m,n\right)L_0^{Vb,k}\left(m,n\right)$$

(1)

where $L_0^{Va,k}\left(m,n\right)$ and $L_0^{Vb,k}\left(m,n\right)$ are low-frequency Laplacian pyramid coefficients of the current frame k in the input video sequences $V_a$ and $V_b$ at position $\left(m, n\right)$ and ${\omega }_{Va}^k\left(m,n\right)$ and ${\omega }_{Vb}^k\left(m,n\right)$ are the local weight coefficients that represent the energy of the pixel environment in a spatial-temporal domain. Low-frequency coefficients represent the lowest level of the pyramid in which the main energy and larger structures of the frame are contained. It means that the weight coefficients for fusing the low-frequency coefficients of the Laplacian pyramid are determined from:

$${\omega }_{Va}^k\left(m,n\right)=\frac{E_{Va}^k\left(m,n\right)+\epsilon }{E_{Va}^k\left(m,n\right)+E_{Vb}^k\left(m,n\right)+\epsilon }$$

(2)

$${\omega }_{Vb}^k\left(m,n\right)=1-{\omega }_{Va}^k\left(m,n\right)$$

(3)

where ε is a small positive constant, to prevent division with 0, set throughout to ${10}^{-6}$. The local spatio-temporal energy E of a central pixel at $m,n$ in frame $t$ and is determined as the total amount of high-frequncy activity, measured through square of local pyramid coeffcient magnitude, in its immediate, 3 × 3 × 3 spatio-temporal neighbourhood according to:

$$E_{\left\{Va,Vb\right\}}^k\left(m,n,t\right)={\displaystyle \sum }_{m=-M/2}^{M/2}{\displaystyle \sum }_{n=-N/2}^{N/2}{\displaystyle \sum }_{\eta =-T/2}^{T/2}{\left|L_0^{\left\{Va,Vb\right\}}\left(x+m,y+n,t+\eta \right)\right|}^2$$

(4)

where $\left\{V_a,V_b\right\}$ signifies the spatial energy computed for video $V_a$ and $V_b$ in turn, for the sake of brevity. Interesting locations around the salient static and moving structures, that we want to preserve in the fused sequence, will have significant pyramid coefficients $L_i^V\left(m,n,t\right)$ leading to high local energy estimates. The next step is to fuse the coefficients of the Laplacian Pyramid L_i^Va(m,n,t) and L_i^Vb(m,n,t) which represent higher frequencies and, therefore finer details in the incoming multi-sensory sequences. Similar to the fusion of large-scale structures, the spatio-temporal energy approach based on a local neighborhood of M × N × T is also used here. The window size has been kept the same at 3.

It is an established practice in the fusion field that for fusing information of higher frequencies derived from multi-resolution decompositions, the choice of the maximum absolute pixel value from either of the inputs is a reliable method of maximizing contrast and preserving the most important input information. However, in our case, we have information from three successive frames, and using the local energy approach a local 3 × 3 × 3 of pyramid pixels will be influenced by each coefficient eliminating the effects of noise and temporal flicker due to shift variance effects of the pyramid decomposition.

Comparing this approach to the simple select-max applied to central frame only, using the objective DQ video fusion performance measure [24] on a representative sequence illustrated in Figure 3, Figure 6 below, we see that the proposed approach improves fusion performance. However, although the increase in DQ is significant, there are still large oscillations through the frames. Figure 7 below shows successive frames obtained by the proposed dynamic fusion where flicker through sequences still causes temporal instability. This is also evident in the difference image obtained between these two frames, in the form of “halo” effects around the person and pixels that have a higher value, although there are no significant changes in the scene background. We appreciate that it is difficult to convey this type of dynamic effect on a still image and include this fused sequence in the Supplementary Material.

Temporally Stable Fusion

Temporal instability is often caused in areas where local pyramid energies of the input images are similar which in turn causes frequent changes of coefficient selection decisions between the inputs across space and time, causing source flicker. This behavior can be remedied through a more advanced fusion approach applied to higher frequency details. Specifically, we can use the spatio-temporal similarity index $S_{Vab}^k\left(m,n\right)$ to compare the input pyramid structures before deciding on the optimal fusion approach [15]. Similarity between inputs at each location is evaluated according to:

$$S_{Vab}^k\left(m,n\right)=\frac{2{{\displaystyle \sum }}_{m=-M/2}^{M/2}{{\displaystyle \sum }}_{n=-N/2}^{N/2}{{\displaystyle \sum }}_{\eta =-T/2}^{T/2}{\left|L_i^{Va}\left(x+m,y+n,t+\eta \right)L_i^{Vb}\left(x+m,y+n,t+\eta \right)\right|}^{}+\epsilon }{E_{Va}^k\left(m,n\right)+E_{Vb}^k\left(m,n\right)+\epsilon }$$

(5)

$S_{Vab}^k$ ranges between 0 and 1, where 1 signifies identical signals and values around 0 indicate very low input similarity. If S is small, below a threshold ξ, one of the inputs is usually dominant and the coefficient from the pyramid with higher local energy is taken for the fused pyramid. If similarity is high, we preserve both inputs in a weighted summation with weight coefficients based on their relative local energies.

$$F_{Li}^k\left(m,n\right)=\{\begin{array}{c}{L}_j^{Va,k}\left(m,n\right),S_{Vab}^k\left(m,n\right)<\xi and{E}_j^{Va}\left(m,n\right)\ge E_j^{Vb}\left(m,n\right)\\ L_j^{Vb,k}\left(m,n\right),S_{Vab}^k\left(m,n\right)<\xi and{E}_j^{Va}\left(m,n\right)<E_j^{Vb}\left(m,n\right)\\ {\omega }_j^{Va}\left(m,n\right)L_j^{Va,k}\left(m,n\right)+{\omega }_j^{Vb}\left(m,n\right)L_j^{Vb,k}\left(m,n\right)\end{array}$$

(6)

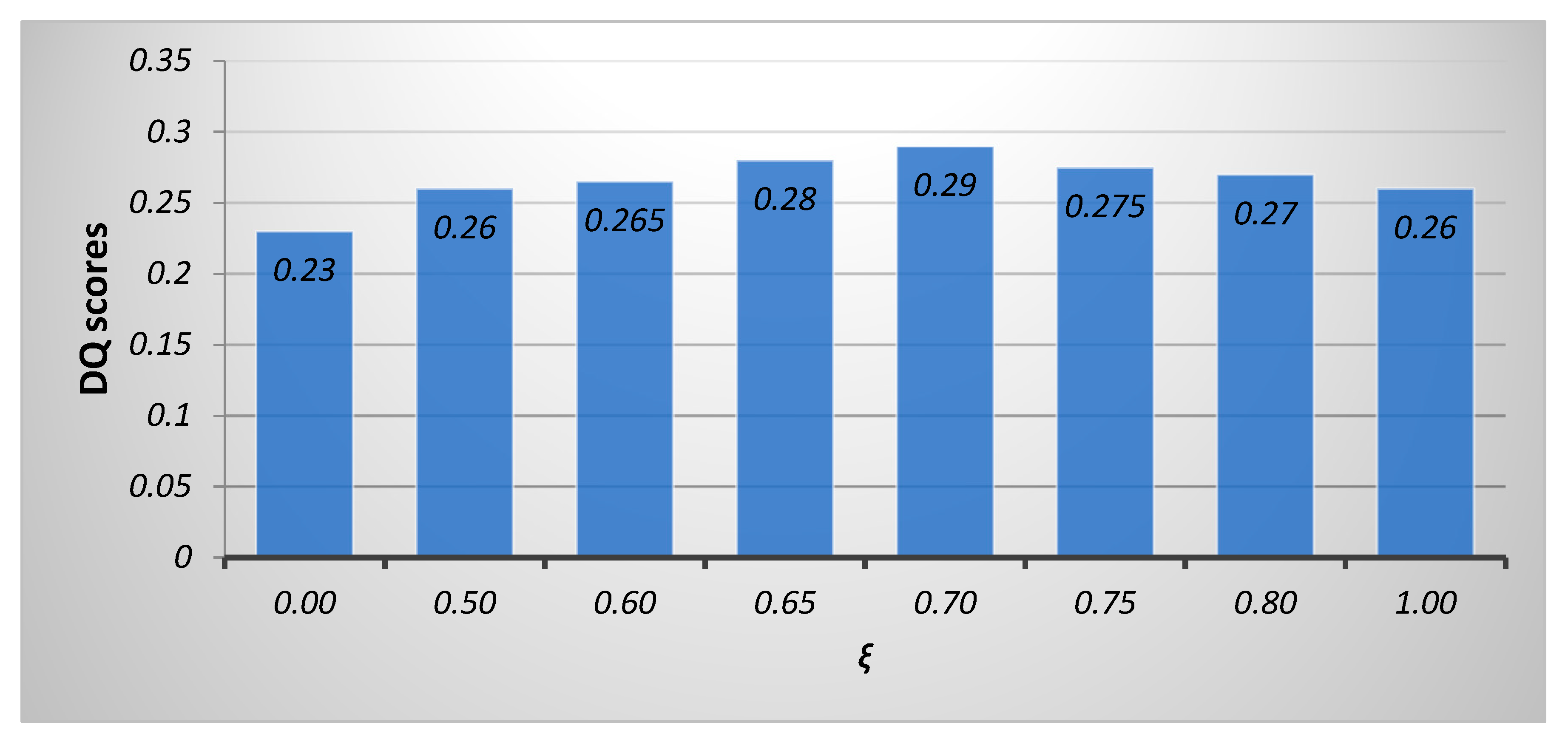
To determine the optimal value of the similarity threshold ξ, we applied the proposed method on a set of six different multi-sensor sequences, varying ξ from 0 to 1 with a step of 0.05. When ξ = 0 resolves to a selection of coefficients with maximum local energy and 1 implies fusion using exclusively linear weighted combination of inputs. We measured the average fusion performance for each tested value of ξ using the dynamic fusion performance measure DQ [24]. The result of this analysis for a relevant subset of threshold values is shown in Figure 8 below, identifying that ξ = 0.7 gives optimal fusion performance.

Figure 9 illustrates the effects of the proposed pyramid fusion approach compared to the static fusion. Pyramid fusion selection maps, static, left, and proposed right, for the frames shown in Figure 3 above (bright pixels are sourced from the visible range and dark ones from the thermal sequence with gray values showing split sourcing in the dynamic fusion case) show a significantly greater consistency in the proposed dynamic method. This directly affects spatio-temporal stability.

4. Results

Performance of the multi-sensor fusion is traditionally measured using subjective and objective measures. Subjective measures derived from collections of subjective scores provided by human observers on representative datasets, are generally considered to be the most reliable measures, since humans are the intended end users of fused video imagery in fields such as surveillance and night vision. Outputs of such subjective evaluation trials are human observer quality measures represented through mean opinion scores – MOS. MOS is a widely used method of subjective quality scores generalization, defined as a simple arithmetic mean of observers’ score for a fused signal i:

$$MO{S}_i=\frac{1}{N_s}{\displaystyle \sum }_1^{N_s}SQ\left(n,i\right)$$

(7)

where SQ(n,i) – subjective quality estimate of fused sequence i by the observer n while N_s is the total number of observers that took part in the trial.

Objective fusion metrics are algorithmic metrics providing a significantly more efficient fusion evaluation compared to subjective trials [60,61]. Even though an extensive field of still fusion objective metrics exists, these methods do not consider temporal data vital for video fusion. Video fusion metrics need to consider temporal stability implying that temporal changes in the fused signal can only be a result of changes in an input signal (any input) and not the result of a fusion algorithm. Furthermore, temporal consistency requires that changes in input sequences have to be represented in fused sequence without delay or contrast change. A direct video fusion metric I was proposed on these principles in [21] based on the calculation of common information in inter-frame-differences (IFDs), of the inputs and fused sequence.

DQ metric based on measuring preservation of spatial and temporal input information in the fused sequence was proposed to explicitly measure video fusion performance [24]. DQ measures the similarity of spatial and temporal gradient information between the inputs and the fused sequences (Figure 10). The evaluation is based on three consecutive frames of all three sequences with spatial information extracted from the current and temporal information from the other two, previous and following, frames using a robust temporal gradient approach. A perceptual gradient preservation model is then applied to evaluate information preservation at each location and time in the sequence. Spatial and temporal preservation estimates are then integrated into a single spatio-temporal information preservation estimate for each location and frame. These localized estimates are then pooled using local perceptual importance estimates into frame scores and then averaged into a single, complete sequence fusion performance score.

We also used the objective video fusion quality metric Q_ST with the structural similarity (SSIM) index and the perception characteristics of human visual system (HVS) [62]. First, for each frame, two sub-indices, i.e., the spatial fusion quality index and the temporal fusion quality index, are defined by the weighted local SSIM indices. Second, for the current frame, an individual-frame fusion quality measure is obtained by integrating the above two sub-indices. Last, the global video fusion metric is constructed as the weighted average of all the individual-frame fusion quality measures. In addition, according to the perception characteristics of HVS, some local and global spatial–temporal information, such as local variance, pixel movement, global contrast, background motion and so on, is employed to define the weights in the metric Q_ST.

Finally, we also evaluate our fusion results with a non-reference objective image fusion metric FMI based on mutual information which calculates the amount of information conducted from the source images to the fused image [63]. The considered information is represented by image features like gradients or edges, which are often in the form of two-dimensional signals.

The performance of the proposed LAP-DIN method was evaluated on a database of dynamic multi-sensor imagery from six different scenarios, Figure 11. The compromises local sharpness for the sake of temporal stability and fewer spatial artifacts, which can be seen in the sharpest SIDWT method.

Figure 12 illustrates its performance alongside the Laplacian pyramid [27] and SIDWT fusion [21], image fusion methods with shift-invariance well suited to dynamic fusion, applied frame by frame. The proposed method is generally no less sharp than the other two methods, see left column, but in some examples the dynamic selection.

The left column shows the static Laplacian pyramid fusion [27], the middle–static SIDWT fusion [21], while the right proposed LAP-DIN fusion, all applied with the same decomposition depth of four. The proposed fusion provides clearer, higher contrast images than the other two methods. Further, a noise mitigation effect is also visible in the second row where the thermal image noise, is transferred into the fused signal by the two static methods, but not the LAP-DIN approach.

4.1. Objective Evaluation

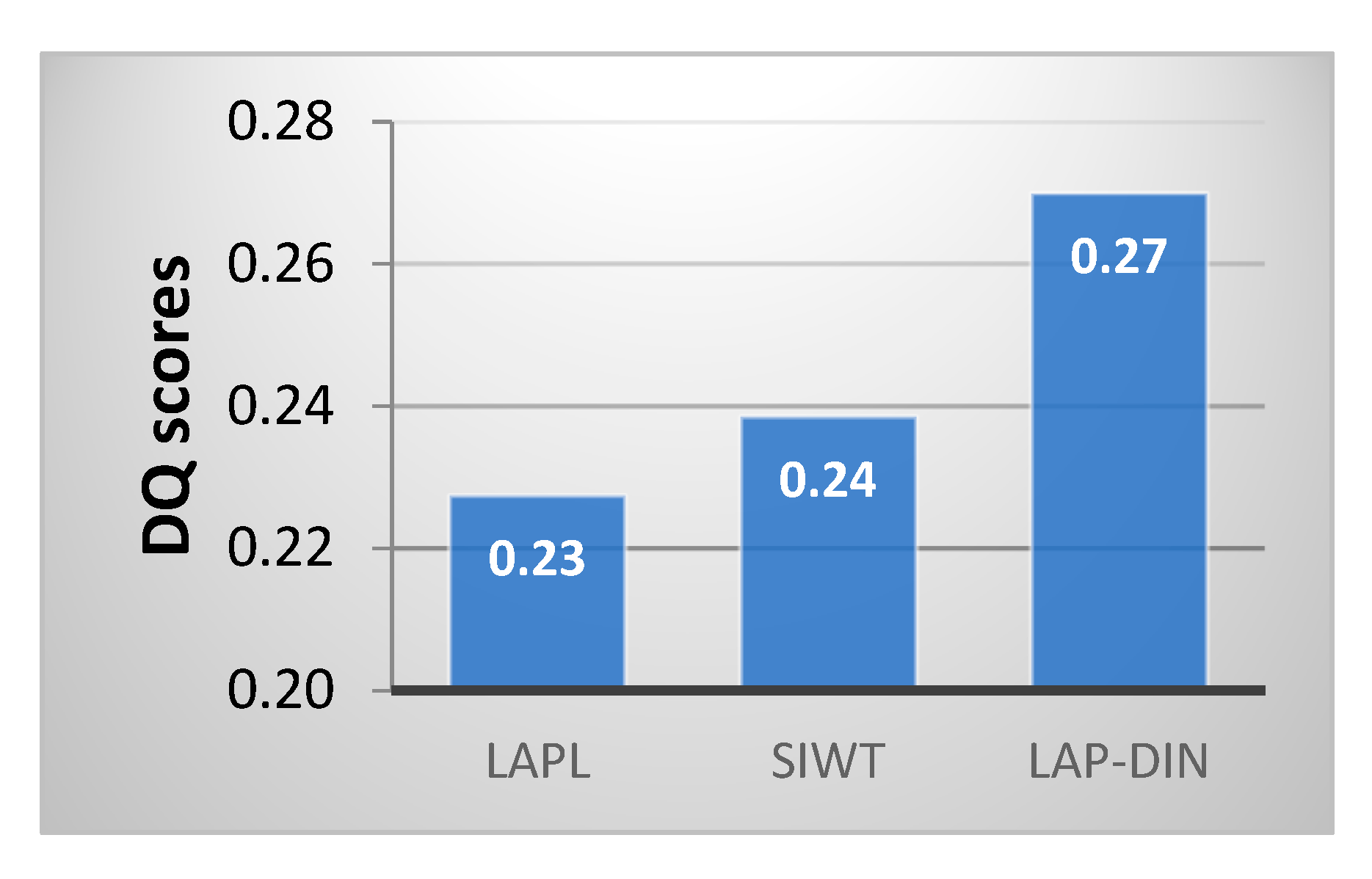
Objective performance evaluation was performed by the DQ and I metrics on the fused video obtained from our test database. DQ scores for the three methods considered first, shown in Figure 13 below and given for all sequences individually in

Table 1. Fusion performance scores for individual sequences.

	LAP	SIWT	LAP-DIN
Seq 1	0.23	0.23	0.26
Seq 2	0.26	0.25	0.30
Seq 3	0.20	0.22	0.23
Seq 4	0.26	0.26	0.29
Seq 5	0.23	0.26	0.28
Seq 6	0.19	0.21	0.23
Mean	0.23	0.24	0.27

, indicate that the LAP-DIN method clearly preserves spatial and temporal input information better overall and for all scenarios individually.

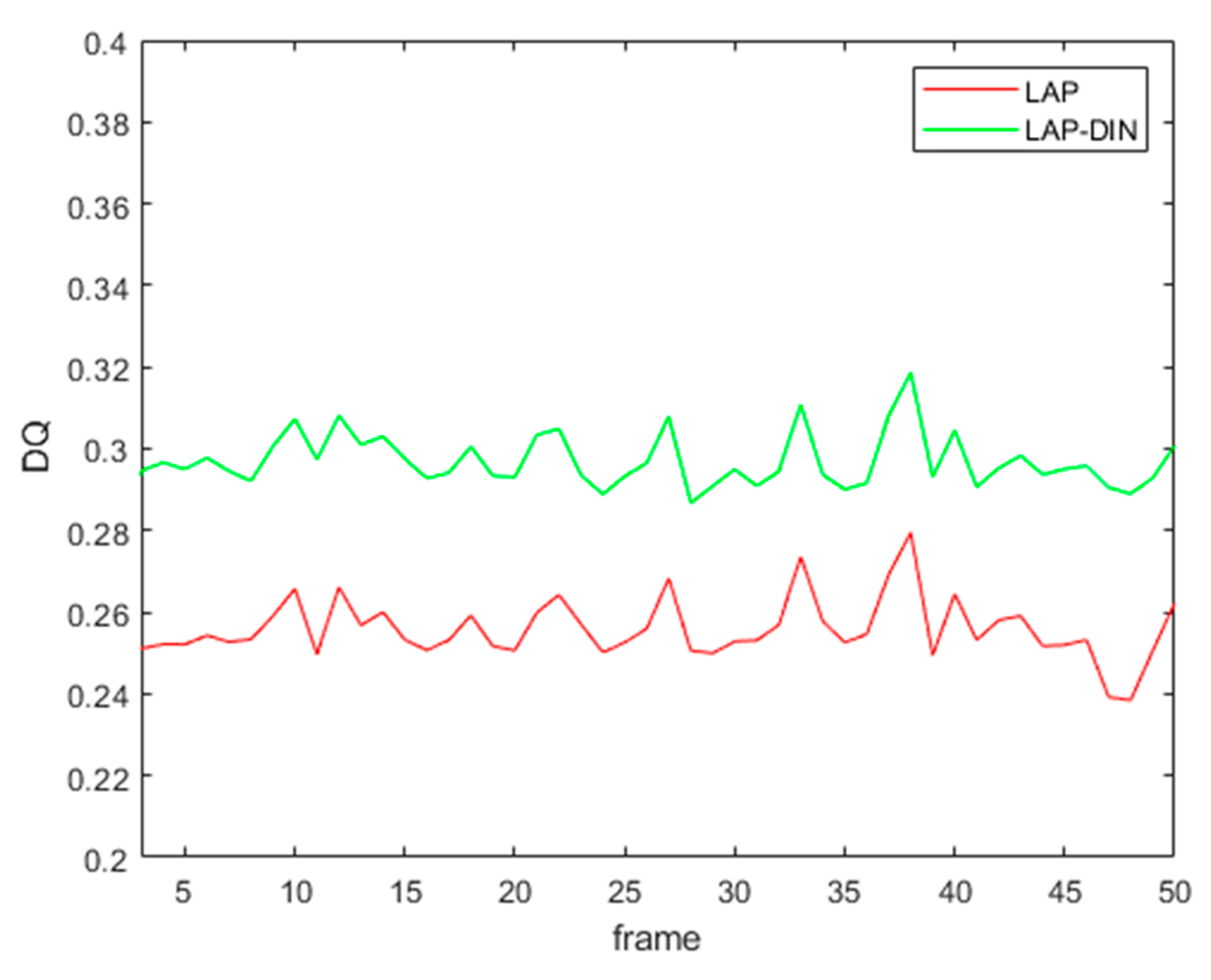
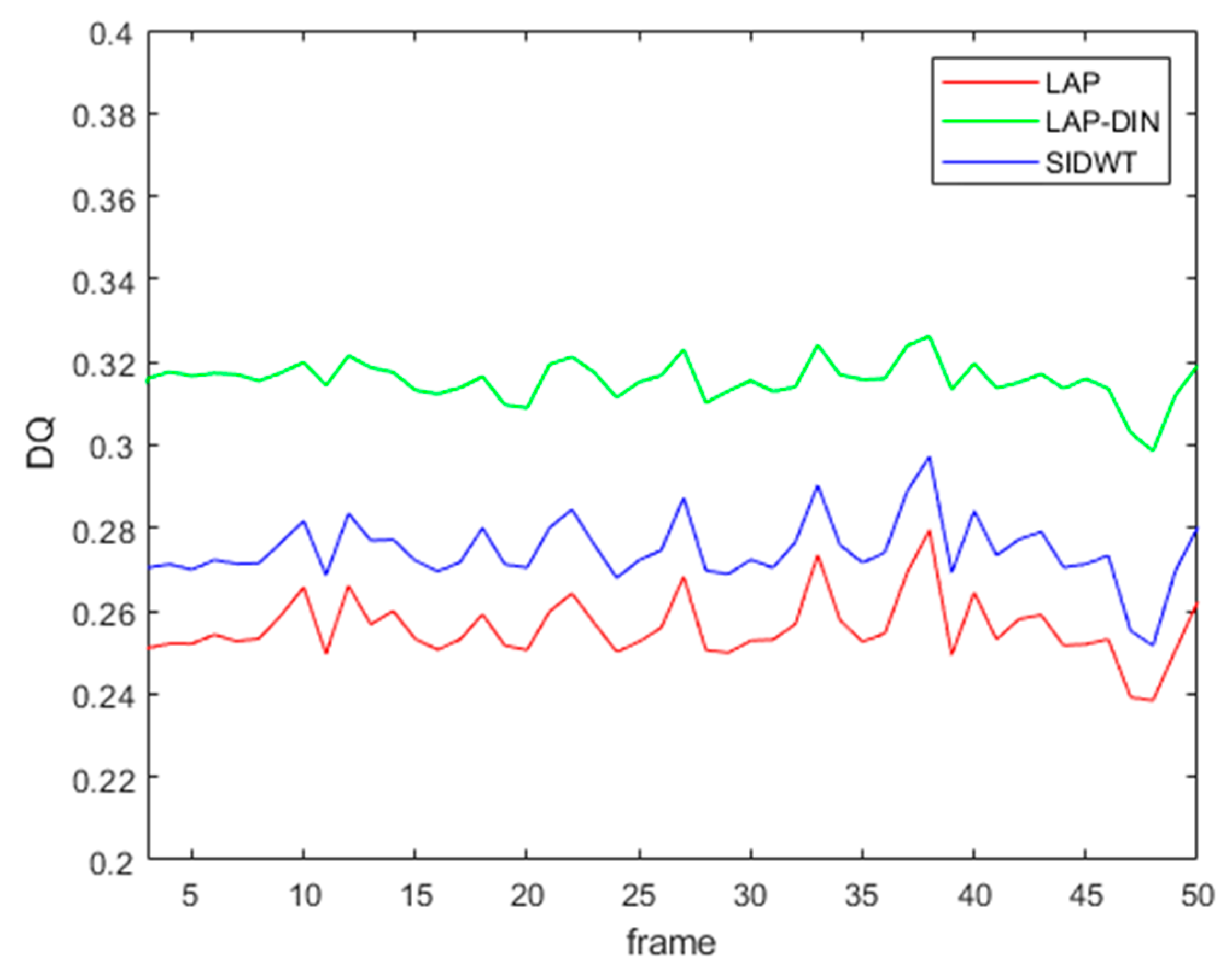
As an indication of temporal stability of fusion scores, DQ values for the first 50 frames of sequence 1 are shown in Figure 14 below. LAP-DIN scores exhibits considerably less temporal variation 0.049 compared to 0.079 and 0.0076 for the LAP and SIDWT static algorithms respectively, on the same fused video section. The remaining score changes are the result of a significant scene movement.

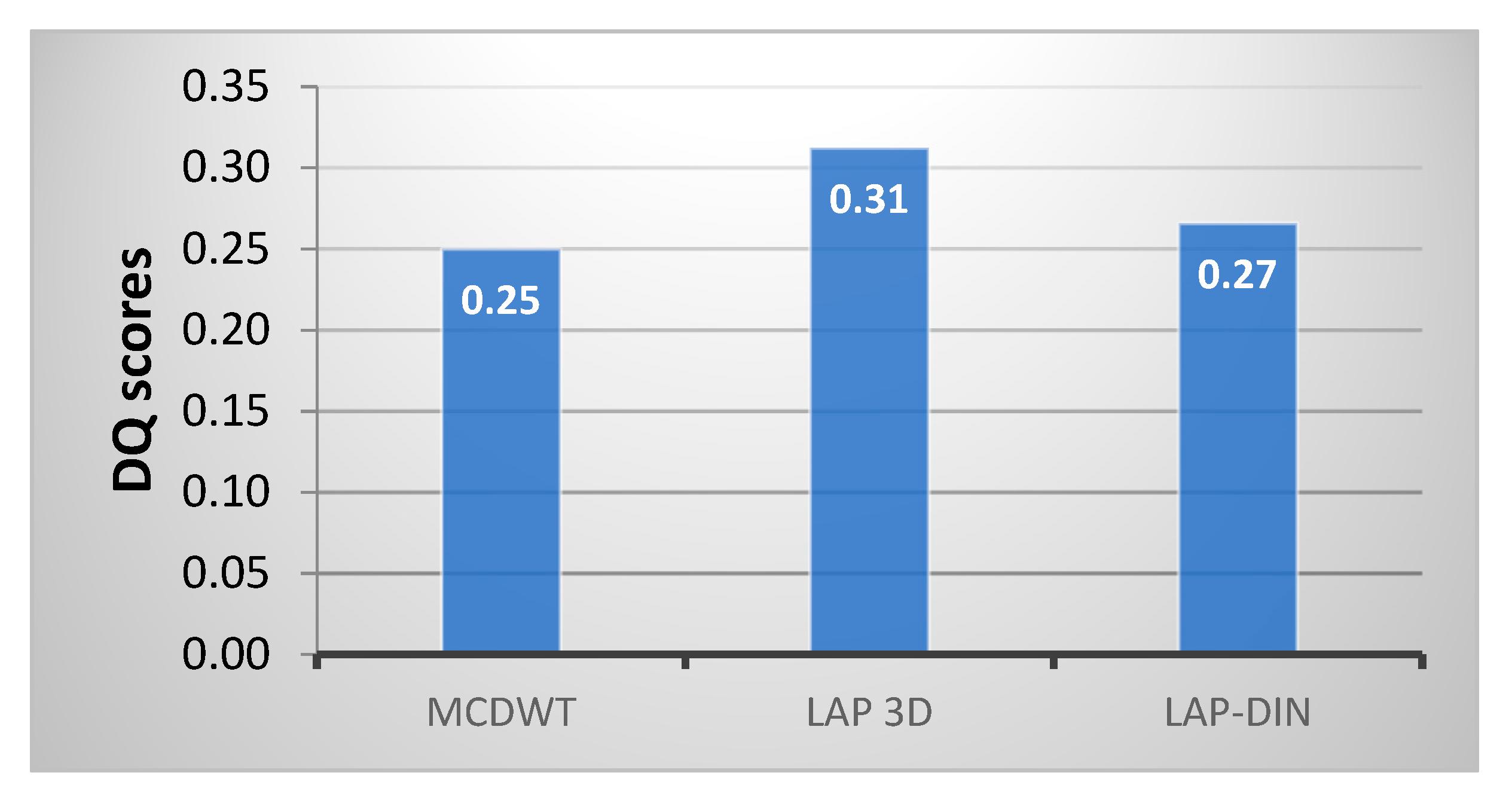
In Figure 15 and

Table 2. Results of objective measure DQ on dataset sequences separately.

	MCDWT	LAP 3D	LAP-DIN
Seq 1	0.24	0.32	0.26
Seq 2	0.26	0.37	0.30
Seq 3	0.23	0.30	0.23
Seq 4	0.22	0.30	0.23
Seq 5	0.26	0.30	0.28
Seq 6	0.30	0.28	0.29
Mean	0.25	0.31	0.27

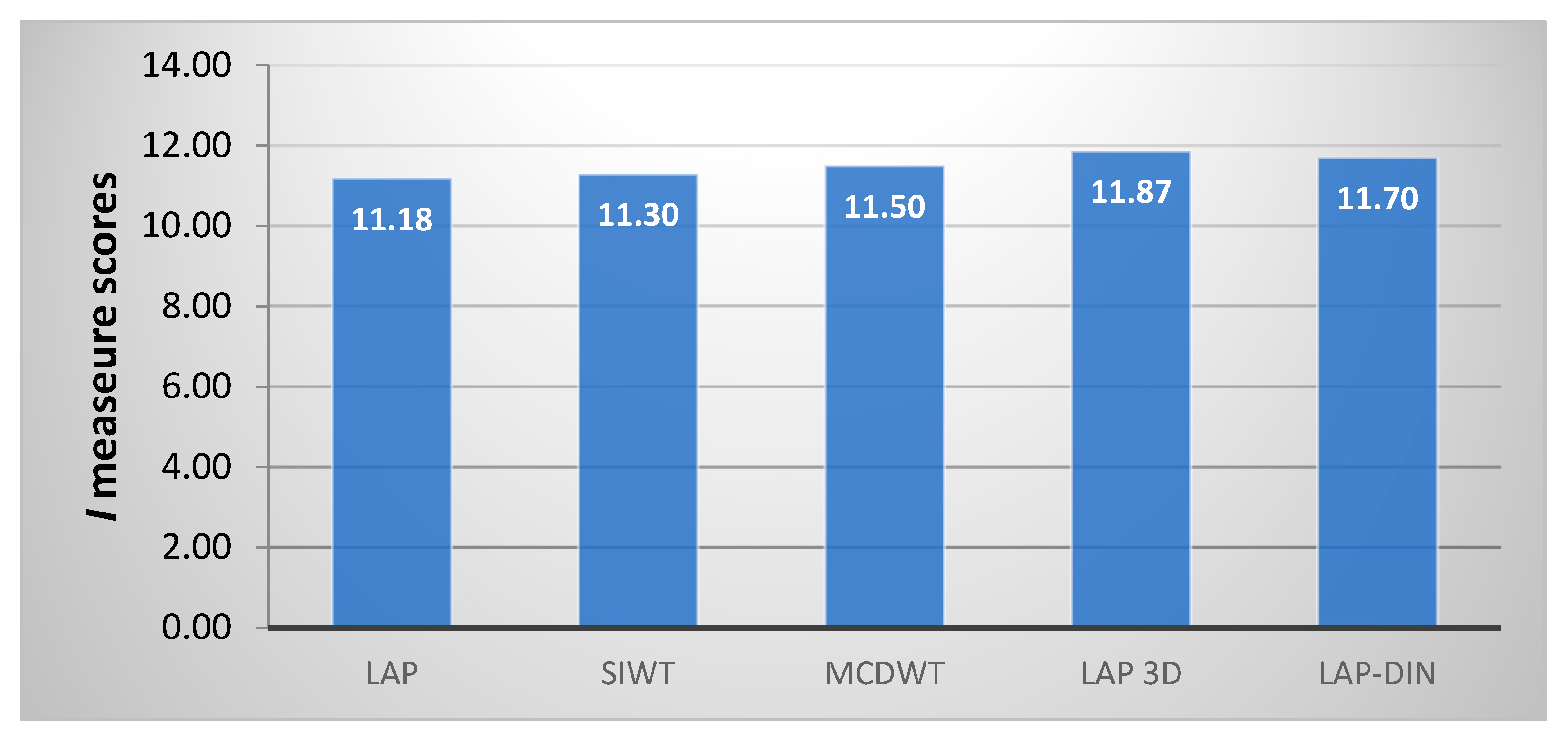
, we compare DQ scores of the proposed method directly with those of the video fusion methods that explicitly deal with temporal information: MCDWT based on motion detection estimation and the discrete wavelet transformation [15] and the non-causal Laplacian 3D pyramid fusion method [54] not suitable for real-time operation. It indicates that the true 3D pyramid is the most successful video fusion technique, followed by the LAP-DIN method and the MCDWT, which is better than static methods.

These findings were confirmed by the I metric [21] as shown in Figure 16 below.

Finally,

Table 3. Results of four objective measures on dataset sequences.

	LAP	SIDWT	MCDWT	LAP 3D	LAP-DIN
DQ	0.23	0.24	0.25	0.31	0.27
I	11.18	11.30	11.50	11.87	11.70
QST	0.87009	0.870064	0.871903	0.878615	0.876745
FMI	0.673145	0.641313	0.661495	0.692034	0.676197

provides the results of the evaluation by four different objective video fusion performance metrics. All the metrics confirm the non-causal 3D Laplacian pyramid fusion as the most successful method, with the proposed method next best, with the exception of the FMI metric, which ranks the conventional Laplacian fusion second. FMI is a static image fusion metric and does not take into account dynamic effects in fused sequences.

4.2. Subjective Evaluation

The proposed video fusion method was also evaluated through formal subjective trials. Observers with general image and video processing research experience but no specific multi-sensor fusion experience were recruited to perform the test in a daylight office environment, until the subjective ratings converged. In all 10 observers completed the trial on six different fusion scenarios displayed in a sequence on a 27” monitor using 1920 × 1080 (full HD) resolution. Participants freely adjusted their position relative to the display and had no time limit. They rated each fused sequence on a scale of 0 to 5, and were free to award equivalent grades (no forced choice).

Each observer was separately induced into the trial by performing an evaluation of two trial video sets which were not included in the analysis. They were explained the aim of the evaluation and various effects of video fusion. Each observer then evaluated the same number, six fused video sets. During the evaluation stage, the upper portion of the display showed the two input video streams and lower portion of the display showed three fused alternatives produced using different fusion algorithms. The order of the fusion methods altered randomly between video sets and observers to avoid positional bias. The sequence duration varied between six and 12 s. Each observer could replay the sequences, which replayed simultaneously, an unlimited number of times until they were satisfied with their assessment and moved onto the next video set. Trial time was not limited.

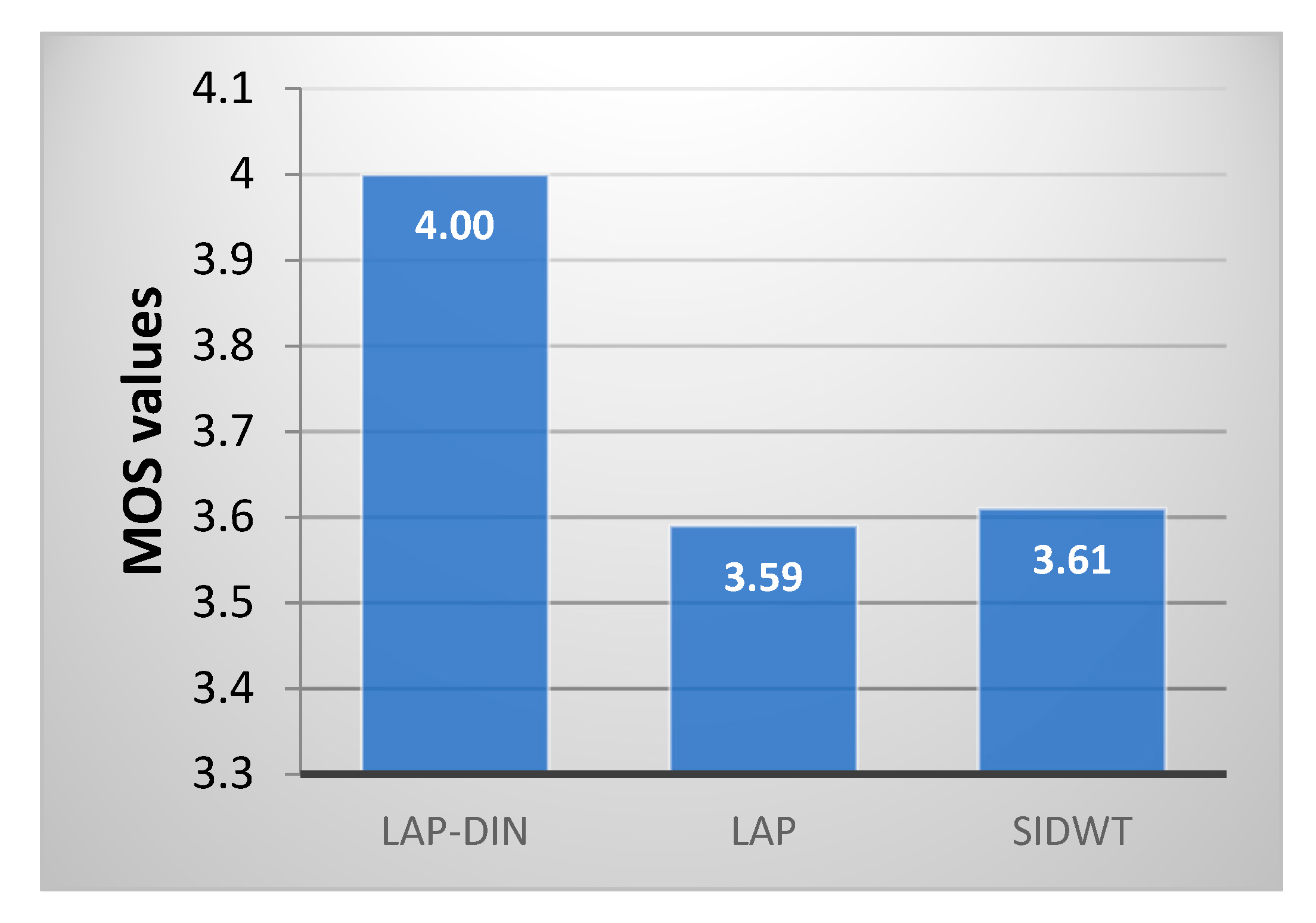
The first test compared the static Laplacian and SIDWT fusion methods applied frame by frame with the proposed LAP-DIN method. Subjective MOS scores for each method, shown in Figure 17 match the results of objective evaluation. The proposed dynamic method outperforms static ones which perform similarly.

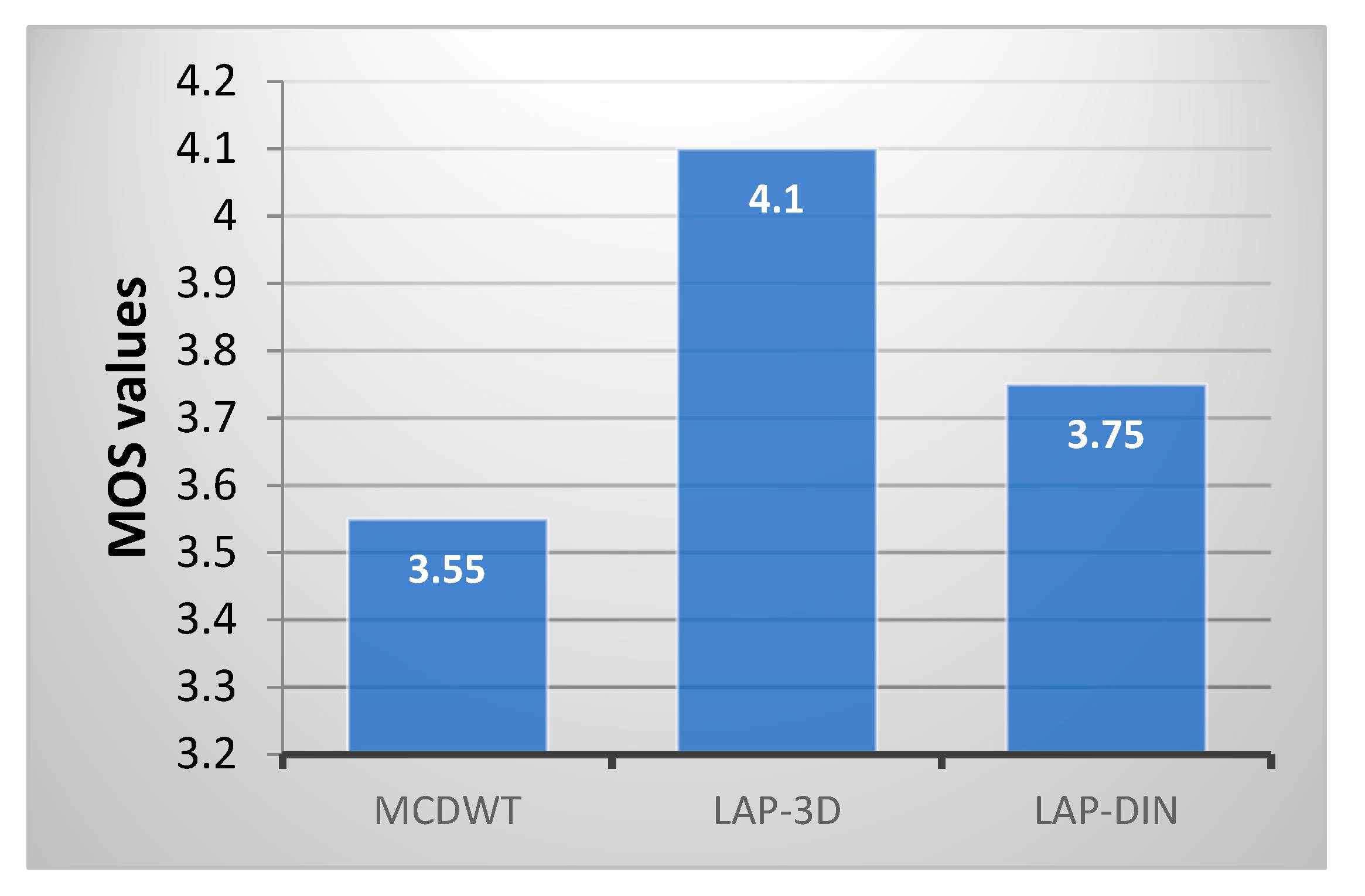
The second subjective trial, run in identical conditions on an identical dataset directly compared three true video/3D fusion methods: MCDWT [15], full 3D pyramid fusion [54] and proposed LAP-DIN method. The results, shown in Figure 18, again support objective metric findings and identify full 3D Laplace pyramid fusion, MOS = 4.1, as the best of the three, followed by proposed LAP-DIN and MCDWT.

This result underlines the well-known fact of the power of hindsight: Full 3D pyramid fusion requires knowledge of the entire signal well into the future and being in possession of all the facts we can more easily arrive at the optimal result. The proposed LAP-DIN fusion trades a single frame latency for a considerable improvement in performance on the fully causal frame-by-frame approach.

An interesting observation is the relative difference of the LAP-DIN MOS between the two trials run in identical conditions on identical data. It reflects the influence of other methods in the trial which generally performed better than those in the first trial, and undermines the value of absolute quality scores but also underlines the value of relative, or ranking scores produced by subjective trials.

4.3. Computational Complexity

Computational complexity, of vital importance in real-time operation, was evaluated for each method on video fusion at resolution of 640 × 480 pixels using the same i7 processor with 8GB of RAM. Results comparing their per-frame cost relative to the static Laplacian fusion are shown in

Table 4. Relative computational complexity of different video fusion methods.

	LAP	SIDWT	MCDWT	LAP-3D	LAP-DIN
Multiple of LAP	1	1.6	1.8	1.75	1.3

. MCDWT is the most demanding due to motion estimation while LAP-DIN is the most efficient among dynamic methods and can be implemented to operate in real-time with 25 frames per second.

5. Conclusions

A new dynamic video fusion method is proposed based on the construction of a fused rolling-multiscale-Laplacian pyramid from equivalent input stream pyramids. The method uses a sophisticated local energy pyramid fusion rule that successfully transfers important structure information from the input video sequences into the fused, achieving considerable temporal stability and consistency. Furthermore, this is achieved with a significantly lower computational complexity compared to other dynamic fusion methods. Comprehensive assessment of the proposed method using subjective and objective evaluation on a number of well-known multi-sensor videos from multiple surveillance scenarios showed that the proposed method performs better than comparable causal video fusion methods. The results also indicate that extending the latency of the fusion process further could add further robustness to the fusion process and we intend to explore this performance-latency boundary in our further work.

Further work on the video fusion will include exploration of different methods to obtain a more compact description of spatio-temporal information. Also, we are planning to make a new database of multi-sensor sequences in different conditions and test the algorithm with subjective and objective tests.