Abstract
This paper presents a novel architecture for ring learning with errors (LWE) cryptoprocessors using an efficient approach in encryption and decryption operations. By scheduling multipliers to work in parallel, the encryption and decryption time are significantly reduced. In addition, polynomial multiplications are conducted using radix-2 and radix-8 multiple delay feedback (MDF) architecture-based number theoretic transform (NTT) multipliers to speed up the multiplication operation. To reduce the hardware complexity of an NTT multiplier, three bit-reverse operations during the NTT and inverse NTT (INTT) processes are removed. Polynomial additions in the ring-LWE encryption phase are also arranged to work simultaneously to reduce the latency. As a result, the proposed efficient-scheduling parallel multiplier-based ring-LWE cryptoprocessors can achieve higher throughput and efficiency compared with existing architectures. The proposed ring-LWE cryptoprocessors are synthesized and verified using Xilinx VIVADO on a Virtex-7 field programmable gate array (FPGA) board. With security parameters and 12,289, the proposed cryptoprocessors using radix-2 single-path delay feedback (SDF), radix-2 MDF, and radix-8 MDF multipliers perform encryption in 4.58 s, 1.97 s, and 0.89 s, and decryption in 4.35 s, 1.82 s, and 0.71 s, respectively. A comparison of the obtained throughput and efficiency with those of previous studies proves that the proposed cryptoprocessors achieve a better performance.
1. Introduction
The internet of things (IoT), with billions of connected devices currently in use, has been developed dramatically during the past decades; therefore, a stronger cryptosystem with the goals of confidentiality, integrity, and authentication has become a necessity. There exist two types of cryptosystems named symmetric cryptography and asymmetric or public key cryptography. The former uses a single key between two parties to enable a secure communication, where the key is kept private from all other parties. Owing to its simplicity, this scheme is widely used. However, a symmetric key algorithm can be used only when the sender and receiver have agreed on the secret key. Asymmetric, or public key cryptosystems use two keys, including one private key and one public key. Whereas the private key is kept secret for the decryption process, the public key is used for encryption and can be revealed to all other parties. The encryption operation is conducted using a public key, and the encrypted message can only be decrypted using the corresponding private key. The security level of these algorithms depends on the difficulty of deriving a private key from a public key. Existing cryptographic primitives such as the symmetric advanced encryption standard (AES) and asymmetric elliptic curve cryptosystems (ECC) [1,2,3] can be applied to achieve the aforementioned security goals. For example, the encryption and decryption operations conducted in ECC are based on an elliptic curve and computation over a Galois field GF or GF, where p and m are prime numbers. In the key generation operation, the receiver selects a random number for its private key and a base point to calculate ECC point multiplication . The public key goes to the sender, who encrypts the input data before sending them to the receiver. At the receiver, the original data can be recovered using the secret key of the receiver and ECC point multiplication operations. However, recent advances in quantum computing intimidate the security of existing cryptographic schemes. The security of ECC and that of Rivest, Shamir, and Adleman (RSA) cryptosystems [4] are based on the difficulty of solving the elliptic-curve discrete logarithm problems and the difficulty of solving certain number theoretic problems, respectively. As early as 1994, Shor [5] proposed an algorithm to solve the integer factorization problem and the discrete logarithm problems in polynomial time when using quantum computers. Therefore, the National Institute of Standards and Technology (NIST) is planning to standardize quantum-resistant cryptosystems such as lattice-based cryptography because the security proofs of lattice-based cryptography are based on the worst-case hardness of the lattice problems, and there are no known algorithms that can efficiently solve them. Learning with errors (LWE) is a well-known lattice-based problem that has attracted significant intention in recent years. In this context, the ring-LWE cryptosystems described in [6,7,8,9,10,11,12] are the most studied lattice-based cryptosystems in terms of both software and hardware. A block diagram of the ring-LWE cryptosystem is described in Figure 1.
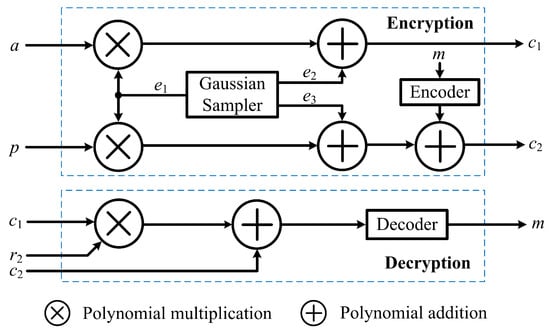
Figure 1.
Block diagram of ring-learning with errors (LWE) cryptosystem.
The ring-LWE public-key cryptosystem operations are conducted in a polynomial ring, normally . These operations include polynomial addition, polynomial multiplication, and modulo reduction. Among them, polynomial multiplication is the most computationally intensive [9] and can be efficiently executed using a number theoretic transform (NTT) based polynomial multiplication. In addition to the significant progress made regarding the theory of lattice-based cryptography, practical implementations of this cryptosystem have recently gained the attention of the research community. Some software implementations of ring-LWE cryptosystems can be found in the literature. In [6], the authors presented efficient techniques to obtain a high-speed computation in ring-LWE encryption and decryption. A high-speed, low-latency software-based ring-LWE cryptographic scheme is introduced in [8] to perform biomedical image storing and transmission. In addition, the processing time of ring-LWE cryptosystems can be considerably improved by employing parallel operations on a graphics processing unit (GPU) [10]. The aforementioned software demonstrations show that the ring-LWE cryptographic scheme offers a higher level of security with lower latency compared with previous cryptosystems. To prove the practicality and efficiency of ring-LWE cryptoprocessor, many hardware deployments have also been conducted in [7,9,13,14]. The study in [13] illustrates that ring-LWE cryptoprocessors require less hardware resources than conventional cryptosystems such as ECC to carry out encryption and decryption operations. In addition, a ring-LWE scheme can operate at a higher frequency than ECC scheme. Therefore, a ring-LWE cryptosystem outperforms ECC in terms of throughput and efficiency. In the design of an NTT multiplier, SDF-architecture based and multiple-path delay commutator (MDC) architecture based schemes have been deployed. An SDF-architecture based multiplier requires less hardware than an MDC-architecture based multiplier; however, it offers lower throughput than an MDC-architecture based multiplier. In [7], high-throughput ring-LWE cryptoprocessors using SDF and MDC-architecture based multipliers are discussed. The results in [7] show that, for ring-LWE encryption and decryption, the throughputs achieved are at gigabits and megabits per second, respectively. However, this architecture requires a significant number of hardware resources and a long computation time because the NTT multipliers operate separately and the NTTs work serially.
In this paper, we present an efficient scheduling architecture to conduct ring-LWE cryptography encryption and decryption operations. To decrease the encryption time, the multipliers used in the proposed ring-LWE encryption operation are scheduled to work concurrently. The adders in the encryption phase also operate simultaneously. Therefore, the encryption latency is reduced by the computation time of one polynomial multiplication and one polynomial addition. In addition, the NTT multipliers are designed using a multiple delay feedback (MDF) architecture to lessen the hardware complexity and speed up the encryption and decryption operations. As a result, with a lower hardware complexity, the proposed ring-LWE cryptoprocessors provide higher throughput and efficiency compared with other designs.
The rest of this paper is organized as follows: Section 2 provides background information on ring-LWE cryptography and an NTT multiplier. In Section 3, the proposed ring-LWE cryptoprocessors using efficient-scheduling parallel multipliers are presented. A performance analysis and comparison are discussed in Section 4. Finally, some concluding remarks are given in Section 5.
2. Ring-LWE Cryptography
2.1. Operations in Ring-LWE Cryptography
The ring-LWE cryptography, a public key cryptosystem introduced by Regev [15] in 2005, is a machine learning problem that is equivalent to the worst-case lattice problems. The ring-LWE cryptosystem is built on a polynomial ring , where is a sufficiently large public prime number, and is the irreducible polynomial. Normally, , where the security parameter n is a power of 2. The ring-LWE distribution on consists of pairs with chosen uniformly random, and , where s is a fixed secret element and e is sampled from a discrete Gaussian distribution with a standard deviation . The procedures of a ring-LWE cryptosystem, including the key generation, encryption, and decryption, are described as follows.
2.1.1. Key Generation
This process generates a private key and public key . The polynomial a is chosen uniformly, and two polynomials and are sampled from the Gaussian distribution . The polynomial becomes the private key, and two polynomials and participate in the public key generation process.
2.1.2. Encryption
The ring-LWE encryption operation encrypts the input message m to the cipher-text . Initially, the input message m is encoded into the polynomial using an encoder. Depending on the i-th coefficient of m, it is encoded as (if ) or 0 (if ). The cipher-text is calculated based on the public key , the encoded message, and three error polynomials , , and sampled from the Gaussian distribution.
2.1.3. Decryption
The decryption operation recovers the original message m from the cipher-text . This operation starts with the calculation of the pre-decoded polynomial
The original message m is recovered from the pre-decoded polynomial using a decoder. The i-th coefficient of the message m is converted to 1 if and only if its corresponding value satisfies the condition ; otherwise, it is converted to 0.
2.2. Arithmetic Operations over a Ring
The operations over ring include polynomial multiplication, polynomial addition, and modulo reduction. Given and in , two polynomials and over the ring can be expressed as follows.
The polynomial multiplication over ring is the arithmetic requiring the longest processing time. Among existing approaches used to execute polynomial multiplication introduced in [7,9,16], the NTT-based algorithm is efficient. If the root of unity in the fast Fourier transform (FFT) is taken from a finite ring instead of a complex number, the NTT can be viewed as a variation of the FFT. Given a primitive n-th root of unity , the NTT of each coefficient of is calculated as follows:
Thus, the inverse number theoretic transform (INTT) is defined as
Assume that and are extended vectors of and by filling n zero elements. The multiplication of two polynomials and can be expressed as forms of NTT and INTT, where ⊙ is a point-wise multiplication.
The negative wrapped convolution can be implemented to avoid zero padding in an NTT multiplication. Considering c to be the negative convolution of and , the negative wrapped convolution can be described as
Define , , and , where , the NTT polynomial multiplication becomes
Using the negative wrapped convolution, the NTT multiplication can be calculated based solely on the n-coefficient. Detail operations of NTT-based polynomial multiplication are described in Algorithm 1.
| Algorithm 1: Number theoretic transform (NTT)-based polynomial multiplication using negative wrapped convolution. |
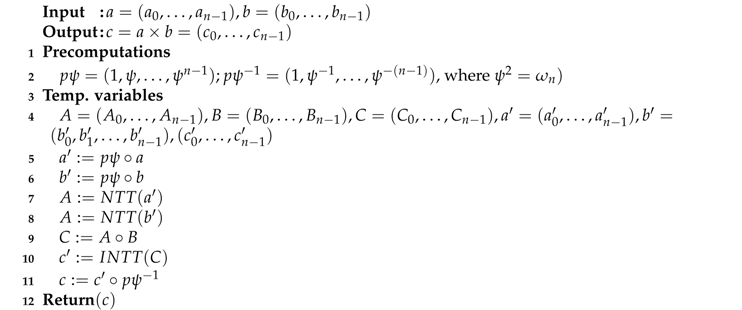 |
The polynomial addition of two polynomials and is simply adding the corresponding coefficients of two polynomials and then applying modulo reduction (MR).
In an MR operation, the coefficients of the resulting polynomial should be reduced by modulus q. To execute this operation, a few MR algorithms are presented in [7,9,17]. Since security parameters used in this study are and 12,289, the SAMS2 algorithm for 12,289 presented in [7] is applied to perform the MR reduction.
2.3. Discrete Gaussian Sampler
In the operations of ring-LWE cryptosystems, polynomials sampled from a discrete Gaussian distribution with a standard deviation are required. In [16,18,19,20,21], the authors present several methods to conduct discrete Gaussian sampling. Among these methods, rejection sampling and inversion sampling are popular choices. In practice, rejection sampling for a discrete Gaussian distribution is slow owing to the high rejection rate for the sampled values, which are far from the center of distribution. The inversion method first generates a random probability and then selects a sample value such that the cumulative distribution up to that sample point is just larger than the randomly generated probability. Since the random probability should be of high precision, this method also requires a large number of random bits. The Knuth–Yao algorithm [16] uses a random walk model for sampling from any non-uniform distribution. However, the output of Knuth–Yao is generated within an unpredictable amount of time [7], and it is therefore not a reliable sampler. In this work, we deploy the linear feedback shift registers (LFSRs) method proposed in [21] because it offers a low complexity with an approximated uniform pseudo-random distribution; hence, it can be exploited to generate an accurate approximation of a Gaussian distribution with a low maximum auto-correlation.
2.4. Ring-LWE Encryption and Decryption Algorithm
In this paper, we use the ring-LWE encryption and decryption algorithms discussed [7]. Furthermore, in the encryption operation, multipliers and adders are scheduled to work in parallel to optimize the computation latency. The detailed algorithms used to perform ring-LWE encryption and decryption operations are presented in Algorithms 2 and 3, respectively. In an encryption operation, the input message m in binary form is converted into a ring polynomial using an encoder. This encoder compares each bit of the input message m to decide if it is encoded as 0 or . To compute the cipher-text , three error polynomials , , and generated from a discrete Gaussian sampler are required. In addition, the public key and error polynomial are transformed using NTT cores. The main part of the encryption algorithm is calculating cipher-texts and using polynomial addition and polynomial multiplication. In this work, we use two temporary variables and to store the multiplication results of two scheduled NTT multipliers and . At the same time, adder calculates the addition between encoded information and error polynomial . The multiplication result is used to compute cipher-text through adder , which adds and error polynomial , whereas is assigned to adder to add with and obtain cipher-text . Note that the additions through two adders and are executed in parallel to speed up the encryption operation.
| Algorithm 2: Ring-learning with errors (LWE) encryption algorithm. |
 |
Algorithm 3 describes the ring-LWE decryption process. Initially, cipher-text is transformed using the NTT and driven to multiplier to compute the multiplication between and . The pre-decoded message is calculated using adder whose inputs are and cipher-text . The original message m is recovered by decoding message . Depending on the value of the i-th coefficient of , the corresponding value of m is decoded as 1 or 0.
| Algorithm 3: Ring-LWE decryption algorithm. |
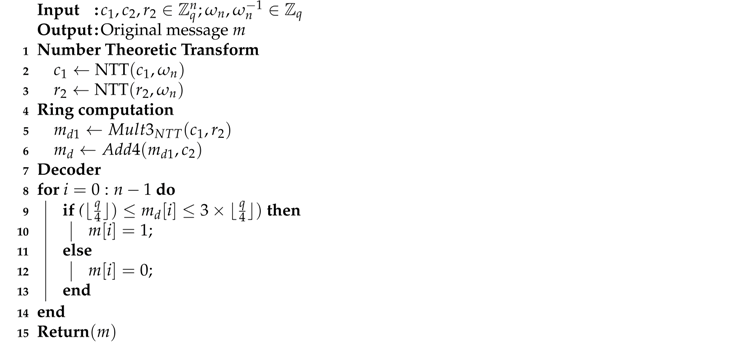 |
3. Proposed Ring-LWE Cryptoprocessor Architectures
3.1. Proposed Ring-LWE Encryption and Decryption Architectures
Figure 2 describes the top module of the proposed ring-LWE cryptoprocessors. The whole processor is directed by control signals generated from a controller. The system includes a Gaussian sampler to generate error polynomials, an encoder to encode the input message m, a decoder that decodes message to recover the original message m, multipliers, adders, and modulus to perform arithmetic operations over ring.
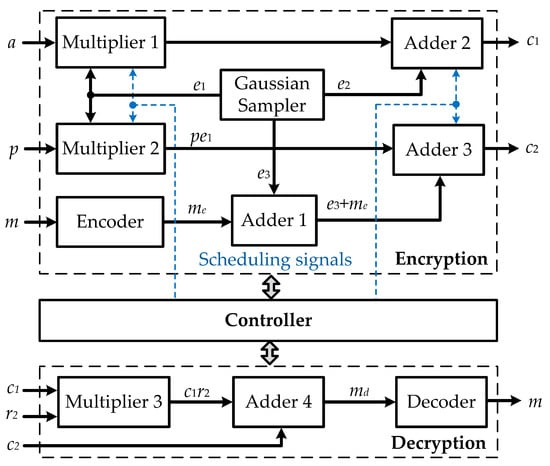
Figure 2.
Proposed top-level ring-LWE cryptopocessors.
To conduct ring-LWE encryption and decryption, the efficient-scheduling parallel multiplier-based architectures shown in Figure 3 is proposed. As can be seen, the ring-LWE encryption architecture used to encrypt the input message m with the public key is illustrated. When the encryption signal is enabled, the input message m is initially encoded using an encoder. A two-input MUX matrix encodes the message m to the ring polynomial . Each bit of the input message m becomes the control signal of each MUX deciding whether bit should be converted into 0 or . The encoded message is then added with the error polynomial generated from a discrete Gaussian distribution through adder . The public key is multiplied with error polynomial using MDF architecture-based multipliers and . These multipliers are controlled by the scheduling signal . When the signal is enabled, two multipliers work simultaneously to reduce the multiplication time. When the multiplications at and are accomplished, two signals and are assigned to 1. The scheduling signals triggers two adders and , where the additions and are executed in parallel, respectively. Once these additions are completed, two signals and are assigned to 1. The output of adder is cipher-text , and the output of adder is cipher-text . The encryption process is thus accomplished.
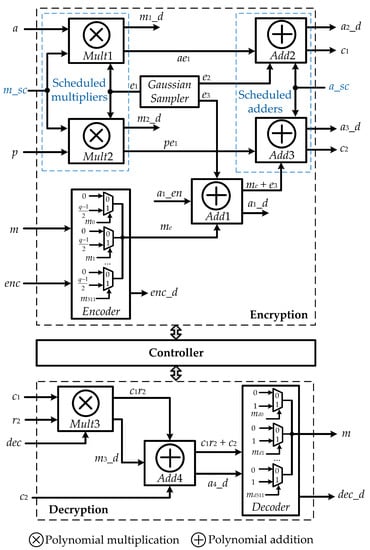
Figure 3.
Proposed efficient-scheduling parallel multiplier-based ring-LWE cryptoprocessor architecture.
The decryption architecture is used to recover the original message m from the cipher-text ) when needed. This process starts when the decryption control signal is enabled. The proposed MDF-architecture based multiplier calculates the multiplication between cipher-text and private key . The signal indicates that this multiplication has been carried out. The output of multiplier is then added with cipher-text through adder enabled by signal . The pre-decoded message is available when signal of adder equals to 1. To recover message m from the pre-decoded message , a decoder with a two-input MUX matrix is used. Each value of the polynomial is compared with and to obtain the control signal of the corresponding MUX. If i-th value of is within this range, the corresponding value of m is decoded as 1; otherwise, it is decoded as 0. Finally, the original message m is completely recovered. The timing diagram of the operations in encryption and decryption phases is described in Figure 4.
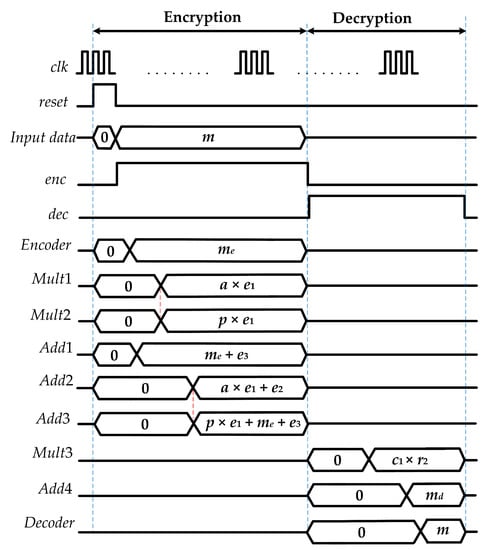
Figure 4.
Timing diagram of proposed ring-LWE cryptoprocessors.
3.2. Proposed NTT Multiplier Architecture
As mentioned previously, polynomial multiplication is an important operation in ring-LWE cryptosystems. Theoretically, an NTT-based polynomial multiplication consists of NTT, INTT, point-wise multiplication, and three bit-reverse processes. To decrease the latency and hardware complexity of the polynomial multiplier, we use the reverse Cooley–Tukey algorithm [22] to remove three bit-reverse operations. The design of the MDF-architecture based NTT multiplier is presented in Figure 5. In detail, Figure 5a describes the top level of the proposed MDF-architecture-based NTT multiplier to conduct the multiplication of two polynomials and . Figure 5b presents the radix-8 MDF-architecture-based NTT multiplier. The multiplication of two input polynomials and is processed using NTT operations NTT and NTT, followed by a point-wise multiplication. The result from the point-wise multiplication is then processed by the INTT block to get the polynomial multiplication result . For the radix-k MDF-architecture based NTT multiplier, n-coefficients of the input polynomial are divided into k paths. Each path consists of coefficients with the indexes of , where , and . The input polynomial with coefficients is allocated as Figure 5c.
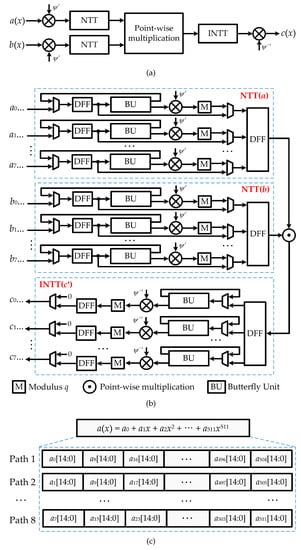
Figure 5.
(a) Data flow of the proposed number theoretic transform (NTT) multiplier, (b) Proposed radix-8 multiple delay feedback (MDF)-architecture based NTT multiplier, and (c) Data structure of the proposed radix-8 MDF-architecture based multiplier.
4. Simulation Results and Comparison
The proposed efficient-scheduling parallel multiplier-based ring-LWE cryptoprocessors were modeled in Verilog HDL, synthesized and implemented in Xilinx VIVADO on a Virtex-7 FPGA platform. Three architectures, namely, radix-2 SDF (radix-2S), radix-2 MDF (radix-2M), and radix-8 MDF (radix-8M) were developed. The simulation results are shown in Table 1.

Table 1.
Implementation results and performance comparison of the proposed ring-learning with errors (LWE) cryptoprocessors.
As can be seen from Table 1, the proposed cryptoprocessors achieved a higher throughput than the architectures in [7,13,16]. It can be explained that the proposed NTT multipliers, as well as adders, were scheduled to work in parallel to speed up the computation time, resulting in an increase in the system throughput. The proposed radix-2S cryptoprocessor required the least amount of hardware resources, whereas the radix-8M architecture provided the highest throughput. Specifically, the proposed radix-2S architecture used only 74.43% and 46.39% of the number of lookup tables (LUTs) and slices in [7] to perform the encryption, respectively. For the ring-LWE encryption, the radix-2S and radix-8M crytoprocessors offered an improvement in throughput of up to 90% compared with the similar architecture presented in [7], while the radix-2M architecture outperformed its predecessor R2M in [7] by approximately 1.5 times in terms of throughput. Although the ring-LWE architectures in [13,16] required a small number of LUTs and slices, the encryption and decryption latencies of these architectures were extremely large. Therefore, these architectures provided a very low throughput. As described in Table 1, the throughput of the proposed radix-2S architecture was about ten times larger than that in [13,16].
The system efficiency was a parameter used to evaluate the performance of the proposed cryptoprocessors and existing studies. This parameter was presented in [23]. As shown in Table 1, the proposed radix-8M architecture achieved the highest encryption efficiency, followed by the radix-2M architecture. The efficiency of the proposed architectures outperformed that of other architectures in general.
5. Conclusions
This paper presents an efficient-scheduling parallel multiplier-based cryptoprocessor architecture to perform the ring-LWE encryption and decryption. By exploiting MDF-architecture based NTT multipliers and scheduling operations of multipliers and adders, the encryption and decryption times are significantly decreased. In addition, the bit-reverse processes in an NTT multiplier are removed to reduce the system hardware complexity. As a result, the proposed cryptoprocessors can lead to a significant reduction in hardware complexity and achieve a much higher throughput and efficiency compared to existing architectures. Therefore, the proposed ring-LWE cryptoprocessors are promising solutions for the security systems that require high throughput, high efficiency, and low latency.
Author Contributions
T.N.T. conceptualized the idea of this research, conducted experiment, collected data, and prepared the original version. H.L. supervised, validated, reviewed, and updated the article.
Funding
This work was supported by MSIT (Ministry of Science, ICT), Korea, under the ITRC support program (IITP-2018-2014-1-00729) supervised by the IITP and in part by the Basic Science Research Program through the NRF funded by the MSIT under Grant 2016R1A2B4015421.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Koblitz, N. Elliptic Curve Cryptosystems. Math. Comput. 1987, 48, 203–209. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Lee, H. Efficient Algorithm and Architecture for Elliptic Curve Cryptographic Processor. J. Semicond. Technol. Sci. 2016, 16, 118–125. [Google Scholar] [CrossRef]
- Choi, P.; Lee, M.K.; Kim, J.H.; Kim, D.K. Low-Complexity Elliptic Curve Cryptography Processor Based on Configurable Partial Modular Reduction over NIST Prime Fields. IEEE Trans. Circuits Syst. II 2018, 65, 1703–1707. [Google Scholar] [CrossRef]
- Rivest, R.L.; Shamir, A.; Adleman, L. A Method for Obtaining Digital Signatures and Public-Key Cryptosystems. ACM Commun. 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Shor, P.W. Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM J. Comput. 1997, 26, 1484–1509. [Google Scholar] [CrossRef]
- Liu, Z.; Azarderakhsh, R.; Kim, H.; Seo, H. Efficient Software Implementation of Ring-LWE Encryption on IoT Processors. IEEE Trans. Comput. 2017. [Google Scholar] [CrossRef]
- Rentería-Mejía, C.P.; Velasco-Medina, J. High-Throughput Ring-LWE Cryptoprocessors. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2017, 25, 2332–2345. [Google Scholar] [CrossRef]
- Tan, T.N.; Lee, H. High-Secure Low-Latency Ring-LWE Cryptography Scheme for Biomedical Images Storing and Transmitting. In Proceedings of the 2018 IEEE International Symposium on Circuits and Systems, Florence, Italy, 27–30 May 2018; pp. 1–4. [Google Scholar]
- Chen, D.D.; Mentens, N.; Vercauteren, F.; Roy, S.S.; Cheung, R.C.C.; Pao, D.; Verbauwhede, I. High-Speed Polynomial Multiplication Architecture for Ring-LWE and SHE Cryptosystems. IEEE Trans. Circuits Syst. I 2015, 62, 157–166. [Google Scholar] [CrossRef]
- Tan, T.N.; Lee, H. High-Performance Ring-LWE Cryptography Scheme for Biometric Data Security. IEIE Trans. Smart Process. Comput. 2018, 7, 97–106. [Google Scholar] [CrossRef]
- Tan, T.N.; Lee, H. High-Secure Fingerprint Authentication System using Ring-LWE Cryptography. IEEE Access 2019, 7, 23379–23387. [Google Scholar] [CrossRef]
- Lyubashevsky, V.; Peikert, C.; Regev, O. On Ideal Lattices and Learning with Errors over Rings. J. ACM 2013, 60, 43:1–43:35. [Google Scholar] [CrossRef]
- Pöppelmann, T.; Güneysu, T. Towards Practical Lattice-Based Public-Key Encryption on Reconfigurable Hardware. In Proceedings of the Selected Areas in Cryptography, Burnaby, BC, Canada, 14–16 August 2013; pp. 68–85. [Google Scholar]
- Rentería-Mejía, C.P.; Velasco-Medina, J. Hardware Design of an NTT-Based Polynomial Multiplier. In Proceedings of the 2014 Southern Conference on Programmable Logic (SPL), Buenos Aires, Argentina, 5–7 November 2014; pp. 1–5. [Google Scholar]
- Regev, O. On Lattices, Learning with Errors, Random Linear Codes, and Cryptography. In Proceedings of the ACM Symposium on Theory of Computing, Baltimore, MD, USA, 22–24 May 2005; pp. 84–93. [Google Scholar]
- Roy, S.S.; Vercauteren, F.; Mentens, N.; Chen, D.D.; Verbauwhede, I. Compact Ring-LWE Cryptoprocessor. In Proceedings of the International Workshop on Cryptographic Hardware and Embedded Systems (CHES 2014), Busan, Korea, 23–26 September 2014; pp. 371–391. [Google Scholar]
- Cao, Z.; Wu, X. An Improvement of the Barrett Modular Reduction Algorithm. Int. J. Comput. Math. 2014, 91, 1874–1879. [Google Scholar] [CrossRef]
- Roy, S.S.; Vercauteren, F.; Verbauwhede, I. High Precision Discrete Gaussian Sampling on FPGAs. In Proceedings of the Selected Areas in Cryptography, Burnaby, BC, Canada, 14–16 August 2013; pp. 383–401. [Google Scholar]
- Du, C.; Bai, G. Towards Efficient Discrete Gaussian Sampling for Lattice-Based Cryptography. In Proceedings of the 2015 International Conference on Field Programmable Logic and Applications (FPL), London, UK, 2–4 September 2015; pp. 1–6. [Google Scholar]
- Liu, Z.; Seo, H.; Roy, S.S.; Großschädl, J.; Kim, H.; Verbauwhede, I. Efficient Ring-LWE Encryption on 8-bit AVR Processors. In Proceedings of the Cryptographic Hardware and Embedded Systems (CHES 2015), Saint-Malo, France, 13–16 September 2015; pp. 663–682. [Google Scholar]
- Condo, C.; Gross, W.J. Pseudo-Random Gaussian Distribution Through Optimised LFSR Permutations. Electron. Lett. 2015, 51, 2098–2100. [Google Scholar] [CrossRef]
- Cooley, J.W.; Tukey, J.W. An Algorithm for the Machine Calculation of Complex Fourier Series. Math. Comput. 1965, 19, 297–301. [Google Scholar] [CrossRef]
- Mahdizadeh, H.; Masoumi, M. Novel architecture for efficient FPGA implementation of elliptic curve cryptographic processor over GF(2163). IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2013, 21, 2330–2333. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).