Cooperative Carrying Control for Multi-Evolutionary Mobile Robots in Unknown Environments
Abstract
:1. Introduction
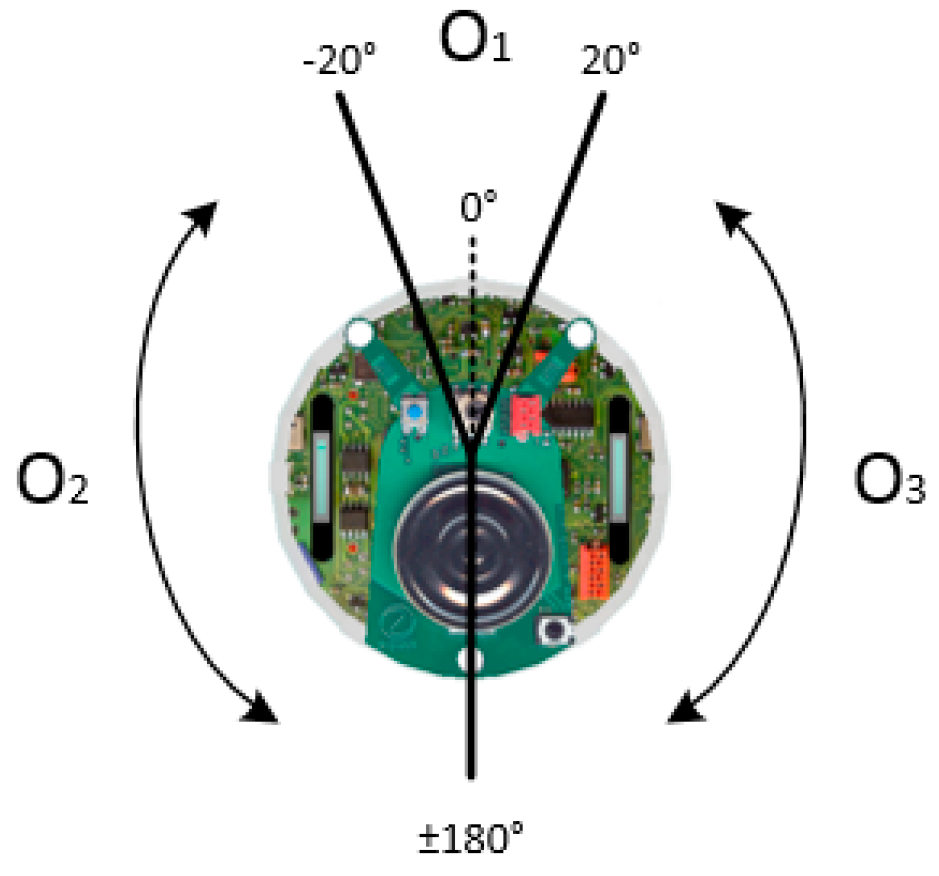
2. Mobile Robot Specifications
3. Proposed Type-2 Fuzzy Controller Based on an Evolutionary Algorithm
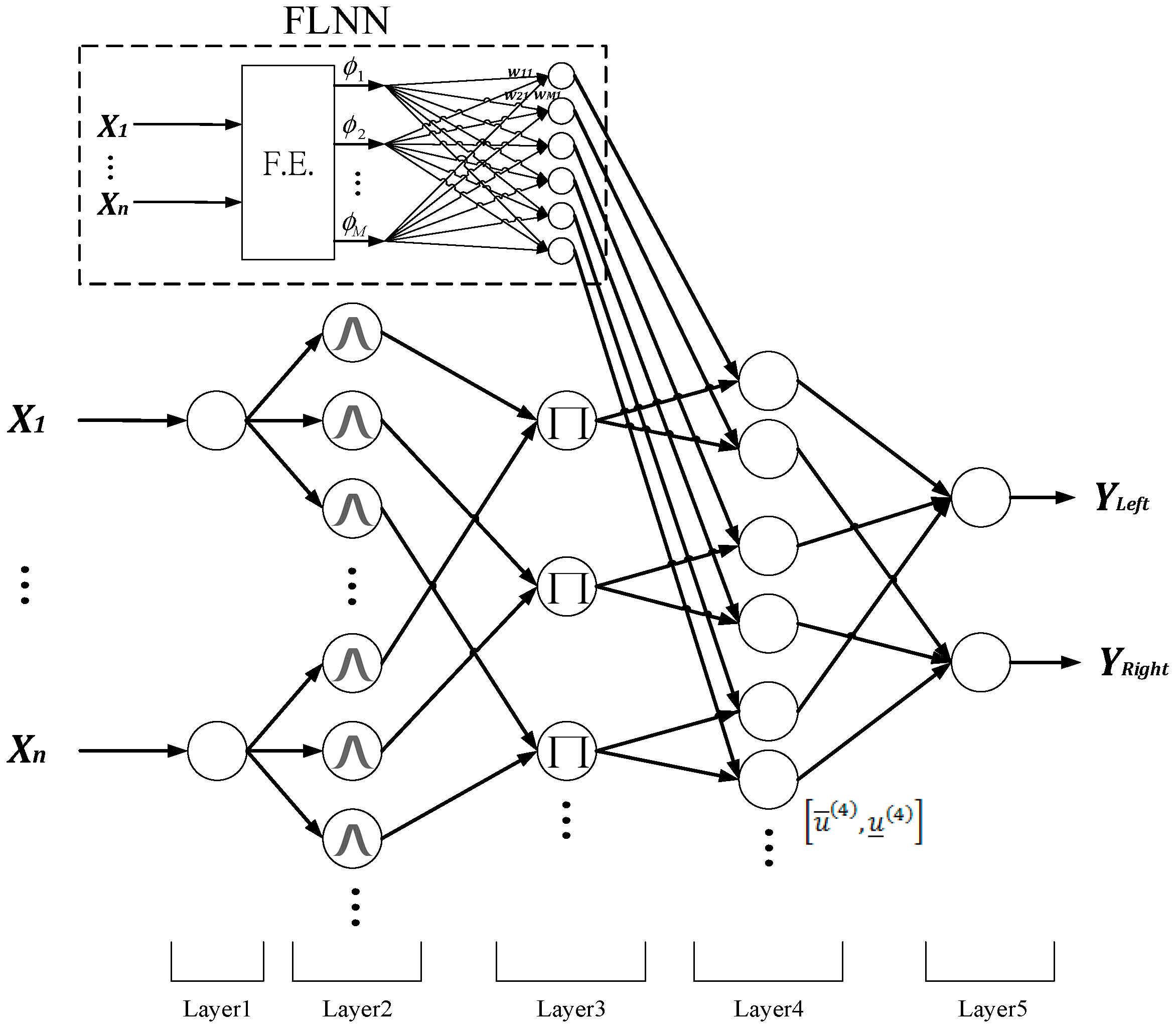
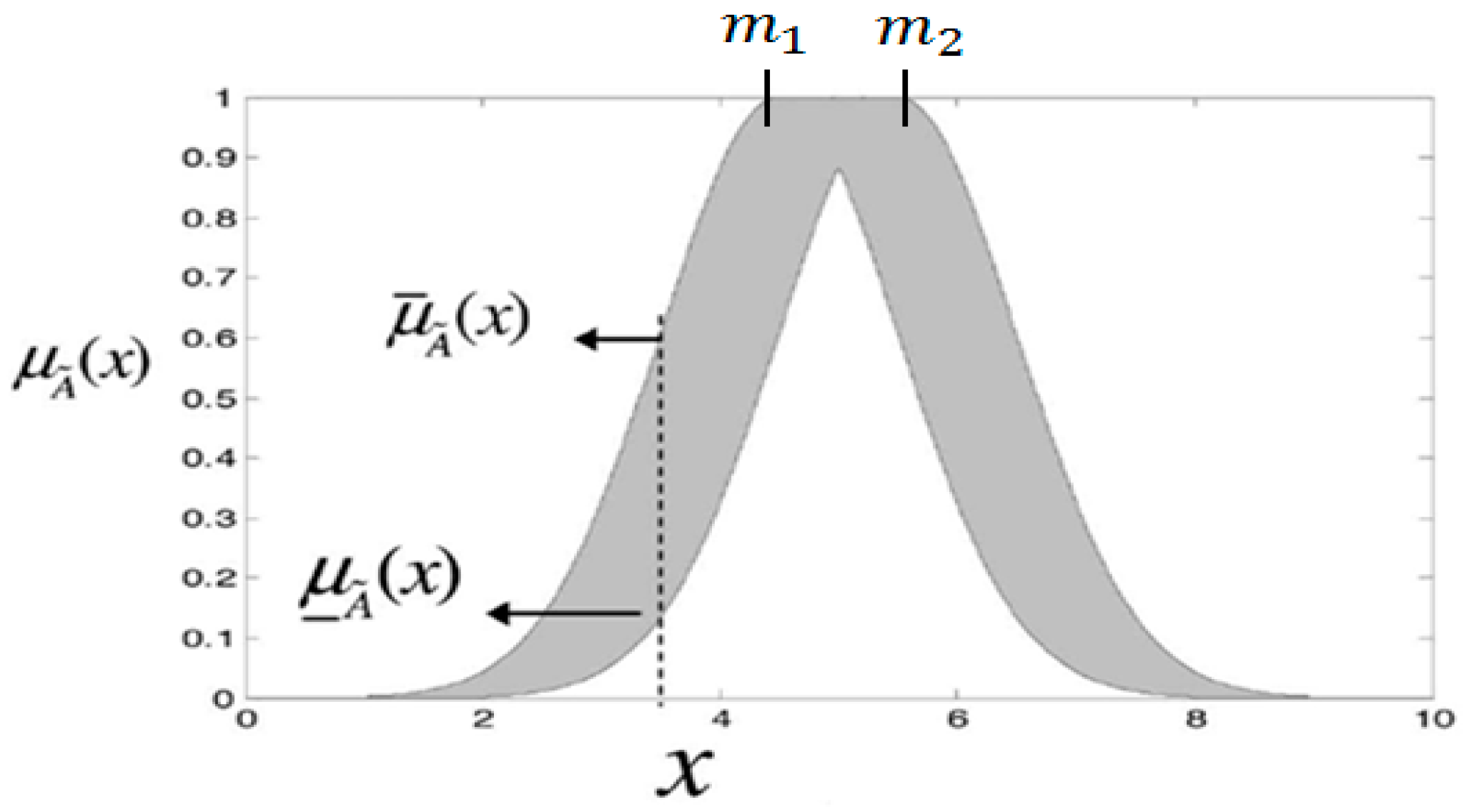
3.1. Interval Type-2 Fuzzy Neural Controller
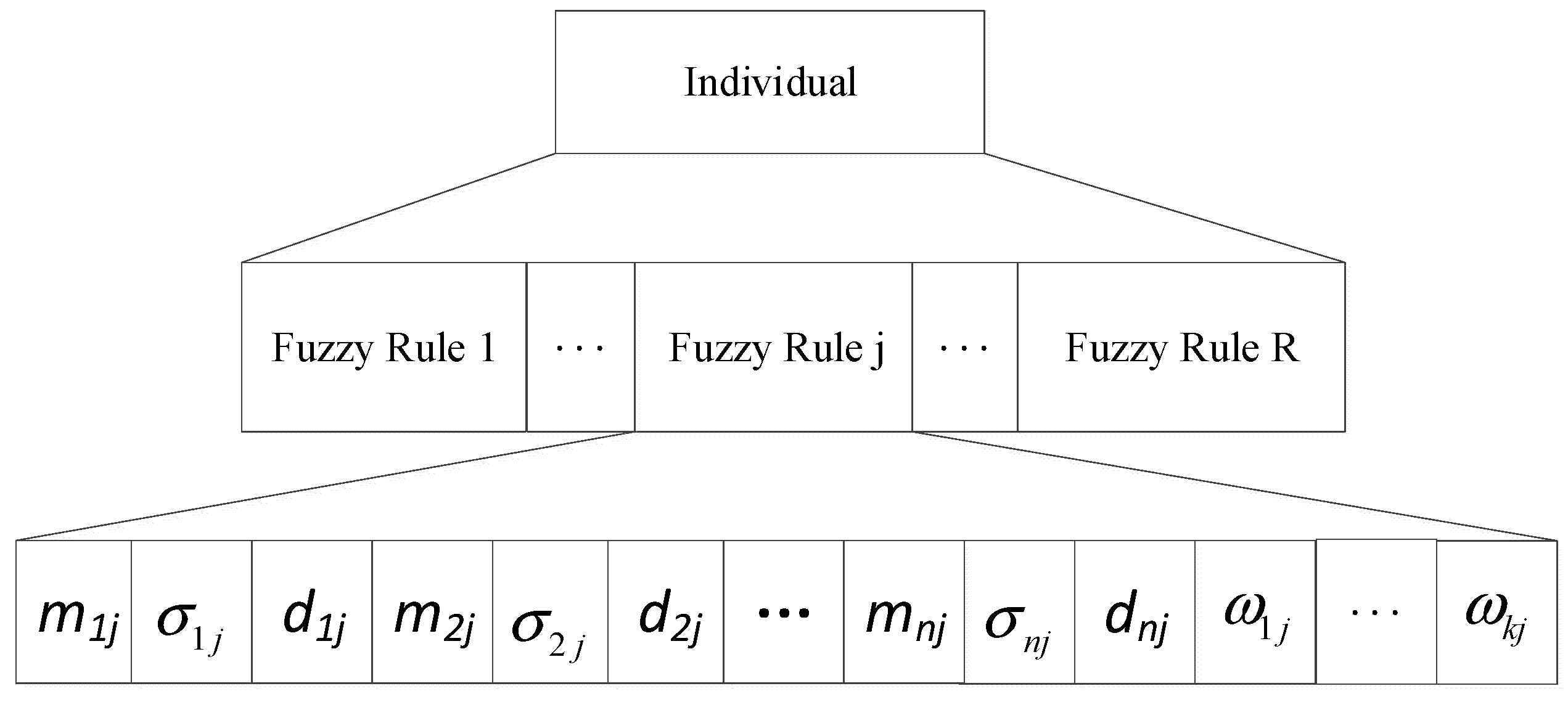
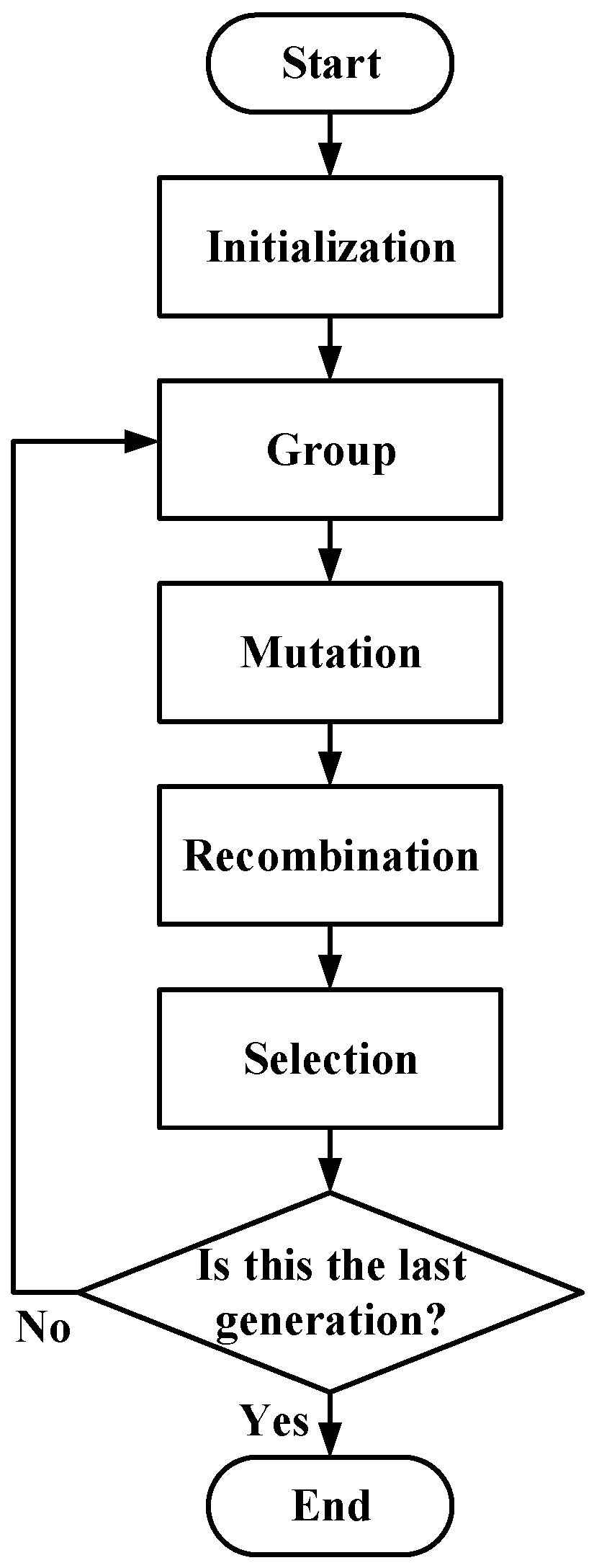
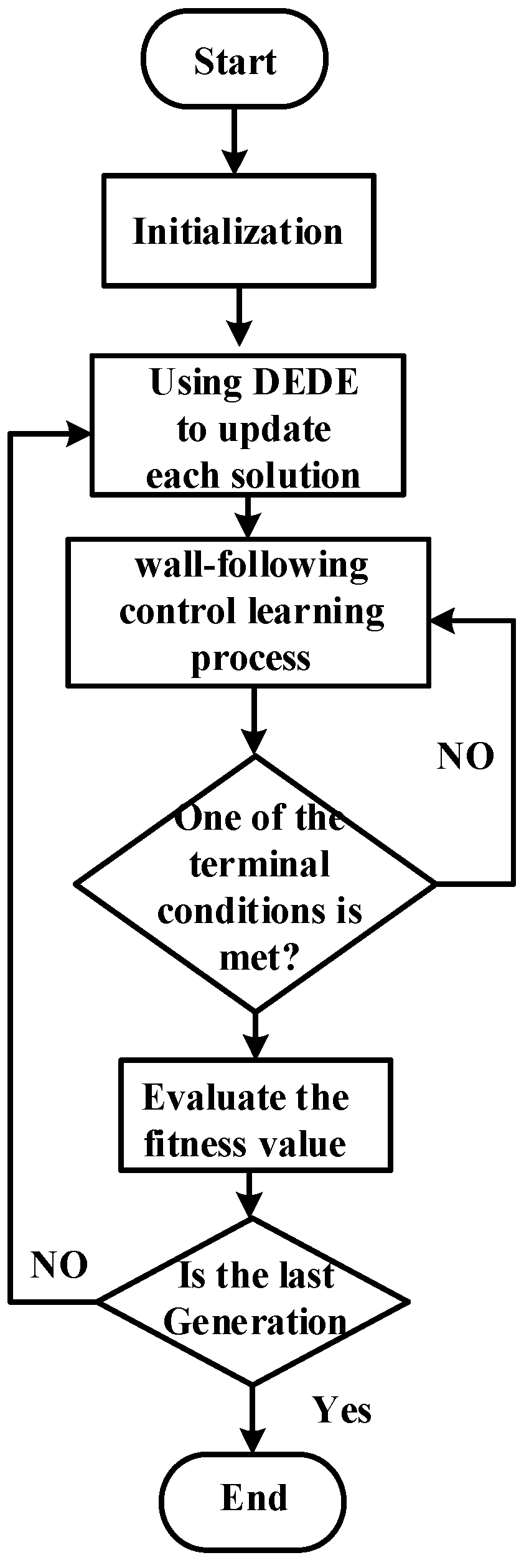
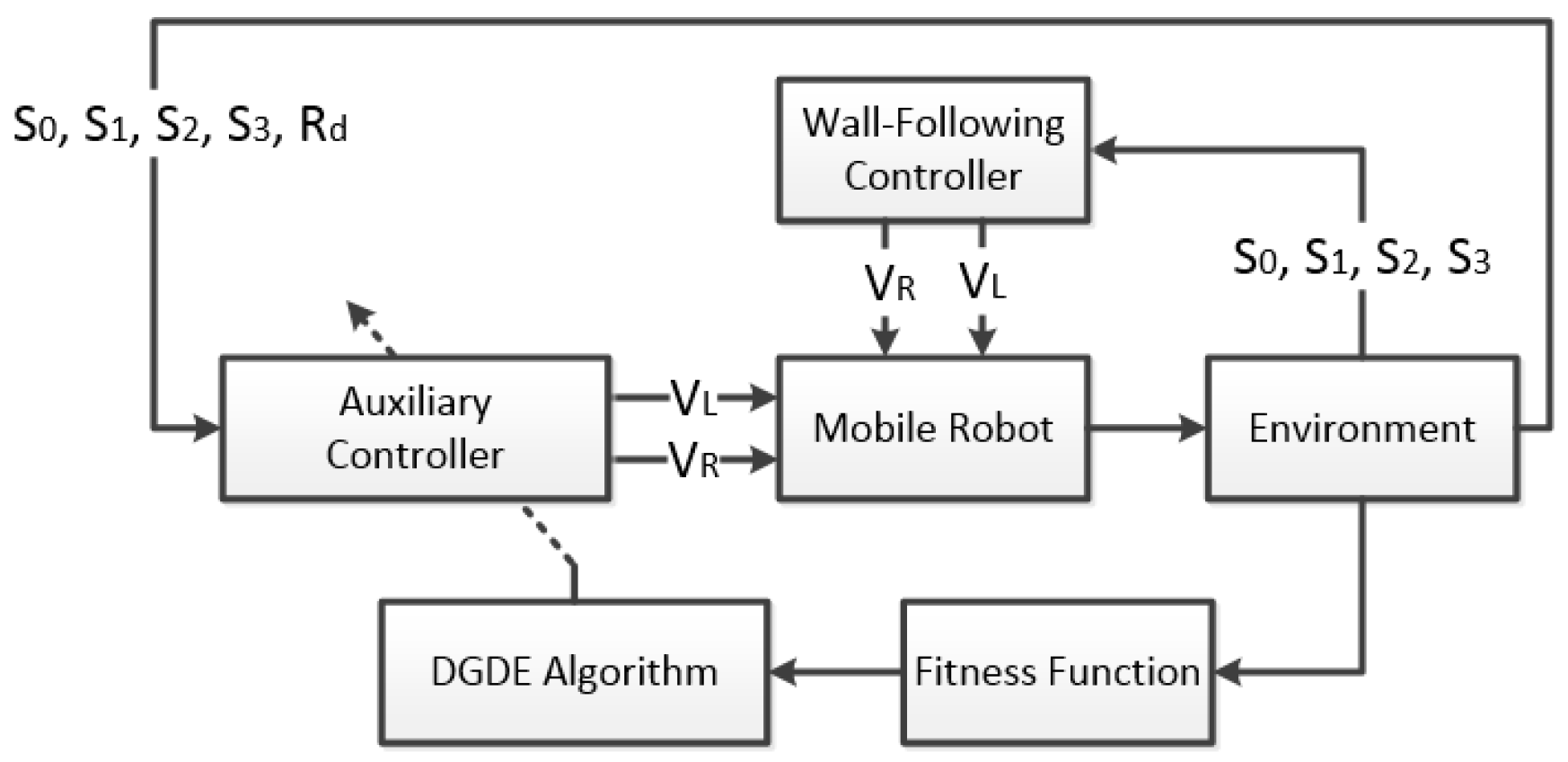
3.2. Proposed DGDE
3.3. Wall-Following Control of Mobile Robots
- If the total moving distance of the mobile robot was larger than the predefined maximal distance of the training environment, the mobile robot successfully moved in a circular path in an unknown environment.
- The mobile robot collided with the wall when the measured distance from any infrared sensor was less than 1 cm, as displayed in Figure 12a.
- The mobile robot deviated from the wall when the measured distance was greater than 6 cm, as displayed in Figure 12b.
- (1)
- : If the moving distance was greater than the predefined value , the robot successfully moved around a circular path in the training environment and set . The sub-fitness function is defined as follows:
- (2)
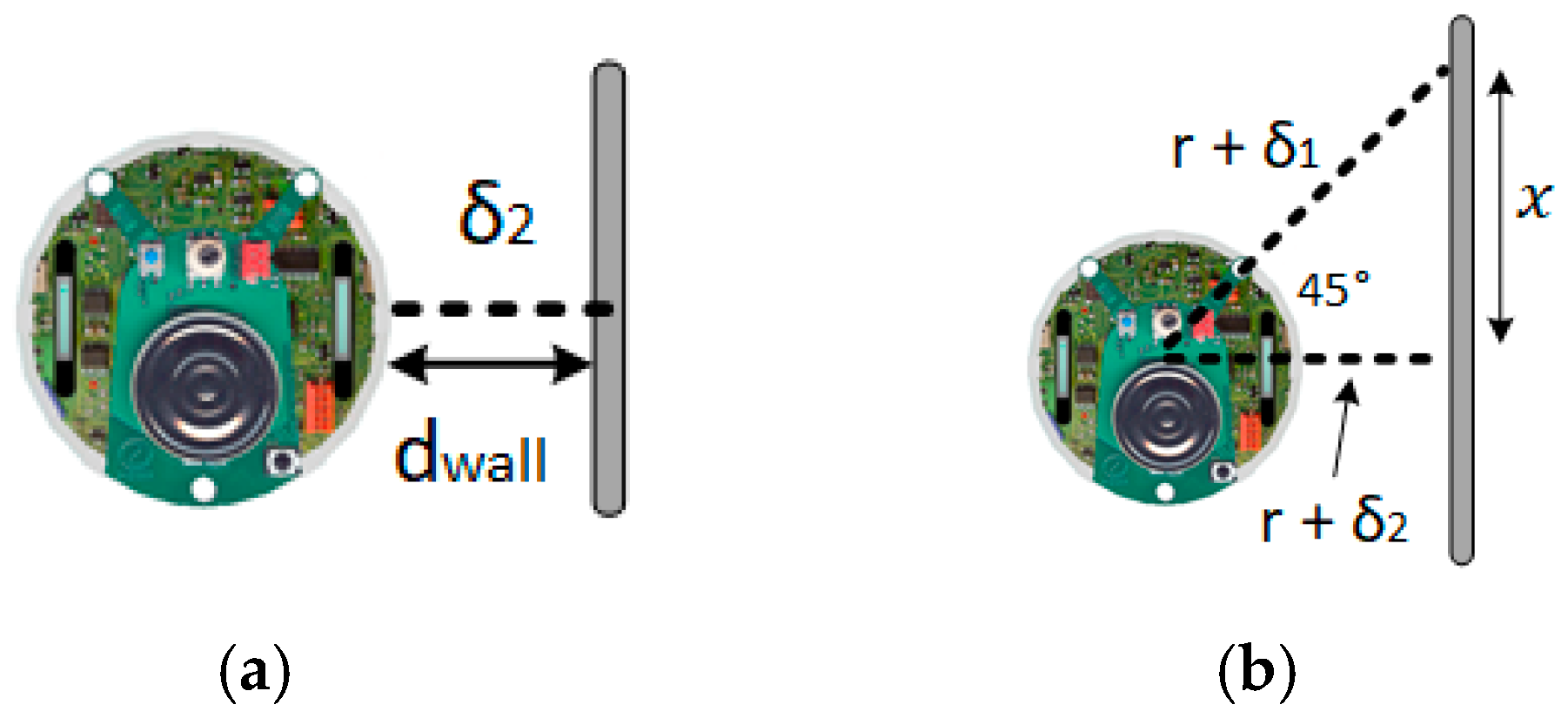
- : The goal of the wall-following control was to maintain a fixed distance between the side of the robot and the wall. Therefore, the sub-fitness function is defined as the average of , where represents the distance between the side of the robot and the wall at each time step, and is defined as follows:where is the pre-defined fixed distance ( = 4 cm), as presented in Figure 13a. is the total number of time steps in a learning process. If the robot remains at a fixed distance from the wall, the value is equal to zero.
- (3)
- : This sub-fitness function was used for evaluating the degree of parallelism between the robot and the wall. If the robot was parallel to the wall, the angle between the robot and wall was 90°. On the basis of the law of cosines, must have the same value as that of , as presented in Figure 13b.where is the radius of the robot; and represent the distance between the sensor 1 and the wall and that between sensor 2 and the wall, respectively, and represents the average value of the degree of parallelism during movement. If the robot is parallel to the wall, is equal to zero.Therefore, the proposed fitness function is defined as follows:
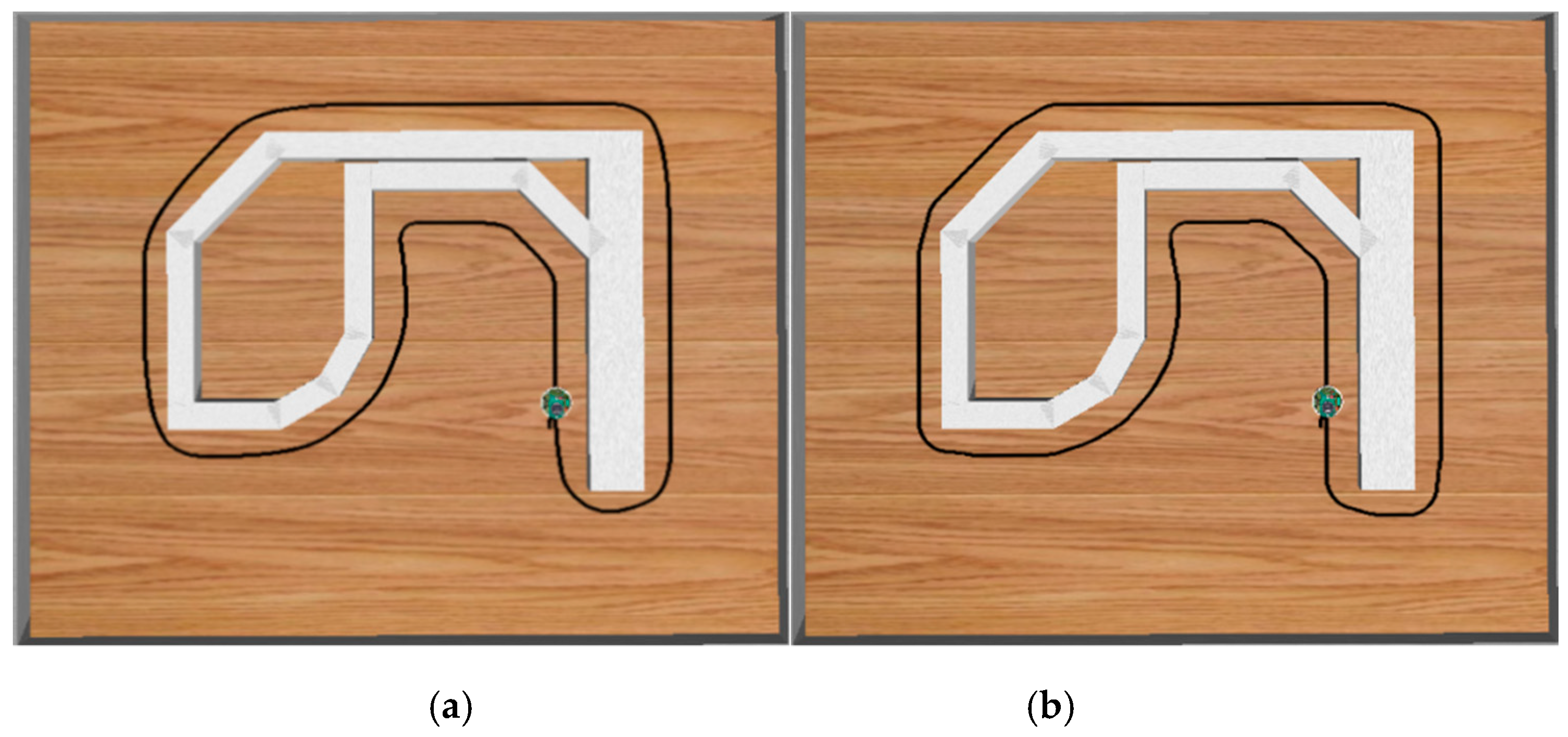
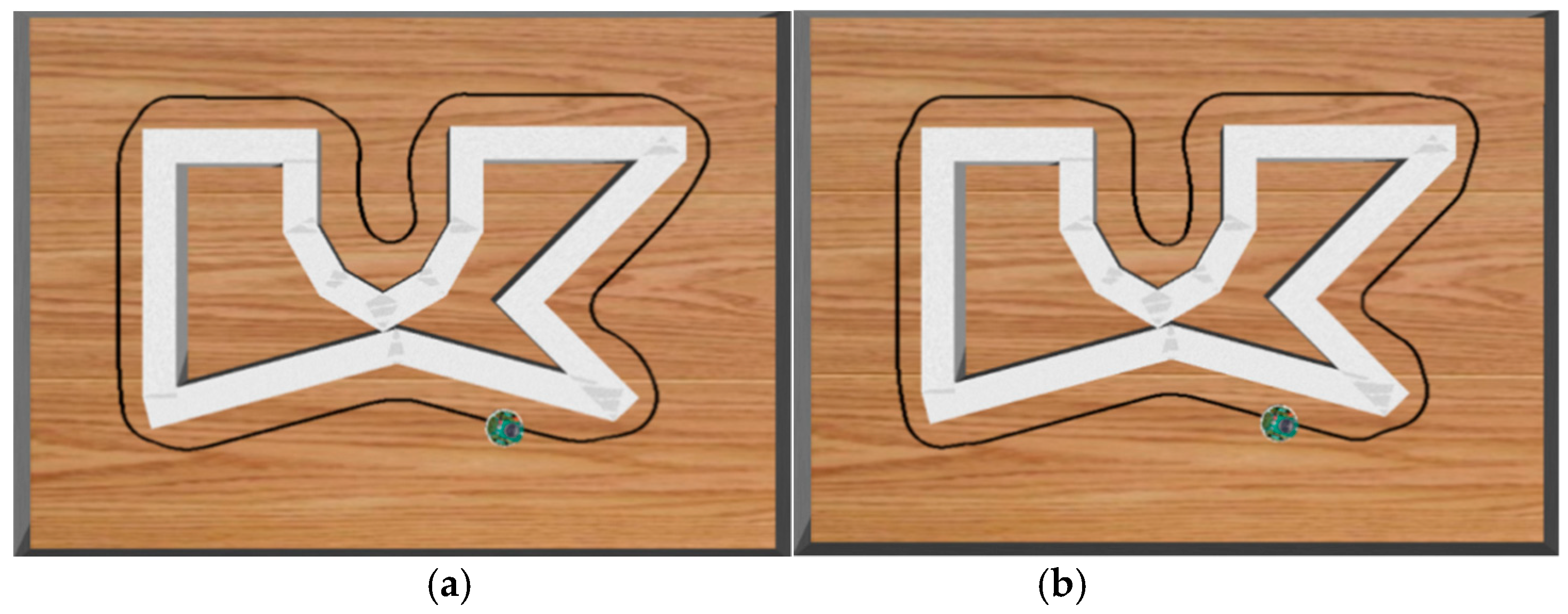
3.4. Experimental Results of the Wall-Following Control
4. Cooperative Carrying and Navigation Control of Multi-Evolutionary Mobile Robots
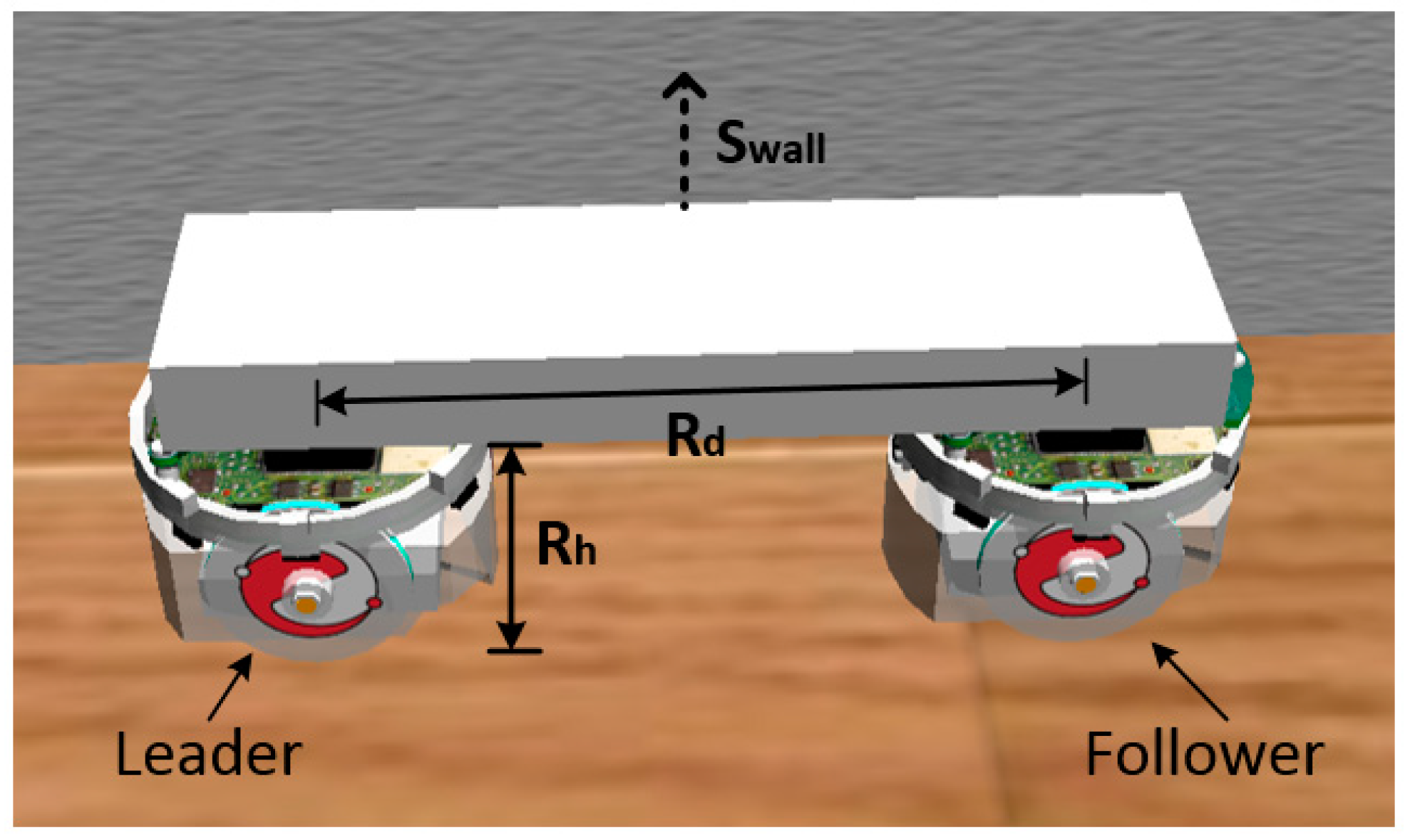
4.1. Wall-Following Control of the Cooperative Carrying Method
- (1)
- If the measured distance from one of the sensors in the follower robot is less than 1 cm, the follower robot collides with the obstacles.
- (2)
- If the measured distance of the sensor is higher than 6 cm, the follower robot deviates from the wall.
- (3)
- If the measured distance between the leader robot and follower robot is less than 10 cm or higher than 20 cm, the leader and follower robots are inferred to be very close or very far.
- (4)
- If the measured distance of the sensor is less than the height of the robot, the object is dropped by robots.
- (5)
- If the measured distance of the sensor is less than 1 cm or greater than 7.5 cm, the object approaches the wall or deviates from the wall.
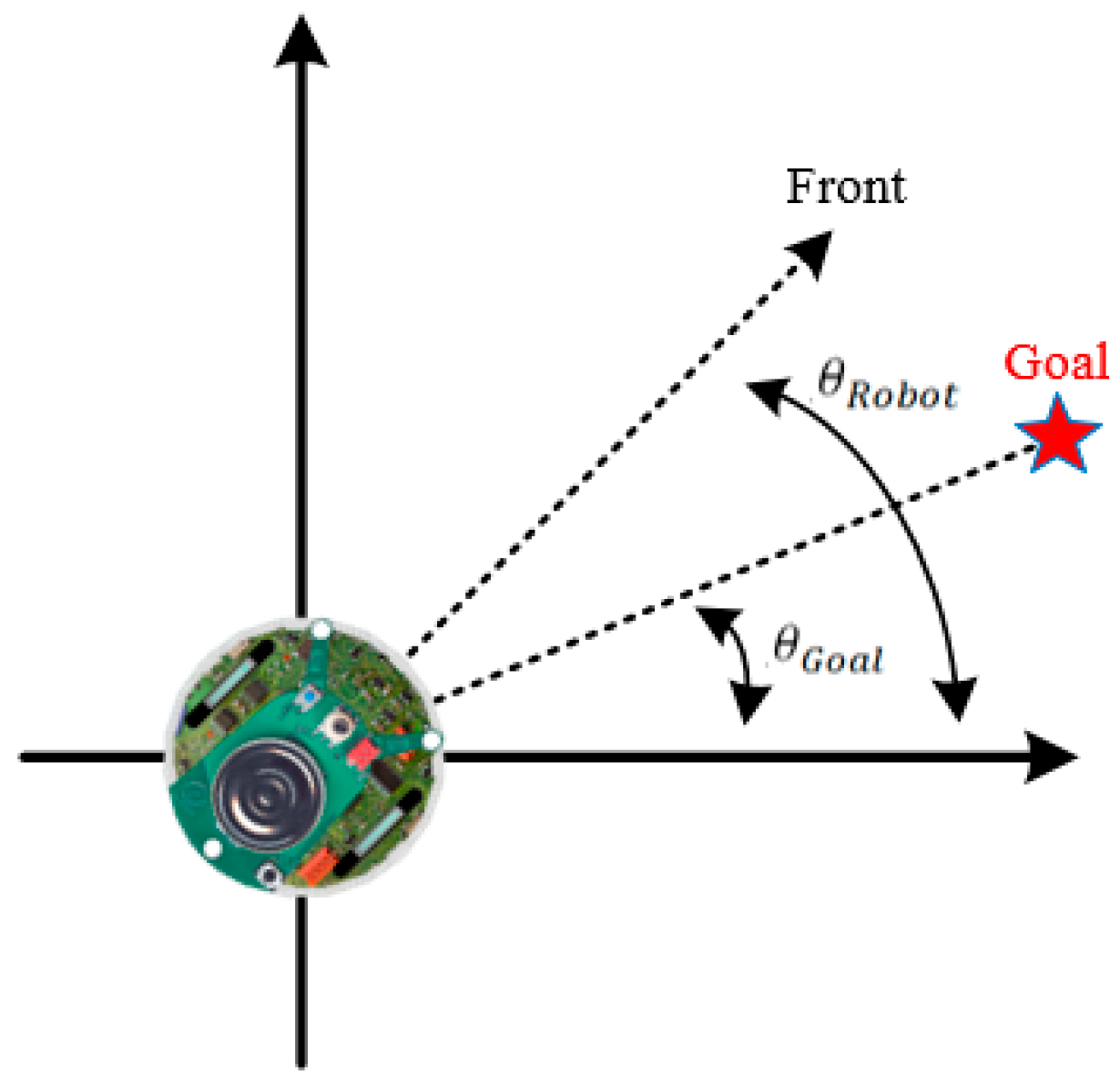
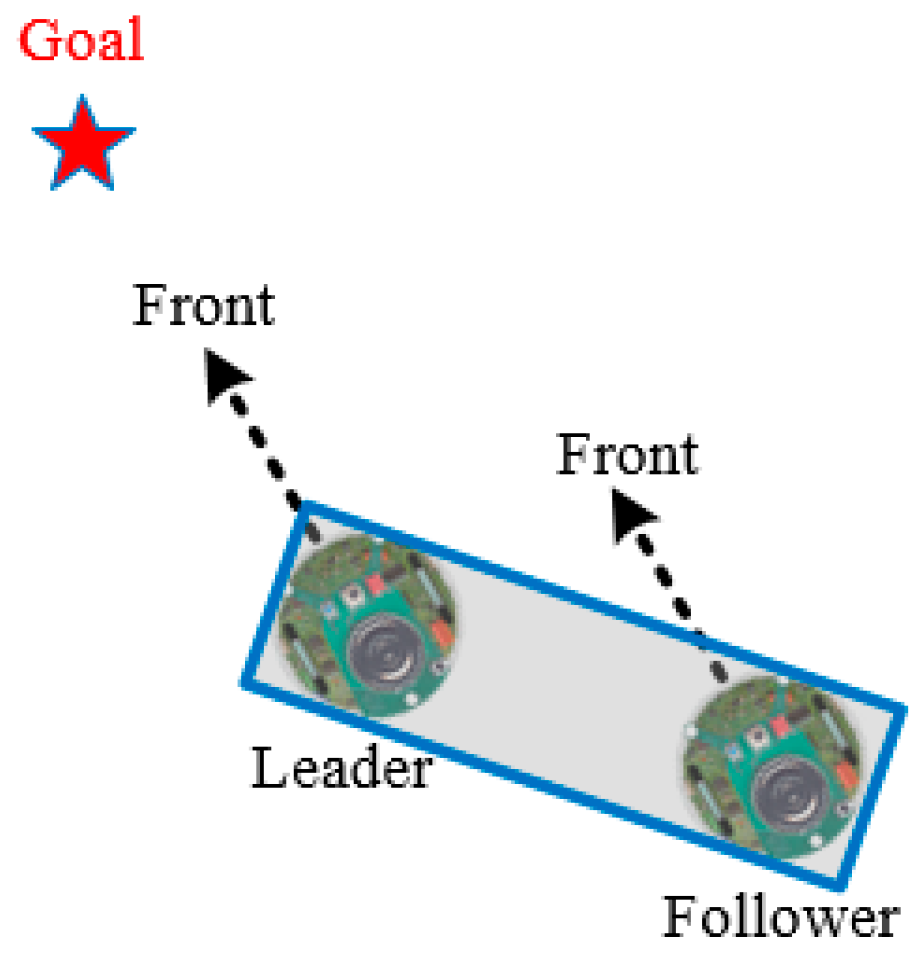
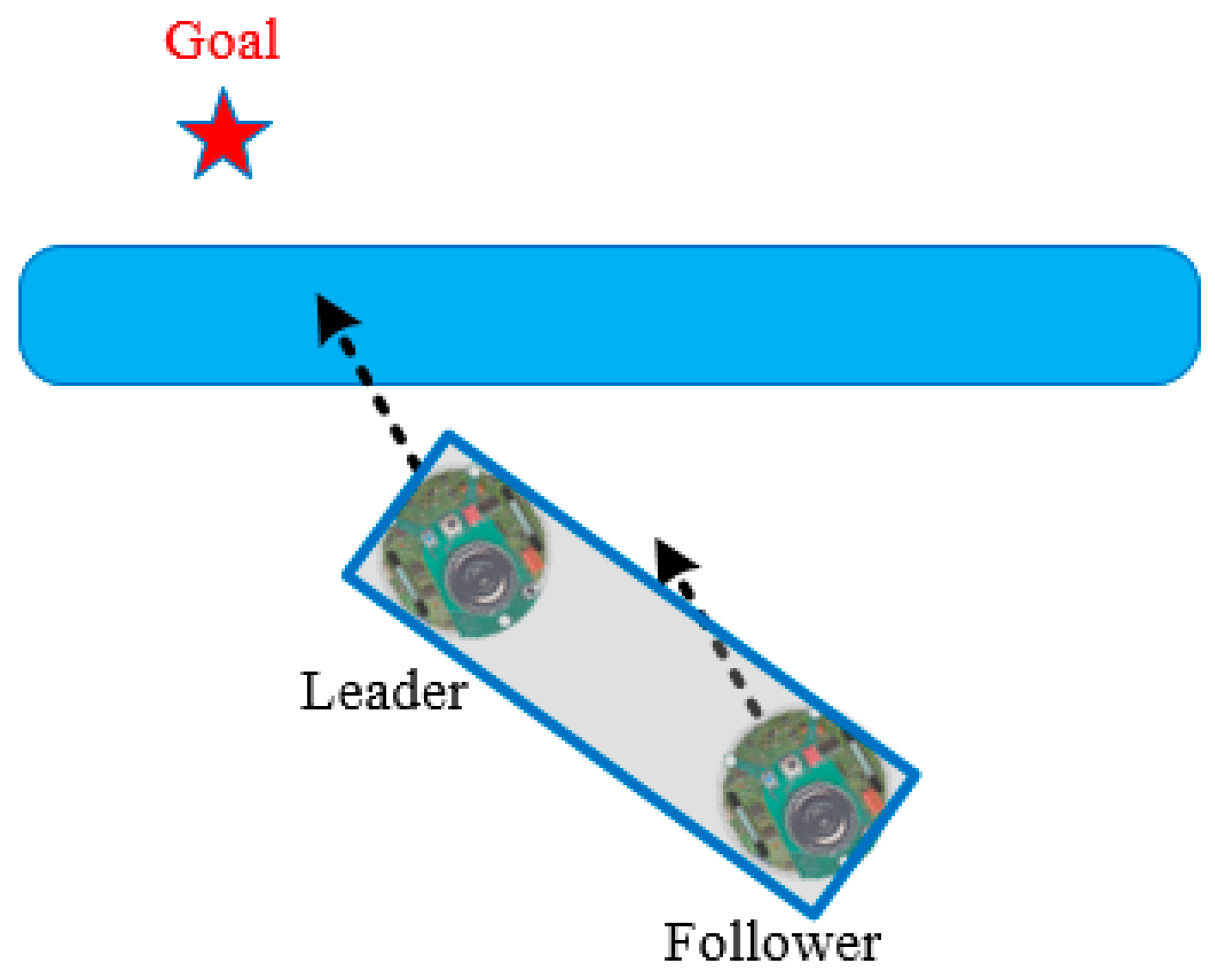
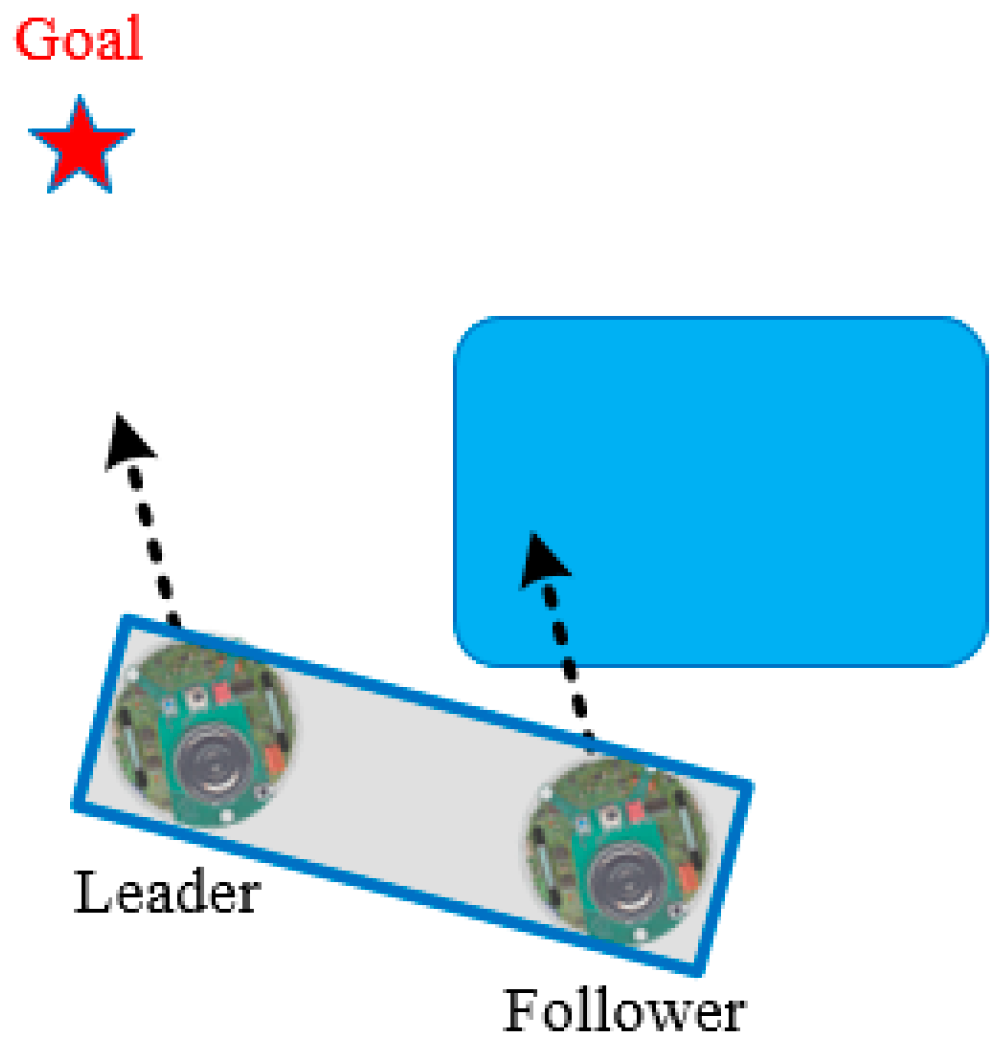
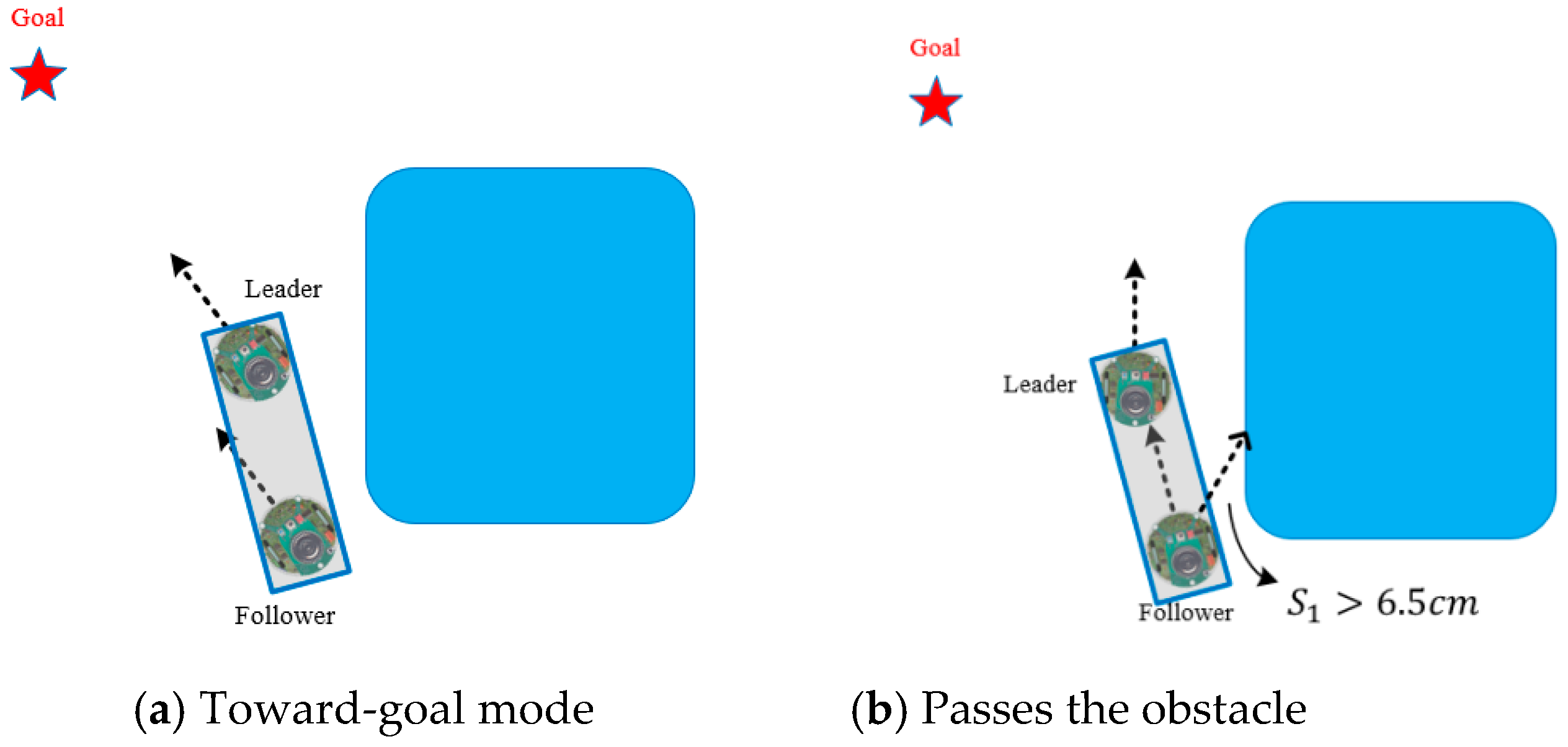
4.2. Navigation Control of Cooperative Carrying
- Left wall-following control:
- (i)
- The goal direction is located at , and or detects obstacles.
- (ii)
- The goal direction is located at , and , , and detect obstacles.
- Right wall-following control:
- (i)
- The goal direction is located at , and or detects obstacles.
- (ii)
- The goal direction is located at , and , , and detect obstacles.
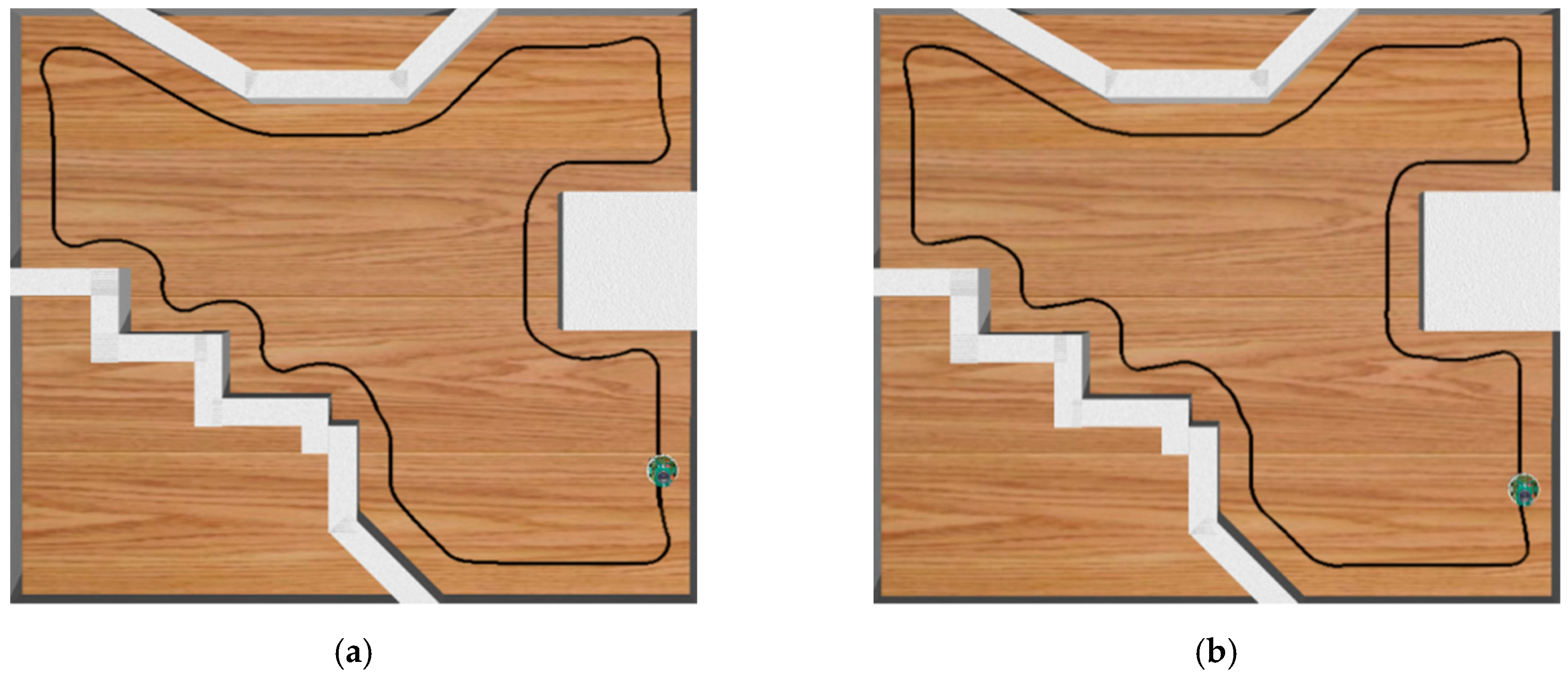
4.3. Experimental Results of Cooperative Carrying Control
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cupertino, F.; Giordano, V.; Naso, D.; Delfine, L. Fuzzy control of a mobile robot. IEEE Robot. Autom. Mag. 2006, 13, 74–81. [Google Scholar] [CrossRef]
- Zhu, A.; Yang, S.X. Neurofuzzy-based approach to mobile robot navigation in unknown environments. IEEE Trans. Syst. Man Cybern. C Appl. Rev. 2007, 37, 610–621. [Google Scholar] [CrossRef]
- Rusu, P.; Petriu, E.M.; Whalen, T.E.; Cornell, A.; Spoelder, H.J.W. Behavior-based neuro-fuzzy controller for mobile robot navigation. IEEE Trans. Instrum. Meas. 2003, 52, 1335–1340. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Hsu, C.H.; Juang, C.F. Multi-objective continuous-ant-colony-optimized FC for robot wall-following control. IEEE Comput. Intell. Mag. 2013, 8, 28–40. [Google Scholar] [CrossRef]
- Anish, P.; Parhi, D.R. Multiple mobile robots navigation and obstacle avoidance using minimum rule based ANFIS network controller in the cluttered environment. Int. J. Adv. Robot. Automn. 2016, 1, 1–11. [Google Scholar]
- Juang, C.F.; Chang, Y.C. Evolutionary group-based particle swarm-optimized fuzzy controller with application to mobile robot navigation in unknown environments. IEEE Trans. Fuzzy Syst. 2011, 19, 379–392. [Google Scholar] [CrossRef]
- Mendel, J.M. Advances in type-2 fuzzy sets and systems. Inf. Sci. 2007, 177, 84–110. [Google Scholar] [CrossRef]
- Mendel, J.M. Type-2 fuzzy sets and systems: An overview. IEEE Comput. Intell. Mag. 2007, 2, 20–29. [Google Scholar] [CrossRef]
- Kim, C.J.; Chwa, D. Obstacle avoidance method for wheeled mobile robots using interval type-2 fuzzy neural network. IEEE Trans. Fuzzy Syst. 2015, 23, 677–687. [Google Scholar] [CrossRef]
- Castillo, O.; Melin, P. A review on the design and optimization of interval type-2 fuzzy controllers. Appl. Soft. Comput. 2012, 12, 1267–1278. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. IEEE Int. Conf. Neural Netw. 1995, 4, 1942–1948. [Google Scholar]
- Dorigo, M.; Caro, G.D. Ant colony optimization: A new meta-heuristic. In Proceedings of the 1999 Congress on Evolutionary Computation, Washington, DC, USA, 6–9 July 1999; Volume 2, pp. 1470–1477. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Passino, K.M. Biomimicry of bacterial foraging for distributed optimization and control. IEEE Control Syst. Mag. 2002, 22, 52–67. [Google Scholar]
- Zhou, Y.; Wang, J.; Zhou, Y.; Qiu, Z.; Bi, Z.; Cai, Y. Differential evolution with guiding archive for global numerical optimization. Appl. Soft Comput. 2016, 43, 424–440. [Google Scholar] [CrossRef]
- Das, S.; Mullick, S.S.; Suganthan, P.N. Recent advances in differential evolution—An updated survey. Swarm Evol. Comput. 2016, 27, 1–30. [Google Scholar] [CrossRef]
- Chang, J.Y.; Lin, Y.Y.; Han, M.F.; Lin, C.T. A functional-link based interval type-2 compensatory fuzzy neural network for nonlinear system modeling. In Proceedings of the 2011 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE 2011), Taipei, Taiwan, 27–30 July 2011; pp. 939–943. [Google Scholar]
- Chen, C.H.; Su, M.T.; Lin, C.J.; Lin, C.T. A hybrid of bacterial foraging optimization and particle swarm optimization for evolutionary neural fuzzy classifier design. Int. J. Fuzzy Syst. 2014, 16, 422–433. [Google Scholar]
- Jhang, J.Y.; Lin, C.J.; Lin, T.C.; Chen, C.C.; Young, K.Y. Using Interval Type-2 Recurrent Fuzzy Cerebellar Model Articulation Controller Based on Improved Differential Evolution for Cooperative Carrying Control of Mobile Robots. Sens. Mater. 2018, 30, 2499–2516. [Google Scholar] [CrossRef]
- Zhang, J.; Sanderson, A.C. JADE: Adaptive differential evolution with optional external archive. IEEE Trans. Evol. Comput. 2009, 13, 945–958. [Google Scholar] [CrossRef]
- Gong, W.; Cai, Z. Differential evolution with ranking-based mutation operators. IEEE Trans. Cybern. 2013, 43, 2066–2081. [Google Scholar] [CrossRef] [PubMed]













| NP | CR | F | Generation | Rule |
|---|---|---|---|---|
| 30 | 0.9 | 0.5 | 3000 | 5,6,7 |
| Number of Rules | DGDE-1 | DGDE-2 | |||||
|---|---|---|---|---|---|---|---|
| Fitness Value | 5 | 6 | 7 | 5 | 6 | 7 | |
| Best | 0.932 | 0.961 | 0.948 | 0.949 | 0.962 | 0.953 | |
| Worst | 0.865 | 0.891 | 0.821 | 0.908 | 0.919 | 0.891 | |
| Average | 0.903 | 0.933 | 0.911 | 0.923 | 0.942 | 0.913 | |
| STD | 0.017 | 0.012 | 0.200 | 0.012 | 0.009 | 0.016 | |
| Number of successful runs | 10 | 10 | 10 | 10 | 10 | 10 | |
| Evaluation Items | Fitness Value | Number of Success Runs | Computation Time (H:M:S) | ||||
|---|---|---|---|---|---|---|---|
| Algorithms | Best | Worst | Average | STD | |||
| DGDE-1 | 0.961 | 0.891 | 0.933 | 0.012 | 10 | 5:01:39 | |
| DGDE-2 | 0.962 | 0.919 | 0.942 | 0.009 | 10 | 4:38:56 | |
| JADE [22] | 0.950 | 0.860 | 0.911 | 0.029 | 10 | 10:11:03 | |
| Rank-DE [23] | 0.958 | 0.867 | 0.922 | 0.025 | 10 | 18:21:05 | |
| DE [14] | 0.941 | 0.262 | 0.786 | 0.184 | 8 | 1:03:38 | |
| PSO [12] | 0.947 | 0.206 | 0.738 | 0.257 | 7 | 5:49:45 | |
| ABC [15] | 0.932 | 0.354 | 0.735 | 0.149 | 8 | 2:57:23 | |
| Evaluation Items | IT2FNC | IT2RFCMAC [23] | ||
|---|---|---|---|---|
| Algorithms | DGDE-1 | DGDE-2 | DGDE | |
| Best | 0.961 | 0.962 | 0.925 | |
| Worst | 0.891 | 0.919 | 0.868 | |
| Average | 0.933 | 0.942 | 0.906 | |
| Evaluation Items | Fitness Value | |||
|---|---|---|---|---|
| Algorithms | Training Environment | Testing Environment 1 | Testing Environment 2 | |
| DGDE-1 | 0.961 | 0.901 | 0.864 | |
| DGDE-2 | 0.962 | 0.899 | 0.872 | |
| JADE [22] | 0.950 | 0.895 | 0.862 | |
| Rank-DE [23] | 0.958 | 0.874 | 0.789 | |
| DE [14] | 0.941 | fail | fail | |
| PSO [12] | 0.947 | 0.828 | 0.721 | |
| ABC [15] | 0.932 | fail | fail | |
| Evaluation Items | Training Environment | Testing Environment 1 | Testing Environment 2 | ||||
|---|---|---|---|---|---|---|---|
| Algorithms | RD (cm) | FWD (cm) | RD (cm) | FWD (cm) | RD (cm) | FWD (cm) | |
| DGDE-1 | 16.18 | 3.81 | 16.54 | 3.61 | 17.03 | 3.42 | |
| DGDE-2 | 15.43 | 3.96 | 15.76 | 3.89 | 17.16 | 4.23 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jhang, J.-Y.; Lin, C.-J.; Young, K.-Y. Cooperative Carrying Control for Multi-Evolutionary Mobile Robots in Unknown Environments. Electronics 2019, 8, 298. https://doi.org/10.3390/electronics8030298
Jhang J-Y, Lin C-J, Young K-Y. Cooperative Carrying Control for Multi-Evolutionary Mobile Robots in Unknown Environments. Electronics. 2019; 8(3):298. https://doi.org/10.3390/electronics8030298
Chicago/Turabian StyleJhang, Jyun-Yu, Cheng-Jian Lin, and Kuu-Young Young. 2019. "Cooperative Carrying Control for Multi-Evolutionary Mobile Robots in Unknown Environments" Electronics 8, no. 3: 298. https://doi.org/10.3390/electronics8030298
APA StyleJhang, J.-Y., Lin, C.-J., & Young, K.-Y. (2019). Cooperative Carrying Control for Multi-Evolutionary Mobile Robots in Unknown Environments. Electronics, 8(3), 298. https://doi.org/10.3390/electronics8030298





