Regulating Scheduler (RSC): A Novel Solution for IEEE 802.1 Time Sensitive Network (TSN)

Abstract

Emerging applications such as industrial automation, in-vehicle, professional audio-video, and wide area electrical utility networks require strict bounds on the end-to-end network delay. Solutions so far to such a requirement are either impractical or ineffective. Flow based schedulers suggested in a traditional integrated services (IntServ) framework are O(N) or O(log N), where N is the number of flows in the scheduler, which can grow to tens of thousands in a core router. Due to such complexity, class-based schedulers are adopted in real deployments. The class-based systems, however, cannot provide bounded delays in networks with cycle, since the maximum burst grows infinitely along the cycled path. Attaching a regulator in front of a scheduler to limit the maximum burst is considered as a viable solution. International standards, such as IEEE 802.1 time sensitive network (TSN) and IETF deterministic network (DetNet) are adopting this approach as a standard. The regulator in TSN and DetNet, however, requires flow state information, therefore contradicts to the simple class-based schedulers. This paper suggests non-work conserving fair schedulers, called ‘regulating schedulers’ (RSC), which function as a regulator and a scheduler at the same time. A deficit round-robin (DRR) based RSC, called nw-DRR, is devised and proved to be both a fair scheduler and a regulator. Despite the lower complexity, the input port-based nw-DRR is shown to perform better than the current TSN approach, and to bind the end-to-end delay within a few milliseconds in realistic network scenarios.

1. Introduction

Various emerging applications such as industrial automation, building automation, inter-vehicle network, in-vehicle network, professional audio video (AV) network, and wide-area electrical utility network require strict delay bounds, which range from a few milliseconds to a few seconds. IEEE 802.1 time sensitive network (TSN) and IETF deterministic network (DetNet) are representative standard groups for dealing such delay requirements on various networks. TSN aims guarantee end-to-end delay and zero packet loss on an Ethernet data plane [1]. IETF’s DetNet has a similar scope with TSN, but is biased on network layer issues [2]. DetNet can be seen as an extension of TSN into routed networks, with IP and MPLS data plane. DetNet claims its scope is limited to a single administrative domain such as campus-area network or private WAN, but does not restrict itself from expanding into wider area networks. DetNet defines the electrical utility networks using time division multiplexing currently to be one of the key use cases [2]. For example, the utility network in Quebec, Canada, which includes 60 generating stations, 513 substations, and 10,500 km of optical fiber, carries instantaneous electrical information (current, voltage, active power, etc.) and real-time commands such as trip, open/close relay, etc. This network has a mixed Layer 2 and Layer 3 topology, and requires the deterministic behavior from the network such as bounded delay/jitter and precise timing. By applying DetNet technology the utility networks can increase the electrical grid’s reliability and efficiency.

TSN and DetNet both cover a wide area of technological aspects, including packet forwarding, time synchronization, path selection, resource reservation, reliable transmission, etc. This paper focuses on the packet forwarding technology. The packet forwarding function includes switching, queueing, and scheduling of packets. The TSN task group (TG) was initiated as the residential Ethernet TG in the IEEE 802.1 working group (WG) around the year 2005 and expanded to the audio video bridge (AVB) TG. Both TGs considered the professional AV traffic transport among nodes in close proximity as the main target. In its early stage, the TGs set a clear performance goal to bind the delay within ”2 ms in seven hops”. This clear goal helped the TGs got the attention from the beginning. The AVB TG in 2012 evolved into the TSN TG with the extended scope for various industrial applications. The residential Ethernet and the AVB TG’s target, the AV applications have a small number of large bandwidth flows. A flow is defined to be a set of packets of the same source-destination processes pair, generated within a relatively limited amount of time. Meanwhile in TSN, the target applications also generate numerous flows with relatively small bandwidth with nodes in a complex, larger area network, such as industrial sensor-actuator networks. For example, IEC/IEEE 60802 TSN Profile for Industrial Automation, a joint project of IEC SC65C/MT9 and IEEE 802 to define TSN profiles for industrial automation, has defined the traffic types of industrial automation and control systems, at the November 2018 meeting. According to this definition, isochronous traffic with 100 byte maximum packet length requires less than 2 ms end-to-end delay, while cyclic traffic with 1000 byte maximum packet length requires 2 ms to 20 ms end-to-end delay. These end-to-end delay requirements will be the primary target of this paper.

There has been a tremendous amount of research activities regarding the end-to-end delay bound in large scale networks, since early 1990s [3,4,5,6,7,8,9,10,11]. While various approaches for such requirements have their pros and cons, meeting delay requirement and implementation simplicity have been incompatible with one another so far. We propose a novel solution that can perform comparatively with the state-of-the-art solutions that are considered as the standard for the TSN and the DetNet, but with a far less complexity.

Our key contribution is schedulers that also perform the regulating function at the same time. This set of schedulers, called the ‘regulating scheduler’ (RSC), are devised by giving a non-work conserving characteristics to fair schedulers. Then a deficit round robin (DRR) based RSC, called nw-DRR, is devised and proved to be both a fair scheduler and a regulator. Despite the lower complexity, the input port-based nw-DRR is shown to perform better than the current TSN approach, and to bind the end-to-end delay within a few milliseconds in realistic network scenarios. In seven-hop networks with a few crossing flows, the maximum end-to-end delay can be bound within 2 ms, if the packet length is limited to be less than 400 bit.

This paper is comprised as follows. The related works to the problem of delay bound are reviewed in Section 2. In Section 3 the RSC and its realization with DRR, nw-DRR, are introduced and formally analyzed. The performance of the nw-DRR is investigated through numerical analysis with an exemplary network topologies in the Section 4. The last section discusses the result, the remaining issues, and possible follow up research activities.

2. Related Works

2.1. TSN Synchronous Approach

As the target applications of the TSN standard have diversified, there emerged two different forwarding approaches in the standard. The first one is the synchronous approach, which includes the cyclic queuing and forwarding (CQF) [12] function. The CQF is rooted from the residential Ethernet TG era’s small number of large bandwidth flows. In the synchronous approach, time is divided into slots, whose start and end times are synchronized across all the nodes in the network. In order to guarantee a bounded delay, the allocation of slots at all the nodes are precisely planned at packet level. A predefined slot has to be allocated to a predefined packet, at every node along the path of the packet. This allocation process, which is not defined in the standard, is quite burdensome in networks even with moderate number of flows. This slot allocation problem is similar to the job-shop scheduling problem [13], which is NP complete. It is shown that with 200 flows the slot allocation takes around 200 s with a contemporary personal computer, even with a heuristic algorithm [13].

The second one is the asynchronous approach, in which the asynchronous traffic shaping (ATS) [14] function takes the central role. The ATS, also called the interleaved regulator, is basically a regulation module in front of a scheduler. In this approach there is no need for the synchronization across the network. The ATS can be seen as a revision of an existing solution stemmed from the IntServ framework, with a modification for a simpler implementation. In the following we will see how the ATS is derived.

2.2. Integrated Services (IntServ) and Latency-Rate (LR) Servers

Binding end-to-end network delay is already achievable with the traditional IntServ framework [3]. Let us look at the theoretical background of IntServ that has been actively researched since the 1990s. The core benefit of the IntServ is that the maximum end-to-end delay of a packet is guaranteed if the following three conditions are met:

• The arrival process of every incoming flow conforms to the flow’s arrival curve.
• The sum of the arrival rates of flows on every link in the network is less than or equal to the link’s bandwidth.
• Every link in the network provides service to each flow with a service process that conforms to a service curve.

More specifically, Condition 1 means that a flow arrival process meets the following inequality.

$$A_i(t_0,t)\le {\rho }_i(t-t_0)+{\sigma }_i,$$

(1)

where $A_i(t_0,t)$ is the amount of the arrived traffic in an arbitrary period $(t_0,t]$ from the flow $i$, ${\rho }_i$ is the average arrival rate, and ${\sigma }_i$ is the maximum burst size of the flow $i$. A burst can be thought as a large number of packets go together with almost no time interval between them. The curve $A_i(t)={\rho }_i(t-t_0)+{\sigma }_i$ is called the arrival curve.

Now let us introduce a set of schedulers that conform to a flow’s service curve therefore meet Condition 3. This set of schedulers is called the latency-rate (LR) servers [10]. We will elaborate on the properties of the LR servers. The mathematical notations frequently appear in this paper are summarized in

Table 1. Mathematical notations used in the paper.

Notation	Meaning
$L_i$	Maximum packet length of flow $i$
$r$	Link capacity
${\rho }_i$	Arrival rate of flow $i$
${\sigma }_i$	Max burst size of flow $i$
${\phi }_i$	Quantum value assigned for flow $i$
${\mathsf{\Theta }}_i^S$	Latency of flow $i\mathrm{at}\mathrm{sever} S$
$D_i$	Delay experienced by packets of flow $i$

.

In the following the definitions and the properties are given according to [10].

Definition 1.

Flow $i$ busy period is the maximum time period $(t_1,t_2]$ that for all $t\subset (t_1,t_2]$ the following inequality holds. $A_i(t_1,t)\ge {\rho }_i(t-t_1)$, where $A_i(t_1,t)$ is the amount of traffic arrived during $(t_1,t]$ from flow $i$.

Note that a flow busy period is not the same with a flow backlogged period, during which a flow always has packet(s) to be served in the scheduler. In the following a start time and a finish time of a period are the arrival time of the first packet’s last bit and the departure time of the last packet’s last bit, respectively.

Definition 2.

Let $t_0$ be the start time of a flow $i$ busy period in server $S$ and $t^{*}$ the finish time of the busy period. Then, server $S$ is an LR server if and only if a nonnegative constant ${C_i}^S$ can be found such that, at every instant in the period $(t_0,t^{*}]$,

$${W_i}^S(t_0,t)\ge max\lceil 0,{\rho }_i(t-t_0-{C_i}^S)\rceil ,$$

(2)

where $W_i(t_0,t)$ is the amount of service given during $(t_0,t]$ to flow $i$.

The minimum ${C_i}^S$ that satisfies (1) is the latency of the flow $i$ at the server $S$ and denoted by ${{\mathsf{\Theta }}_j}^S$. The curve $W_i(t)=max\lceil 0,{\rho }_i(t-t_0-{C_i}^S)\rceil$ derived from the inequality (2) is called the service curve. If a service given to a flow satisfies (2) then it conforms to the service curve. Condition 3 above means that a scheduler at an output port has to satisfy the inequality (2). Therefore, LR servers are the key functional elements of the IntServ framework. For an LR server, only two parameters, service curve ${\rho }_i$ and latency ${{\mathsf{\Theta }}_j}^S$ define the service curve. LR servers have the following properties [10].

Property 1.

If a flow traverses two adjacent LR servers, it is equivalent for the flow to traverse a single LR server with the latency equal to the sum of the latencies of the two adjacent LR servers.

Property 1 means the series of LR servers can be seen as a single LR server with a latency equal to the sum of the latencies of the LR servers in series.

Property 2.

If a flow $i$ traverses only LR servers $S_j$ in its path, then the end-to-end delay experienced by the packets in the flow is bounded by the following inequality.

$$D_i\le \frac{{\sigma }_i-L_i}{{\rho }_i}+{\displaystyle \sum }_{j=1}^k{{\mathsf{\Theta }}_j}^{S_j}$$

(3)

Property 2 means the maximum end-to-end delay is the sum of latencies of the LR servers plus the single delay term caused by the initial max burst. As in Property 3, the maximum burst of a flow increases as it passes the LR servers, yet it does not affect the delay. This property is called “pay burst only once”.

Property 3.

If a flow $i$ conforms to the arrival curve with parameters $\left\{{\rho }_i,{\sigma }_i\right\}$, i.e. $A_i(t_0,t)\le {\rho }_i(t-t_0)+{\sigma }_i$, then after traversing an LR server $S$ it follows the curve $({\rho }_i,{\sigma }_i+{{\mathsf{\Theta }}_i}^S{\rho }_i)$, i.e. the maximum burst increases as much as ${\rho }_i{{\mathsf{\Theta }}_i}^S$. In other word, if $t_0$ is the start time of a busy period, then$W_i(t_0,t)\le {\rho }_i(t-t_0)+{\sigma }_i+{\rho }_i{{\mathsf{\Theta }}_i}^S$.

Note that a service process for a flow at a scheduler is identical to the arrival process to the next scheduler. Now we have defined the LR servers and its important properties. Fair schedulers that can guarantee sustainable service rate to every flow fall into this category. The ideal generalized processor sharing (GPS) [4], packetized-GPS [4], self-clocked fair queuing [5], and virtual clock [7], which are all based on the “virtual finish time”, are LR servers. Round robin based deficit round robin (DRR) [8] and weighted round robin (WRR) are also LR servers. Virtual finish time-based LR servers generally have smaller latencies but are more complex to implement. DRR and WRR are easier to implement and therefore widely deployed. These LR servers’ latencies are proportional to the maximum packet size and the maximum burst size of a flow.

The application service procedure in the IntServ is composed of the connection establishment phase and the data transfer phase. In connection establishment phase, a flow specifies its input parameters $\left\{{\rho }_i,{\sigma }_i\right\}$, then the network checks if the traversing nodes have enough bandwidth, reserve the bandwidth for the flow, then admit the flow and guarantee the service. The admitted flows are placed in its own queues and serviced fairly with schedulers at the output ports of relaying nodes in the data transfer phase. The LR servers in an IntServ network work as a scheduler and provide a fair share of the resource. The series of LR servers form a single virtual LR server to a flow, according to Property 1. The maximum delay of the flow then limited by (3).

The flow-based scheduling function is a key component of the IntServ, yet its complexity prohibits practical implementation. Flow based schedulers suggested in the IntServ framework are O(N) or O(log N), when N is the number of flows in the scheduler. N can be tens of thousands in core networks. Due to such complexity, flow-based schedulers have not been deployed.

2.3. Alternatives to the IntServ

As a consequence, a simpler solution with the class based scheduling emerged. A class is a coarser set of packets, which is a set of packets of similar performance requirements. This solution is adopted in the differentiated services (DiffServ) [15] framework. The DiffServ categorizes the whole traffic into eight classes and schedules the queues according to the classes. In the DiffServ, however, the connection establishment and the admission to a network are still flow basis. A flow specifies its input parameters $\left\{{\rho }_i,{\sigma }_i\right\}$, then the network checks if the traversing nodes have enough bandwidth, reserve the bandwidth for the flow, then admit the flow and guarantee the service. After connection establishment, in data transfer phase, at the boundary of a network a flow is regulated. Regulation is a process to enforce the arrival process of a flow to conform to its arrival curve. Packets of a flow that does not conform to the negotiated arrival curve may be delayed or dropped if necessary. A properly regulated flow will conform to the arrival curve in (1) after the regulation. The leaky bucket [16] and the token bucket [17,18] are the commonly implemented regulators.

After the regulation process at the network boundary, a flow is put into the network relaying nodes. At the output of the relaying nodes a flow is put into a proper class. The packets in a class is placed into a single queue. Then the queues for different classes are scheduled accordingly. The scheduler used in the DiffServ network is the strict priority (SP) scheduler. In an SP scheduler, among the packets queued, the packet with the highest priority is selected to be served. It is shown that the strict priority scheduler is also an LR server [11] for a flow, but its latency is a function of the sum of all the other flows’ maximum burst sizes as

$${{\mathsf{\Theta }}_i}^{SP}=\frac{{\sigma }^{SP}-{\sigma }_i^{SP}+2L}{r^{SP}},$$

(4)

where ${\sigma }^{SP}$ is the sum of maximum bursts of all the flows in the SP scheduler.

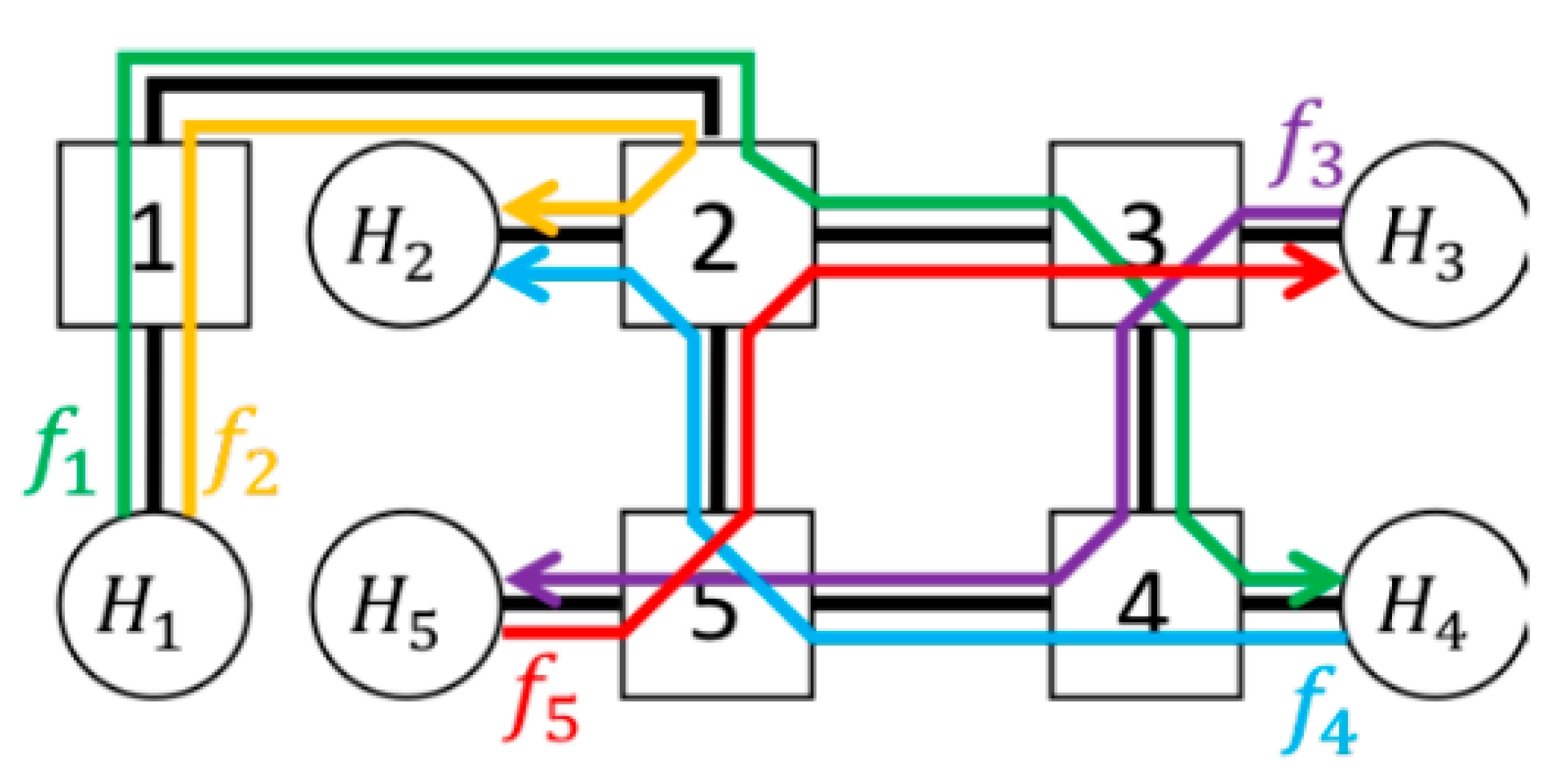
DiffServ is suitable for the applications with the performance metrics such as average delay and packet loss rate, but not for ones with the strict delay bounds. This is because the class-based SP scheduler in the DiffServ cannot provide guaranteed delay for networks with cycle. The burst increases infinitely along the cycle. Consider the following network topology depicted in Figure 1. Nodes 1-4 forms a cycle. The flows traversing node 1-4 are higher priority flows. They affect to each other as follows. Flow 1 shares the queue at the node 1 with flow 4. Flow 1’s latency at the node 1, ${{\mathsf{\Theta }}_1}^{SP1}$, is a function of the max burst of flow 4 arriving to the node 1, ${\sigma }_4^{SP1}$. Since the max burst of the flow 1 arriving to the node 2, ${\sigma }_1^{SP2}$, is a function of the latency ${{\mathsf{\Theta }}_1}^{SP1}$, it is also a function of ${\sigma }_4^{SP1}$. In other words,

$${\sigma }_1^{SP2}=f({\sigma }_4^{SP1}).$$

(5)

Now, flow 1 affects flow 2 the same way as flow 4 does to flow 1, i.e., ${\sigma }_2^{SP3}=f({\sigma }_1^{SP2})=f({\sigma }_4^{SP1})$. It eventually evolves to the point where ${\sigma }_4^{SP1}=f({\sigma }_4^{SP1})$. The only value that satisfies this equation for ${\sigma }_4^{SP1}$ is infinity.

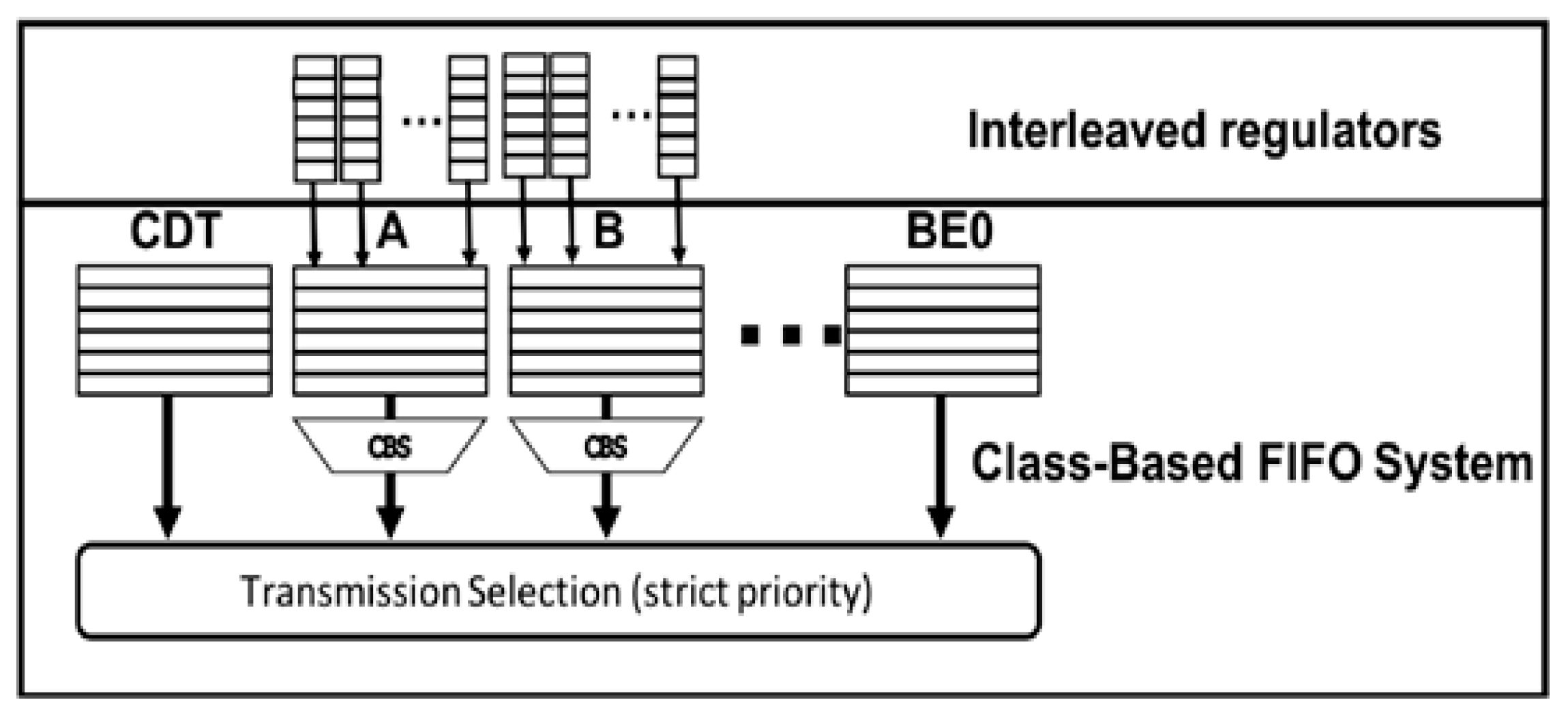
One possible solution for the infinitely increasing burst is the regulation per flow at every node. Therefore, a regulator placed right before the class-based scheduler has been considered [6,9].

Figure 2 depicts such a system architecture [6,9]. In Figure 2, a connection is synonymous to a flow. The max burst size of a flow at the output of the system in Figure 2 is proportional to the sum of all the flows in a queue. The max burst size, however, is reduced drastically by the regulator at the next node. The packets in the flow under regulation may suffer from additional delays at the regulator, but it is shown that the maximum delay does not increase with the addition of the regulator [9,19]. It can be interpreted that the packets with large enough delays are not delayed further at the regulator.

In the system of Figure 2, the central scheduler is relieved from per-flow scheduling task. The complexity goes to the parallel distributed regulators, however. Since the distributed regulators have most of complexity, compare to the flow-based schedulers, the regulator-scheduler system is more plausible for implementation. This architecture has not been widely accepted though, due to the massive number of regulators.

2.4. TSN Asynchronous Approach

TSN’s asynchronous approach has also suggested a regulator-scheduler pair for each output port. The regulation function in the TSN is performed by the aforementioned ATS module, which was originally called the interleaved regulator [14]. ATS places queues per-input port for higher priority class. After the regulation with the ATS, the TSN schedules with strict priority scheduling with queues assigned to each classes. ATS, however, still needs to maintain flow states, find the flow to which the packet at the head of the queue belongs, decides whether the packet is to be regulated based on the flow state. Therefore, it does not completely remove the per-flow complexity [20,21].

Figure 3 depicts the architecture of the TSN asynchronous approach. ATS maintains the queue per input port, for class A and B. A and B indicates the high priority traffic Class A and Class B, while BE0 stands for Best Effort Class 0 traffic. The CDT (control data traffic) represents the highest priority traffic for control and management. There are usually eight classes excluding CDT. Class A and B are further regulated by the credit based shaper (CBS). The CBS has been adopted in the standard at the early stage of standardization activity, before the asynchronous approach was introduced. The reason for the existence of CBS is now unclear. It was meant to prevent the exhaustion of link bandwidth by the high priority traffic, but a part of its function is now duplicated with ATS.

3. Proposed Scheduler and Its Analysis

3.1. Proposed Approach

This paper proposes a simpler alternative for end-to-end delay guarantee, the regulating scheduler (RSC). The RSC can be thought as a non-work conserving version of fair schedulers. In order to build an RSC, a fair scheduler is modified to make their queues always filled with a virtual packet if there is no actual packet waits for the service. The virtual packet receives the service but it just disappear after the service rather than be transferred to the next node. When an actual packet arrives, the virtual packet in that queue, if existing, is removed even if it was in the middle of a service. By this modification all the queues look backlogged and the queue under observation will be served at a steady pace. Therefore, the traffic served out from the queue under observation is strictly regulated. Intuitively, a burst increases at a node as follows. At a certain moment, a single queue is full of traffic while all the other queues are empty. The incoming burst to the queue arrives right before the queued burst’s service time. They merged together and served instantly, and becomes a larger burst. The RSC prevents the instant service of a large amount of traffic from a single queue by having the other backlogged queues.

We carefully devised a pure per input port RSC for the TSN environment. Its operation can be described as the following. The whole traffic is divided into high priority and low priority traffic. The high priority traffic includes CDT, Class A, and Class B. The low priority traffic includes the rest. At an output port of a relaying node such as switch and router the high priority traffic is divided based on their input ports and allocated to different queues. The low priority traffic is allocated to another queue at the output port. Therefore, if there are N input ports, (N+1) queues will be established. These queues are scheduled with a DRR scheduler [8] but based on the RSC principle. The algorithm detail will follow in Section 3.3. This scheduler is the main contribution of this paper, which is called nw-DRR (the non-work conserving DRR).

Figure 4 depicts the proposed input-port based nw-DRR’s architecture. It replaces the whole system depicted in Figure 3. One can easily see the simplicity of the proposed system’s architecture. We analyze and prove that the nw-DRR is a scheduler and a regulator at the same time in Section 3.3. We also prove that nw-DRR is a fair scheduler with the same {latency, service rate} parameters with the original DRR before modification. It is also shown that the input-port based nw-DRR can guarantee end-to-end delay within the required bounds of a few milliseconds.

3.2. DRR Scheduler

DRR’s complexity depends heavily on its parameter, deficit value. Larger the deficit easier to implement, but with larger latency. DRR works as the follows [8].

• Each queue is assigned a deficit value (δ) and a quantum value (φ).
• Deficit value is variable but initialized to zero. Quantum value is fixed and determined to be proportional to the arrival rate of the traffic to the queue. For example, if arrival rates to two queues are 1 Mbps and 2 Mbps then quantum value of the latter queue should be twice to the one of the former. The quantum values of two queues can be set to be 10 byte and 20 byte, or 50 byte and 100 byte, respectively as well. It is shown that a smaller quantum gives a smaller latency [10]. A smaller quantum makes the operation of the scheduler slower, however.
• Each backlogged queue takes a turn, and a complete cycle of turns of backlogged queues is called a frame ($F$).
• At the start of each turn a queue increases the deficit value as much as the quantum value.
• If the deficit value is larger or equal to the packet length at the head of the queue, then serve the packet. After service of the packet, the deficit is reduced as much as the packet length. Repeat the Step 5 as long as the condition holds.
• If the queue becomes empty then reset deficit to zero.
• Proceed to the next backlogged queue, and go to the Step 4.

The latency of a DRR server, in case the deficit value is smaller than the max packet length, is given as the follows [22].

$${{\mathsf{\Theta }}_i}^{DRR}=\frac{1}{r}\left[(F-{\phi }_i)\left(1+\frac{L_i}{{\phi }_i}\right)+{\displaystyle \sum }_{n=1}^N{L}_n\right]$$

(6)

where $F$ is the sum of all ${\phi }_i$ of active flows in the server, and N is the number of active flows. The significant term in (6) is $F$ and ${{\displaystyle \sum }}_{n=1}^N{L}_n$. $F$ can be reduced by reducing deficit values locally, but sum of max packet lengths of each queue is not easily controlled.

3.3. DRR Scheduler as a Regulator

From now on, we will show that a DRR scheduler can work as a regulator, with a proper modification in line with the RSC principle. The following theorems show that a general DRR scheduler bounds the work given to a flow within a certain limit.

Theorem 1.

Assume that flow $i$ is continuously backlogged during time period (a,b]. Assume that the flow is served k turns during (a,b]. The work given to the flow during this period is bounded by the following inequality.

$$\mathrm{k}{\phi }_i-{\delta }_i^k\le W_i(a,b)\le \mathrm{k}{\phi }_i+{\delta }_i^0,$$

(7)

where ${\delta }_i^k$ is the deficit value at the finish time of k_th round during (a,b].

Proof. 

See the proof of Theorem 4.2 in [8]. □

Theorem 2 generalizes the result of Theorem 1 without using k and the deficit value terms.

Theorem 2.

During any time period ($a$, $b$] within a flow $i$ backlog period, the work given to the flow is bounded by the following inequality.

$$W_i(a,b)\le {\rho }_i\frac{F_{max}}{f}(b-a)+{\phi }_i+L_i,$$

(8)

where $f$ is the sum of quantum values of the flows that have been always backlogged during (a,b], and $F_{max}$ is the sum of quantum values of all the flows in the scheduler, in an imaginary situation where the sum of arrival rates of all the flows equals to the link capacity.

Proof. 

Let $t_k$ be the finish time of k_th round, counting from $a$. Let $t_0=a$. Duration of a round $t_k-t_{k-1}=\frac{1}{r}{\displaystyle \sum }_{j\in B_k}({\phi }_j+{\delta }_j^{k-1}-{\delta }_j^k)$, where $B_k$ is the set of flows that are continuously backlogged during $(t_{k-1},t_k\rceil$. During $(t_{k-1},t_k\rceil$ the elements of $B_k$ are not changed. Let B be the set of flows that are continuously backlogged during $(t_0,t_k\rceil$. For any k, $B\subset B_k$. The following equation holds. $t_k-t_{k-1}=\frac{1}{r}{\displaystyle \sum }_{j\in B}({\phi }_j+{\delta }_j^{k-1}-{\delta }_j^k)$. By summing up the equation for all k, we get $t_k-t_0\ge k\frac{f}{r}+\frac{1}{r}{\displaystyle \sum }_{j\in B}({\delta }_j^0-{\delta }_j^k)\ge \frac{f}{r}(k-1)$, since ${\displaystyle \sum }_{j\in B}{\delta }_j^0\ge 0$ and ${\displaystyle \sum }_{j\in B}{\delta }_j^k\le f$. Therefore $k\le \frac{r}{f}(t_k-t_0)+1$. From Theorem 1, during $(t_0,t_k\rceil$.

$$W_i(t_0,t_k)\le \mathrm{k}{\phi }_i+{\delta }_i^0\le \frac{r}{f}(t_k-t_0){\phi }_i+{\phi }_i+{\delta }_i^0\le {\rho }_i\frac{F_{max}}{f}(t_k-t_0)+{\phi }_i+L_i,$$

(9)

because $L_i\le {\delta }_i^0$ and ${\rho }_i/r={\phi }_i/F_{max}$. In other words, the deficit values cannot be larger than the maximum packet length $L_i$, at all the round finish time instants including $t_0$. Furthermore, the flow arrival rate is proportional to the quantum value of the flow, and $F_{max}$ is so to the link capacity r. Therefore, for arbitrary time instant b between $t_k$ and $t_{k+1}$,

$$W_i(a,b)=W_i(a,t_k)\le {\rho }_i\frac{F_{max}}{f}(t_k-a)+{\phi }_i+L_i\le {\rho }_i\frac{F_{max}}{f}(b-a)+{\phi }_i+L_i,$$

(10)

and the theorem follows. □

From Theorem 2, if a DRR scheduler satisfies two conditions 1) the sum of arrival rates of flows is equal to the link capacity and 2) all the queues in the scheduler are always backlogged, then the work given to the scheduler is bounded as the following inequality.

$$W_i(a,b)\le {\rho }_i(b-a)+{\phi }_i+L_i,$$

(11)

which is the inequality for the amount of work of a regulator with maximum burst size ${\phi }_i+L_i$, or an arrival curve of a flow {${\rho }_i$, ${\phi }_i+L_i$} where ${\phi }_i+L_i$ is the max burst size.

As the next step, we will introduce a modified DRR that satisfies the two conditions given above, and show that it indeed works as a regulator with inequality (11). Consider a DRR scheduler that is modified to work with the following algorithm.

• Assign a queue for a virtual flow $v$, which has the arrival rate equals to the difference of the link capacity and the sum of the arrival rates of all the flows in the scheduler. (${\rho }_v=r-{\displaystyle \sum }_{i\in H}{\rho }_i$.) Flow $v$ will serve the low priority traffic, whose arrival rates are not predefined.
• If a queue, including the queue for $v$, is empty then place a virtual packet in the queue immediately, so that all the queues are never empty. The length of the virtual packet is set to the quantum value of the queue. In other words, the virtual packet is sized such that it can be served in a single turn.
• The virtual packet is served the same way with the actual packets. After the service virtual packets do not leave the scheduler, though.
• Consider an actual packet arrives to the queue with a virtual packet. If the virtual packet was not in a service then remove the virtual packet. If it was during a service then immediately stop serving the virtual packet, set the deficit value to 0, and proceed to the next queue.

The above scheduler may serve a virtual packet even when actual packets are waiting in the other queues, therefore is non-work conserving. This is called the nw-DRR scheduler.

3.4. Properties of the nw-DRR

The following theorem proves the nw-DRR gives the same service curve, i.e.,

$${W_i}^{nw-DRR}(t_0,t)\ge max\lceil 0,{\rho }_i(t-t_0-{{\mathsf{\Theta }}_i}^{DRR})\rceil ,$$

(12)

with the original DRR scheduler that does not generate virtual packets.

Theorem 3.

The nw-DRR is an LR server with the same service rate and latency with the DRR server that does not generate any virtual packets.

Proof. 

Assume N flows arrive to an nw-DRR, thus there are N queues. It is sufficient to prove that for all the packets in an arbitrary flow $i$, $i\in \left\{1,\dots ,N\right\}$, there exists a work conserving DRR scheduler that serves later than or equal to the nw-DRR would. □

Let all the other flows, except the flow under observation $i$, have the same arrival rates with those with the nw-DRR but sufficiently large maximum burst sizes to make their queues always be backlogged during the flow $i$ backlog period. Recall that the max burst size does not affect the latency of a flow with a DRR scheduler. Furthermore upon the start of the flow $i$ backlogged period, let the service of the (i+1)_th queue start. Let us call this work conserving server DRR*. Intuitively, DRR* gives the worst case DRR service to $i$ in terms of packet service finish time.

Now we will come back to the nw-DRR scheduler. Let us call $p_k$, $k=0,1,\dots ,K$, the packets arrive during a flow $i$ backlog period. $p_0$ arrives to a queue with a virtual packet, but nw-DRR removes the virtual packet just before the $p_0$’s arrival. This is true even if that virtual packet was under service, in which case the (i+1)_th queue’s service starts upon the $p_0$’s arrival. Therefore, $p_0$ does not see that it is non-work conserving. The subsequent packets $p_k$, $k=1,\dots ,K$, arrive to a backlogged queue and do not see that it is non-work conserving, as well. Therefore, the service times of $p_k$, $k=0,1,\dots ,K$, of the nw-DRR are always earlier than or equal to those of the DRR*. The theorem follows.

By Theorem 3, the nw-DRR is an LR server with the same {latency, service rate} parameters with the ordinary work-conserving DRR. Let $i$ be a set of packets assigned to the $i$_th queue in the nw-DRR. We will call $i$ the flow aggregate. The maximum delay experienced by packets in a flow-aggregate $i$ in an nw-DRR’s is given as

$$D_i\le \frac{{\sigma }_i-L_i}{{\rho }_i}+{\mathsf{\Theta }}_i^{nw-DRR}.$$

(13)

Here, ${\mathsf{\Theta }}_i^{nw-DRR}$ is the latency of the nw-DRR server and equals to a work conserving DRR scheduler, given in (6).

Consider a node architecture with nw-DRR at the output ports, as depicted in Figure 5. Let us calculate the maximum burst of $i_q^{D+1}$. Let us denote it with ${\sigma }_q$. $i_q^{D+1}$ is the set of flows from the input port q to the output port under observation of the node (D+1). We argue that ${\sigma }_q\le {\sigma }_{I^D}$, and ${\sigma }_{I^D}\le {\displaystyle \sum }_p({\phi }_p+L_p)$, therefore

$${\sigma }_q\le {{\displaystyle \sum }}_p({\phi }_p+L_p).$$

(14)

Similarly, we can argue that ${\sigma }_p\le {\displaystyle \sum }_o({\phi }_o+L_o)$, if the input port p is connected to an nw-DRR scheduler in the upstream node (D-1), with $o$ representing the input ports to the output port under observation in the node (D-1).

The first argument above (${\sigma }_q\le {\sigma }_{I^D}$) holds. For any $t$ and $t_0$, $t>t_0$,

$$\begin{gathered} \begin{array}{ll}{A}_{I^D}(t_0,t)& ={\displaystyle {\displaystyle \sum }_q}{A}_{i_q^{D+1}}(t_0,t)={\displaystyle {\displaystyle \sum }_q}({\sigma }_{i_q^{D+1}}+{\rho }_{i_q^{D+1}}(t-t_0))\\ & ={\displaystyle \sum }_q{\sigma }_{i_q^{D+1}}+{\displaystyle \sum }_q{\rho }_{i_q^{D+1}}(t-t_0)={\sigma }_{I^D}+{\rho }_{I^D}(t-t_0),\mathrm{and}\end{array} \\ {\displaystyle {\displaystyle \sum }_q}{\rho }_{i_q^{D+1}}(t-t_0)={\rho }_{I^D}(t-t_0). \end{gathered}$$

Therefore ${\displaystyle \sum }_q{\sigma }_{i_q^{D+1}}={\sigma }_{I^D}$, and ${\sigma }_q\triangleq {\sigma }_{i_q^{D+1}}\le {\sigma }_{I^D}$, for any q. The second argument (${\sigma }_{I^D}\le {\displaystyle \sum }_p({\phi }_p+L_p)$) also holds because of (11).

We can now calculate the delay of packets in $i_p^D$ at the node D. The delay of $i_p^D$ is bounded by (13), where ${\rho }_i$, $L_i$, and ${\mathsf{\Theta }}_i^{nw-DRR}$ can be easily obtained by letting $i_p^D$ be the aggregate of all the flows traverse from the input port p to the output port under observation at the node D. The maximum burst of $i_p^D$, ${\mathsf{\sigma }}_p$, can be obtained similarly with (14).

4. Case Study

4.1. Case of a Network with a Cycle

In this subsection we investigate the performance of the nw-DRR with an exemplary network depicted in Figure 6, which was suggested in [19] for the study of the performance of the TSN asynchronous forwarding module in Figure 3. By adopting the already studied network topology, we can clearly compare the performance of the two solutions head to head. The flow under observation, $f_1$, starts from the host 1, traverses the node 1, 2, 3, 4, and then sinks to the host 4. All the other flows from $f_2$ to $f_5$ have the same parameters with $f_1$. Low priority traffic also exists and occupies the low priority traffic queue in each nw-DRR.

We calculated the maximum end-to-end delay while varying the maximum packet length that applies the same to both high and low priority traffic, the max input burst size, the flow input data rate, and the quantum size, and fixing the link capacity, as in

Table 2. Parameter values used for the case study.

Parameter	Value
L (Maximum packet length)	400–3200 bit
$r$ (Link capacity)	100 Mbps
${\rho }_i$ (Arrival rate of a flow)	10–40 Mbps
${\sigma }_i$ (Max initial burst size of a flow)	400–3200 bit
${\phi }_i$ (Quantum value assigned for a flow with ${\rho }_i$)	80–400 bit

.

The delay at a node is calculated with (13). At the first node $f_1$ and $f_2$ share a queue, since they enter the node with the same port. The maximum burst at the first node is equal to the max packet length. Therefore the delay of $f_1$ at the first node satisfies the inequality $D_{f1}^1\le {\mathsf{\Theta }}_1^1$, where ${\mathsf{\Theta }}_1^1=\frac{1}{r}\left[\left(\frac{r}{{\rho }_i}-2{\phi }_i\right)\left(1+\frac{L}{2{\phi }_i}\right)+2L\right]$ from (6). The delay of $f_1$ at the nodes from 2 to 4 satisfies the inequality

$$D_{f1}^j\le \frac{{\sigma }_1^j-L}{{\rho }_i}+{\mathsf{\Theta }}_1^j,$$

(15)

where ${\mathsf{\Theta }}_1^j=\frac{1}{r}\left[\left(\frac{r}{{\rho }_i}-{\phi }_i\right)\left(1+\frac{L}{{\phi }_i}\right)+3L\right]$ with j is the node identifier that j = 2, 3, or 4. ${\sigma }_1^j$ in (15) is the max burst into the queue of the output port of node j, to which $f_1$ belongs. ${\sigma }_1^j$ is calculated with (14), and in our case

$${\sigma }_1^j\le 2({\phi }_i+L),$$

(16)

for all j = 2, 3, or 4, since there are always two flows in the queue in the previous node j-1.

Figure 7 shows the maximum end-to-end delay of $f_1$ with varying max packet size from 400 bit to 3200 bit, flow arrival rate from 10 Mbps to 40 Mbps, and a fixed quantum value at 80 bit. It is shown that the max packet length and the input data rate are both significant parameters for the delay. The input data rate is inversely proportional to the max delay. One can consider to increase the input data rate during the connection setup phase, while actual amount of traffic remains unchanged, in order to reduce the max delay.

The

Table 3. End-to-end delay bound at sample parameter sets (ms) with the fixed quantum value at 80 bit.

$\mathit{L}\backslash {\mathit{\rho }}_{\mathit{i}}$	10 Mbps	40 Mbps
400 bit	0.364	0.109
1000 bit	0.796	0.249
3200 bit	2.38	0.76

shows the exact values of the max end-to-end delay at sample parameter value sets.

As in Table 3, with the quantum value 80 bit and flow arrival rate 10 Mbps, the maximum end-to-end delay is around 2 ms even when the max packet length is 400 Byte. If we can limit the max packet length to 50 Byte, the max delay reduces to 0.364 ms.

Next, we investigated how the max end-to-end delay changes when the quantum size varies. The smaller quantum size implies more computational burden to the scheduler.

Figure 8 shows that the quantum size does not significantly affects the delay. When the max packet length becomes larger, the effect of the quantum value becomes even less significant. One can choose to use a relatively large quantum value in case the complexity is one of key design issues, without sacrificing the delay performance too much.

Next, we compare our performance with the ATS system in [19]. It is revealed that the ATS system shows the max end-to-end delay of 0.70 ms when the max packet length 1000 bit, flow arrival rate 20 Mbps [19]. The same parameter set gives 0.431 ms with quantum value 80 bit and 0.575 ms with quantum value 400 bit in our result, which can be found at

Table 4. End-to-end delay bound at sample parameter sets (ms) with the flow arrival rate at 20 Mbps.

$\mathit{L}\backslash {\mathit{\phi }}_{\mathit{i}}$	80 bit	400 bit
400 bit	0.194	0.338
1000 bit	0.431	0.575
3200 bit	1.30	1.444

. This result is summarized in

Table 5. End-to-end delay bound comparison with [19] (ms) with the maximum packet size 1000bit and the flow arrival rate at 20Mbps.

[19]	This Paper with ${\phi }_i$ = 80 bit	This Paper with ${\phi }_i$ = 400 bit
0.70	0.431	0.575

.

The performances of two different approaches are remarkably similar, while ours is slightly better. This is encouraging considering the simplicity of the proposed architecture.

4.2. Case of a Seven-Hop Network

In this subsection a network with a flow that traverses seven hops is considered. The early residential Ethernet TG defined the “2 ms delay bound in seven hops” as an ultimate performance goal for the strictest applications. We will investigate if this goal can be met with the proposed RSC. Consider the following topology depicted partly in Figure 9. There are 6 relaying nodes between the source and the destination of the flow, which makes up seven hops between the source and the destination. All the nodes have multiples input and output ports. The flow under observation enters the input port 1 and then departs from the output port 1, in every bridge node. A flow with the same specification with the flow under observation comes in at every other input port and then leaves at the output port 1. The set of such flows from all the input ports is called crossing flows. The crossing flows in a node shares the output ports with the flow under observation, but are separated to different output ports at the next node. This pattern continues at the subsequent nodes. This type of tandem networks is suitable for the investigation of the delay performance of schedulers with flow aggregation [23]. Although not specified in the figure, there exists low priority traffic at every output port. This setup of flows makes the network quite busy and large-scale.

As in Section 4.1, we set the parameters within a predefined range specified in

Table 6. Parameter values used for the case study.

Parameter	Value
L (Maximum packet length)	400–1600 bit
$r$ (Link capacity)	100 Mbps
${\rho }_i$ (Arrival rate of a flow)	10 Mbps
${\sigma }_i$ (Max initial burst size of a flow)	400–1600 bit
${\phi }_i$ (Quantum value assigned for a flow with ${\rho }_i$)	80 bit
$N$-1 (Number of crossing flows in a node)	1–8

. We fixed the values of ${\rho }_i$, ${\phi }_i$. The number of crossing flows, $N$-1, varies from 1 to 8, which makes the number of ports, $N$, from 2 to 9. The number of queues in an RSC scheduler is then $N$+1, because of the low priority traffic queue.

Let us call $f_1$ the flow under observation. The delay of $f_1$ at the nodes from 1 to 6 satisfies the inequality

$$D_{f1}^j\le \frac{{\sigma }_1^j-L}{{\rho }_i}+{\mathsf{\Theta }}_1^j,$$

(17)

where ${\mathsf{\Theta }}_1^j=\frac{1}{r}\left[\left(\frac{r}{{\rho }_i}-{\phi }_i\right)\left(1+\frac{L}{{\phi }_i}\right)+\left(N+1\right)L\right]$ with j is the node identifier that j = 1, …, 6. ${\sigma }_1^j$ in (17) is the max burst into the queue of the output port of node j, to which $f_1$ belongs. ${\sigma }_1^j$ is calculated with (14), and in our case

$${\sigma }_1^j\le N({\phi }_i+L),$$

(18)

for j = 2, …, 6, since there are always $N$ high priority queues in the scheduler in the previous node j-1. The maximum burst at the first node is equal to the max initial burst, which is same with the packet length in our case. Therefore ${\sigma }_1^1={\sigma }_1=L.$

Figure 10 shows the maximum end-to-end delay of $f_1$, ${{\displaystyle \sum }}_{j=1}^6{D}_{f_1}^j$ with varying max packet size from 400 bit to 1600 bit, number of crossing flows from 1 to 8, fixed flow arrival rate at 10 Mbps, and a fixed quantum value at 80 bit.

As depicted in Figure 10, even when the number of crossing flows is eight, which represents quite a busy network, the end-to-end delay bound can be near 2 ms if we set the maximum packet length to be less than 400 bit.

Table 7. End-to-end delay bound (mc) at sample parameter sets with the fixed arrival rate at 10 Mbps.

$\mathit{L}\backslash \mathit{N}$	2	9
400 bit	0.327	2.175
1600 bit	1.08	7.632

shows that with the maximum packet size 400 bit, or 50 byte, even if the number of crossing flows at every node is 8, the maximum delay is 2.175 ms, which is around the IEEE TSN’s ultimate performance goal of the “2 ms with seven hops”.

5. Discussion

A method of building a regulating scheduler (RSC) from a fair scheduler is proposed in this paper, which has non-work conserving characteristic. Possibility of the RSC as a delay bounding module is investigated. Especially, the DRR scheduler is modified to be an RSC, the nw-DRR. The nw-DRR is proved to be an LR server, with the same {latency, service rate} parameters with the original DRR server. The nw-DRR is then applied to work as an input-port based scheduler. At an output port of a relaying node the high priority traffic is divided based on their input ports and allocated to different queues. The low priority traffic is allocated to another queue at the output port. Therefore, if there are N input ports, (N+1) queues will be established.

The input-port based scheduling prevents the ill-behaving flows from overwhelming the network, if applied at the boundary of a network. As such it can guarantee the fair resource sharing among all the flows in the high priority class, without per-flow scheduling. For example, if the first Ethernet switch from a flow’s source host employs an input port-based RSC at the output ports, then automatically the flow is regulated, therefore shares only a fair amount of network resources.

Low priority traffic also benefits from an RSC since they do not suffer from the exhaustion, the bandwidth monopoly by high priority traffic. Low priority traffic is assigned a single queue in an RSC and guaranteed to receive the remaining available bandwidth without any resource reservation process. This property fits well to the “best-effort” traffic class, literally, and is in line with the available bit rate (ABR) service paradigm defined in the ATM networks [24].

The performance of the nw-DRR was investigated with realistic network topologies. The first network examined has a cycle, so the class-based scheduler would not meet any delay bound requirement. It was shown that in over various network parameters range, the nw-DRR bounds the delay within a few milliseconds. The network topology was adopted from [19] to compare the performance of the nw-DRR with that of the ATS approach of TSN. While the two perform similarly, ours was slightly better in the given parameter set. Moreover, our architecture is simpler in two ways. First, it is purely input port-based. Second, the regulator and the scheduler are in one piece. Despite the simplicity, the performance was acceptable. It is shown that the max packet length and the input data rate are both significant parameters for the delay. The input data rate is inversely proportional to the max delay. One can consider to increase the input data rate during the connection setup phase, while actual amount of traffic remains unchanged, in order to reduce the max delay. The quantum size does not significantly affect the delay. When the max packet length becomes larger, the effect of the quantum value becomes even less significant. One can choose to use a relatively large quantum value in case the complexity is one of key design issues, without sacrificing the delay performance too much. In the second network examined, a flow under observation traverses seven-hops with a number of crossing flows. Even with eight crossing flows at every node, which represents quite a busy network, if we set the maximum packet length to be less than 400 bit, then the maximum end-to-end delay bound is around the IEEE TSN’s ultimate performance goal of “2 ms with seven hops”.

The non-work conserving nature of the proposed scheduler may increase the average delay. The guarantee on the delay bound, however, is crucial in emerging applications. Therefore, the RSC will play a key role in such application networks. Various fair schedulers can be modified to be an RSC. The DRR’s latency depends on the sum of max packet lengths of each queues (${{\displaystyle \sum }}_{n=1}^N{L}_n$), which makes it too large in situations with many input ports, and thus many queues in the nw-DRR. The virtual-finish time based LR servers’ latency is usually dominated by the max packet length, not their sum, therefore will be more suitable to TSN. In future work, the possibility of modifying a virtual finish time based LR server to an RSC will be investigated. Although they are more complex, input port-based implementation will mitigate the complexity greatly.