Joint Estimation of Doppler Stretch and Time Delay of Wideband Echoes for LFM Pulse Radar Based on Sigmoid-FRFT Transform under the Impulsive Noise Environment
Abstract
:1. Introduction
2. Signal Model and Noise Model
2.1. Wideband Signal Model
2.2. Distribution Noise Model
3. Sigmoid Fractional Fourier Transform
3.1. Fractional Fourier Transform
3.2. FRFT of LFM Signal
3.3. Sigmoid Transform
3.4. Definition of the Sigmoid-FRFT
4. Parameter Estimation Based on Sigmoid Fractional Fourier Transform (Sigmoid-FRFT)
4.1. Estimation of Doppler Stretch and Time Delay based on Sigmoid-FRFT
4.2. Boundedness of Sigmoid-FRFT to the Noise
4.3. Robustness of Sigmoid-FRFT to the Noise
4.4. Complexity Analysis
5. Simulation Results
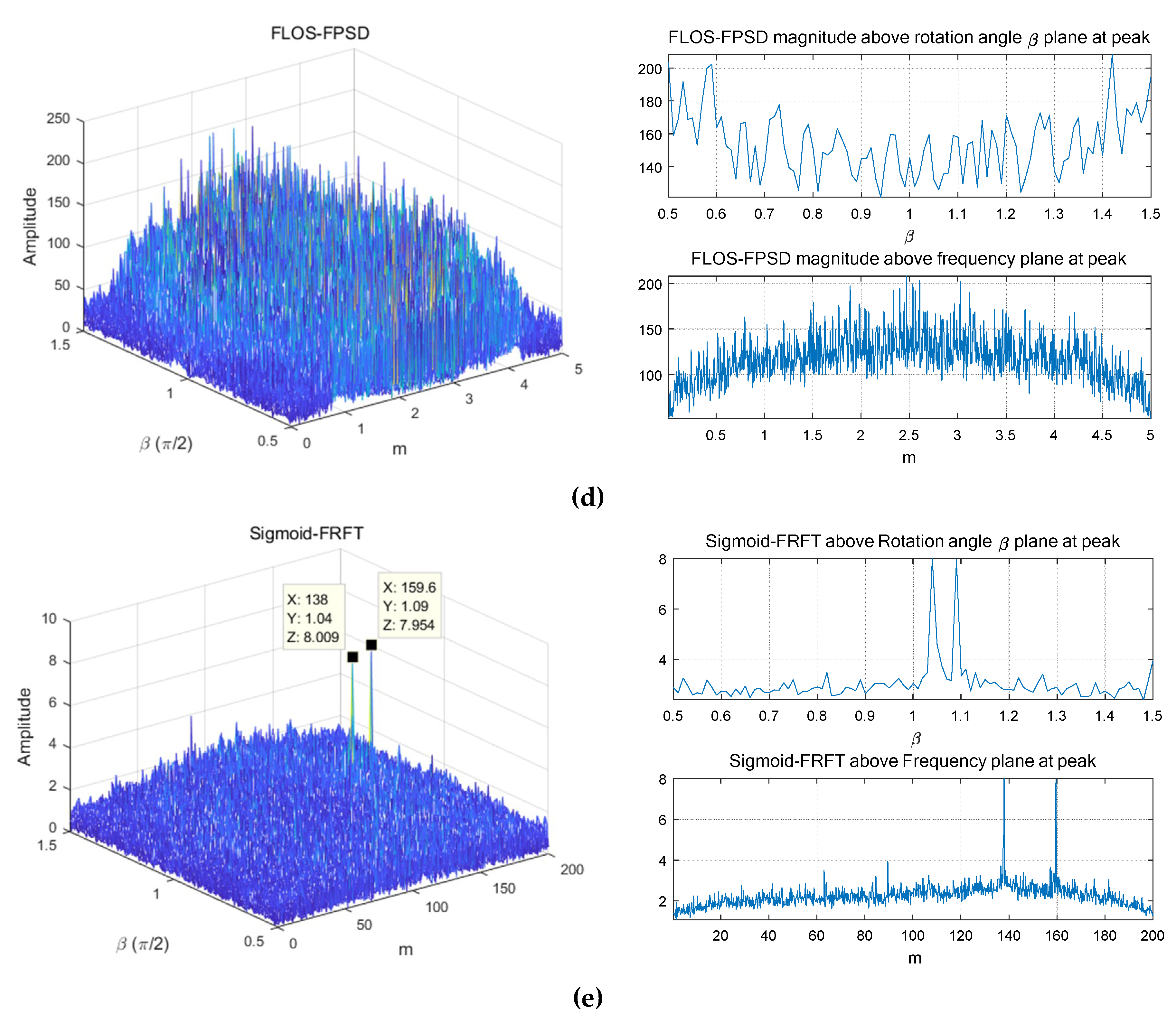
5.1. Simulation 1: FRFT, FLOS-FC, FLOS-FPSD, and Sigmoid-FRFT for a Single Estimation for Two Targets
5.2. Simulation 2: Estimation Accuracy with Respect to GSNR
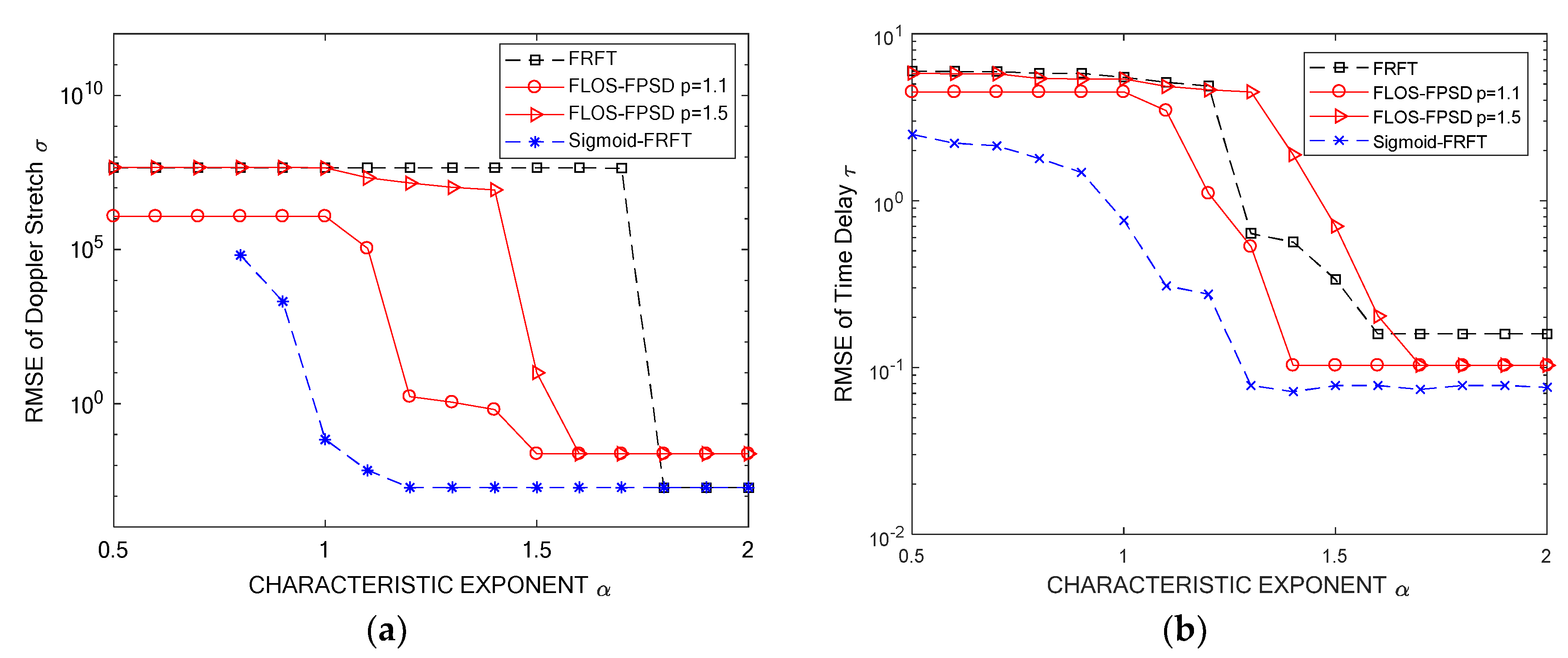
5.3. Simulation 3: Estimation Accuracy with Respect to Characteristic Exponent
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Geroleo, F.; Brandt-Pearce, M. Detection and estimation of LFMCW radar signals. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 405–418. [Google Scholar] [CrossRef]
- Govoni, M.; Li, H.; Kosinski, J. Low probability of interception of an advanced noise radar wavefor m with linear-FM. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1351–1356. [Google Scholar]
- Zhang, X.; Li, H.; Liu, J.; Himed, B. Joint delay and Doppler estimation for passive sensing with direct-path interference. IEEE Trans. Signal Process. 2016, 64, 630–640. [Google Scholar] [CrossRef]
- Qiu, T.; Wang, H.; Zhang, Y.; Bao, H. Non-linear transform-based robust adaptive latency change estimation of evoked potentials. Methods Arch. 2002, 41, 331–336. [Google Scholar]
- Niu, X.; Ching, P.; Chan, Y. Wavelet based approach for joint time delay and Doppler stretch measurements. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 1111–1119. [Google Scholar] [CrossRef]
- Zhao, Y.; Yu, H.; Wei, G.; Ji, F.; Chen, F. Parameter estimation of wideband underwater acoustic multipath channels based on fractional Fourier transform. IEEE Trans. Signal Process. 2016, 64, 5396–5408. [Google Scholar] [CrossRef]
- Li, S.; He, R.; Lin, B.; Sun, F. DOA estimation based on sparse representation of the fractional lower order statistics in impulsive noise. IEEE CAA J. Autom. Sin. 2018, 5, 860–868. [Google Scholar] [CrossRef]
- Ma, X.; Nikias, C. Joint estimation of time delay and frequency delay in impulsive noise using fractional lower order statistics. IEEE Trans. Signal Process. 1996, 44, 2669–2687. [Google Scholar]
- Long, J.; Wang, H.; Li, P.; Fan, H. Applications of fractional lower order time frequency representation to machine bearing fault diagnosis. IEEE CCA J. Autom. Sin. 2017, 4, 734–750. [Google Scholar] [CrossRef]
- Al-Manie, M.A.; Wang, J.W. Time-frequency analysis by evolutionary periodogram with application in gear fault diagnosis. Int. J. Wavelets Multiresolut. Inf. Process. 2010, 8, 679–693. [Google Scholar] [CrossRef]
- Dong, G.; Chen, J. Noise resistant time frequency analysis and application in fault diagnosis of rolling element bearings. Mech. Syst. Signal Process. 2002, 33, 212–236. [Google Scholar] [CrossRef]
- Li, L.; Qiu, T.S. Parameter estimation based on fractional power spectrum under alpha-stable distribution noise environment in wideband bistatic MIMO radar system. AEU Int. J. Electron. Commun. 2013, 67, 947–954. [Google Scholar] [CrossRef]
- Li, L.; Qiu, T. Parameter estimation based on fractional lower order statistics and fractional correlation in wideband bistatic MIMO radar system. J. Commun. 2014, 9, 745–750. [Google Scholar] [CrossRef]
- Gonzalez, J.; Griffith, D.; Arce, G. Zero-order statistics: A mathematical framework for the characterization of very impulsive signal. IEEE Trans. Signal Process. 2006, 54, 3839–3851. [Google Scholar] [CrossRef]
- Li, L.; Younan, N.; Shi, X. A novel parameter estimation method based on a tuneable Sigmoid in alpha-stable distribution noise environments. Sensors 2018, 18, 3012. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Qiu, T. A novel phase parameter estimation method of quadratic FM signal based on Sigmoid fractional ambiguity function in impulsive noise environment. AEU Int. J. Electron. Commun. 2018, 93, 268–276. [Google Scholar] [CrossRef]
- Chen, R.; Wang, Y. Efficient detection of chirp signals based on the fourth-order original moment of fractional spectrum. Circ. Syst. Signal Process. 2014, 33, 1585–1596. [Google Scholar] [CrossRef]
- Kang, X.; Tao, R.; Zhang, F. Multiple-parameter discrete fractional transform and its applications. IEEE Trans. Signal Process. 2016, 64, 3402–3417. [Google Scholar] [CrossRef]
- Zhang, F.; Tao, R. Power spectral estimation and its application in fractional Fourier domain. Acta Electron. Sin. 2008, 36, 1723–1727. [Google Scholar]
- Brodersen, K.H.; Daunizeau, J.; Mathys, C.; Chumbley, J.R.; Buhmann, J.M.; Stephan, K.E. Variational Bayesian mixed-effects inference for classification studies. Neuroimage 2013, 76, 345–361. [Google Scholar] [CrossRef] [Green Version]
- Saini, N.; Sinha, A. Face and palmprint multimodal biometric systems using Gabor–Wigner transform as feature extraction. Pattern Anal. Appl. 2015, 18, 921–932. [Google Scholar] [CrossRef]
- Lang, H.; Zhang, J.; Zhang, X.; Meng, J. Ship classification in SAR Image by joint feature and classifier selection. IEEE Geosci. Remote Sens. Lett. 2016, 13, 212–216. [Google Scholar] [CrossRef]
- Tao, R.; Zhang, F.; Wang, Y. Fractional power spectrum. IEEE Trans. Signal Process. 2008, 56, 4199–4206. [Google Scholar]
- Yu, L.; Qiu, T.S.; Luan, S.Y. Robust joint estimation for time delay and Doppler frequency shift based on generalized sigmoid cyclic cross-ambiguity function. IET Radar Sonar Navig. 2017, 11, 721–728. [Google Scholar]
- Tao, R.; Deng, B.; Wang, Y. Research of fractional Fourier transform in signal processing. SCI China Ser. E 2006, 36, 113–136. [Google Scholar] [CrossRef]




© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Younan, N.H.; Shi, X. Joint Estimation of Doppler Stretch and Time Delay of Wideband Echoes for LFM Pulse Radar Based on Sigmoid-FRFT Transform under the Impulsive Noise Environment. Electronics 2019, 8, 121. https://doi.org/10.3390/electronics8020121
Li L, Younan NH, Shi X. Joint Estimation of Doppler Stretch and Time Delay of Wideband Echoes for LFM Pulse Radar Based on Sigmoid-FRFT Transform under the Impulsive Noise Environment. Electronics. 2019; 8(2):121. https://doi.org/10.3390/electronics8020121
Chicago/Turabian StyleLi, Li, Nicolas H. Younan, and Xiaofei Shi. 2019. "Joint Estimation of Doppler Stretch and Time Delay of Wideband Echoes for LFM Pulse Radar Based on Sigmoid-FRFT Transform under the Impulsive Noise Environment" Electronics 8, no. 2: 121. https://doi.org/10.3390/electronics8020121
APA StyleLi, L., Younan, N. H., & Shi, X. (2019). Joint Estimation of Doppler Stretch and Time Delay of Wideband Echoes for LFM Pulse Radar Based on Sigmoid-FRFT Transform under the Impulsive Noise Environment. Electronics, 8(2), 121. https://doi.org/10.3390/electronics8020121





