Using Approximate Computing and Selective Hardening for the Reduction of Overheads in the Design of Radiation-Induced Fault-Tolerant Systems

Abstract

Fault mitigation techniques based on pure software, known as software-implemented hardware fault tolerance (SIHFT), are very attractive for use in COTS (commercial off-the-shelf) microprocessors because they do not require physical modification of the system. However, these techniques cause software overheads that may affect the efficiency and costs of the overall system. This paper presents a design method of radiation-induced fault-tolerant microprocessor-based systems with lower execution time overheads. For this purpose, approximate computing and selective fault mitigation software-based techniques are used; thus it can be used in COTS devices. The proposal is validated through a case study for the TI MSP430 microcontroller. Results show that the designer can choose among a wide spectrum of design configurations, exploring different trade-offs between reliability, performance, and accuracy of results.

1. Introduction

The susceptibility of modern systems to radiation effects has been increasing mainly due to technological scaling [1]. Therefore, mission critical systems need to be protected against this kind of fault. while these faults may be transient (also known as soft errors) and not only permanent, they might affect the behavior of the system, causing malfunctions or crashes in modern electronic systems [2,3].

In order to address this problem, researchers have proposed fault tolerance techniques that range from changes to the materials and manufacturing processes of the chip, to several alternatives at the design level, including mitigation approaches based on hardware, software, or both, i.e., hybrid methods [4,5]. In particular, in microprocessor-based systems, since the fault mitigation techniques based on pure software, also known as software-implemented hardware fault tolerance (SIHFT) [6], do not require physical modification of the components of the system; they are attractive for use in COTS (commercial off-the-shelf) devices. However, many of the SIHFT techniques are based on software redundancy, so they can cause significant overheads (mainly execution time overheads), which can make these mitigation techniques inappropriate in many cases.

To reduce these overheads, researchers have proposed mitigation schemes based on selective or partial redundancy [7,8]. These proposals are based on protecting only essential parts of the system, so fault coverage is also sacrificed. In addition, recent works have proposed to use the approximate computing (AC) paradigm to reduce the overheads in the design of fault tolerant systems [9,10].

The AC paradigm seeks to improve performance and energy efficiency by taking advantage of the flexibility of some applications to tolerate inaccurate results [11]. The works that use AC in the design of fault tolerant systems achieve low overheads at the expense of accuracy in the results. While these works have shown a good trade-off between fault coverage, overhead, and the accuracy of results, most of them are based on AC hardware techniques, so they cannot be applied to COTS devices.

In this paper, we propose using software-based AC techniques along with SIHFT strategies to reduce overheads associated with the design of fault-tolerant systems based on COTS processors. Our proposal is based on applying the full implementation of SIHFT techniques, as well as selective protection techniques, to increase the design space. Since this proposal is completely based on software, it can be applied in COTS processors. The validation of the presented method was carried out through a case study using the Texas Instruments MSP430 microcontroller and four test programs. The results are evaluated in terms of overhead, percentage of error in the results, and coverage of faults. The last is done with fault injection campaigns through fault simulation, which are based on incremental tests to determine the number of injections to be performed.

The remainder of this paper is organized as follows. Section 2 presents the background and the related works. Section 3 describes the proposed design method. Section 4 presents a case study used to validate the proposal. The obtained results are shown and discussed in Section 5. Finally, Section 6 presents conclusions and future work.

2. Background and Related Works

2.1. Radiation Effects and Soft Errors

The effects of radiation on semiconductors can be classified into cumulative effects and single event effects (SEEs). The first ones, as their name implies, are due to the prolonged exposure of materials to radiation, and can usually cause changes in the electrical properties of the materials of electronic components [3]. Moreover, SEEs originate from the impact of high-energy particles on semiconductor materials, generating deposition and transportation of charges. The effects of SEEs can be permanent or transient. The latter are known as ‘soft errors’ [2]. If the impact of a high energy particle causes the generation of an electron-hole pair, a bit flip may occur. When the bit flip occurs in a storage element, such as a memory cell or a flip-flop, the effect is known as single event upset (SEU). When the change of the bit occurs in a combinational circuit, the effect is called single event transient—SET [3].

2.2. Software-Based Fault Tolerance

Hardware-based hardening techniques, although effective, are not always suitable mainly due to their high costs and because they require physical modifications to the components of the system. In the case of COTS components, such as commercial microprocessors and microcontrollers, hardening techniques based on software modifications are very attractive. They are also known as software-implemented hardware fault tolerance (SIHFT) techniques [6].

These techniques can be used to protect the control flow [12,13] or the data flow [7,14,15] of a microprocessor. The SIHFT techniques are based on software redundancy at different levels. Each level of granularity implies a level of protection, but it also has associated overheads.

For instance, a representative example of these techniques is SWIFT-R [16], which uses triple modular redundancy (TMR) at the instruction level of the software for the detection and correction of faults. It is based on the creation of three copies of the data to be protected, and then, through majority voters, it is able to detect and correct faults.

2.3. Approximate Computing (AC)

Several applications can accept results with some degree of inaccuracy. This feature can be used, through the approximate computing paradigm, to improve the efficiency of a system [11]. The improvements can be made in the performance of the system, when executing a task in a shorter time; in energy, by reducing the power consumption that is normally required for a given task; and in area, when the size of the chips is reduced due to the use of approximated logic circuits or to an increase in the density of semiconductor memories [17].

Approximate computing (AC) can be achieved by means of different techniques at the hardware and software levels [18]. At the hardware level [19,20,21], inaccurate but more efficient components can be used. Additionally, software-based AC techniques [22,23] prevent physical modification of the system to obtain approximated results. At the software level, the aim is to increase efficiency by reducing calculations or access to memory. The most important AC techniques at the software level include:

• Bit width reduction: This technique is based on precision reduction (number of bits that would normally be used) in floating-point numbers. In this way, energy efficiency and performance can be improved by sacrificing accuracy in the results [24]. On the other hand, when using the highest precision available in a microprocessor, code execution could take more time, so energy consumption would increase. On the other hand, if the representation of the data to put into operation is done using a smaller number of bits, it could have a lower energy consumption by reducing the accuracy in the result.
• Float point to fixed point conversion: Following the same principle of the prior technique, a floating-point variable can be replaced by a fixed-point variable [25]. The computation of real data type operations using a fixed-point number representation could be executed faster than operations using a floating point representation. For instance, this technique could be used for the computation of arithmetical operations in systems that lack a floating point unit (FPU), such as small microcontrollers.
• Code perforation: This technique identifies sections of code that can be discarded, without greatly affecting the results, to reduce computational costs. An example is to reduce the number of iterations in a loop, i.e., loop perforation [26,27]. This is a technique that transforms a loop to execute a subset of iterations of the original loop. By executing fewer iterations, the perforated loop will have a shorter execution time. Nevertheless, reducing iterations in a loop changes the result obtained with the original loop. Sometimes that difference may not be significant, but in other cases, the percentage of error between the results can be considerable, so the designer must establish a trade-off between accuracy of results and execution time.
• Synchronization elision: In multi-core systems, one of the most time-consuming tasks is synchronization. This technique implies a relaxing synchronization in parallel applications to reduce the associated costs [28]. Traditional relaxing synchronization techniques are based on the identification of scenarios where synchronization is not necessary. In contrast, this new technique takes advantage of the possibility of reducing the accuracy in the result without having a great impact on the behavior of the application. In this way, the synchronization is relaxed to improve performance at the expense of inexact results.

It should be noted that the applicability of the AC techniques mentioned above depends strongly on the type of application, that is, on the nature of the algorithm to be approximated. Firstly, each technique fits to particular conditions of the applications; for example, in programs lacking iterative loops, it would not be valid to implement loop perforation. The float-point to fixed-point conversion could be a suitable alternative instead. As mentioned earlier, AC techniques are worthy only in applications that have the flexibility to tolerate inaccuracy in the results. Applications classified as RMS (recognition, mining and synthesis) have been characterized by tolerating inaccurate results. These applications include several fields, such as: Digital signal processing, machine learning, and computer vision, among others. More recently, the scope of the AC paradigm has also been extended to the design of fault-tolerant systems [9,29,30].

2.4. Fault Tolerance with Approximate Computing Techniques

Thanks to the opportunity that AC provides to improve performance and energy efficiency, different researchers have used AC techniques to reduce overheads associated with redundancy in fault mitigation schemes [18]. These works have shown good results by compensating the costs of fault tolerance techniques with the speed-up obtained through AC. However, most of the works presented are at the circuit level [10,31,32,33,34] or require special architecture [9,29,35,36], so hardware modifications are still necessary. This means that those works are not suitable for COTS processors.

More recently, fault tolerance proposals have been reported using AC techniques at the software level. In [30], a proposal is presented to reduce overheads in NMR (N-modular redundancy) schemes. The method is based on the use of exact and approximate versions of tasks that are executed in different cores. In [37,38], the authors analyze the intrinsic fault tolerance that characterizes some algorithms of an iterative nature, and how the approximation affects their fault tolerance. Through experiments based on pulsed laser and fault emulation tests, it was demonstrated that the capability to tolerate errors depends on the algorithm, the number of iterations (approximation level) and the region where the faults occur.

In [39], the authors propose a technique to detect errors at the software level, with lower overheads. The technique is based on the duplication with comparison (DWC) technique, which consists in duplicating a software task and comparing the generated data to detect errors. To reduce the overheads associated with traditional DWC, the tasks to be duplicated are approximated using software AC techniques.

In addition, as part of our previous work [40], we recently explored the combination of SIHFT techniques (fully implemented) and AC approaches to reduce overheads in fault tolerant COTS systems. The research showed that it is possible to reduce, and in some cases eliminate, the overheads associated with redundancy by applying AC techniques to the programs before hardening them. The difference with the current work is mainly based on the inclusion of selective hardening techniques, which broaden the design space, unexplored in previous works.

3. Proposed Method

Similarly to other approaches, we propose to use software-only fault mitigation techniques in order to design a fault-tolerant embedded systems suitable for COTS devices. However, as the main drawback of SIHFT methods is the non-negligible overheads in terms of code size and execution time, we also propose a twofold strategy to reduce this impact. The objectives are first to reduce the overheads by means of selective hardening based on software, and second to compensate the protection overheads through the speed-ups achieved using approximate computing techniques based on software.

Therefore, the workflow of the proposed approach is composed of three main stages: Approximation, selective hardening, and validation. This workflow can be seen in Figure 1. We propose to perform an approximation of the program before it is hardened. In this way, it is possible to reduce the execution time overheads that result from applying the selective fault mitigation strategies at the software level.

Figure 1. Proposed workflow for the reduction of overheads in the design of fault-tolerant systems by using approximate computing and selective hardening techniques.

It is important to clarify that, in the proposed approach, the approximation stage is isolated to the hardening stage. However, the speed-ups reached in the first stage should compensate for the execution time overheads of the hardening stage.

3.1. Approximation stage

The first stage is responsible for receiving the source code of the program (in C/C++ language) as an input, and performing its transformation according to the more suitable relaxation for the application. The choice of the AC technique is based on the characteristics of the program that will be approximated, as well as on the device to be used. For instance, in programs with large loops, a suitable AC technique would be ‘loop perforation’. This technique involves reducing the number of iterations in a loop. Therefore, the approximation of the program reduces the execution time, but at the same time decreases the accuracy of the results. The designer must analyze the type of routine that will be approximated, and, according to its nature, choose an appropriate approximation technique.

At this point, it is necessary to quantify the gains of the relaxation given by the approximation techniques; for example, the speed-up in terms of performance of the program. In addition, to ensure good enough results, a quality metric must be established. The quality metric depends on each test program. Some examples of quality metrics that can be used are distortion [26], mean relative error and mean pixel difference [41].

This stage (approximation) is carried out at the source code level, and results in the generation of n approximate source code versions. Each of the approximate versions of the original program must comply with a predefined quality metric, i.e., the resulting error must not exceed a certain threshold.

3.2. Selective Hardening Stage

After obtaining the n approximate versions of the original program, they are hardened to protect the data flow, employing software-based fault mitigation techniques. As most SIHFT techniques are based on low-level (assembly code) instruction transformation rules and operations within the microprocessor register file, the hardening stage must be carried out using the assembly code of the several approximate versions of the program. This permits to get fine-grained control of the resources of the microprocessor accessible from the ISA (instruction set architecture).

For this reason, the approximate versions generated in the previous stage must be compiled to obtain their assembly code. After that, each of the n approximate versions is hardened, obtaining m hardened and approximate versions. The number of m versions depends on the number of SIHFT techniques that have been evaluated and the selective number of protected versions that can be generated by each one of these SIHFT techniques. The total number of k versions generated at this stage is given by $k=n\ast m$.

At this stage, it is very important to analyze the overheads associated with the hardening. Notice, that in many cases they might have been compensated by the speed-up of the prior approximation stage. Therefore, we should explore jointly the trade-offs between execution time overheads from the hardening, and accuracy in the results and speed-ups from the approximation stage.

Then, the final versions of the program are assembled to generate k executable files and pass them to the next stage: Validation.

3.3. Validation Stage

The last stage consists in evaluating the k approximate and hardened programs obtained in the previous stages. Validation is done by comparing each version with the original program in terms of fault coverage, the percentage of error in the results and the execution time of overheads. This step is performed by means of fault injection tools to analyze the fault coverage, and simulators/emulators to determine the execution times and the percentage of error in the results.

The effectiveness of the hardening step is validated by fault injection campaigns. The fault model is the bit-flip model, in which only a single bit is affected during each program execution. This model is useful to simulate the effects of a single event upset (SEU). Injected faults are classified according to their effect in the system as follows [42]:

• SDCs (silent data corruption): When the program completes its execution with erroneous output results.
• unACEs (unnecessary for architecturally correct execution): When the program obtains the expected results.
• Hangs: For abnormal terminations of the program or infinite loops.

Target bits of the system that, when affected by a fault, cause faults classified as SDC and ’hangs’ are considered together as ACE, i.e., necessary for the architecturally correct execution of the system.

To estimate reliability improvements, we propose to use the mean work to failure (MWTF) metric [43]. The MWTF takes into account the trade-off between performance and reliability, and can be calculated as follows:

$$MWTF=\frac{amountofworkcompleted}{numberoferrorsencountered}$$

(1)

$$MWTF=\frac{1}{rawerrorrate·AVF·executiontime}$$

(2)

where the AVF (architectural vulnerability factor) is the probability that a fault becomes an error. It is calculated as follow:

$$AVF=\frac{numberofACEbits}{totalnumberofbits}$$

(3)

4. Case Study

4.1. Experimental Setup

As previously mentioned, the Texas Instruments MSP430 microcontroller was used to validate the effectiveness of the proposal presented. This 16-bit microcontroller with Von Neumann architecture was chosen primarily for its extended use in low-power embedded systems and mission-critical systems. Moreover, thanks to its low energy consumption, it has been widely used in space applications, such as picosatellites, where the probabilities of radiation-induced faults are higher [44,45,46]. This device has a microprocessor register file comprised of 16 registers in total: The first four registers are special purpose registers, and the last 12 registers are general purpose registers.

Instead of using a well-known benchmark set (such as MiBench, available at: http://vhosts.eecs.umich.edu/mibench/), we used four representative concept tests with programs that could be implemented in the microcontroller. This decision was made due to the limitations in terms of microcontroller resources. The first two test programs are implementations of iterative algorithms to calculate the Euler number (Euler) and the natural logarithm of 2 (ln2), respectively. The algorithms were restricted to working only with integer data. The selection of this pair of algorithms is because they are based on convergent series. Its iterative nature allows us to evaluate the behavior of this type of algorithm against approximation techniques such as loop perforation. In addition, an implementation of the Sobel image filter and the Emboss image filter were used to validate the applicability of the proposal. These algorithms are widely used in the field of image processing, within edge detection algorithms for images. They create images highlighting the edges of a given image. In this case, implementations these algorithms were made in the microcontroller. To do so, we worked with small images of 55 × 55 pixels. The resulting (output) and the original image (input), were stored in the RAM memory of the microcontroller.

When evidencing the iterative nature of the algorithms used, it was decided to use loop perforation as an AC technique at the approximation stage. The reduction of the number of iterations of the ‘for’ loops of each algorithm was done by hand. In the case of the first two programs (ln2 and Euler), since they are based on convergent series, the upper limits of the conditional expressions in the ‘for’ statements were reduced, as shown in the code fragments presented in Figure 2.

Figure 2. Code fragments for the loop perforation of convergent series: ln2 and Euler. On the left the original code, on the right the approximated code, where ITER_APROX < ITER_ORIG.

The code fragment on the left represents the original loop. The upper limit of the conditional expression in the ‘for’ statement is represented by the $ITER\_ORIG$ variable. This value corresponds to the maximum number of iterations. In the case where ln2 is 1000 and in the case where Euler is 8, approximated versions are obtained from the original code by halving the maximum number of iterations (i.e., $ITER\_APPROX$ variable in the code on the right) for each version.

The cases of the filter programs (Sobel and Emboss) are somewhat different. Since they are based on a two-dimensional convolution, these algorithms do not have large iterative loops. Instead, the programs are based on nested cycles. Therefore, the perforation was done by increasing the step of the iteration variable, as observed in the code fragments shown in Figure 3. Again, the code on the right represents the perforated loop, and the one on the left represents the original one.

Figure 3. Code fragments for the loop perforation in the image filters: Sobel and Emboss. On the left the original code, on the right the approximate code. The loop step is different.

In this way, the different approximate versions were obtained for each test program. To determine the percentage of error in the result and the speed-up in execution time, an instruction set simulator (ISS) was used. Since this technique is applied in the high-level source code (in C language), it can be extended to other architectures.

In the next stage, the SHE (software hardening environment) [47] tool was used to automate the hardening process. SHE operates at the registry level, implementing S-SWIFT-R [7], which is a selective variation of SWIFT-R [16]. With this tool it is possible to implement complete or selective hardening, allowing the designer to choose the register or registers to protect. Since the four special-purpose registers of the MSP430 file register are not accessible from the ISA (instruction set architecture), only the general-purpose registers were protected with this technique.

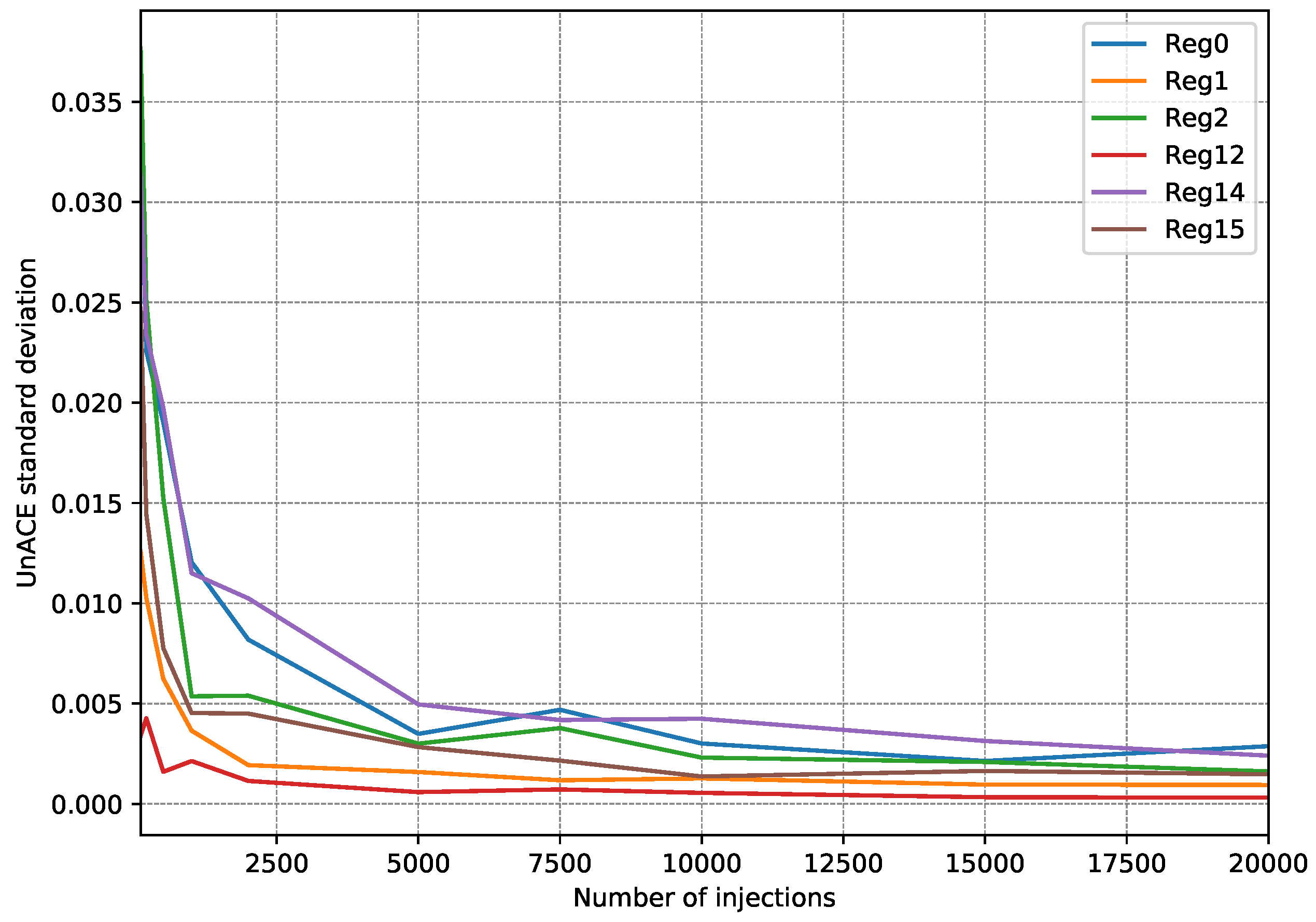
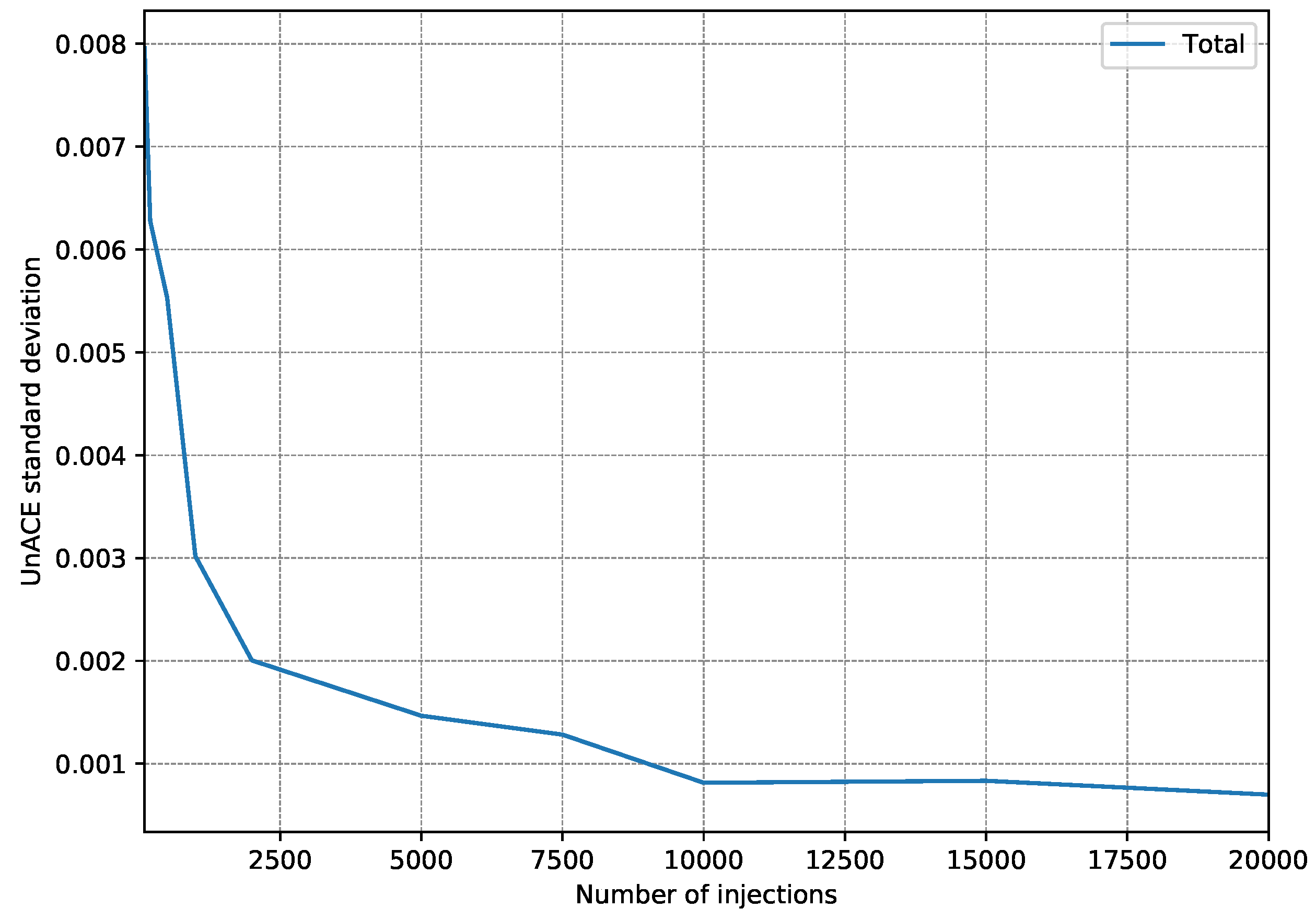
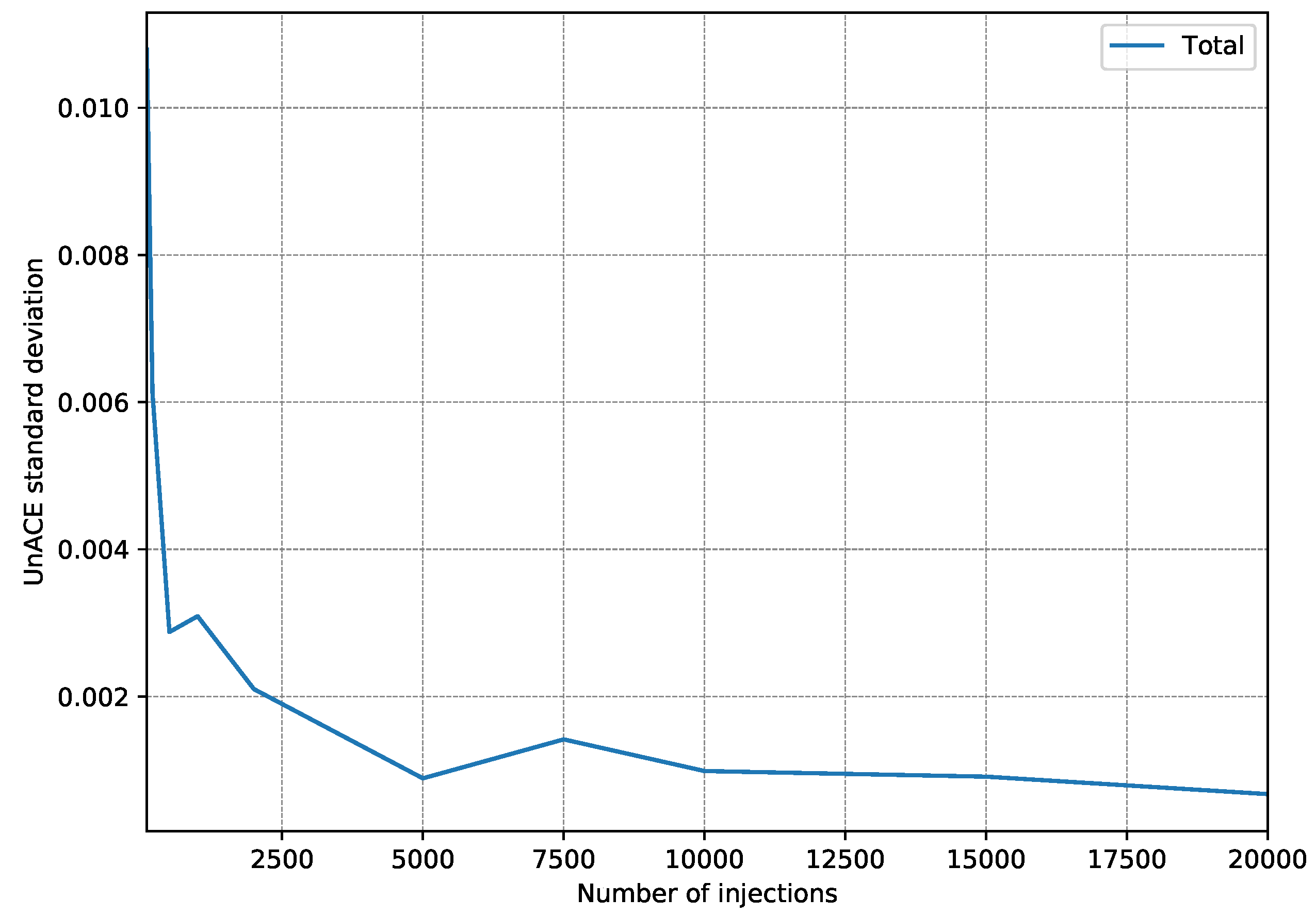
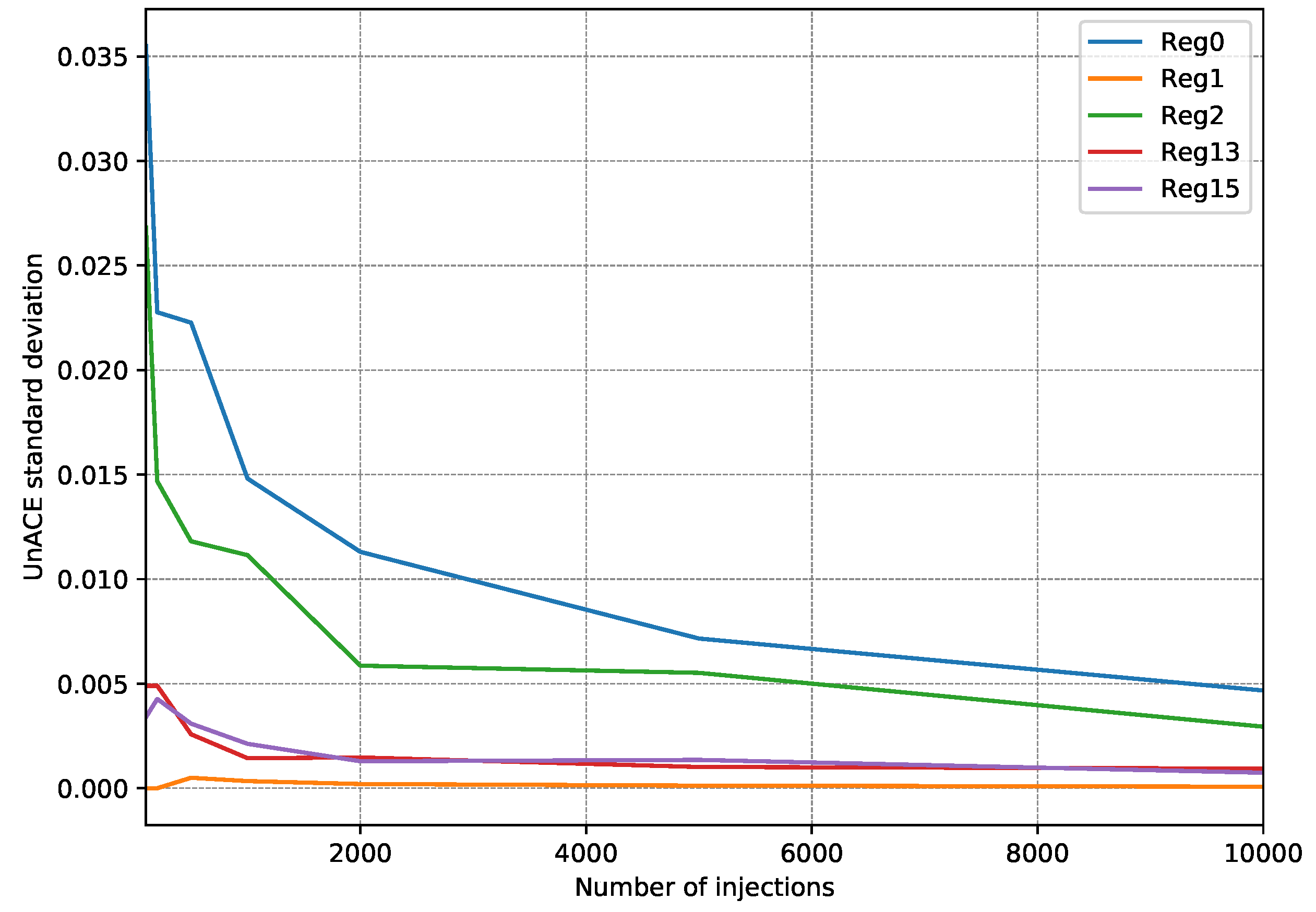
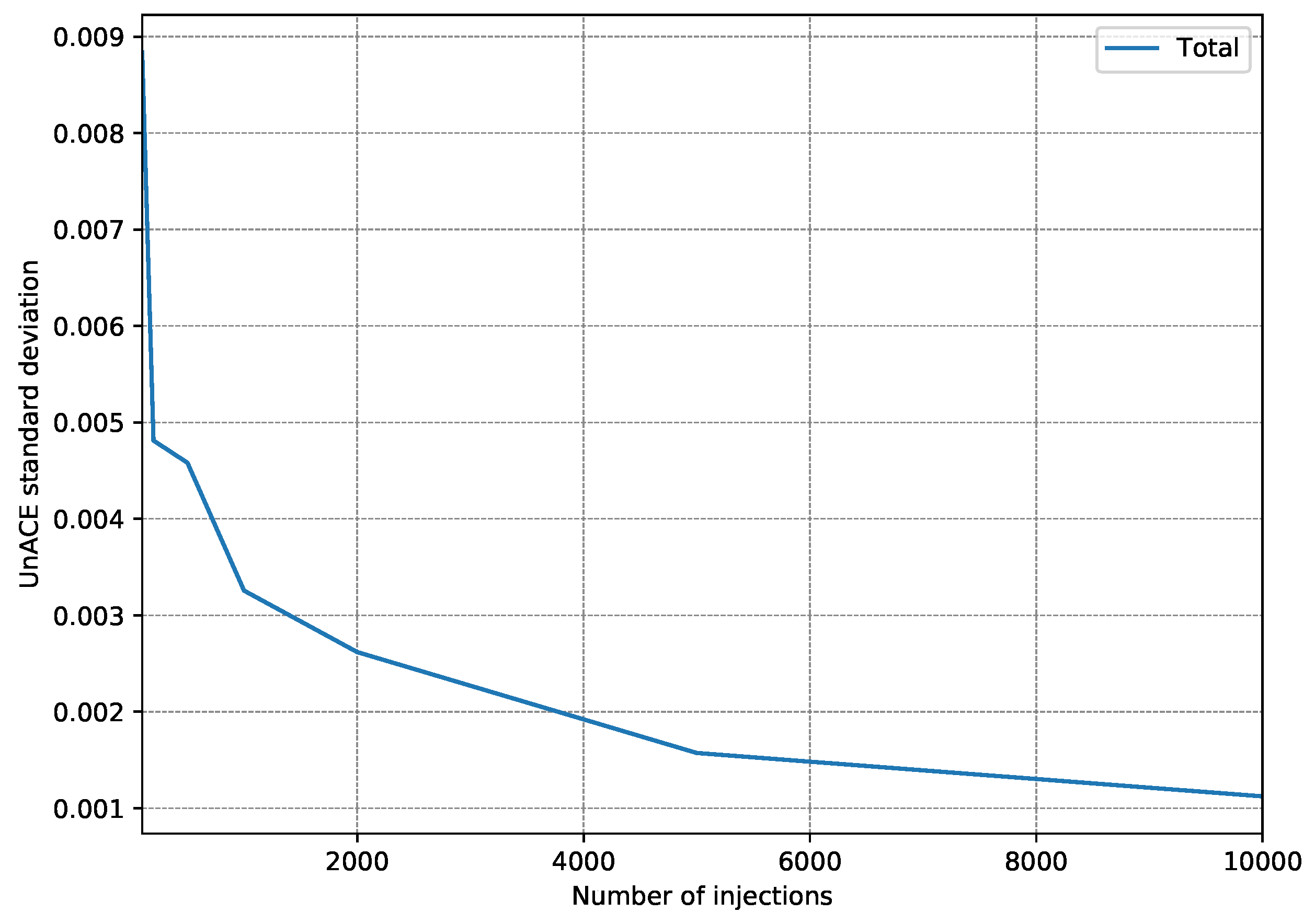
4.2. Fault Injection Campaigns

To validate the efficiency of the hardening stage, fault injection tests were carried out in the hardened and non-hardened programs in different approximation versions. The injections were made through fault simulation using the MiFIT tool [48].

Before carrying out the fault injection campaigns, it is necessary to estimate the number of faults to be injected in each register. A low number of injections would not give statistically significant results. On the other hand, the higher the number of faults to inject, the longer the simulation time. Therefore, it is necessary to find a trade-off between the minimum number of faults to be injected and the significance of the results. To solve this problem, an incremental injection campaign was carried out. For each one of the test programs, several campaigns were carried out increasing the number of injections every time, to analyze the differences in the results. The procedure for incremental testing is explained below:

• First, 15 fault injection campaigns were carried out, injecting 100 faults per register (a single fault per execution).
• After each injection campaign, the faults classified as unACE are totalized. Only registers used in the test program are taken into account since injection into a register that is not used would always be classified as unACE.
• With the 15 campaign results, the standard deviation is calculated to estimate how scattered they are.
• The whole procedure is repeated, each time increasing the number of injections per register to be performed.

Incremental tests were performed for the Euler program, the ln2 program and the Sobel filter program. One of the two filters was chosen since the algorithm for both is essentially the same, and therefore the registers used in each one are also the same. The hardened versions of the precise programs were used to perform the incremental tests since these versions have the longest execution time (highest number of instructions).

The results of the incremental tests can be seen in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9. The x-axis of each figure corresponds to the number of faults injected per register. The y-axis shows the standard deviation of the result for each case.

Figure 4. Standard deviation of unnecessary for architecturally correct execution (unACE) results for Euler program (all registers).

Figure 5. Standard deviation of UnACE results for Euler program (total).

Figure 6. Standard deviation of unACE results for the ln2 program (all registers).

Figure 7. Standard deviation of unACE results for the ln2 program (total).

Figure 8. Standard deviation of UnACE results for the Sobel filter (all registers).

Figure 9. Standard deviation of unACE results for the Sobel filter (total).

Figure 4 and Figure 5 correspond to the standard deviation of the results classified as unACE for the Euler program. Figure 4 shows the standard deviation for each register affected by the injections. It can be seen that the standard deviation decreases as the number of injections increases. The same behavior is observed for the total unACE classification in Figure 5.

The standard deviation for the data classified as unACE of the ln2 program can be seen in Figure 6 and Figure 7. As in the case of the Euler program, it can be seen that by increasing the number of injections per register, the results obtained in the fault injection campaigns are less dispersed. It should be noted that according to the incremental tests carried out, it is observed that the dispersion in the results for the ln2 program increases slightly from 5000 to 7500 injections per register, but then decays again after 7500 faults (Figure 7).

Finally, Figure 8 and Figure 9 show the results of the incremental tests for the Sobel filter. Again, the reduction in the dispersion of the results is evidenced by increasing the number of injections per register.

Analyzing the results of the incremental tests, as can be seen, the standard deviation tends to decrease as the number of injections increases. Moreover, the reduction in the standard deviation is less drastic with each increase in injected faults. With more than 10,000 injections per register, the standard deviation tends to stabilize. The value for this number of injections is smaller than $1\%$ for all cases. For this reason, it was determined to carry out fault injection campaigns with 10,000 injections per register, for a total of 160,000 injections for every version of the programs to be further evaluated. This value is consistent with the model presented in [49], in which the number of injections to be carried out in a fault injection campaign can be determined according to an error margin and a level of confidence. For our case, 10,000 injections per register, there is a margin of error of $3.86\%$ with a confidence level of $99.8\%$, taking into account that the MSP430 is a microcontroller with 16 registers of 16 bits.

5. Results and Discussion

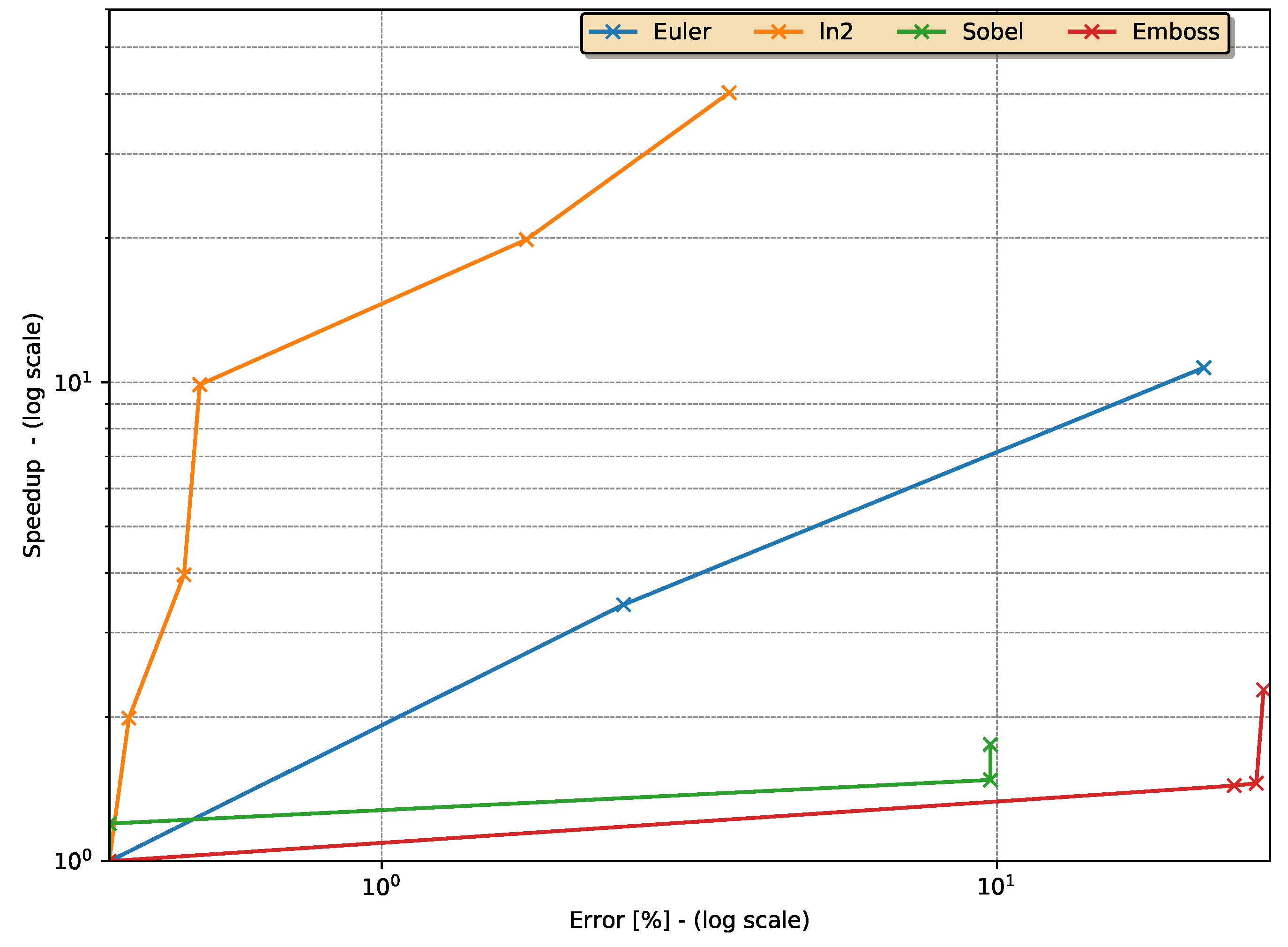
5.1. Approximation Speed-Up vs. Error Percentage

As a result of applying the loop perforation technique in the test programs, different approximate versions were obtained for each of them: 5 for the calculation of the natural logarithm of 2 (ln2), 2 for the calculation of the Euler number, and 3 versions for each one of the filters (Sobel and Emboss). With each level of approximation, the speed-up of the programs increases, as does the error in the result.

Figure 10 shows the error rate and speed-up of the approximate versions for each test program. The horizontal axis corresponds to the percentage of error and the vertical axis to the speed-up, both axes on a logarithmic scale. The speed-up is the division between the number of cycles of the original program over the number of cycles of the approximate version. It is a dimensionless measure. Each line represents a test program. The approximate versions of each program are represented with a marker (x). It can be seen that the program that has the best results on the approximation is ln2 since it has the highest speed-ups with a lower percentage of error.

Figure 10. Error vs. speed-up of approximated versions.

As can be seen in Figure 10, the results differ substantially between each test program. This is due to the specific characteristics of each algorithm used. While all algorithms have an iterative nature (which is why we used loop perforation as the AC technique), the loops of each program are not the same. For example, the algorithms that show the best results (ln2 and Euler) are based on convergent series. In these cases the final iterations of the programs do not modify the results considerably. In the case of ln2, the series converges more slowly than in the case of Euler, i.e., it needs more iterations. Moreover, the image filters (Sobel and Emboss) are implemented using more ‘for’ statements (nested loops), but with fewer iterations. While the algorithm of the two filters is essentially the same, the matrix of weights used for the Sobel filter contains some values with zeros, so discarding a few iterations would not affect the result in some cases.

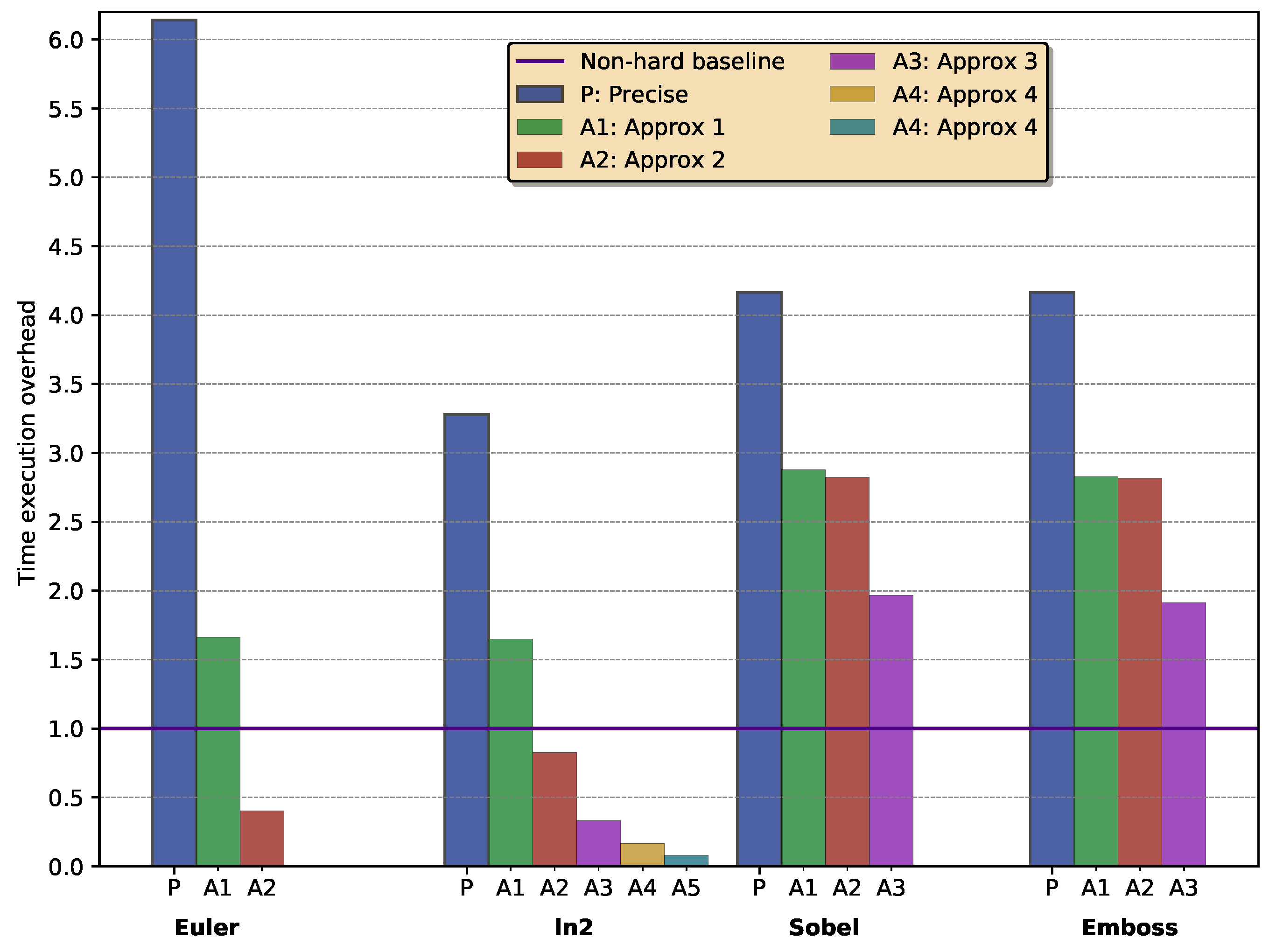
5.2. Execution Time Overheads

As a result of hardening, execution time overheads are generated, as shown in Figure 11. The horizontal axis presents all the hardened versions of each test program (P: Precise, and its approximations, e.g., A1, A2, etc.), whereas the vertical axis corresponds to the normalized execution time overhead. The time execution overhead is the relationship between the execution time of the hardened version and the original one. In this case, initially, the complete hardening of each version (SWIFT-R) was performed. That is, all registers used in each algorithm were protected.

Figure 11. Execution time overheads of the hardened (precise and approximate) versions of the programs using SWIFT-R.

The Figure 11 shows that the highest overheads correspond to the hardened precise versions of each program, as expected. The highest overhead corresponds to the precise version of the Euler program ($6.14\times$), which indicates that hardening this algorithm implies a high cost.

Moreover, it is observed that higher levels of approximation have lower overheads. For some approximate versions, the speed-up achieved in the approximate stage is so high that the overheads associated with hardening are less than $1\times$. This means that a hardened and optimized version of the original program is obtained. Such is the case of the second approximate version of the Euler logarithm (A2), with an overhead of less than $0.5\times$, and the versions A2 to A5 of the ln2 program, with overheads of less than $0.8\times$.

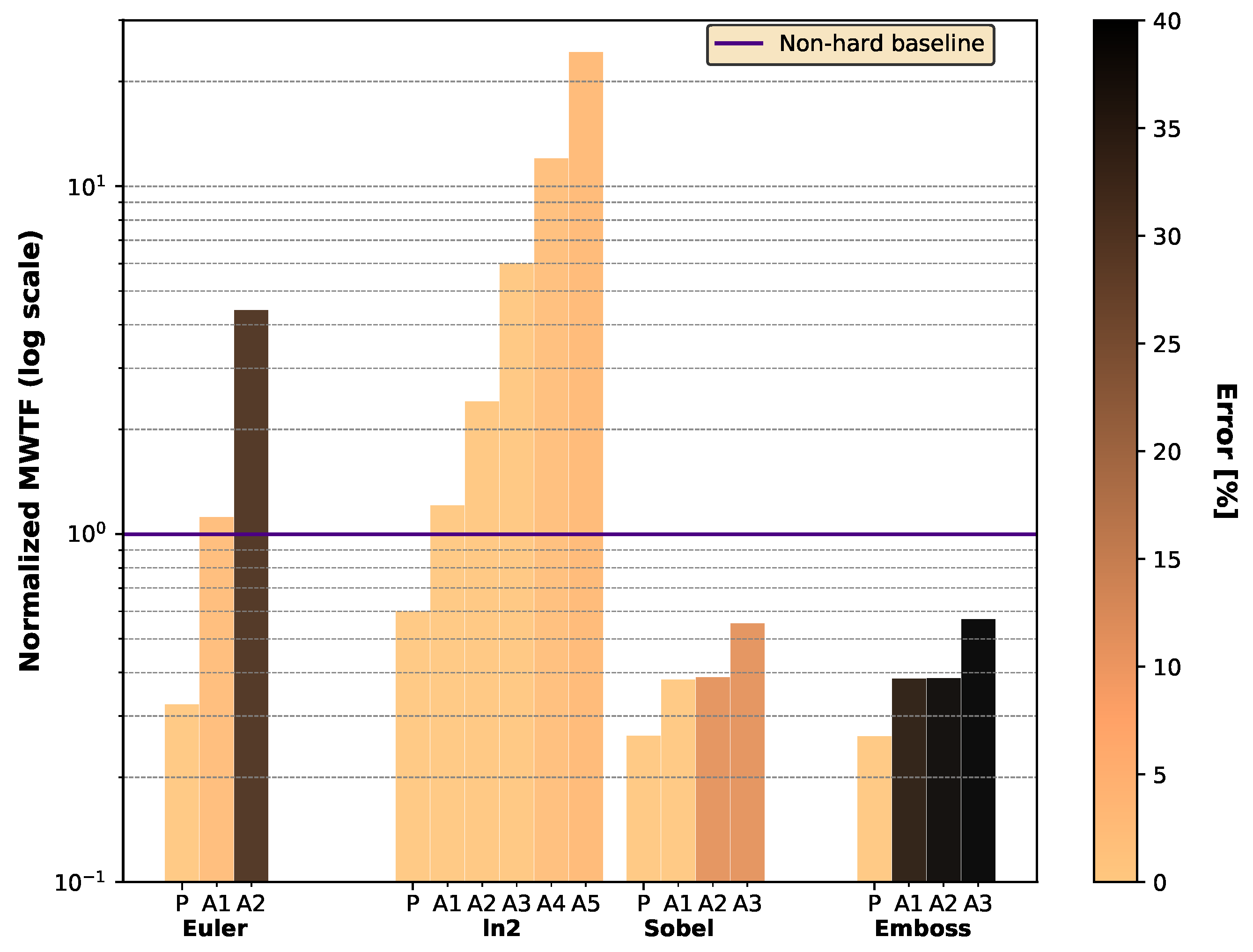
5.3. Reliability and Error Percentage

As mentioned in Section 3, the MWTF is a metric that represents a trade-off between the fault coverage achieved by the hardening and its execution time overhead. For this case, the normalized MWTF was determined for each version of the program as follows:

$$Norm.MWTF=\frac{ACEbitsnonhard}{ACEbitshardversion}·\frac{1}{Timeoverhead}$$

The normalized MWTF (in logarithmic scale) can be seen in the vertical axis of Figure 12. The different versions of the test programs are shown on the x-axis of the same figure. The percentage of error in the results of the different versions is also shown using colors. Darker tones represent higher percentages of error.

Figure 12. Normalized MWTF for the different versions of the programs and percentages of error in the results.

It should be noted that the accuracy in the results is dependent on each algorithm. For instance, the ln2 program has an error percentage below $3\%$ for the highest approximation level, while in the case of the Emboss filter, the error percentages exceed $30\%$. This indicates that ln2 is an algorithm very susceptible to approximation (employing loop perforation), unlike the algorithms corresponding to the filters.

It can be seen that the MWTF increases with each level of approximation. This is because relaxed programs require a shorter execution time. This means that the approximated versions of the programs will be less time exposed to faults. So the probability of a fault occurring during a program execution will be lower. The highest MWTF ($24.37\times$) corresponds to the most approximated version of ln2 (A5), which is consistent with the low overhead obtained for this version.

However, it should be also noted that in some cases the MWTF was less than the non-hardened baseline ($1.0\times$), such as for the filters. This means that, although the hardening technique improves the fault coverage, the overheads are so high that they are not compensated with the speed-up reached in the approximation stage. Therefore, it can be affirmed that although these versions have higher fault coverage, their reliability is lower than the original program (without hardening). The same situation can be observed for all the hardened precise versions of the test programs (P columns).

According to the results observed in Figure 12, it can also be concluded that the program that best behaves with the proposed method is ln2. This affirmation is based on two main reasons: First, as mentioned above, ln2 is the algorithm most susceptible to approximation (the loss of precision in the results is very low); and second, this algorithm has the highest MWTF, greater than $1.0\times$ for all approximate versions. The first approximate version of ln2 has a normalized MWTF of $1.2\times$ with an error in the results of less than $1\%$. As mentioned earlier, the higher approximated version of this algorithm reaches a normalized MWTF greater than $24\times$ with an error percentage below $3\%$. In the case of the algorithm for the calculation of the Euler number, there are two approximate versions with normalized MWTFs of $1.2\times$ and $4.4\times$, and error percentages of $1.88\%$ and $26.41\%$, respectively.

Results show that, reducing the execution time overheads by means of approximations, it is possible to improve the reliability of a system. This is observed in the increase of the normalized MWTF for the approximate versions. On the other hand, although the approximation of the programs modifies the expected results, in some cases these changes could be negligible.

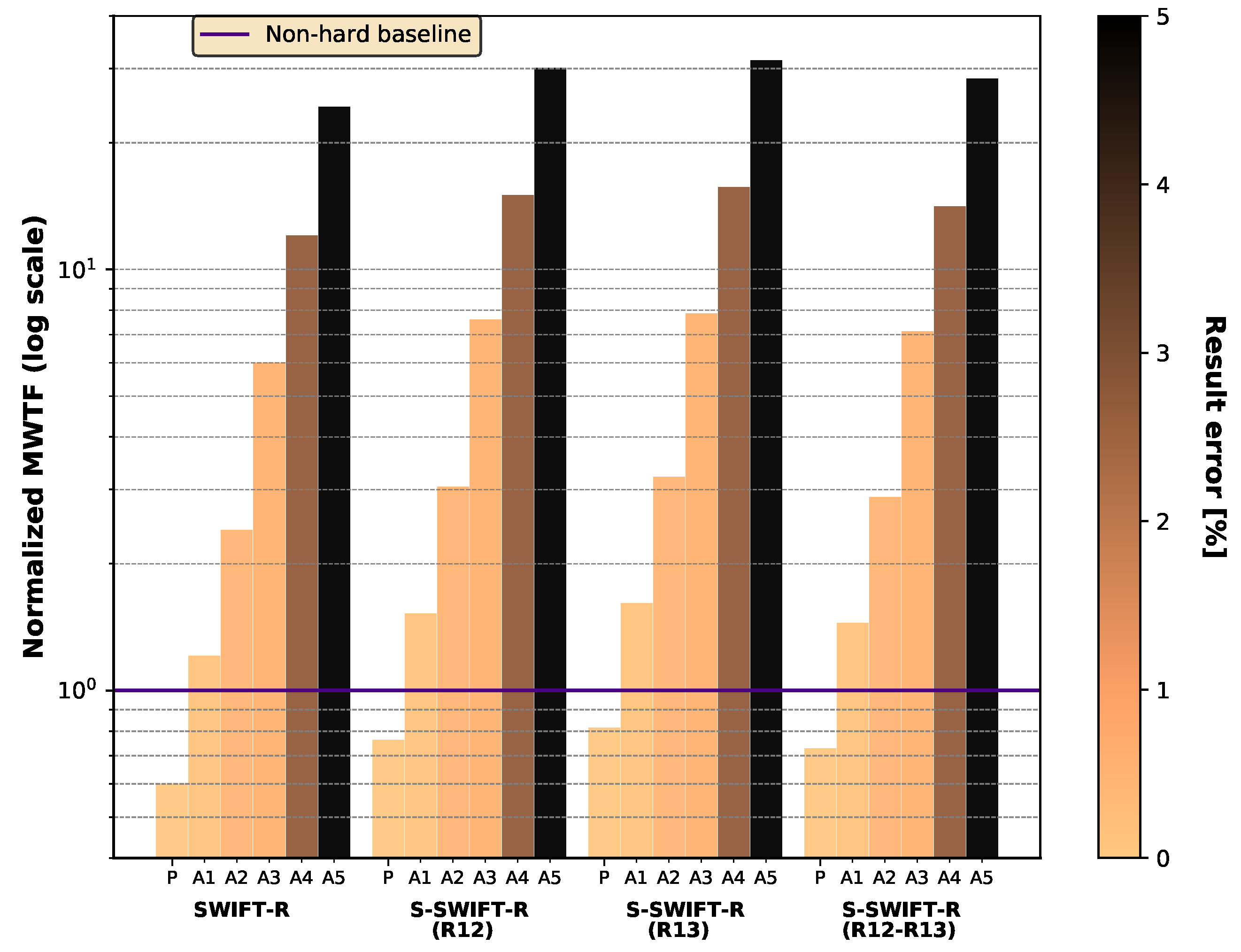
5.4. Selective Hardening

To explore new possibilities in the design space, S-SWIFT-R (selective hardening) was applied to the ln2 program. This test program was chosen over the others because it is the algorithm with more approximated versions. This means a wider design space to explore in detail jointly with selective hardening. Three additional versions of the program were obtained by hardening two of the registers that achieved the highest level of protection with SWIFT-R. The three new versions correspond to the protection of the R12 register, the protection of the R13 register and the protection of the two registers at the same time (R12 and R13).

The results of the tests carried out on the selective versions of the ln2 program are shown in Figure 13. The different versions can be seen using groups of bars. The first group on the left corresponds to the fully hardened version of the program. The others correspond to selective versions. As in the previous case, the percentage of error in the results is represented by color. Likewise, the y-axis represents the standardized MWTF in the logarithmic scale, and the different hardening versions can be seen on the x-axis.

Figure 13. Normalized mean work to failure (MWTF) metric for the ln2 program: Complete and selective hardening using S-SWIFT-R, jointly with the percentage of error in the results (color bar).

It can be seen that the highest MWTF corresponds to the selective version, where only the R13 register hardened. Therefore, it can be affirmed that reliability depends on the protected registers. In this case, although R13 is not the register most affected by faults, it is the one that best results in terms of reliability that can be delivered when protected. The results show that, by protecting only the R13 register, higher reliability is obtained than even by applying total hardening. The obtained MWTF by hardening the R13 register of the most approximated version is $31.47\times$, while with the full hardening the MWTF is $24.37\times$ for the same version. When only the R12 register is protected, a normalized MWTF of $30.2\times$ can be reached, while if R12 and R13 are jointly protected, a maximum normalized MWTF of $28.49\times$ is obtained.

With these results, we can observe that not necessarily protecting more registers in a microcontroller implies greater reliability. Sometimes the overheads generated by hardening several registers are so high that the fault coverage does not compensate for the additional exposure time that the hardened system will have.

Experiments show that it is possible to explore new possibilities in the design space by combining complete and selective hardening strategies with approximate computing techniques. This allows the designer to choose from a wide range of fault tolerance solutions, with a different trade-off between reliability, performance, and accuracy of results.

6. Conclusions and Future Work

A method to reduce overheads associated with redundancy in the design of radiation-induced fault-tolerant systems with SIHFT techniques was presented. The proposed method combines AC techniques at the software level with selective hardening strategies. This combination compensates for overheads derived from hardening techniques and increases the spectrum in the design space. The proposal was validated through a case study, using the TI MSP430 microcontroller and four programs with concept test. Results showed that, with the proposed method, the overheads associated with traditional SIHFT techniques were reduced while increasing the reliability of the system. It was also observed that the error in the result, as well as the reduction of overheads, depends on the program to be hardened. Through selective hardening tests, it was shown that in some cases protecting a single register is better, in terms of reliability, than performing a complete hardening.

As future work, it is intended to further validate the proposal through complementary case studies by applying it to other architectures (specifically ARM and RISC-V) and to use more complex test programs to implement selective and total hardening. It is also planned to validate the method through radiation tests. In addition, we plan to explore possible approximated hardening strategies that involve AC techniques combined with fault tolerance approaches in a non-isolated way to optimize results.