Area-Efficient Pipelined FFT Processor for Zero-Padded Signals

Abstract

This paper proposes an area-efficient fast Fourier transform (FFT) processor for zero-padded signals based on the radix-2${}^2$ and the radix-2${}^3$ single-path delay feedback pipeline architectures. The delay elements for aligning the data in the pipeline stage are one of the most complex units and that of stage 1 is the biggest. By exploiting the fact that the input data sequence is zero-padded and that the twiddle factor multiplication in stage 1 is trivial, the proposed FFT processor can dramatically reduce the required number of delay elements. Moreover, the 256-point FFT processors were designed using hardware description language (HDL) and were synthesized to gate-level circuits using a standard cell library for 65 nm CMOS process. The proposed architecture results in a logic gate count of 40,396, which can be efficient and suitable for zero-padded FFT processors.

1. Introduction

The fast Fourier transform (FFT) is a mathematical algorithm for reducing the computational complexity of the discrete Fourier transform (DFT) and is widely used for frequency analysis [1,2,3]. The zero-padded FFT offers increased frequency resolution by extending the length of the input data sequence in the time domain by padding with zeros at the tail of the discrete-time signal. Because of this, it has been widely used for wireless communications and radar systems that require high-frequency resolution [4,5,6,7,8,9].

The radix-2 and radix-4 algorithms are the most widely used for implementing FFT processors because of their simple architectures. For pipeline architectures, the radix-4 algorithm has a smaller number of non-trivial multiplications than the radix-2 algorithm [10]. However, the radix-4 algorithm complicates the control of butterfly architectures more than the radix-2 algorithm. Thus, radix-2${}^2$ and radix-2${}^3$ algorithms have been proposed to reduce the complexity of high-radix algorithms. The radix-2${}^2$ algorithm has the same number of non-trivial multiplications as the radix-4 algorithm but maintains the butterfly architecture of the radix-2 algorithm. Similarly, the radix-2${}^3$ algorithm has the same number of non-trivial multiplications as the radix-8 algorithm [11,12,13,14]. The pruned FFT algorithm can also be applied to the zero-padded signals to reduce the computational complexity and many studies have been conducted [15,16,17,18,19,20]. However, the pruned FFT processor based on the pipeline architecture requires an additional memory unit corresponding to FFT-length to re-arrange data sequence [20].

Single-path delay feedback (SDF) pipeline FFT architectures are commonly used because they have the smallest number of non-trivial multiplications compared with other pipeline architectures, such as single-path delay commutator (SDC) and multi-path delay commutator (MDC). However, as the number of FFT points increases, the SDF architecture requires significantly more circuit area because of the delay elements for data reordering [21,22,23,24,25,26].

In this paper, we propose an area-efficient FFT processor for zero-padded signals by taking advantage of the fact that the data sequence is zero-padded and that the twiddle factor (TF) operation in stage 1 is a trivial multiplication in the radix-2${}^2$ and radix-2${}^3$ algorithms. The rest of this paper is organized as follows. In Section 2, we review the zero-padded FFT. The hardware architecture of the proposed FFT processor is described in Section 3. In Section 4, we compare the proposed zero-padded FFT architecture with conventional architectures. Finally, Section 5 concludes the paper.

2. Zero-Padded FFT

The DFT for complex data sequence $x\left(n\right)$ of length $N$ is defined as

$$X\left(k\right)=\sum _{n=0}^{N-1}x\left(n\right)W_N^{nk},0\le k\le N-1,$$

(1)

where the twiddle factor is

$$W_N^{nk}=e^{-j\left(\frac{2\pi nk}{N}\right)}=cos\left(\frac{2\pi nk}{N}\right)-jsin\left(\frac{2\pi nk}{N}\right),$$

(2)

when analyzing the resolution of the DFT, there are two factors to consider. The first one is the spectral resolution, which refers to the algorithm’s capability to detect closely spaced spectral components. The second one is the frequency resolution, which is the definition of the distance between frequency bins. Whereas the spectral resolution can only be increased by increasing the time window of the signal, the frequency resolution is determined by the number of input data points in the sequence given to the DFT [27,28,29,30]. A longer data sequence is usually obtained by using the zero-padding method, which is described below.

Assume that a new data sequence $y\left(n\right)$ is created by zero-padding the original data sequence $x\left(n\right)$ of length $N$ to a length of $M$.

$$y\left(n\right)=\left\{\begin{array}{c}x\left(n\right),0\le n\le N-1\hfill \\ 0,N\le n\le M-1\hfill \end{array}\right..$$

(3)

The $M$ points of the DFT are calculated as

$$Y\left(k\right)=\sum _{n=0}^{M-1}y\left(n\right)W_M^{nk},0\le k\le M-1.$$

(4)

Based on the divide-and-conquer algorithm, indices $n$ and $k$ can be written as

$$n=\frac{M}{2}{n}_1+\frac{M}{4}{n}_2+n_3,$$

(5)

$$k=k_1+2k_2+4k_3,$$

(6)

where $0\le n_1\le 1$, $0\le k_1\le 1$, $0\le n_2\le 1$, $0\le k_2\le 1$, $0\le n_3\le \frac{M}{4}-1$ and $0\le k_3\le \frac{M}{4}-1$. Replacing Equations (5) and (6) in Equation (4), we obtain

$$\begin{array}{c}Y\left(k\right)=\sum _{n_3=0}^{\frac{M}{4}-1}\sum _{n_2=0}^1\sum _{n_1=0}^1\left(y\left(\frac{M}{2}{n}_1+\frac{M}{4}{n}_2+n_3\right)W_2^{n_1{k}_1}{W}_4^{n_2\left(k_1+2k_2\right)}{W}_M^{n_3\left(k_1+2k_2+4k_3\right)}\right)\\ =\sum _{n_3=0}^{\frac{M}{4}-1}\sum _{n_2=0}^1\left(B_{\frac{M}{2}}^{k_1}\left(\frac{M}{4}{n}_2+n_3\right)\times W_4^{n_2\left(k_1+2k_2\right)}{W}_M^{n_3\left(k_1+2k_2+4k_3\right)}\right).\end{array}$$

(7)

In Equation (7), the butterfly operation is given by

$$\begin{array}{c}{B}_{\frac{M}{2}}^{k_1}\left(\frac{M}{4}{n}_2+n_3\right)=\sum _{n_1=0}^{1}y\left(\frac{M}{2}{n}_1+\frac{M}{4}{n}_2+n_3\right)W_2^{n_1{k}_1}\\ =y\left(\frac{M}{4}{n}_2+n_3\right)+{(-1)}^{k_1}y\left(\frac{M}{2}+\frac{M}{4}{n}_2+n_3\right).\end{array}$$

(8)

Assuming that $M$ is 2$N$ in order to increase the frequency resolution twice, samples from $y\left(N\right)$ to $y(2N-1)$ are set to zero so that Equation (8) can be simplified as follows:

$$B_{\frac{M}{2}}^{k_1}\left(\frac{M}{4}{n}_2+n_3\right)=y\left(\frac{M}{4}{n}_2+n_3\right).$$

(9)

Therefore, Equation (7) can be summarized as follows

$$\begin{array}{c}Y\left(k_1+2k_2+4k_3\right)=\sum _{n_3=0}^{\frac{M}{4}-1}\sum _{n_2=0}^1\left({\left(-j\right)}^{n_2{k}_1}y\left(\frac{M}{4}{n}_2+n_3\right)W_2^{n_2{k}_2}{W}_M^{n_3\left(k_1+2k_2+4k_3\right)}\right)\hfill \\ =\sum _{n_3=0}^{\frac{M}{4}-1}H\left(k_1,k_2,n_3\right)W_M^{n_3\left(k_1+2k_2\right)}{W}_{M/4}^{n_3{k}_3},\end{array}$$

(10)

where the output of the stage 2 butterfly $H(k_1,k_2,n_3)$ is expressed as shown in Equation (11):

$$\begin{array}{c}H\left(k_1,k_2,n_3\right)=\sum _{n_2=0}^1{\left(-j\right)}^{n_2{k}_1}y\left(\frac{M}{4}{n}_2+n_3\right)W_2^{n_2{k}_2}\\ =y\left(n_3\right)+{\left(-1\right)}^{k_2}{\left(-j\right)}^{k_1}y\left(\frac{M}{4}+n_3\right).\end{array}$$

(11)

Alternatively, assuming that $M$ is 4$N$ in order to increase the frequency resolution four times, samples from $y\left(N\right)$ to $y(4N-1)$ are zero so that Equation (11) can be simplified as follows:

$$H(k_1,k_2,n_3)=y\left(n_3\right).$$

(12)

Therefore, Equation (10) can be summarized as follows:

$$Y\left(k_1+2k_2+4k_3\right)=\sum _{n_3=0}^{\frac{M}{4}-1}y\left(n_3\right)W_M^{n_3\left(k_1+2k_2\right)}{W}_{M/4}^{n_3{k}_3}.$$

(13)

Similarly, even if the frequency resolution is increased by more than four times, $y(M/4+n3)$ in Equation (11) becomes zero and the radix-2${}^2$ algorithm is derived as shown in Equation (13). When increasing the frequency resolution by more than four times using the radix-2${}^3$ algorithm, $M$ points of the DFT are derived as shown in Equation (14) in a way similar to the radix-2${}^2$ algorithm:

$$\begin{array}{c}Y\left(k_1+2k_2+4k_3+8k_4\right)=\sum _{n_4=0}^{\frac{M}{8}-1}\sum _{n_3=0}^1\left(y\left(\frac{M}{8}{n}_3+n_4\right)W_8^{n_3\left(k_1+2k_2\right)}{W}_2^{n_3{k}_3}{W}_M^{n_4\left(k_1+2k_2+4k_3\right)}{W}_{M/8}^{n_4{k}_4}\right)\end{array}$$

(14)

where $0\le n_1\le 1$, $0\le k_1\le 1$, $0\le n_2\le 1$, $0\le k_2\le 1$, $0\le n_3\le 1$, $0\le k_3\le 1$, $0\le n_4\le \frac{M}{8}-1$ and $0\le k_4\le \frac{M}{8}-1$.

3. Proposed Hardware Architecture

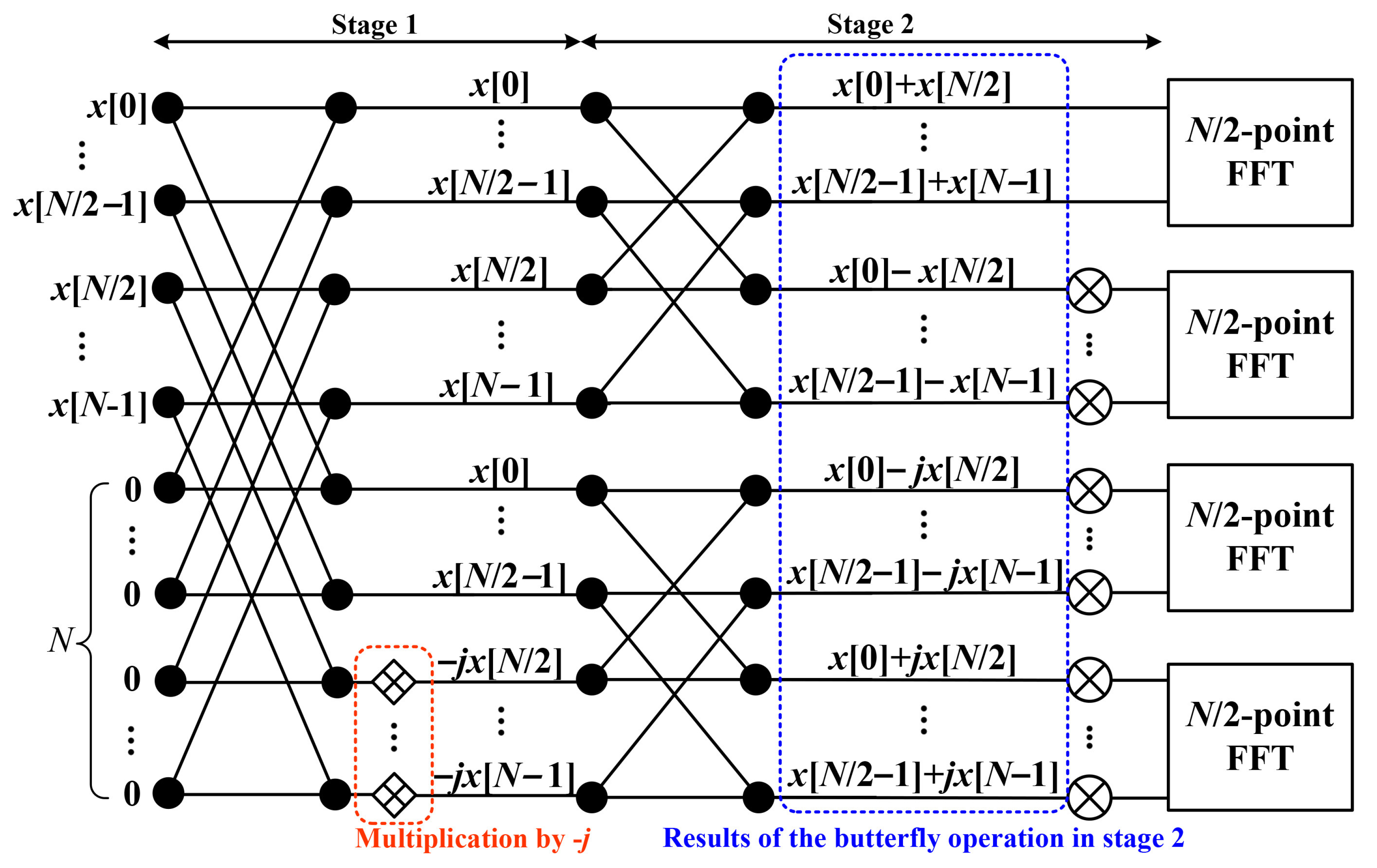
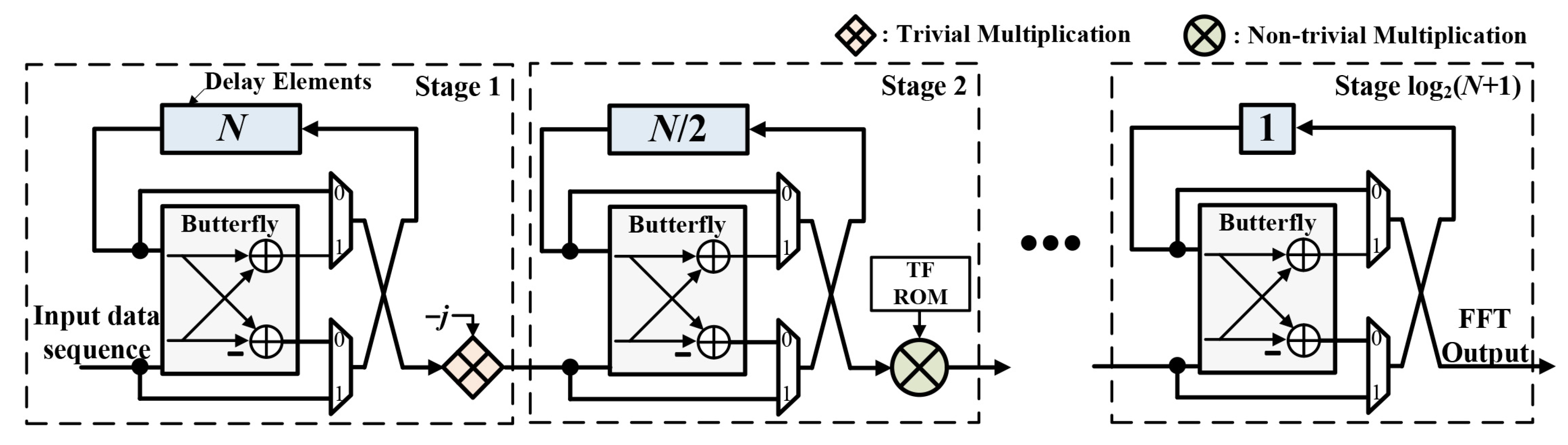
3.1. Double Frequency Resolution

In order to double the frequency resolution, the tail of input data sequence $x\left(n\right)$ of length $N$ is padded with $N$ zeros to double its length in the time domain. The FFT signal flow graph (SFG) of the radix-2${}^2$ algorithm for a zero-padded signal with double frequency resolution is shown in Figure 1. To implement the zero-padded FFT using the conventional radix-2${}^2$ SDF architecture, delay elements of length $N$ are required for data sequence reordering in stage 1 and the length of the delay elements required for each stage is reduced by half each time as shown in Figure 2. That is, in order to implement the FFT processor for a zero-padded signal of length 2$N$ using the conventional radix-2${}^2$ SDF architecture, delay elements with a total length of 2$N-1$ are required [31]. As a result, the number of delay elements notably increases with the FFT data points. To solve this problem, we propose the hardware architecture depicted in Figure 3 by using the feedback path of the SDF architecture and exploiting the trivial multiplication of stage 1.

The data flow of the proposed hardware architecture is shown in Figure 4. First, $x\left[0\right]$ to $x[N/2-1]$ go through the delay elements of stage 2 for the butterfly operation of stage 2. After $N$/2 cycles, $x[N/2]$ to $x[N-1]$ are entered into the butterfly unit of stage 2 and $x\left[0\right]$ to $x[N/2-1]$ are simultaneously outputted from the delay elements of stage 2. $x\left[0\right]$ to $x[N/2-1]$, which are now the output of the delay elements of stage 2, are delayed by the delay elements of length $N/2$ of stage 1; at the same time $x\left[0\right]$ to $x[N/2-1]$ and $x[N/2]$ to $x[N-1]$ perform the butterfly operation in stage 2. The outputs of the butterfly unit of stage 2 are $\left(x\right[0]+x[N/2\left]\right)$ to $\left(x\right[N/2-1]+x[N-1\left]\right)$ and $\left(x\right[0]-x[N/2\left]\right)$ to $\left(x\right[N/2-1]-x[N-1\left]\right)$. $\left(x\right[0]+x[N/2\left]\right)$ to $\left(x\right[N/2-1]+x[N-1\left]\right)$ are transferred into stage 3 and $\left(x\right[0]-x[N/2\left]\right)$ to $\left(x\right[N/2-1]-x[N-1\left]\right)$ are fed back to the delay elements of stage 2. After $N$ cycles, $x\left[0\right]$ to $x[N/2-1]$, which are now the output of the delay elements of stage 1, are entered into the delay elements of stage 2.

In addition, the feedback data $\left(x\right[0]-x[N/2\left]\right)$ to $\left(x\right[N/2-1]-x[N-1\left]\right)$ are multiplied by the TF ROM and then transferred into stage 3. At the same time, $\left(x\right[0]-x[N/2\left]\right)$ to $\left(x\right[N/2-1]-x[N-1\left]\right)$ are entered into the delay elements of stage 1. After 3$N/2$ cycles, $x\left[0\right]$ to $x[N/2-1]$ are outputted from the delay elements of stage 2 and $\left(x\right[0]-x[N/2\left]\right)$ to $\left(x\right[N/2-1]-x[N-1\left]\right)$ are outputted from the delay elements of stage 1. Consequently, $(-jx[N/2\left]\right)$ to $(-jx[N-1\left]\right)$ can be obtained by subtracting $x\left[0\right]$ to $x[N/2-1]$ from $\left(x\right[0]-x[N/2\left]\right)$ to $\left(x\right[N/2-1]-x[N-1\left]\right)$ and then via multiplication by $-j$. Additionally, $x\left[0\right]$ to $x[N/2-1]$ and $(-jx[N/2\left]\right)$ to $(-jx[N-1\left]\right)$ perform the butterfly operation in stage 2. The butterfly unit outputs of stage 2 from $\left(x\right[0]-jx[N/2\left]\right)$ to $\left(x\right[N/2-1]-jx[N-1\left]\right)$ are transferred into stage 3 and $\left(x\right[0]+jx[N/2\left]\right)$ to $\left(x\right[N/2-1]+jx[N-1\left]\right)$ are fed back to delay elements of stage 2. Thus, it can be verified that the outputs of the stage 2 butterfly unit are equal to the results of the stage 2 butterfly operation shown in Figure 1. Therefore, this demonstrates that the number of delay elements in stage 1 can be reduced by 50% compared with the conventional architecture. Besides, multiplication by $-j$ is a trivial multiplication that consists of changing the positions of the integer and imaginary parts of the complex number and the butterfly unit of stage 1 can be omitted as shown in Equation (9).

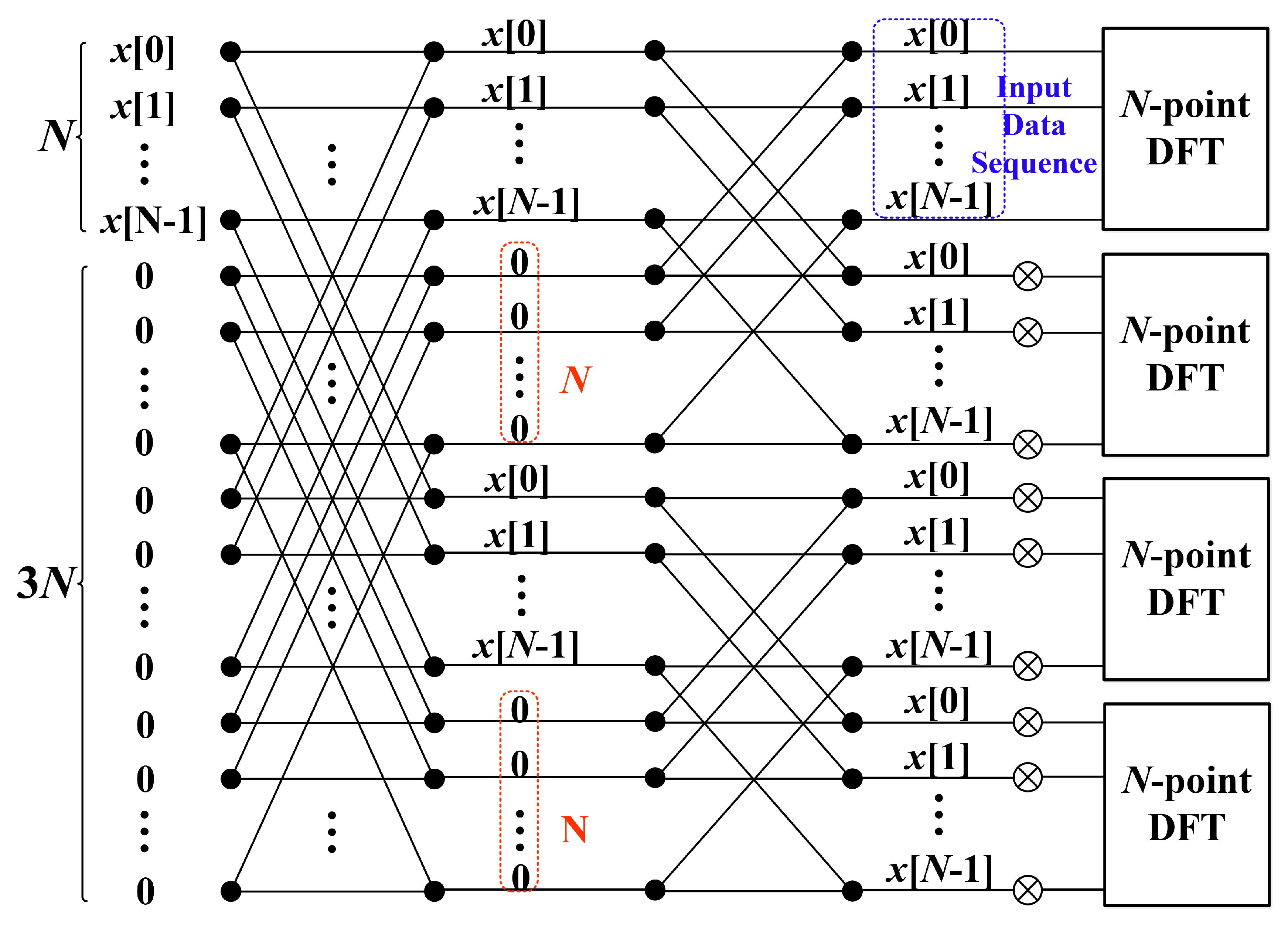
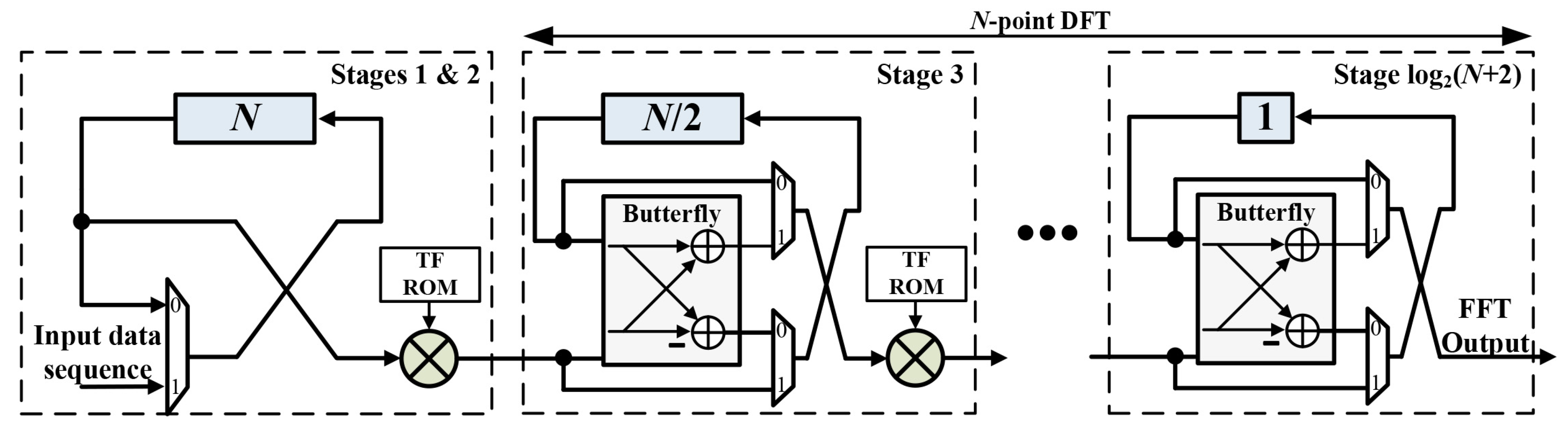
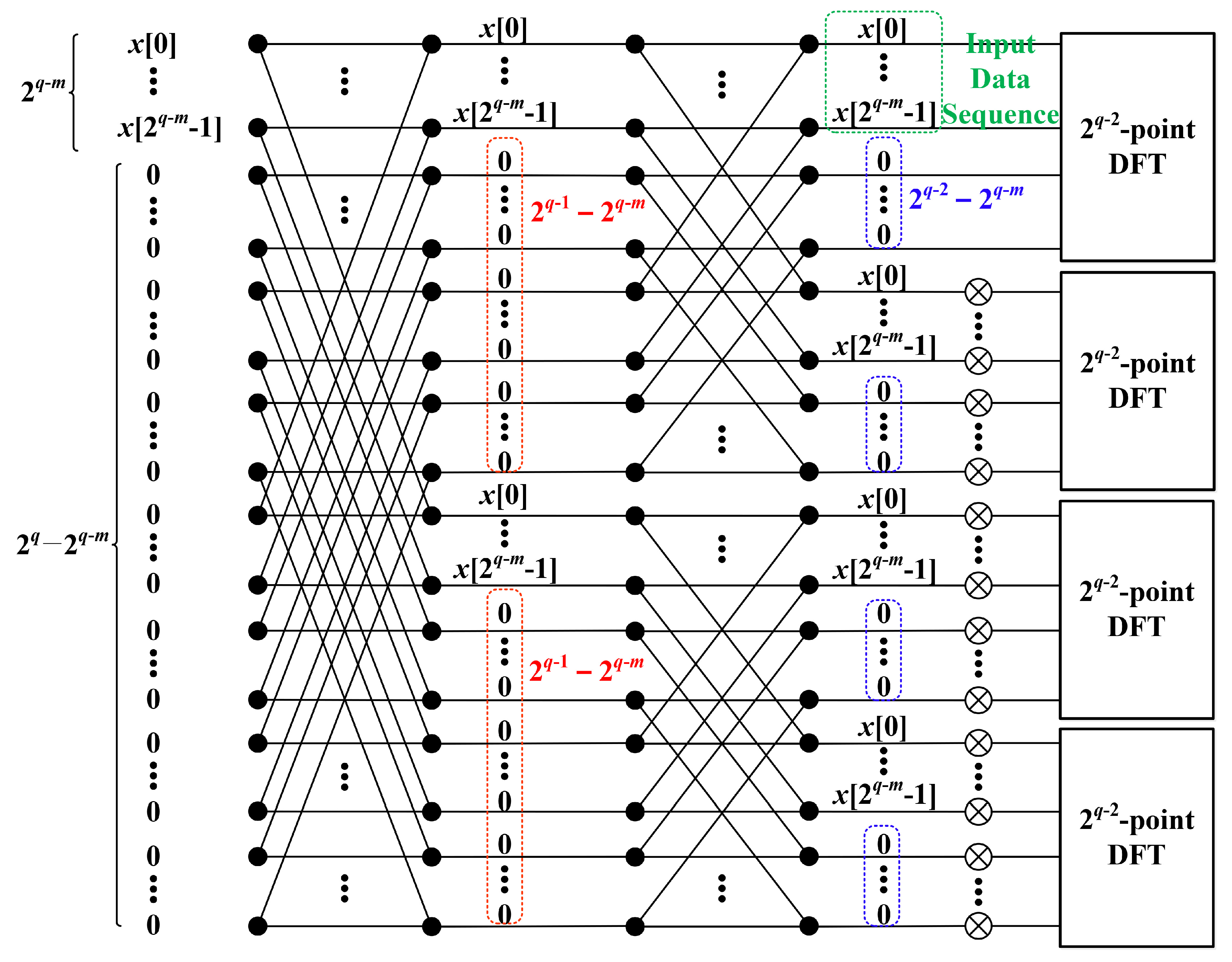
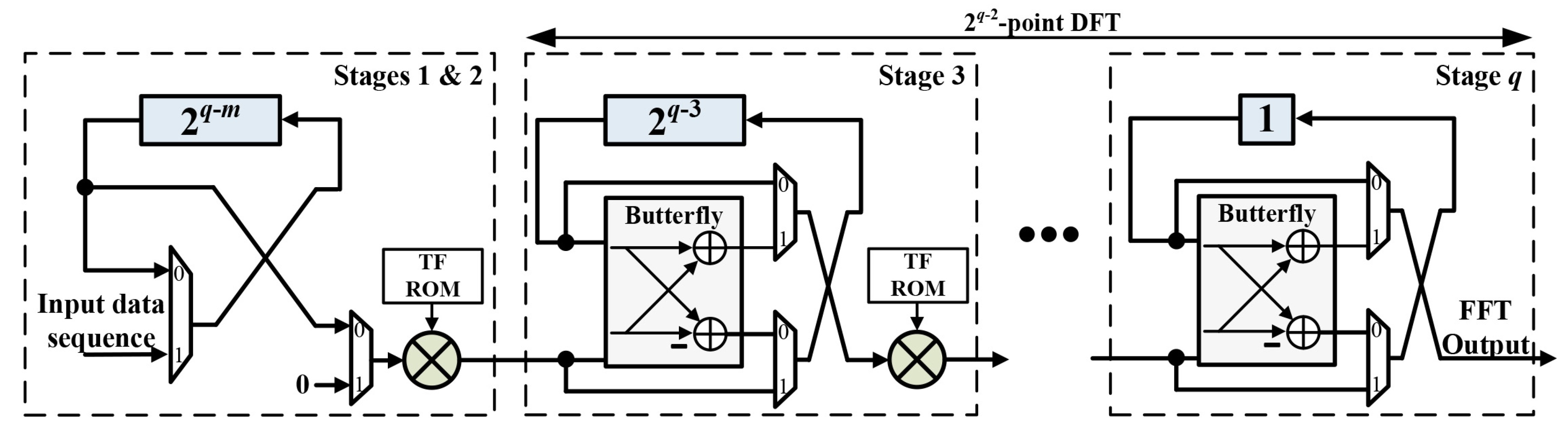
3.2. Four-Times Frequency Resolution

When the tail of an input data sequence of length $N$ is padded with 3$N$ zeros, the number of data points in the sequence in the time domain becomes 4$N$ and, consequently, the frequency resolution increases by a factor of 4. The DFT for a 4$N$-long zero-padded signal is expressed in Equation (13) and the corresponding SFG is depicted in Figure 5. As can be seen from the SFG, the outputs of stage 1 from $B_{\frac{M}{2}}^{k_1}\left(N\right)$ to $B_{\frac{M}{2}}^{k_1}(2N-1)$ and from $B_{\frac{M}{2}}^{k_1}\left(3N\right)$ to $B_{\frac{M}{2}}^{k_1}(4N-1)$ are zeros. Hence, the outputs from the butterfly unit in stage 2 are repeated in the input data sequence four times. Therefore, the hardware architecture at stage 1 and stage 2 of the SDF for a zero-padded signal with four times the frequency resolution requires $N$ delay elements and one complex multiplier, as illustrated in Figure 6.

In the proposed hardware architecture, an input data sequence of length $N$ is delayed using $N$ delay elements and the delayed data sequence is fed back to the delay elements and simultaneously transferred to a complex multiplier for multiplying by the TF. As a result, the input data sequence is repeated four times. After the calculations of stages 1 and 2 are completed, an $N$-point DFT calculation with $lo{g}_{2}N$ stages is performed. In other words, the proposed SDF architecture for a zero-padded signal with four times the frequency resolution can reduce the total number of delay elements by 50% compared with the conventional SDF architecture by eliminating stage 1, which has the largest number of delay elements.

3.3. 2${}^m$-Times Frequency Resolution

When the tail of an input data sequence of length 2${}^{(q-m)}$ is padded with 2${}^q-$2${}^{(q-m)}$ zeros, the frequency resolution increases by a factor of 2${}^m$, where $m$ is 2 or more and $q$ is $m+1$ or more. Figure 7 shows the SFG when a data sequence of length 2${}^q$ is decomposed using the radix-2${}^2$ algorithm. Among the outputs from the stage 1, from $B_{\frac{M}{2}}^{k_1}\left(2^{q-m}\right)$ to $B_{\frac{M}{2}}^{k_1}(2^{q-1}-1)$ and from $B_{\frac{M}{2}}^{k_1}(2^{q-1}+2^{q-m})$ to $B_{\frac{M}{2}}^{k_1}(2^q-1)$ are zeros and the outputs from $B_{\frac{M}{2}}^{k_1}\left(0\right)$ to $B_{\frac{M}{2}}^{k_1}(2^{q-m}-1)$ and from $B_{\frac{M}{2}}^{k_1}\left(2^{q-1}\right)$ to $B_{\frac{M}{2}}^{k_1}(2^{q-1}+2^{q-m}-1)$ are repeatedly generated in the same form as the input data sequence. In addition, the outputs from the butterfly unit in stage 2 are repeated four times for an input data sequence of length 2${}^{(q-m)}$ and $(2^{q-2}+2^{q-m})$ zeros. Therefore, the hardware architecture at stages 1 and 2 of the SDF for a zero-padded signal with $2^m$-times frequency resolution requires 2${}^{(q-m)}$ delay elements and one complex multiplier. Additionally, a multiplexer for $(2^{q-2}+2^{q-m})$ zeros is required for the stage 2 butterfly outputs, as illustrated in Figure 8.

In the proposed hardware architecture, the input data sequence of length 2${}^{q-m}$ is delayed using delay elements of length 2${}^{q-m}$ and the delayed input data sequence is simultaneously transferred to a complex multiplier and to delay elements of length 2${}^{q-m}$. As a result, in the outputs from the butterfly unit in stage 2, the input data sequence and the zeros are repeated. After the calculations of stage 1 and stage 2 are completed, 2${}^{q-2}$-point DFT calculations are performed over $q-2$ stages. In other words, the proposed SDF architecture for a zero-padded signal with 2${}^m$-times frequency resolution eliminates stage 1, which has the largest number of delay elements. Moreover, in the case of eight-times frequency resolution or higher and because the input of the 2${}^{q-2}$-point DFT calculations is zero-padded after the operations of stage 2, the number of the delay elements in the 2${}^{q-2}$-point FFT processors can be reduced in the same way as in the proposed hardware architecture.

4. Comparison

Table 1. Comparison of pipeline hardware architectures for the computation of a 2${}^q$-point zero-padded FFT on complex-valued data (frequency resolution is assumed to be increased by a factor of 2${}^m$).

Pipelined Architecture	Complex Adder	Complex Multipliers	Delay Elements	Latency (Cycles)
SDF Radix-2	2$q$	$q-1$	2${}^q-1$	2${}^q$
SDF Radix-4	4$q$	$q/2-1$	2${}^q-1$	2${}^q$
SDF Radix-2${}^2$	2$q$	$q/2-1$	2${}^q-1$	2${}^q$
SDF Split Radix-2	2$q$	$q/2-1$	2${}^q-1$	2${}^q$
SDC Radix-4	3$q$/2	$q/2-1$	2${}^{q+1}-1$	2${}^q$
Proposed SDF Radix-2${}^2$ ($m$ : Odd/Even)	(Odd : 2$q-$2$m$+1 Even : 2$q-$2$m$)	$q/2-1$	$(m+2)$(2${}^{q-m-1}$)$-1$	$(m+2)$(2${}^{q-m-1}$)

shows a comparison of the hardware area and performance between the conventional pipelined FFT architecture and the proposed hardware architecture for a zero-padded signal of length 2${}^q$ when the frequency resolution is increased by a factor of 2${}^m$. This Table includes the number of complex adders, complex multipliers and delay elements. The latency is also presented in terms of the number of cycles. Because all the architectures process single-path data, their throughput is one sample per clock cycle. Additionally, the number of complex multipliers is the same as in the radix-2${}^2$ SDF architecture but it can be seen that the number of complex adders is reduced by 2$m$ compared with the radix-2${}^2$ SDF architecture. Most notably, compared with the conventional hardware architecture (in which the number of delay elements seriously increases with FFT length and the number of data paths), the proposed hardware architecture reduces the number of the delay elements significantly. Moreover, latency is significantly reduced compared with other single-path pipeline architectures.

In order to confirm the superiority of the proposed architecture, we implemented two 256-point FFT processors with the proposed and conventional radix-2${}^2$ SDF architectures. For four-times frequency resolution, the tail of an input data sequence of length 64 is padded with 192 zeros. A 12-bit word for real and imaginary data paths was selected to satisfy the requirement for a signal-to-quantization noise-ratio (SQNR) of 40 dB. We designed the zero-padded FFT processor for integration in frequency modulated continuous wave (FMCW) radar signal processor and confirmed that the performance degradation due to quantization noise is minimized when the SQNR is above 40 dB. In addition, in the case of FFT processor for orthogonal frequency division multiplexing (OFDM) baseband processor, it is presented in Reference [32] that there is no effect of quantization noise when the SQNR is 40 dB or more.

Two FFT processors were designed using hardware description language (HDL) and synthesized to gate-level circuits using a standard cell library of 65 nm CMOS process.

Table 2. Comparison of logic synthesis results of a 256-point four-times frequency resolution zero-padded FFT on complex-valued data.

Block Name	SDF Radix-2${}^{\mathbf{2}}$	Proposed	Reduction (%)
Butterfly Unit	7192	6293	12.5
Non-trivial Multiplier	13,783	13,783	0
Delay Elements	40,800	20,320	50.2
Total	61,775	40,396	34.6

shows comparison results for logic gate count. As depicted in this Table, the proposed architecture can reduce the gate count by 34.6% compared to the conventional architecture owing to the reduction of 50.2% for delay elements.

Table 3. Comparison of the proposed FFT processor with previous research results.

	[33]	[34]	[35]	[36]	This Work
FFT Length	128–2048	1024–8192	128–2048	4–2048	256
FFT Architecture	SDF	SDF	SDF	SDF	SDF
Frequency (MHz)	40	112	40	500	300
Word Length (Bit)	16	12	12	14	12
Technology	180	180	90	40	65
Execution Time/FFT Length @ 20MHz (ns)	50	50	N.A.	N.A.	28
Area (mm${}^2$)	6.76	3.52	0.783	0.36	0.18
Normailzed Area	80.14	35.31	37.13	86.42	22.50

shows comparison results between this work and other FFT processors in References [33,34,35,36]. For a fair comparison, we normalized the area as

$$A_{norm}=\frac{\mathrm{Area}\times {10}^3}{{(Tech/65\mathrm{nm})}^2\times {log}_{2}N},$$

(15)

where $N$ and $Tech$ are the FFT length and the process technology in nanometers, respectively. As shown in Table 3, the normalized area of the proposed FFT processor is the smallest among different FFT processors because it can significantly reduce the number of delay elements.

5. Conclusions

In this paper, we proposed an area-efficient FFT processor for zero-padded signals based on the radix-2${}^2$ and radix-2${}^3$ SDF pipeline architectures by taking advantage of the fact that the input data sequence is zero-padded that and the twiddle factor multiplication in stage 1 is trivial. The proposed FFT processor can dramatically reduce the required the number of delay elements. For four-times frequency resolution, the tail of an input data sequence of length 64 is padded with 192 zeros, the number of delay elements can be reduced by 50.2% and we demonstrated that the proposed architecture is efficient and suitable for zero-padded FFT processors.