A Hybrid Asymptotic-FVTD Method for the Estimation of the Radar Cross Section of 3D Structures
Abstract
:1. Introduction
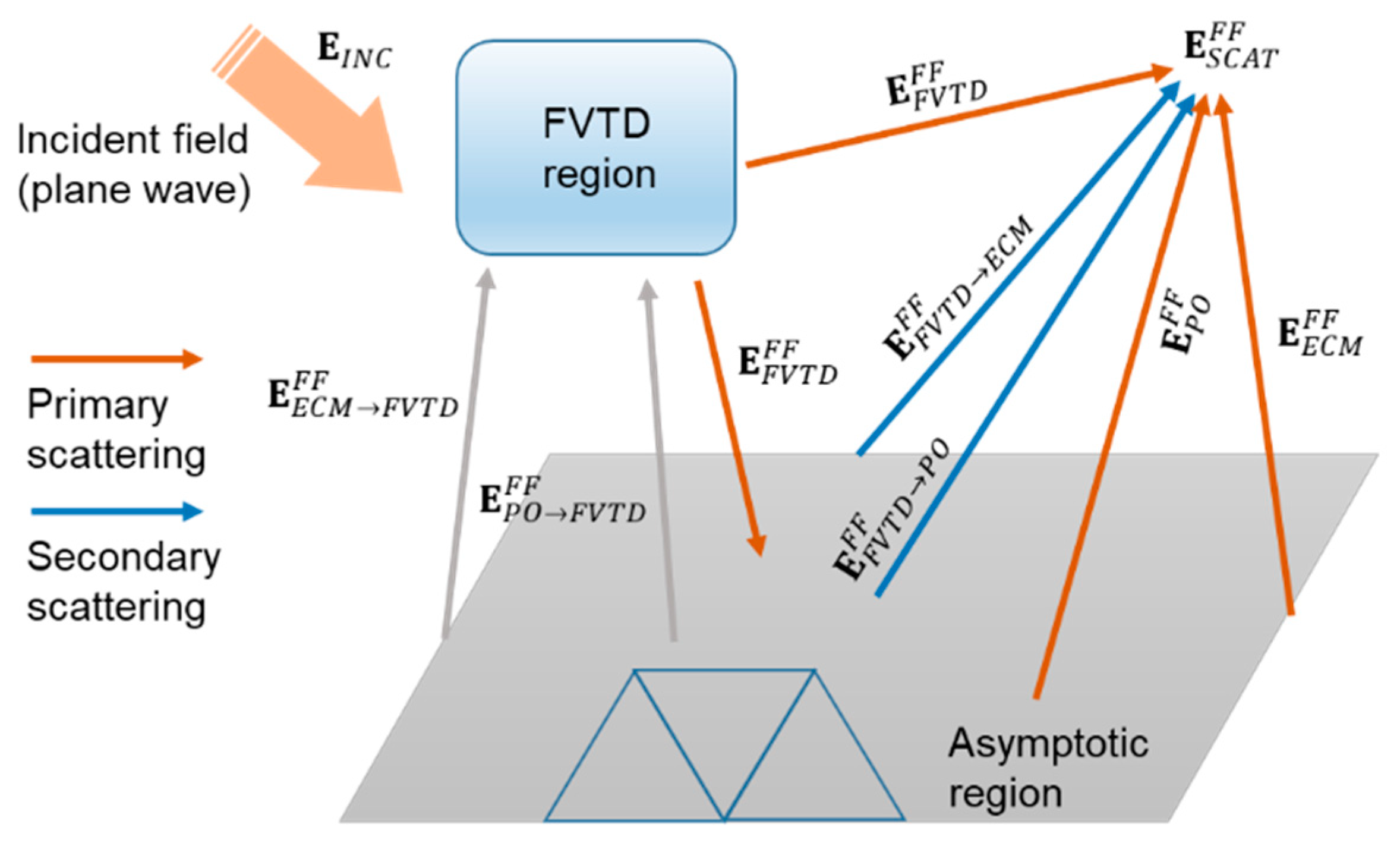
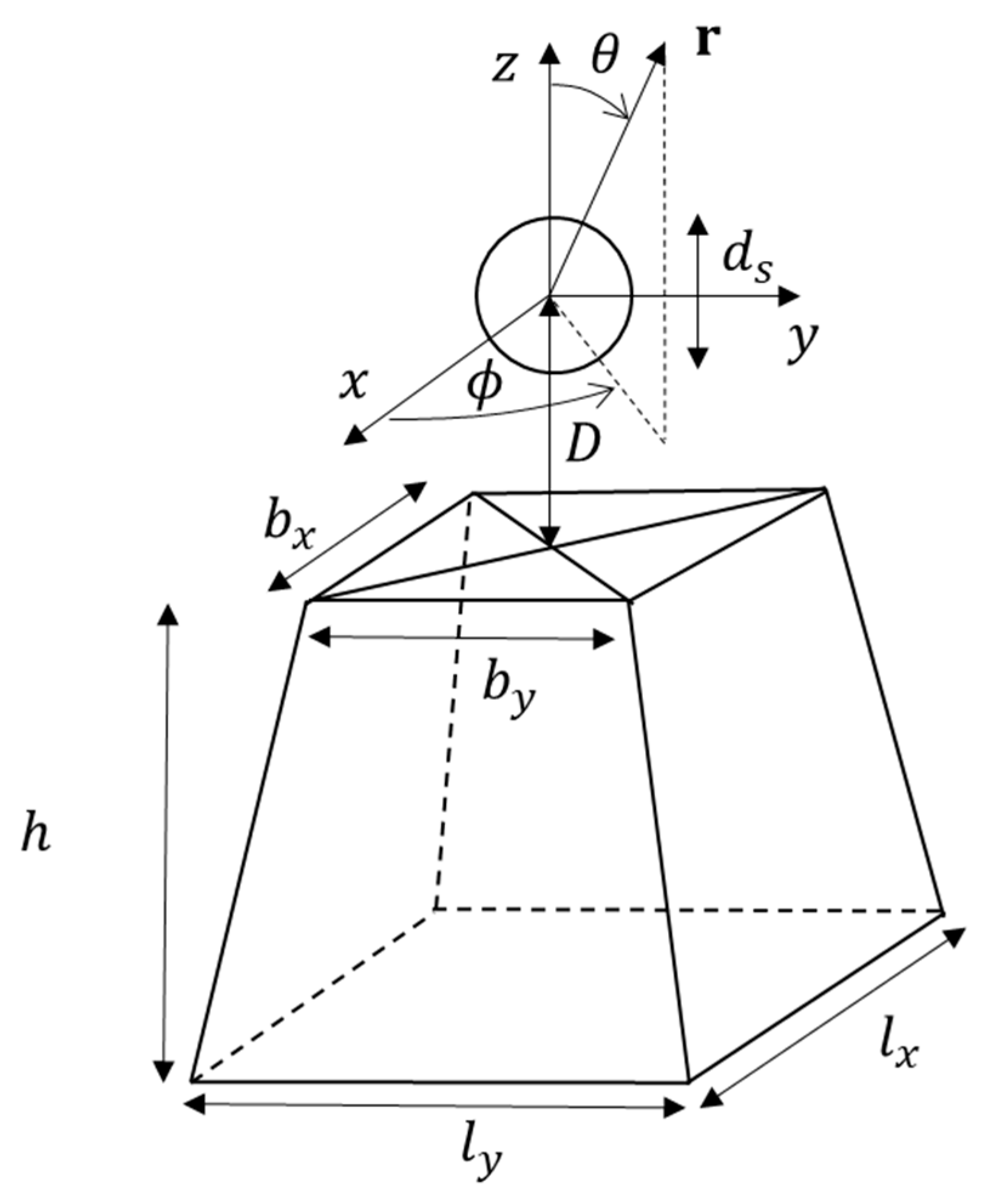
2. Formulation of the Hybrid Method
2.1. Scattered Field from the FVTD Region
2.2. Scattered Field from the Asymptotic Region
2.3. Scattered Fields Due to the Coupling between Regions
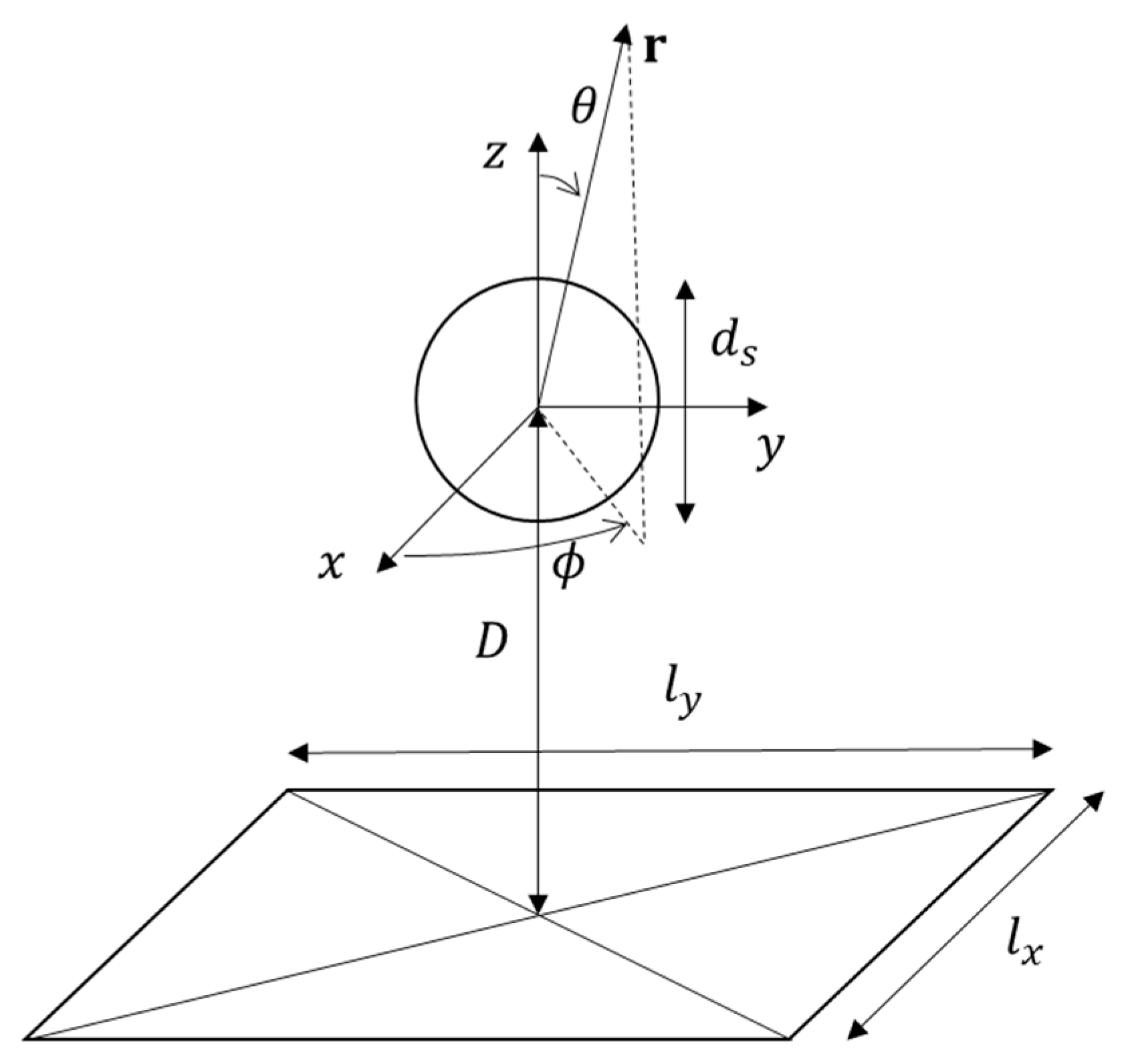
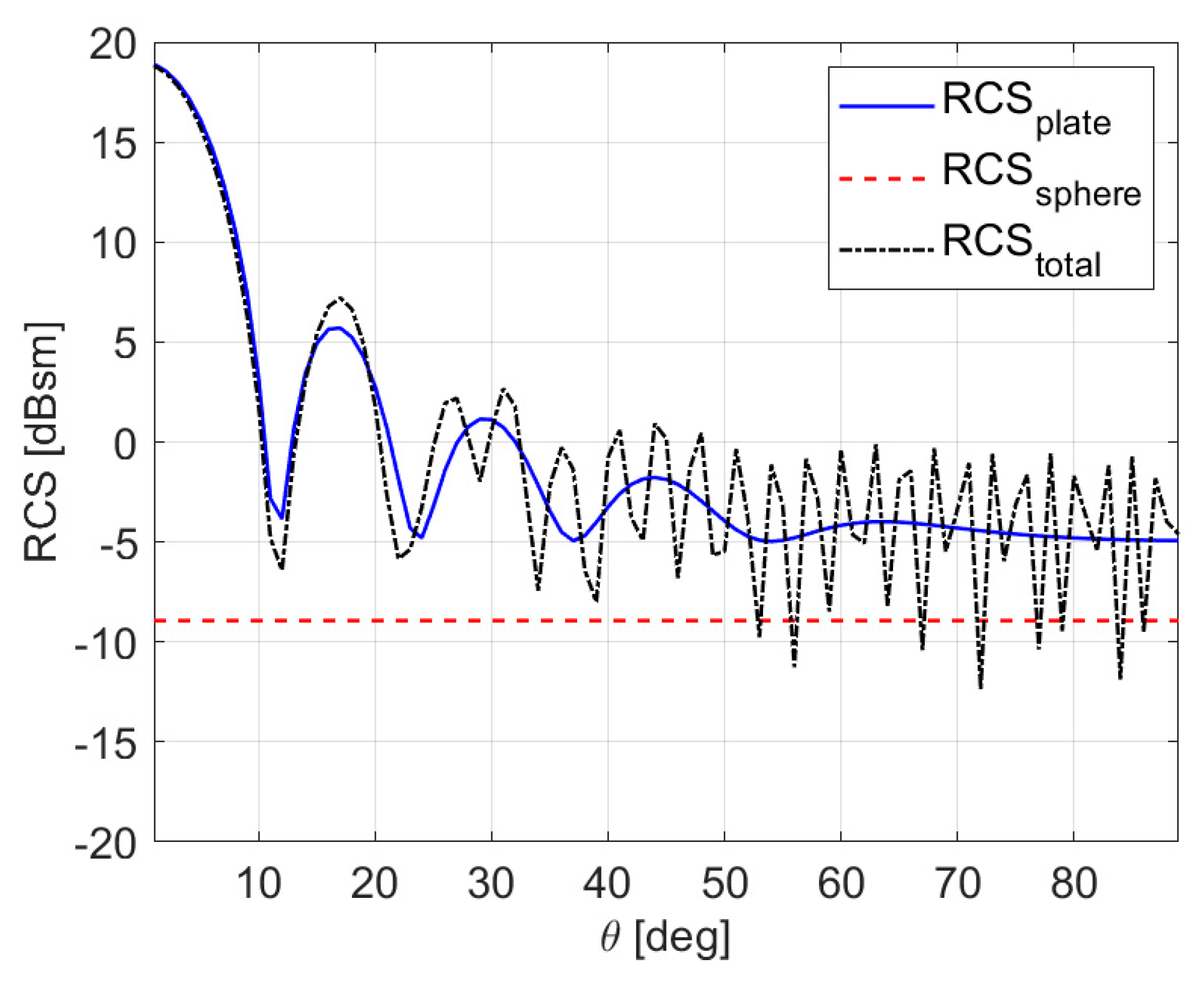
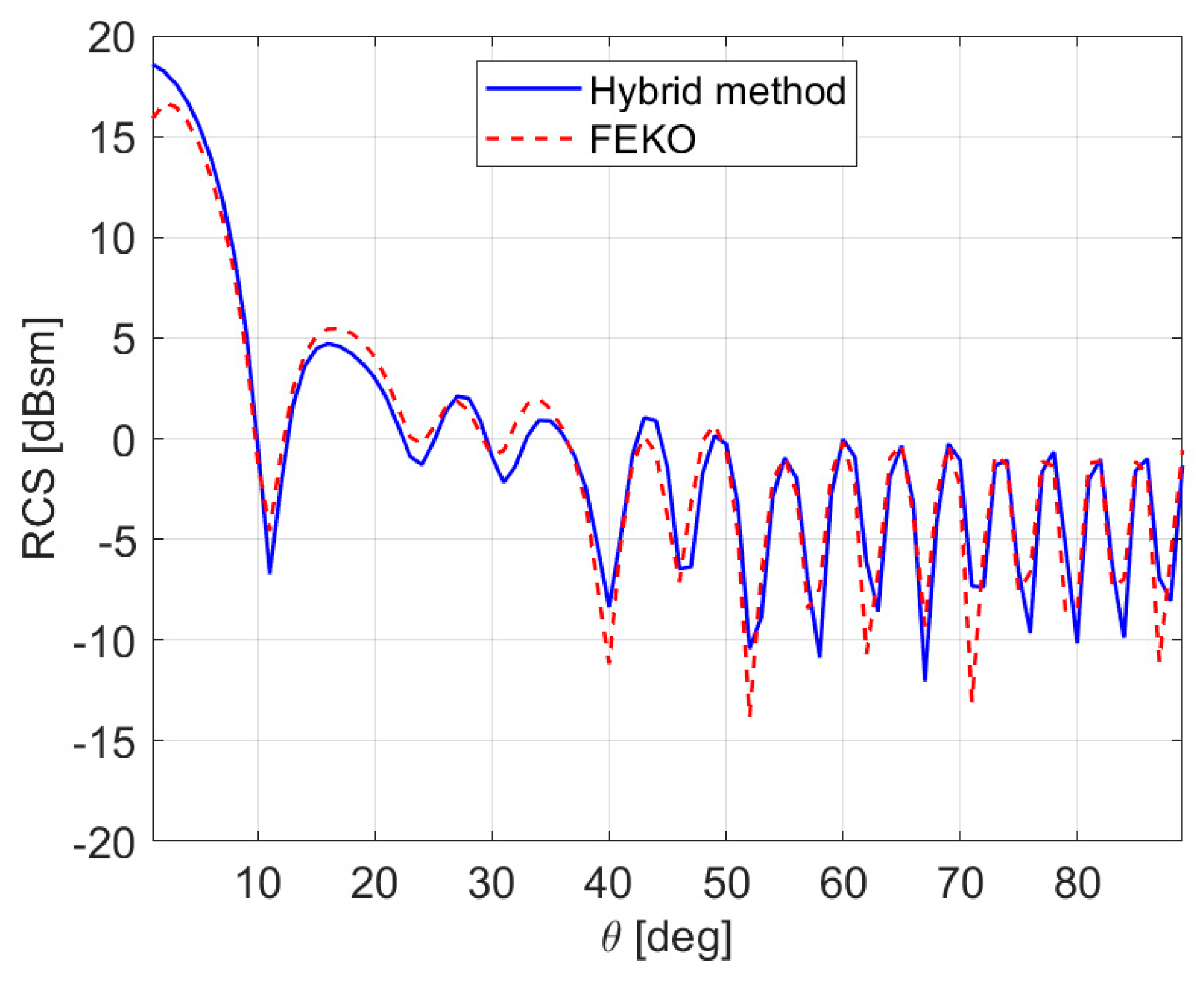
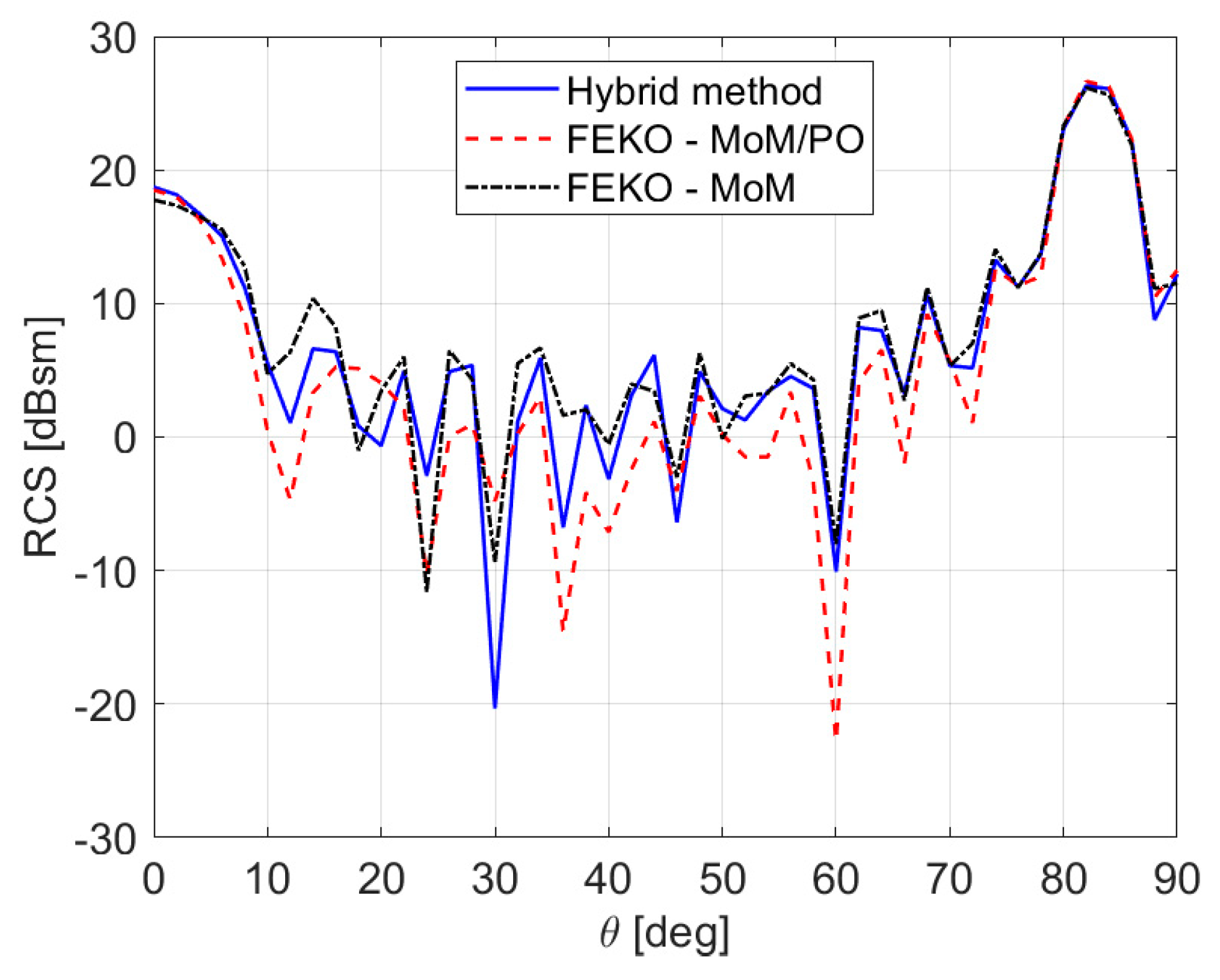
3. Numerical Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rao, S.M. Time Domain Electromagnetics; Academic Press: San Diego, CA, USA, 1999; ISBN 978-0-08-051924-1. [Google Scholar]
- Davidson, D.B. Computational Electromagnetics for Rf and Microwave Engineering, 2nd ed.; Cambridge University Press: Cambridge, UK, 2010; ISBN 978-0-511-91890-2. [Google Scholar]
- Fumeaux, C.; Baumann, D.; Leuchtmann, P.; Vahldieck, R. A generalized local time-step scheme for efficient FVTD simulations in strongly inhomogeneous meshes. IEEE Trans. Microw. Theory Tech. 2004, 52, 1067–1076. [Google Scholar] [CrossRef]
- Frezza, F.; Pajewski, L.; Ponti, C.; Schettini, G. Through-wall electromagnetic scattering by N conducting cylinders. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2013, 30, 1632–1639. [Google Scholar] [CrossRef] [PubMed]
- Harrington, R.F. Field Computation by Moment Methods; IEEE: Piscataway, NJ, USA, 1993; ISBN 978-0-7803-1014-8. [Google Scholar]
- Taflove, A.; Hagness, S.C. Computational Electrodynamics: The Finite-Difference Time-Domain Method, 3rd ed.; Artech House: Boston, MA, USA, 2005; ISBN 1-58053-832-0. [Google Scholar]
- Ramahi, O.M.; Subramanian, V.; Archambeault, B. A simple finite-difference frequency-domain (FDFD) algorithm for analysis of switching noise in printed circuit boards and packages. IEEE Trans. Adv. Packag. 2003, 26, 191–198. [Google Scholar] [CrossRef]
- Clemens, M.; Weiland, T. Discrete electromagnetism with the finite integration technique. Prog. Electromagn. Res. 2001, 32, 65–87. [Google Scholar] [CrossRef]
- Paknys, R. Applied Frequency-Domain Electromagnetics; John Wiley & Sons: Hoboken, NJ, USA, 2016; ISBN 978-1-118-94054-9. [Google Scholar]
- Pregla, R.; Helfert, S. Analysis of Electromagnetic Fields and Waves: The Method of Lines; John Wiley & Sons: Hoboken, NJ, USA, 2008; ISBN 978-0-470-05850-3. [Google Scholar]
- Knott, E.F.; Shaeffer, J.; Tuley, M. Radar Cross Section, 2nd ed.; SciTech Publishing: Raleigh, NC, USA, 2004; ISBN 978-1-891121-25-8. [Google Scholar]
- Liu, Z.L.; Wang, X.; Wang, C.F. Installed performance modeling of complex antenna array mounted on extremely large-scale platform using fast MoM-PO hybrid framework. IEEE Trans. Antennas Propag. 2014, 62, 3852–3858. [Google Scholar] [CrossRef]
- Moneum, M.A.A.; Shen, Z.; Volakis, J.L.; Graham, O. Hybrid PO-MoM analysis of large axi-symmetric radomes. IEEE Trans. Antennas Propag. 2001, 49, 1657–1666. [Google Scholar] [CrossRef]
- Obelleiro, F.; Taboada, J.M.; Rodríguez, J.L.; Rubiños, J.O.; Arias, A.M. Hybrid moment-method physical-optics formulation for modeling the electromagnetic behavior of on-board antennas. Microw. Opt. Technol. Lett. 2000, 27, 88–93. [Google Scholar] [CrossRef]
- Çivi, Ö.A.; Pathak, P.H.; Chou, H.T.; Nepa, P. Hybrid uniform geometrical theory of diffraction—Moment method for efficient analysis of electromagnetic radiation/scattering from large finite planar arrays. Radio Sci. 2000, 35, 607–620. [Google Scholar] [CrossRef]
- Braaten, B.D.; Nelson, R.M.; Mohammed, M.A. Electric field integral equations for electromagnetic scattering problems with electrically small and electrically large regions. IEEE Trans. Antennas Propag. 2008, 56, 142–150. [Google Scholar] [CrossRef]
- Vipiana, F.; Francavilla, M.A.; Vecchi, G. EFIE modeling of high-definition multiscale structures. IEEE Trans. Antennas Propag. 2010, 58, 2362–2374. [Google Scholar] [CrossRef]
- Mei, X.; Zhang, Y.; Lin, H. A new efficient hybrid SBR/MoM technique for scattering analysis of complex large structures. In Proceedings of the 2015 IEEE International Conference on Computational Electromagnetics, Hong Kong, China, 2–5 February 2015; pp. 306–308. [Google Scholar]
- Chen, M.; Zhao, X.W.; Zhang, Y.; Liang, C.H. Analysis of antenna around nurbs surface with iterative MoM-PO technique. J. Electromagn. Waves Appl. 2006, 20, 1667–1680. [Google Scholar] [CrossRef]
- Liu, Z.L.; Wang, C.F. Efficient iterative method of moments-physical optics hybrid technique for electrically large objects. IEEE Trans. Antennas Propag. 2012, 60, 3520–3525. [Google Scholar] [CrossRef]
- Yang, L.X.; Ge, D.B.; Wei, B. FDTD/TDPO hybrid approach for analysis of the EM scattering of combinative objects. Prog. Electromagn. Res. 2007, 76, 275–284. [Google Scholar] [CrossRef]
- Faghihi, F.; Heydari, H. Time domain physical optics for the higher-order FDTD modeling in electromagnetic scattering from 3-D complex and combined multiple materials objects. Prog. Electromagn. Res. 2009, 95, 87–102. [Google Scholar] [CrossRef]
- Chia, T.T.; Burkholder, R.J.; Lee, R. The application of FDTD in hybrid methods for cavity scattering analysis. IEEE Trans. Antennas Propag. 1995, 43, 1082–1090. [Google Scholar] [CrossRef]
- Lepvrier, B.L.; Loison, R.; Gillard, R.; Pouliguen, P.; Potier, P.; Patier, L. A new hybrid method for the analysis of surrounded antennas mounted on large platforms. IEEE Trans. Antennas Propag. 2014, 62, 2388–2397. [Google Scholar]
- Chou, H.T.; Hsu, H.T. Hybridization of simulation codes based on numerical high and low frequency techniques for the efficient antenna design in the presence of electrically large and complex structures. Prog. Electromagn. Res. 2008, 78, 173–187. [Google Scholar] [CrossRef]
- Burkholder, R.J.; Kim, Y.; Pathak, P.H.; Lee, J.F. Green’s function approach for interfacing UTD with FEM for a conformal array antenna on a large platform. In Proceedings of the Fourth European Conference on Antennas and Propagation, Barcelona, Spain, 12–16 April 2010; pp. 1–4. [Google Scholar]
- Burkholder, R.J.; Pathak, P.H.; Sertel, K.; Marhefka, R.J.; Volakis, J.L.; Kindt, R.W. A hybrid framework for antenna/platform analysis. ACES J. 2006, 21, 177–195. [Google Scholar]
- Tzoulis, A.; Eibert, T.F. A hybrid FEBI-MLFMM-UTD method for numerical solutions of electromagnetic problems including arbitrarily shaped and electrically large objects. IEEE Trans. Antennas Propag. 2005, 53, 3358–3366. [Google Scholar] [CrossRef]
- Yee, K.S.; Chen, J.S. The finite-difference time-domain (FDTD) and the finite-volume time-domain (FVTD) methods in solving Maxwell’s equations. IEEE Trans. Antennas Propag. 1997, 45, 354–363. [Google Scholar] [CrossRef]
- Bonnet, P.; Ferrieres, X.; Issac, F.; Paladian, F.; Grando, J.; Alliot, J.C.; Fontaine, J. Numerical Modeling of Scattering Problems Using a Time Domain Finite Volume Method. J. Electromagn. Waves Appl. 1997, 11, 1165–1189. [Google Scholar] [CrossRef]
- Baumann, D.; Fumeaux, C.; Vahldieck, R. Field-based scattering-matrix extraction scheme for the FVTD method exploiting a flux-splitting algorithm. IEEE Trans. Microw. Theory Tech. 2005, 53, 3595–3605. [Google Scholar] [CrossRef]
- Fumeaux, C.; Baumann, D.; Vahldieck, R. Finite-volume time-domain analysis of a cavity-backed Archimedean spiral antenna. IEEE Trans. Antennas Propag. 2006, 54, 844–851. [Google Scholar] [CrossRef]
- Baumann, D.; Fumeaux, C.; Hafner, C.; Li, E.P. A modular implementation of dispersive materials for time-domain simulations with application to gold nanospheres at optical frequencies. Opt. Express 2009, 17, 15186–15200. [Google Scholar] [CrossRef] [PubMed]
- Bozza, G.; Caviglia, D.D.; Ghelardoni, L.; Pastorino, M. Cell-centered finite-volume time-domain method for conducting media. IEEE Microw. Wirel. Compon. Lett. 2010, 20, 477–479. [Google Scholar] [CrossRef]
- Almpanis, G.; Fumeaux, C.; Vahldieck, R. The trapezoidal dielectric resonator antenna. IEEE Trans. Antennas Propag. 2008, 56, 2810–2816. [Google Scholar] [CrossRef]
- Yee, K.S.; Chen, J.S. Conformal hybrid finite difference time domain and finite volume time domain. IEEE Trans. Antennas Propag. 1994, 42, 1450–1455. [Google Scholar] [CrossRef]
- Ferrieres, X.; Parmantier, J.P.; Bertuol, S.; Ruddle, A.R. Application of a hybrid finite difference/finite volume method to solve an automotive EMC problem. IEEE Trans. Electromagn. Compat. 2004, 46, 624–634. [Google Scholar] [CrossRef]
- Chatterjee, A.; Myong, R.S. Efficient implementation of higher-order finite volume time-domain method for electrically large scatterers. Prog. Electromagn. Res. 2009, 17, 233–254. [Google Scholar] [CrossRef]
- Cerruti, M.; Pastorino, M.; Randazzo, A. A hybrid FVTD-PO approach for the characterization of antennas on large platforms in naval applications. In Proceedings of the 2015 MTS IEEE OCEANS, Genoa, Italy, 8–21 May 2015; pp. 1–5. [Google Scholar]
- Lax, P.; Wendroff, B. Systems of conservation laws. Commun. Pure Appl. Math. 1960, 13, 217–237. [Google Scholar] [CrossRef]
- Domingo, M.; Torres, R.P.; Catedra, M.F. Calculation of the RCS from the interaction of edges and facets. IEEE Trans. Antennas Propag. 1994, 42, 885–888. [Google Scholar] [CrossRef]
- Balanis, C.A. Advanced Engineering Electromagnetics, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012; ISBN 978-0-470-58948-9. [Google Scholar]
- Ufimtsev, P.Y. Fundamentals of the Physical Theory of Diffraction; IEEE: Hoboken, NJ, USA, 2007; ISBN 978-0-470-09771-7. [Google Scholar]
- Electromagnetic Simulation Software|Altair FEKO. Available online: https://altairhyperworks.com/product/FEKO (accessed on 17 November 2019).
| Distance [m] | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| NRMSE | 0.118 | 0.072 | 0.055 | 0.056 | 0.056 |
| Plate side [m] | 0.5 | 1 | 2 |
|---|---|---|---|
| NRMSE | 0.142 | 0.056 | 0.048 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fedeli, A.; Pastorino, M.; Randazzo, A. A Hybrid Asymptotic-FVTD Method for the Estimation of the Radar Cross Section of 3D Structures. Electronics 2019, 8, 1388. https://doi.org/10.3390/electronics8121388
Fedeli A, Pastorino M, Randazzo A. A Hybrid Asymptotic-FVTD Method for the Estimation of the Radar Cross Section of 3D Structures. Electronics. 2019; 8(12):1388. https://doi.org/10.3390/electronics8121388
Chicago/Turabian StyleFedeli, Alessandro, Matteo Pastorino, and Andrea Randazzo. 2019. "A Hybrid Asymptotic-FVTD Method for the Estimation of the Radar Cross Section of 3D Structures" Electronics 8, no. 12: 1388. https://doi.org/10.3390/electronics8121388
APA StyleFedeli, A., Pastorino, M., & Randazzo, A. (2019). A Hybrid Asymptotic-FVTD Method for the Estimation of the Radar Cross Section of 3D Structures. Electronics, 8(12), 1388. https://doi.org/10.3390/electronics8121388







