A Power Calculation Algorithm for Single-Phase Droop-Operated-Inverters Considering Linear and Nonlinear Loads HIL-Assessed
Abstract
:1. Introduction
2. Materials and Methods
2.1. Droop Principle-Based Control Scheme
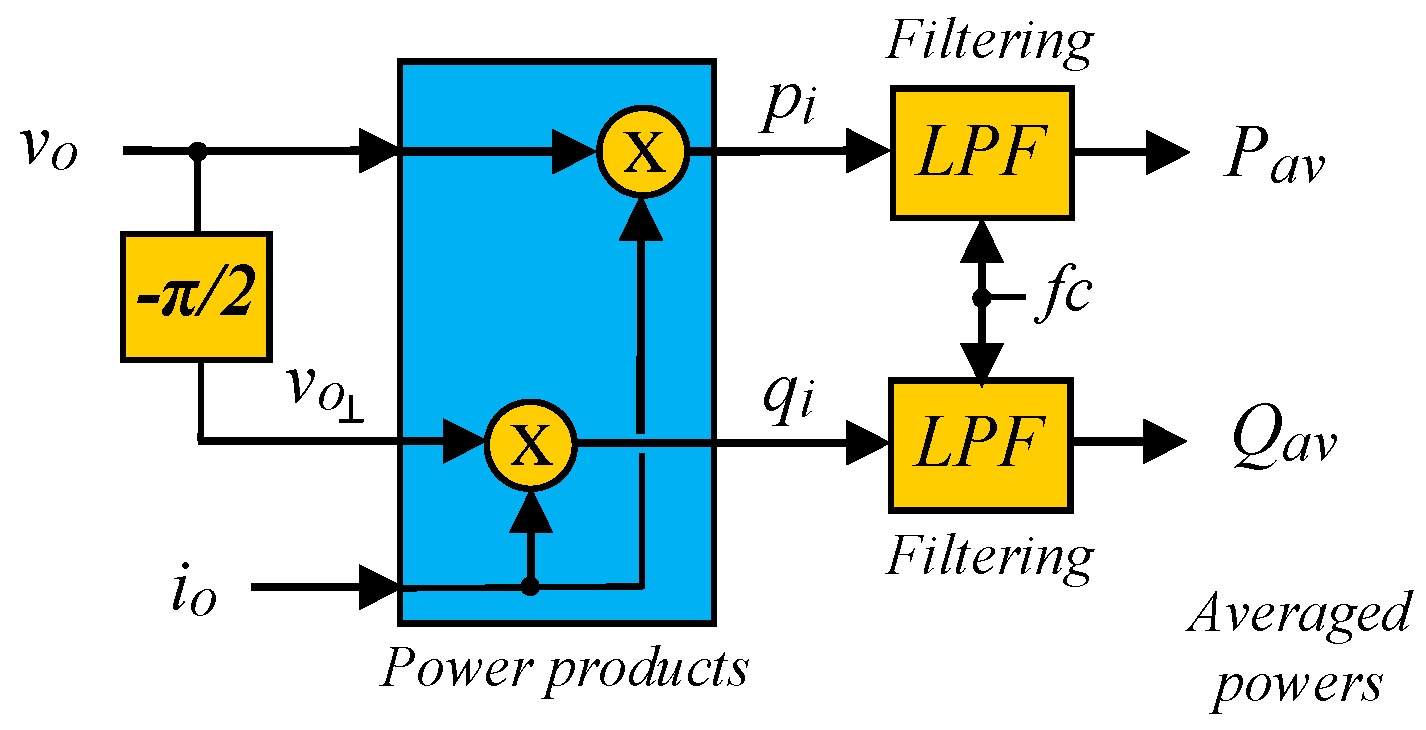
2.2. Conventional P-Q Calculation Schemes
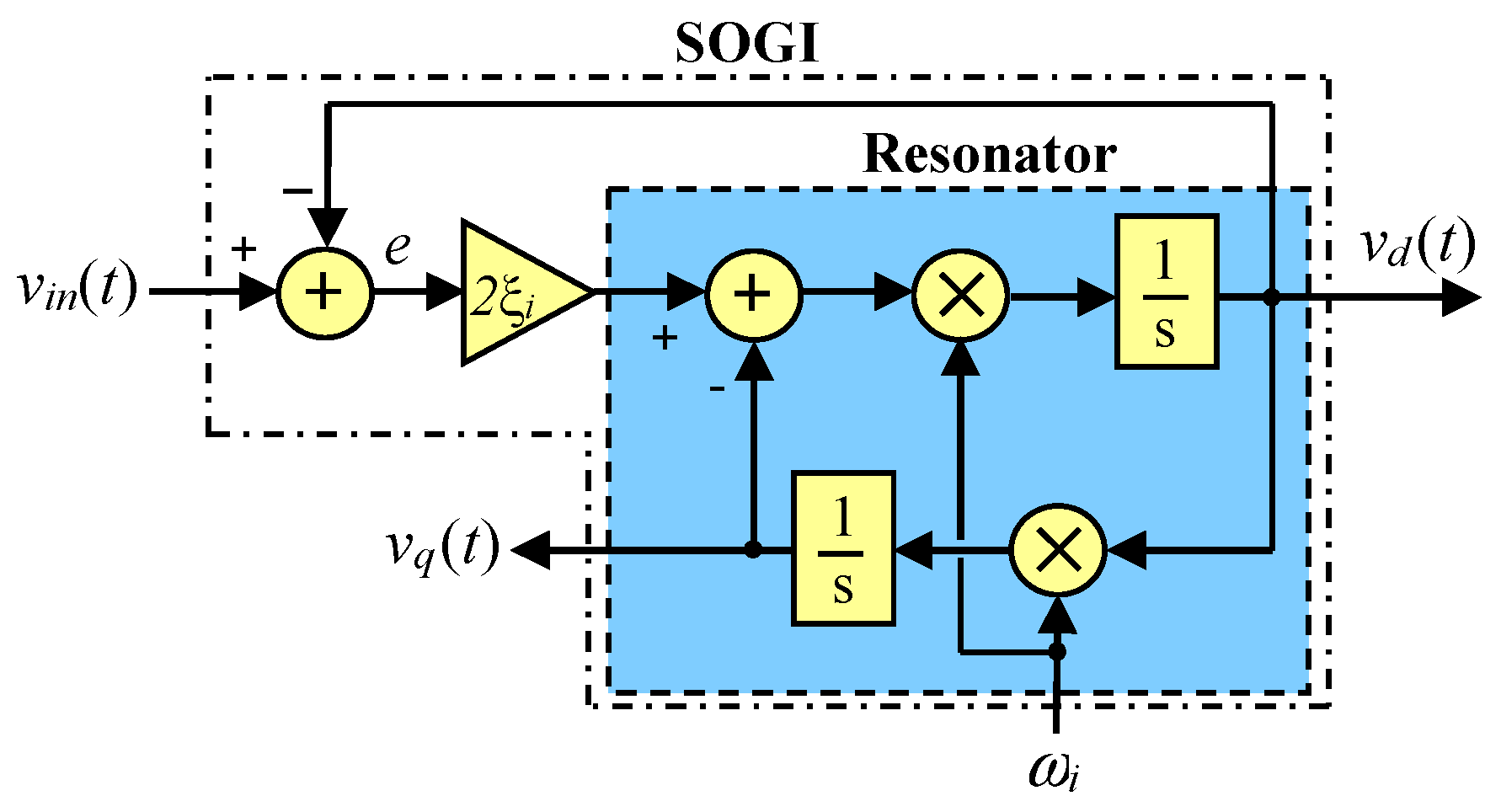
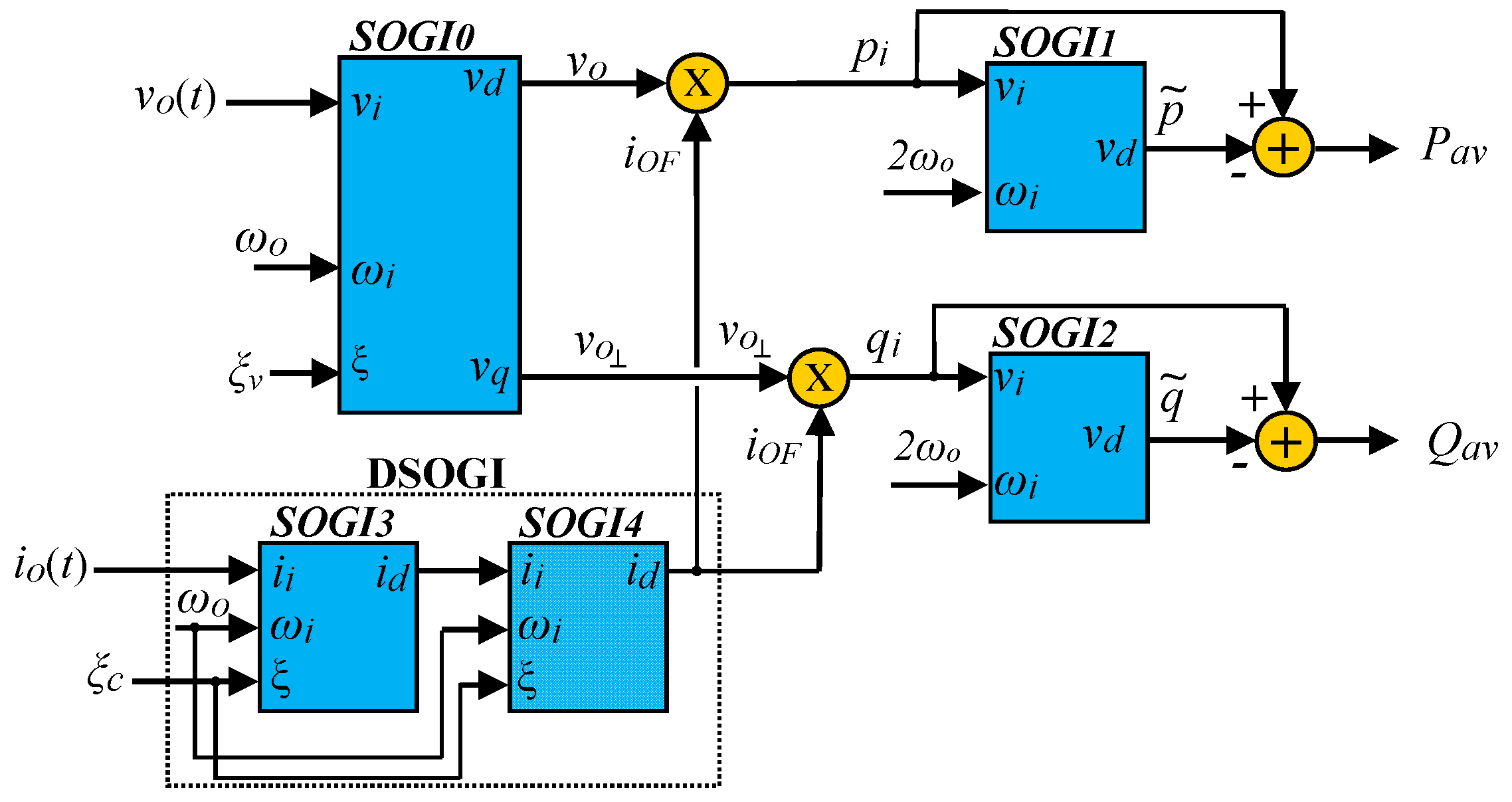
2.3. The SOGI and DSOGI Approach
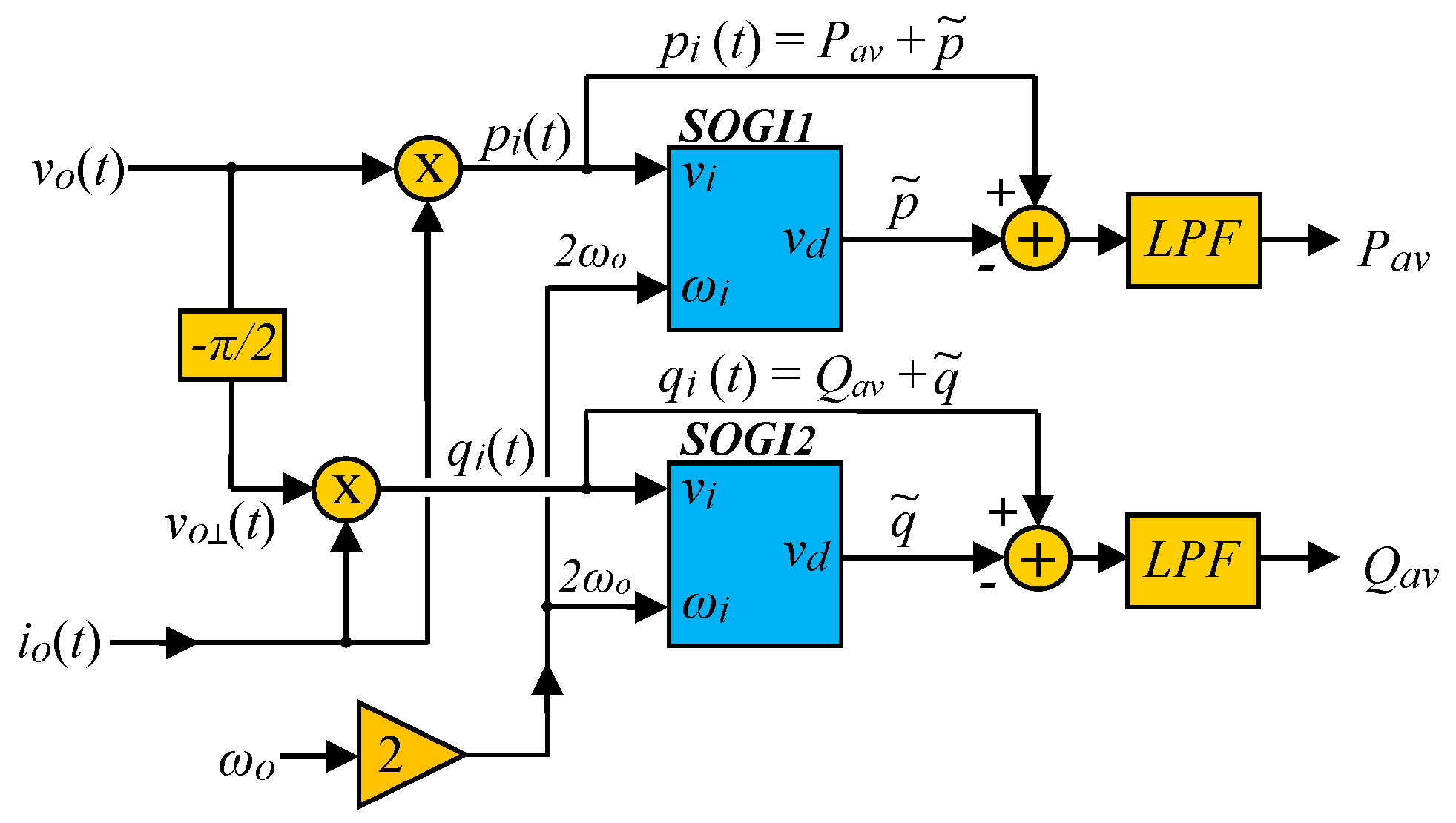
2.4. Advanced P-Q Calculation Scheme
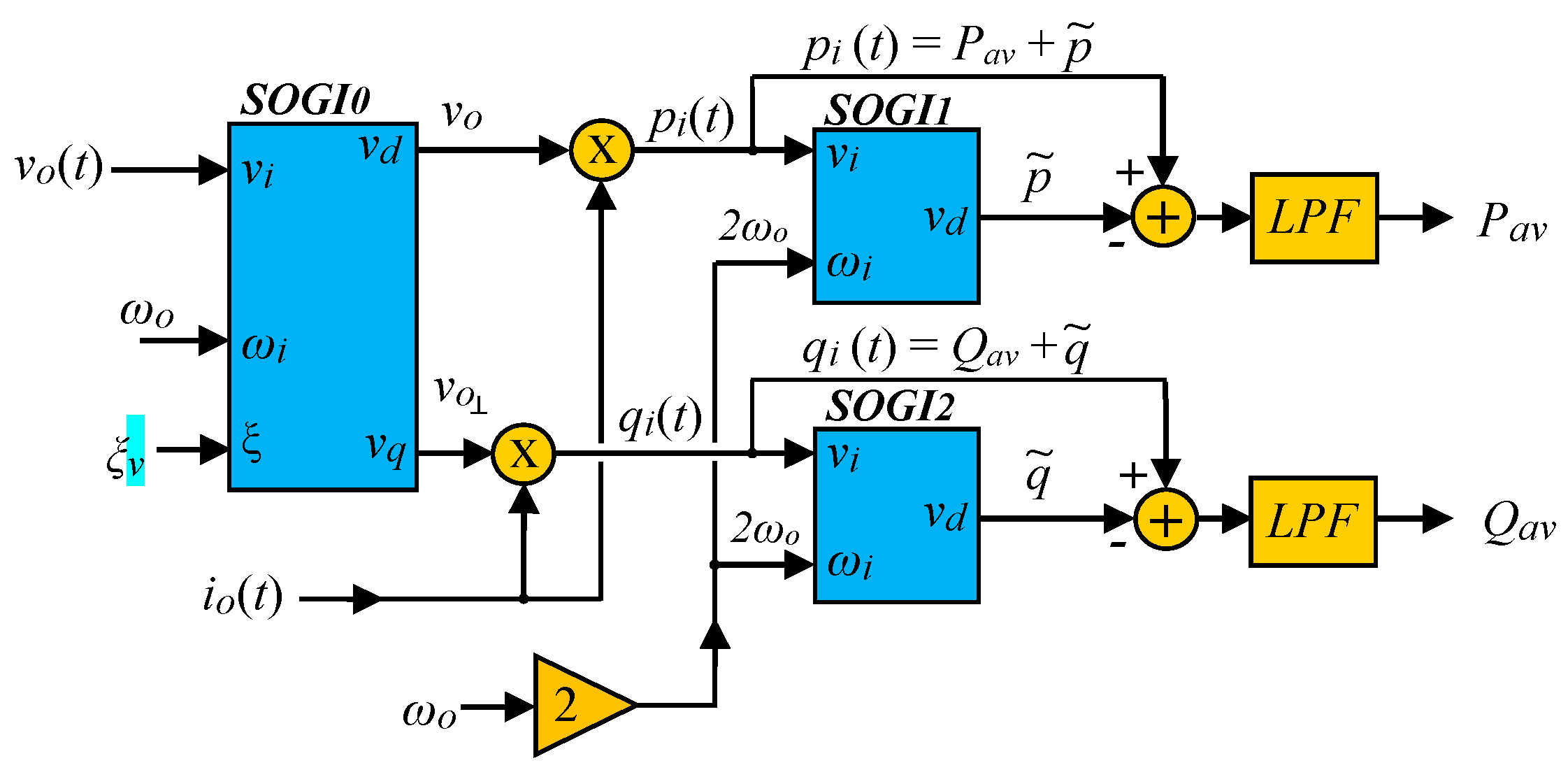
2.5. Proposed P-Q Calculation Scheme
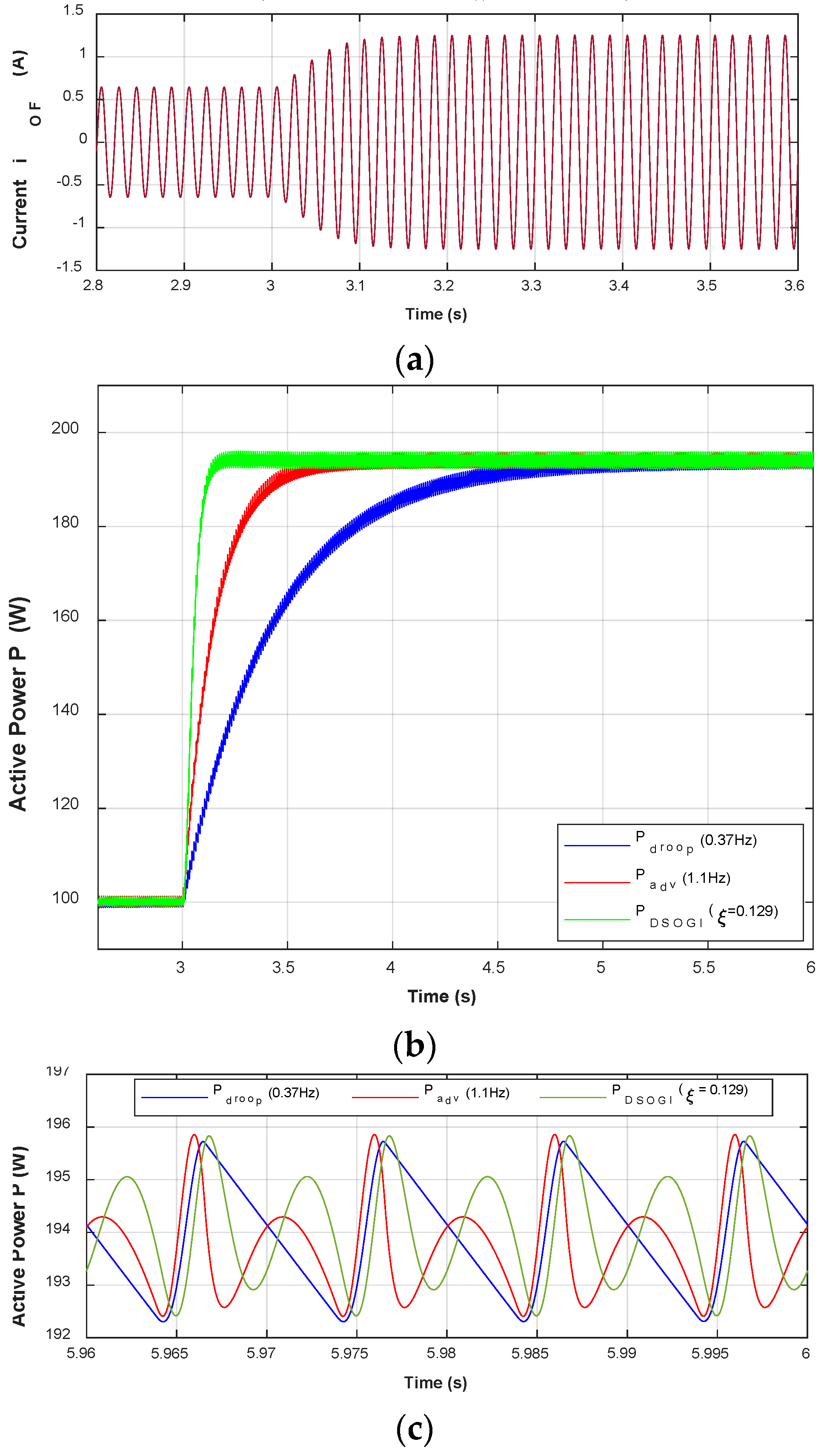
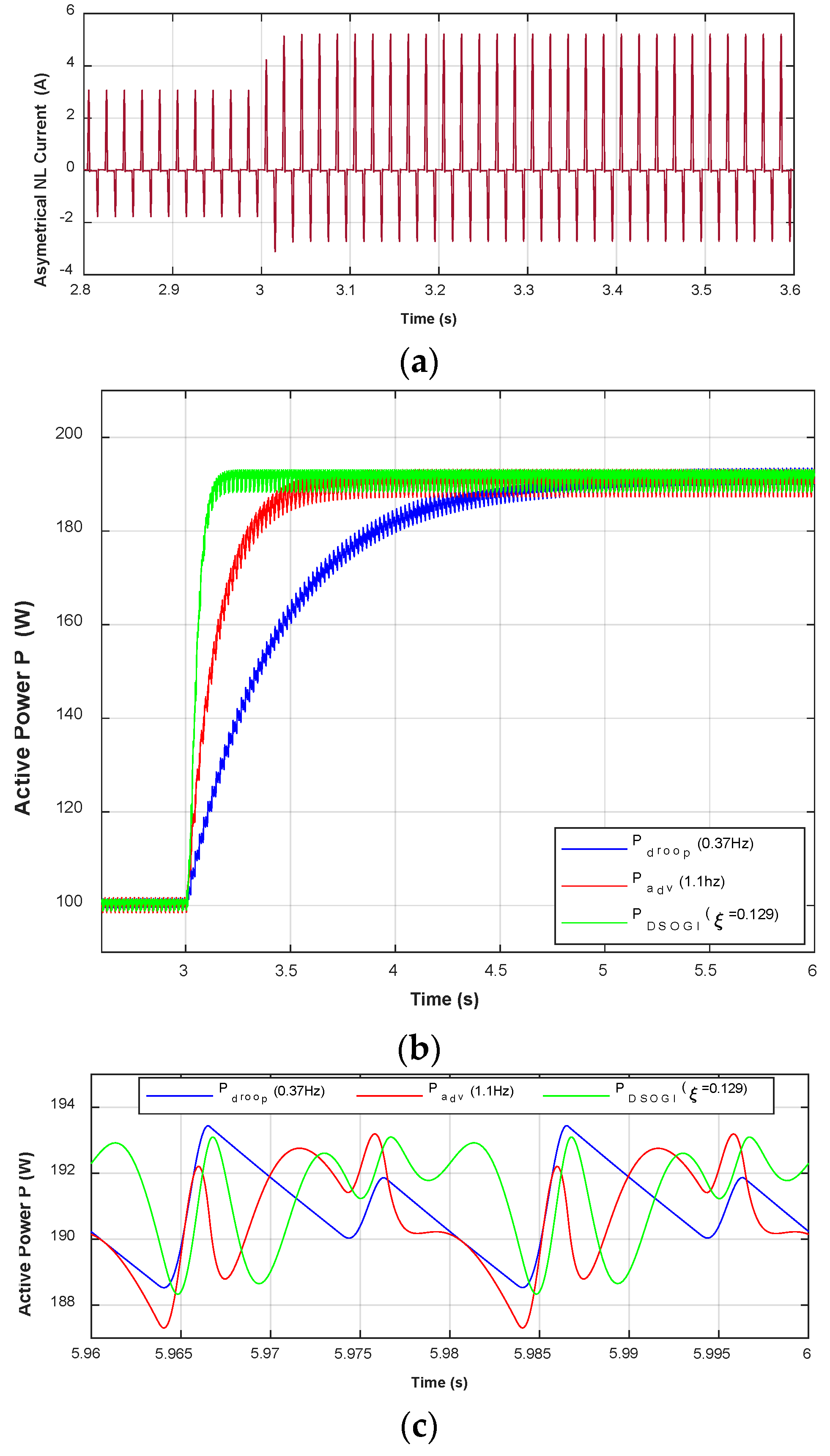
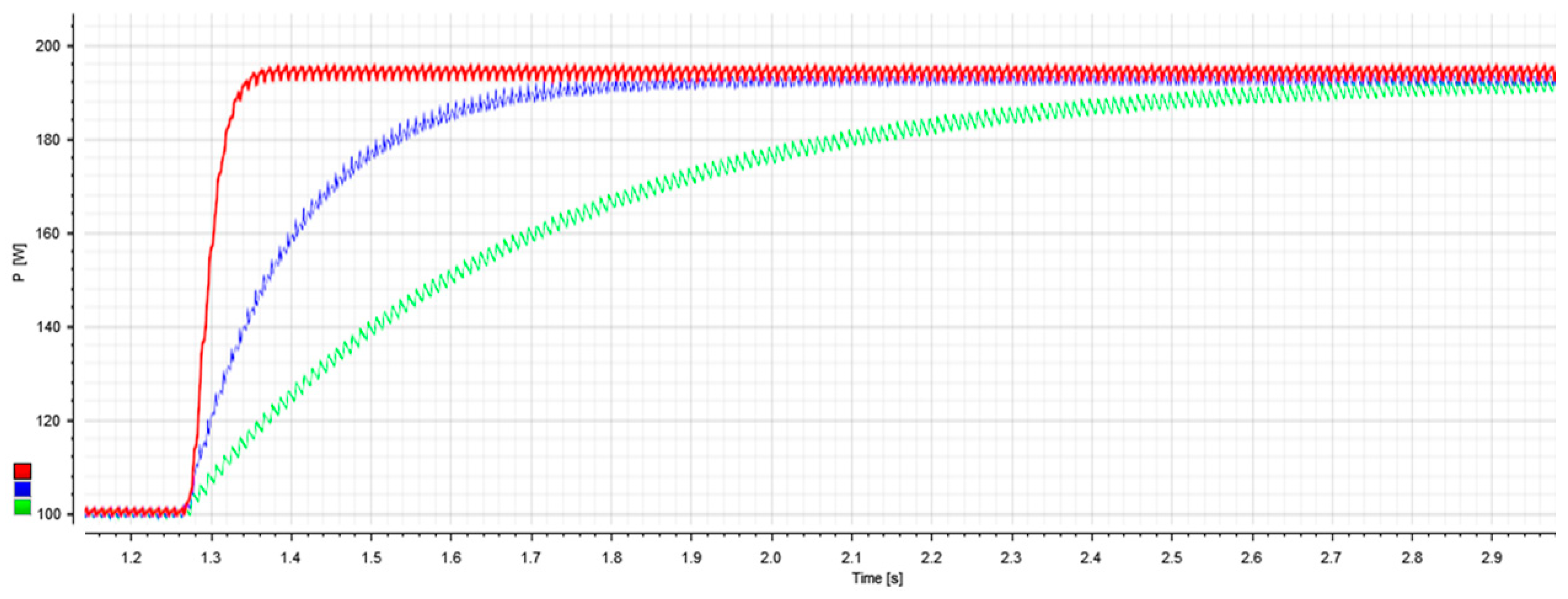
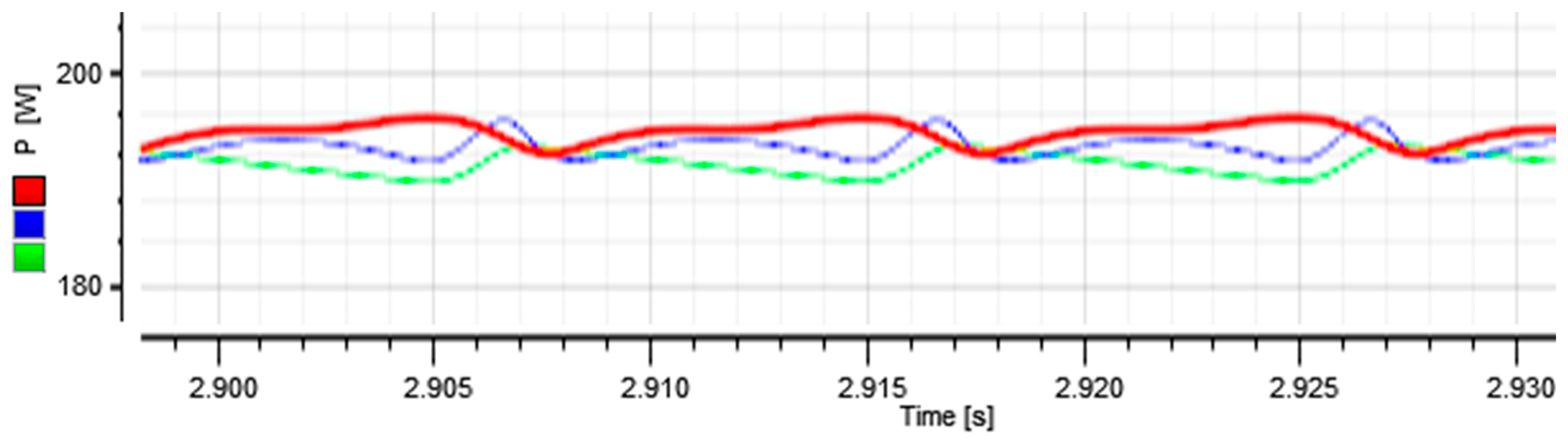
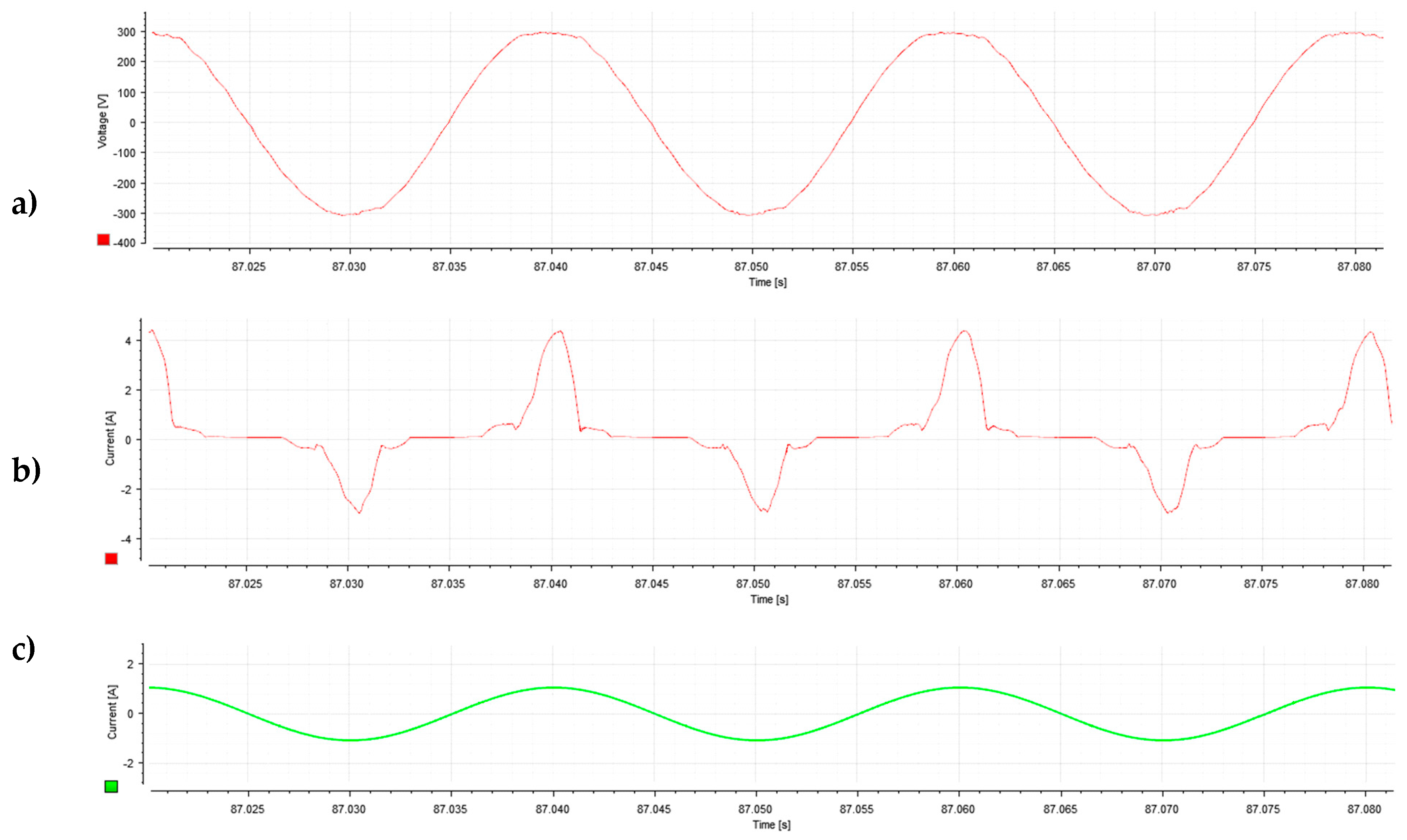
3. Experimental Results
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Kim, J.-H.; Lee, Y.-S.; Kim, H.-J.; Han, B.-M. A New Reactive-Power Sharing Scheme for Two Inverter-Based Distributed Generations with Unequal Line Impedances in Islanded Microgrids. Energies 2017, 10, 1800. [Google Scholar] [CrossRef]
- Ren, B.; Sun, X.; Chen, S.; Liu, H. A Compensation Control Scheme of Voltage Unbalance Using a Combined Three-Phase Inverter in an Islanded Microgrid. Energies 2018, 11, 2486. [Google Scholar] [CrossRef]
- Ma, J.; Wang, X.; Liu, J.; Gao, H. An Improved Droop Control Method for Voltage-Source Inverter Parallel Systems Considering Line Impedance Differences. Energies 2019, 12, 1158. [Google Scholar] [CrossRef]
- Coelho, E.A.A.; Cortizo, P.C.; Garcia, P.F.D. Small signal stability for single phase inverter connected to stiff AC system. In Proceedings of the Record of the IEEE Industry Applications Conf. 34th IAS Annual Meeting (Cat. No.99CH36370), Phoenix, AZ, USA, 1999; Volume 4, pp. 2180–2187. [Google Scholar]
- Soshinskaya, M.; Graus, W.H.J.; Guerrero, J.M.; Vasquez, J.C. Microgrids: experiences barriers and success factors. Renew. Sustain. Energy Rev. 2014, 40, 659–672. [Google Scholar] [CrossRef]
- Araújo, L.S.; Narváez, D.I.; Siqueira, T.G.; Villalva, M.G. Modified droop control for low voltage single phase isolated microgrids. In Proceedings of the IEEE Int. Conf. on Automatica (ICA-ACCA), Curico, Chile, 19–21 October 2016; pp. 1–6. [Google Scholar]
- IEEE. IEEE Standard Definitions for the Measurement of Electric Power Quantities Under Sinusoidal, Nonsinusoidal, Balanced or Unbalanced Conditions; IEEE Standard 1459-2010; IEEE: New York, NY, USA, 2000; pp. 1–52. [Google Scholar]
- Lu, J.; Wen, Y.; Zhang, Y.; Wen, W. A novel power calculation method based on second order general integrator. In Proceedings of the IEEE 8th Int. Power Electronics and Motion Control Conf. (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 1975–1979. [Google Scholar]
- Andrade, E.T.; Ribeiro, P.E.M.J.; Pinto, J.O.P.; Chen, C.L.; Lai, J.S.; Kees, N. A novel power calculation method for droop-control microgrid systems. In Proceedings of the 2012 27th Annual IEEE Applied Power Electronics Conf. and Exp. (APEC), Vladivostok, Russia, 9–10 September 2012; pp. 2254–2258. [Google Scholar]
- Ren, Z.; Gao, M.; Mo, Q.; Liu, K.; Yao, W.; Chen, M.; Qian, Z. Power Calculation Method Used in Wireless Parallel Inverters Under Nonlinear Load Conditions; IEEE: New York, NY, USA, 2010. [Google Scholar]
- Furtado, E.C.; Aguirre, L.A.; Torres, L.A.B. UPS Parallel Balanced Operation Without Explicit Estimation of Reactive Power—A Simpler Scheme. In Circuits and Systems II: Express Briefs; IEEE Trans. Eds.; IEEE: New York, NY, USA, 2008; pp. 1061–1065. [Google Scholar]
- Guerrero, J.; Matas, J.; Vicuna, L.G.; Castilla, M.; Miret, J. Decentralized Control for Parallel Operation of Distributed Generation Inverters Using Resistive Output Impedance. In Industrial Electronics; IEEE Trans. Eds.; IEEE: New York, NY, USA, 2007; pp. 994–1004. [Google Scholar]
- Silva, S.A.; Novochadlo, R.; Modesto, R.A. Single-phase PLL structure using modified p-q theory for utility connected systems. In Proceedings of the IEEE PESC, Rhodes, Greece, 15–19 June 2008; pp. 4706–4711. [Google Scholar]
- Wang, H.; Yue, X.; Pei, X.; Kang, Y. A new method of power calculation based on parallel inverters. In Proceedings of the IEEE EPE-PEMC, Novi Sad, Serbia, 28–30th October 2009; pp. 1573–1576. [Google Scholar]
- Wei, Y.; Xu, D.; Ma, K. A Novel Accurate Active and Reactive Power Calculation Method for Paralleled UPS System. In Proceedings of the APEC, Singapore, 15–16 November 2009; pp. 1269–1275. [Google Scholar]
- Ren, Z.; Gao, M.; Mo, Q.; Liu, K.; Yao, W.; Chen, M.; Qian, M. Power calculation method used in wireless parallel inverters under nonlinear load conditions. In Proceedings of the 25th Annual IEEE Applied Power Electronics Conf. and Exp., Palm Springs, CA, USA, 21–25 February 2010; pp. 1674–1677. [Google Scholar]
- Akagi, H.; Watanabe, E.; Aredes, M. Instantaneous Power Theory and Application to Power Conditioning; IEEE Press Series in Power Engineering; IEEE: New York, NY, USA, 2007; pp. 5–28. [Google Scholar]
- Gao, M.; Yang, S.; Jin, C.; Ren, Z.; Chen, M.; Qian, Z. Analysis and experimental validation for power calculation based on p-q theory in single-phase wireless-parallel inverters. In Proceedings of the 26th Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Hyderabad, India, 16–18 December 2011; pp. 620–624. [Google Scholar]
- Matas, J.; Castilla, M.; d. Vicuña, L.G.; Miret, J.; Vasquez, J.C. Virtual Impedance Loop for Droop-Controlled Single-Phase Parallel Inverters Using a Second-Order General-Integrator Scheme. In Power Electronics; IEEE Trans. Eds.; IEEE: New York, NY, USA, 2010; pp. 2993–3002. [Google Scholar]
- Tolani, S.; Sensarma, P. An improved droop controller for parallel operation of single-phase inverters using R-C output impedance. In Power Electronics, Drives and Energy Systems (PEDES), Bengaluru; IEEE Trans. Eds.; IEEE: New York, NY, USA, 2012; pp. 1–6. [Google Scholar]
- Yang, Y.; Blaabjerg, F. A new power calculation method for single-phase grid-connected systems. In IEEE International Symposium on Industrial Electronics; IEEE Eds.; IEEE: New York, NY, USA, 2013; pp. 1–6. [Google Scholar]
- Guerrero, J.M.; Berbel, N.; Matas, J.; de Vicuna, L.G.; Miret, J. Decentralized Control for Parallel Operation of Distributed Generation Inverters in Microgrids Using Resistive Output Impedance. In Proceedings of the IECON 2006—32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 7–10 November 2006; pp. 5149–5154. [Google Scholar]
- Mariachet, J.E.; Matas, J.; Martín, H.; Abusorrah, A. Power Calculation Algorithm for Single-Phase Droop-Operated Inverters Considering Nonlinear Loads. Renew. Energy Power Qual. J. 2018, 1, 16. [Google Scholar]
- Song, H.; Nam, K. Dual current control scheme for PWM converter under unbalanced input voltage conditions. In Ind. Electron; IEEE Trans. Eds.; IEEE: New York, NY, USA, 1991; pp. 953–959. [Google Scholar]
- IEEE Standard Definitions for the Measurement of Electric Power Quantities Under Sinusoidal; Nonsinusoidal, Balanced, or Unbalanced Conditions-Redline; IEEE: New York, NY, USA, 2010; pp. 1–52, 1459-2010 (Revision of IEEE Std 1459-2000)-Redline, 19 March 2010.
- Matas, J.; Castilla, M.; Miret, J.; Vicuna, L.G.; Guzman, R. An adaptive prefiltering method to improve the speed/accuracy tradeoff of voltage sequence detection methods under adverse grid conditions. IEEE Trans. Ind. Electron. 2014, 61, 2139–2151. [Google Scholar] [CrossRef]
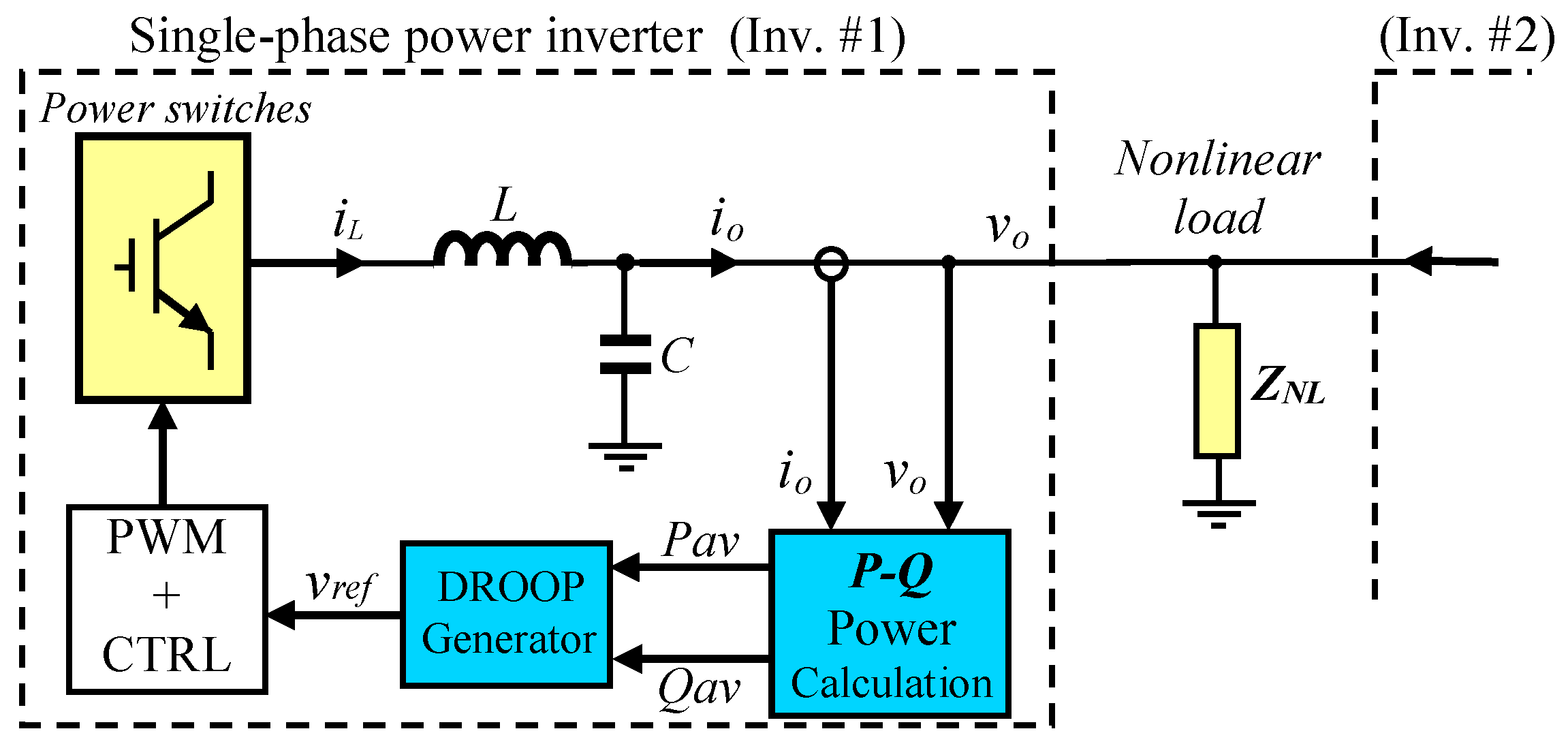
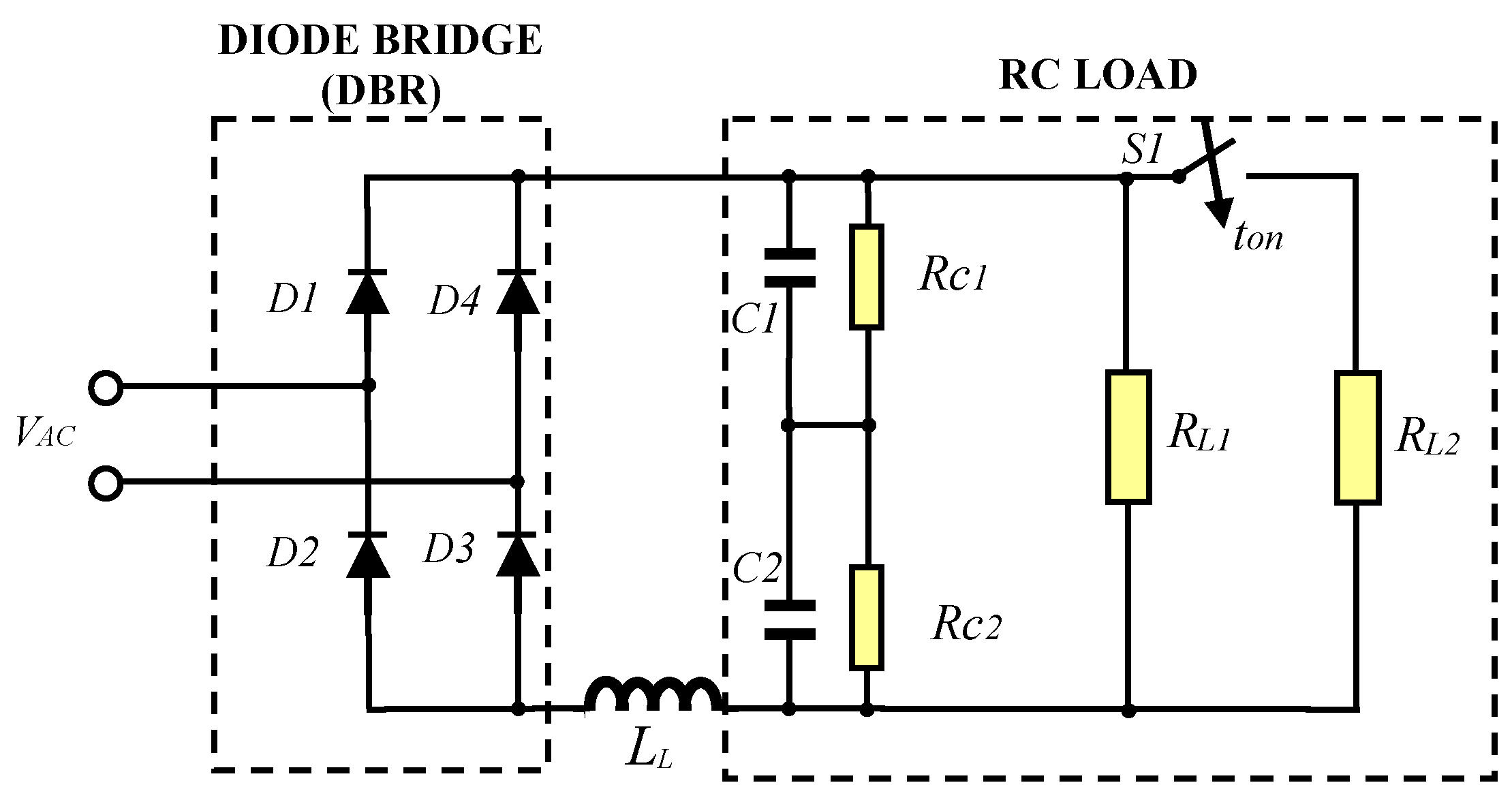
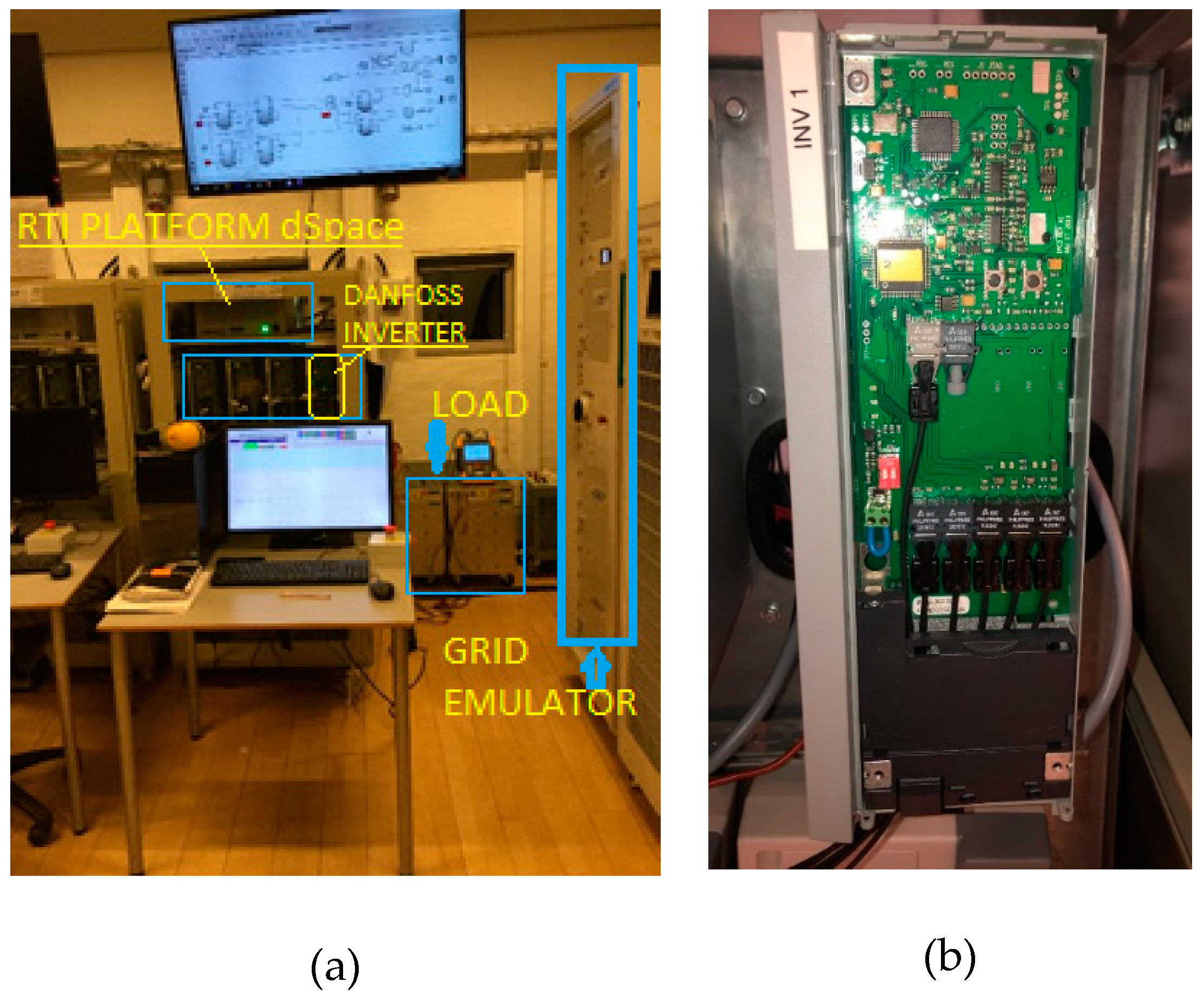
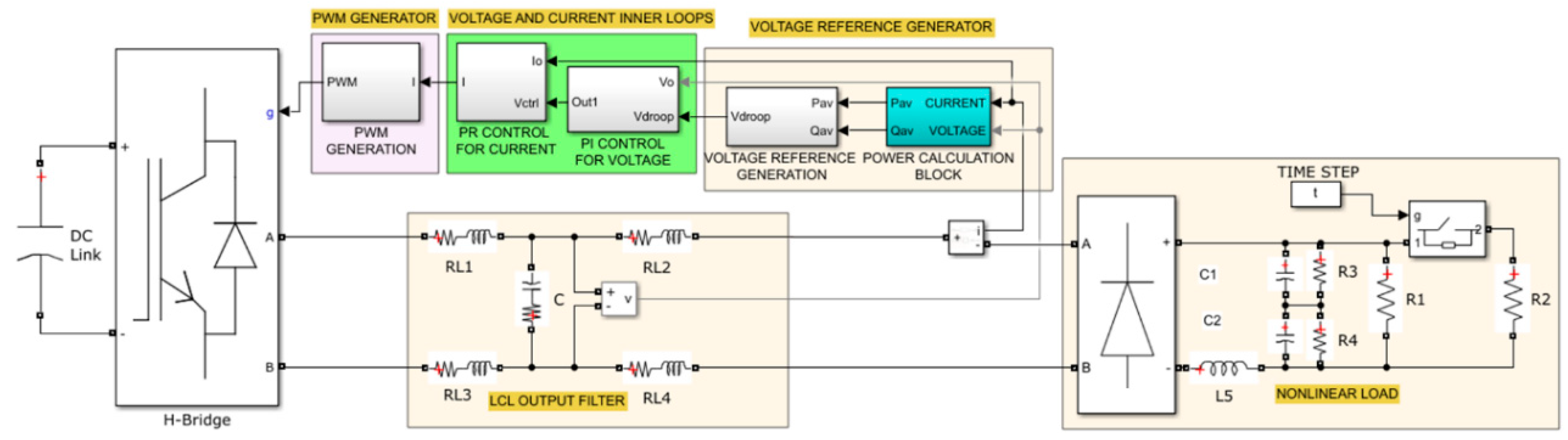

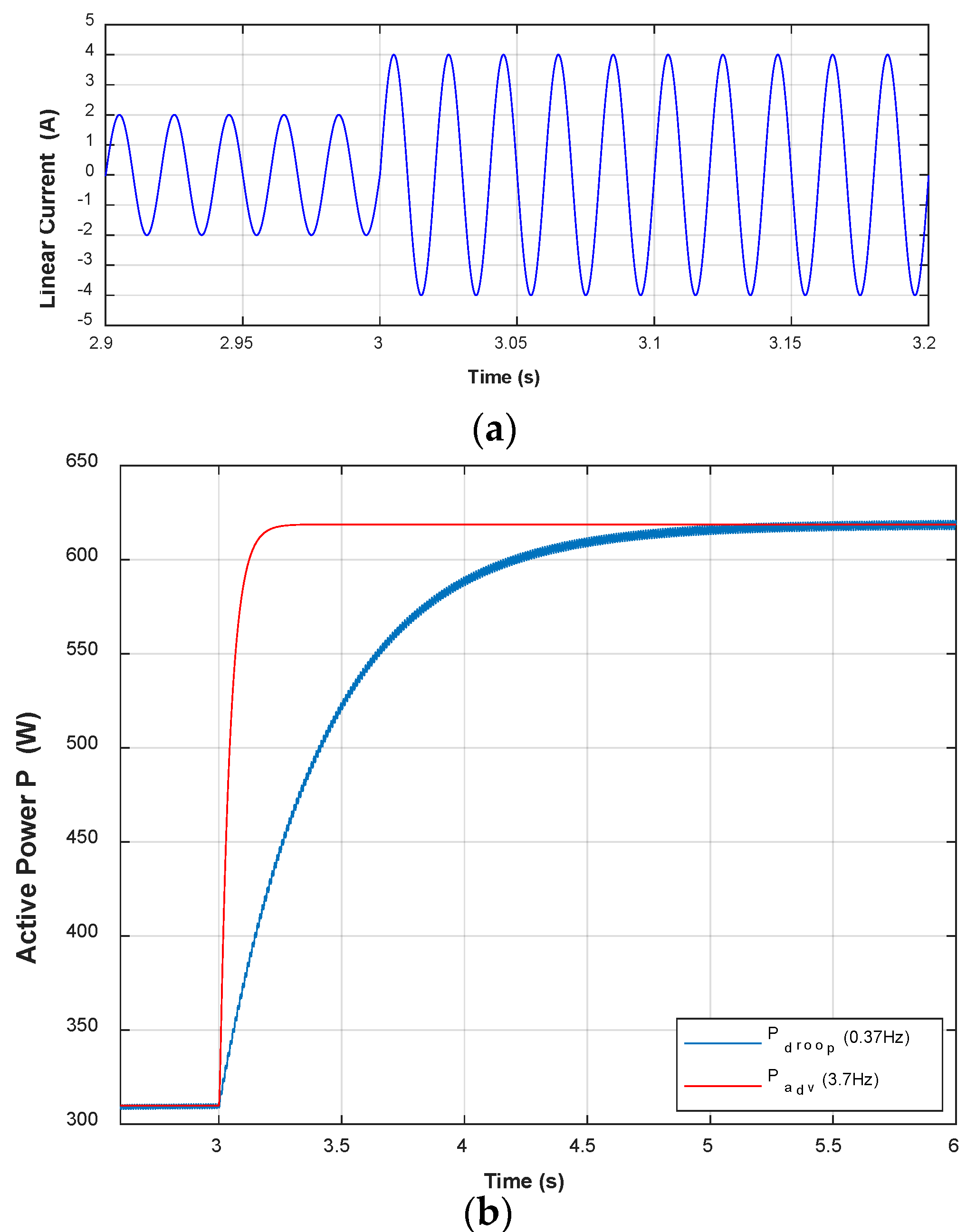
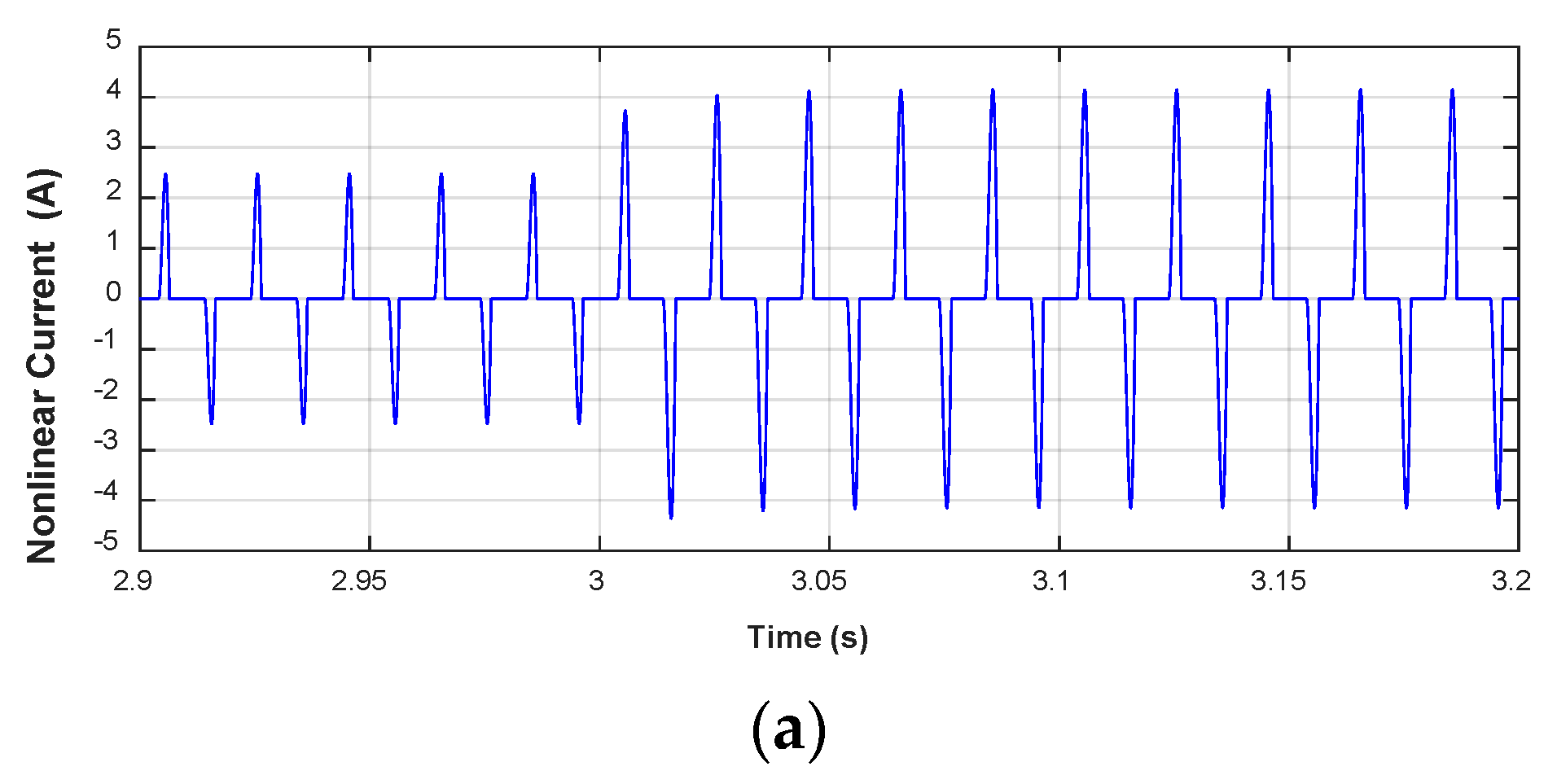
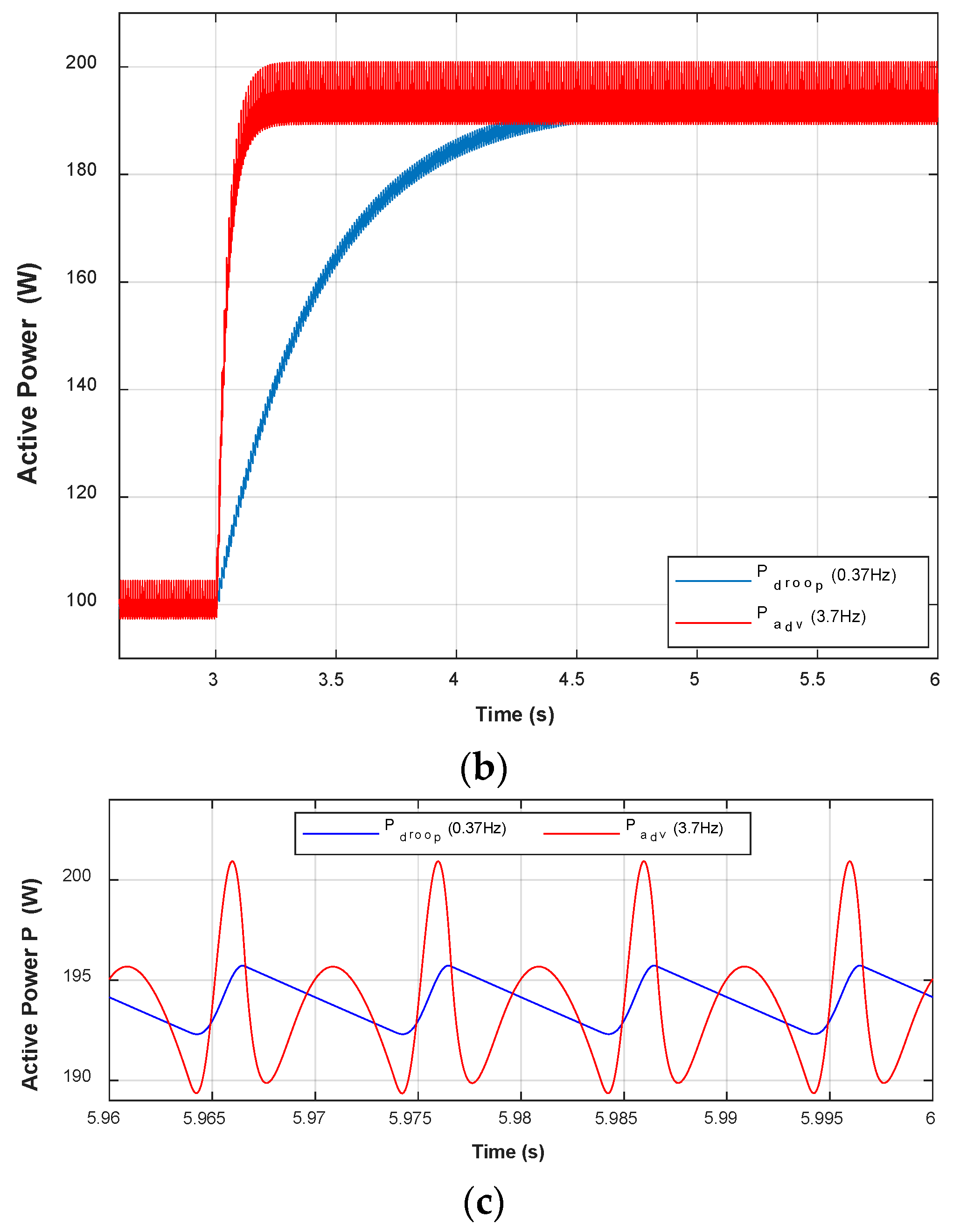


| Parameter | Value |
|---|---|
| LC Filter | 1.8 mH; 25 µF |
| Switching frequency, fs | 10 kHz |
| RonD1-D4 | 0.01 Ω |
| 84 µH | |
| C1, C2 | 470 µF |
| 37 kΩ | |
| 960 Ω |
| Parameter | Value |
|---|---|
| Vn | 311 V |
| ωo | 2π50 rad/s |
| DBR RESISTOR LOAD FOR T < 3S | 950 Ω |
| DBR RESISTOR LOAD FOR T > 3S | 471.8 Ω |
| THD io(t) | 215% |
| ξ0 | 0.7 |
| ξ1 = ξ2 | 1 |
| Parameter | Value |
|---|---|
| PDROOP | 325 ms |
| PADV | 165 ms |
| PDSOGI | 66 ms |
| Parameter | Value |
|---|---|
| RL1 = RL2 = RL3 = RL4 | 1.8 mH; 0.01 Ω |
| RC branch | 25 µF; 1 Ω |
| Switching frequency, fs | 10 kHz |
| RonD1 and D4/ RonD2 and D3 | 0.01 Ω/ 1 Ω |
| LL | 84 µH |
| C1 = C2/ Rc1 = Rc2 | 470 µF/37 kΩ |
| 960 Ω |
| P-Q Algorithm | Settling Time Matlab (ms)/(%reduction) | Settling Time HIL (ms)/(%reduction) | Settling Time VSI (ms) /(%reduction) |
|---|---|---|---|
| Conventional, Pdroop | 760 / (---) | 780 / (---) | 930 (---) |
| Advanced, Padv | 310 / (59%) | 330 / (58%) | 360 (61%) |
| Proposed, PDSOGI | 130 / (83%) | 140 / (82%) | 180 (80%) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Mariachet, J.; Matas, J.; Martín, H.; Li, M.; Guan, Y.; Guerrero, J.M. A Power Calculation Algorithm for Single-Phase Droop-Operated-Inverters Considering Linear and Nonlinear Loads HIL-Assessed. Electronics 2019, 8, 1366. https://doi.org/10.3390/electronics8111366
El Mariachet J, Matas J, Martín H, Li M, Guan Y, Guerrero JM. A Power Calculation Algorithm for Single-Phase Droop-Operated-Inverters Considering Linear and Nonlinear Loads HIL-Assessed. Electronics. 2019; 8(11):1366. https://doi.org/10.3390/electronics8111366
Chicago/Turabian StyleEl Mariachet, Jorge, Jose Matas, Helena Martín, Mingshen Li, Yajuan Guan, and Josep M. Guerrero. 2019. "A Power Calculation Algorithm for Single-Phase Droop-Operated-Inverters Considering Linear and Nonlinear Loads HIL-Assessed" Electronics 8, no. 11: 1366. https://doi.org/10.3390/electronics8111366
APA StyleEl Mariachet, J., Matas, J., Martín, H., Li, M., Guan, Y., & Guerrero, J. M. (2019). A Power Calculation Algorithm for Single-Phase Droop-Operated-Inverters Considering Linear and Nonlinear Loads HIL-Assessed. Electronics, 8(11), 1366. https://doi.org/10.3390/electronics8111366









