Motion Planning of a Second-Order Nonholonomic Chained Form System Based on Holonomy Extraction

Abstract

This paper proposes a motion planning algorithm for dynamic nonholonomic systems represented in a second-order chained form. The proposed approach focuses on the so-called holonomy resulting from a kind of motion that traverses a closed path in a reduced configuration space of the system. According to the author’s literature survey, control approaches that make explicit use of holonomy exist for kinematic nonholonomic systems but does not exist for dynamic nonholonomic systems. However, the second-order chained form system is controllable. Also, its structure analogizes with the one of the first-order chained form for kinematic nonholonomic systems. These survey and perspectives brought a hypothesis that there exists a specific control strategy for extracting holonomy of the second-order chained form system to the author. To verify this hypothesis, this paper shows that the holonomy of the second-order chained form system can be extracted by combining two appropriate pairs of sinusoidal inputs. Then, based on such holonomy extraction, a motion planning algorithm is constructed. Furthermore, the effectiveness is demonstrated through some simulations including an application to an underactuated manipulator.

1. Introduction

Nonholonomic systems—dynamical systems with non-integrable differential constraints—have attracted attention as challenging robotic systems in the fields of motion planning and control [1,2,3,4]. The most symbolical control problem is characterized by Brockett’s theorem [5]. It provides a well-known fact that nonholonomic systems cannot be stabilized by using pure smooth state feedback control. According to the kind of constraints, the nonholonomic systems are generally classified into two types: kinematic ones and dynamic ones. The former, which are subject to velocity constraints, include a wheeled mobile robot without or with trailers [1], a snakeboard [1] and a trident snake robot [6]; the latter, which are subject to acceleration constraints, include an underactuated manipulator [7,8,9,10], a surface vessel [11,12], and a blimp [13].

Nonholonomic systems have an intrinsic property that a part of states is impossible to change by an individual control input. The key to control such states is to combine the effects of multiple control inputs in order to extract a kind of motion expressed by Lie brackets. For a class of kinematic nonholonomic systems, holonomy (or geometric phase) is defined as “the extent to which a closed path in the base space fails to be closed in the configuration space” [14], where the base space is a reduced configuration space. The effect which corresponds to Lie brackets is generated by periodic control inputs. It can be said as the essential motion of kinematic nonholonomic systems. In fact, several control approaches utilize the holonomy [1,14,15,16,17,18,19,20].

Table 1 summarizes main control approaches proposed so far for nonholonomic systems. The control approaches are classified into three groups by the type of constraints and also, in each group, sorted by the published year. From Table 1, the following points can be seen:

Table 1. Comparison of conventional control approaches.

Constraints	Reference	Canonical Form	Application${}^{*}$	Control Approach	Explicit Use of Holonomy
	[14]	Partially FL	Knife-edge, etc.	MP w/sinusoids	Yes
	[20]	1st-order CF	Vehicle, etc.	MP w/sinusoids	Yes
	[1]	1st-order CF	Multifingered robot hand	MP w/sinusoids	Yes
	[15]	Left-invariant	—	MP w/sinusoids	Yes
	[21]	Partially FL	Acrobot, etc.	Stab. by nonlinear FB	No
	[22]	1st-order CF	Unicycle robot	Traj. tracking	No
Kinematic	[18]	1st-order non-CF	—	Stab. by Switched FB	Yes
	[19]	Cross CF	—	Stab. by Switched FB	Yes
	[16]	—	Knife-edge	MP	Yes
	[17]	—	Rolling disk	MP	Yes
	[23]	1st-order CF	Firetruck, etc.	Stab. by AISMC	No
	[24]	—	Rolling disk	Traj. tracking	No
	[7]	—	R${}_{\mathrm{a}}$-R${}_{\mathrm{u}}$ UAM	Stab. to EM	No
	[11]	—	Surface vehicle	Stab. to EM	No
	[8]	2nd-order CF	2P${}_{\mathrm{a}}$-R${}_{\mathrm{u}}$ UAM	Stab. to traj.	No
	[10]	3rd-link’s acc.	2R${}_{\mathrm{a}}$-R${}_{\mathrm{u}}$ UAM	Stab. to composite traj.	No
	[9]	2nd-order CF	2R${}_{\mathrm{a}}$-R${}_{\mathrm{u}}$ UAM	Traj. design (≈ MP)	No
	[25]	2nd-order CF	2P${}_{\mathrm{a}}$-R${}_{\mathrm{u}}$ UAM	Stab. by discont. FB w/non-regular FL	No
	[26]	Last-link’s PFL	$(n-1)$X${}_{\mathrm{a}}$-R${}_{\mathrm{u}}$ UAM	Traj. tracking w/dynamic FL	No
Dynamic	[27,28]	2nd-order CF	2P${}_{\mathrm{a}}$-R${}_{\mathrm{u}}$ UAM	Traj. tracking w/cascaded BS	No
	[28]	2nd-order CF	2R${}_{\mathrm{a}}$-R${}_{\mathrm{u}}$ UAM	Stab. by Homogeneous FB	No
	[29]	port-Hamiltonian	2R${}_{\mathrm{a}}$-R${}_{\mathrm{u}}$ UAM	Stab. by IDA-PBC	No
	[30]	2nd-order CF	2P${}_{\mathrm{a}}$-R${}_{\mathrm{u}}$ UAM	Traj. tracking & stab.	No
	[13]	2nd-order CF	Underactuated AUV	Stab. by discontinuous FB	No
	[31]	2nd-order CF	—	Stab. based on MPC	No
	[32]	2nd-order CF	Underactuated hovercraft	Stab. by Hölder continuous FB	No
	[23]	2nd-order CF	2P${}_{\mathrm{a}}$-R${}_{\mathrm{u}}$ UAM	Stab. by AISMC	No
	This paper	2nd-order CF	2R${}_{\mathrm{a}}$-R${}_{\mathrm{u}}$ UAM	MP w/sinusoids	Yes
3rd	[23]	3rd-order CF	2P${}_{\mathrm{a}}$-R${}_{\mathrm{u}}$ UAM w/jerk	Stab. by AISMC	No

* Note: As for the type of UAM, this table adopts the same notation as in Reference [26]. For instance, $(n-1)$X${}_a$-R${}_u$ means that the first $n-1$ actuated joints are prismatic (P${}_a$) or revolute (R${}_a$) and the last unactuated joint is revolute (R${}_u$).

• As a canonical form for nonholonomic systems, the chained form is often used over all kinds of constraints.
• Many studies have been attracted to a feedback control problem related Brockett’s theorem independently of the type of constraints.
• For kinematic nonholonomic systems, there are some control approaches that explicitly use holonomy especially in motion planning; for dynamic or third-order nonholonomic systems, there is no such control approach.

On the other hand, by comparing the first- and second-order chained form systems, it can be found that the structures are similar unless the number of integrators is different. This perspective and the above-mentioned survey led the author to a hypothesis that there exists an appropriate pair of sinusoids to extract holonomy of the second-order chained form system.

Motivated by the hypothesis, this paper addresses a motion planning problem for the second-order chained form system. A class of dynamic nonholonomic systems can be represented as the second-order chained form by transforming the generalized coordinates and control inputs appropriately [8,9,12]. The second-order chained form system is described as a type of affine systems which is nonlinear controllable. Inspired by the structural difference and analogy between the first- and second-order chained form systems, it is found that a combination of two appropriate pairs of sinusoidal inputs can be used to extract the holonomy. This verifies the hypothesis. The idea of holonomy extraction is available directly to motion planning. The proposed motion planning algorithm can be applied to an underactuated manipulator. Its effectiveness is demonstrated by some simulation results.

The main contributions of the proposed approach are emphasized as follows:

• A specific way to extract holonomy of the second-order chained form system was proposed. Based on holonomy extraction, a motion planning algorithm was constructed.
• The holonomy-based motion planning algorithm was applied to an underactuated manipulator. The usefulness of the proposed algorithm was validated through some simulation results.
• To the best of the author’s knowledge, no control approach that makes explicit use of the holonomy for the second-order chained form system has been previously reported as shown in Table 1.

This paper has improved the preliminary results of the author’s previous studies [33,34]. In Reference [33], the author has first proposed a specific strategy of holonomy extraction for the second-order chained form system. In addition to that, this paper presents another strategy (see Remark 1). The holonomy obtained in each strategy was also visualized in some phase spaces to understand the differences (see Figures 2 and 4). In Reference [34], the author has applied the holonomy-based motion planning algorithm into an underactuated manipulator and discussed singularities of the system transformation therein. Instead of such discussion, this paper examine an effect from the parameters of control inputs (see the second last paragraph in Section 4, that is, the paragraph before Remark 5).

The rest of the paper is organized as follows. In Section 2, a system representation of the second-order chained form system is given and then its controllability is confirmed. In Section 3, to extract the holonomy of the system, appropriate pairs of sinusoids is concretely provided; based on the maneuver of holonomy extraction, a motion planning algorithm is also proposed. In Section 4, the algorithm is applied to an underactuated manipulator. In the last section, the paper is concluded with directions for future work.

2. Second-Order Nonholonomic Chained Form System and Its Controllability

Consider the following second-order chained form system:

$$\left\{\begin{array}{c}{\ddot{\xi }}_1=u_1\hfill \\ {\ddot{\xi }}_2=u_2\hfill \\ {\ddot{\xi }}_3={\xi }_2{u}_1,\hfill \end{array}\right.$$

(1)

which is one canonical representation for a class of dynamic nonholonomic systems. This system can be obtained from the original dynamical model via an appropriate transformation of the generalized coordinates and control inputs. By defining a state vector by $\mathit{z}={[z_1,z_2,\cdots ,z_6]}^{\top }:={[{\xi }^{\top },{\dot{\xi }}^{\top }]}^{\top }(\xi :={[{\xi }_1,{\xi }_2,{\xi }_3]}^{\top })$, in state space form, (1) is represented as an affine nonlinear system

$$\frac{{\displaystyle \mathrm{d}}}{{\displaystyle \mathrm{d}t}}\mathit{z}=\mathit{f}\left(\mathit{z}\right)+{\mathit{g}}_1\left(\mathit{z}\right)u_1+{\mathit{g}}_2\left(\mathit{z}\right)u_2,$$

(2)

where

$$\begin{array}{cccccccccccccc}\hfill \mathit{f}\left(\mathit{z}\right)& :=[\hfill & z_4\hfill & ,\hfill & z_5\hfill & ,\hfill & z_6\hfill & ,\hfill & 0\hfill & ,\hfill & 0& ,& 0& {]}^{\top },\end{array}$$

(3)

$$\begin{array}{cccccccccccccc}\hfill {\mathit{g}}_1\left(\mathit{z}\right)& :=[\hfill & 0\hfill & ,\hfill & 0\hfill & ,\hfill & 0\hfill & ,\hfill & 1\hfill & ,\hfill & 0& ,& z_2& {]}^{\top },\end{array}$$

(4)

$$\begin{array}{cccccccccccccc}\hfill {\mathit{g}}_2\left(\mathit{z}\right)& :=[\hfill & 0\hfill & ,\hfill & 0\hfill & ,\hfill & 0\hfill & ,\hfill & 0\hfill & ,\hfill & 1& ,& 0& {]}^{\top }.\end{array}$$

(5)

Note that the system (2) has equilibrium points at ${\mathit{z}}_e:={[{\left({\xi }^{★}\right)}^{\top },{\mathbf{0}}_3^{\top }]}^{\top },{\xi }^{★}\in {\mathbb{R}}^3$ with $u_1=u_2=0$.

According to Sussmann’s theorem [35], the small-time local controllability (STLC) of the affine system (2) is easily confirmed. For a Lie bracket $\mathit{h}$, let ${\delta }_0\left(\mathit{h}\right)$, ${\delta }_1\left(\mathit{h}\right)$ and ${\delta }_2\left(\mathit{h}\right)$ be defined as the number of times that $\mathit{f}$, ${\mathit{g}}_1$ and ${\mathit{g}}_2$ occur in $\mathit{h}$, respectively. If ${\delta }_0\left(\mathit{h}\right)$ is odd and ${\delta }_i\left(\mathit{h}\right)$ is even for each $i=1,2$, the bracket $\mathit{h}$ is called “bad”; otherwise, the bracket $\mathit{h}$ is called “good”. Also, let ${\sum }_{i=0}^2{\delta }_i\left(\mathit{h}\right)$ be defined as the degree of $\mathit{h}$. Then, in the Philip Hall bases [1] of (2), the non-zero vector fields at ${\mathit{z}}_e$ are as follows:

$$\begin{array}{cccccccccccccc}\hfill {\mathit{g}}_1\left({\mathit{z}}_e\right)& =[\hfill & 0\hfill & ,\hfill & 0\hfill & ,\hfill & 0\hfill & ,\hfill & 1\hfill & ,\hfill & 0& ,& z_2^{★}& {]}^{\top },\end{array}$$

(6)

$$\begin{array}{cccccccccccccc}\hfill {\mathit{g}}_2\left({\mathit{z}}_e\right)& =[\hfill & 0\hfill & ,\hfill & 0\hfill & ,\hfill & 0\hfill & ,\hfill & 0\hfill & ,\hfill & 1& ,& 0& {]}^{\top },\end{array}$$

(7)

$$\begin{array}{cccccccccccccc}\hfill [\mathit{f},{\mathit{g}}_1]\left({\mathit{z}}_e\right)& =[\hfill & -1\hfill & ,\hfill & 0\hfill & ,\hfill & -z_2^{★}\hfill & ,\hfill & 0\hfill & ,\hfill & 0& ,& 0& {]}^{\top },\end{array}$$

(8)

$$\begin{array}{cccccccccccccc}\hfill [\mathit{f},{\mathit{g}}_2]\left({\mathit{z}}_e\right)& =[\hfill & 0\hfill & ,\hfill & -1\hfill & ,\hfill & 0\hfill & ,\hfill & 0\hfill & ,\hfill & 0& ,& 0& {]}^{\top },\end{array}$$

(9)

$$\begin{array}{cccccccccccccc}\hfill [{\mathit{g}}_2,[\mathit{f},{\mathit{g}}_1]]\left({\mathit{z}}_e\right)& =[\hfill & 0\hfill & ,\hfill & 0\hfill & ,\hfill & 0\hfill & ,\hfill & 0\hfill & ,\hfill & 0& ,& 1& {]}^{\top },\end{array}$$

(10)

$$\begin{array}{cccccccccccccc}\hfill [{\mathit{g}}_1,[\mathit{f},{\mathit{g}}_2]]\left({\mathit{z}}_e\right)& =[\hfill & 0\hfill & ,\hfill & 0\hfill & ,\hfill & 0\hfill & ,\hfill & 0\hfill & ,\hfill & 0& ,& 1& {]}^{\top },\end{array}$$

(11)

$$\begin{array}{cccccccccccccc}\hfill [{\mathit{g}}_2,[\mathit{f},[\mathit{f},{\mathit{g}}_1]]]\left({\mathit{z}}_e\right)& =[\hfill & 0\hfill & ,\hfill & 0\hfill & ,\hfill & -2\hfill & ,\hfill & 0\hfill & ,\hfill & 0& ,& 0& {]}^{\top },\end{array}$$

(12)

$$\begin{array}{cccccccccccccc}\hfill [[\mathit{f},{\mathit{g}}_1],[\mathit{f},{\mathit{g}}_2]]\left({\mathit{z}}_e\right)& =[\hfill & 0\hfill & ,\hfill & 0\hfill & ,\hfill & -1\hfill & ,\hfill & 0\hfill & ,\hfill & 0& ,& 0& {]}^{\top }.\end{array}$$

(13)

Six appropriate vector fields out of (6)–(13) can span ${\mathbb{R}}^6$, which means that the system is locally accessible. In other words, the so-called Lie Algebra Rank Condition (LARC) is satisfied. On the other hand, all bad brackets , $\mathit{f}$, $[{\mathit{g}}_1,[\mathit{f},{\mathit{g}}_1]]$ and $[{\mathit{g}}_2,[\mathit{f},{\mathit{g}}_2]]$, are zero vector fields at ${\mathit{z}}_e$. This obviously can be expressed by linear combinations of good brackets of lower degree Thus the second-order chained form system (1) is small-time local controllable at ${\mathit{z}}_e$.

From the above-mentioned controllability analysis, there exists an admissible control input such that the system can be steered from any equilibrium point to its neighborhood for a small time. This, however, does not imply that a specific control input is obtained. As a specific solution, the subsequent section presents a motion planning algorithm that makes use of holonomy extraction.

3. Motion Planning Based on Holonomy Extraction

This section considers a motion planning problem of the second-order chained form system and presents an algorithm to solve it. The key idea is to extract holonomy of the system by using sinusoidal inputs. Based on that, the proposed algorithm can be simply constructed.

3.1. Problem Formulation

The following motion planning problem is addressed in this paper:

Problem 1.

Suppose that the second-order chained form system (1) (or (2)) is given. Then, find a control input $\mathit{u}\left(t\right)={[u_1\left(t\right),u_2\left(t\right)]}^{\top }$ which steers the system between initial and final equilibrium points: $(\xi \left(t_0\right),\dot{\xi }\left(t_0\right))=({\xi }_0,{\mathbf{0}}_3)$ and $(\xi \left(t_f\right),\dot{\xi }\left(t_f\right))=({\xi }^{★},{\mathbf{0}}_3)$, on a given time interval $[t_0,t_f]$.

The affine system (2) can be divided into two parts: the double-integrator part with respect to $(z_1,z_2,z_4,z_5)(=({\xi }_1,{\xi }_2,{\dot{\xi }}_1,{\dot{\xi }}_2))$; and the residual part with respect to $(z_3,z_6)(=({\xi }_3,{\dot{\xi }}_3))$. The former is linear controllable, so it is easy to control the four states. The latter nonlinear part is what we should focus on here. According to the controllability analysis in the last section, displacement of only $z_6(={\dot{\xi }}_3)$ requires the third-order Lie brackets such as (10) and (11); displacement of only $z_3(={\xi }_3)$ requires the fourth-order Lie brackets such as (12) and (13). In general, however, handling higher-order Lie brackets is quite difficult [6].

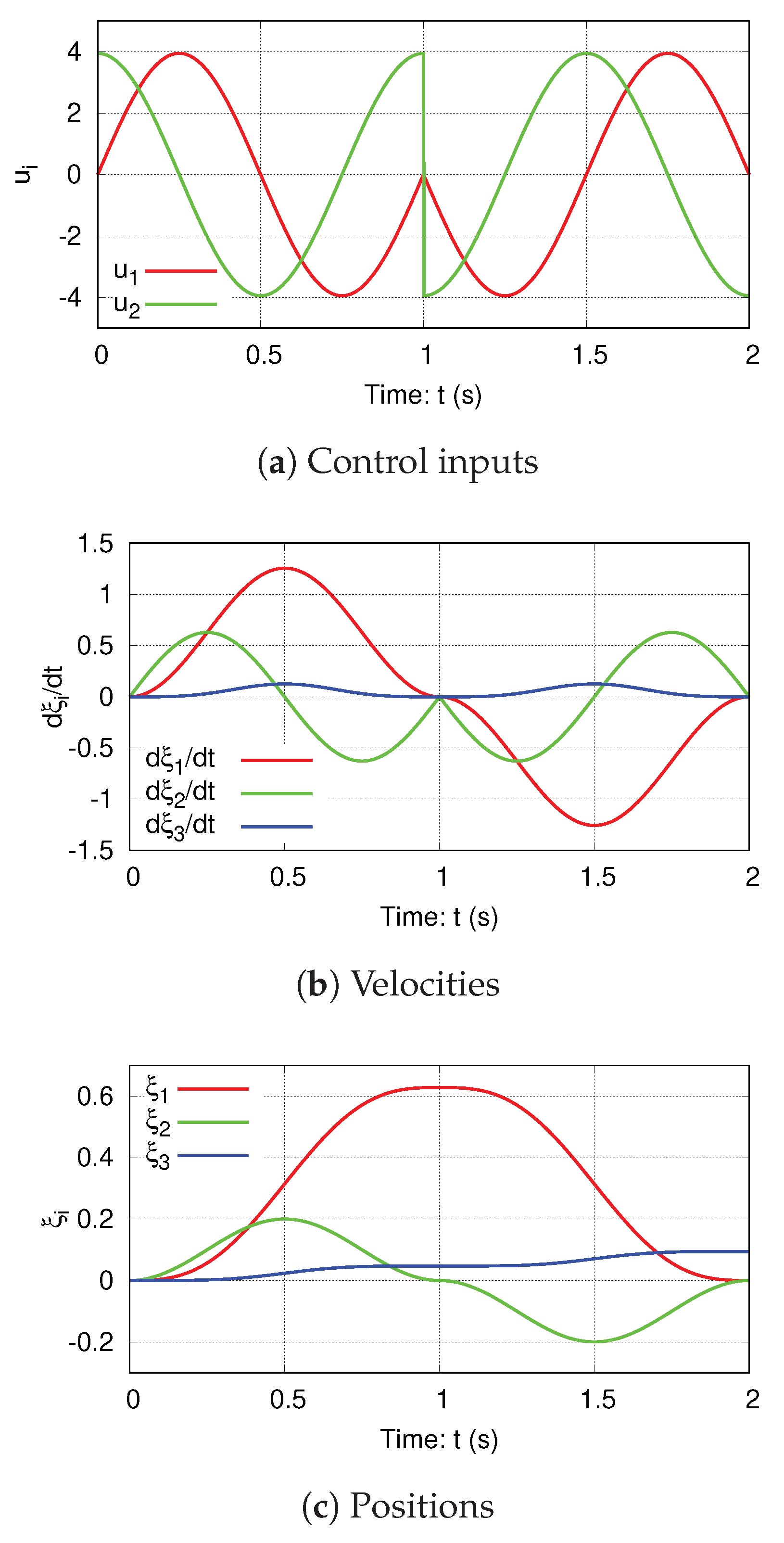
3.2. Holonomy Extraction by Using Sinusoidal Inputs

For the difficulty to obtain displacement of ${\xi }_3$ and ${\dot{\xi }}_3$, this subsection presents how to break it through by using sinusoidal inputs.

What we should do for verifying the hypothesis presented in Section 1 is to find an appropriate pair of sinusoids such that displacement of ${\xi }_3$ and ${\dot{\xi }}_3$ is obtained as holonomy—a kind of motion that traverses a closed path in a reduced configuration space of $({\xi }_1,{\xi }_2,{\dot{\xi }}_1,{\dot{\xi }}_2)$. Note that the motion planning problem we address is based on the equilibrium points, that is, $\dot{\mathit{\xi }}={\mathbf{0}}_3$. So, the desired holonomy is the one to excite ${\xi }_3$ to be a certain value and ${\dot{\xi }}_3$ to be zero.

Now consider two control inputs of zero-mean sinusoidal functions with angular frequency $\omega$, that is, period $T=2\pi /\omega$ and amplitude $a{\omega }^2$, $b{\omega }^2$, where a and b are positive constants. The time span for applying control inputs is also assumed to be composed of two periods: $[0,T)$ and $[T,2T]$. By direct calculation, we analyze how the system is steered by a pair of given sinusoidal inputs over each period. First, let the initial equilibrium point be $\xi \left(0\right)={\xi }_0:={[{\xi }_{10},{\xi }_{20},{\xi }_{30}]}^{\top }$, $\dot{\xi }\left(0\right)={\mathbf{0}}_3$ and let the pair of control inputs over the first period $[0,T)$ be

$$u_1\left(t\right)=a{\omega }^{2}sin\omega t,u_2\left(t\right)=b{\omega }^{2}cos\omega t.$$

(14)

Then, the trajectories of ${\xi }_1,{\xi }_2$ and their time derivatives become

$$\begin{array}{cc}\hfill {\dot{\xi }}_1\left(t\right)& =a\omega -a\omega cos\omega t,\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill {\xi }_1\left(t\right)& ={\xi }_{10}+a\omega t-asin\omega t,\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill {\dot{\xi }}_2\left(t\right)& =b\omega sin\omega t,\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill {\xi }_2\left(t\right)& ={\xi }_{20}+b-bcos\omega t.\hfill \end{array}$$

(18)

Consequently, the values at $t=T$ are

$$\begin{array}{cc}\hfill {\dot{\xi }}_1\left(T\right)& =0,\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill {\xi }_1\left(T\right)& ={\xi }_{10}+a\omega T={\xi }_{10}+\underset{\Delta {\xi }_1\left(T\right)}{\underbrace{2\pi a}},\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill {\dot{\xi }}_2\left(T\right)& =0,\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill {\xi }_2\left(T\right)& ={\xi }_{20}\hfill \end{array}$$

(22)

From (18), the trajectories of ${\xi }_3$ and its time derivative are given by

$$\begin{array}{cc}\hfill {\dot{\xi }}_3\left(t\right)& =a\omega \left({\xi }_{20}+\frac{3}{4}b\right)-a\omega ({\xi }_{20}+b)cos\omega t+\frac{1}{4}ab\omega cos2\omega t,\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill {\xi }_3\left(t\right)& ={\xi }_{30}+a\omega \left({\xi }_{20}+\frac{3}{4}b\right)t-a({\xi }_{20}+b)sin\omega t+\frac{1}{8}absin2\omega t.\hfill \end{array}$$

(24)

Hence, we obtain the values of ${\xi }_3$ and ${\dot{\xi }}_3$ at $t=T$ as follows:

$$\begin{array}{cc}\hfill {\dot{\xi }}_3\left(T\right)& =0,\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill {\xi }_3\left(T\right)& ={\xi }_{30}+a\omega \left({\xi }_{20}+\frac{3}{4}b\right)T={\xi }_{30}+\underset{\Delta {\xi }_3\left(T\right)}{\underbrace{2\pi a\left({\xi }_{20}+\frac{3}{4}b\right)}}.\hfill \end{array}$$

(26)

At this moment, each non-zero displacement from the initial value is expressed as $\Delta {\xi }_1\left(T\right)$ and $\Delta {\xi }_3\left(T\right)$ in (20) and (26), respectively. As one of a pair of control inputs such that ${\xi }_1\left(2T\right)={\xi }_{10}$, ${\xi }_2\left(2T\right)={\xi }_{20}$ and ${\xi }_3\left(2T\right)\ne {\xi }_{30}$ at $t=2T$, we choose the following pair of sinusoidal functions over the second period $[T,2T]$:

$$u_1\left(t\right)=-a{\omega }^{2}sin\omega t,u_2\left(t\right)=-b{\omega }^{2}cos\omega t.$$

(27)

Note that (27) is the sign inversion of (14). By using (19)–(22), the trajectories of ${\xi }_1,{\xi }_2$ and their time derivatives can be written as

$$\begin{array}{cc}\hfill {\dot{\xi }}_1\left(t\right)& =-a\omega +a\omega cos\omega t,\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill {\xi }_1\left(t\right)& ={\xi }_{10}+4\pi a-a\omega t+asin\omega t,\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill {\dot{\xi }}_2\left(t\right)& =-b\omega sin\omega t,\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill {\xi }_2\left(t\right)& ={\xi }_{20}-b+bcos\omega t.\hfill \end{array}$$

(31)

Their values at $t=2T$ are also computed as

$$\begin{array}{cc}\hfill {\dot{\xi }}_1\left(2T\right)& =0,\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill {\xi }_1\left(2T\right)& ={\xi }_{10},\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill {\dot{\xi }}_2\left(2T\right)& =0,\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill {\xi }_2\left(2T\right)& ={\xi }_{20}.\hfill \end{array}$$

(35)

Since the trajectory of ${\xi }_2$ behaves according to (31), ${\xi }_3$ and ${\dot{\xi }}_3$ over $[T,2T]$ can be expressed by

$$\begin{array}{cc}\hfill {\dot{\xi }}_3\left(t\right)& =-a\omega \left({\xi }_{20}-\frac{3}{4}b\right)+a\omega ({\xi }_{20}-b)cos\omega t+\frac{1}{4}ab\omega cos2\omega t,\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill {\xi }_3\left(t\right)& ={\xi }_{30}+2a\omega {\xi }_{20}T-a\omega \left({\xi }_{20}-\frac{3}{4}b\right)t+a({\xi }_{20}-b)sin\omega t+\frac{1}{8}absin2\omega t.\hfill \end{array}$$

(37)

Finally, from (36) and (37), the reaching values at $t=2T$ are provided as

$$\begin{array}{cc}\hfill {\dot{\xi }}_3\left(2T\right)& =0,\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill {\xi }_3\left(2T\right)& ={\xi }_{30}+\frac{3}{2}ab\omega T={\xi }_{30}+\underset{\Delta {\xi }_3\left(2T\right)}{\underbrace{3\pi ab}}.\hfill \end{array}$$

(39)

Therefore, the results (32)–(35), (38) and (39) mean that combining two pairs of sinusoidal inputs (14) and (27), that is,

$$\left\{\begin{array}{ccccc}{u}_1\left(t\right)=a{\omega }^{2}sin\omega t\hfill & \mathrm{and}& u_2\left(t\right)=b{\omega }^{2}cos\omega t,\hfill & \mathrm{for}& t\in [0,T)\hfill \\ u_1\left(t\right)=-a{\omega }^{2}sin\omega t\hfill & \mathrm{and}& u_2\left(t\right)=-b{\omega }^{2}cos\omega t,\hfill & \mathrm{for}& t\in [T,2T],\hfill \end{array}\right.$$

(40)

provides the desired holonomy. This verified the hypothesis. Although this approach is heuristic and constructive, it brings the obvious relationship between parameters of the inputs and the magnitude of the holonomy. In fact, the displacement of ${\xi }_3$ at $t=2T$, that is, $\Delta {\xi }_3\left(2T\right)$ with the parameters: a and b; the displacement of ${\xi }_3$ at $t=T$, that is, the $\Delta {\xi }_3\left(T\right)$ state, depends on not only a and b but also ${\xi }_{20}$.

Figure 1 shows the control inputs with $a=b=0.1,\omega =2\pi (i.e.,T=1)$, the resultant velocities and positions. Also, Figure 2 depicts the trajectories in various phase spaces. Trajectories of velocities and positions were (not analytically but) numerically obtained. The simulator was developed in C with the GNU Scientific Library [36]. The embedded eight-th order Runge-Kutta Prince-Dormand method with nine-th order error estimate (rk8pd) was selected as an ODE solver, where an absolute and relative errors were set to ${10}^{-12}$ and 0, respectively.

Figure 1. Time plots, derived from Reference [33].

Figure 2. Trajectories. Only (a) is derived from Reference [33].

From Figure 1b,c, it can be observed that a positive displacement with respect to ${\xi }_3$ is obtained by two-period motion. Since $a=b=0.1$ in (39), the magnitude of the holonomy is computed as $\Delta {\xi }_3\left(2\right)\approx 9.4\times {10}^{-2}$. Figure 2 shows the holonomy in six different types of phase spaces, which visualizes that the displacement of ${\xi }_3$ results from a kind of motion that traverses a closed path in a reduced configuration space of $({\xi }_1,{\xi }_2,{\dot{\xi }}_1,{\dot{\xi }}_2)$. In particular, Figure 2b,f present that the motion to extract the holonomy is characterized by two closed circular paths in the reduced configuration space.

In fact, it is verified that the same displacement as in (39) is obtained by combining two pairs of sinusoidal inputs (14) and (27) in the reverse order of (40), that is,

$$\left\{\begin{array}{ccccc}{u}_1\left(t\right)=-a{\omega }^{2}sin\omega t\hfill & \mathrm{and}& u_2\left(t\right)=-b{\omega }^{2}cos\omega t,\hfill & \mathrm{for}& t\in [0,T)\hfill \\ u_1\left(t\right)=a{\omega }^{2}sin\omega t\hfill & \mathrm{and}& u_2\left(t\right)=b{\omega }^{2}cos\omega t,\hfill & \mathrm{for}& t\in [T,2T].\hfill \end{array}\right.$$

(41)

Let us synthesize (40) and (41) as follows:

$$\left\{\begin{array}{ccccc}{u}_1\left(t\right)=\pm a{\omega }^{2}sin\omega t\hfill & \mathrm{and}& u_2\left(t\right)=\pm b{\omega }^{2}cos\omega t,\hfill & \mathrm{for}& t\in [0,T)\hfill \\ u_1\left(t\right)=\mp a{\omega }^{2}sin\omega t\hfill & \mathrm{and}& u_2\left(t\right)=\mp b{\omega }^{2}cos\omega t,\hfill & \mathrm{for}& t\in [T,2T].\hfill \end{array}\right.$$

(42)

Also, we can easily confirm that the following pairs of control inputs other than (42) yield a positive displacement of ${\xi }_3$:

$$\left\{\begin{array}{ccccc}{u}_1\left(t\right)=\pm a{\omega }^{2}cos\omega t\hfill & \mathrm{and}& u_2\left(t\right)=\mp b{\omega }^{2}sin\omega t,\hfill & \mathrm{for}& t\in [0,T)\hfill \\ u_1\left(t\right)=\mp a{\omega }^{2}cos\omega t\hfill & \mathrm{and}& u_2\left(t\right)=\pm b{\omega }^{2}sin\omega t,\hfill & \mathrm{for}& t\in [T,2T].\hfill \end{array}\right.$$

(43)

Moreover, two appropriate pairs of sinusoidal inputs such that a negative displacement with respect to ${\xi }_3$ can be obtained include the following forms:

$$\begin{array}{cc}\hfill & \left\{\begin{array}{ccccc}{u}_1\left(t\right)=\pm a{\omega }^{2}sin\omega t\hfill & \mathrm{and}& u_2\left(t\right)=\mp b{\omega }^{2}cos\omega t,\hfill & \mathrm{for}& t\in [0,T)\hfill \\ u_1\left(t\right)=\mp a{\omega }^{2}sin\omega t\hfill & \mathrm{and}& u_2\left(t\right)=\pm b{\omega }^{2}cos\omega t,\hfill & \mathrm{for}& t\in [T,2T],\hfill \end{array}\right.\hfill \end{array}$$

(44)

$$\begin{array}{cc}\hfill & \left\{\begin{array}{ccccc}{u}_1\left(t\right)=\pm a{\omega }^{2}cos\omega t\hfill & \mathrm{and}& u_2\left(t\right)=\pm b{\omega }^{2}sin\omega t,\hfill & \mathrm{for}& t\in [0,T)\hfill \\ u_1\left(t\right)=\mp a{\omega }^{2}cos\omega t\hfill & \mathrm{and}& u_2\left(t\right)=\mp b{\omega }^{2}sin\omega t,\hfill & \mathrm{for}& t\in [T,2T].\hfill \end{array}\right.\hfill \end{array}$$

(45)

Remark 1.

The common strategy among (42)–(45) is, in the second period, to keep $\Delta {\xi }_3\left(T\right)$ while canceling $\Delta {\xi }_1\left(T\right)$ or $\Delta {\xi }_2\left(T\right)$ arisen over the first period. To accomplish it, (42)–(45) in the second period make use of the sinusoidal inputs which are the sign inversion of those over the first period. Alternatively, we can employ a fact that ${\xi }_3$ and ${\dot{\xi }}_3$ are not driven by only either $u_1$ or $u_2$. For example, if we adopt

$$u_1\left(t\right)=-a{\omega }^{2}sin\omega t,u_2\left(t\right)=0$$

(46)

instead of (27), then $\Delta {\xi }_3\left(2T\right)=(3/2)\pi ab$. Note that the magnitude of the holonomy resulted from a pair of (14) and (46) is half of the one resulted from a pair of (14) and (27). The control inputs and the resultant states with $a=b=0.1,\omega =2\pi$ are shown in Figure 3. Then, the magnitude of the holonomy is computed as $\Delta {\xi }_3\left(2\right)\approx 4.7\times {10}^{-2}$. Figure 4 visualizes the holonomy of this case in six different types of phase spaces. By contrast with Figure 2b,f, it can be seen that the holonomy in Figure 4b,f is extracted by traversing one closed circular path in the reduced configuration space. The alternative way such as (46) is applicable not only to (42) but also to (43)–(45) as follows:

$$\begin{array}{cc}\hfill & \left\{\begin{array}{ccccc}{u}_1\left(t\right)=\pm a{\omega }^{2}sin\omega t\hfill & \mathrm{and}& u_2\left(t\right)=\pm b{\omega }^{2}cos\omega t,\hfill & \mathrm{for}& t\in [0,T)\hfill \\ u_1\left(t\right)=\mp a{\omega }^{2}sin\omega t\hfill & \mathrm{and}& u_2\left(t\right)=0,\hfill & \mathrm{for}& t\in [T,2T],\hfill \end{array}\right.\hfill \end{array}$$

(47)

$$\begin{array}{cc}\hfill & \left\{\begin{array}{ccccc}{u}_1\left(t\right)=\pm a{\omega }^{2}cos\omega t\hfill & \mathrm{and}& u_2\left(t\right)=\mp b{\omega }^{2}sin\omega t,\hfill & \mathrm{for}& t\in [0,T)\hfill \\ u_1\left(t\right)=0\hfill & \mathrm{and}& u_2\left(t\right)=\pm b{\omega }^{2}sin\omega t\hfill & \mathrm{for}& t\in [T,2T],\hfill \end{array}\right.\hfill \end{array}$$

(48)

$$\begin{array}{cc}\hfill & \left\{\begin{array}{ccccc}{u}_1\left(t\right)=\pm a{\omega }^{2}sin\omega t\hfill & \mathrm{and}& u_2\left(t\right)=\mp b{\omega }^{2}cos\omega t,\hfill & \mathrm{for}& t\in [0,T)\hfill \\ u_1\left(t\right)=\mp a{\omega }^{2}sin\omega t\hfill & \mathrm{and}& u_2\left(t\right)=0,\hfill & \mathrm{for}& t\in [T,2T],\hfill \end{array}\right.\hfill \end{array}$$

(49)

$$\begin{array}{cc}\hfill & \left\{\begin{array}{ccccc}{u}_1\left(t\right)=\pm a{\omega }^{2}cos\omega t\hfill & \mathrm{and}& u_2\left(t\right)=\pm b{\omega }^{2}sin\omega t,\hfill & \mathrm{for}& t\in [0,T)\hfill \\ u_1\left(t\right)=0\hfill & \mathrm{and}& u_2\left(t\right)=\mp b{\omega }^{2}sin\omega t,\hfill & \mathrm{for}& t\in [T,2T].\hfill \end{array}\right.\hfill \end{array}$$

(50)

Figure 3. Time plots.

Figure 4. Trajectories.

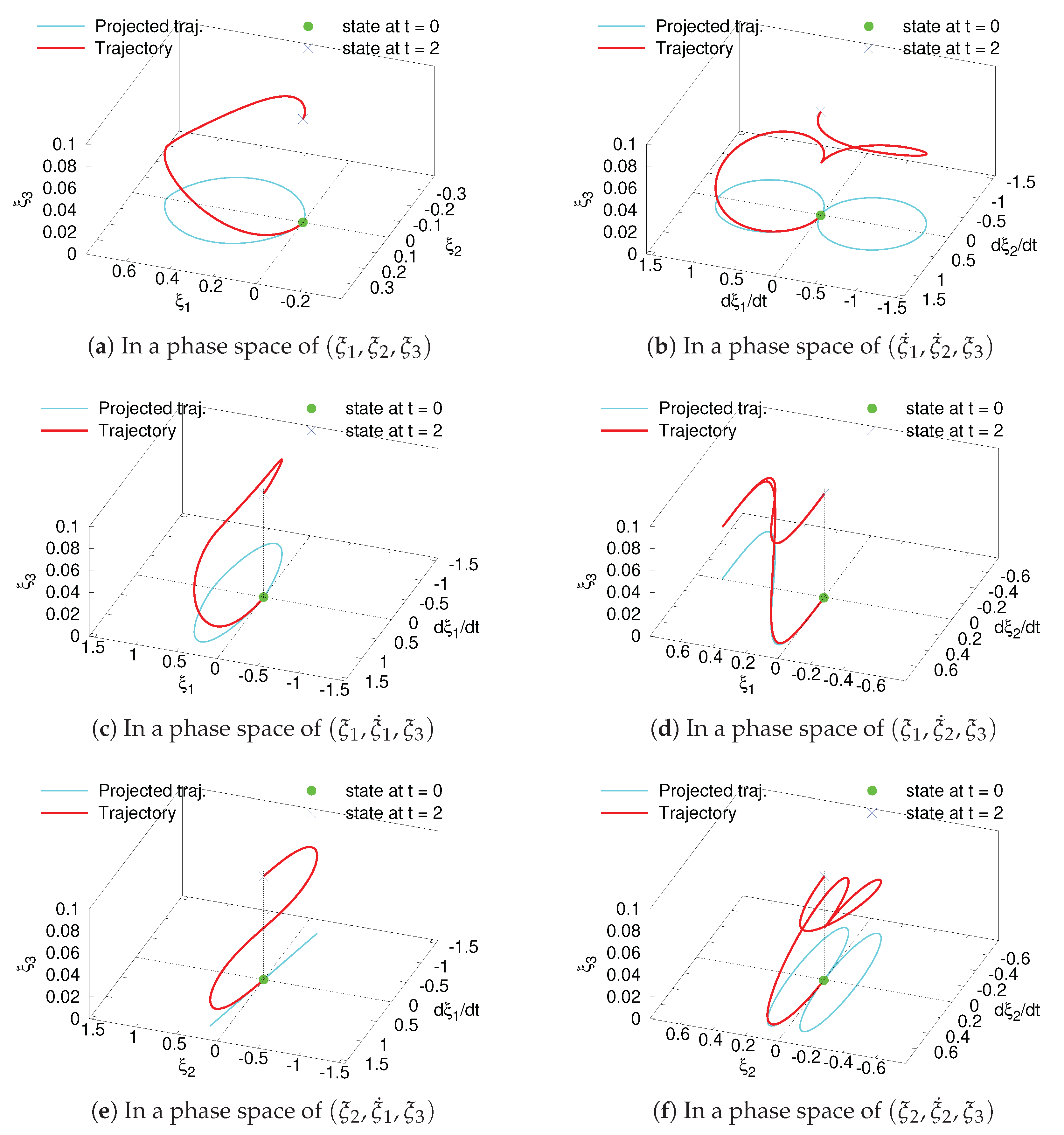
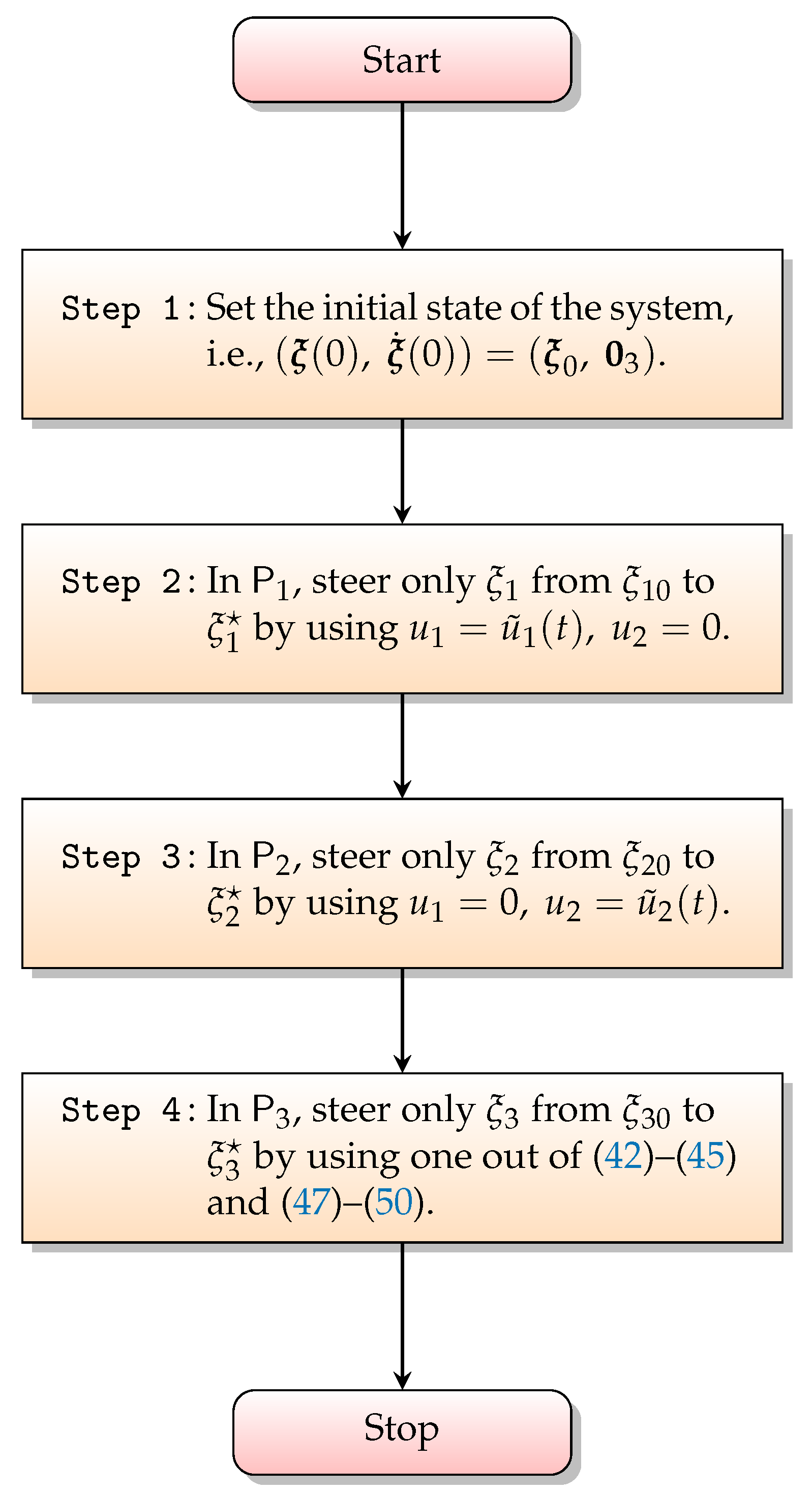
3.3. Holonomy-Based Motion Planning Algorithm

Based on the holonomy extraction of the previous subsection, a motion planning algorithm can be easily constructed.

Here, let us assume the following points:

• The entire motion planning consists of three phases: ${\mathsf{P}}_1$, ${\mathsf{P}}_2$ and ${\mathsf{P}}_3$. Also, the periods of ${\mathsf{P}}_1$ and ${\mathsf{P}}_2$ are T, whereas that of ${\mathsf{P}}_3$ is $2T$.
• At the beginning and end of each phase, the system (1) stops; that is to say, each velocity is zero.
• Let ${\tilde{u}}_i\left(t\right)$, $i=1,2$, be an appropriate sinusoidal function whose period is T.

The basic algorithm of motion planning to steer from an equilibrium point $({\xi }_0,{\mathbf{0}}_3),{\xi }_0={[{\xi }_{10},{\xi }_{20},{\xi }_{30}]}^{\top }$ to the other equilibrium point $({\xi }^{★},{\mathbf{0}}_3),{\xi }^{★}={[{\xi }_1^{★},{\xi }_2^{★},{\xi }_3^{★}]}^{\top }$ is as follows (see Figure 5 as the corresponding flowchart):

Figure 5. The algorithm of motion planning.

Step 1:

Set the initial state of the system, that is, $(\xi \left(0\right),\dot{\xi }\left(0\right))=({\xi }_0,{\mathbf{0}}_3)$.

Step 2:

In ${\mathsf{P}}_1$, steer only ${\xi }_1$ from ${\xi }_{10}$ to ${\xi }_1^{★}$ by using $u_1={\tilde{u}}_1\left(t\right),u_2=0$.

Step 3:

In ${\mathsf{P}}_2$, steer only ${\xi }_2$ from ${\xi }_{20}$ to ${\xi }_2^{★}$ by using $u_1=0,u_2={\tilde{u}}_2\left(t\right)$.

Step 4:

In ${\mathsf{P}}_3$, steer only ${\xi }_3$ from ${\xi }_{30}$ to ${\xi }_3^{★}$ by using one out of (42)–(45) and (47)–(50).

Note that Steps 1–3 are replaceable.

Now let us consider an example of motion planning from an initial state $(0,0,0,0,0,0)$ to a desired state $(1,1,1,0,0,0)$ for four seconds (i.e., $T=1$). As control inputs such that the control objective is achieved, we adopt

$$\left\{\begin{array}{ccccc}{u}_1\left(t\right)=a_{\mathsf{P}{}_1}{\omega }^{2}sin\omega t\hfill & \mathrm{and}& u_2\left(t\right)=0,\hfill & \mathrm{for}& t\in [0,1)\hfill \\ u_1\left(t\right)=0\hfill & \mathrm{and}& u_2\left(t\right)=b_{\mathsf{P}{}_2}{\omega }^{2}sin\omega t,\hfill & \mathrm{for}& t\in [1,2)\hfill \\ u_1\left(t\right)=a_{\mathsf{P}{}_3}{\omega }^{2}sin\omega t\hfill & \mathrm{and}& u_2\left(t\right)=b_{\mathsf{P}{}_3}{\omega }^{2}cos\omega t,\hfill & \mathrm{for}& t\in [2,3)\hfill \\ u_1\left(t\right)=-a_{\mathsf{P}{}_3}{\omega }^{2}sin\omega t\hfill & \mathrm{and}& u_2\left(t\right)=-b_{\mathsf{P}{}_3}{\omega }^{2}cos\omega t,\hfill & \mathrm{for}& t\in [3,4].\hfill \end{array}\right.$$

(51)

The system starts to move from the initial state at $t=0$, through

$$\begin{array}{cc}\hfill {\xi }_1\left(1\right)& ={\xi }_1\left(0\right)+2\pi a_{\mathsf{P}{}_1}+{\dot{\xi }}_1\left(0\right)=2\pi a_{\mathsf{P}{}_1},\hfill \end{array}$$

(52)

$$\begin{array}{cc}\hfill {\xi }_2\left(1\right)& ={\xi }_2\left(0\right)=0,\hfill \end{array}$$

(53)

$$\begin{array}{cc}\hfill {\xi }_3\left(1\right)& ={\xi }_3\left(0\right)=0,\hfill \end{array}$$

(54)

$$\begin{array}{cc}\hfill {\dot{\xi }}_i\left(1\right)& ={\dot{\xi }}_i\left(0\right)=0,i=1,2,3,\hfill \end{array}$$

(55)

at $t=1$ and

$$\begin{array}{cc}\hfill {\xi }_1\left(2\right)& ={\xi }_1\left(1\right)=2\pi a_{\mathsf{P}{}_1},\hfill \end{array}$$

(56)

$$\begin{array}{cc}\hfill {\xi }_2\left(2\right)& ={\xi }_2\left(1\right)+2\pi b_{\mathsf{P}{}_2}+{\dot{\xi }}_2\left(1\right)=2\pi b_{\mathsf{P}{}_2},\hfill \end{array}$$

(57)

$$\begin{array}{cc}\hfill {\xi }_3\left(2\right)& ={\xi }_3\left(1\right)=0,\hfill \end{array}$$

(58)

$$\begin{array}{cc}\hfill {\dot{\xi }}_i\left(2\right)& ={\dot{\xi }}_i\left(1\right)=0,i=1,2,3,\hfill \end{array}$$

(59)

at $t=2$ and lastly reaches the following final states:

$$\begin{array}{cc}\hfill {\xi }_1\left(4\right)& ={\xi }_1\left(2\right)=2\pi a_{\mathsf{P}{}_1},\hfill \end{array}$$

(60)

$$\begin{array}{cc}\hfill {\xi }_2\left(4\right)& ={\xi }_2\left(2\right)=2\pi b_{\mathsf{P}{}_2},\hfill \end{array}$$

(61)

$$\begin{array}{cc}\hfill {\xi }_3\left(4\right)& ={\xi }_3\left(2\right)+3\pi a_{\mathsf{P}{}_3}{b}_{\mathsf{P}{}_3}=3\pi a_{\mathsf{P}{}_3}{b}_{\mathsf{P}{}_3},\hfill \end{array}$$

(62)

$$\begin{array}{cc}\hfill {\dot{\xi }}_i\left(4\right)& ={\dot{\xi }}_i\left(2\right)=0,i=1,2,3.\hfill \end{array}$$

(63)

Therefore, the results (60)–(62) indicate the following things:

• to realize ${\xi }_i\left(4\right)=1(i=1,2)$, $a_{\mathsf{P}{}_1}$ and $b_{\mathsf{P}{}_2}$ must be

  $$\begin{array}{c}\left\{\begin{array}{ccc}{a}_{\mathsf{P}{}_1}=\frac{1}{2\pi },\hfill & \mathrm{for}& t\in [0,1)\hfill \\ b_{\mathsf{P}{}_2}=\frac{1}{2\pi },\hfill & \mathrm{for}& t\in [1,2),\hfill \end{array}\right.\hfill \end{array}$$

  (64)
• to realize ${\xi }_3\left(4\right)=1$, $a_{\mathsf{P}{}_3}$ and $b_{\mathsf{P}{}_3}$ should be assigned as, for example,

  $$\begin{array}{c}{a}_{\mathsf{P}{}_3}=b_{\mathsf{P}{}_3}=\frac{1}{\sqrt{3\pi }},\mathrm{for}t\in [2,4].\hfill \end{array}$$

  (65)

Figure 6 depicts the control inputs with (64) and (65), the resultant velocities and positions. From Figure 6b,c, it can be confirmed that the state arrives at $(1,1,1,0,0,0)$, that is, the desired motion is successfully planned.

Figure 6. Time plots.

Remark 2.

The control inputs with (64) and (65) have switching points between $\mathsf{P}{}_1$ and $\mathsf{P}{}_2$, between $\mathsf{P}{}_2$ and $\mathsf{P}{}_3$ and in the middle of $\mathsf{P}{}_3$. The corresponding effect cannot be found in the resultant velocities and positions. In a practical situation, however, a combination with feedback control should be required to compensate the occurred error. This is included in future work.

Remark 3.

Note that there exists freedom to choose $a_{\mathsf{P}{}_3}$ and $b_{\mathsf{P}{}_3}$. The freedom can be utilized for designing the motion of the system. Under the above-mentioned control objective, you can choose $a_{\mathsf{P}{}_3}$ and $b_{\mathsf{P}{}_3}$ such that $a_{\mathsf{P}{}_3}{b}_{\mathsf{P}{}_3}=1/\left(3\pi \right)$. Its example of use will be shown in the next section.

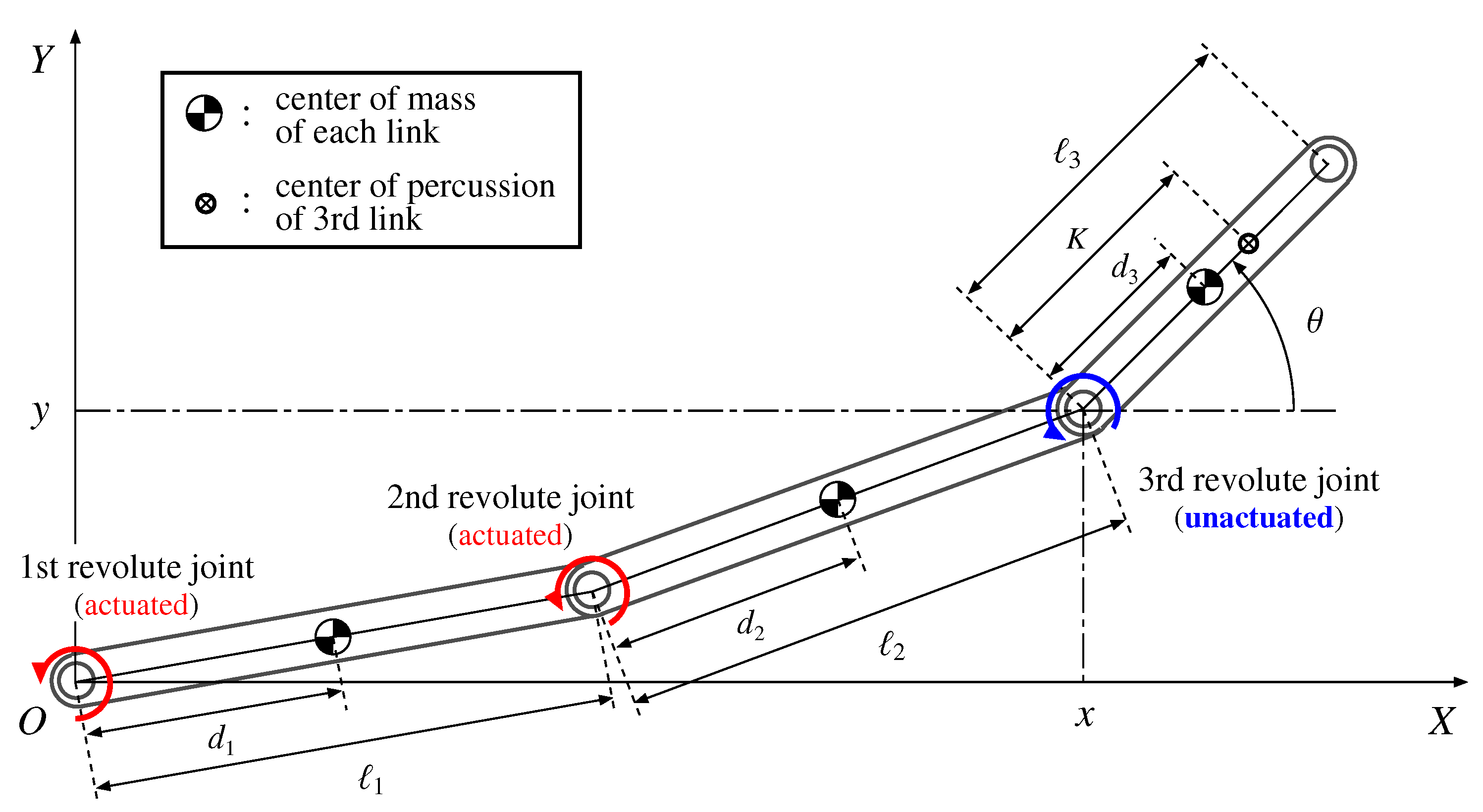
4. Application to Rest-to-Rest Motion of a Three-Joint Manipulator with Passive Third Joint

This section applies the proposed algorithm into a rest-to-rest motion of an underactuated planar manipulator that moves in a horizontal plane. The manipulator has three joints whose third joint is passive (i.e., unactuated) as depicted in Figure 7.

Figure 7. A three-joint manipulator with passive third joint, derived from Reference [29].

The main variables and parameters are defined as in Table 2.

Table 2. Definition of main variables and parameters.

${\mathit{q}}_{\mathit{i}}$	: (relative) angle of the i-th joint ($\mathit{i}=1,2,3$);
${\tau }_i$	: torque for the i-th joint ($i=1,2$);
${\ell }_i$	: length of the i-th link ($i=1,2,3$);
$d_i$	: distance between the i-th joint and the center of mass of the i-th link ($i=1,2,3$);
$m_i$	: mass of the i-th link ($i=1,2,3$);
$I_i$	: moment of inertia mass of the i-th link ($i=1,2,3$);
K	: distance between the third joint and the center of percussion of the third link;
$(x,y)$	: position of the center of percussion of the third link in the frame $O-XY$;
$\theta$	: orientation of the third link with respect to the X-axis;
${\alpha }_1$	: linear acceleration along the third link;
${\alpha }_2$	: angular acceleration with respect to $\theta$.

For simplicity, assume that there is no external disturbance such as load, friction, linear and nonlinear damping acting on each joint. Then, based on Lagrange’s equation of motion, the dynamics of the manipulator is given by

$$\mathit{M}\left(\mathit{q}\right)\ddot{\mathit{q}}+\mathit{c}\left(\mathit{q},\dot{\mathit{q}}\right)=\left[\begin{array}{c}{\tau }_{12}\\ 0\end{array}\right],$$

(66)

where $\mathit{q}={[q_1,q_2,q_3]}^{\top }$ and ${\tau }_{12}={[{\tau }_1,{\tau }_2]}^{\top }$ are vectors of joint angles and torques, respectively. Note that (66) does not include the gravitational term because the dynamics is not affected from gravitational forces. See Appendix A for the details of the inertia matrix $\mathit{M}\left(\mathit{q}\right)$ and the centrifugal and Coriolis term $\mathit{c}\left(\mathit{q},\dot{\mathit{q}}\right)$.

Yoshikawa, et al. [9] considered the same case, and also gave a set of coordinate and input transformation that can transform system (66) to

$$\ddot{\chi }=\left[\begin{array}{cc}cos\theta & 0\\ sin\theta & 0\\ 0& 1\end{array}\right]\alpha ,$$

(67)

where $\chi :={[x,y,\theta ]}^{\top }$ and $\alpha ={[{\alpha }_1,{\alpha }_2]}^{\top }$. In addition, using the coordinate transformation

$$\left[\begin{array}{c}{\xi }_1\\ {\xi }_2\\ {\xi }_3\end{array}\right]=\left[\begin{array}{c}x-K\\ tan\theta \\ y\end{array}\right],$$

(68)

where $K:=(I_3+m_3{d}_3^2)/\left(m_3{d}_3\right)$ and the input transformation

$$\left[\begin{array}{c}{\alpha }_1\\ {\alpha }_2\end{array}\right]=\left[\begin{array}{c}{u}_{1}sec\theta \\ u_2{cos}^2\theta -2{\dot{\theta }}^{2}tan\theta \end{array}\right]$$

(69)

can transform system (67) to the second-order chained form system (1) [9]. Note that both transformation are singular at $\theta =\pm \pi /2$.

We here suppose a motion from $(\chi \left(0\right),\dot{\chi }\left(0\right))=({\chi }_0,{\mathbf{0}}_3)$ to $(\chi \left(t_f\right),\dot{\chi }\left(t_f\right))=({\chi }^{★},{\mathbf{0}}_3)$ that is subject to $\theta \left(t\right)\ne \pm \pi /2fort=0,t_f$. The correspondence between (67) and (1) implies that the system (67) with the input transformation (69) can be controlled by the motion planning algorithm presented in Section 3.3. Then, a control procedure for achieving such motion is as follows (see Figure 8 as the corresponding diagram):

Figure 8. Diagram for holonomy-based motion planning with (68) and (69).

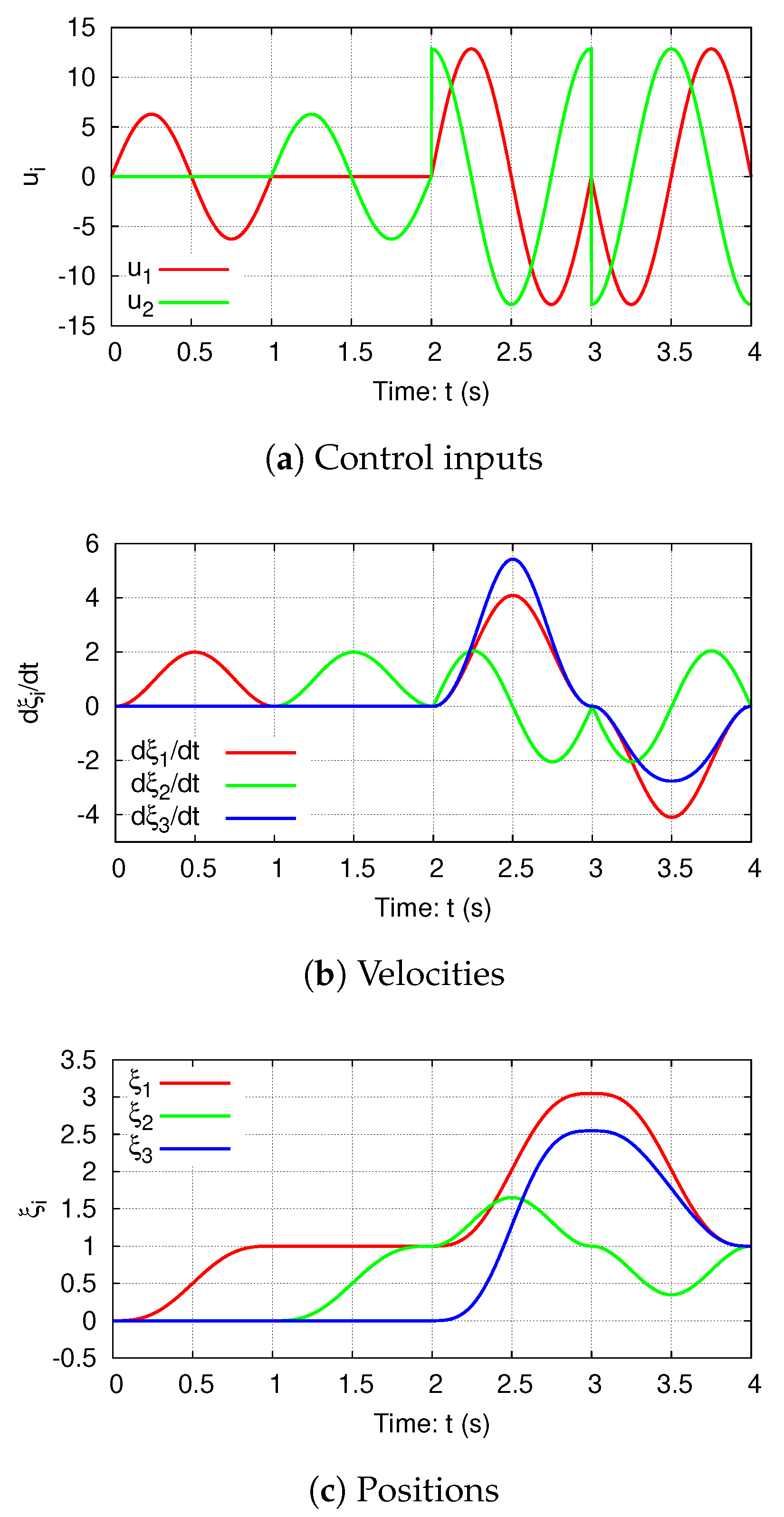
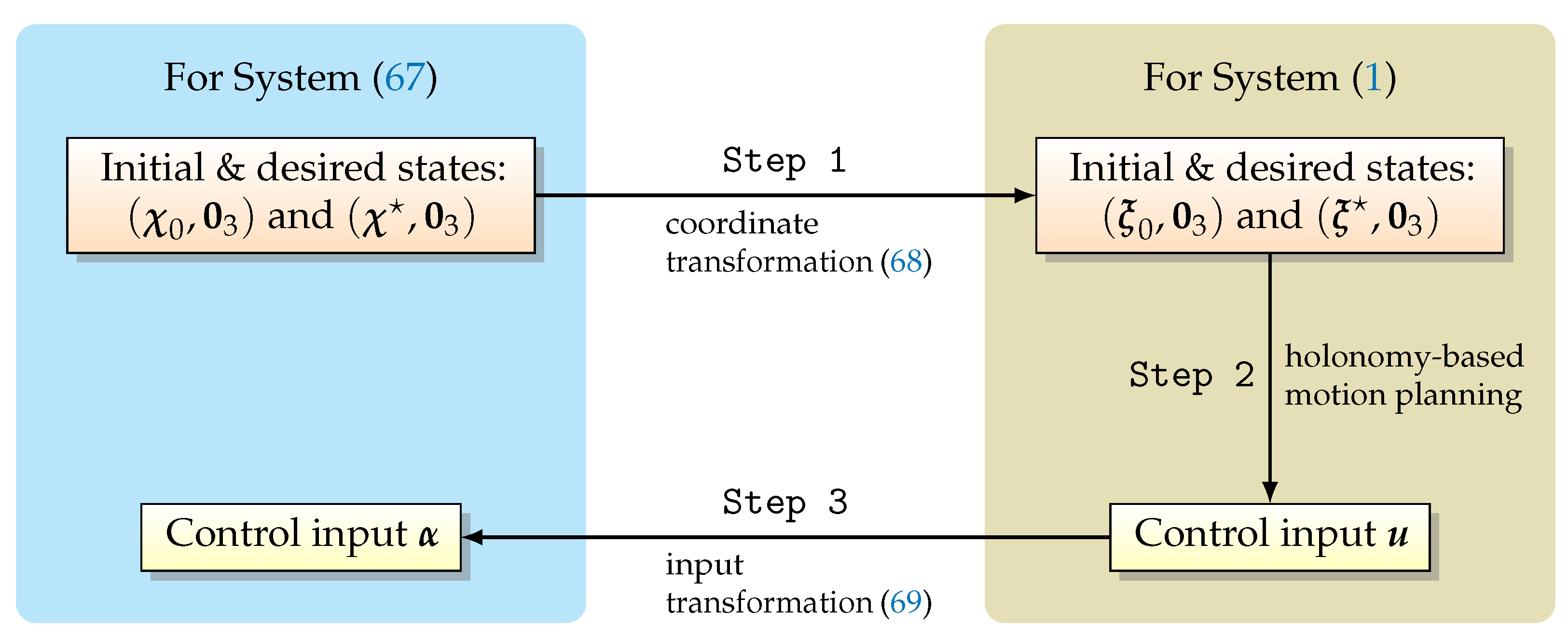
Step 1:

For a given initial position ${\chi }_0$ and a desired position ${\chi }^{★}$, compute their corresponding positions ${\xi }_0$ and ${\xi }^{★}$ by using (68).

Step 2:

Plan motion so as to steer the system (1) from $(\xi \left(0\right),\dot{\xi }\left(0\right))=({\xi }_0,{\mathbf{0}}_3)$ to $(\xi \left(t_f\right),\dot{\xi }\left(t_f\right))=({\xi }^{★},{\mathbf{0}}_3)$ by using the holonomy-based motion planning algorithm presented in the last section. As a result, the corresponding sinusoidal inputs $\mathit{u}$ is obtained.

Step 3:

Apply the sinusoidal inputs $\mathit{u}$ to the system (67) through the input transformation (69).

Remark 4.

Suppose that the state and input of the system (1) are bounded and also both $\theta \left(0\right)$ and $\theta \left(t_f\right)$ are not $\pm \pi /2$. Then, $\theta \left(t\right),t\in (0,t_f)$ does not reach either singular points $\pm \pi /2$ because the singular points corresponds to ${\xi }_2=\pm \infty$. See a simple solution in Reference [34] if a rest-to-rest motion problem with either $\theta \left(0\right)=\pm \pi /2$ or $\theta \left(t_f\right)=\pm \pi /2$ is addressed.

Let us consider that a three-joint underactuated manipulator with $m_3=0.6kg$, ${\ell }_3=0.6m$, $d_3={\ell }_3/2$, $I_3=4.5\times {10}^{-3}kg·m^2$, that is, $K=3.3\times {10}^{-1}m$ conducts a rest-to-rest motion from ${\chi }_0={[0,0,0]}^{\top }$ to ${\chi }^{★}={[1m,1m,0]}^{\top }$. Then, ${\chi }_0$ and ${\chi }^{★}$ correspond to ${\xi }_0={[-3.3\times {10}^{-1},0,0]}^{\top }$ and ${\xi }^{★}={[6.7\times {10}^{-1},0,1]}^{\top }$, respectively. The following set of control inputs to (1) can be applied:

$$\left\{\begin{array}{ccc}{u}_1\left(t\right)=a_{\mathsf{P}{}_1}{\omega }^{2}sin\omega t\hfill & u_2\left(t\right)=0,\hfill & t\in [0,1]\hfill \\ u_1\left(t\right)=a_{\mathsf{P}{}_2}{\omega }^{2}cos\omega t\hfill & u_2\left(t\right)=-b_{\mathsf{P}{}_2}{\omega }^{2}sin\omega t,\hfill & t\in (1,2]\hfill \\ u_1\left(t\right)=0\hfill & u_2\left(t\right)=b_{\mathsf{P}{}_2}{\omega }^{2}sin\omega t,\hfill & t\in (2,3]\hfill \end{array}\right.$$

with $a_{\mathsf{P}{}_1}=1/\left(2\pi \right)$ and $(a_{\mathsf{P}{}_2},b_{\mathsf{P}{}_2})$ such that $a_{\mathsf{P}{}_2}{b}_{\mathsf{P}{}_2}=2/\left(9\pi \right)$ holds.

Simulations were performed for three kinds of $(a_{\mathsf{P}{}_2},b_{\mathsf{P}{}_2})$: $(2/3,1/(3\pi \left)\right)$, $(\sqrt{2}/\left(3\sqrt{\pi }\right),\sqrt{2}/\left(3\sqrt{\pi }\right))$ and $(1/(3\pi ),2/3)$. As the simulation results, Figure 9, Figure 10 and Figure 11 show positions, velocities, and control inputs of (67). From Figure 9, the following facts can be observed:

Figure 9. Time plots.

Figure 10. Time plot of control inputs.

Figure 11. Motion trajectories of the third link.

• the desired rest-to-rest motion on $(\chi ,\dot{\chi })$ is achieved;
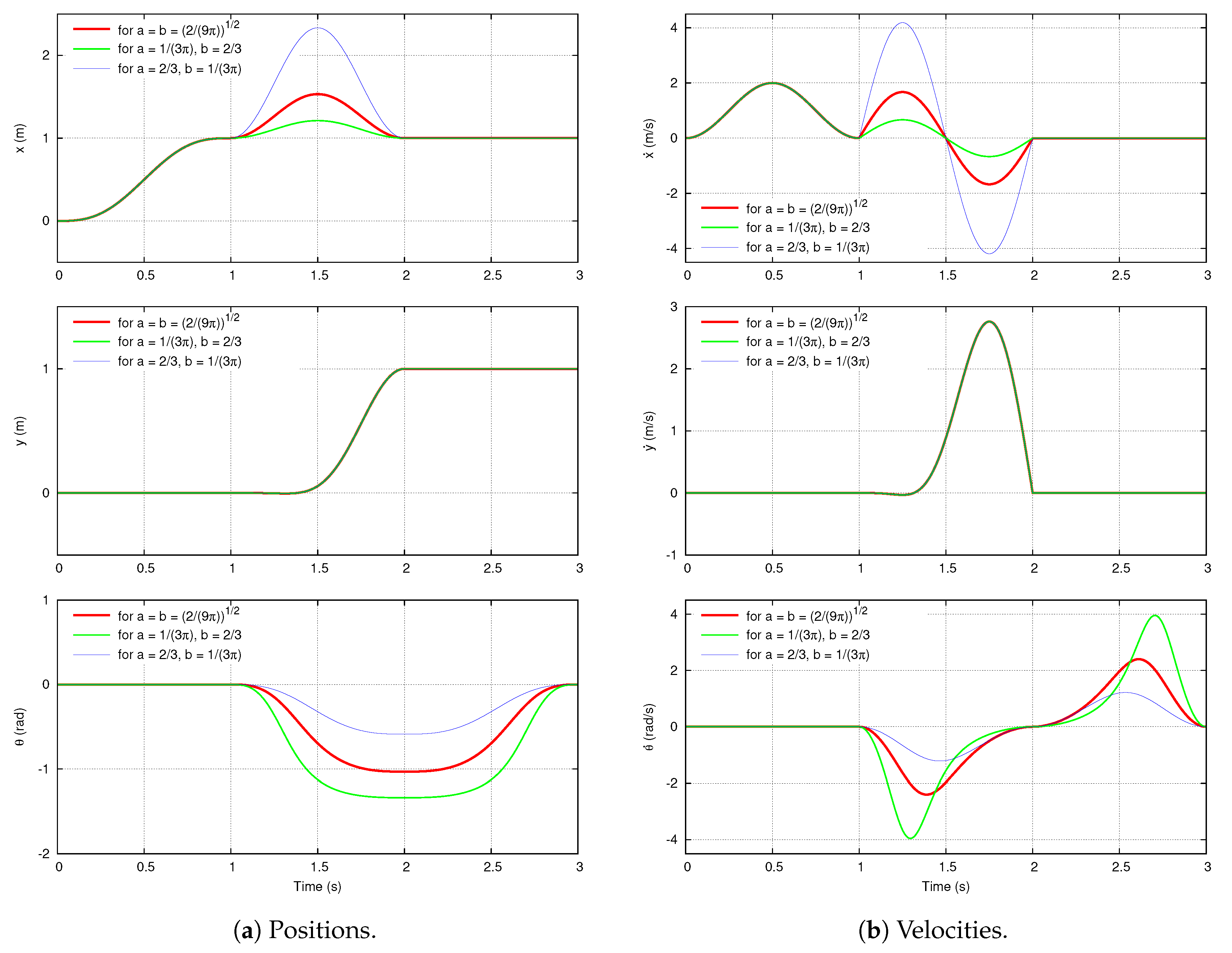
• If $a_{\mathsf{P}{}_2}$ is greater than $b_{\mathsf{P}{}_3}$, then, on the basis of the case when $a_{\mathsf{P}{}_2}=b_{\mathsf{P}{}_3}$, $\left|{\int }_1^{2}x\left(t\right)\mathrm{d}t\right|$ becomes bigger and $\left|{\int }_1^3\theta \left(t\right)\mathrm{d}t\right|$ becomes smaller; that is to say, the third link moves broadly in direction of x-axis while its orientation varies slightly smaller.
• If $a_{\mathsf{P}{}_2}$ is less than $b_{\mathsf{P}{}_3}$, then, on the basis of the case when $a_{\mathsf{P}{}_2}=b_{\mathsf{P}{}_3}$, $\left|{\int }_1^{2}x\left(t\right)\mathrm{d}t\right|$ becomes smaller and $\left|{\int }_1^3\theta \left(t\right)\mathrm{d}t\right|$ becomes bigger; that is to say, the third link moves narrowly in direction of x-axis while its orientation varies slightly larger.

The last two facts indicate that the freedom in choosing $a_{\mathsf{P}{}_3}$ and $b_{\mathsf{P}{}_3}$ can be used for obstacle avoidance. If there is an obstacle in the gray-hatched area of Figure 11, choosing $a_{\mathsf{P}{}_3}$ and $b_{\mathsf{P}{}_3}$ such that $a_{\mathsf{P}{}_3}$ is less than $b_{\mathsf{P}{}_3}$ can make the third link avoid colliding to the obstacle. Therefore, the simulation results illustrated the effectiveness of the proposed algorithm.

Remark 5.

To avoid a collision with an obstacle in the real world, it is necessary to detect the obstacle and measure the distance between the obstacle and the manipulator. For achieving such things, e.g., an optical 3D laser measurement system [37] and a stereo vision system [38] would be useful.

5. Conclusions

In this paper, a holonomy-based motion planning algorithm for the second-order chained form system was proposed. First, it was shown that a combination of two appropriate pairs of sinusoidal inputs extracts the holonomy. This verified the hypothesis that motivated this study. Next, the idea of holonomy extraction was directly used to construct a motion planning algorithm. Finally, the effectiveness of the proposed algorithm was confirmed from the simulation results including an application to an underactuated manipulator.

This algorithm is heuristic but simple and useful. By adopting specific sinusoids as control inputs, the relationship between parameters of control inputs and the magnitude of the holonomy was revealed. Also, it was found that the freedom to choose the parameters can be utilized for designing the motion of the system. Accordingly, the proposed algorithm will provide a new perspective on how to control dynamic nonholonomic systems.

Future work will include experimental validation and generalization of the controlled systems and control inputs. In particular, a combination with feedback control should be needed in practice to make the proposed approach robust against the modeling error and external disturbance. Also, to enlarge applicable systems, an extension to an underactuated system under the gravity will be considered.