Abstract
The paper deals with the generation of optimal trajectories for industrial robots in machining and additive manufacturing applications. The proposed method uses an Ant Colony algorithm to solve a kinodynamic motion planning problem. It exploits the kinematic redundancy that is often present in these applications to optimize the execution of trajectory. At the same time, the robot kinematics and dynamics constraints are respected and robot collisions are avoided. To reduce the computational burden, the task workspace is discretized enabling the use of efficient network solver based on Ant Colony theory. The proposed method is validated in robotic milling and additive manufacturing real-world scenarios.
1. Introduction
The growing demand for advanced industrial robotic applications such as machining and additive manufacturing highlights the importance of motion planning algorithms in this field [1,2]. As a consequence of this trend, a strong effort has been put into the improvement of the algorithm efficiency, especially in terms of reduction of the computing time. Moreover, researchers have investigated path and/or trajectory planners that are able to avoid collisions also taking into account the robot dynamics constraints [3,4,5,6].
The easiest motion planning problem consists in finding a collision-free point-to-point trajectory from a starting configuration to an end configuration without any constraints on the intermediate points. This problem is often addressed by means of path planning algorithms, which compute a suitable path between the points without taking into account constraints on velocity, accelerations, and torques [7,8,9,10]. The trajectory is then obtained by using a suitable time parametrization of the path [11,12]. Other approaches also consider constraints on velocity, acceleration and motor torque during the planning phase [13,14]. This class of problems is known as kinodynamic motion planning [15].
The lack of constraints on the intermediate points is an important drawback in many applications. For example, one might want to keep the robot tool oriented toward the floor during the whole trajectory for safety reasons. Recent works addresssed problem of this kind when the closed form of the constraints is not known a priori [16,17]. In this paper, we consider a more specific but still important class of trajectories, in which the number of degrees of freedom of the task is smaller than the one of the robot. This is a common scenario, as technological tasks often require to constrain only some of the Cartesian coordinates and velocities. Thus, the kinematic redundancy of the robot with respect to the task can be exploited to optimize a desired criterion [18,19,20,21]. It is worth stressing that, in this kind of tasks, path constraints are known a priori. This is a fundamental difference with respect to [16], because the dimension of the problem can be reduced by only exploring the subspace given by the kinematic redundancy.
The robotic machining and the additive manufacturing tasks are two significant technological examples where the use of industrial robots has become important and the motion planning strategies cover a crucial role [20,21]. However, the use of dedicated motion planning algorithms for these kind of applications is not common in the literature and in industry.
Thank to the improvements of robots kinematics and dynamics performance, the use of industrial robots in the field of machining applications has profitably increased during the last years [22]. However, industrial robots still have low kinematics and dynamics performance if compared to CNC machines, hence a kinodynamic motion planning can be a suitable solution to tackle such limitations. In machining tasks, kinematics constraints strictly depend on the process and hence by the adopted tool. In general, all the machining processes using a rotating tool have at least one redundant degree of freedom (DoF). The redundancy permits to choose an optimized robot configuration among an infinite set of solutions, as also clarified in Figure 1. Depending on the technological requirements of the specific machining task the redundant DoF/DoFs can be optimized to improve the process results [23].
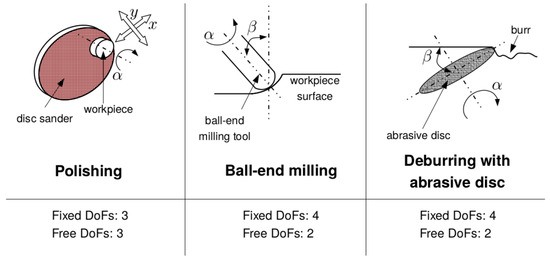
Figure 1.
Example of machining tasks with the free DoFs.
Another emerging field for industrial robots is represented by the additive manufacturing and laser cladding, that is, metal material deposition with techniques such as laser metal deposition or electron beam melting [24,25,26]. The kinematic constraints with laser metal deposition technique consists in keeping the translation speed constant and identifying the best tilt of the laser head with respect to the underlying surface. [27,28,29,30] highlight that the process is feasible, although not optimal, for a large range of relative orientations between the deposition axis and the line perpendicular to the surface. Thus, it is possible to optimize the trajectory in order to keep the tilt angle as small as possible and respecting also kinodynamic constraints at the same time.
In particular, the main axis of the operating tool and the axis perpendicular to the surface to be machined/coated define an angle that should be always kept within certain limits depending on the specific process. As consequence, there is always (i) an operative redundancy (the rotation around the main axis of the operating tool) and (ii) a range of permitted angles around the axis perpendicular to the surface. The operative redundancy, namely the allowed cone around the axis perpendicular to the surface, can be exploited to find an optimal orientation able to satisfy both the technological constraints and the robot kinematics/dynamics limits. Figure 2 describes the general idea of these motion planning issues in additive manufacturing. Pipe welding [20] and gluing [31] applications can also be described with a similar optimization problem.
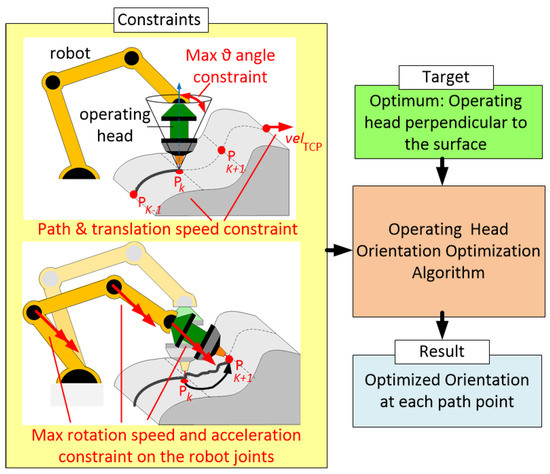
Figure 2.
Scheme of kinodynamic constraints and desired targets for the residual DoFs optimization in defining a laser head or deburring tool orientation.
Although a-priori knowledge of closed-form Cartesian constraints reduces the complexity of the problem, it is not trivial to find the solution of the optimization problem. Indeed, the problem is PSPACE-hard [32], highly nonlinear and the constraints make the feasible subset of the configuration space disconnected due to direct kinematics is surjective but not necessary injective. Moreover, to obtain an effective obstacles avoidance, collision checks are mandatory with a consequent increment of the computing time. Thus, solvers face local minima and computational burden issues. Many works proposed tailored solutions on the specific application or the number of redundant DoFs: welding [20,33], machining and 5-axes applications [34,35], additive manufacturing [21]. However, there is a lack of a general solution for the entire family of problems. Looking at the 5-axes CNC machines, some works deal with a simplified version (because of the lower number of DoFsand the particular structure of CNC machines) of the technologically constrained planning problem. In [36] a complete overview of motion planning for CNC machines is presented. In particular, the focus of the paper is on the definition of the tool orientation in order to: avoid collisions with gauges, preserve the position within joints limits, and get smooth speed profiles. Moreover, [37] investigated the optimization of the orientation of the cutting tools in 5-axes machines. Unfortunately, most of the assumptions valid for a 5-axes CNC machine do not hold for industrial robots, where high rotation speed leads to high dynamic effort with resulting motion inaccuracies and vibrations.
This work proposes a unified framework to deal with kinodynamic motion planning applied to machining, welding, gluing, and additive manufacturing tasks. This allows us to cope with different technological constraints and objectives, avoiding the need of tailored solutions.
The approach is based on the formulation of the redundant task as a net, whose vertices are the admissible joint configurations and the edges are the movements between two subsequent configurations. In this formulation, path constraints define the set of admissible joint configurations, that is, the vertices of the net. Then, kinodynamics constraints determine the admissible edges. The resulting net represents the constrained motion planning problem.
The paper shows examples of industrial processes that can be expressed in this framework. It is worth noticing that also complex tasks can be addressed, such as the minimization of elastic deformations during milling processes. Moreover, the discrete nature of the approach also permits to set a trade-off between the quality of the solution and the computational time. This is especially true considering that the granularity of the discretization directly affects the number of collision checks that the algorithm needs to perform, which represent the main bottleneck from the computational point of view.
To solve the discrete motion planning problem, we propose a modified Ant Colony Optimization algorithm. Ant colony optimization is a meta-heuristic technique to find optimal path through graphs [38]. It is inspired by the behavior of some species of ants to find the optimal route from the anthill to food resources. The idea behind the algorithm is that the ants release a pheromone track on the nodes, which attracts other ants. This track evaporates through iterations but is reinforced by other ants if the nodes belong to good paths. In the end, the high-pheromone tracks converge to the optimal route from the starting point to the goal. Ant colony optimization is particularly suitable for nonlinear high-dimensional discrete optimization problems, which makes it a good candidate for the problem at hand. Different variants of the ant colony algorithm have been proposed in the literature, as detailed in [39]. In this paper, we combine two strategies to develop an improved Ant Colony solver. First, we exploit the rank-based ant-colony strategy proposed in [40], in which only the best ants of each iteration are selected to update the pheromone trails. This approach is very promising for the problem considered in this paper, because it makes possible to dramatically reduce the computational burden by performing lazy collision checking (namely, to check collisions only for the most promising vertexes). Then, we use the modified version of the Ant Colony algorithm proposed in [41] to avoid premature convergence to local minima, which is a typical issue in motion planning problems. In the proposed approach, a rank-based ant-colony with pheromone saturation is used to solve the planing problem. Comparison with other ant-colony approaches shows its effectiveness to manage redundancy in technological trajectories.
The proposed approach is applied to a real-work milling and additive manufacturing scenarios, where the deflection of the robot tool is successfully minimized throughout the process. Moreover, the proposed algorithm shows faster convergence rate compared to other Ant Colony Optimization solvers.
The paper is organized as follows. Section 7 introduces the notation used in the paper. Definitions related to the technological processes and constraints are given in Section 2. Section 3 describes the proposed framework and the definition of the motion planning problem as a discrete optimization problem. Section 4 focuses on the application of the proposed framework to common technological tasks in industrial processes. Section 5 describes the modified Ant Colony Optimization solver used in this work. Then, case study on machining applications is discussed in Section 6, where the proposed solver is compared with other ant-colony strategies. Conclusions are drawn in Section 7.
2. Technological Trajectories And Constraints
Technological trajectories are typically generated by CAM software as an ordered set of couples containing tool center point coordinates and the tool z-axis orientations, and the corresponding time instant. Therefore, it is possible to define:
Definition 1.
A technological path is a set of N desired transformation matrices, each denoted as , .
Definition 2.
A technological trajectory is a technological path where an execution time instant is assigned to each kth pose.
Definitions 1 and 2 define the user input to the optimization problem. Given a technological trajectory, the desired velocity and acceleration twist vectors and can be derived through numerical differentiation.
Notice that a technological trajectory does not define a unique Cartesian trajectories, but it corresponds to a family of possible Cartesian trajectories that have to satisfy some hard constraints (for example, the position of the tool center point) and some soft constraints (for example, limitations of the maximum tilt of a laser with respect to the surface). Hard constraints are mathematically represented as a set of equalities, whereas soft constraints can be modeled as a set of inequalities. It is worth stressing that time parametrization is an input for the motion planner, as well as the number of trajectory steps N.
Definition 3.
The path hard constraints are a set of equality constraints that limit the pose of the tool with respect to the base such that, for all :
The path soft constraints are a set of inequality constraints that limit the pose of the tool with respect to the base such that, for all :
Definition 4.
Kinodynamics hard constraints are defined as a set of equality constraints that limit the tool velocity and acceleration with respect to the base such that, for all :
Definition 5.
Kinodynamics soft constraints are defined as a set of inequality constraints that limit the tool velocity and acceleration with respect to the base such that, for all :
3. Proposed Framework for Task Formalization
By considering constraints (1)–(2), the set of feasibile Cartesian paths can be defined as the set of all possible transformation matrices that satisfy (1) and (2) at each step k, that is:
Technological tasks typically have a small number of redundant DoFs. For example, milling and deburring tasks require 5 DoFs and are typically performed by a 6-DoF manipulator. The exploration of the subset of Cartesian given by the redundancy is therefore practical. In particular, such space can be discretized and, for each sample, the closed-form inverse kinematics of the manipulator can be solved. We therefore refer to as the discretization of the continuous set . Inverse kinematic problem is then solved for all the elements of . Details about the discretization process for different technological tasks are described in Section 4.1 and Section 4.2.
Definition 6.
For each k, the feasible configuration set is the set of all joint configurations which correspond to a transformation matrix in and that respect the joint limits, that is:
The elements of each set are the net vertex. The joint configuration is the element of set , while is the corresponding transformation matrix. The transition between the element of set to the element of set is the net edge.
In order to check if constraints (3)–(4) are satisfied, it is necessary to know the edges that connect to . We therefore define a network path as follows.
Definition 7.
A network path p is an ordered sequence that connects the configuration sets .
This idea is also clarified in Figure 3. Given a network path p, it is possible to compute the finite-difference approximations of Cartesian velocities, joint velocities, joint accelerations, and joint efforts. Joint velocity and acceleration at step k are computed as:
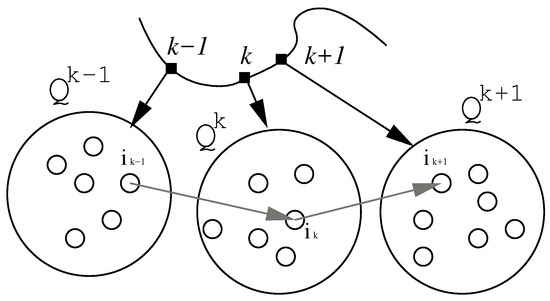
Figure 3.
Network representation of the possible joint configuration evolution.
Joint effort can be computed using inverse dynamics:
Velocity and acceleration twists are computed as:
In order to evaluate the goodness of the paths, it is necessary to define a cost function which depends on both the vertices and the edges. Vertex costs depend only on the path, while edge costs depend on kinodynamics quantities. The following definition of the trajectory planning problem therefore can be applied:
Definition 8.
The robot trajectory optimization is a minimization problem defined as follows:
where:
and where and are cost functions depending respectively on the vertices and the edges of the network path.
4. Examples of Common Technological Tasks
Based on the definitions given above, two typical problems of additive manufacturing, welding, and gluing applications are discussed in details: (i) a 5-DoF task, typical of machining applications, where the goal is to execute the trajectory by minimizing the deflections caused by the material removing forces; (ii) a 3-DoF task, where the goal is to reduced the angle between the end-effector and the surface normal to the tool z-axis.
4.1. 5-DoF Tasks
In 5-DoF tasks (such as deburring and milling), path hard constraints are related to the end-effector position and its z-axis orientation, while there are no soft path constraints. Path constraints are therefore given by:
Moreover, machining tasks require hard constraints on end-effector Cartesian linear velocity, that is, for all :
The redundancy can be exploited to optimize the manipulator stiffness along the direction of the cutting forces of the milling process. A possible choice of is therefore the squared norm of the so-called Cartesian Compliance Index, that is:
where is the -norm weighted by vector M, and is a vector representing angular and linear deflections of the end-effector due to the milling force. The Cartesian Compliance Index is a scalar measure that represents the weighted norm of deflections introduced by robot elasticity. Minimizing this index improves quality of the technological task.
Deflection is computed as
where is the wrench vector given by the torque and the force generated by the milling process at the step k, J is the geometric Jacobian matrix, and K is the joint stiffness matrix. Milling force is computed by using model proposed in [42], force application point is the end-effector frame origin the milling torque is null.
The edge cost function is chosen as the sum of the squared norms of the joint velocity and acceleration vectors, that is:
where and are weighting constants.
Since there is only one redundant DoF, uniform gridding can be applied without curse of dimensionality. As mentioned in Section 3, the redundant degree of freedom is uniformly sampled between its limits obtaining a set of transformation matrices. Inverse kinematics is then computed to compute sets . The discretization step can be chosen as a trade-off between the computational burden and the quality of the solution.
4.2. 3-DoF Tasks
In 3-DoF tasks (such as additive manufacturing, welding and gluing), path hard constraints are related to the end-effector position and its z-axis orientation. The following path constraints should therefore hold for all :
Soft path constraints consist in imposing the z-axis of to be inside a cone with aperture equal to such that, for all :
These tasks also require hard constraints on end-effector Cartesian linear velocity, that is, for all :
Vertex cost is the norm of the angle between the z-axis of the end effector and the z-axis of the desired pose, that is:
Edge cost term minimizes the sum of squared norms of the joint velocity and acceleration vectors as in the 5-DoF case (14).
Since redundancy subspace is three-dimensional, memory footprint can be a limit factor. In this case, uniform random sampling can be used. By using ZYX Euler angles coordinates, the y- and x-axis are rotated by a randomly sampled angle in , while the z-axis angle is randomly sampled in . Then, the resulting transformation matrix is stored if (16) is respected. In order to avoid oversampling in some regions of the redundant subspace, a new sample is discarded if the distance with the closest sample is smaller than a chosen threshold. The number of samples can be chosen as a trade-off between computational burden and the quality of the solution.
5. Ant Colony Optimization Algorithm
The robot trajectory optimization stated in Definition 8 is a discrete optimization problem that can be solve by means of an Ant Colony Optimization solver. The proposed solver uses a strategy [41], where a rank-based selection of the best m ants contribute to pheromone updates [40].
The quantity of pheromone added to the vertex depends on the quality of the ant network path (namely, it is inversely proportional to the related cost function). The pheromone evaporation is performed by applying an exponential decay after the passage of all ants. In order to avoid early stalling, the values of the pheromone is bounded between and as in [41]. The ants choose the next vertex based on a probability inversely proportional to the vertex cost . Such probability is given by:
where is the probability to go from vertex to , is the pheromone value of vertex , is the cardinality of ,
and has a small value to avoid division by zero.
Thus, the Ant Colony algorithm can be summarized as:
- Set is discretized into set , sampling in redundancy subspace;
- Set is obtained by solving the inverse kinematic problem for all elements of ;
- The pheromone value of each vertex is initialized equal to ;
- Each ant randomly selects the next vertex based on the transition probability Equation (19);
- Ants are ranked based on the path cost;
- m best ants are selected, collision checking is performed on the vertexes which are selected the first time. If an ant path is in collision, this ant is replaced by the next ant in the ranking;
- The best solution found since the beginning of the whole optimization is added to the set of the best ants found at the current iteration;
- The best ants update the pheromone values of the vertexes of their path by adding a quantity that is inversely proportional to the cost function of its entire network path, that is:
- The pheromone evaporation is performed for all the vertexes
- If termination conditions are not satisfied, go to step 4.
Termination conditions are the convergence of ants to the best path and the convergence of the pheromone level to a steady value, as suggested in [43]. It is worth highlighting that if in Step 6 there are less the m ants with a feasible path, all of them are selected. If no ant provides a feasible path, the optimization problem is aborted.
6. Case Studies
6.1. Milling Task
Algorithm effectiveness is analyzed in the milling task scenario shown in Figure 4. As stated in Section 4.1, the redundancy optimization criterion consists in minimizing the deflections caused by milling forces.

Figure 4.
Redundant DoF of the robot during the milling task. The redundant DoF is the rotation around the z-axis of the world frame denoted .
Weighting vector M in (12) is set equal to
by imposing that a linear deflection equal to 1 [mm] has the same influence of an angular deflection equal to 1 [deg], and neglecting deflections around the redundant axis. Weighting factors are set equal to and , respectively.
The considered robot model is a 6-DoF Comau NS16. The algorithm runs on a laptop equipped with a Intel Core i7-8565U, 16 GB RAM-LPDDR3 and a 512 GB SSD. The stiffness matrix was derived by following the identification procedure described in Chapter 4 of [44] and is equal to:
The transformation matrix between the robot base frame and the workspace frame is
while the transformation matrix between the robot flange and the end-effector frame is
The milling trajectory is a 100 [mm] × 100 [mm] square with rounded corner (radius 5 [mm]), the center of the square is shifted by 50 [mm] from the the workspace origin along x and y directions, as shown in Figure 5, where also milling forces are represented. The milling parameters are in Table 1.
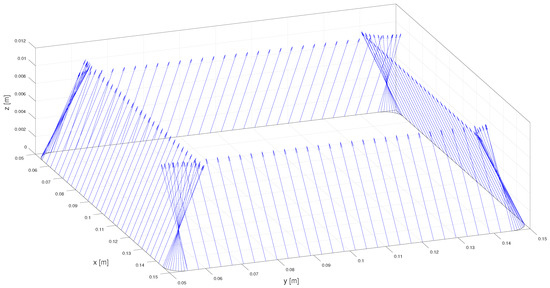
Figure 5.
Milling path with the required force field (blue arrows).

Table 1.
Technological parameters used to compute the milling forces described in [42]. Parameters are referred to aluminum milling.
The milling path is discretized in 157 points. In each of them, the redundancy angle is discretized by using 721 values equally spaced in the range [−,] (namely, sampling step equal to 0.5 [deg]). By computing the inverse kinematic for each value of the redundancy angle, the cardinality of sets varies between 1442 and 1868, depending on joint limits and possible collisions. Memory footprint of each vertex is 64 Byte (6 double variables for joint configuration, one double variable for the cost , one double variable for pheromone value), the footprint of the all net vertexes is 16 Mbyte.
We denote with RBMM (Rank-Based Max-Min) the solver proposed in Section 5. We compare it with:
- a standard Ant Colony Optimization solver (denoted as ACO) [38];
- a rank-based Ant Colony approach (denoted as RB) [40];
- a Ant Colony approach (denoted as MM) [41];
- a local solver (denoted as LS) where is selected as the vertex with minimum cost in and, for each step k, the next vertex is selected as the vertex with minimum cost in which can be reached from with a feasible transition.
In order to compare different algorithms performances, Problem (7) is solved 10 times for each algorithm. The chosen performance indices are the root mean square value of the Cartesian Compliance Index () and the time taken by the algorithm to find a solution. Table 2 shows the average value and the standard deviation of the indices for the different methods. On the one hand, RBMM and MM converge to a better solution thanks to the pheromone saturation, which avoids stagnation in local minima. On the other hand, RBMM and RM show lower computational times, thank to the rank-based ant selection and the consequent reduction of collision checking. Notice that LS gives the worst solution, due to its deterministic and local nature.

Table 2.
Average and standard deviation of the Cartesian Compliance Index (root mean square value) and of the computational time.
The obtained deflection trends during the 10 runs of RBMM algorithm are shown in Figure 6, highlighting the algorithm repeatability.
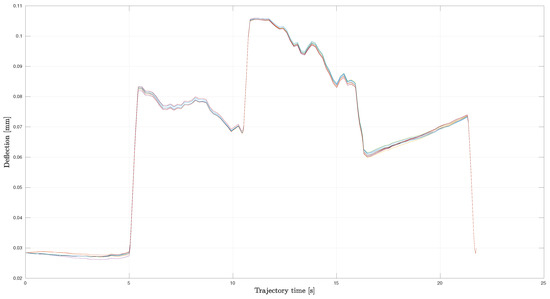
Figure 6.
Deflection (Cartesian Compliance Index) trends obtained during 10 runs of the proposed algorithm.
6.2. Additive Manufacturing
An additive manufacturing task is considered. The technological path is a spiral defined as
where is the curvilinear abscissa
The curve is depicted in Figure 7.
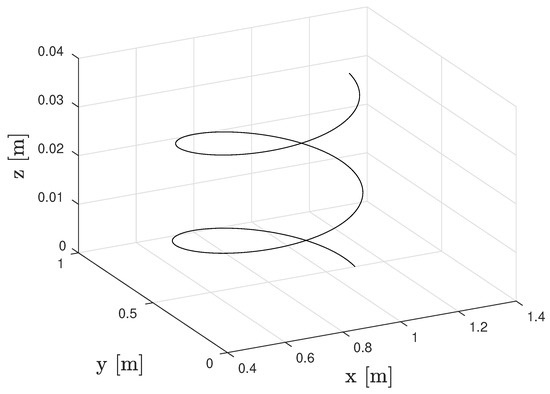
Figure 7.
Additive manufacturing technological path.
The end-effort has to follow the curve during the time period with the following timing law
In this way, the modulus of Cartesian velocity is constant when , as shown in Figure 8.
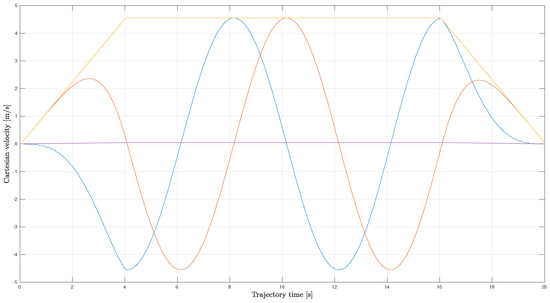
Figure 8.
Trends of Cartesian velocity. Blue line: x-component. Red line: y-component. Violet line: z-component. Yellow line: modulus.
The considered robot model is a 6-DoF Comau NS16, while the algorithm runs on a laptop equipped with a Intel Core i7-8565U, 16 GB RAM-LPDDR3 and a 512 GB SSD.
The additive path is discretized in 200 points. The cone apperture is set equal to [deg]. In each of them, 2356 uniform-distributed transformation matrices respecting (16) are considered. By computing the inverse kinematic for each value of the redundancy angle, the cardinality of sets varies between 9424 and 18,848, depending on joint limits and possible collisions. As in Section 6.1, memory footprint of each vertex is 64 Byte, the footprint of the all net vertexes is 171 Mbyte.
The comparison is made by using the same algorithm of Section 6.1. In order to compare different algorithms performances, Problem (7) is solved 10 times for each algorithm. The chosen performance indices are the root mean square value of the angle (in degrees) w.r.t. the nominal path and the time taken by the algorithm to find a solution.
Table 3 shows the average value and the standard deviation of the indices for the different methods. Considerations of Section 6.1 are confirmed also in this case study. RBMM and MM converge to a better solution avoiding stagnation in local minima. Moreover, RBMM and RM show lower computational times, thank to the rank-based ant selection and the consequent reduction of collision checking. Finally, LS gives the worst solution, due to its deterministic and local nature.

Table 3.
Average and standard deviation of the angle between computed and nominal path. (root mean square value) and of the computational time.
Also in this case, the algorithm repeatability is shown in Figure 9, where results of 10 runs are depicted.
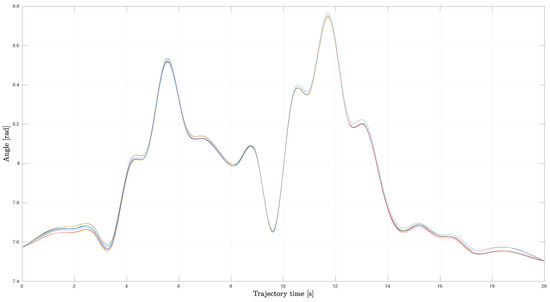
Figure 9.
Angle between computed and nominal path trends obtained during 10 runs of the proposed algorithm.
7. Conclusions
This paper has proposed a unified motion planning framework to deal with under-defined Cartesian trajectories in technological applications, such as milling, additive manufacturing, welding, and gluing applications. In particular, we have used this framework to formulate two common technological problems by taking into account their particular technological requirements. The proposed formulation is based on the discretization of the configuration space: the allowed Cartesian space is sampled and a closed-form inverse kinematics is applied to obtain an admissible set of joint configurations for each point of the task. This leads to a discrete optimization problem, which is solved by a modified Ant Colony Optimization solver based on Rank-based and strategies. Notice that the formulation of the problem implicitly respects the constraints of the robot such as position, velocity, acceleration, and torque limits. The effectiveness of the method is demonstrated in real-word milling and additive manufacturing scenarios. Results show that the proposed approach is able to optimize the task by also taking into account complex elastic behaviours during the process, such as the deflection of the robot tool. A comparison with other Ant Colony solvers shows that the proposed algorithm has faster converge rate and it has a better repeatability then other Ant Colony Optimization implementations.
Author Contributions
M.B., S.M. and G.N. designed the Ant Colony solver. M.F. and N.P. worked on the problem formalization, P.M. dealed with additive manufacturing case study, E.V. worked on the machining case study.
Funding
No funding was received for this work.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| n | number of degrees of freedom of the robot |
| q | joint configuration vector |
| joint velocity vector | |
| joint acceleration vector | |
| joint effort vector | |
| transformation matrix from frame b to frame a | |
| origin of frame b in frame a | |
| linear velocity of the origin of frame b in frame a | |
| angular velocity of frame b in frame a | |
| linear acceleration of the origin of frame b in frame a | |
| angular acceleration of frame b in frame a | |
| velocity twist vector from frame b to frame a, defined as | |
| acceleration twist vector from frame b to frame a, defined as | |
| transformation matrix from robot end-effector frame to workpiece frame w | |
| transformation matrix from CAM output frame to workpiece frame w at trajectory sample k | |
| N | number of samples of the desired trajectory |
The following functions describe the kinematics and dynamics equation of the robot:
| - | is the forward kinematic function of the robot; |
| - | is the velocity forward kinematic function; |
| - | is the acceleration forward kinematic function; |
| - | is the inverse dynamics function; |
| - | is the collision function, which is equal to 1 in case of one or more collisions, 0 otherwise. |
The following sets describe the feasible conditions:
| - | admissible joint configuration set where and are, respectively, the lower and upper joint limits; |
| - | admissible joint velocities set where and are, respectively, the lower and upper joint velocity limits; |
| - | admissible joint effort set where and are, respectively, the lower and upper joint effort limits; |
| - | admissible Cartesian velocities set where , , , and are, respectively, the lower and upper linear and angular velocity limits. |
References
- Mohanan, M.; Salgoankar, A. A survey of robotic motion planning in dynamic environments. Robot. Auton. Syst. 2018, 100, 171–185. [Google Scholar] [CrossRef]
- Erdos, G.; Kovács, A.; Váncza, J. Optimized joint motion planning for redundant industrial robots. CIRP Ann. Manuf. Technol. 2016, 65, 451–454. [Google Scholar] [CrossRef]
- LaValle, S.M. Planning Algorithms; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Jaillet, L.; Cortés, J.; Siméon, T. Sampling-Based Path Planning on Configuration-Space Costmaps. IEEE Trans. Robot. 2010, 26, 635–646. [Google Scholar] [CrossRef]
- Devaurs, D.; Simeon, T.; Cortes, J. Enhancing the transition-based RRT to deal with complex cost spaces. In Proceedings of the IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 17 October 2013; pp. 4120–4125. [Google Scholar] [CrossRef]
- Adiyatov, O.; Varol, H.A. A novel RRT*-based algorithm for motion planning in Dynamic environments. In Proceedings of the IEEE International Conference on Mechatronics and Automation, Takamatsu, Japan, 6–9 August 2017; pp. 1416–1421. [Google Scholar] [CrossRef]
- Choudhury, S.; Gammell, J.D.; Barfoot, T.D.; Srinivasa, S.S.; Scherer, S. Regionally accelerated batch informed trees (RABIT*): A framework to integrate local information into optimal path planning. In Proceedings of the IEEE International Conference on Robotics and Automation, Stockholm, Sweden, 16–21 May 2016; pp. 4207–4214. [Google Scholar] [CrossRef]
- Gammell, J.D.; Srinivasa, S.S.; Barfoot, T.D. Informed RRT*: Optimal sampling-based path planning focused via direct sampling of an admissible ellipsoidal heuristic. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 2997–3004. [Google Scholar] [CrossRef]
- Salzman, O.; Halperin, D. Asymptotically-optimal Motion Planning using lower bounds on cost. In Proceedings of the IEEE International Conference on Robotics and Automation, Seattle, WA, USA, 26–30 May 2015; pp. 4167–4172. [Google Scholar] [CrossRef]
- Schulman, J.; Ho, J.; Lee, A.; Awwal, I.; Bradlow, H.; Abbeel, P. Finding locally optimal, collision-free trajectories with sequential convex optimization. In Proceedings of the Robotics: Science and Systems, Berlin, Germany, 24–28 June 2013. [Google Scholar] [CrossRef]
- Kunz, T.; Stilman, M. Time-optimal trajectory generation for path following with bounded acceleration and velocity. In Robotics: Science and Systems; MIT Press: Cambridge, MA, USA, 2013; Volume 8, pp. 209–216. [Google Scholar]
- Faroni, M.; Beschi, M.; Pedrocchi, N.; Visioli, A. Predictive Inverse Kinematics for Redundant Manipulators with Task Scaling and Kinematic Constraints. IEEE Trans. Robot. 2019, 35, 278–285. [Google Scholar] [CrossRef]
- Zucker, M.; Ratliff, N.; Dragan, A.D.; Pivtoraiko, M.; Klingensmith, M.; Dellin, C.M.; Bagnell, J.A.; Srinivasa, S.S. CHOMP: Covariant Hamiltonian optimization for motion planning. Int. J. Robot. Res. 2013, 32, 1164–1193. [Google Scholar] [CrossRef]
- Kalakrishnan, M.; Chitta, S.; Theodorou, E.; Pastor, P.; Schaal, S. STOMP: Stochastic trajectory optimization for motion planning. In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011. [Google Scholar] [CrossRef]
- Donald, B.; Xavier, P.; Canny, J.; Reif, J. Kinodynamic motion planning. J. ACM 1993, 40, 1048–1066. [Google Scholar] [CrossRef]
- Kingston, Z.; Moll, M.; Kavraki, L.E. Sampling-based methods for motion planning with constraints. Annu. Rev. Control. Robot. Auton. Syst. 2018, 1, 159–185. [Google Scholar] [CrossRef]
- Kingston, Z.; Moll, M.; Kavraki, L.E. Exploring implicit spaces for constrained sampling-based planning. Int. J. Robot. Res. 2019, 38, 1151–1178. [Google Scholar] [CrossRef]
- Sabourin, L.; Subrin, K.; Cousturier, R.; Gogu, G.; Mezouar, Y. Redundancy-based optimization approach to optimize robotic cell behaviour: Application to robotic machining. Ind. Robot. 2015, 42, 167–178. [Google Scholar] [CrossRef]
- Fang, H.; Ong, S.; Nee, A. Robot path planning optimization for welding complex joints. Int. J. Adv. Manuf. Technol. 2017, 90, 3829–3839. [Google Scholar] [CrossRef]
- Shahabi, M.; Ghariblu, H.; Beschi, M. Obstacle avoidance of redundant robotic manipulators using safety ring concept. Int. J. Comput. Integr. Manuf. 2019, 32, 695–704. [Google Scholar] [CrossRef]
- Magnoni, P.; Pedrocchi, N.; Thieme, S.; Legnani, G.; Tosatti, L.M. Optimal planning in robotized cladding processes on generic surfaces. Robotica 2018. [Google Scholar] [CrossRef]
- Iglesias, I.; Sebastián, M.; Ares, J. Overview of the State of Robotic Machining: Current Situation and Future Potential. Procedia Eng. 2015, 132, 911–917. [Google Scholar] [CrossRef]
- Sadílek, M.; Čep, R.; Budak, I.; Soković, M. Aspects of using tool axis inclination angle. Stroj. Vestnik/J. Mech. Eng. 2011, 57, 681–688. [Google Scholar] [CrossRef]
- Nowotny, S.; Scharek, S.; Beyer, E.; Richter, K. Laser beam build-up welding: Precision in repair, surface cladding, and direct 3D metal deposition. J. Therm. Spray Technol. 2007, 16, 344–348. [Google Scholar] [CrossRef]
- Gao, J.; Chen, X.; Yilmaz, O.; Gindy, N. An integrated adaptive repair solution for complex aerospace components through geometry reconstruction. Int. J. Adv. Manuf. Technol. 2008, 36, 1170–1179. [Google Scholar] [CrossRef]
- Denkena, B.; Boess, V.; Nespor, D.; Floeter, F.; Rust, F. Engine blade regeneration: A literature review on common technologies in terms of machining. Int. J. Adv. Manuf. Technol. 2015, 81, 917–924. [Google Scholar] [CrossRef]
- Calleja, A.; Tabernero, I.; Fernández, A.; Celaya, A.; Lamikiz, A.; de Lacalle, L.L. Improvement of strategies and parameters for multi-axis laser cladding operations. Opt. Lasers Eng. 2014, 56, 113–120. [Google Scholar] [CrossRef]
- Lalas, C.; Tsirbas, K.; Salonitis, K.; Chryssolouris, G. An analytical model of the laser clad geometry. Int. J. Adv. Manuf. Technol. 2007, 32, 34–41. [Google Scholar] [CrossRef]
- Liu, J.; Li, L. In-time motion adjustment in laser cladding manufacturing process for improving dimensional accuracy and surface finish of the formed part. Opt. Laser Technol. 2004, 36, 477–483. [Google Scholar] [CrossRef]
- Xu, M.; Li, J.; Jiang, J.; Li, B. Influence of Powders and Process Parameters on Bonding Shear Strength and Micro Hardness in Laser Cladding Remanufacturing. Procedia CIRP 2015, 29, 804–809. [Google Scholar] [CrossRef]
- Pastras, G.; Fysikopoulos, A.; Chryssolouris, G. A theoretical investigation on the potential energy savings by optimization of the robotic motion profiles. Robot. Comput. Integr. Manuf. 2019. [Google Scholar] [CrossRef]
- Latombe, J.C. Robot Motion Planning; Kluwer Academic Publishers: Boston, MA, USA, 1991. [Google Scholar]
- Chen, C.; Hu, S.; He, D.; Shen, J. An approach to the path planning of tube-sphere intersection welds with the robot dedicated to J-groove joints. Robot. Comput. Integr. Manuf. 2013, 29, 41–48. [Google Scholar] [CrossRef]
- Léger, J.; Angeles, J. Off-line programming of six-axis robots for optimum five-dimensional tasks. Mech. Mach. Theory 2016, 100, 155–169. [Google Scholar] [CrossRef]
- Subrin, K.; Sabourin, L.; Gogu, G.; Mezouar, Y. Intrinsic redundancy to optimize the robotic cell behavior: Application to robotic machining. In Proceedings of the 21ème Congrès Français de Mécanique, Bordeaux, France, 26–30 August 2013; pp. 2–7. [Google Scholar]
- Lasemi, A.; Xue, D.; Gu, P. Recent development in CNC machining of freeform surfaces: A state-of-the-art review. Comput. Aided Des. 2010, 42, 641–654. [Google Scholar] [CrossRef]
- Sellmann, F.; Haas, T.; Nguyen, H.; Weikert, S.; Wegener, K. Orientation smoothing for 5-axis machining using quasi-redundant degrees of freedom. Int. J. Autom. Technol. 2016, 10, 262–271. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Chandra Mohan, B.; Baskaran, R. A survey: Ant Colony Optimization based recent research and implementation on several engineering domain. Expert Syst. Appl. 2012, 39, 4618–4627. [Google Scholar] [CrossRef]
- Hartl, R.F. A New Rank Based Version of the Ant System—A Computational Study Bernd Bullnheimer; Institute of Management Science, University of Vienna: Vienna, Austria, 1997. [Google Scholar]
- Stützle, T.; Hoos, H.H. Max-Min Ant System. Future Gener. Comput. Syst. 2000, 16, 889–914. [Google Scholar] [CrossRef]
- Altintas, Y. Manufacturing Automation Metal Cutting Mechanics, Machine Tool Vibrations, and CNC Design; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Zhang, Z.; Feng, Z.; Ren, Z. Approximate termination condition analysis for ant colony optimization algorithm. In Proceedings of the World Congress on Intelligent Control and Automation, Jinan, China, 23 August 2010; pp. 3211–3215. [Google Scholar] [CrossRef]
- Villagrossi, E. Robot Dynamics Modelling and Control for Machining Applications. Ph.D. Thesis, University of Brescia, Brescia, Italy, December 2016. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).