An Ultra-Wideband Bandpass Filter with a Notch Band and Wide Upper Bandstop Performances
Abstract
:1. Introduction
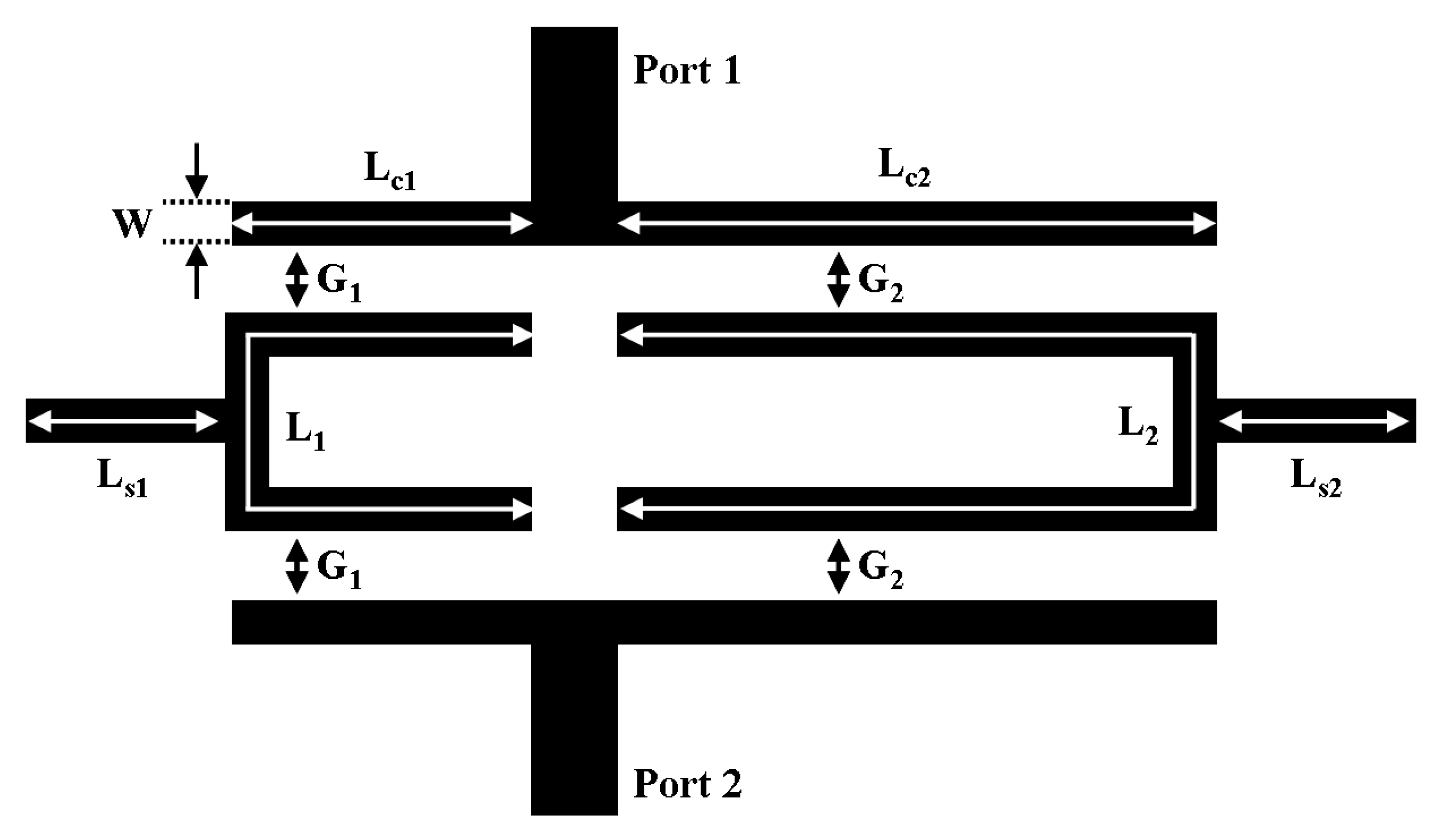
2. Design Procedure
2.1. Step 1: Determining Centered Frequency of the Passband
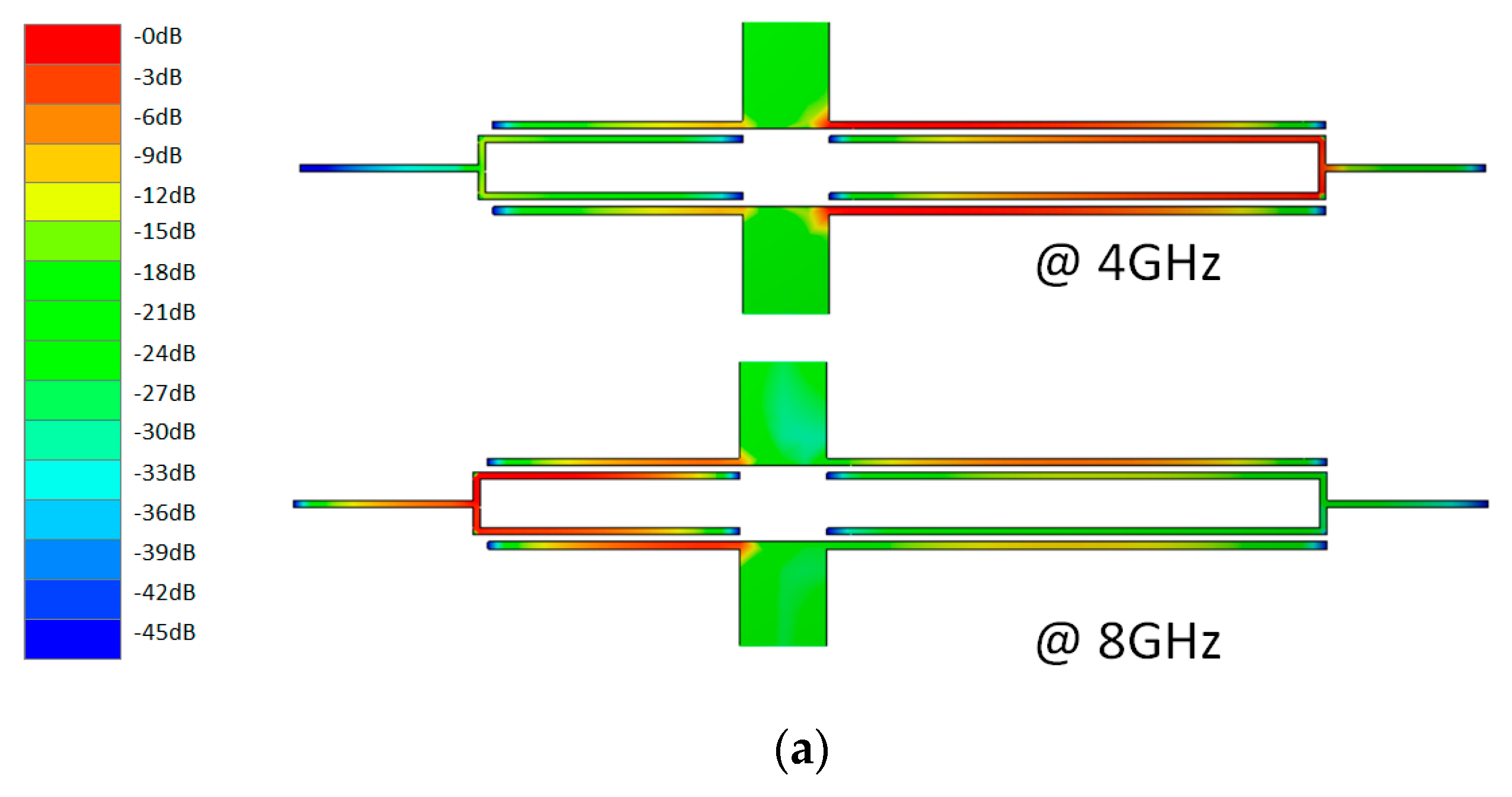
2.2. Step 2: Forming the Wideband Response
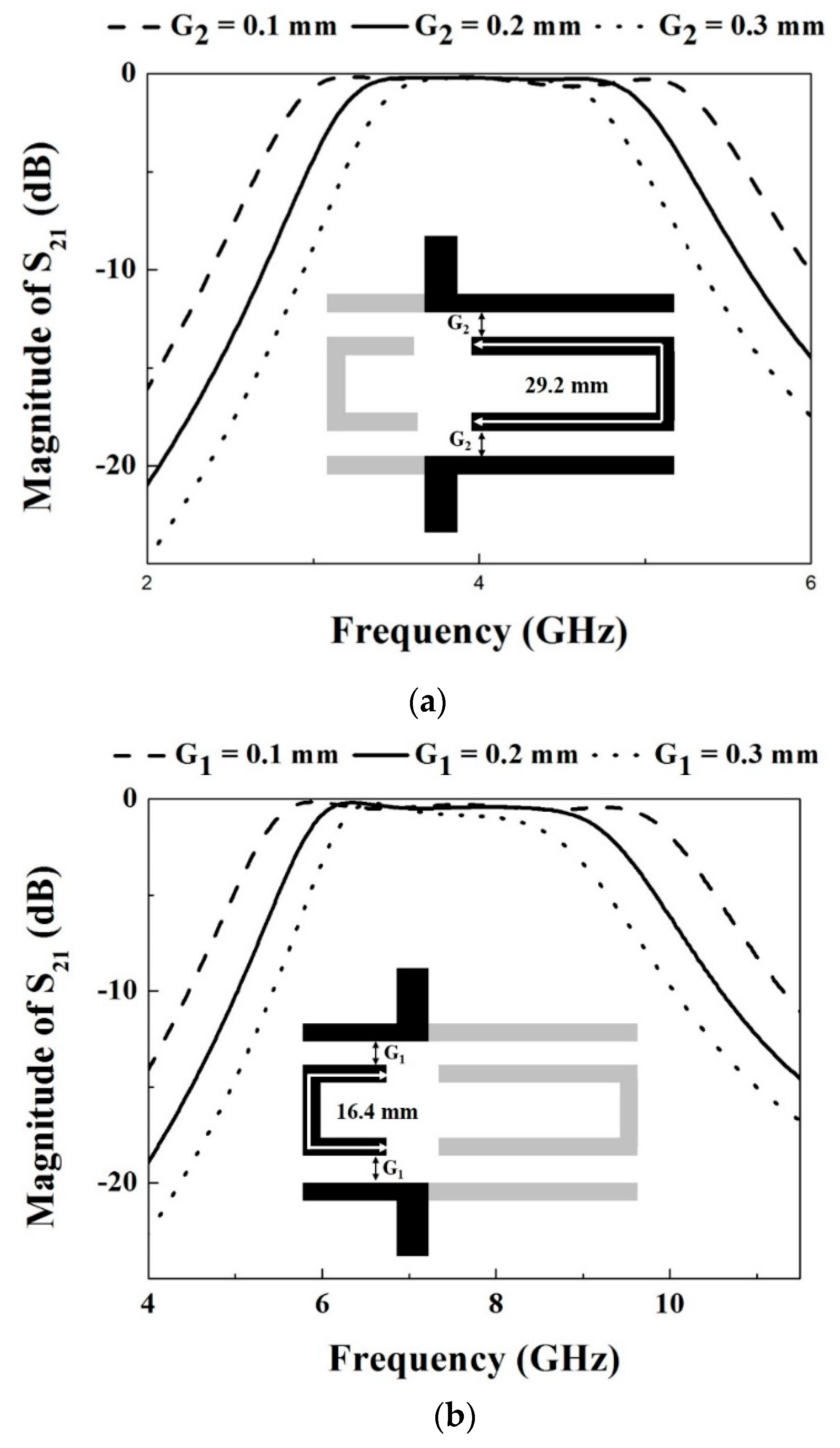
2.3. Step 3: Combining Two UWB Responses
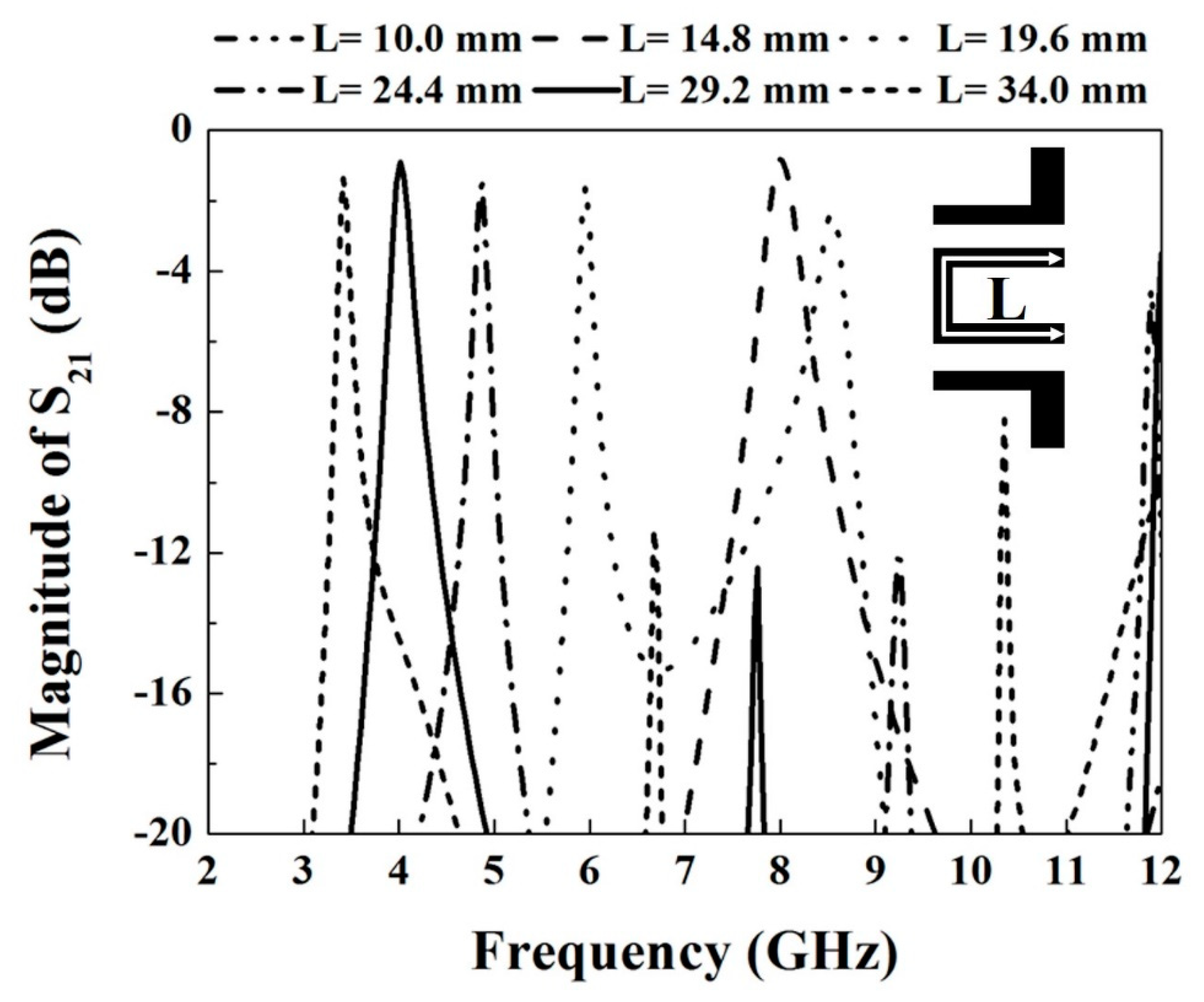
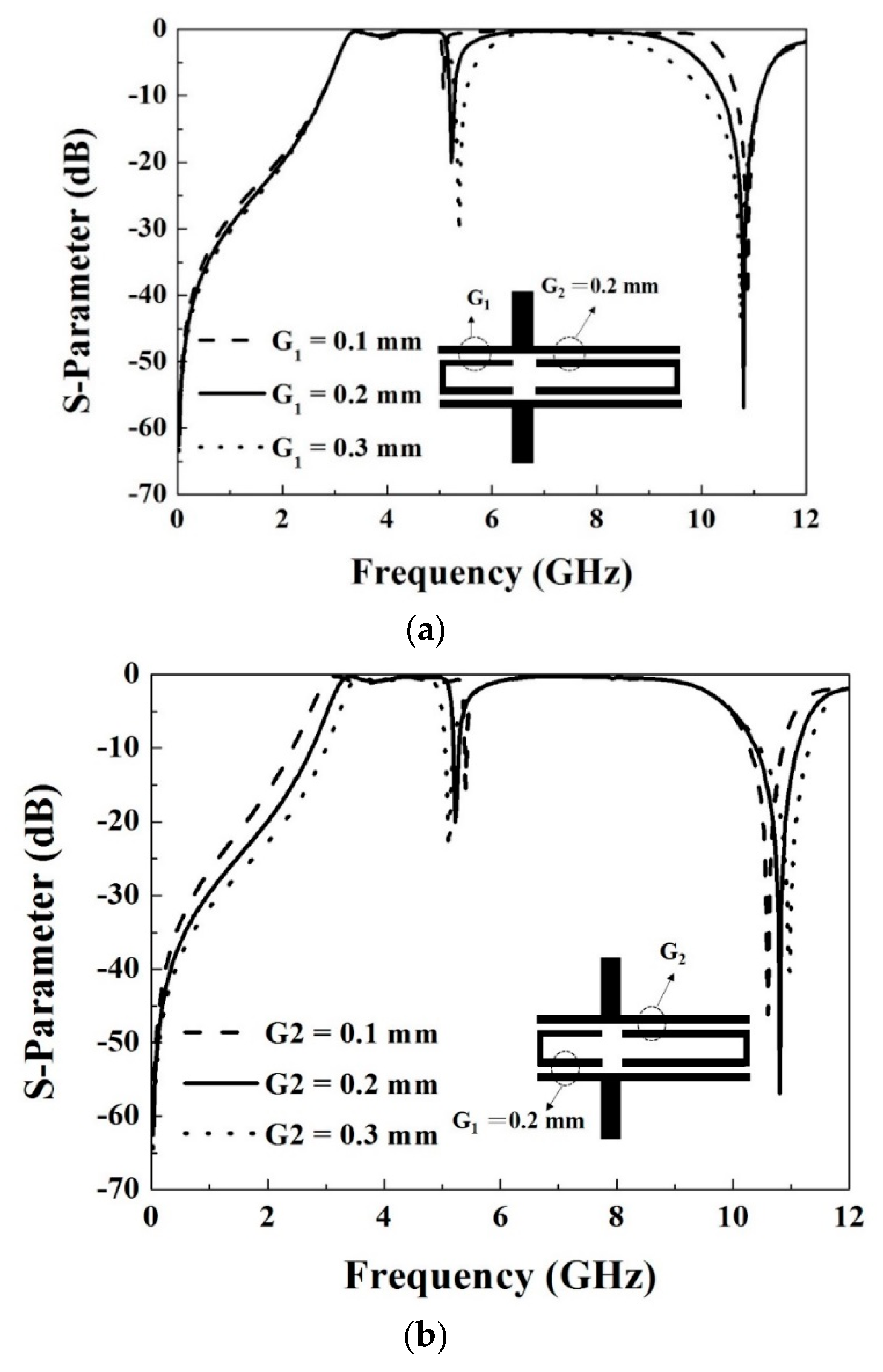
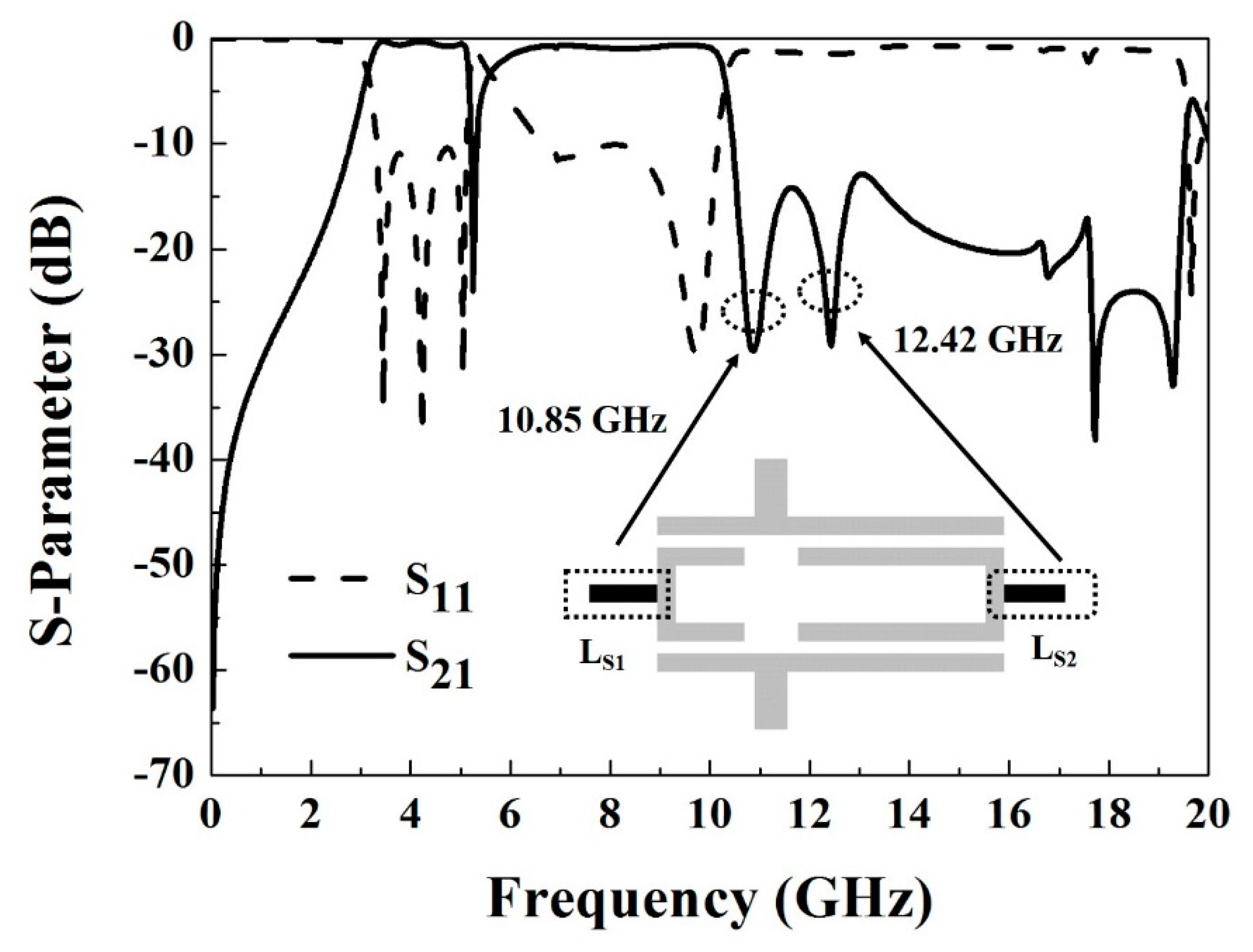
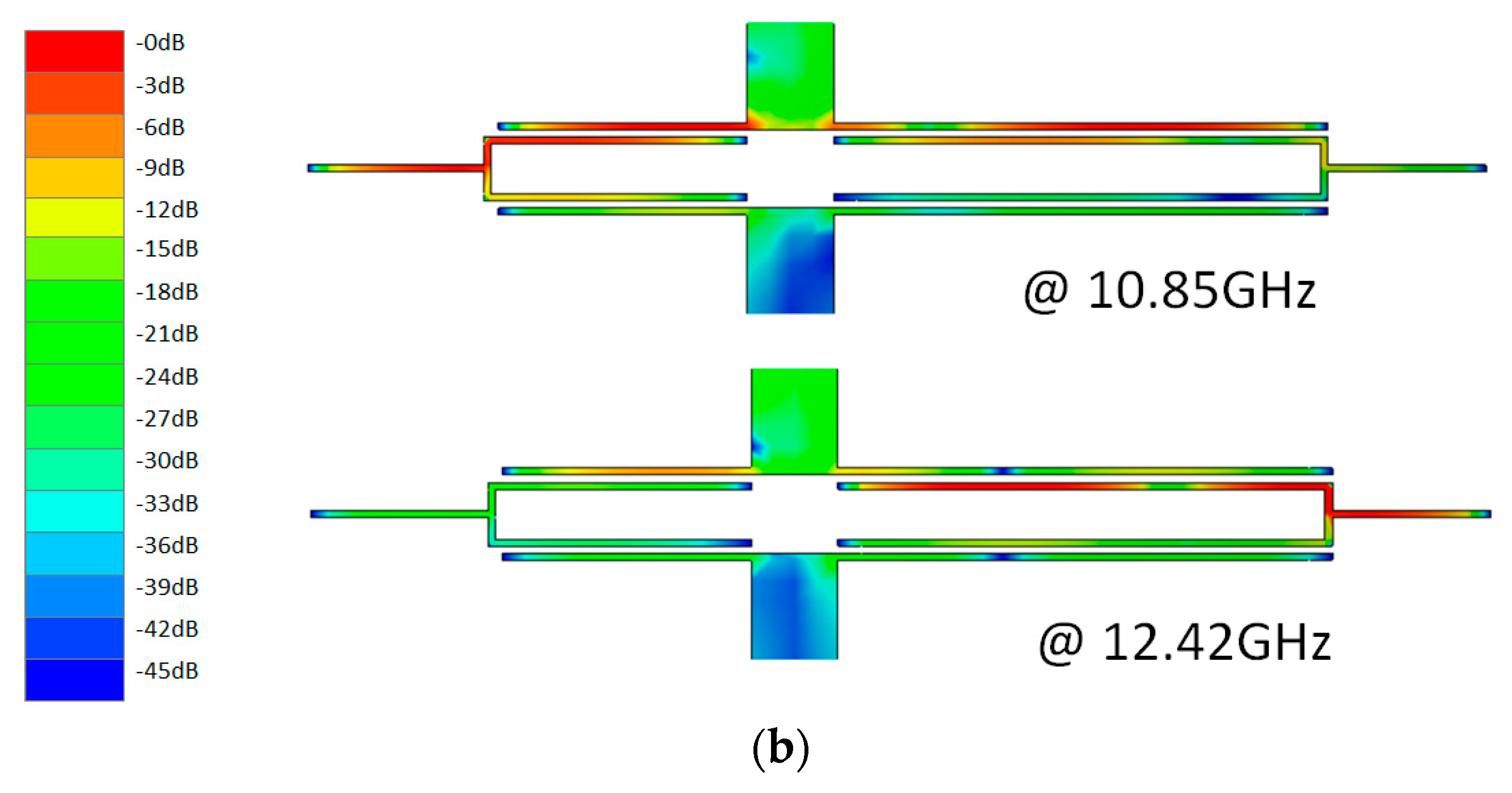
2.4. Step 4: Forming the Transmission Zeros
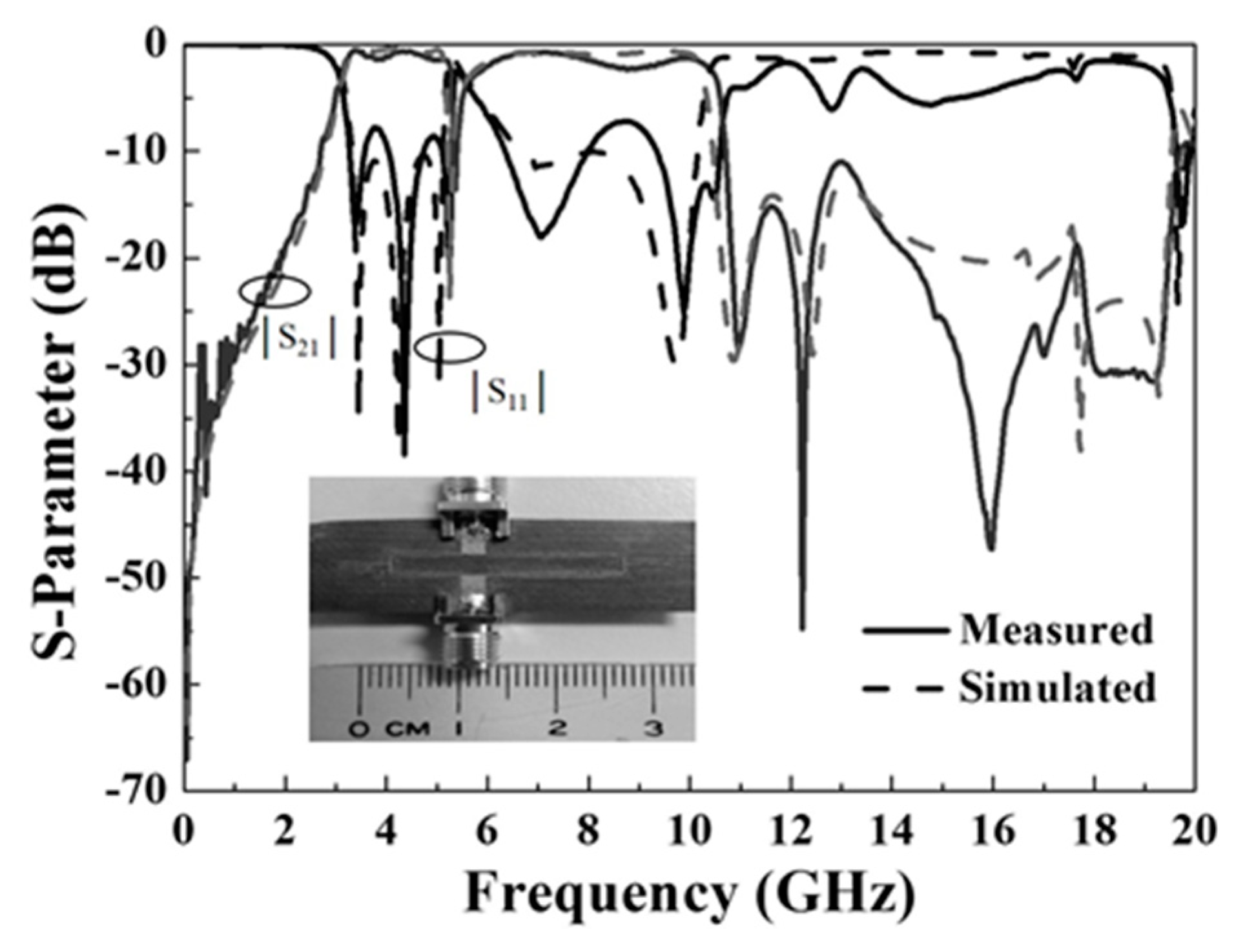
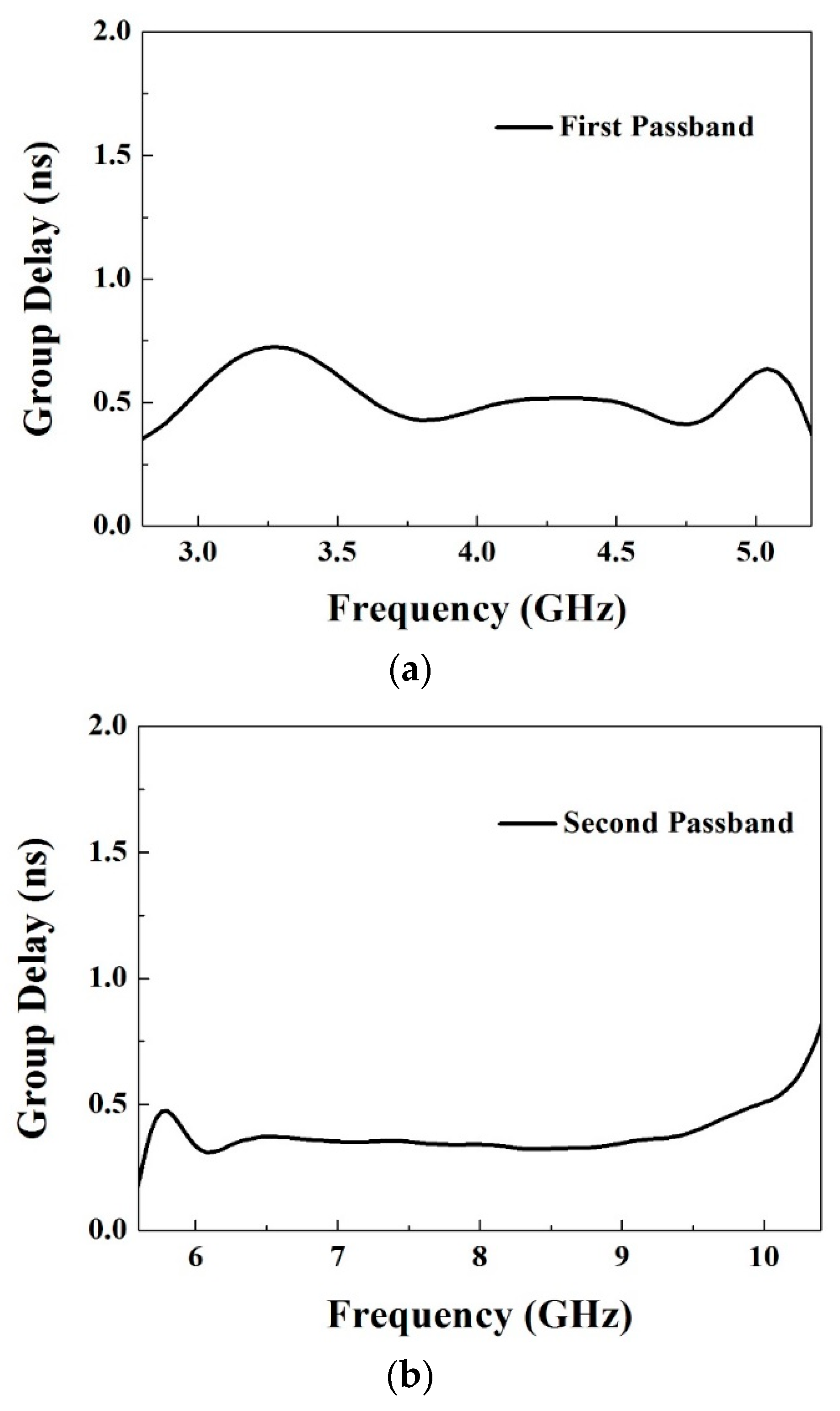
3. Experimental Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Federal Communication Commission. Revision of Part 15 of the Commission’s Rules Regarding Ultra-Wideband Transmission Systems; ET-Docket 98-153, FCC02-48; Federal Communication Commission: Washington, DC, USA, 2002.
- Kim, C.H.; Chang, K. Ultra-wideband (UWB) ring resonator bandpass filter with a notched band. IEEE Microw. Wirel. Compon. Lett. 2011, 21, 206–208. [Google Scholar] [CrossRef]
- Hao, Z.C.; Hong, J.S.; Parry, J.P.; Hand, D.P. Ultra-wideband bandpass filter with multiple notch bands using nonuniform periodical slotted ground structure. IEEE Trans. Microw. Theory Technol. 2009, 57, 3080–3088. [Google Scholar]
- Hung, C.Y.; Weng, M.H.; Su, Y.K. Design of compact and sharp rejection UWB BPFs using interdigital stepped-impedance resonators. IEICE Electron. Lett. 2007, 90, 1652–1654. [Google Scholar] [CrossRef]
- Wong, S.W.; Zhu, L. Implementation of compact UWB bandpass filter with a notch-band. IEEE Microw. Wirel. Compon. Lett. 2008, 18, 10–12. [Google Scholar] [CrossRef]
- Chang, Y.C.; Kao, C.H.; Weng, M.H.; Yang, R.Y. Design of the compact wideband bandpass filter with low loss, high selectivity and wide stopband. IEEE Microw. Wirel. Compon. Lett. 2008, 18, 187–189. [Google Scholar] [CrossRef]
- Song, Y.; Yang, G.M.; Geyi, W. Compact UWB bandpass filter with dual notched bands using defected ground structures. IEEE Microw. Wirel. Compon. Lett. 2014, 24, 230–232. [Google Scholar] [CrossRef]
- Liu, J.B.; Ding, W.H.; Chen, J.H.; Zhang, A. New ultra-wideband filter with sharp notched band using defected ground structure. Prog. Electromagn. Res. Lett. 2019, 83, 99–105. [Google Scholar] [CrossRef]
- Deng, K.; Feng, W. Wideband bandpass filter with multiple transmission zeros and compact size. Microw. Opt. Technol. Lett. 2016, 58, 2452–2455. [Google Scholar] [CrossRef]
- Zhang, Z.C.; Liu, H. A ultra compact wideband bandpass filter using a quadmode stub-loaded resonator. Prog. Electromagn. Res. Lett. 2018, 77, 35–40. [Google Scholar] [CrossRef]
- Li, Y.; Choi, W.W.; Tam, K.W.; Zhu, L. Novel wideband bandpass filter with dual notched bands using stub-loaded resonators. IEEE Microw. Wirel. Compon. Lett. 2017, 27, 25–27. [Google Scholar]
- Choudhary, D.K.; Chaudhary, R.K. A compact via-less metamaterial wideband bandpass filter using split circular rings and rectangular stub. Prog. Electromagn. Res. Lett. 2018, 72, 99–106. [Google Scholar] [CrossRef]
- Ji, X.C.; Ji, W.S.; Feng, L.Y.; Tong, Y.Y.; Zhang, Z.Y. Design of a novel multi-layer wideband bandpass filter with a notched band. Prog. Electromagn. Res. Lett. 2019, 82, 9–16. [Google Scholar] [CrossRef]
- Li, Z.; Wu, K.L. Direct synthesis and design of wideband bandpass filter with composite series and shunt resonators. IEEE Trans. Microw. Theory Technol. 2017, 65, 3789–3800. [Google Scholar] [CrossRef]
- Hameed, M.; Xiao, G.; Qiu, L.; Xiong, C.; Hameed, T. Multiple-mode wideband bandpass filter using split ring resonators in a rectangular waveguide cavity. Electronics 2018, 7, 356. [Google Scholar] [CrossRef]
- Hameed, M.; Xiao, G.; Najam, A.I.; Qiu, L.; Hameed, T. Quadruple-mode wideband bandpass filter with improved out-of-band rejection. Electronics 2019, 8, 300. [Google Scholar] [CrossRef]
- Zeland Software, Inc. IE3D Simulator; Zeland Software, Inc.: Fremont, CA, USA, 2002. [Google Scholar]
- Ye, C.S.; Su, Y.K.; Weng, M.H.; Hung, C.Y.; Tang, R.Y. Design of the compact parallel-coupled lines wideband bandpass filters using image parameter method. Prog. Electromagn. Res. 2010, 100, 153–173. [Google Scholar] [CrossRef]
- Hong, J.-S.; Lancaster, M.J. Microstrip Filters for RF/Microwave Applications; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Pozar, D.M. Microwave Engineering, 4th ed.; Wiley: New York, NY, USA, 2012; ISBN 978-0-470-63155-3. [Google Scholar]
| Ref. [8] | Ref. [9] | Ref. [10] | Ref. [11] | Ref. [12] | Ref. [13] | This Work | |
|---|---|---|---|---|---|---|---|
| Center frequency (GHz) | 5 | 1.1 | 4 | 3 | 2.3 | 5 | 5 |
| |S11| (dB) | 12 | 13 | 14 | 11.7 | >13 | 15 | 10 |
| |S21| (dB) | 1.2 | 0.2 | 1.4 | 2.1 | 0.35 | 2 | 2 |
| 3-dB FBW (%) | 100 | 110 | 45 | 107 | 80 | 100 | 100 |
| Circuit Size (λg × λg) | Unknown | 0.15 × 0.12 | 0.30 × 0.10 | 0.89 × 0.46 | 0.53 × 0.43 | 0.74 × 0.42 | 0.70 × 0.28 |
| Number of notched band | 1 | 0 | 0 | 2 | 0 | 1 | 1 |
| Wide stopband | No | Yes | No | No | No | Yes | Yes |
| Defected ground | Yes | No | No | Yes | No | Yes | No |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weng, M.-H.; Hsu, C.-W.; Lan, S.-W.; Yang, R.-Y. An Ultra-Wideband Bandpass Filter with a Notch Band and Wide Upper Bandstop Performances. Electronics 2019, 8, 1316. https://doi.org/10.3390/electronics8111316
Weng M-H, Hsu C-W, Lan S-W, Yang R-Y. An Ultra-Wideband Bandpass Filter with a Notch Band and Wide Upper Bandstop Performances. Electronics. 2019; 8(11):1316. https://doi.org/10.3390/electronics8111316
Chicago/Turabian StyleWeng, Min-Hang, Che-Wei Hsu, Siang-Wen Lan, and Ru-Yuan Yang. 2019. "An Ultra-Wideband Bandpass Filter with a Notch Band and Wide Upper Bandstop Performances" Electronics 8, no. 11: 1316. https://doi.org/10.3390/electronics8111316
APA StyleWeng, M.-H., Hsu, C.-W., Lan, S.-W., & Yang, R.-Y. (2019). An Ultra-Wideband Bandpass Filter with a Notch Band and Wide Upper Bandstop Performances. Electronics, 8(11), 1316. https://doi.org/10.3390/electronics8111316






