Application of Reservoir Computing for the Modeling of Nano-Contact Vortex Oscillator
Abstract
:1. Introduction
2. Background and Related Work
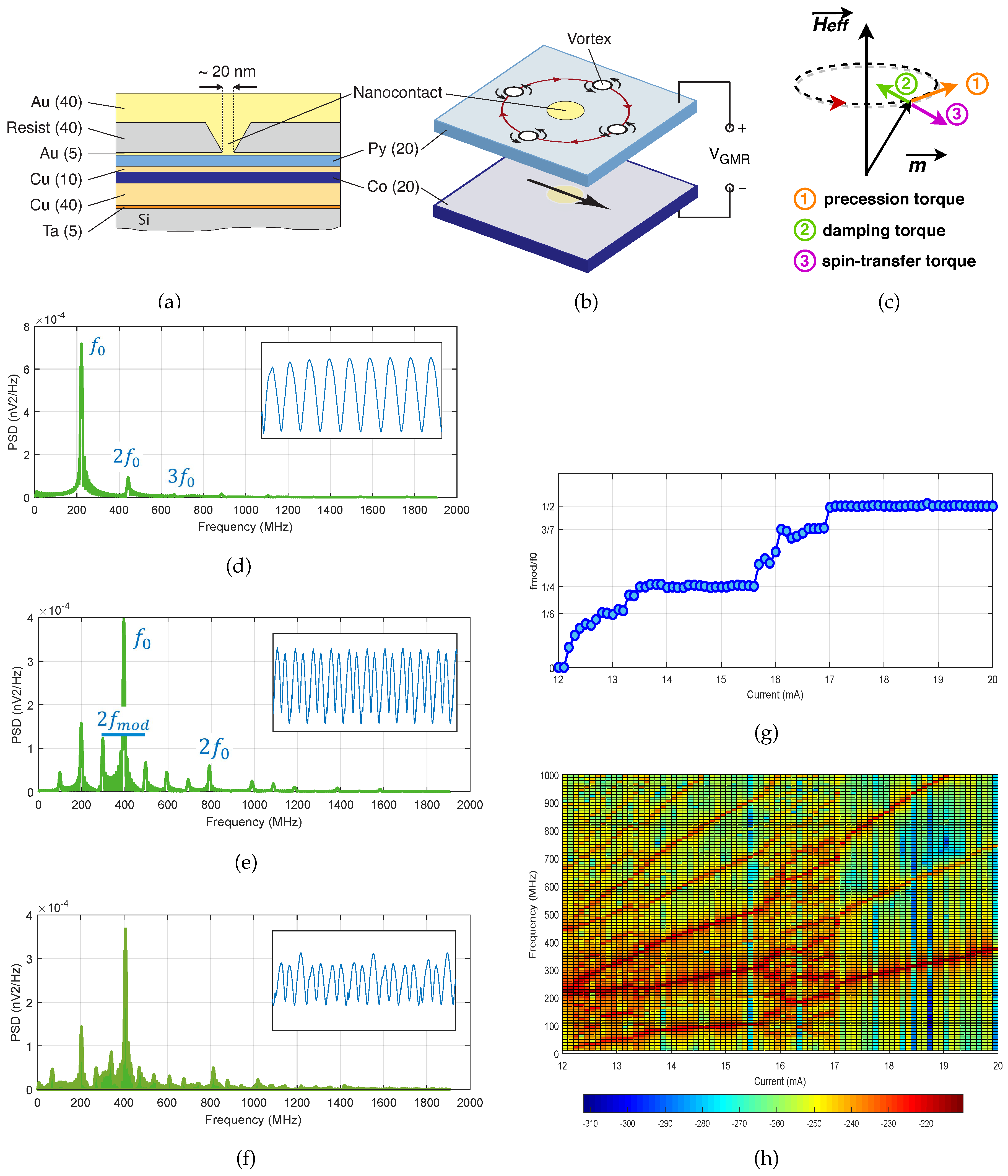
2.1. NCVO and the Physics Behind It
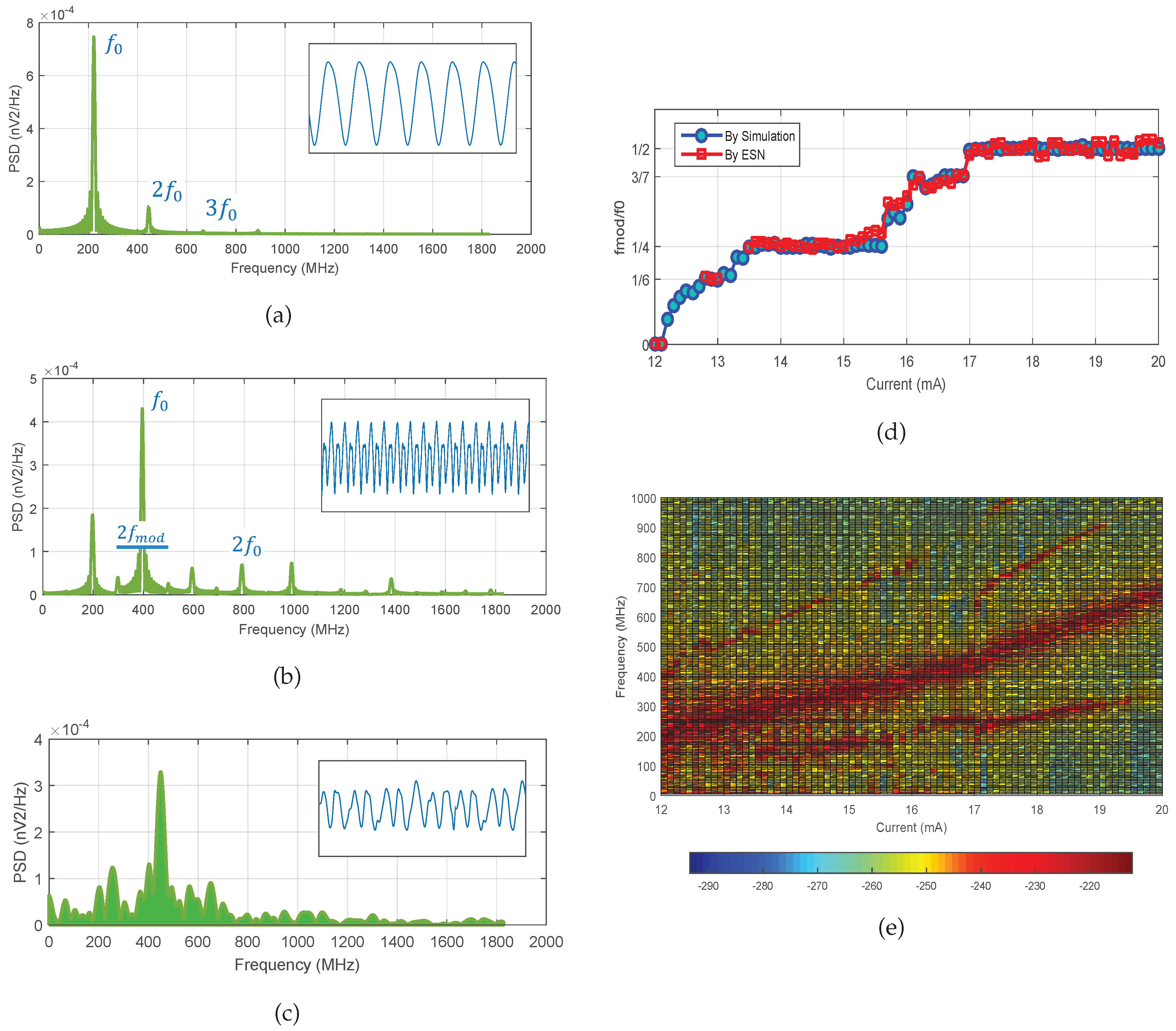
- No-modulation mode: This mode appears for currents I in the range mA. The vortex revolves around the NC continuously. No change of polarity takes place. Thus, only a fundamental mode, which denotes the gyration frequency, is obtained with its harmonics in the power spectrum (see Figure 1d).
- Modulation mode: This modulation frequency comes from a periodic relaxation of the vortex dynamics due to the core reversal. In this mode, the power spectrum shows two sideband frequencies associated with the gyration frequency (see Figure 1e). , which denotes the vortex polarity reversal, is said to be commensurably locked to . As a result, the vortex fulfills complete cycles around the NC before dropping toward the center to invert its direction.
- Chaotic mode: As its name indicates, the vortex revolves with no definite rules. The vortex may drop at any time toward the center due to the non-compatibility of the gyration and modulation frequencies (see Figure 1f).
2.2. Modelling Methods
3. Proposed Models
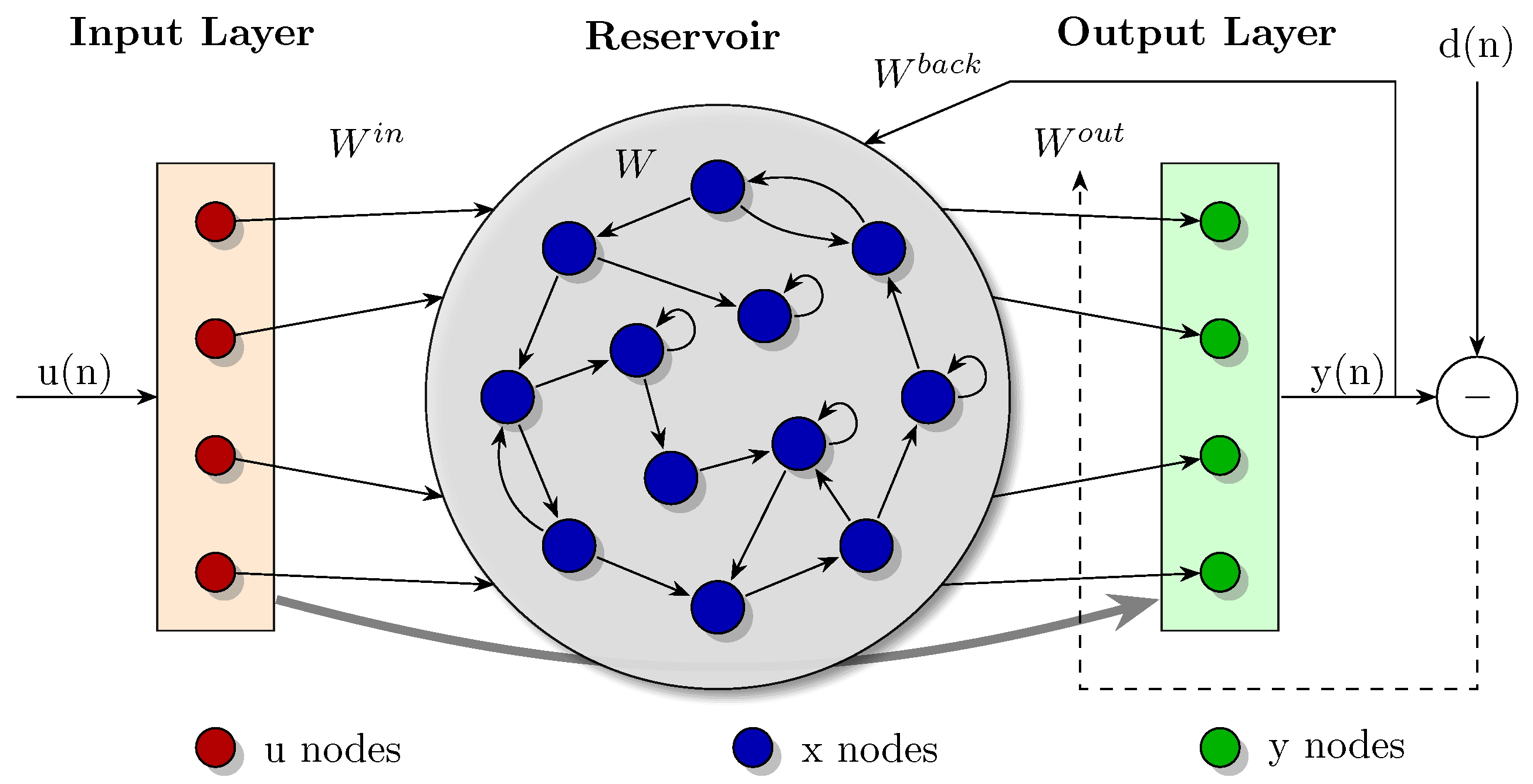
3.1. Echo State Network
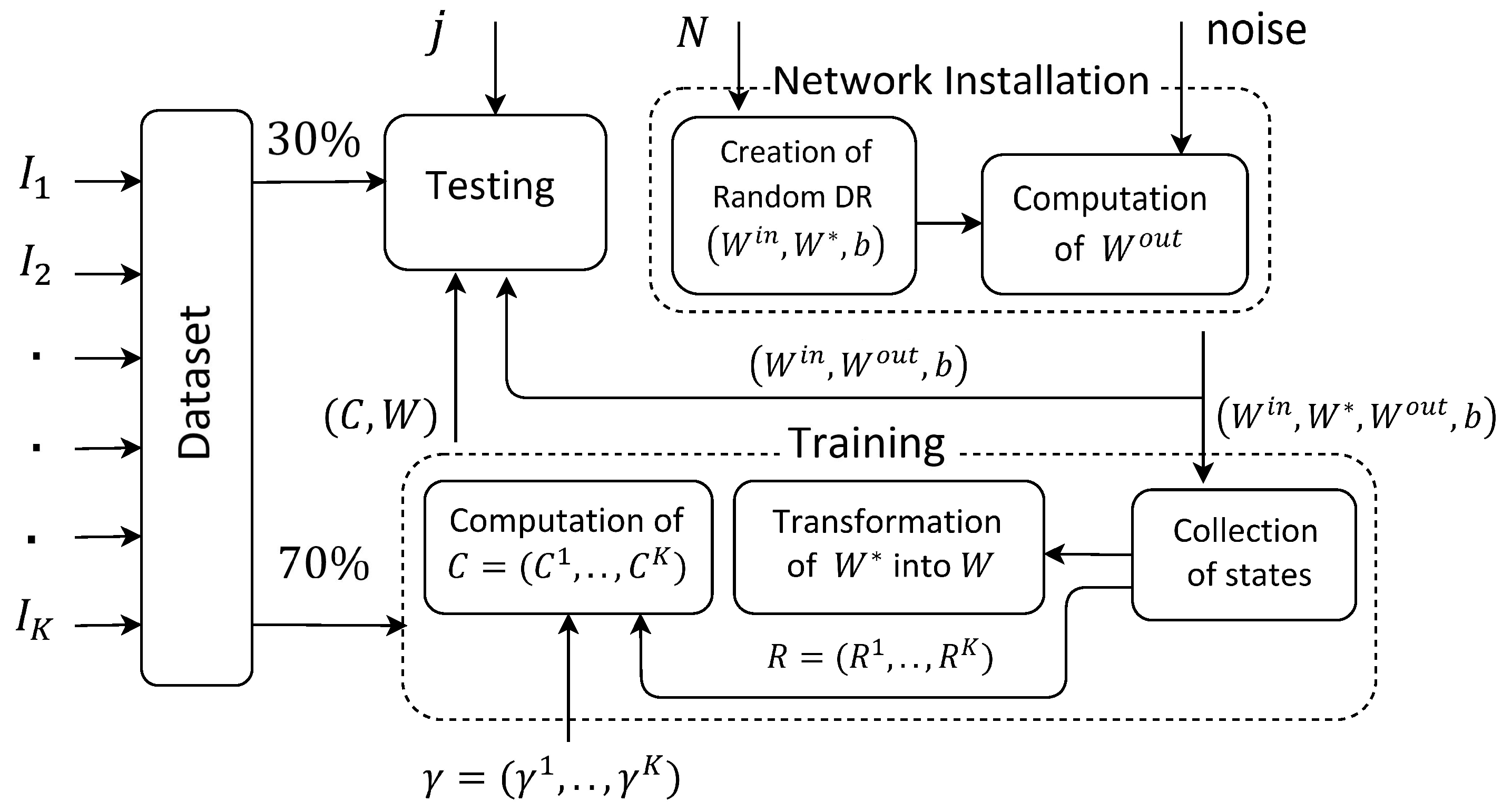
3.2. Conceptors-Driven Network
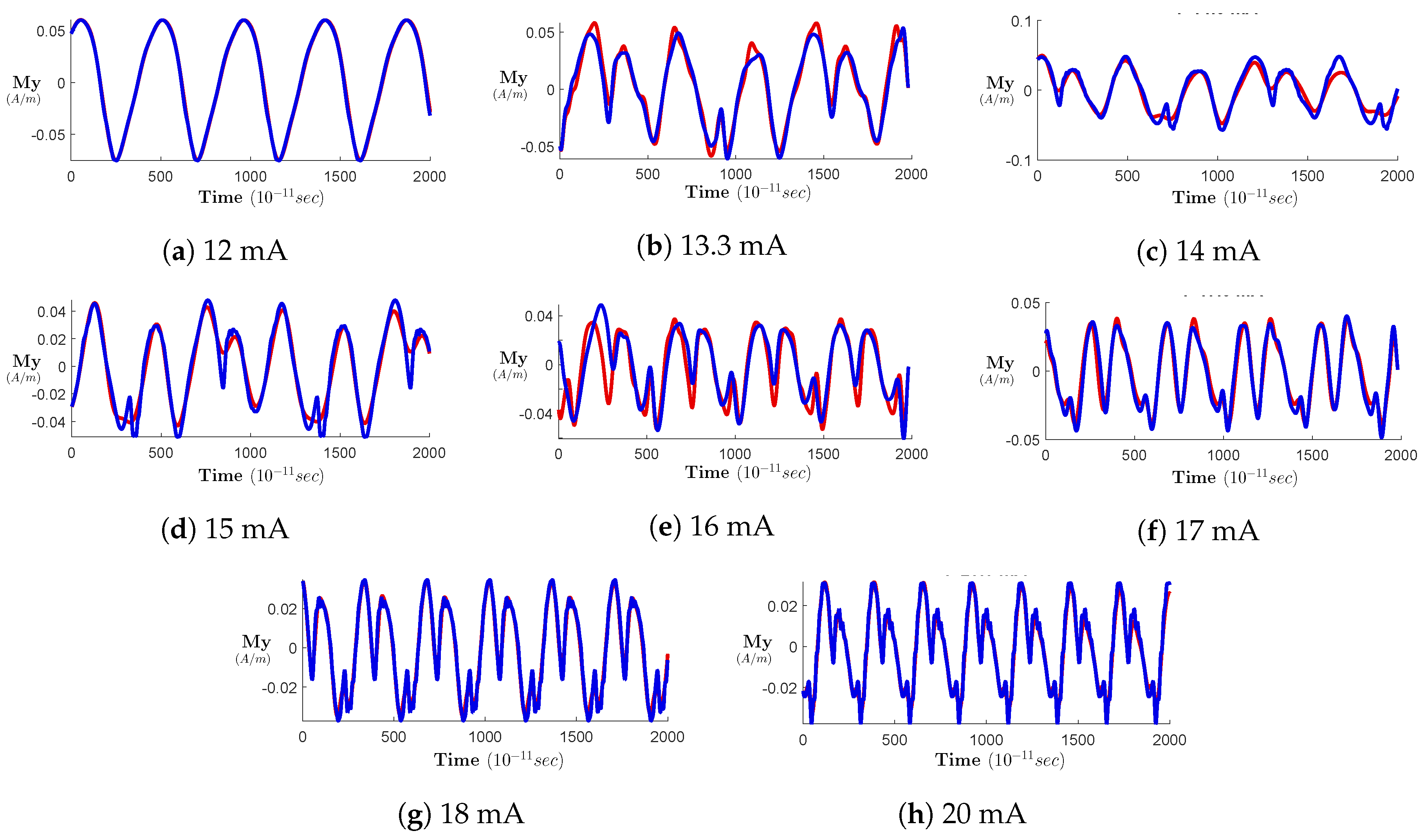
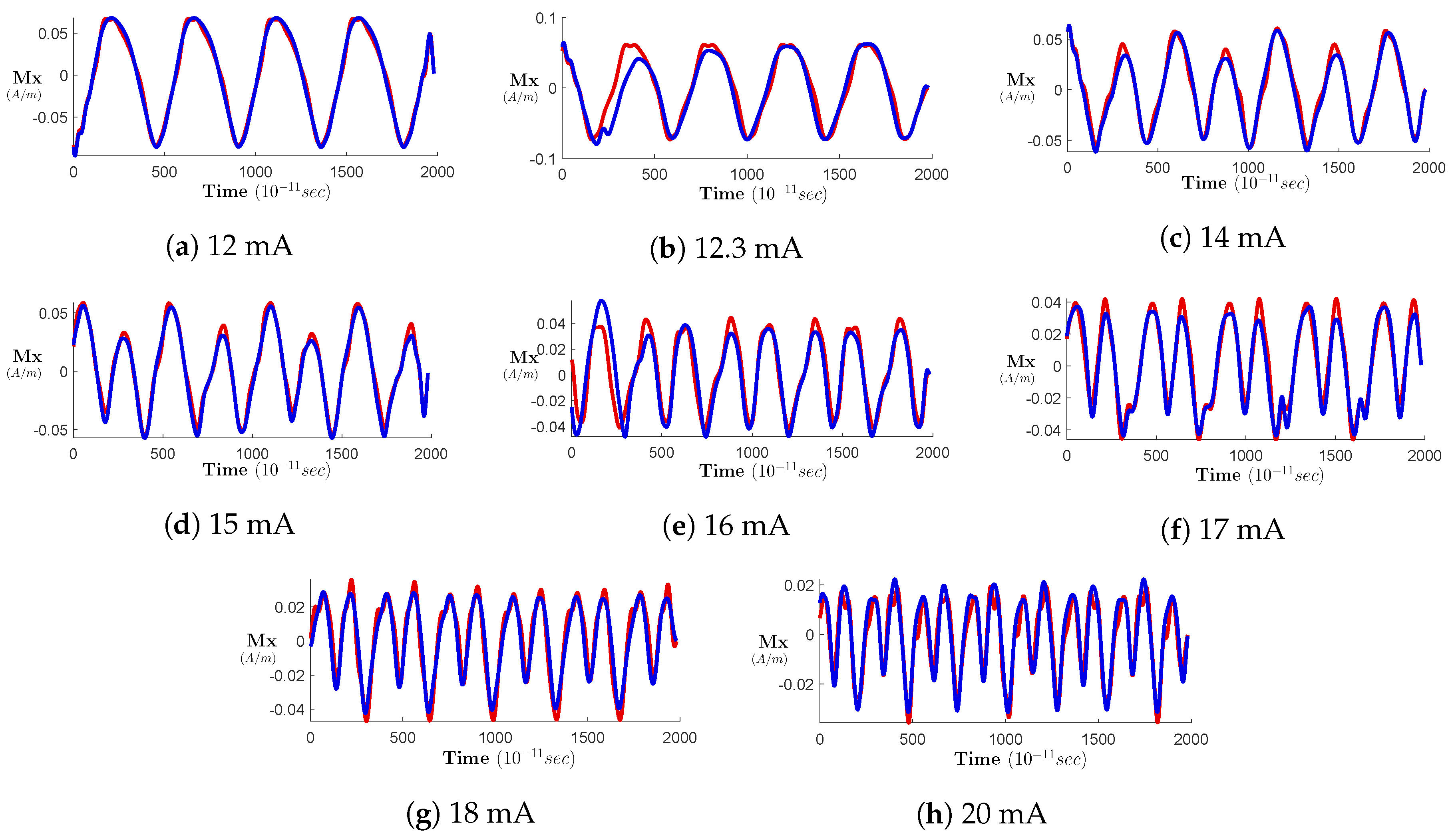
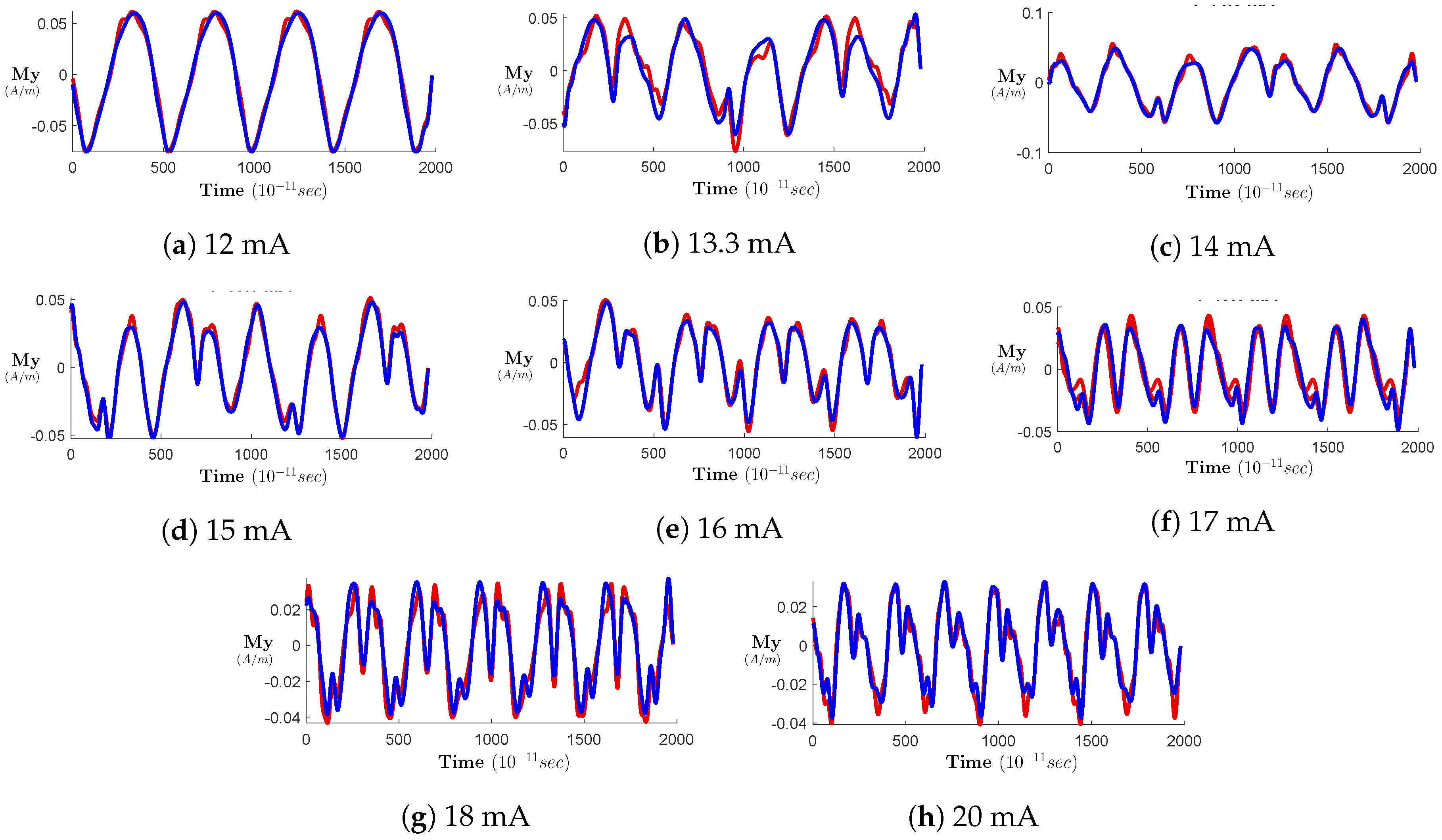
4. Results and Discussion
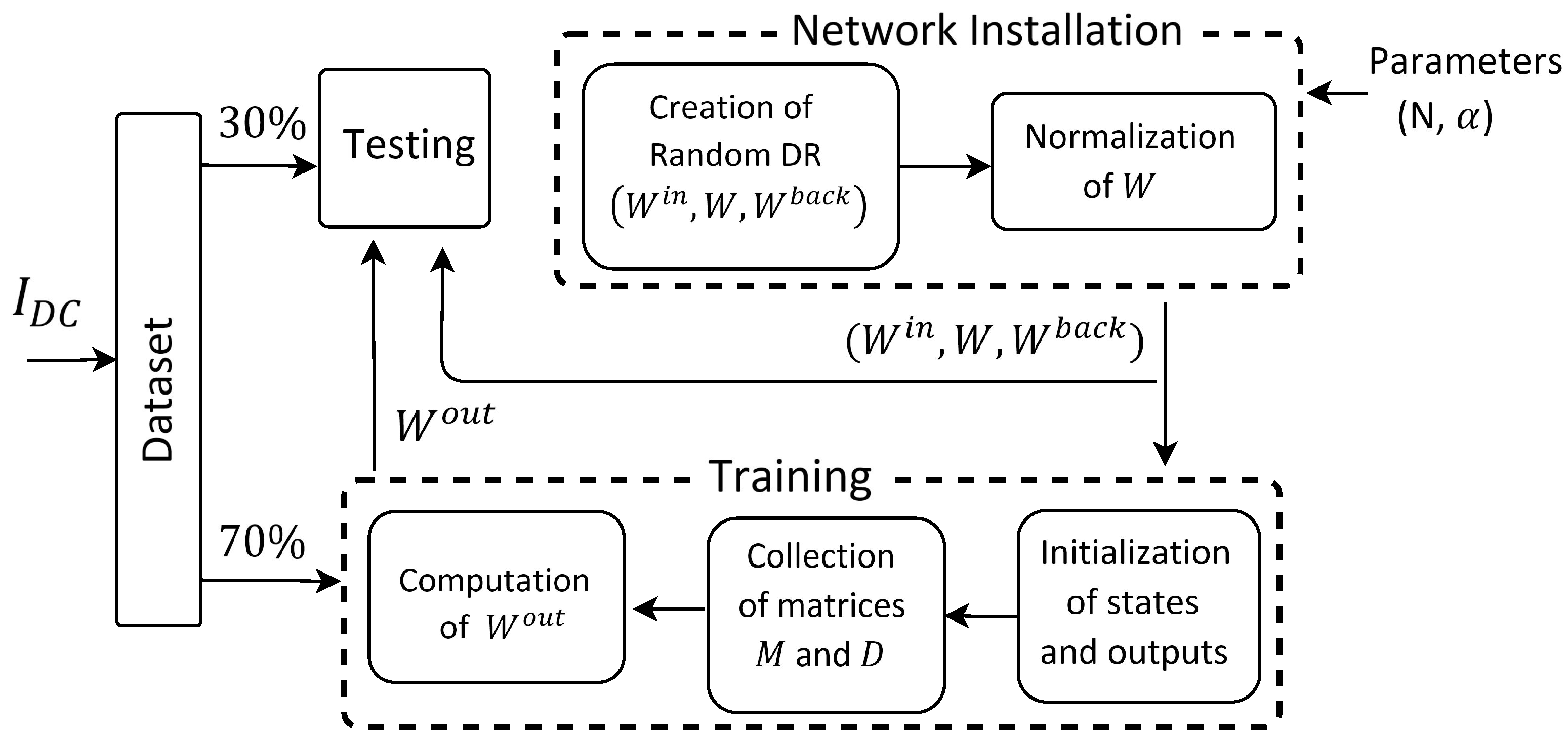
4.1. Simulation Setup
4.2. Generated Data from the Proposed Models
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wolf, W.; Jerraya, A.; Martin, G. Multiprocessor system-on-chip (mpsoc) technology. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2008, 27, 1701–1713. [Google Scholar] [CrossRef]
- Taylor, M.B. A landscape of the new dark silicon design regime. IEEE Micro 2013, 33, 8–19. [Google Scholar] [CrossRef]
- Sharbati, M.T.; Du, Y.; Torres, J.; Ardolino, N.D.; Yun, M.; Xiong, F. Low-power, electrochemically tunable graphene synapses for neuromorphic computing. Adv. Mater. 2018, 30, 1802353. [Google Scholar] [CrossRef] [PubMed]
- Eichwald, I.; Breitkreutz, S.; Ziemys, G. György Csaba, Wolfgang Porod, and Markus Becherer. Majority logic gate for 3d magnetic computing. Nanotechnology 2014, 25, 335202. [Google Scholar] [CrossRef] [PubMed]
- Grollier, J.; Querlioz, D.; Stiles, M.D. Spintronic nanodevices for bioinspired computing. Proc. IEEE 2016, 104, 2024–2039. [Google Scholar] [CrossRef] [PubMed]
- Castelvecchi, D. Quantum computers ready to leap out of the lab in 2017. Nat. News 2017, 541, 9. [Google Scholar] [CrossRef]
- Di Ventra, M.; Pershin, Y.V. Just add memory. Sci. Am. 2015, 312, 56–61. [Google Scholar] [CrossRef]
- Kuo, D. Chaos and its computing paradigm. IEEE Potentials 2005, 24, 13–15. [Google Scholar] [CrossRef]
- Kia, B.; Kia, S.; Lindner, J.F.; Sinha, S.; Ditto, W.L. Noise tolerant spatiotemporal chaos computing. Chaos Interdiscip. J. Nonlinear Sci. 2014, 24, 043110. [Google Scholar] [CrossRef]
- Beyki, M.; Yaghoobi, M. Chaotic logic gate: A new approach in set and design by genetic algorithm. Chaos Solitons Fractals 2015, 77, 247–252. [Google Scholar] [CrossRef]
- Piper, J.R.; Sprott, J.C. Simple autonomous chaotic circuits. IEEE Trans. Circuits Syst. II Express Briefs 2010, 57, 730–734. [Google Scholar] [CrossRef]
- Tchitnga, R.; Nguazon, T.; Louodop Fotso, P.H.; Gallas, J.A.C. Chaos in a single op-amp–based jerk circuit: Experiments and simulations. IEEE Trans. Circuits Syst. II Express Briefs 2015, 63, 239–243. [Google Scholar] [CrossRef]
- Srisuchinwong, B.; Munmuangsaen, B.; Ahmad, I.; Suibkitwanchai, K. On a simple single-transistor-based chaotic snap circuit: A maximized attractor dimension at minimized damping and a stable equilibrium. IEEE Access 2019, 7, 116643–116660. [Google Scholar] [CrossRef]
- Yogendra, K.; Fan, D.; Shim, Y.; Koo, M.; Roy, K. Computing with coupled spin torque nano oscillators. In Proceedings of the 2016 21st Asia and South Pacific Design Automation Conference (ASP-DAC), Macau, China, 25–28 January 2016; pp. 312–317. [Google Scholar]
- Petit-Watelot, S.; Kim, J.-V.; Ruotolo, A.; Otxoa, R.M.; Bouzehouane, K.; Grollier, J.; Vansteenkiste, A.; Van de Wiele, B.; Cros, V.; Devolder, T. Commensurability and chaos in magnetic vortex oscillations. Nat. Phys. 2012, 8, 682. [Google Scholar] [CrossRef]
- Pathak, J.; Lu, Z.; Hunt, B.R.; Girvan, M.; Ott, E. Using machine learning to replicate chaotic attractors and calculate lyapunov exponents from data. Chaos Interdiscip. J. Nonlinear Sci. 2017, 27, 121102. [Google Scholar] [CrossRef]
- Legenstein, R.; Maass, W. What makes a dynamical system computationally powerful. In New Directions in Statistical Signal Processing: From Systems to Brain; MIT Press: Cambridge, MA, USA, 2007; pp. 127–154. [Google Scholar]
- Sterman, J.D. System dynamics modeling: tools for learning in a complex world. Calif. Manag. Rev. 2001, 43, 8–25. [Google Scholar] [CrossRef]
- Aguirre, L.A.; Letellier, C. Modeling nonlinear dynamics and chaos: A review. In Mathematical Problems in Engineering; Hindawi: London, UK, 2009. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Volos, C.; Akgul, A.; Pham, V.; Stouboulos, I.; Kyprianidis, I. A simple chaotic circuit with a hyperbolic sine function and its use in a sound encryption scheme. Nonlinear Dyn. 2017, 89, 1047–1061. [Google Scholar] [CrossRef]
- Hénon, M. A two-dimensional mapping with a strange attractor. In The Theory of Chaotic Attractors; Springer: Berlin, Germany, 1976; pp. 94–102. [Google Scholar]
- Yang, Q.; Bai, M. A new 5d hyperchaotic system based on modified generalized lorenz system. Nonlinear Dyn. 2017, 88, 189–221. [Google Scholar] [CrossRef]
- Laiphrakpam, D.S.; Khumanthem, M.S. Cryptanalysis of symmetric key image encryption using chaotic rossler system. Optik 2017, 135, 200–209. [Google Scholar] [CrossRef]
- Boccara, N. Modeling complex systems. In Modeling Complex Systems: Graduate Texts in Contemporary Physics; Springer-Verlag New York, Inc.: New York, NY, USA, 2004; ISBN 978-0-387-40462-2. [Google Scholar]
- Lewin, R. Complexity: Life at the Edge of Chaos; University of Chicago Press: Chicago, IL, USA, 1999. [Google Scholar]
- Bar-Yam, Y. Dynamics of Complex Systems; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Murray, J.D. Mathematical Biology, 2nd ed.; Springer: Berlin, Germany, 1993. [Google Scholar]
- Hardin, G. The competitive exclusion principle. Science 1960, 131, 1292–1297. [Google Scholar] [CrossRef]
- Bellen, A.; Zennaro, M. Numerical Methods for Delay Differential Equations; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Zuniga-Aguilar, C.J.; Coronel-Escamilla, A.; Gomez-Aguilar, J.F.; Alvarado-Martinez, V.M.; Romero-Ugalde, H.M. New numerical approximation for solving fractional delay differential equations of variable order using artificial neural networks. Eur. Phys. J. Plus 2018, 133, 75. [Google Scholar] [CrossRef]
- Sompolinsky, H.; Crisanti, A.; Sommers, H.-J. Chaos in random neural networks. Phys. Rev. Lett. 1988, 61, 259. [Google Scholar] [CrossRef] [PubMed]
- Derrida, B.; Gardner, E.; Zippelius, A. An exactly solvable asymmetric neural network model. EPL (Europhys. Lett.) 1987, 4, 167. [Google Scholar] [CrossRef]
- Gray, R.M. Toeplitz and circulant matrices: A review. Found. Trends Commun. Inf. Theory 2006, 2, 155–239. [Google Scholar] [CrossRef]
- Han, H.-G.; Guo, Y.-N.; Qiao, J.-F. Nonlinear system modeling using a self-organizing recurrent radial basis function neural network. Appl. Soft Comput. 2018, 71, 1105–1116. [Google Scholar] [CrossRef]
- Xing, F.Z.; Cambria, E.; Zou, X. Predicting evolving chaotic time series with fuzzy neural networks. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 3176–3183. [Google Scholar]
- Din, Q.; Elsadany, A.A.; Ibrahim, S. Bifurcation analysis and chaos control in a second-order rational difference equation. Int. J. Nonlinear Sci. Numer. Simul. 2018, 19, 53–68. [Google Scholar] [CrossRef]
- Jaeger, H. The “echo state” approach to analysing and training recurrent neural networks-with an erratum note. Bonn Ger. Ger. Natl. Res. Cent. Inf. Technol. GMD Tech. Rep. 2001, 148, 13. [Google Scholar]
- Jaeger, H. Tutorial on Training Recurrent Neural Networks, Covering BPPT, RTRL, EKF and the “Echo State Network” Approach; GMD-Forschungszentrum Informationstechnik: Bonn, Germany, 2002; Volume 5. [Google Scholar]
- Furlanello, T.; Zhao, J.; Saxe, A.M.; Itti, L.; Tjan, B.S. Active Long Term Memory Networks. arXiv 2016, arXiv:1606.02355. [Google Scholar]
- Jaeger, H. Using conceptors to manage neural long-term memories for temporal patterns. J. Mach. Learn. Res. 2017, 18, 387–429. [Google Scholar]
- Vansteenkiste, A.; Leliaert, J.; Dvornik, M.; Helsen, M.; Garcia-Sanchez, F.; Van Waeyenberge, B. The design and verification of mumax3. AIP Adv. 2014, 4, 107133. [Google Scholar] [CrossRef]
- Petit-Watelot, S.; Otxoa, R.M.; Manfrini, M. Electrical properties of magnetic nanocontact devices computed using finite-element simulations. Appl. Phys. Lett. 2012, 100, 083507. [Google Scholar] [CrossRef]
- Létang, J.; Petit-Watelot, S.; Yoo, M.-W.; Devolder, T.; Bouzehouane, K.; Cros, V.; Kim, J.-V. Modulation and phase-locking in nanocontact vortex oscillators. arXiv 2019, arXiv:1906.08492. [Google Scholar] [CrossRef]
- Lukoševičius, M. A practical guide to applying echo state networks. In Neural Networks: Tricks of the Trade; Springer: Berlin, Germany, 2012; pp. 659–686. [Google Scholar]

| MSE of | MSE of | |||
|---|---|---|---|---|
| I (mA) | Conceptor-Driven | ESN | Conceptor-Driven | ESN |
| 12 | ||||
| 13 | ||||
| 14 | ||||
| 15 | ||||
| 16 | ||||
| 17 | ||||
| 18 | ||||
| 19 | ||||
| 20 | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ismail, A.R.; Jovanovic, S.; Petit-Watelot, S.; Rabah, H. Application of Reservoir Computing for the Modeling of Nano-Contact Vortex Oscillator. Electronics 2019, 8, 1315. https://doi.org/10.3390/electronics8111315
Ismail AR, Jovanovic S, Petit-Watelot S, Rabah H. Application of Reservoir Computing for the Modeling of Nano-Contact Vortex Oscillator. Electronics. 2019; 8(11):1315. https://doi.org/10.3390/electronics8111315
Chicago/Turabian StyleIsmail, Ali Rida, Slavisa Jovanovic, Sébastien Petit-Watelot, and Hassan Rabah. 2019. "Application of Reservoir Computing for the Modeling of Nano-Contact Vortex Oscillator" Electronics 8, no. 11: 1315. https://doi.org/10.3390/electronics8111315
APA StyleIsmail, A. R., Jovanovic, S., Petit-Watelot, S., & Rabah, H. (2019). Application of Reservoir Computing for the Modeling of Nano-Contact Vortex Oscillator. Electronics, 8(11), 1315. https://doi.org/10.3390/electronics8111315






