X-Band High-Efficiency Continuous Class B Power Amplifier GaN MMIC Assisted by Input Second-Harmonic Tuning
Abstract
:1. Introduction
2. Efficiency Enhancement Methods of Continuous Class B Mode
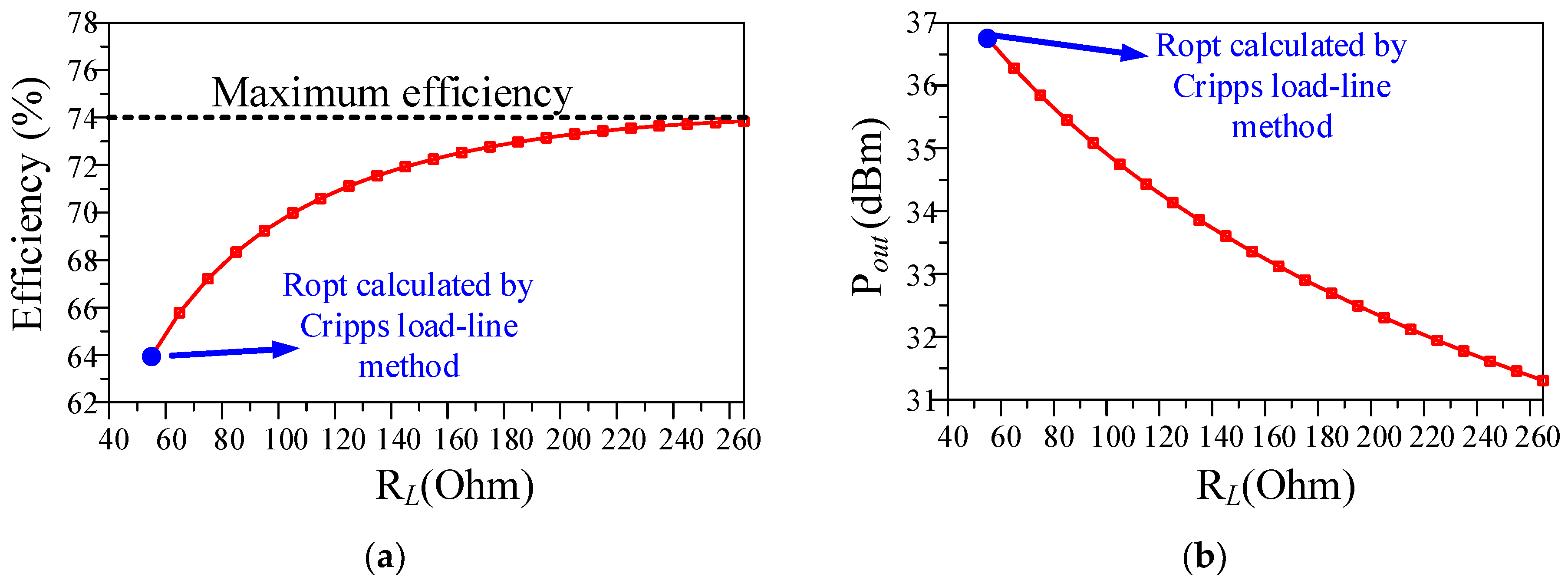
2.1. The Choice of Ropt for Efficiency Enhancement
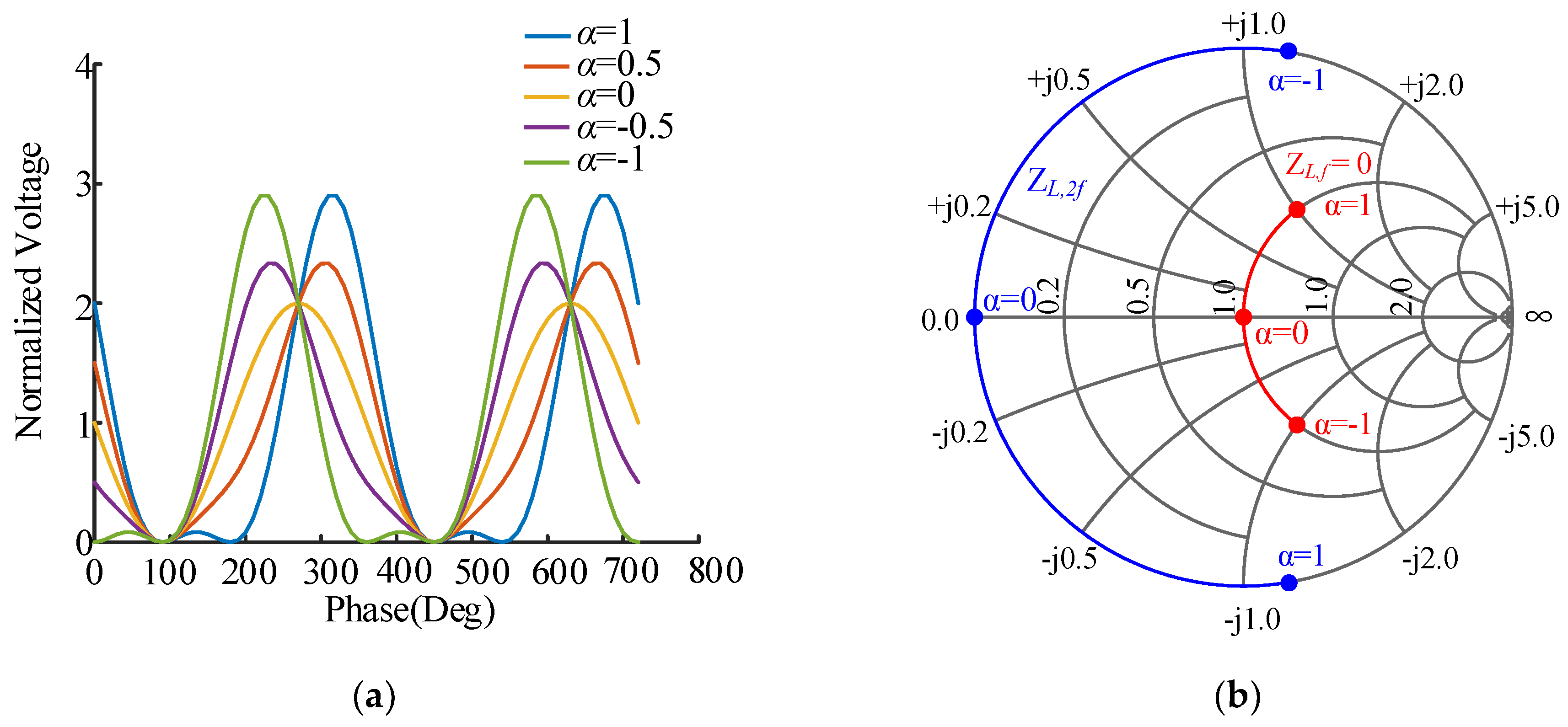
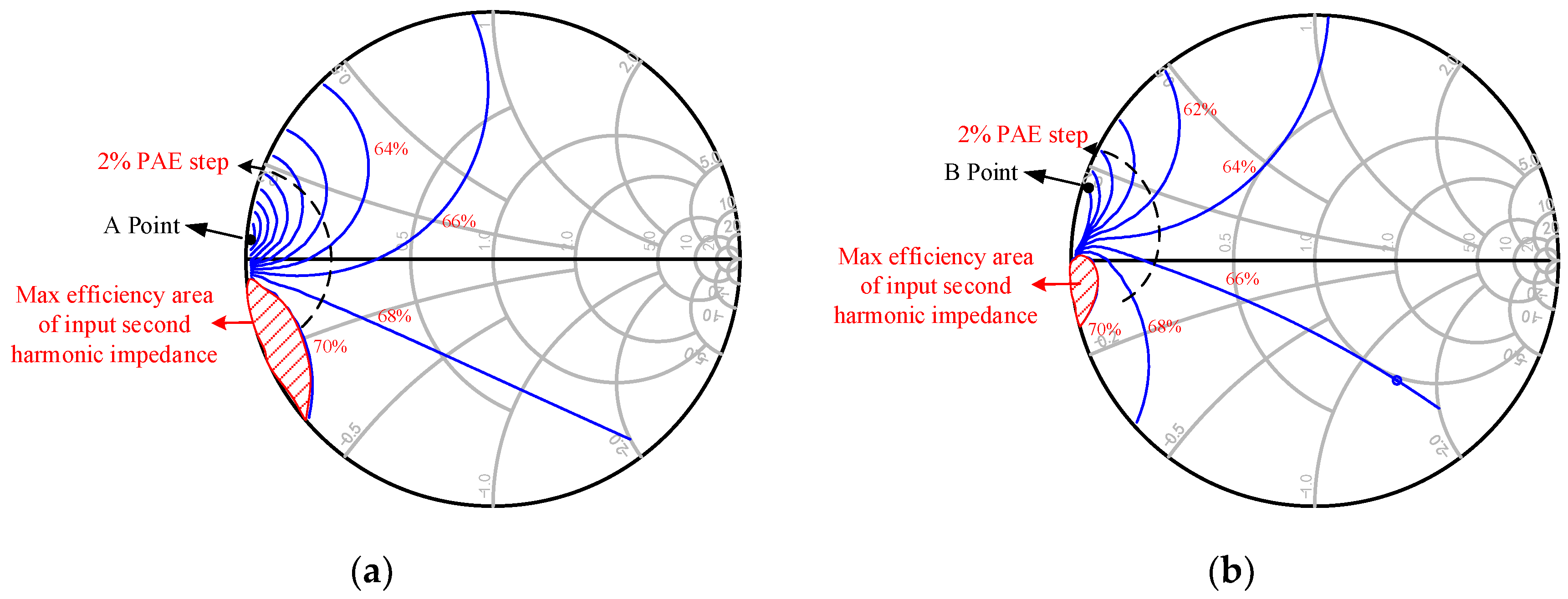
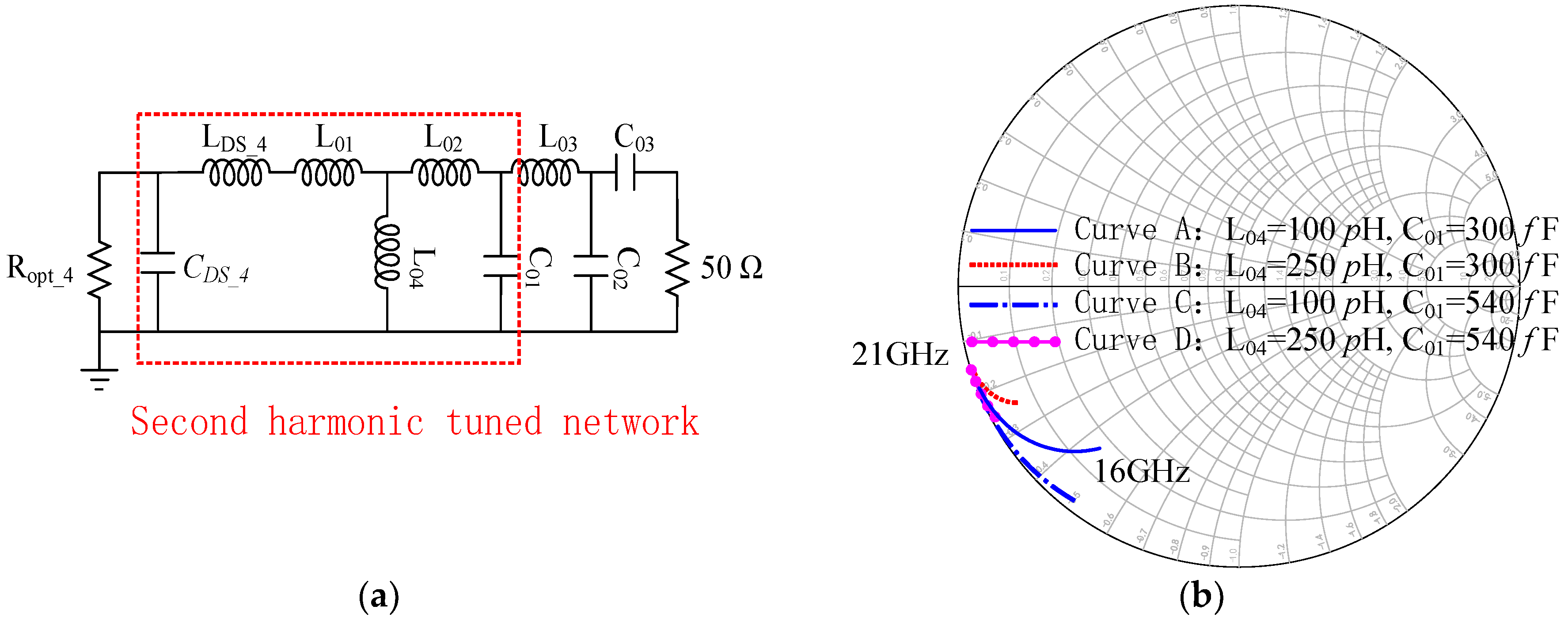
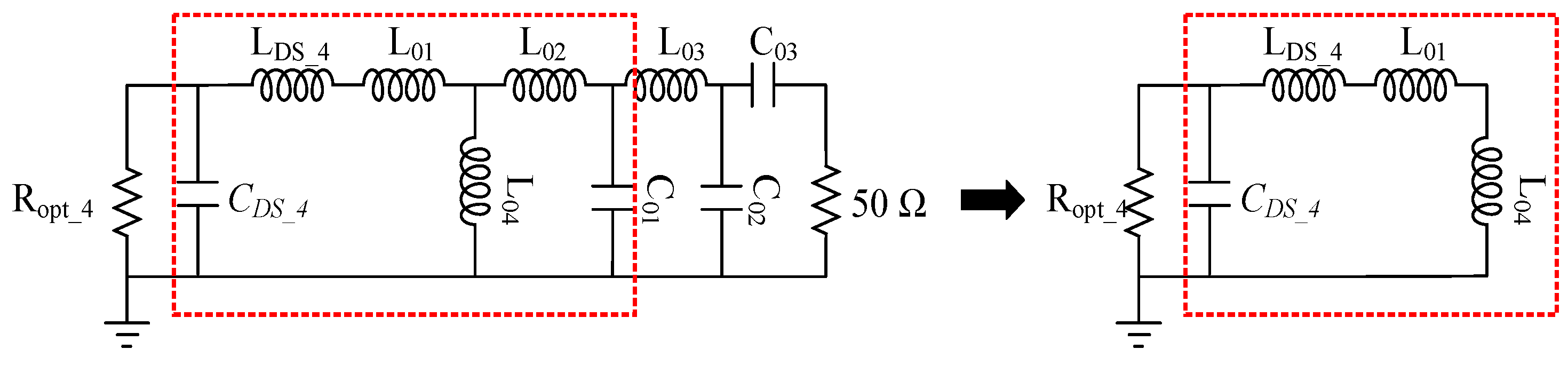
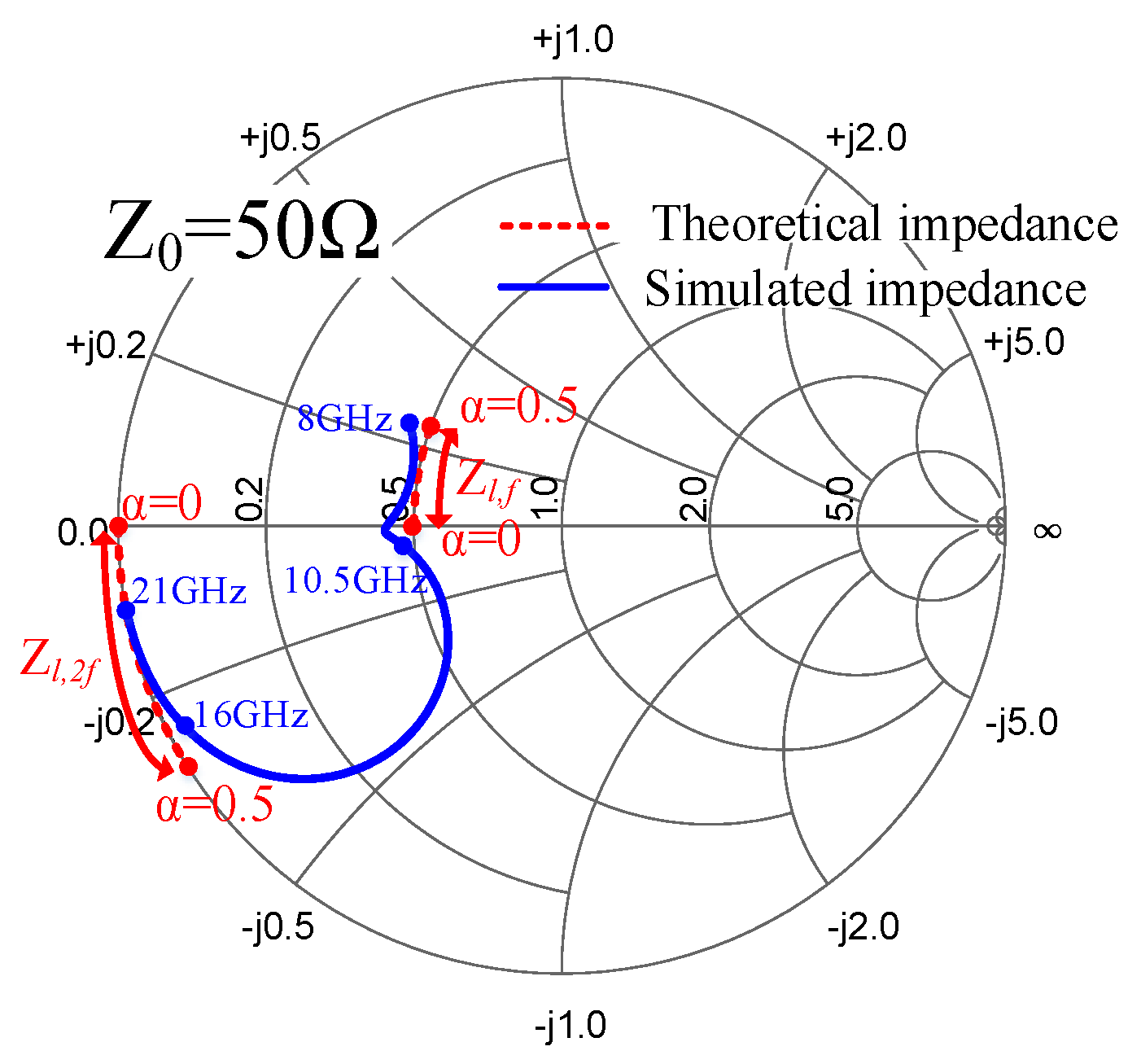
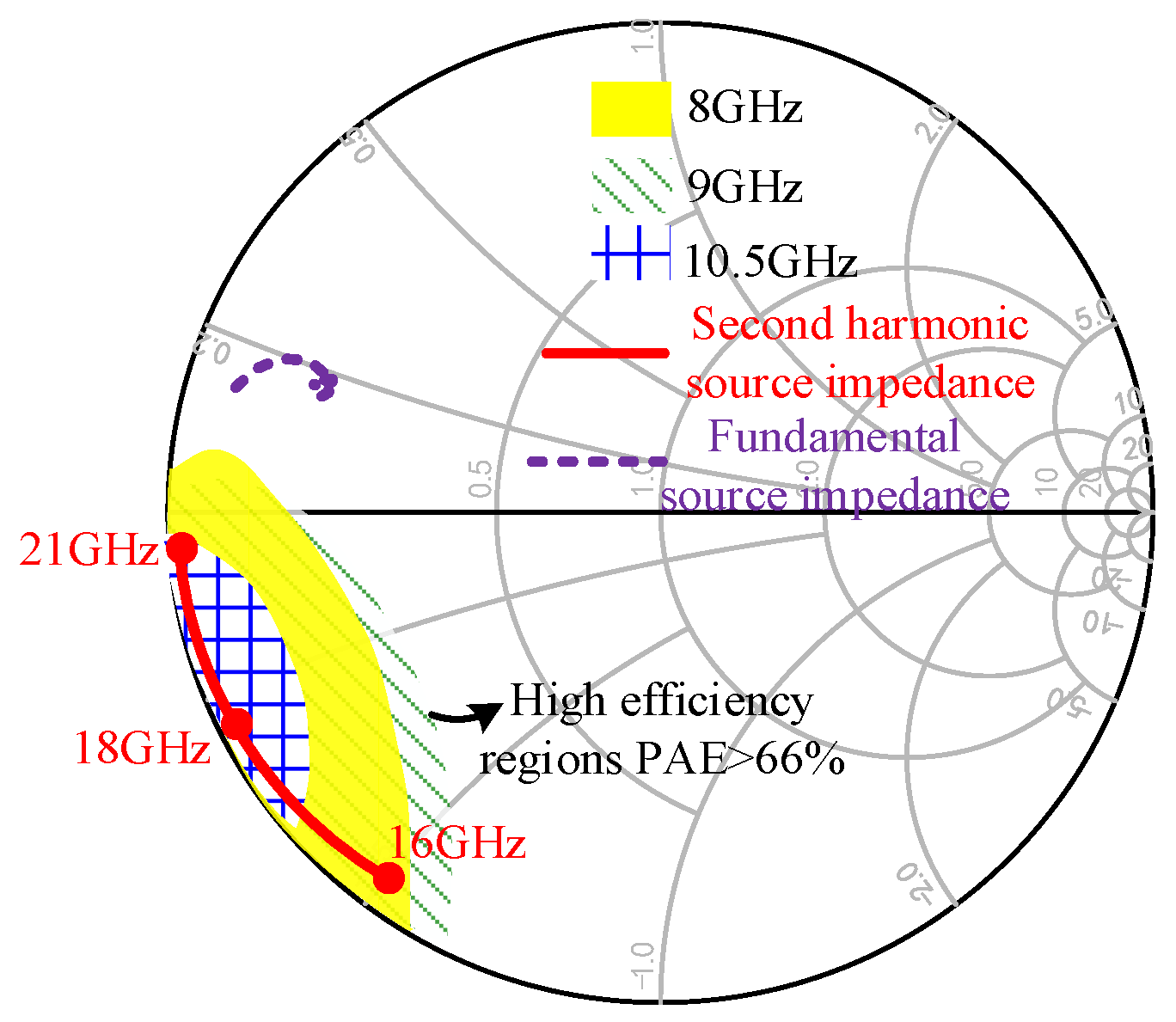
2.2. Input Second Harmonic Tuned in Continuous Class B Mode For Efficiency Enhancment
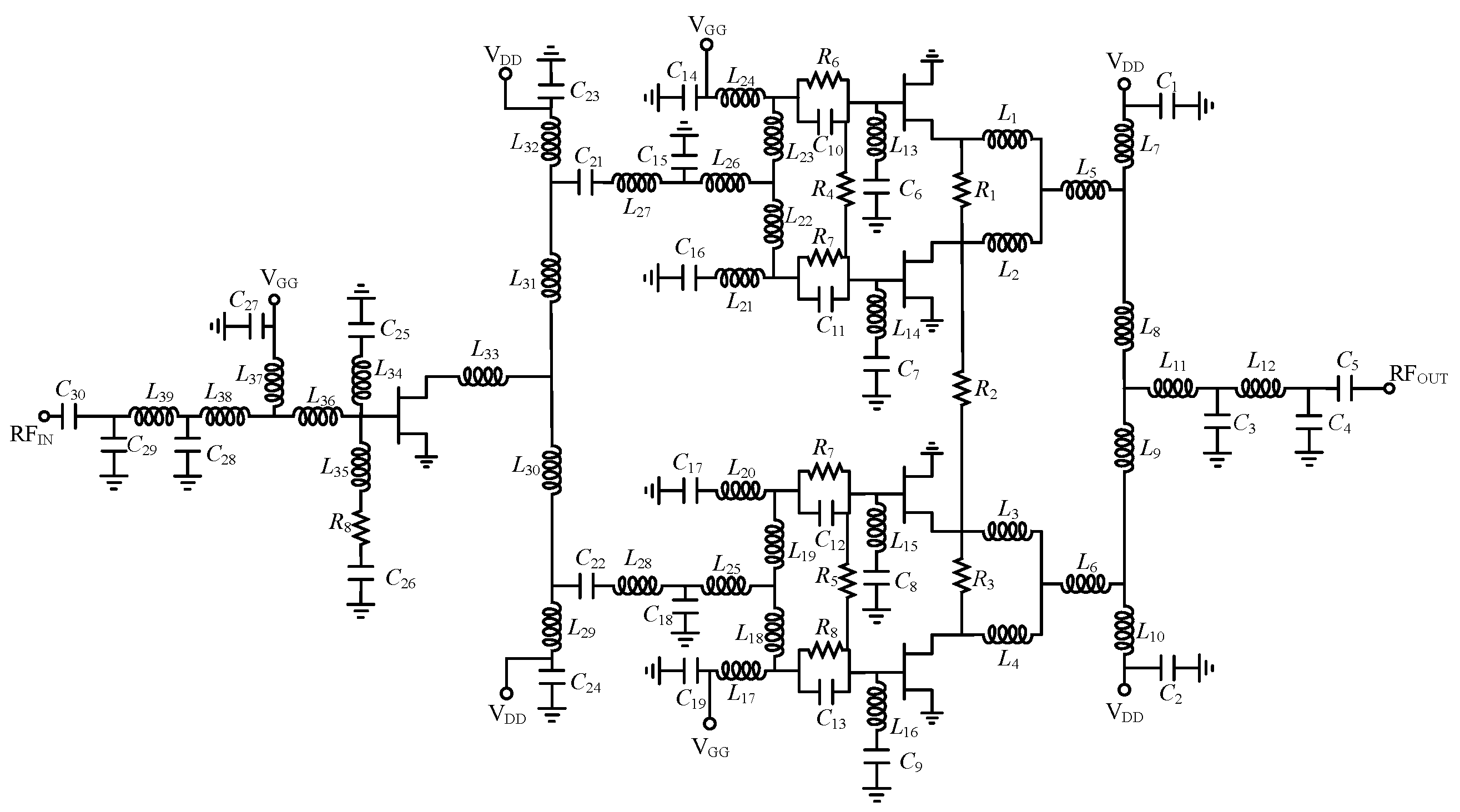
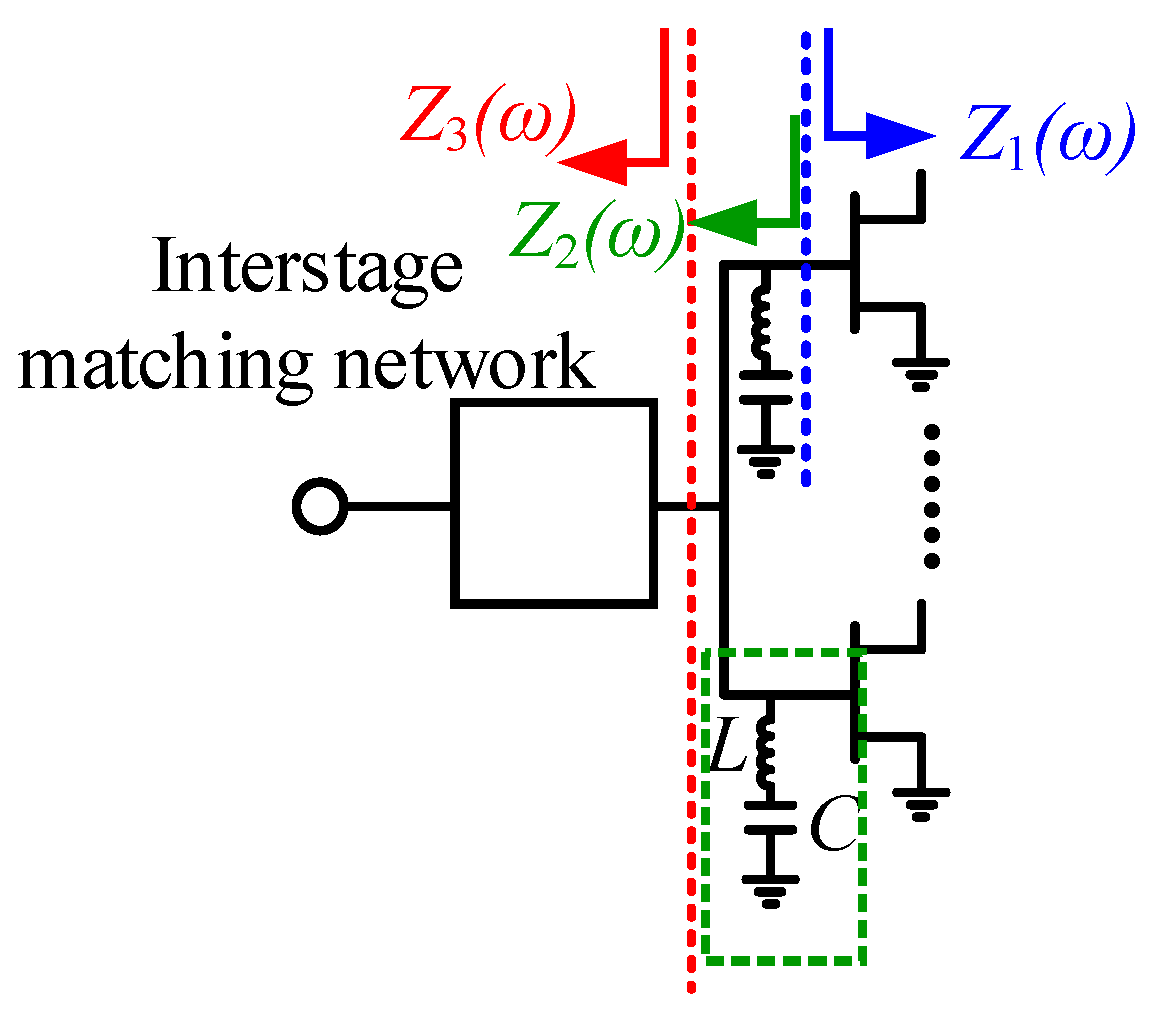
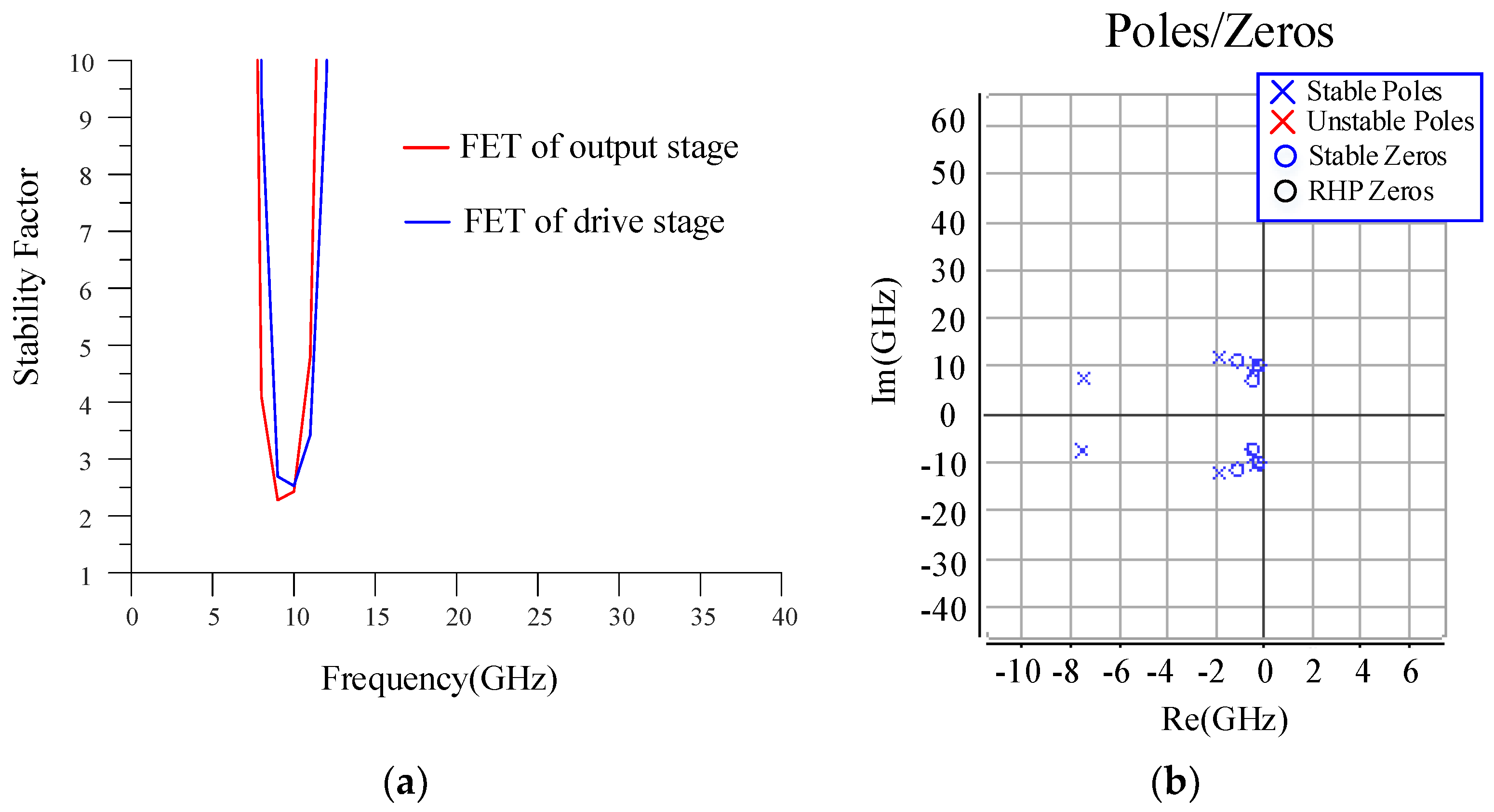
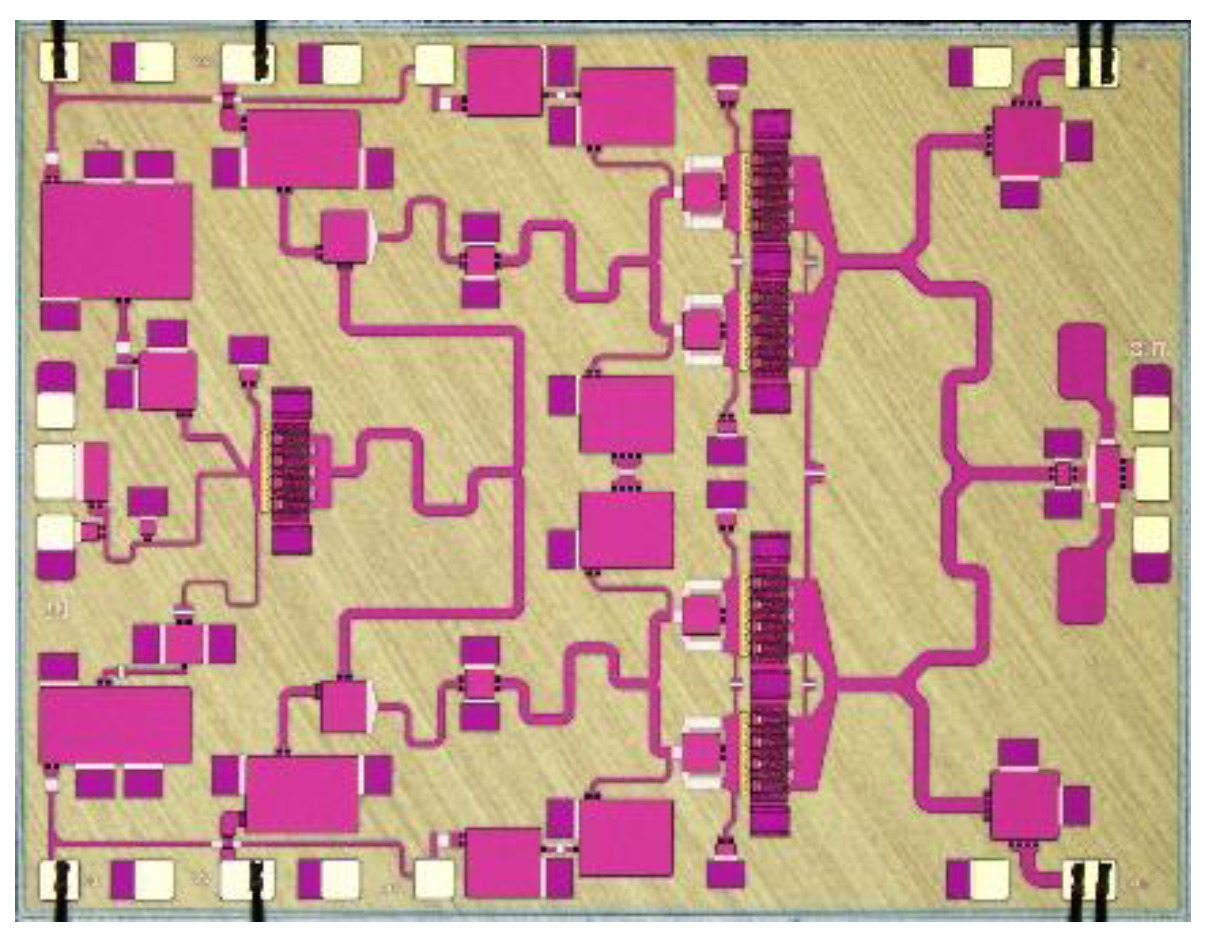
3. Circuit Design
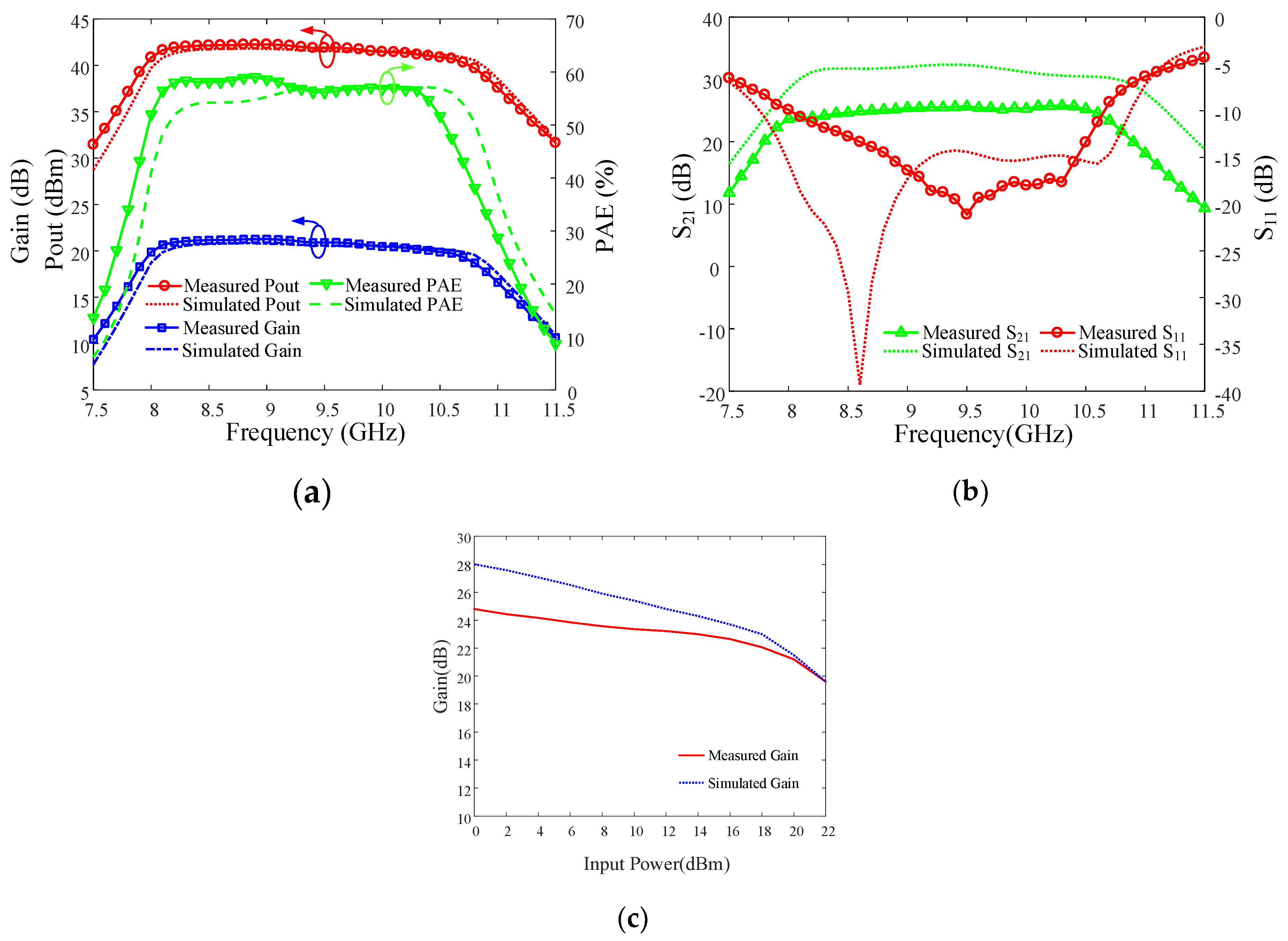
4. Measurement Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tasker, P.J.; Carrubba, V.; Wright, P.; Lees, J.; Benedikt, J.; Cripps, S.; Wideband, P.A. Design: The “Continuous” Mode of Operation. In Proceedings of the IEEE Compound Semiconductor Integrated Circuit Symposium (CSICS), La Jolla, CA, USA, 14–17 October 2012; pp. 1–4. [Google Scholar]
- Cipriani, E.; Colantonio, P.; Giannini, F. Class F-C X-band MMIC GaN power amplifier: An extension of waveform engineering approach. In Proceedings of the Integrated Nonlinear Microwave and Millimeter-wave Circuits Workshop Digest, Graz, Australia, 20–21 April 2017; pp. 1–4. [Google Scholar]
- Gao, S.; Butterworth, P.; Sambell, A.; Sanabria, C.; Xu, H.; Heikman, S.; Mishra, U.; York, R.A. Microwave Class-F and Inverse Class-F Power Amplifiers Designs using GaN Technology and GaAs pHEMT. In Proceedings of the European Microwave Conference Digest, Manchester, UK, 10–13 September 2006; pp. 439–496. [Google Scholar]
- Forouzanfar, M.; Feghhi, R.; Baseri, J.; Joodaki, M. High efficiency 8.8–9.6 GHz class J power amplifier. In Proceedings of the 16th Mediterranean Microwave Symposium, Abu Dhabi, UAE, 14–16 November 2016; pp. 1–4. [Google Scholar]
- Liu, B.; Mao, M.; Boon, C.C.; Choi, P.; Khanna, D.; Fitzgerald, E.A. A Fully Integrated Class-J GaN MMIC Power Amplifier for 5-GHz WLAN 802.11ax Application. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 434–436. [Google Scholar] [CrossRef]
- Cripps, S.; Tasker, P.J.; Clarke, A.L.; Lees, J.; Benedikt, J. On the Continuity of High Efficiency Modes in Linear RF Power Amplifiers. IEEE Microw. Wirel. Compon. Lett. 2009, 19, 665–667. [Google Scholar] [CrossRef]
- Powell, J.R.; Uren, M.J.; Martin, T.; McLachlan, A.; Tasker, P.; Woodington, S.; Bell, J.; Saini, R.; Benedikt, J.; Cripps, S.C. GaAs X-band high efficiency(>65%) Broadband (>30%) amplifier MMIC based on the Class B to Class J continuum. In Proceedings of the IEEE MTT-S International Microwave Symposium, Baltimore, MD, USA, 5–10 June 2011; pp. 1–4. [Google Scholar]
- Cripps, S.C. RF Power Amplifiers for Wireless Communications, 2nd ed.; Artech House: Norwood, MA, USA, 2006; pp. 21–27. [Google Scholar]
- Pedro, J.C.; Nunes, L.C.; Cabral, P.M. A Simple Method to Estimate the Output Power and Efficiency Load-Pull Contours of Class-B Power Amplifiers. IEEE Trans. Microw. Theory Tech. 2015, 63, 1239–1249. [Google Scholar] [CrossRef]
- Sharma, T.; Srinidhi, E.R.; Darraji, R.; Holmes, D.G.; Staudinger, J.; Jones, J.K.; Ghannouchi, F.M. High-Efficiency Input and Output Harmonically Engineered Power Amplifiers. IEEE Trans. Microw. Theory Tech. 2017, 66, 1002–1014. [Google Scholar] [CrossRef]
- Colantonio, P.; Giannini, F.; Limiti, E. High Efficiency RF and Microwave Solid State Power Amplfiers; John Wiley & Sons Ltd.: West Sussex, UK, 2009; p. 303. [Google Scholar]
- Canning, T.; Tasker, P.; Cripps, S. Waveform Evidence of Gate Harmonic Short Circuit Benefits for High Efficiency X-Band Power Amplifiers. IEEE Trans. Microw. Theory Tech. 2013, 23, 439–441. [Google Scholar] [CrossRef]
- Colantonio, P.; Giannini, F.; Leuzzi, G.; Limiti, E. High efficiency low-voltage power amplifier design by second-harmonic manipulation. Int. J. RF Microw. Comput. Aided Eng. 2000, 10, 19–32. [Google Scholar] [CrossRef]
- Colantonio, P.; Giannini, F.; Leuzzi, G.; Limiti, E. Multiharmonic manipulation for highly efficient microwave power amplifiers. Int. J. RF Microw. Comput. Aided Eng. 2001, 11, 366–384. [Google Scholar] [CrossRef]
- Anakabe, A.; Ayllón, N.; Collantes, J.M.; Mallet, A.; Soubercaze-Pun, G.; Narendra, K. Automatic Pole-Zero Identification Multivariable Large-Signal Stability Analysis of RF and Microwave Citcuits. In Proceedings of the 40th European Microwave Conference, Paris, France, 28–30 September 2010; pp. 477–480. [Google Scholar]
- Sardin, D.; Reveyrand, T.; Popovi´c, Z. X-band 10 W MMIC High-Gain Power Amplifier with up to 60% PAE. In Proceedings of the 2014 9th European Microwave Integrated Circuit Conference, Rome, Italy, 6–7 October 2014; pp. 393–396. [Google Scholar]
- Resca, D.; Raffo, A.; Falco, D.S.; Scappaviva, F.; Vadalà, V.; Vannini, G. X-Band GaN Power Amplifier for Future Generation SAR Systems. IEEE Microw. Wirel. Compon. Lett. 2014, 24, 266–268. [Google Scholar] [CrossRef]
- Bae, K.T.; Lee, L.K.; Kang, B.; Sim, S.; Jeon, L.; Kim, D.W. X-Band GaN Power Amplifier MMIC with a Third Harmoninc-Tuned Circuit. Electronics 2017, 6, 103. [Google Scholar] [CrossRef]
- Couturier, A.M.; Poitrenaud, N.; Serru, V.; Dionisio, R.; Fontecavc, J.J.; Camiade, M. 50% High Efficiency X-Band GaN MMIC Amplifier for Space Applications. In Proceedings of the 48th European Microwave Conference, Madrid, Spain, 23–27 September 2018; pp. 352–355. [Google Scholar]
- Piotrowicz, S.; Ouarch, Z.; Chartier, E.; Aubry, R.; Callet, G.; Floriot, D.; Jacquet, J.-C.; Jardel, O.; Morvan, E.; Reveyrand, T.; et al. 43W, 52% PAE X-Band AlGaN/GaN HEMTs MMIC Amplifiers. In Proceedings of the 2010 IEEE MTT-S International Microwave Symposium Digest, Anaheim, CA, USA, 23–28 May 2010; pp. 505–508. [Google Scholar]

| Reference | Technology | Operation Mode | Frequency (GHz) | Pout (dBm) | PAE (%) | Gp (dB) | Pulse/Duty (μs, %) |
|---|---|---|---|---|---|---|---|
| [16] | 0.15 μm GaN | Class AB, output 2nd and 3rd harmonic tuned | 10–10.5 | 40 | 45–61 | 19 | Continuous Wave |
| [17] | 0.25 μm GaN | Class AB | 8.8–10.4 | 40–41 | 38–44 | 17–18 | 50, 15 |
| [18] | 0.25 μm GaN | Class AB, 3rd harmonic tuned | 8.5–10.5 | 43.2–44.7 | 35–37 | 16–19.1 | 100, 10 |
| [19] | 0.25 μm GaN | Class AB, input and output 2nd harmonic tuned | 7.8–8.8 | 43.5 | 50–52 | 18.5 | Continuous Wave |
| [20] | 0.25 μm GaN | Class AB | 8.5–11 | 43–46.5 | 33–52 | 13–16.5 | 20, 10 |
| This work | 0.25 μm GaN | Continuous class B, input 2nd harmonic tuned | 8–10.5 | 40.8–42.2 | 51.7–59 | 19.8–21.2 | 100, 10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, C.; Gao, Y.; Chen, W.; Huang, J.; Wang, Z.; Mo, J.; Yu, F. X-Band High-Efficiency Continuous Class B Power Amplifier GaN MMIC Assisted by Input Second-Harmonic Tuning. Electronics 2019, 8, 1312. https://doi.org/10.3390/electronics8111312
Jin C, Gao Y, Chen W, Huang J, Wang Z, Mo J, Yu F. X-Band High-Efficiency Continuous Class B Power Amplifier GaN MMIC Assisted by Input Second-Harmonic Tuning. Electronics. 2019; 8(11):1312. https://doi.org/10.3390/electronics8111312
Chicago/Turabian StyleJin, Chen, Yuan Gao, Wei Chen, Jianhua Huang, Zhiyu Wang, Jiongjiong Mo, and Faxin Yu. 2019. "X-Band High-Efficiency Continuous Class B Power Amplifier GaN MMIC Assisted by Input Second-Harmonic Tuning" Electronics 8, no. 11: 1312. https://doi.org/10.3390/electronics8111312
APA StyleJin, C., Gao, Y., Chen, W., Huang, J., Wang, Z., Mo, J., & Yu, F. (2019). X-Band High-Efficiency Continuous Class B Power Amplifier GaN MMIC Assisted by Input Second-Harmonic Tuning. Electronics, 8(11), 1312. https://doi.org/10.3390/electronics8111312




