An FPGA-Based 16-Bit Continuous-Time 1-1 MASH ΔΣ TDC Employing Multirating Technique
Abstract
1. Introduction
2. Background
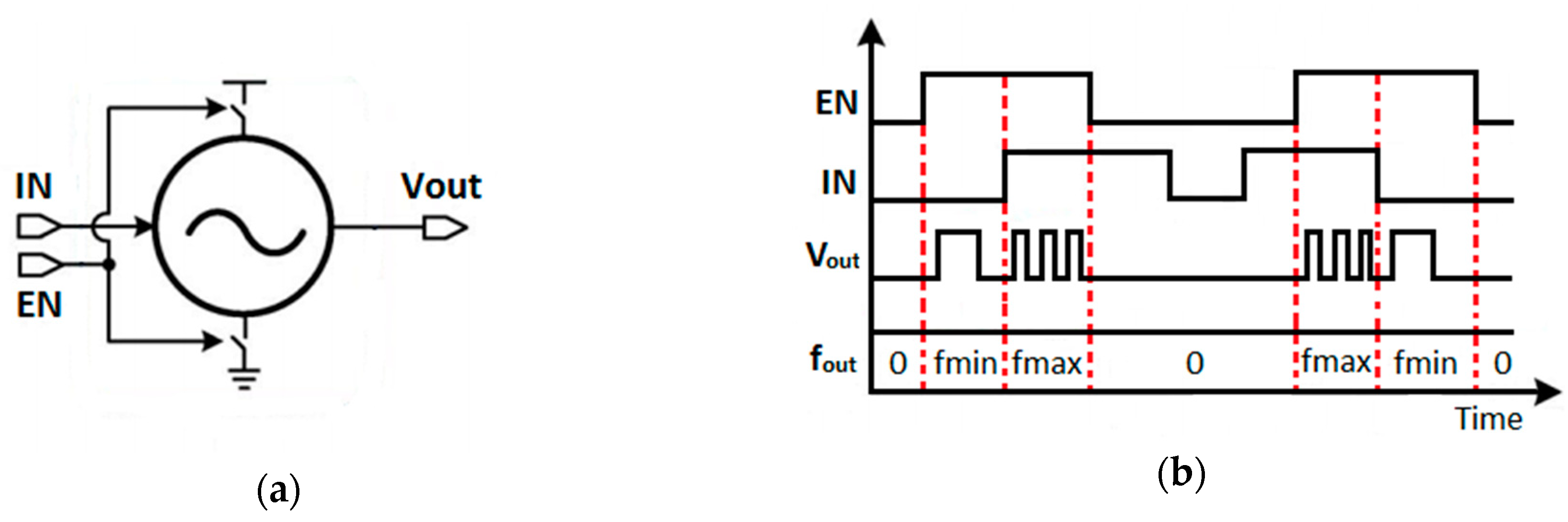
2.1. Gated Switched-Ring Oscillator-Time-to-Digital Converter (GSRO-TDC)
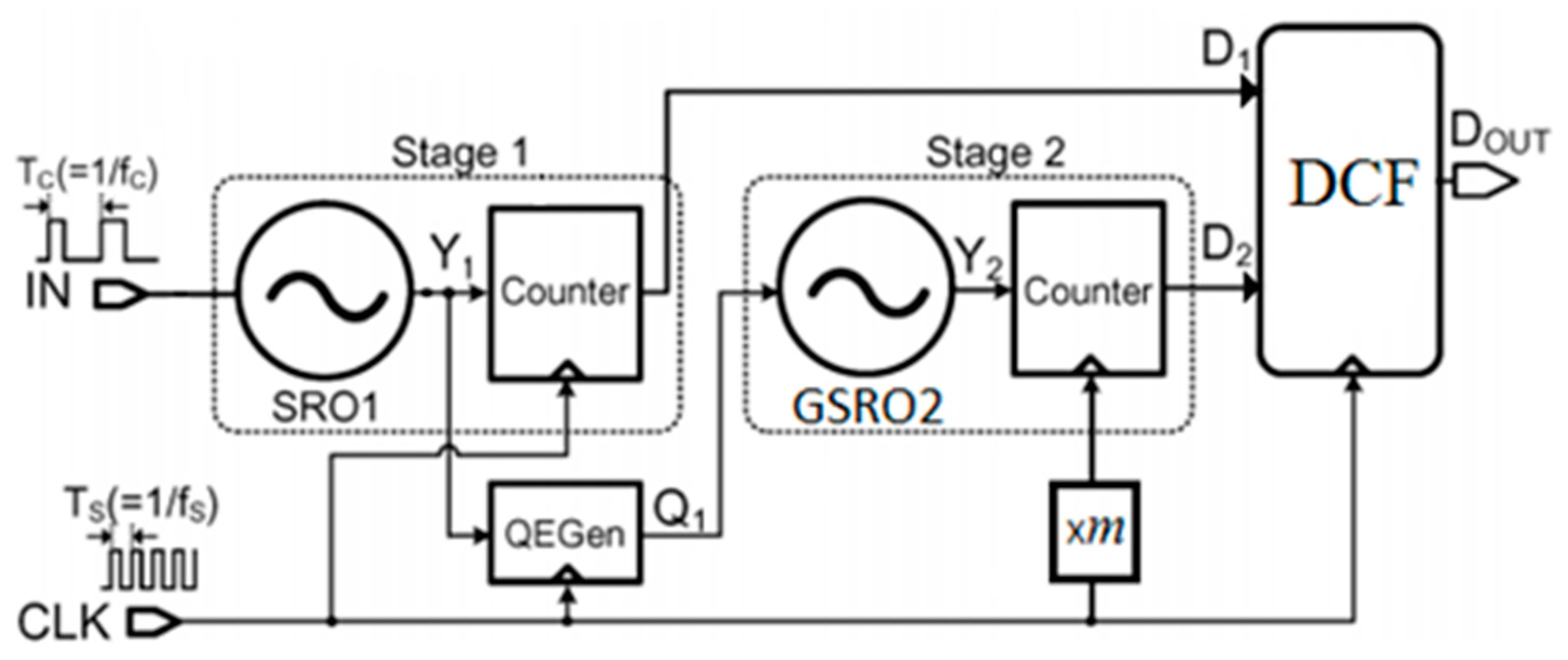
2.2. Multirating Technique in ∆∑ Multi-Stage Noise-Shaping (MASH) Converters
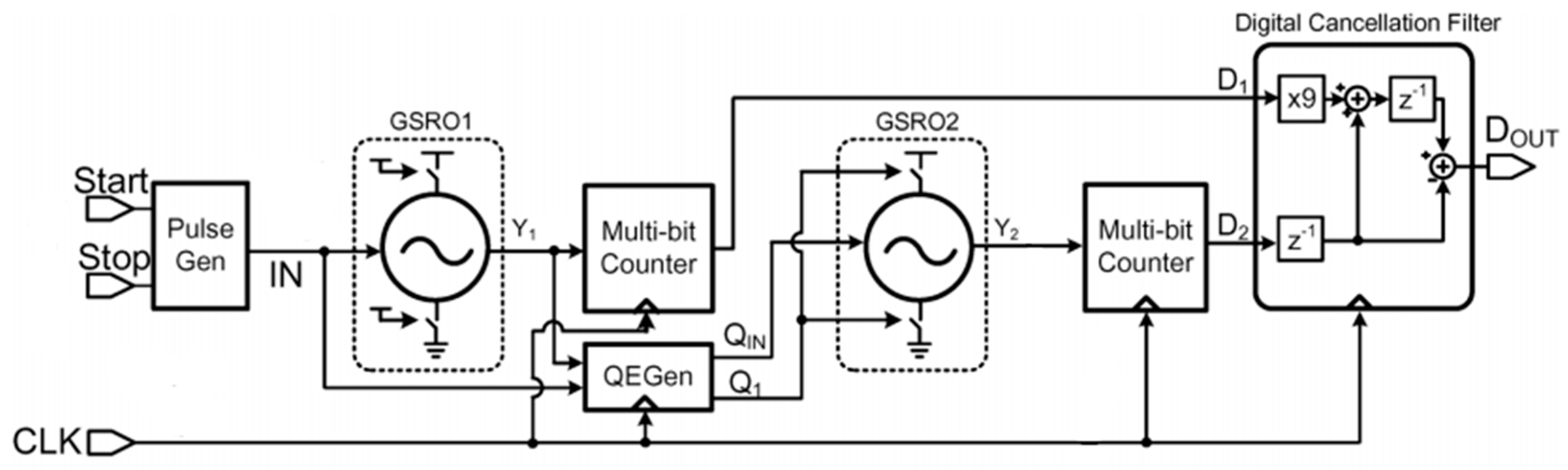
3. Proposed FPGA-Based 1-1 MASH ∆∑ TDC
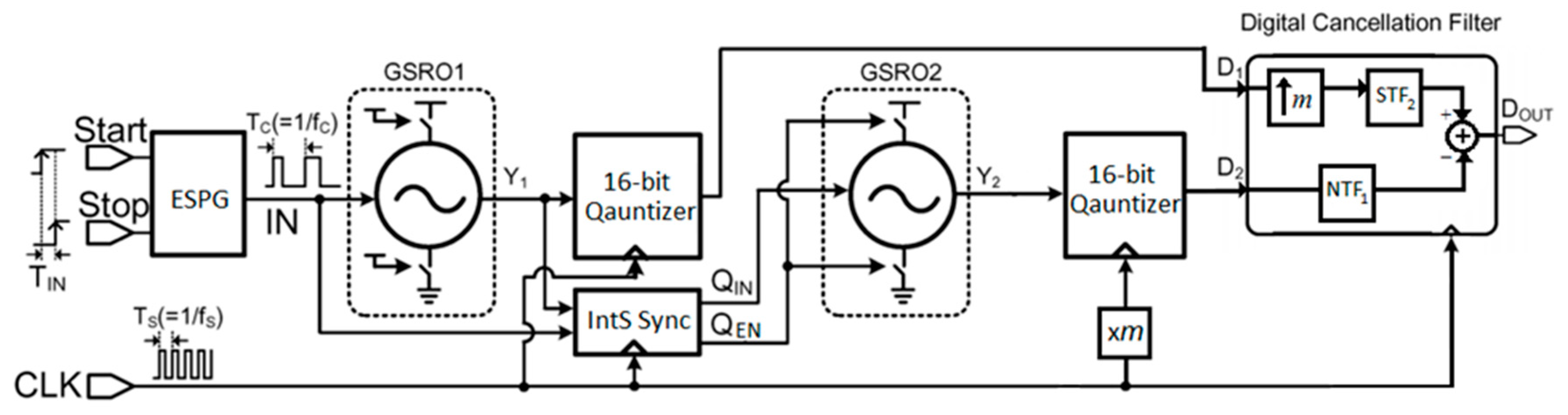
4. Implementation Details
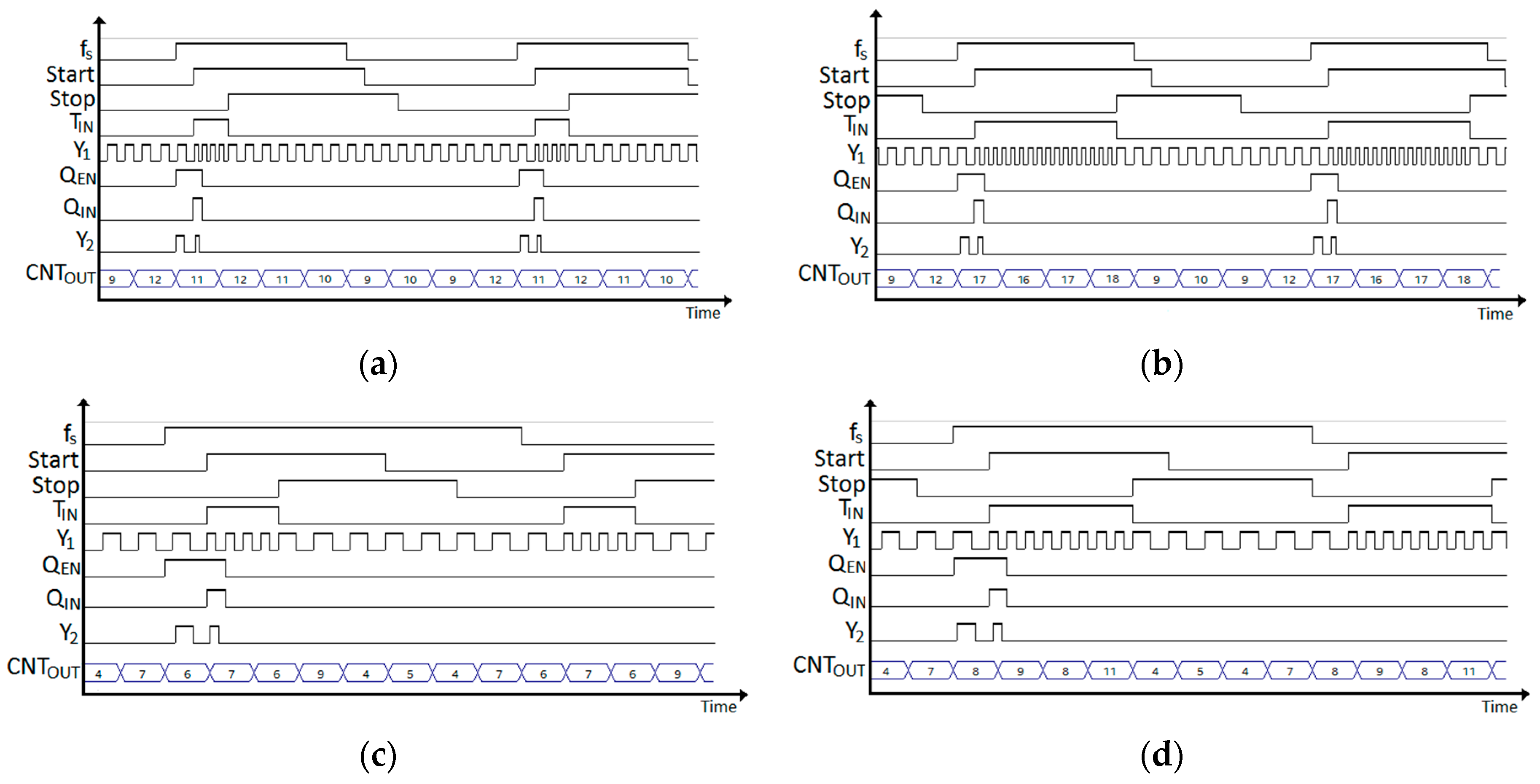
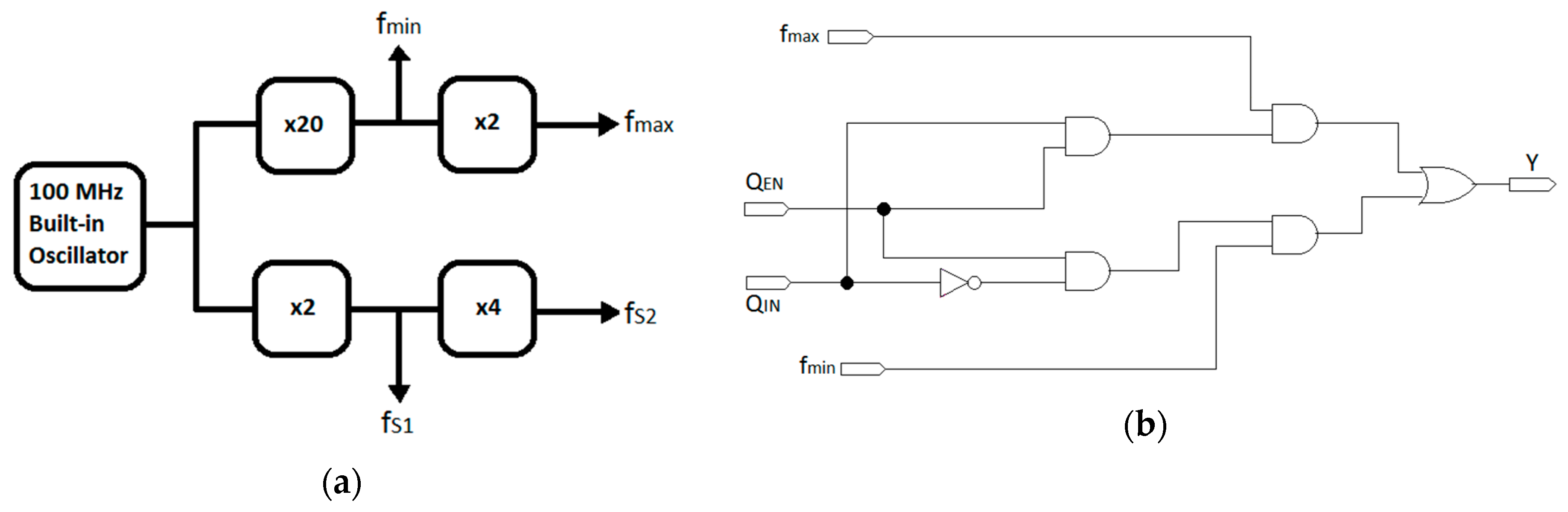
4.1. GSRO and Sampling Clocks
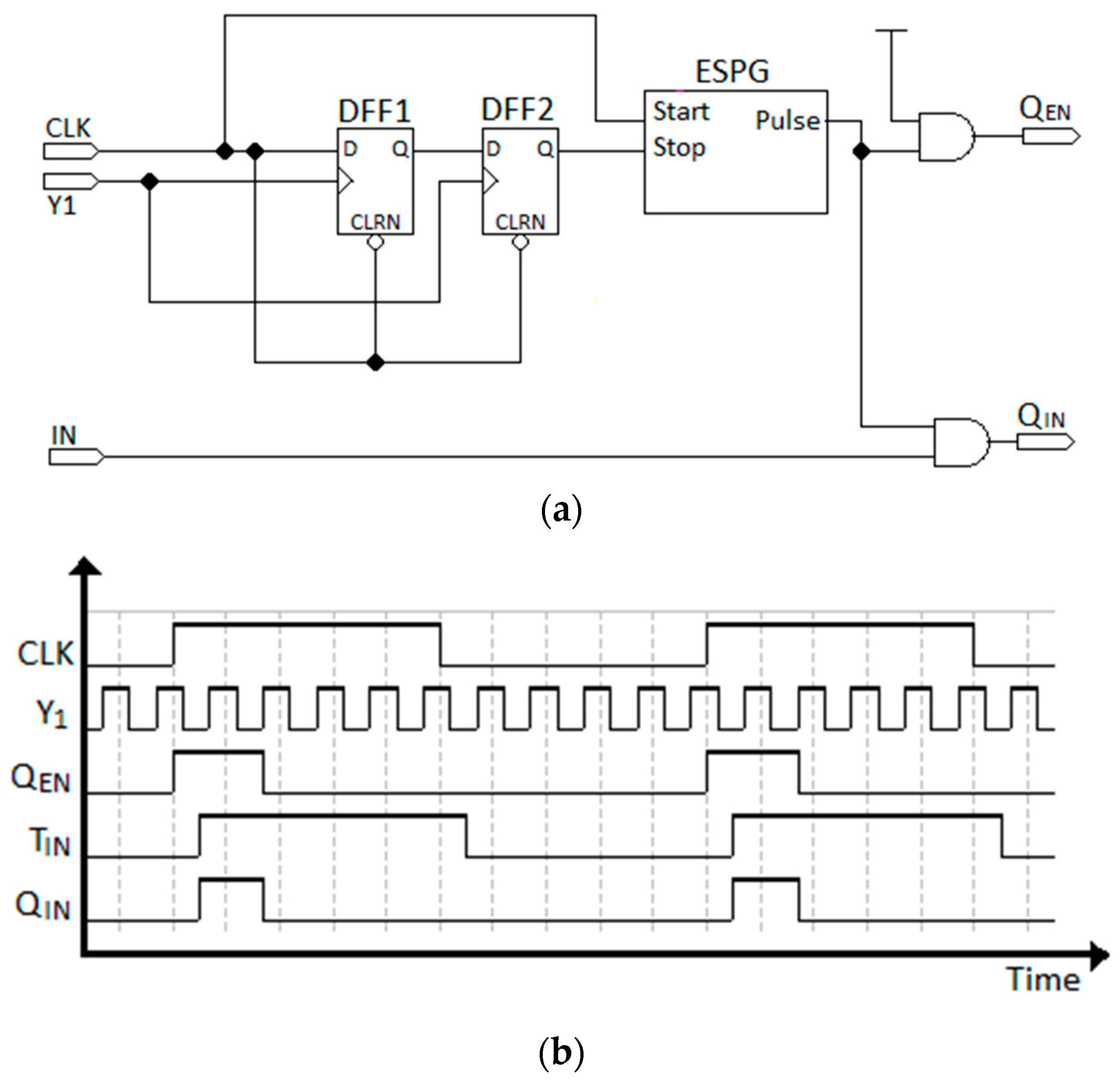
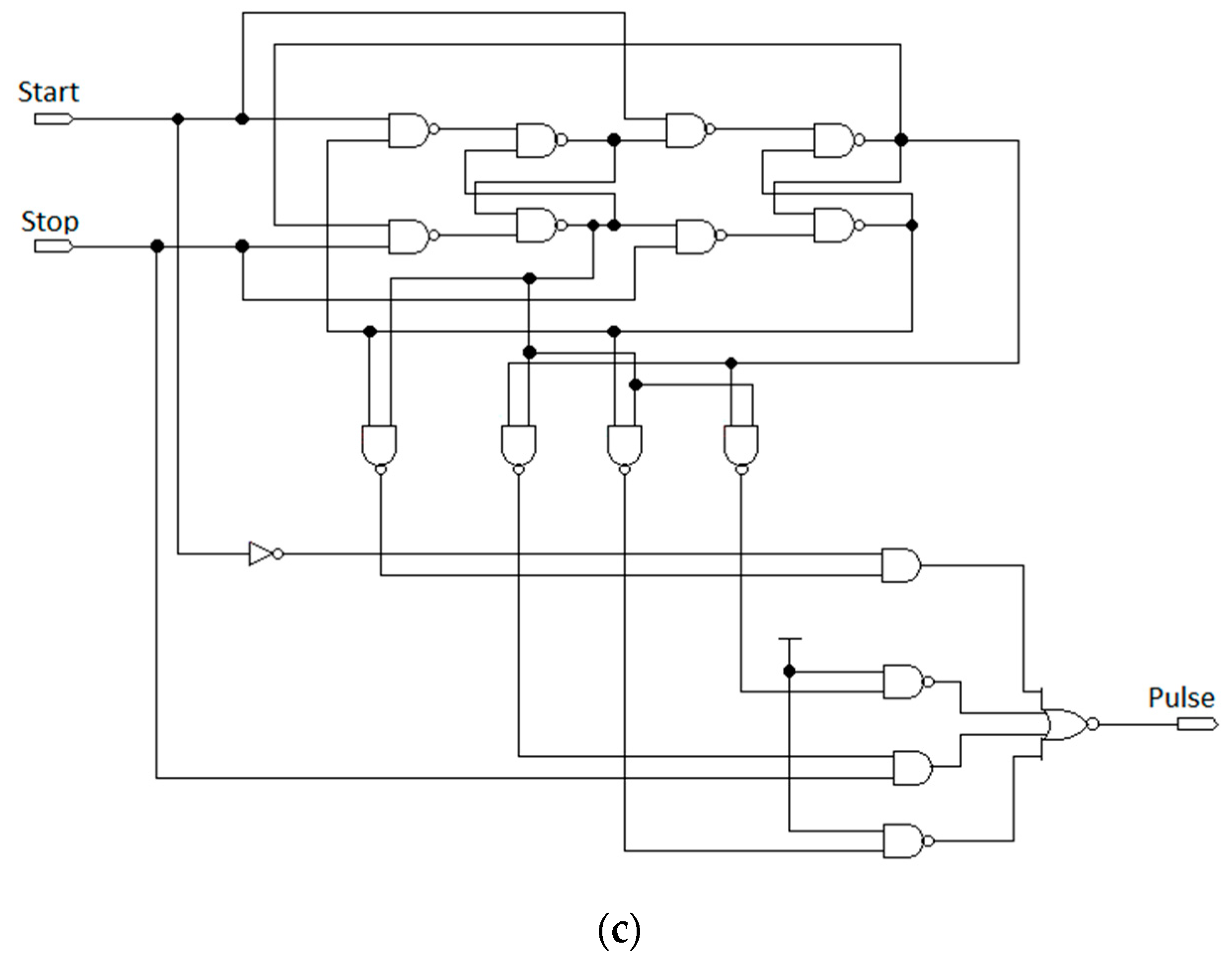
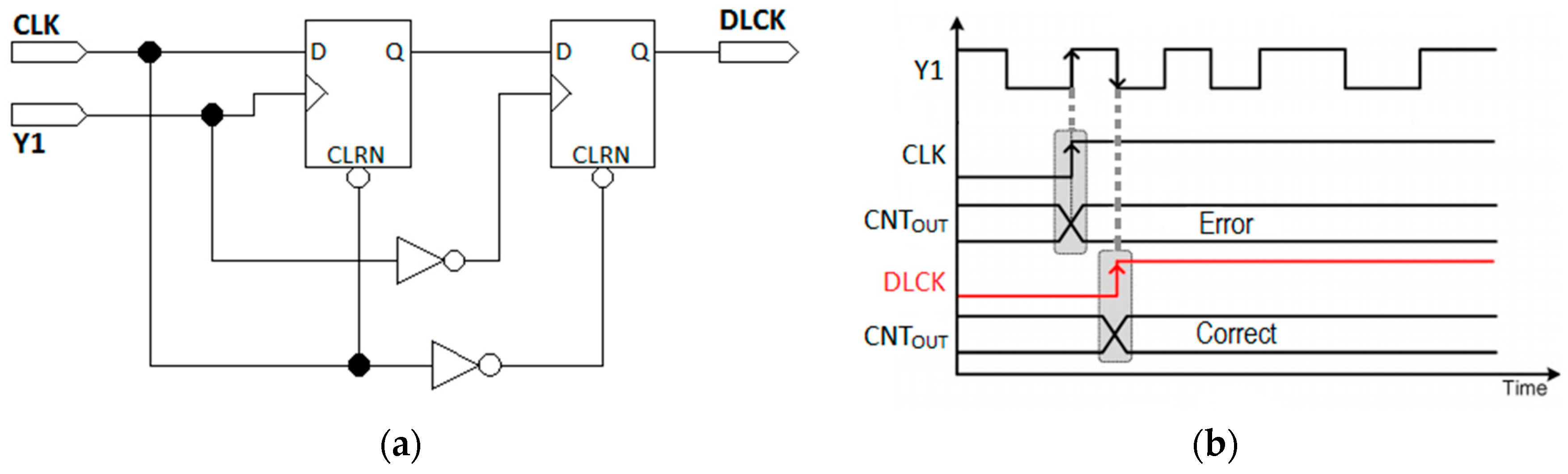
4.2. Interstage Synchronizer (IntS Sync)
4.3. The 16-Bit Quantizer
4.4. Digital Cancellation Filter (DCF)
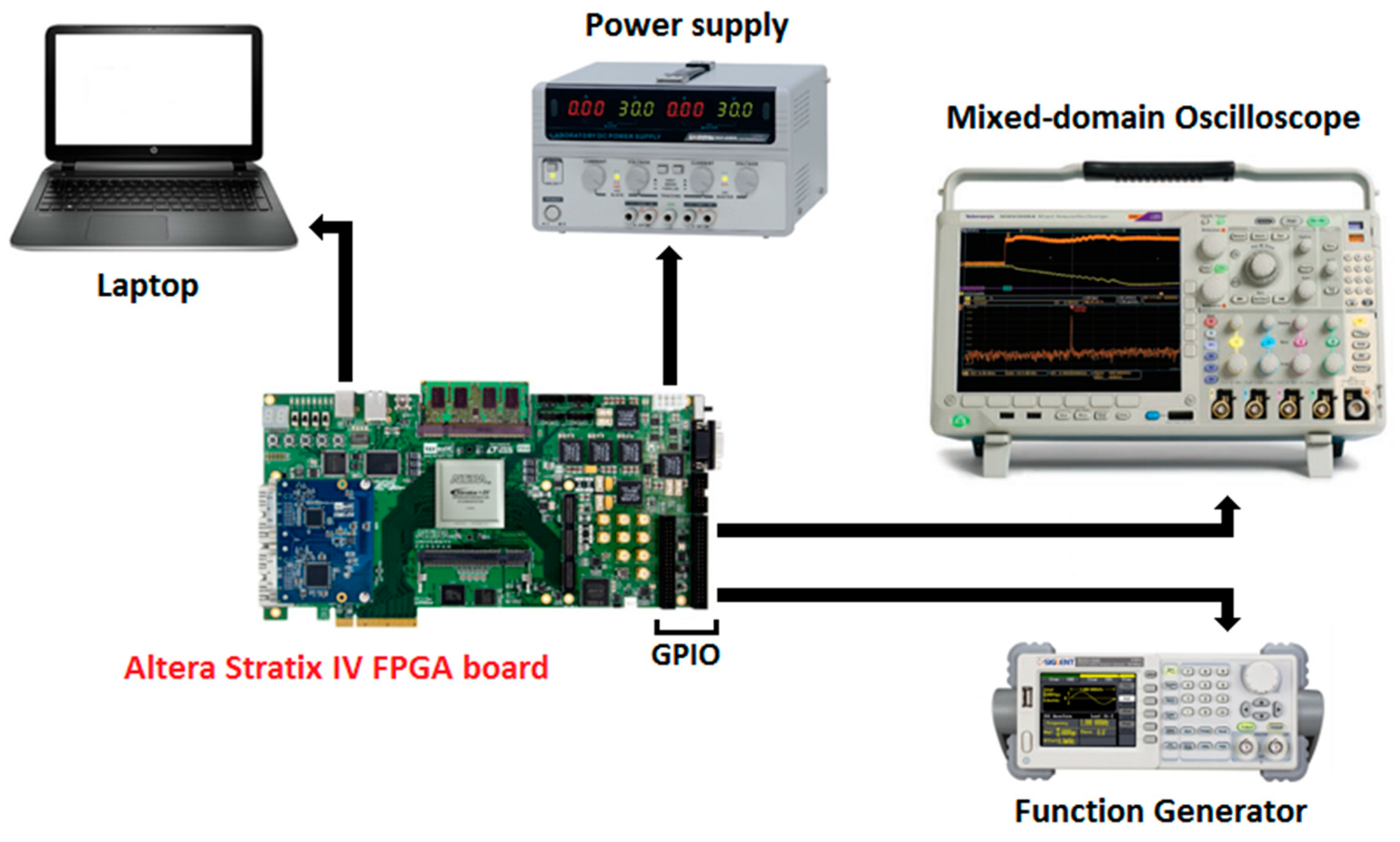
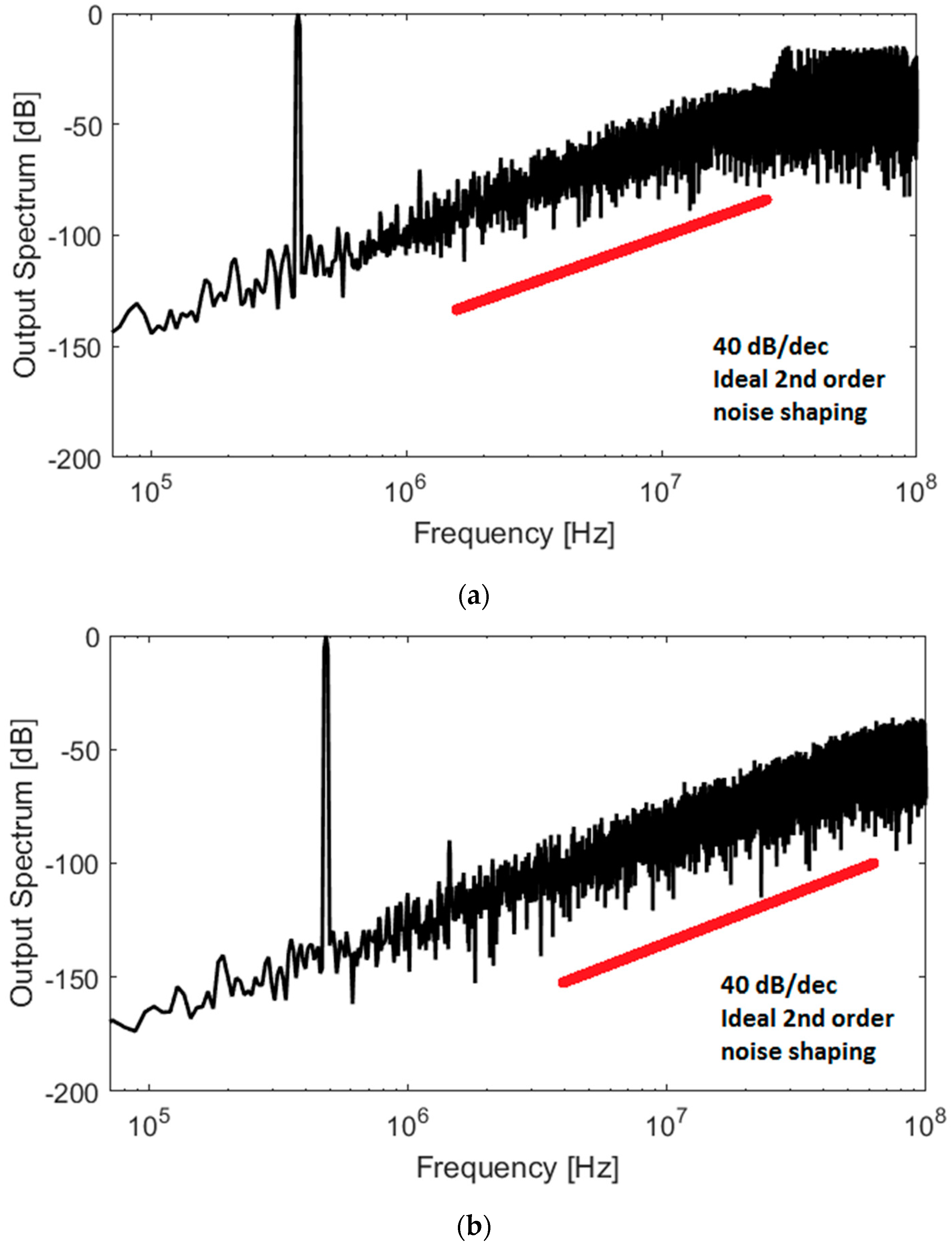
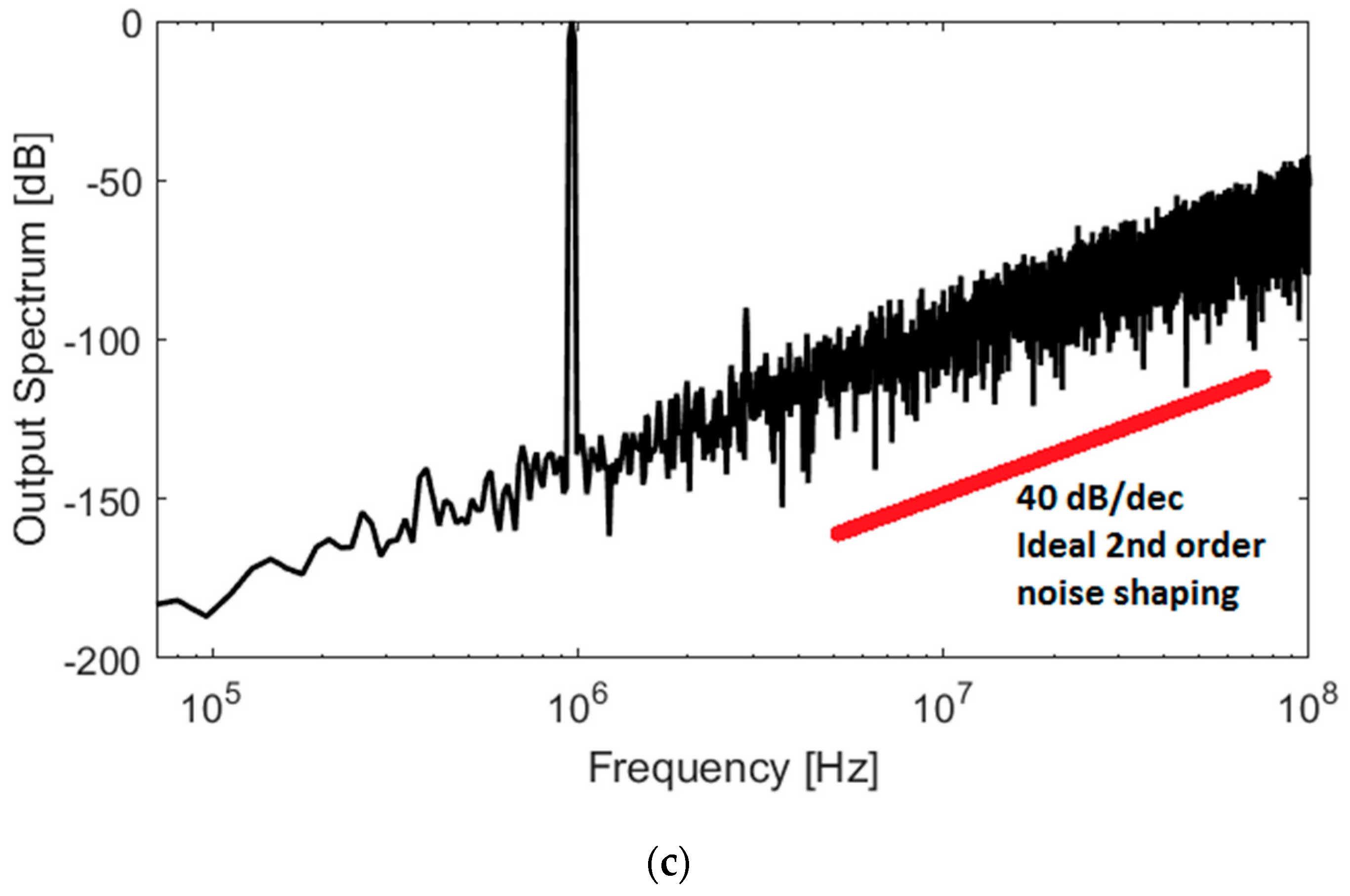
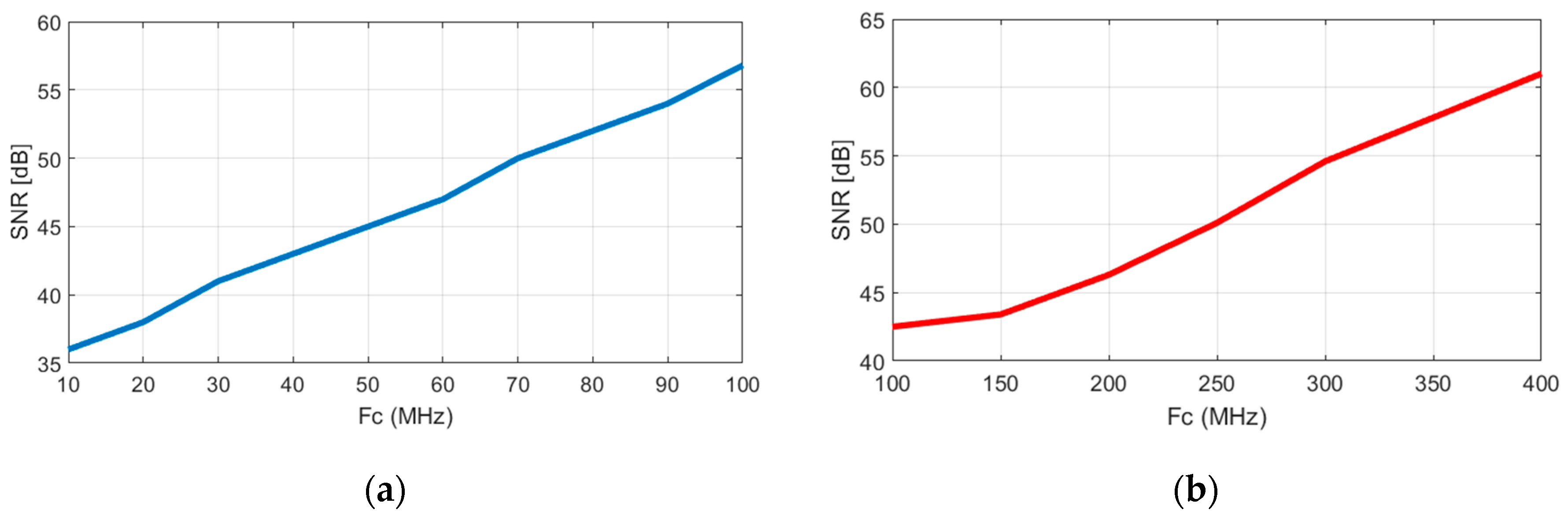
5. Measured Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yan, N.; Ma, L.; Xu, Y.; Chen, S.; Liu, X.; Xiang, J.; Min, H. A Low Power All-Digital PLL With −40dBc In-Band Fractional Spur Suppression for NB-IoT Applications. IEEE Access 2019, 7, 7897–7904. [Google Scholar] [CrossRef]
- Liu, Y.; Constandinou, T.G.; Georgiou, P. A 32 × 32 ISFET Array with In-Pixel Digitisation and Column-Wise TDC for Ultra-Fast Chemical Sensing. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Sapporo, Japan, 26–29 May 2019; pp. 1–5. [Google Scholar]
- Hussein, A.; Vasadi, S.; Paramesh, J. A 50–66-GHz Phase-Domain Digital Frequency Synthesizer with Low Phase Noise and Low Fractional Spurs. IEEE J. Solid State Circuits 2017, 52, 3329–3347. [Google Scholar] [CrossRef]
- Alkurwy, S.; Sawal, H.M.A.; Shabiul Islam, M.; Idros, F. A low power memoryless ROM design architecture for a direct digital frequency synthesizer. Turkish J. Electr. Eng. & Comput. Sci. 2017, 25, 4023–4032. [Google Scholar]
- Ibrahim, S.H.; Sawal, H.M.A.; Shabiul Islam, M. Hardware Implementation of 32-Bit High-Speed Direct Digital Frequency Synthesizer. Sci. World J. 2014, 2014, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, S.H.; Sawal, H.M.A.; Shabiul Islam, M. Implementation of a 32-Bit High-Speed Phase Accumulator for Direct Digital Frequency Synthesizer. Asian J. Sci. Res. 2014, 7, 118–124. [Google Scholar] [CrossRef]
- Nguyen, V.; Duong, D.; Chung, Y.; Lee, J.W. A Cyclic Vernier Two-Step TDC for High Input Range Time-of-Flight Sensor Using Startup Time Correction Technique. Sensors 2018, 18, 3948. [Google Scholar] [CrossRef]
- Lu, P.; Wu, Y.; Andreani, P. A 2.2-ps Two-Dimensional Gated-Vernier Time-to-Digital Converter with Digital Calibration. IEEE Trans. Circuits Syst. II Express Briefs 2016, 63, 1019–1023. [Google Scholar] [CrossRef]
- Yu, W.; Kim, J.; Kim, K.; Cho, S. A time-domain high-order MASH ADC using voltage-controlled gated-ring oscillator. IEEE Trans. Circuits Syst. I Reg. Papers 2013, 60, 856–866. [Google Scholar] [CrossRef]
- Kim, J.S.; Seo, Y.H.; Suh, Y.; Park, H.J.; Sim, J.Y. A 300-MS/s, 1.76-ps-resolution, 10-b asynchronous pipelined time-to-digital converter with on-chip digital background calibration in 0.13-µm CMOS. IEEE J. Solid State Circuits 2013, 48, 516–526. [Google Scholar] [CrossRef]
- Kim, K.; Kim, Y.H.; Yu, W.; Cho, S. A 7 bit, 3.75 ps resolution two-step time-to-digital converter in 65 nm CMOS using pulse-train time amplifier. IEEE J. Solid State Circuits 2013, 48, 1009–1017. [Google Scholar] [CrossRef]
- Kim, K.S.; Yu, W.; Cho, S. A 9 b, 1.12 ps resolution 2.5 b/stage pipelined time-to-digital converter in 65 nm CMOS using time-register. In Proceedings of the Symposium on VLSI Circuits, Kyoto, Japan, 12–14 June 2013; pp. 1007–1016. [Google Scholar]
- Seo, Y.H.; Kim, J.S.; Park, H.J.; Sim, J.Y. A 1.25 ps resolution 8 b cyclic TDC in 0.13 µm CMOS. IEEE J. Solid State Circuits 2012, 47, 736–743. [Google Scholar] [CrossRef]
- Chung, H.; Ishikuro, H.; Kuroda, T. A 10-Bit 80-MS/s decision-select successive approximation TDC in 65 nm CMOS. IEEE J. Solid State Circuits 2012, 47, 1232–1241. [Google Scholar] [CrossRef]
- Gande, M.; Maghari, N.; Oh, T.; Moon, U.K. A 71 dB dynamic range third-order TDC using charge-pump. In Proceedings of the Symposium on VLSI Circuits (VLSIC), Honolulu, HI, USA, 13–15 June 2012; pp. 168–169. [Google Scholar]
- Young, B.; Kwon, S.; Elshazly, A.; Hanumolu, P.K. A 2.4 ps resolution 2.1 mW second-order noiseshaped time-to-digital converter with 3.2 ns range in 1 MHz bandwidth. In Proceedings of the IEEE Custom Integrated Circuits Conference, San Jose, CA, USA, 19–22 September 2010; pp. 1–4. [Google Scholar]
- Straayer, M.Z.; Perrott, M.H. A multi-path gated ring oscillator TDC with first-order noise shaping. IEEE J. Solid State Circuits 2009, 44, 1089–1098. [Google Scholar] [CrossRef]
- Elshazly, A.; Rao, S.; Young, B.; Hanumolu, P.K. A 13 b 315 fsrms 2 mW 500 MS/s 1 MHz bandwidth highly digital time-to-digital converter using switched ring oscillators. In Proceedings of the IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 20–24 February 2012; pp. 464–466. [Google Scholar]
- Konishi, T.; Okuno, K.; Izumi, S.; Yoshimoto, M.; Kawaguchi, H. A 61-dB SNDR 700 µm2 second-order all-digital TDC with low-jitter frequency shift oscillator and dynamic flipflops. In Proceedings of the Symposium on VLSI Circuits (VLSIC), 13–15 June 2012; pp. 190–191. [Google Scholar]
- Yu, W.; Kim, K.S.; Cho, S.H. A 148 fsrms integrated noise 4 MHz bandwidth second-order ∆∑ time-to-digital converter with gated switched-ring oscillator. IEEE Trans. Circuits Syst. I Reg. Papers 2014, 61, 2281–2289. [Google Scholar] [CrossRef]
- Zaliasl, S.; Saxena, S.; Hanumolu, P.K.; Mayaram, K.; Fiez, T.S. A 12.5-bit 4 MHz 13.8 mW MASH Modulator with Multirated VCO-Based ADC. IEEE Trans. Circuits Syst. I Reg. Papers 2012, 59, 1604–1613. [Google Scholar] [CrossRef]
- Chandrasekaran, S.T.; Jayaraj, A.; Danesh, M.; Sanyal, A. A Highly Digital Second-Order Oversampling TDC. IEEE Solid State Circuits Lett. 2018, 1, 114–117. [Google Scholar] [CrossRef]
- Liu, Q.; Edward, A.; Zhou, D.; Silva-Martinez, J. A Continuous-Time MASH 1-1-1 Delta–Sigma Modulator with FIR DAC and Encoder-Embedded Loop-Unrolling Quantizer in 40-nm CMOS. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2018, 26, 756–767. [Google Scholar] [CrossRef]
- Dayanik, M.B.; Weyer, D.; Flynn, M.P. A 5GS/s 156MHz BW 70dB DR continuous-time sigma-delta modulator with time-interleaved reference data-weighted averaging. In Proceedings of the Symposium on VLSI Circuits (VLSIC), Kyoto, Japan, 5–8 June 2017. [Google Scholar]
- Edward, A.; Liu, Q.; Briseno-Vidrios, C.; Kinyua, M.; Soenen, E.G.; Karşılayan, A.I.; Silva-Martinez, J. A 43-mW MASH 2-2 CT ∑∆ Modulator Attaining 74.4/75.8/76.8 dB of SNDR/SNR/DR and 50 MHz of BW in 40-nm CMOS. IEEE J. Solid State Circuits 2017, 52, 448–459. [Google Scholar] [CrossRef]
- Li, H.; Breyne, L.; Van Kerrebrouck, J.; Verplaetse, M.; Wu, C.Y.; Demeester, P.; Torfs, G. A 21-GS/s Single-Bit Second-Order Delta–Sigma Modulator for FPGAs. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 482–486. [Google Scholar] [CrossRef]
- Tan, Y.T.; Bhuyan, M.S.; Sawal, H.M.A.; Shabiul Islam, M. FPGA Realization of Fault Diagnostic Manufacturing Equipment Using Fuzzy Expert System. Res. J. Appl. Sci. 2014, 9, 53–59. [Google Scholar]
- Moubark, A.M.; Mohd Ali, M.A.; Sanusi, H.; Sawal, H.M.A. FPGA Implementation of Low Power Digital QPSK Modulator Using Verilog HDL. J. Appl. Sci. 2013, 13, 385–392. [Google Scholar] [CrossRef]
- Marufuzzaman, M.; Ibne Reaz, M.; Rahman, L.F.; Chang, T.G. FPGA Based Precise and High Speed Current dq PI Controller for FOC PMSM Drive. Curr. Nanosci. 2014, 10, 394–401. [Google Scholar] [CrossRef]
- Straayer, M.Z. Noise Shaping Techniques for Analog and Time to Digital Converters Using Voltage Controlled Oscillators. Ph.D. Thesis, MIT, Cambridge, MA, USA, 2008. [Google Scholar]
- Kim, J.; Jang, T.K.; Yoon, Y.G.; Cho, S. Analysis and design of voltage-controlled oscillator based analog-to-digital converter. IEEE Trans. Circuits Syst. I Reg. Papers 2010, 57, 18–30. [Google Scholar]

| [25] | [24] | [23] | [22] | [20] | This work | ||
|---|---|---|---|---|---|---|---|
| Process (nm) | 40 | 40 | 40 | 65 | 65 | 40-FPGA | |
| Shaping order | 4 | 3 | 3 | 2 | 2 | 2 | |
| fBW (MHz) | 50.3 | 156 | 50.5 | 2.5 | 4 | 9.6 | |
| Trange (ns) | N/A | N/A | N/A | 4.5 | 4 | 4.5 | |
| fS (MHz) | 1000 | 5000 | 3000 | 205 | 400 | 200 - 800 | 400 - 1600 |
| DR (dB) | 76.8 | 70 | 68.2 | 52.6 | 79.6 | 84.2 | 86.2 |
| Tint,rms (fs,rms)1 | N/A | N/A | N/A | 3752 | 148 | 98.2 | 78 |
| SNR (dB) | 75.8 | 66.6 | 68 | 56 | N/A | 56.8 | 61.02 |
| Resolution (ps)2 | N/A | N/A | N/A | 13 | 0.51 | 0.34 | 0.27 |
| Power (mW) | 43 | 233 | 19 | 0.63 | 6.72 | 6.233 | 7.843 |
| FoM (dB)4 | 167.5 | 158.3 | 162.4 | 148 | 167 | 176 | 177 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mouri Zadeh Khaki, A.; Farshidi, E.; Hamid MD Ali, S.; Othman, M. An FPGA-Based 16-Bit Continuous-Time 1-1 MASH ΔΣ TDC Employing Multirating Technique. Electronics 2019, 8, 1285. https://doi.org/10.3390/electronics8111285
Mouri Zadeh Khaki A, Farshidi E, Hamid MD Ali S, Othman M. An FPGA-Based 16-Bit Continuous-Time 1-1 MASH ΔΣ TDC Employing Multirating Technique. Electronics. 2019; 8(11):1285. https://doi.org/10.3390/electronics8111285
Chicago/Turabian StyleMouri Zadeh Khaki, Ahmad, Ebrahim Farshidi, Sawal Hamid MD Ali, and Masuri Othman. 2019. "An FPGA-Based 16-Bit Continuous-Time 1-1 MASH ΔΣ TDC Employing Multirating Technique" Electronics 8, no. 11: 1285. https://doi.org/10.3390/electronics8111285
APA StyleMouri Zadeh Khaki, A., Farshidi, E., Hamid MD Ali, S., & Othman, M. (2019). An FPGA-Based 16-Bit Continuous-Time 1-1 MASH ΔΣ TDC Employing Multirating Technique. Electronics, 8(11), 1285. https://doi.org/10.3390/electronics8111285






