Photographic Noise Performance Measures Based on RAW Files Analysis of Consumer Cameras
Abstract
:1. Introduction
2. Theoretical Background
2.1. Noise in CMOS Image Sensors
- The read noise is decomposed in two independent components: pre and post amplifier noises. For low ISOs, the post amplifier term is the dominant one and for large ISOs the input read noise is the most important. The gain of the amplifier is related to the ISO dial in the camera: double the ISO, double the gain G. The RAW domain values in DU can be input-referred to the domain dividing by the gain factor, e.g., . Since these two components are independent, the read noise is:
- In modern cameras, the ADC noise has been reduced so much that not only for high ISOs, but even at base ISO (typically ISO 100). It means that the read noise can be simplified to only the input read noise . Since signal is also amplified by the same factor G, the output remains approximately constant for all ISOs. As a consequence, the sensor that shows this behavior is named ISO-invariant.
- The read noise drops at a certain ISO. To achieve this, a single amplifier model is not enough; since the output noise is , it must at least double when ISO is doubled. The way to model this behavior is by using a two stage amplification, where first is a low noise amplifier. From base ISO to the ISO where the sensor changes from a low to high gain mode, the read noise increases with ISO. At that ISO it drops and above that ISO it grows again. These sensors are called dual gain sensors and they allow to increase the dynamic range at high ISOs as we will analyze later. The read noise model for a dual sensor is:where , is the pre first amplifier noise, is the pre second amplifier noise and is the downstream noise. For low ISOs (low gain mode), , thus the model in Equation (3) is simplified to Equation (2); however, at some ISO, the pixel commutes to high gain mode, and so is reduced at that ISO.
2.2. Signal to Noise Ratio, Exposure and ISO
- Even for poor noise performance sensors (large read noise), if exposure can be set so that light arriving to the pixel corresponding to the darkest area of the scene is high enough to guarantee that the photon noise is dominant, the is as good as the one you would get with an ideal perfect sensor, since , independent of the sensor. The limit on increasing the exposure is given by the full well capacity (when the sensor saturates and highlights are burnt). The higher is the full well capacity of the pixel, the better, since the greater is the before saturation.
- In the deepest shadows (small signal values S), the key factor is the read noise. The smaller is the read noise, the better.
- If you increase exposure, the grows more quickly in the shadows than in the highlights. Doubling the exposure doubles the in the shadows where the read noise dominates and improves the in the highlights by a factor of . Therefore, in situations of very low exposure, such as night photography, each additional captured photon is priceless.
- Increasing exposure is not the same as increasing “exposure”. For photon noise to be dominant, it must be satisfied that or its equivalent in electrons . If you raise the ISO (greater G), it increases , but the read noise also grows with G. The best way to ensure that photon noise is much larger than read noise is by doing s very large, that is, G small for the same value of S. Thus, the condition must be understood as: the exposure s should be as large as possible.
- If the extra photon is captured because the aperture size is increased (lower f-stop), the depth of field is reduced; if you are photographing a landscape you do not want a shallow depth of field.
- If extra light is achieved because the exposure time is increased, there is a risk of trepidation (photography with no tripod) or missing the moment (fast action photography).
- If exposure time is so long that the sensor heats up too much, dark current noise begins to be a major problem.
2.3. Dynamic Range
2.4. Photographic Noise Performance Measurements
2.4.1. Same Format but Different Resolution Sensors
2.4.2. Any Format and Resolution Sensor
3. Materials and Methods
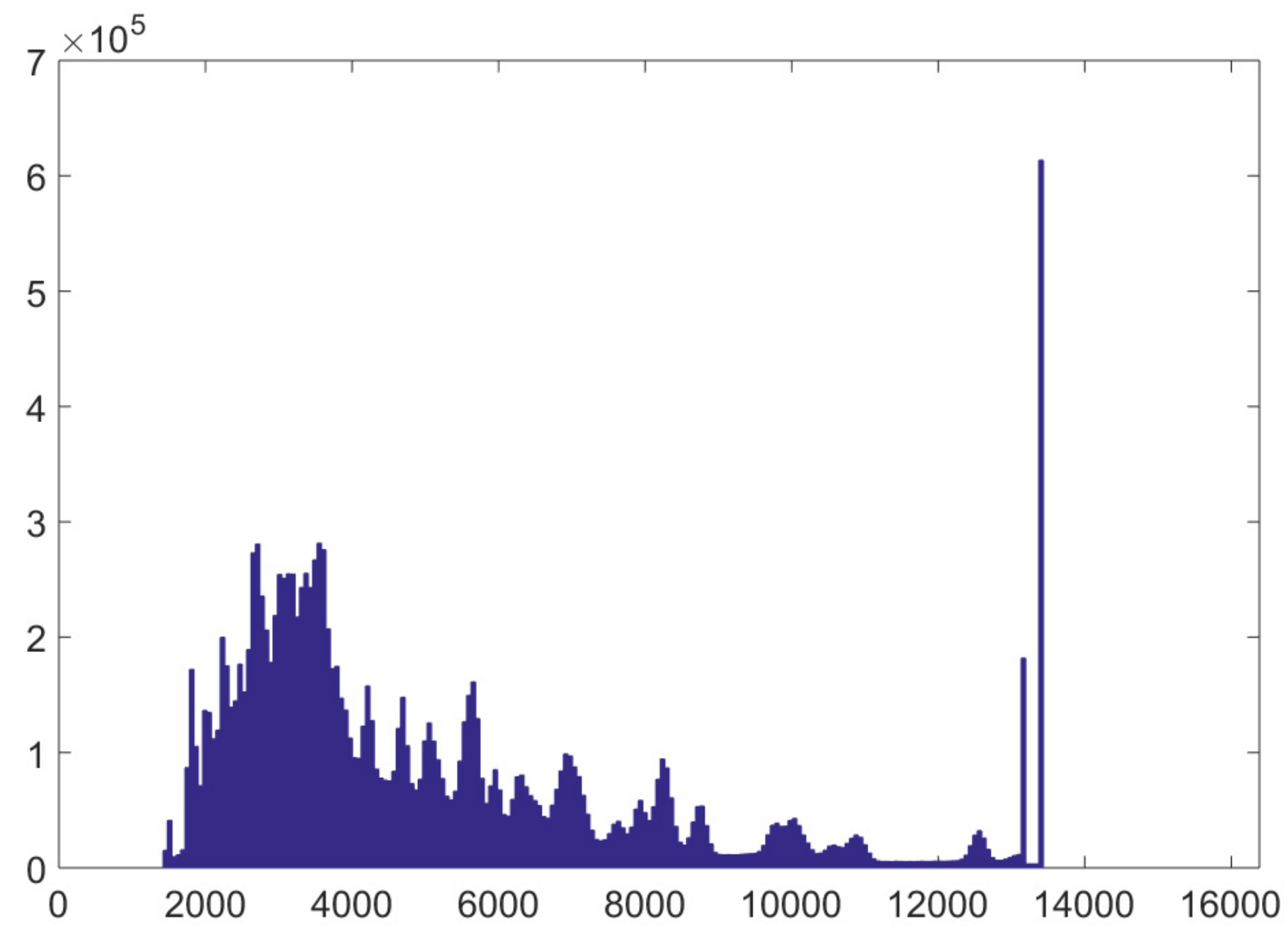
3.1. Description and Source of Material
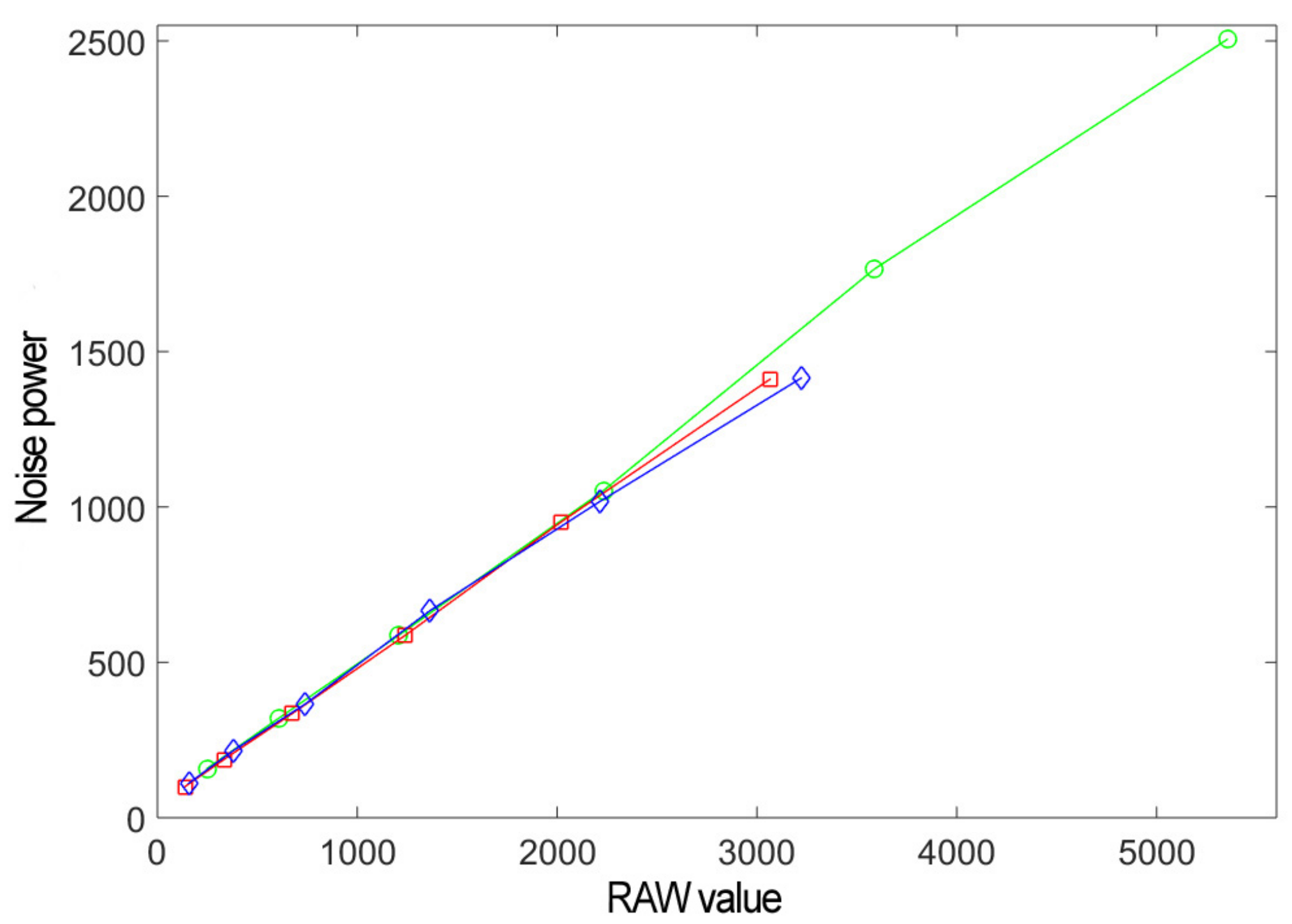
3.2. Experiment: Canon 50D Noise Model at ISO 100
4. Results
4.1. Canon 50D Analysis
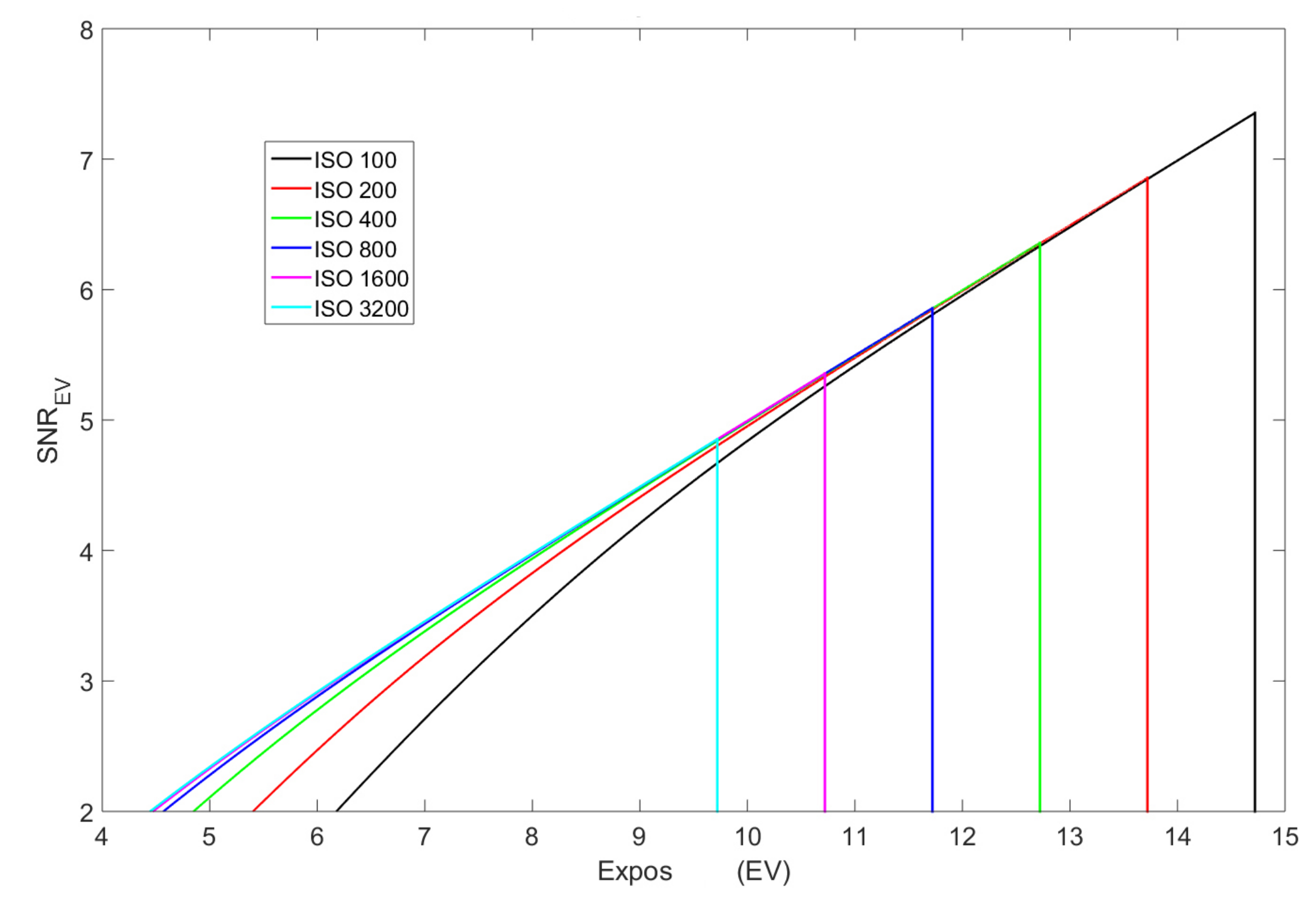
4.1.1. Canon 50D: Signal to Noise Ratio Curves
4.1.2. Canon 50D: , Exposure and ISO
4.1.3. Canon 50D: Read Noise Model and Exposure
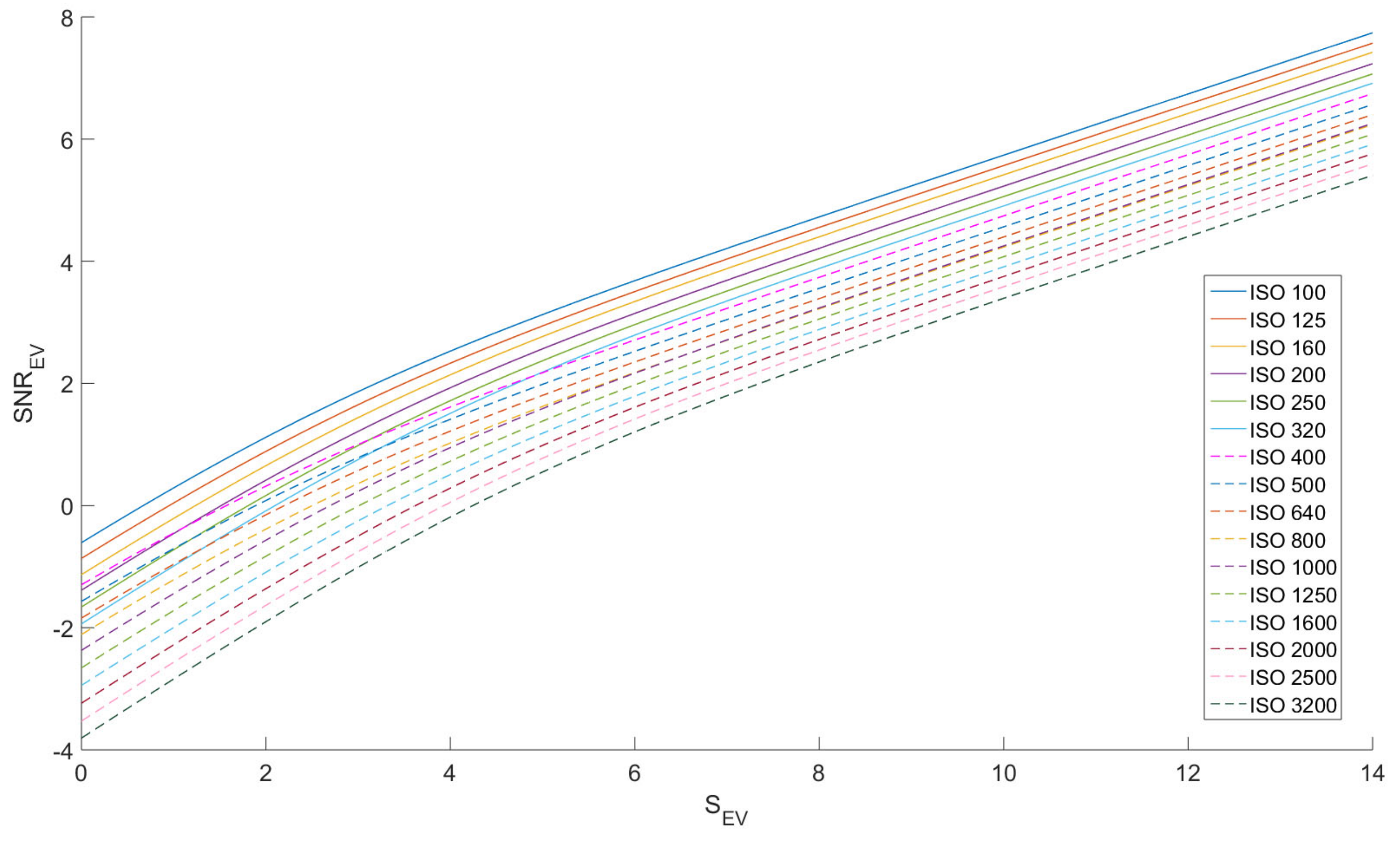
4.2. and ISO for Dual Gain ISO Invariant Sensors
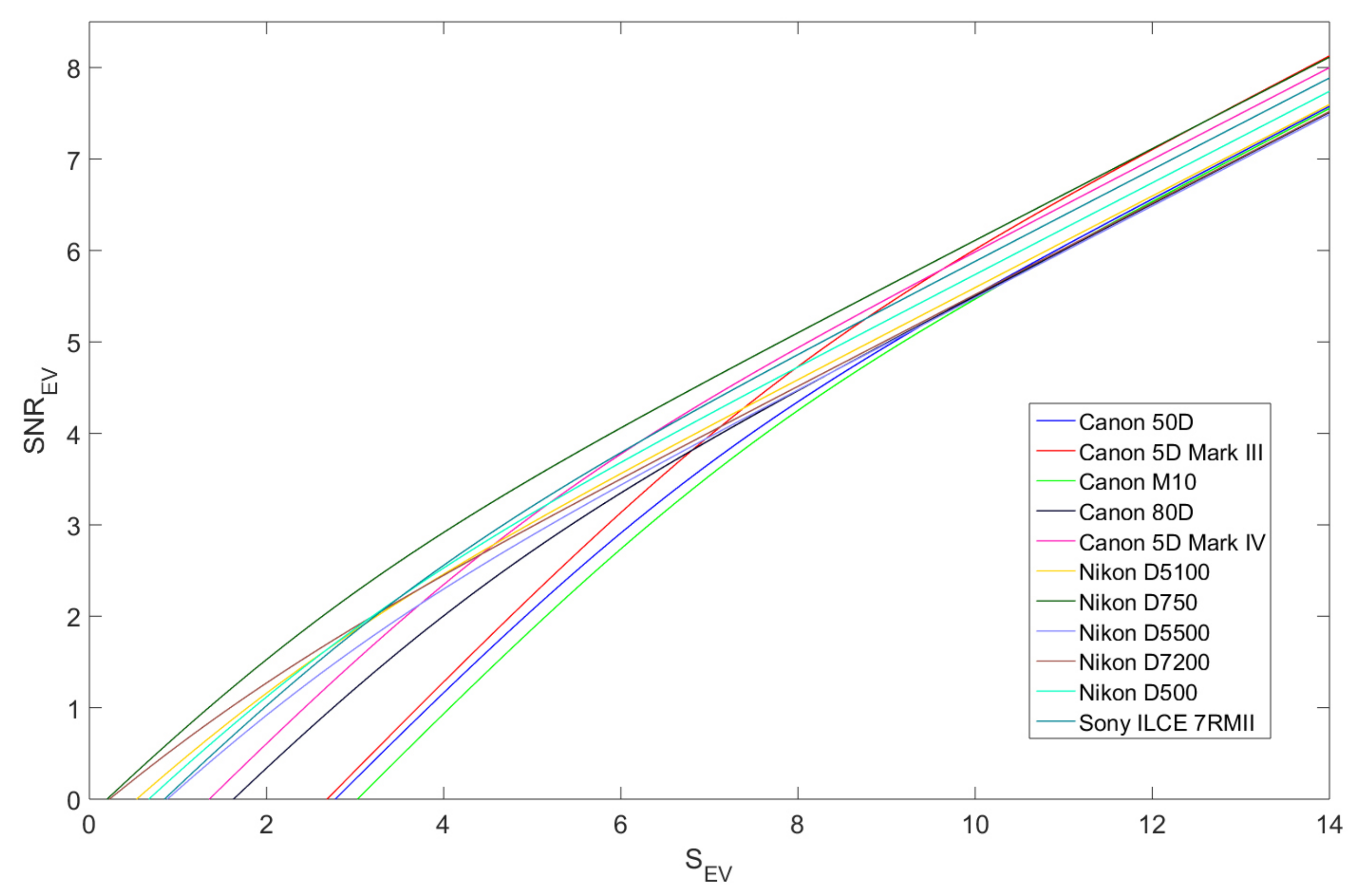
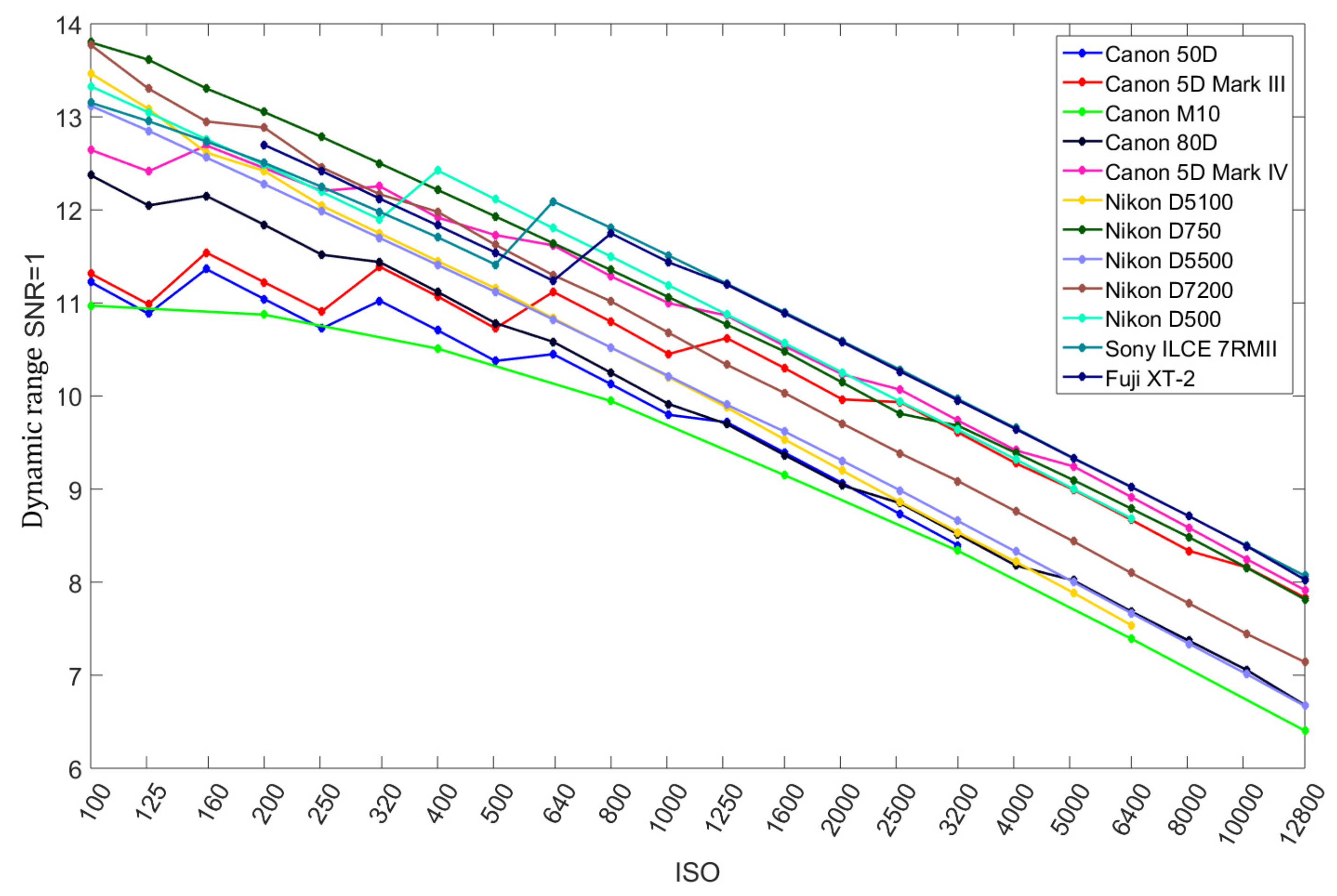
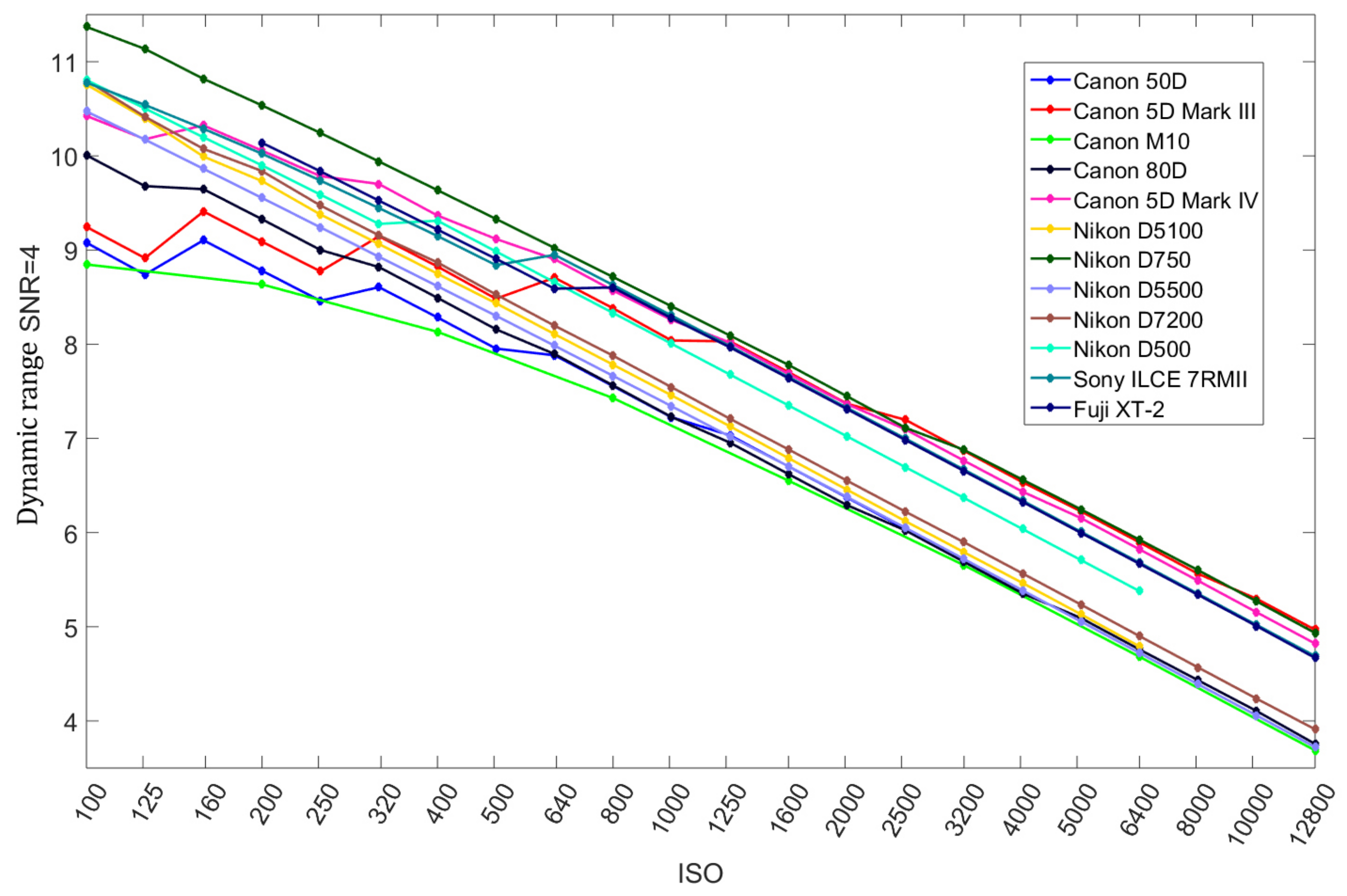
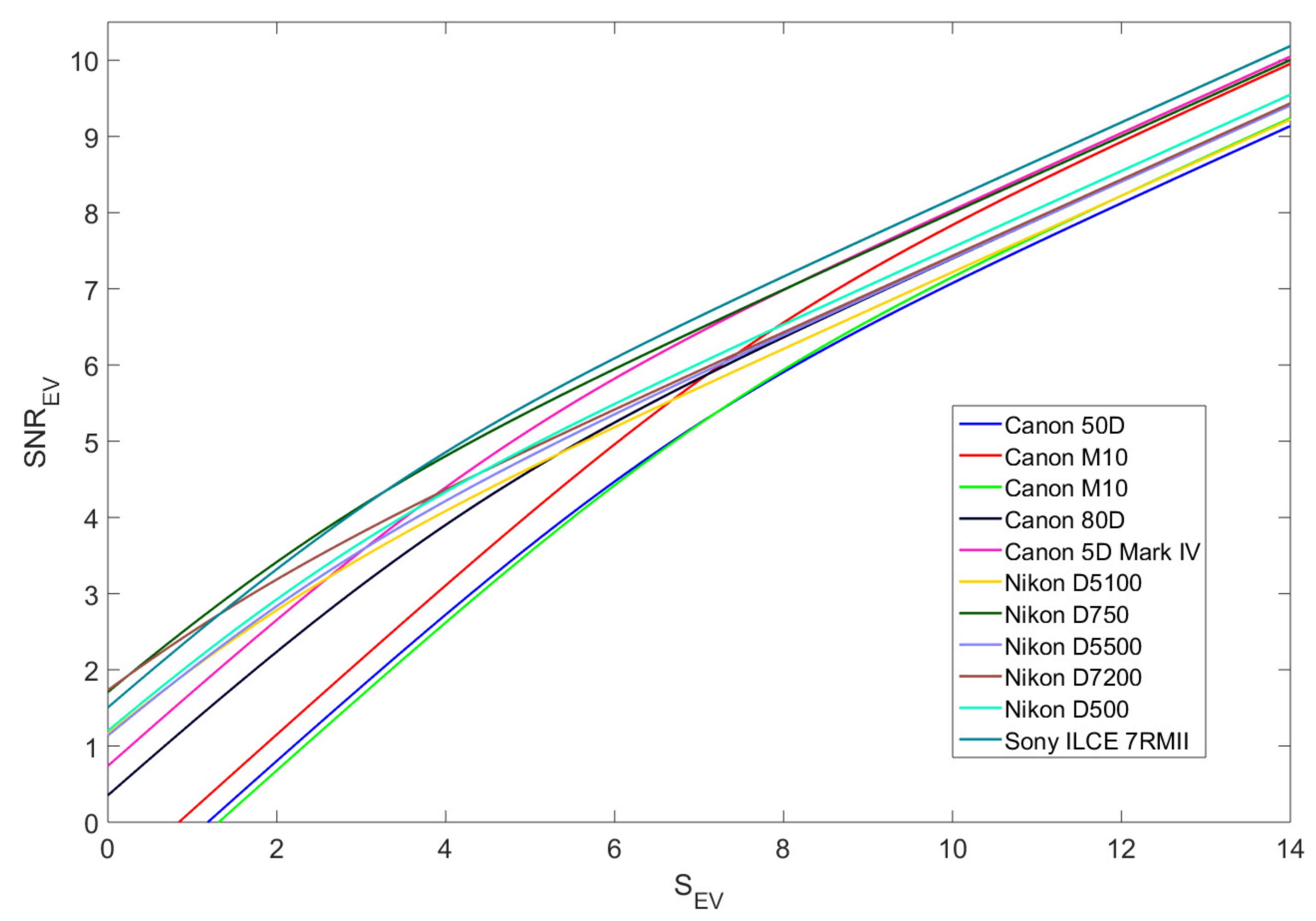
4.3. Comparative Performance Evaluation
4.3.1. Pixel Curves
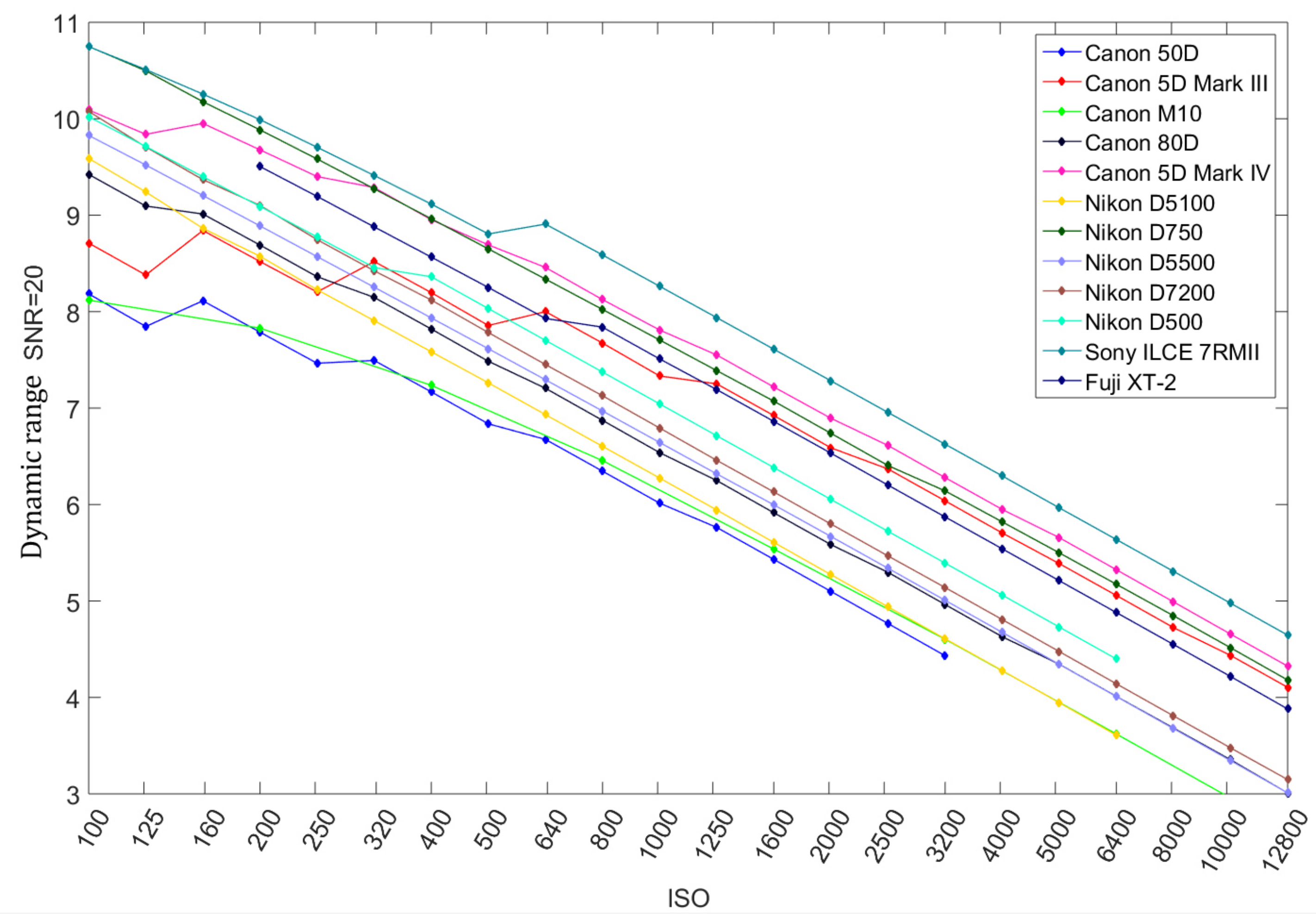
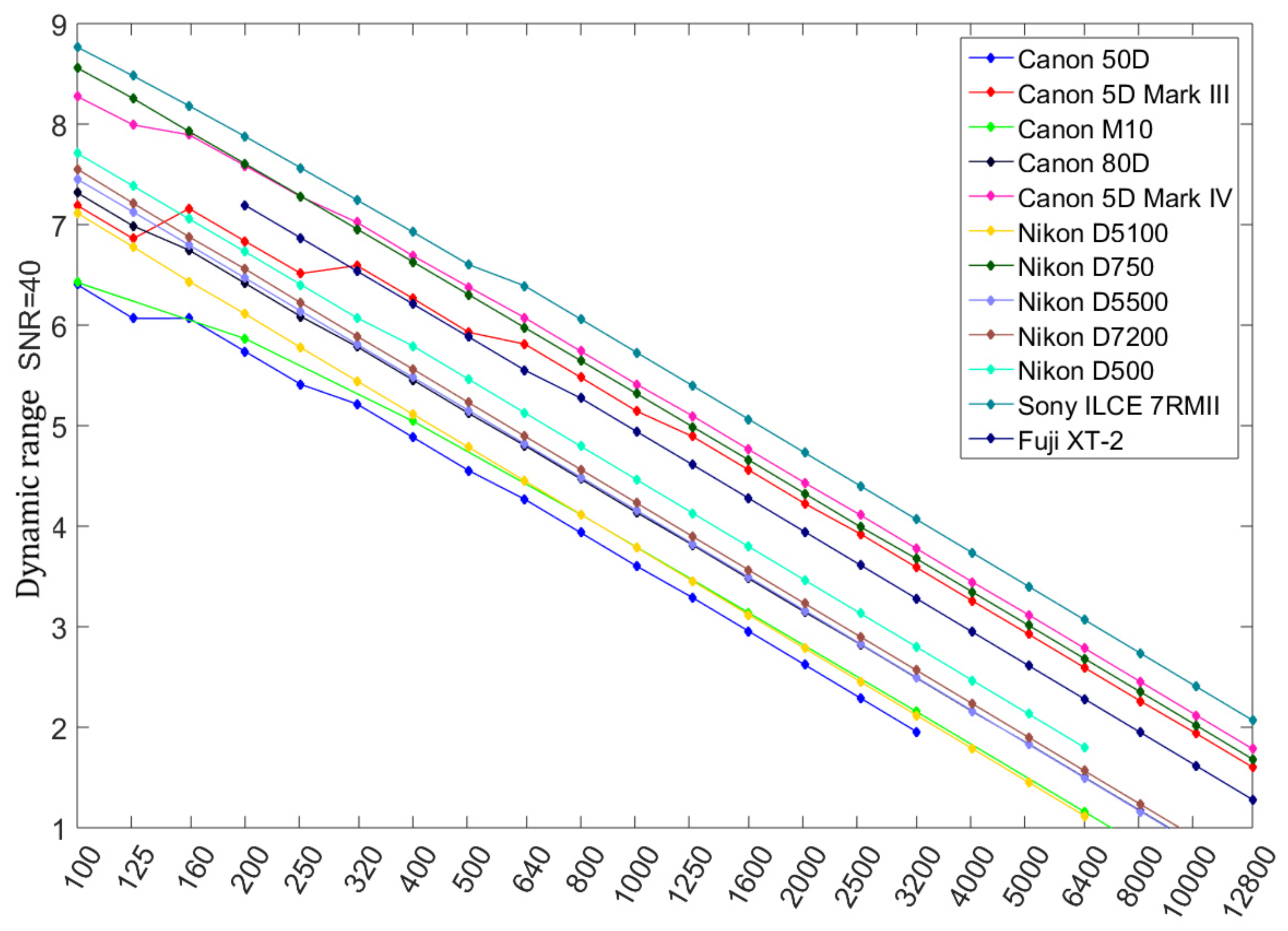
4.3.2. Pixel Dynamic Range
4.3.3. Photo Level Results
5. Discussion and Conclusions: How to Expose in Digital Photography
Funding
Acknowledgments
Conflicts of Interest
References
- Camera Imaging Products Association: Digital Cameras Report. Available online: http://cipa.jp/stats/dc_e.html (accessed on 1 September 2019).
- Gye, L. Picture This: the Impact of Mobile Camera Phones on Personal Photographic Practices. Continuum 2007, 21, 279–288. [Google Scholar] [CrossRef]
- Fontaine, R. The state of the art of smartphone imagers. In Proceedings of the International Image Sensor Conference, Snowbird, UT, USA, 23–27 June 2019; p. R6. Available online: https://www.imagesensors.org/PastWorkshops/2019Workshop/2019Papers/R01.pdf (accessed on 10 September 2019).
- Bhandari, A.; Raskar, R. Signal Processing for Time-of-Flight Imaging Sensors: An introduction to inverse problems in computational 3-D imaging. IEEE Signal Process. Mag. 2016, 33, 45–58. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, C.; Hao, P. New color filter arrays of high light sensitivity and high demosaicking performance. In Proceedings of the 2011 18th IEEE International Conference on Image Processing, Brussels, Belgium, 11–14 September 2011; pp. 3153–3156. [Google Scholar] [CrossRef]
- Chan, C.C.; Chen, H.H. Improving the Reliability of Phase Detection Autofocus. Electron. Imaging 2018, 2018, 241-1–241-5. [Google Scholar] [CrossRef]
- Kirkpatrick, K. The edge of Computational Photography. Commun. ACM 2019, 62, 14–16. [Google Scholar] [CrossRef]
- Koppal, S.J. A Survey of Computational Photography in the Small: Creating intelligent cameras for the next wave of miniature devices. IEEE Signal Process. Mag. 2016, 33, 16–22. [Google Scholar] [CrossRef]
- Knowledge Sourcing Intelligence LLP. CMOS Image Sensor Market: Forecasts from 2019 to 2024. Technical Report. May 2019. Available online: https://www.knowledge-sourcing.com/report/cmos-Image-sensor-market (accessed on 5 September 2019).
- Photonstophotos.net. Available online: http://photonstophotos.net (accessed on 3 September 2019).
- Dxomark. Available online: http://dxomark.com (accessed on 3 September 2019).
- Boukhayma, A.; Peizerat, A.; Enz, C. Temporal Readout Noise Analysis and Reduction Techniques for Low-Light CMOS Image Sensors. IEEE Trans. Electron Devices 2016, 63, 72–78. [Google Scholar] [CrossRef]
- Igual, J. Noise in CMOS Image Sensors: A Photographic Analysis of Noise Models in Consumer Cameras. Sensors 2019. submitted. [Google Scholar]
- Vargas-Sierra, S.; Liñán-Cembrano, G.; Rodríguez-Vázquez, Á. A 151 dB High Dynamic Range CMOS Image Sensor Chip Architecture With Tone Mapping Compression Embedded In-Pixel. IEEE Sens. J. 2015, 15, 180–195. [Google Scholar] [CrossRef]
- Photography—Electronic Still-Picture Imaging—Noise Measurements; International Organization for Standardization: Geneva, Switzerland, 2017.
- Photography—Digital Still Cameras—Determination of Exposure Index, ISO Speed Ratings, Standard Output Sensitivity, and Recommended Exposure Index; International Organization for Standardization: Geneva, Switzerland, 2019.
- Baer, R. ISO Sensitivity. In Proceedings of the IEEE 2005 ISSCC Circuit Design Forum: Characterization of Solid-State Image Sensors, San Francisco, CA, USA, 6–10 February 2005. [Google Scholar]
- Hassan, N.B.; Huang, Y.; Shou, Z.; Ghassemlooy, Z.; Sturniolo, A.; Zvanovec, S.; Luo, P.; Le-Minh, H. Impact of Camera Lens Aperture and the Light Source Size on Optical Camera Communications. In Proceedings of the 2018 11th International Symposium on Communication Systems, Networks Digital Signal Processing (CSNDSP), Budapest, Hungary, 18–20 July 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Hirsch, J.; Curcio, C.A. The spatial resolution capacity of human foveal retina. Vis. Res. 1989, 29, 1095–1101. [Google Scholar] [CrossRef]
- Deering, M.F. The limits of human vision. In Proceedings of the 2nd International Immersive Projection Technology Workshop, Ames, IA, USA, 11–12 May 1998; Volume 2. [Google Scholar]
- Janesick, J.R. Photon Transfer; SPIE Optical Engineering Press: Bellingham, WA, USA, 2007; p. 280. [Google Scholar]
- Xrite. ColorChecker Classic Chart. Available online: https://xritephoto.com/colorchecker-classic (accessed on 25 August 2019).
- Wang, F.; Theuwissen, A.J.P. Linearity analysis of a CMOS image sensor. Electron. Imaging 2017, 11, 84–90. [Google Scholar] [CrossRef]
- Wakashima, S.; Kusuhara, F.; Kuroda, R.; Sugawa, S. Analysis of pixel gain and linearity of CMOS image sensor using floating capacitor load readout operation. In Proceedings of the SPIE—The International Society for Optical Engineering, San Francisco, CA, USA, 20 March 2015; Volume 9403. [Google Scholar] [CrossRef]
- Wang, F.; Han, L.; Theuwissen, A.J.P. Development and Evaluation of a Highly Linear CMOS Image Sensor with a Digitally Assisted Linearity Calibration. IEEE J. Solid-State Circuits 2018, 53, 2970–2981. [Google Scholar] [CrossRef]








| Camera | Dimensions | Mp | Pixel Size | k |
|---|---|---|---|---|
| Canon 50D | 15.1 | 4.7 | 2.23 | |
| Canon 5DMIII | 22.3 | 6.3 | 4.83 | |
| Canon M10 | 18 | 4.3 | 2.17 | |
| Canon 80D | 24 | 3.7 | 2.03 | |
| Canon 5DMIV | 30.1 | 5.4 | 4.00 | |
| Nikon D5100 | 16.2 | 4.8 | 2.29 | |
| Nikon D750 | 24 | 6 | 4.69 | |
| Nikon D5500 | 24.2 | 3.9 | 1.97 | |
| Nikon D7200 | 24 | 3.9 | 2.05 | |
| Nikon D500 | 20.9 | 4.2 | 2.79 | |
| Sony 7RMII | 42 | 4.5 | 3.42 | |
| Fuji XT-2 | 24 | 3.9 | 1.69 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Igual, J. Photographic Noise Performance Measures Based on RAW Files Analysis of Consumer Cameras. Electronics 2019, 8, 1284. https://doi.org/10.3390/electronics8111284
Igual J. Photographic Noise Performance Measures Based on RAW Files Analysis of Consumer Cameras. Electronics. 2019; 8(11):1284. https://doi.org/10.3390/electronics8111284
Chicago/Turabian StyleIgual, Jorge. 2019. "Photographic Noise Performance Measures Based on RAW Files Analysis of Consumer Cameras" Electronics 8, no. 11: 1284. https://doi.org/10.3390/electronics8111284
APA StyleIgual, J. (2019). Photographic Noise Performance Measures Based on RAW Files Analysis of Consumer Cameras. Electronics, 8(11), 1284. https://doi.org/10.3390/electronics8111284





