Abstract
Gated integrating measurement method represents a widely used approach when fast, repetitive analogue signals are concerned. In this work a compact synchronized gated-integrator prototype has been realized and preliminary characterized. Front-end electronics is based on the mature high-precision switched-integrator transimpedance-amplifier IVC102 whose output is connected to a precision LT1991 inverting amplifier, whereas analogue-to-digital conversion, as well as timing control circuitry, are performed by a high-efficiency LPC845 microcontroller. Synchronizing signal detection with the external trigger generated in coincidence with a source, the proposed circuitry amplifies and integrates the signal only when the pulse is generated, displaying excellent performances in terms of linearity, sensitivity and signal-to-noise ratio. Hence, the proposed solution represents an affordable alternative to continuous-time regime measurement-techniques, usually adopted in radiation dosimetry where accuracy and sensitivity are strict requirements for treatment quality assurance.
1. Introduction
Gated integration represents an adequate approach for repetitive pulsed signal conditioning. In particular, a gated-integrator is able to synchronize signal detection to the external trigger generated in coincidence with a source having a repetition rate fR. In a typical application there is a need of measuring short time signals with the possibility to open the acquisition window just around the signal occurrence. Gated integrator instruments can reach gate widths as low as dozens of picoseconds and, therefore, are used to process fast analogue signals. Widely employed in X-ray particles physics [1], they may be useful also for clinical apparatus using strongly ionization radiation for cancer treatment, like linear accelerators (LINACs).
Usually, in order to guarantee adequate accuracy, the measurement method employed in X-ray or fast excimer laser intensity diagnostics are based on the integration of the detector signal in a continuous time regime [2]. Moreover, despite its intrinsic optimized performance, a synchronized gated-integrating measurement method has not yet been applied in radiation dosimetry where repetitive intense pulsed radiations are employed [3]. For example, a LINAC apparatus used in radiotherapy treatments generates X-ray pulses having a duration from a few to a few tens of microseconds, with a repetition rate up to a few hundreds of Hz. Figure 1 shows an example of signal generated by a LINAC (Clinac iX, Varian Medical Systems, Inc., Palo Alto, CA, USA): for each packet, the rising edge of the electron current impinging onto the heavy-metal target and generating the X-rays pulses, occurs 12 µs (TD) after the rising edge of synchronism signal and it is only 4 µs wide. For fast devices able to detect such X-ray sources [2,4], considering a typical maximum repetition rate of 360 Hz, a duty cycle as low as about 0.1% is found for the transduced current signal.
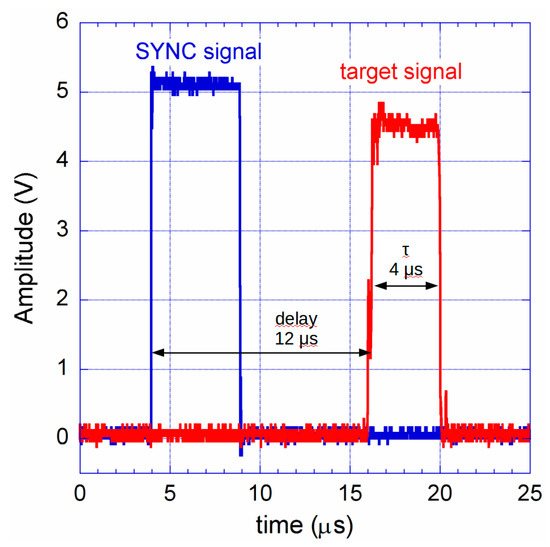
Figure 1.
Example of an electron pulse (red curve, 4 µs wide) generated by a LINAC apparatus and impinging onto a heavy metal target to produce an equivalent X-ray pulse. The blue curve shows the produced sync signal 12 µs before the target electrons’ current-pulse rising edge.
Electrometers used for dosimeter charge-signal acquisition integrate continuously in time, providing a measure of the absorbed dose with a relatively high number of impinging radiation pulses [5]. This operational procedure requires then periods of time where only noise signals, mainly sourced by electromagnetic interference (EMI) generated by the LINAC apparatus itself, are integrated, resulting in a non-optimized signal-to-noise ratio (SNR). Conversely, the synchronized-integration relies on the incoherent nature of noise to guarantee good performance in terms of SNR. Indeed, repeating measurements N times at fR frequency, the signal contribution increases of a factor N, whereas stationary random noise accumulates proportionally to √N. Hence, for a truly repetitive input signal, averaging N samples will improve the SNR by a √N quantity, also assuring good performances in terms of precision and sensitivity [6,7,8,9]. In addition, when repetitive narrow pulsed signals are concerned, synchronized integration can be performed in a time interval just around the pulse, nulling the integrated noise contribution in the “dead time” between two pulses, hence increasing the SNR in comparison to a continuous-time measurement approach.
It has to be observed that the evolution in the radiotherapy field has led to the development of sophisticated techniques (such as intensity modulated radiation therapy, IMRT, and stereotactic body radiation therapy [10,11]) that provides for the use of appropriately-shaped narrow beams and turned along different angles. For these advanced techniques, detectors, with an active volume lower than 1 mm3 are required as an alternative to the common ionization chambers used in clinical dosimetry. Hence, in this field accurate dose measurements are necessary for the quality assurance required in treatment planes definition. In such a field, diamond is considered one of the best candidates for the realization of highly sensitive, radiation hard detectors [12]. In addition, due to its tissue equivalence [13], diamond would find application for IMRT monitoring [14,15], as well as for the fabrication of microdosimeters [16]. Within these contexts, a gated integrator (GI) appears to be an appropriate solution to meet the requirements of narrow pulsed signal conditioning. In this work the characterization of a compact GI prototype is illustrated, emulating the noisy conditions found in a real environment. Front-end electronics of the circuit is based on the mature high precision charge integrator IVC102 which shows excellent performances for low-level signal conditioning [17,18,19,20]. To acquire either sourcing or sinking input currents, integrator output is then connected to a LT1991 gain-selectable amplifier. Integrating highly-matched and low-thermal coefficient resistors, as well as a low noise op-amp, the LT1991 represents a good solution for one-chip precision amplifier realization. Analogue-to-digital conversion, system control and external interface are performed by an LPC845 microcontroller equipped with an ARM Cortex-M0+ processor. The LPC845 assures high power efficiency, to be applied for smart and portable equipment fabrication. The high versatile state configurable timer (SCT) used for measurement timing control allows to tail measurement parameters for the particular input conditions. Furthermore, a method able to drastically reduce offset errors induced by detector bias current is also discussed and verified, as well as non-ideality of charge transfer during hold and reset integrator switched phases. The main added values of the proposed prototype are compactness and cost effectiveness compared to instruments and methodologies typically adopted, for example, in the mentioned clinical dosimetry of fast X-ray pulses.
2. Circuit Description
Front-End Electronics and Integration Cycle
Figure 2 shows the schematic of the proposed gated-integrator prototype. The front-end electronics is based on the IVC102 high-precision switched integrator transimpedance amplifier (by Texas Instruments Inc., Dallas, Texas, USA). IVC102 chip integrates three high quality metal/oxide capacitors characterized by low leakage, excellent dielectric characteristics (typical non-linearity of ±0.005%) and temperature stability (±25 ppm/°C). They can be connected to obtain an integration capacitance of 10 pF, 30 pF, 40 pF, 60 pF, 70 pF, 90 pF or 100 pF. IVC102 output has been coupled to a gain-selectable amplifier LT1991 (by Texas Instruments Inc., Dallas, Texas, USA) configured as inverting amplifier whose non-inverting input is biased properly in order to measure both sinking and sourcing currents. Indeed, the LT1991 internal highly-matched resistors are used to create a VDD/4 voltage at op-amp non-inverting input to obtain, at IVC102 reset, a VDD/2 output voltage, i.e., in the middle of the ADC-input dynamics. The LT1991 output voltage is digitally converted by the 12-bit successive approximation A/D converter integrated in the LPC845 microcontroller (by NXP Semiconductors, Eindhoven, The Netherlands).
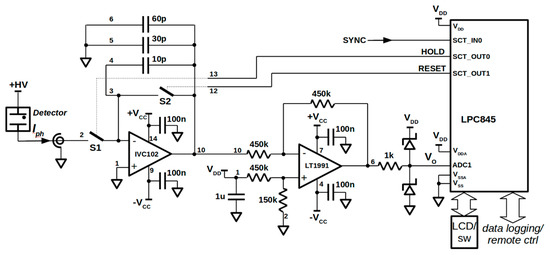
Figure 2.
Schematic of the proposed prototype. A microcontroller unit based on the LPC845 is dedicated to A/D conversion, as well as timing control and external interface.
A dual power supply voltage VCC = ±15 V was used for both the IVC102 and the LT1991 ICs, whereas the microcontroller unit, hence its internal ADC, is supplied at VDD = 3 V. Two Schottky diodes have been inserted to prevent any damage of the ADC input induced by voltages outside its VDD − VSS input dynamics. Figure 3 shows the realized prototype. The analogue front-end has been enclosed between two copper-clad boards connected to ground. An LPC845-BRK board was used for digital circuitry and the system was inserted in an aluminum box connected to line earth.
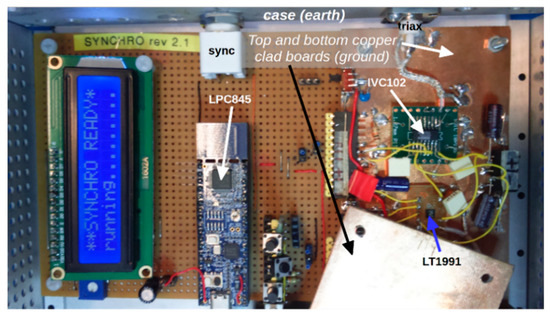
Figure 3.
Picture of the prototype used for circuit characterization. Analogue circuitry was enclosed between two copper boards connected to ground (upper board opened) and the circuit was installed in an aluminum box connected to line earth. A triaxial connector has been used for input signal.
In principle, an integration measurement cycle starts by resetting the IVC102 output to 0 V, by closing its internal switch S2. Hence, the integration begins by opening S2 and closing S1, so the charge is transferred to the selected integration capacitor (10 pF for the most sensitive range as chosen for the characterization described in this work. Unused internal capacitor pins have been connected to analogue ground). The SCT integrated in the LPC845 microcontroller has been used to generate the control signals for the internal IVC102 S1 and S2 MOS switches, HOLD and RESET signals, respectively. Figure 4 shows an example of the performed reset-integration-hold phases. At t1 the reset of integration feedback capacitor CINT is removed (RESET high) and integration starts after a while, at t2, closing S1 switch (HOLD low). Integration is maintained in the Ti = t3 − t2 time period: integrated charge is given by QINT = CINT VO expression, where VO is the voltage acquired by the ADC. Although VO of Figure 4a refers to IVC102 input left float, it has to be noted that Ti has been centred around the sync front edge at which the input signal is synchronized. VO amplitude is maintained opening S1 at t3, and an A/D conversion can be performed. Finally, S2 is closed at t4 and a new cycle can start. The diagram in Figure 4a highlights the effect induced by internal MOS switches commutations. In particular, due to charge transfer during MOS S1 commutations, two ∆VQ voltage steps of few mV, equal in amplitude but opposite in sign, are observed at the start and at the end of the integration period. Therefore, to zero any A/D conversion errors greatly reducing accuracy for low level signals, the charge integration result is measured as the voltage difference between the value VA acquired before (pre-hold phase) and the value VB acquired after the integration period (hold phase). It is worth to observe that when the IVC102 input is connected to a source (as the test fixture used for circuit characterization described in the following section), a charge transfer asymmetry is found, due to the unavoidable additional capacitance inserted at the integrator input. In this case, also the mentioned VB − VA differential measurement is not able to guarantee an adequate measurement accuracy. Figure 4b illustrates such an effect: for the adopted connection, the absolute value of voltage step when S1 is closed is greater than that when the switch is reopened. In such a case, the VB − VA quantity contains an unpredictable offset error related to the particular capacitance value of the cable/device connected at the integrator input.
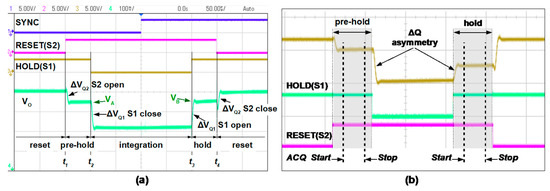
Figure 4.
(a) Signal acquisition is performed in two phases, “pre-hold” and “hold”, before and after the integration period; (b) charge transfer asymmetry observed when the sensor/cable is connected.
In commercially-available boxcar units [21] it is possible to perform a second acquisition with the same window length to suppress the noise baseline. In fact, a similar approach is also used for low level signals in CMOS image sensors. Such technique called CDS (correlated double sampling) removes the noise by differencing sampled values taken from the same pixel before and immediately after the measurement onto similar capacitances. Hence, in our case to cancel measurement error due to charge-transfer asymmetry, mostly affecting precision at the lowest input levels, for GI prototype signal acquisition has been doubled: one measurement is synchronized with the sync signal front-edge; a second acquisition is performed in the time interval between two pulses. The asymmetry of charge transferred during switch commutations is counterbalanced by calculating the result of the measurement as the difference between the voltage (VB − VA) acquired when the pulse is present and the differential voltage (VB0 − VA0) acquired during “zero-measurement” (pulse absent).
An SCT peripheral integrated into the LPC845 microcontroller allows advanced timing control operations with or without a small CPU intervention, as well as supporting user-defined events and states based on external signals or on match conditions. In our case the SCT was used as a 32-bit up-counter timer, with a clock frequency fCK of 30 MHz, to manage six events in order to generate the switches control signals synchronized to the input sync signal. A sketch of the timing diagram adopted for the GI prototype is reported in Figure 5. Event EV0 is generated when the rising edge of the sync signal arrives. At every occurrence of event EV0, SCT has been programmed to automatically capture into the Cap[0] register the timer-counter value and then resets the timer-counter register itself. At start-up (not shown in the figure), i.e., during the first cycle, SCT allows to have a precise measure (ideally within 33 ns at fCK = 30 MHz) of period T between two successive sync pulses, in our experiments fixed to about 2.778 ms (360 Hz of pulse repetition rate).
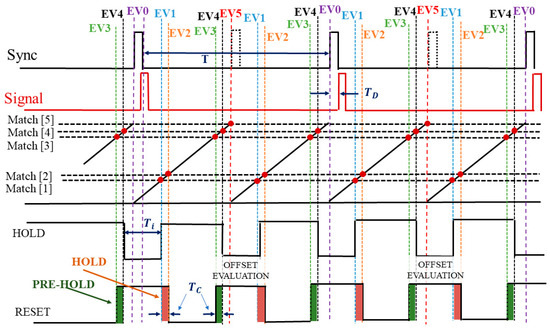
Figure 5.
Time diagram of SCT control signals for HOLD and RESET switches synchronized with sync pulses. Red dots represent a match (1..5) condition for timer counter generating a corresponding event (EV1..5).
Match[5] register is then loaded with the calculated T/2 value (around 1.389 ms) in order to add event EV5 used to perform the mentioned “zero-measurement” in the following cycles. EV5 also resets the timer counter. After such a start-up first cycle, in periodic regime, capture on EV0 represents a measure of a “new” T/2 value, whereas the overall time period T between two pulses is updated as the sum of previous Match[5] content and actual Cap[0] quantity. A new T/2 value is then calculated and stored in the Match[5] register to be used for the next cycle. The other four events (EV1–EV4) determine a symmetric integration time interval around the signal pulse and the microcontroller performs A/D conversions in the two pre-hold and hold periods.
Table 1 reports equations and match values, both in µs and SCT clock counts, generating EV1-EV5 events. Values are calculated for an integration time Ti = 100 µs, an ADC acquisition/processing time TC = 50 µs, a time delay between the pulse signal arrival and the sync front edge TD = 12 µs, and assuming for T the nominal 2777.8 µs value. Obviously, Match[1] and Match[2] values do not depend on the particular measured period, whereas Match[3], Match[4], and obviously Match[5] contents are a function of the actual T measurement.

Table 1.
Match values related to EV1-EV5 events calculated as a function of measurement parameters Ti, TD, and TC, and the measured T value (see text).
3. Circuit Characterization
3.1. Experimental Setup
Figure 6 illustrates the setup adopted for the GI prototype characterization. A test fixture has been realized to emulate the presence of a real detector generating repetitive current pulses 10 µs wide in the 1 nA–3 µA range (i.e., 10−14–3 × 10−11 C) immersed in a noisy environment. Additive white noise (at a bandwidth 10 MHz, amplitude greater than 10 mVPP), provided by an Agilent 33220A waveform generator, is superimposed to the pulsed signal via a 1 MΩ resistor. Both circuit prototype and test fixture have been enclosed in aluminum boxes connected to line–earth in order to reduce unintentional external EMI contributions. A Keithley 6221 AC/DC precision current source was used to generate controlled and repeatable charge packets. The GI integrator input sync was connected to the 6221 trigger out. For circuit characterizations, a square wave at 360 Hz with 0.36% of duty cycle has been used to source 10 µs wide current pulses.
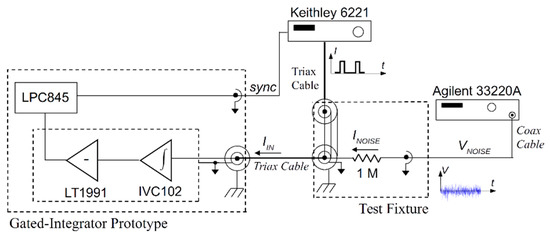
Figure 6.
Measurement setup adopted for the circuit prototype characterization. A real device connected at the integrator input has been emulated by a test fixture sourced by a precision AC-DC current generator (Keithley 6221) coupled to an Agilent 33220A waveform generator used to inject a controlled additional white noise current.
Figure 7a shows an example of generated repetitive current pulses. Signal has been acquired by an oscilloscope (Agilent, DSO-X 3024A) as the output voltage difference across a 3900 Ω resistor. Moreover, Figure 7b shows the resulting 1 µApp current pulse with the maximum addition of white noise signal in our test.
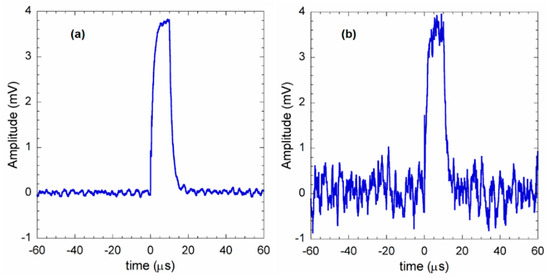
Figure 7.
(a) Example pulsed signals injected at GI prototype input here acquired as the voltage difference across a 3900 Ω resistor. (b) Same signal of (a) but with noise addition (SNR of about 20 dB).
A differential measurement method previously described allows to ideally counterbalance any error induced by offset originated by continuous bias current of a detector connected at the integrator input. Figure 8 illustrates the time diagram observed when injecting a 10 nA DC current superimposed to 1 µApp pulses. To highlight the effect, the integration period has been fixed to 1 ms. The slope of VO curves during the half period in which the pulse is absent is equal to that observed in presence of the pulse. Hence, according to the equation reported in the figure, signal conversion is not affected by any offset errors since (VB − VA) − (VB0 − VA0) amplitude only depends on the ΔV voltage step induced by input pulse.
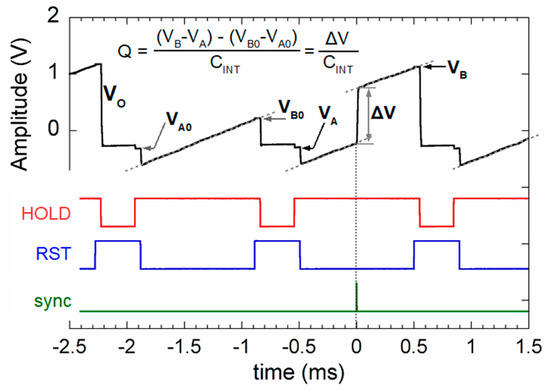
Figure 8.
Time diagram related to GI output VO for a 10 nA DC current superimposed to a 1 µApp, 10 µs wide, AC pulse. ΔV voltage step, related to the injected charge, can be correctly acquired by means of the implemented differential measurement method according to the reported equation.
3.2. Characterization Results
Gated integration, relying the incoherent nature of noise components, allows to increase the signal to noise ratio of a repetitive input signal. As pointed out in the introduction, a SNR increase as N1/2 would be obtained repeating signal integration and averaging N samples. By means of the setup indicated in the previous paragraph, a preliminary circuit characterization was performed to verify such a behaviour. A 100 nA constant current (sourced by Keithley 6221) was injected in the input. Note differential “zero-measurement”, which would have given null results, was disabled. White noise signal was added via an Agilent 33220A waveform generator set for a 50 mVpp amplitude. Figure 9 reports data of the performed characterization (Ti = 60 µs). In particular, for each N, SNR values have been estimated as the ratio between the mean value of ADC output and the observed standard deviation. Recorded values fairly reproduce the expected SNR ~ N1/2 (dotted line).
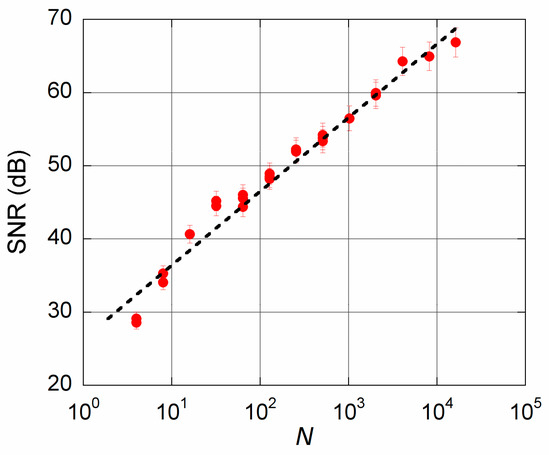
Figure 9.
SNR of ADC output values as a function of gated integrated samples. The dotted line represents the expected SNR ~ N1/2 behaviour.
Designed for pulsed signal conditioning, the circuit was then characterized injecting 10 µs-wide current pulses in the 1 nA–3 µA interval in order to generate charge packets in the range 0.01–30 pC. As indicated by data reported in Figure 10a, obtained as mean value of 512 pulses acquisition (N = 512) with an integration time period of 40 µs, the system shows excellent linearity over more than three decades of the impinged charge packets. In order to quantify the linearity error, we calculated the residuals between experimental ADC values and the linear fit straight line of data in Figure 10a. Figure 10b shows that the absolute value of the residuals is lower than 0.4%.
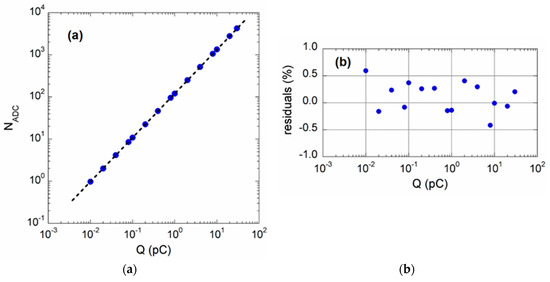
Figure 10.
(a) ADC output as a function of the charge packets injected by a precision current source (Keithley 6221). Each data point (blue dots) is obtained as the average of 512 successive pulses. The dotted line represents linear fit of experimental data. (b) The residuals were calculated by the difference of experimental ADC values and those calculated by linear best fit of data.
To demonstrate the effectiveness of the implemented measurements method, Figure 11 reports data obtained for input charge packets in the lowest range of tenths of pC without performing any measurement in the time period between two pulses (“zero-measurement” described in the previous paragraph). It is worth to mention that the non-linearity error is now greater than 5%, highlighting the effectiveness of the implemented differential acquisition method to null any offset contribution. It is pointed out here that compensation errors, such as the asymmetric MOS switch charge transfer, are induced by the unavoidable presence of a bias current.
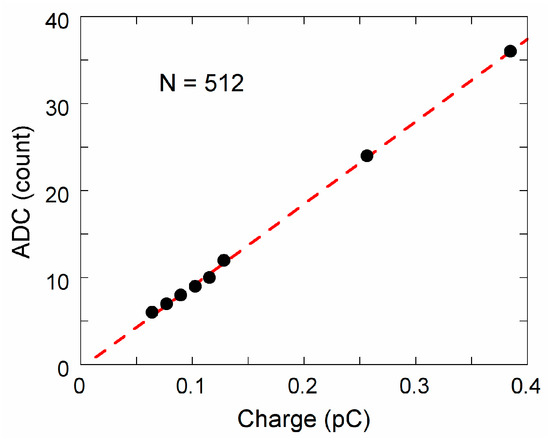
Figure 11.
The results obtained for ADC counts without performing the “zero measurement” in the range of tenths of pC. Each data point (black dots) is the average value of 512 input pulses. The dotted line represents linear best fit of experimental data. A non-linearity up to 5% is observed.
One key advantage of the realized GI prototype synchronized to a source is the possibility to reduce integration to a time period tailored on the input pulse width. Therefore, the method would guarantee good performance in SNR terms in comparison to the measurements usually performed in a continuous time regime. To verify how noise influenced the acquisitions in the realized prototype, we performed measurements as a function of integration time Ti for different noise amplitudes. In particular, 10 pC charge packets sourced by a Keithley 6221 generator (set to generate a square wave of 1 µApp amplitude, a frequency fR = 360 Hz, and a duty cycle of 0.36%) were injected into the GI input by means of the test fixture of Figure 6. During the measurements, the signal was kept constant, whereas the noise amplitude was increased from 3% to 50% of the peak signal, i.e., an SNR in the 20–50 dB range. Similarly, to what done for characterizations reported in Figure 10 and Figure 11, the microcontroller unit calculated the mean value of N = 512 successive input pulses, as well as the variance according to:
where qi represents the ith acquired charge pulse (in ADC counts). The acquisition of N samples was repeated 32 times in order to evaluate both q and σq2 dispersions (however displaying changes within the resolution of data reported in this work). The data in Figure 12 refer to the measured variance σq2 as a function of Ti between 40 µs and 1 ms. The results clearly display the expected linear behaviour of σq2 on the integration time period when white noise is concerned (see Appendix A) [6,22]. Moreover, as also expected, curves referring to different noise amplitudes are scaled as the power of input noise itself (as also indicated by Equation (6) reported in Appendix A). The experimental data clearly indicate that best results are gained at the lowest integration period, highlighting the effectiveness of synchronized gated-integration in drastically reducing the detrimental effect due to a noisy environment.
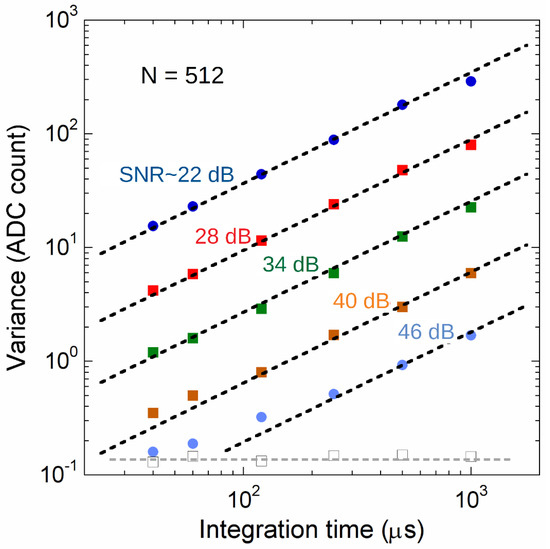
Figure 12.
Variance values as a function of the integration time period obtained for different white current noise amplitudes. A minimum constant value is observed (open squares) and related to the intrinsic system resolution.
To underline the good performance of the implemented system, we also compared the results acquired by the GI prototype to those furnished by a high-performance Keithley 6517A electrometer. Comparison has been performed with the same 10 pC input pulse repetitive signal used for data reported in Figure 12 and the results are summarized in Table 2. For the GI prototype, Ti was set to 40 µs. Error values were calculated as the difference between the maximum and the minimum of the recorded values during 30 s of observation and reported in the columns of Table 2 also as the percentage on the average quantity. The Keithley electrometer was set into current measurement mode. For each value of the injected noise, the relative measurement was enabled in order to null the contribution of the offset current induced by noise source (~1 nA). Compared to the expected 3.6 nA (1 µA × 0.36%) value, the electrometer displayed highly dispersive results on the average current, ranging from 3.61 nA to 3.70 nA, strongly dependent on the noise amount. The percentage error of the results, mostly within 1.4%, becomes 3.6% at the highest noise amplitude (SNR ~20 dB). Conversely, for the same input conditions, data acquired by the GI prototype were highly stable, with an average n value between 1345 and 1346. It is worth noting that such results correspond to an input charge pulse amplitude of:
where for CINT has been used the nominal 10 pF value, whereas the VDD measured 3.1 V. The reading error was significantly lower than that observed for the electrometer, spanning 0.09%–0.89%.
Q = N VDD CINT/212 = 10.18 pC

Table 2.
Noise performances of gated integrator circuit (Ti = 40 µs) and a Keithley 6517A electrometer for 10 pC, 10 µs wide, input charge pulses sourced by an AC/DC current source (Keithley 6221) injected by means of the test fixture illustrated in Section 2.
4. Concluding Remarks
By exploiting the excellent performances of commercially available components, a compact and high-precision gated integrator prototype has been realized and characterized. The system has been mainly thought for conditioning and acquisition of repetitive input pulsed signals in which a sync trigger is provided. In such a context, timing circuitry, based on versatile state configurable timer embedded into the microcontroller (also used for signal acquisition and processing) was designed to synchronize the integration period to the source sync signal, as well as to easily adapt measurements on the pulse width, assuring the highest SNR and sensitivity. In addition, by adopting a differential two phases acquisition standard procedure, measuring the signal also within the time period between two consecutive pulses, we greatly reduced the offset induced by unavoidable asymmetric charge transfer during MOS switch commutation induced by the particular value of detector/connection-cable capacitances, as well as offset errors due to bias currents.
Experimental results demonstrated excellent performance of the proposed circuit in terms of linearity in the 10 fC–30 pC range for 10 µs width by using an integration time period of 40 µs centred around each pulse. A non-linearity relative error lower than ±0.4% has been achieved over more than three order of magnitude. Circuit characterization has been also performed emulating a real noisy environment usually found when fast pulsed sources are involved. Compared to results provided by an unsynchronized precision current meter, as usually adopted for pulse signals acquisition, proposed GI prototype demonstrated excellent performance with data dispersed only within less than 1% when peak-to-peak noise is comparable to the input pulses amplitude. Furthermore, investigations of prototype performances have been compared between both industrial and specifically-designed laboratory research gated integrator systems in Table 3.

Table 3.
Comparison of performances of gated integrator systems found in scientific literature and commercial webpages (see references reported in the first column).
It has to be observed that commercially available systems are mainly developed for voltage inputs. Moreover, our prototype shows higher resolution when compared to the other current/charge input systems. Industrial systems designed for ultrafast-narrow input pulses provides the possibility of extremely low gate opening times, reaching repetition rates in the GHz regime. On the other hand, added values of the circuit proposed in this work are compactness, cost effectiveness and versatility and it would find application for pulsed sources diagnostics where adequate accuracy is required, as in X-rays dosimetry for radiotherapy. In such a context, work is currently in progress to evaluate the long-term stability and temperature dependence of the proposed circuit, as well as to test it in a real clinical environment.
Author Contributions
Conceptualization: S.P., M.G. and S.S.; data curation: S.P., A.O. and S.S.; investigation: S.P. and S.S.; software: S.S.; supervision: M.C.R.; validation: A.O., M.G., D.M.T., M.C.R. and S.S.; visualization: S.S.; writing—original draft: S.P., A.O., D.M.T. and S.S.; writing—review and editing: S.P., A.O., M.G., D.M.T., M.C.R. and S.S.
Funding
This research received no external funding.
Acknowledgments
The authors would like to thank Marco Pacilli, Fabrizio Imperiali and Gennaro Conte for technical support and for fruitful discussions.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Signal Variance vs. Integration Time
The signal acquired by the instrument is given by a combination of a current pulse (e.g., related to photons impinging the detector) and a time varying, zero mean, noise contribution. The latter can be expressed as the superposition of frequency dependent components whose amplitudes depend on the noise power spectral density. If white noise is concerned, each component at fi con be expressed by:
where is the constant power density in A2/Hz and is a random phase shift varying uniformly in the [0, 2π] interval. Being the phase shift at fi and fj (i ≠ j) uncorrelated, a mean value for the overall noise contribution is found. The signal is acquired by integrating in the time interval [0, τ], so that the net of the noise amplitude is expressed as:
with a mean value equal to zero and a variance calculated as the second moment of (τ):
Due to uncorrelated nature of the phase shift, previous equation can be calculated as:
The mean value is calculated as the average for varying in the interval [0, 2π]:
which, rewritten in the integral form for , gives:
Equation (6) demonstrates that the variance of signal induced by white noise is proportional to the integration time , as well as to the noise power density.
References
- Hertlein, M.P.; Scholl, A.; Cordones, A.A.; Lee, J.H.; Engelhorn, K.; Glover, T.E.; Barbrel, B.; Sun, C.; Steier, C.; Portmann, G.; et al. X-rays only when you want them: Optimized pump–probe experiments using pseudo-single-bunch operation. J. Synchrotron Radiat. 2015, 22, 729–735. [Google Scholar] [CrossRef] [PubMed]
- Girolami, M.; Allegrini, P.; Conte, G.; Trucchi, D.M.; Ralchenko, V.G.; Salvatori, S. Diamond detectors for UV and X-ray source imaging. IEEE Electron Device Lett. 2011, 33, 224–226. [Google Scholar] [CrossRef]
- Podgorsak, E.B. Radiation Oncology Physics; Int. At. Energy Agency: Vienna, Austria, 2005; pp. 123–271. ISBN 9201073046. [Google Scholar]
- Salvatori, S.; Rossi, M.C.; Galluzzi, F. Dynamic performance of UV photodetectors based on polycrystalline diamond. IEEE Trans. Electron Devices 2000, 47, 1334–1340. [Google Scholar] [CrossRef]
- Khan, F.M.; Gibbons, J.P. Khan’s the Physics of Radiation Therapy; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2014. [Google Scholar]
- Collier, J.L.; Goddard, B.J.; Goode, D.C.; Marka, S.; Telle, H.H. A low-cost gated integrator boxcar averager. Meas. Sci. Technol. 1996, 7, 1204. [Google Scholar] [CrossRef]
- Reichert, J.; Townsend, J. Gated Integrator for Repetitive Signals. Rev. Sci. Instrum. 1964, 35, 1692–1697. [Google Scholar] [CrossRef]
- Weng, X. Ultrafast, high precision gated integrator. In AIP Conference Proceedings; AIP: New York, NY, USA, 1995; Volume 333, pp. 260–266. [Google Scholar]
- Shenoy, R.K.; Ramakrishna, J.; Jeffrey, K.R. A simple and inexpensive two channel boxcar integrator. Pramana 1979, 13, 1–7. [Google Scholar] [CrossRef]
- Brugmans, M.J.P.; van der Horst, A.; Lebesque, J.V.; Mijnheer, B.J. Beam intensity modulation to reduce the field sizes for conformal irradiation of lung tumors: A dosimetric study. Int. J. Radiat. Oncol. Biol. Phys. 1999, 43, 893–904. [Google Scholar] [CrossRef]
- De Jaeger, K.; Hoogeman, M.S.; Engelsman, M.; Seppenwoolde, Y.; Damen, E.M.; Mijnheer, B.J.; Boersma, L.J.; Lebesque, J.V. Incorporating an improved dose-calculation algorithm in conformal radiotherapy of lung cancer: Re-evaluation of dose in normal lung tissue. Radiother. Oncol. 2003, 69, 1–10. [Google Scholar] [CrossRef]
- Trucchi, D.M.; Allegrini, P.; Bellucci, A.; Calvani, P.; Galbiati, A.; Girolami, M. Resistant and sensitive single-crystal diamond dosimeters for ionizing radiation. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2013, 718, 373–375. [Google Scholar] [CrossRef]
- Gorka, B.; Nilsson, B.; Svensson, R.; Brahme, A.; Ascarelli, P.; Trucchi, D.M.; Conte, G.; Kalish, R. Design and characterization of a tissue-equivalent CVD-diamond detector for clinical dosimetry in high-energy photon beams. Phys. Medica 2008, 24, 159–168. [Google Scholar] [CrossRef]
- Almaviva, S.; Ciancaglioni, I.; Consorti, R.; De Notaristefani, F.; Manfredotti, C.; Marinelli, M.; Milani, E.; Petrucci, A.; Prestopino, G.; Verona, C.; et al. Synthetic single crystal diamond dosimeters for Intensity Modulated Radiation Therapy applications. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2009, 608, 191–194. [Google Scholar] [CrossRef]
- Tromson, D.; Rebisz-Pomorska, M.; Tranchant, N.; Isambert, A.; Moignau, F.; Moussier, A.; Marczewska, B.; Bergonzo, P. Single crystal CVD diamond detector for high resolution dose measurement for IMRT and novel radiation therapy needs. Diam. Relat. Mater. 2010, 19, 1012–1016. [Google Scholar] [CrossRef]
- Zahradnik, I.A.; Pomorski, M.T.; De Marzi, L.; Tromson, D.; Barberet, P.; Skukan, N.; Bergonzo, P.; Devès, G.; Herault, J.; Kada, W.; et al. scCVD Diamond Membrane based Microdosimeter for Hadron Therapy. Phys. Status Solidi. 2018, 215, 1800383. [Google Scholar] [CrossRef]
- Salvatori, S.; Masarone, N.; di Nucci, G.; Conte, G. Compact front-end electronics for low-level current sensor measurements. Electron. Lett. 2006, 42, 682–684. [Google Scholar] [CrossRef]
- Salvatori, S.; Conte, G. Precision integrator sparks current-ratio-to-frequency converter. EDN 2007, 52, 110–114. Available online: https://www.edn.com/design/analog/4314711/Precision-integrator-sparks-current-ratio-to-frequency-converter (accessed on 27 October 2019).
- Salvatori, S.; Conte, G. Integrator enables simple ohmmeter with gigohm range. EDN 2007, 52, 104–108. Available online: https://www.edn.com/design/analog/4315271/Integrator-enables-simple-ohmmeter-with-gigohm-range (accessed on 27 October 2019).
- D’Antonio, E.; Salvatori, S.; Oliva, P.; Patanè, F.; Girolami, M.; Trucchi, D.M. High Precision Integrator for CVD-Diamond Detectors for Dosimetric Applications. In Proceedings of the 2018 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Rome, Italy, 11–13 June 2018; pp. 1–6. [Google Scholar]
- See for Example UHF-BOX Boxcar Averager; Zurich Instruments AG: Zurich, Switzerland; Available online: https://www.zhinst.com/products/uhfli/uhf-box# (accessed on 27 October 2019).
- McDowell, E.J.; Cui, X.; Yaqoob, Z.; Yang, C. A generalized noise variance analysis model and its application to the characterization of 1/f noise. Opt. Express 2007, 15, 3833–3848. [Google Scholar] [CrossRef] [PubMed]
- Leontein, S.; Westlin, E. Destructive Beam Profile Monitor Electronics Using Gated Current Integrators. In Proceedings of the 6th European Particle Accelerator Conference, Stockholm, Sweden, 22–26 June 1998; p. e-proc. 1550. [Google Scholar]
- Gated Integrator GA100; Artifex Engineering GmbH & Co KG.: Emdem Germany; Available online: https://www.artifex-engineering.com/index.php/en/instruments-2/gated-integrating-amplifiers/gia100 (accessed on 27 October 2019).
- SR250 Gated Integrator; Stanford Research Systems: Sunnyvale, CA, USA; Available online: https://www.thinksrs.com/ products/sr250.html (accessed on 27 October 2019).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).