Measurement of the PMSM Shaft Position with An Absolute Encoder

Abstract

The most critical aspect of assessing a permanent magnet synchronous motor is the problem of correctly measuring the position of the synchronous motor shaft. The purpose of this article was to show the effects of employing an absolute encoder to control a synchronous motor with permanent magnets while encountering disturbances. This problem is often overlooked, but it appears from time to time. The correct measurement of the shaft position eliminates improper motor operation characterized by jerking. The article showed that despite momentary erroneous readings of the shaft’s position, it was still possible to control the permanent magnet synchronous motor (PMSM). This also allows for correct measurement of the motor speed. This paper originally proposed an adaptive correction method for a rotary encoder.

1. Introduction

Recent advances in car design have been driven, in part, by the dynamic development of electric drives. The most promising advance in this respect seems to be the permanent magnet synchronous motor (PMSM) due to its low weight, small size, high efficiency, and high torque. Electric motors with permanent magnets NdFeB [1] simplify the motor structure. The motor stator is usually similar to the stator of induction motors and the rotor contains permanent magnets. The magnets and the armature winding are positioned so that the electromotive force (EMF) generated as a result of rotation is sinusoidal. A characteristic feature of PMSM motors is a wide range of speed control [1,2,3]. Permanent magnet motors lack commutators, so the weight of the drive design is significantly transferred toward the electronic control of the electric motor. Motors with permanent magnets demonstrate high efficiency, high torque, and low weight, all of which are highly important for vehicle design.

In order to obtain a smooth regulation of the rotational speed of the drive system with a PMSM, the angle of the motor shaft must be measured correctly. Errors in the measurement of the shaft angle cause unstable operation of the motor, jerking, or excessive current consumption, which can even damage the PMSM. Therefore, it is very important that the position measured by the encoder is correct. Unfortunately, the encoder works in conditions of strong interference, which means the central unit must check and correct the measured position by the encoder at all times. This allows for smooth speed control and stable operation of the PMSM. Detection of information loss error for the incremental encoder was presented in [4]. There are also methods of sensor less control of the PMSM, but due to the high precision of the control, the article focused on the control system using an absolute encoder [5,6]. In conventional position sensorless permanent magnet (PM) machine drives, the rotor position is obtained from the phase-locked loop (PLL) with the regulation of spatial signal in estimated back electromotive force (EMF) voltages. Due to the sinusoidal distribution of back-EMF voltages, a small-signal approximation is assumed in the PLL in order to estimate the position [7,8,9,10,11]. In the sensorless control method, the stator current is measured to estimate the speed of the motor. When the PMSM sensorless control is used in an electric vehicle, it sometimes causes another problem. When the motor is running in steady state and is suddenly given a large load that has reverse torque direction, a problem will arise [12,13,14]. Therefore, an original method was proposed that obtained good results when the PMSM is operating in such adverse conditions.

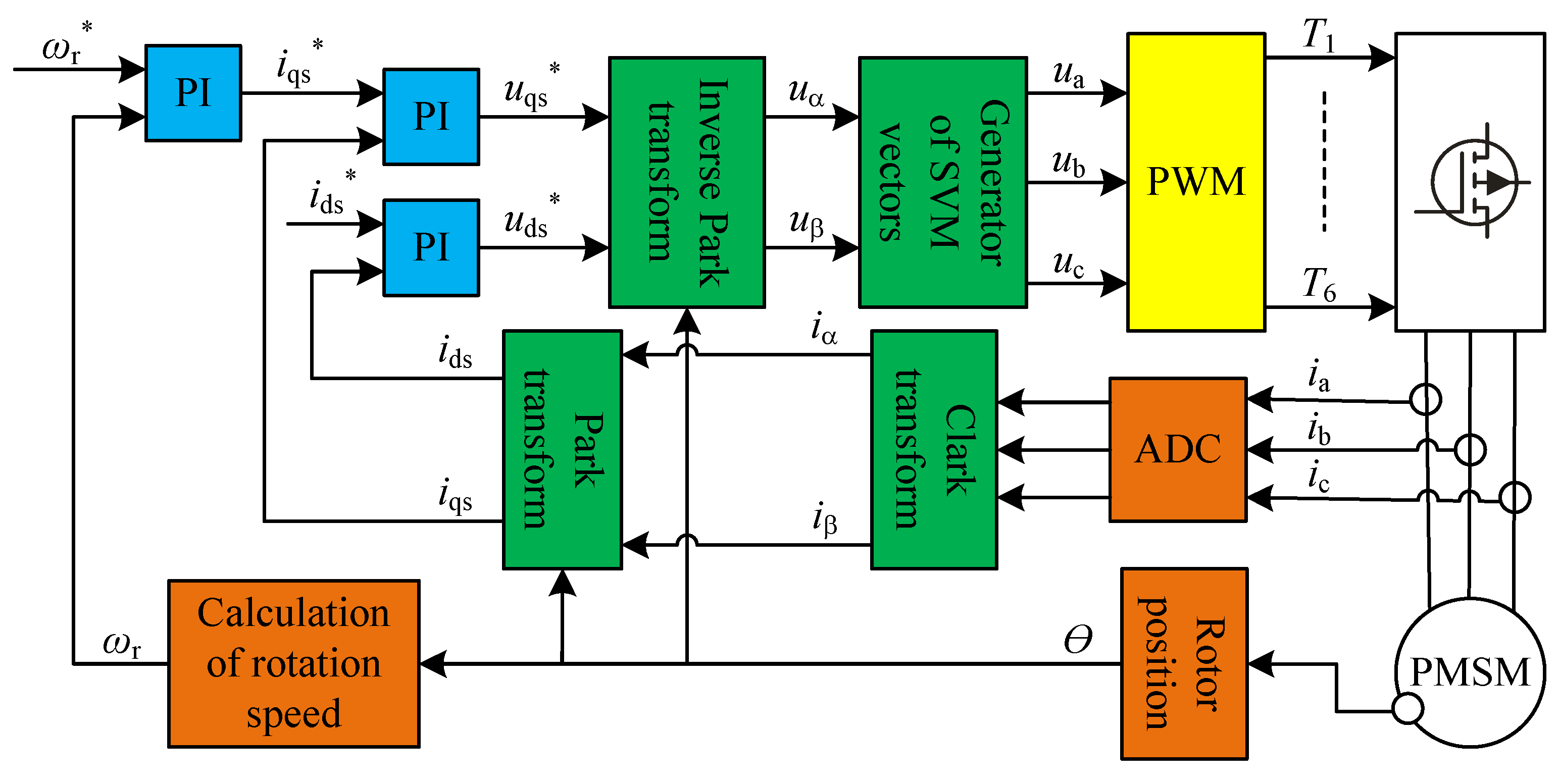
2. Control Unit for PMSM

One of the typical PMSM motor control systems is field oriented control (FOC), the idea of which is presented in Figure 1 [15].

In order to enable fast calculations, the control was performed in a dq-axis rotating system. Two transforms were carried out. First, a three-phase stationary system was converted into a stationary two-axis reference frame. The second transform consisted in the rotation of the foregoing two-axis reference system. Those transforms, respectively referred to as Clarke and Park transforms, enabled substitution of three analog converter (AC) parameters by two digital converter (DC) parameters. As a result, calculations for these two DC signals were much simpler and enabled the subsequent inverse transform to recover the actual three-phase AC results. The signal path (d) refers to magnetic flux, while the signal path (q) is related to torque.

The importance of the feedback for PMSM control provides the current, voltage, and angle of rotation. With appropriate scaling of the signals (i_a, i_b, and i_c) in the analog-to-digital converter (ADC), a Clarke transformation with rotating coordinate system (d, q) was performed to generate the two-phase system (i_a, i_b). As a result of these calculations, currents (i_ds, i_qs) were obtained. In the next step, the currents (i_ds, i_qs) and (i_ds*, i_qs*) were served on proportional integral (PI) controllers that set new values of the voltages (u_qs*, u_ds*). Values of these voltages were subjected to the inverse Park transform (using the information on the rotor position θ), which produced a voltage (u_α, u_β). Based on this, the voltages (u_a, u_b, u_c) were generated. The respective rectangular waveforms for controlling the power transistors T₁–T₆ of the inverter were produced by the pulse width modulation (PWM) block. The θ was position angle of the rotor [16,17,18]. The power unit produced a voltage three-phase inverter with an amplitude and offset [19,20]. The equations for Clarke and Park transformations are presented in Equation (1) and Equation (2), respectively:

$$\left[\begin{array}{c}{i}_{\mathsf{\alpha }}\\ i_{\mathsf{\beta }}\end{array}\right]=\left[\begin{array}{ccc}1& -\frac{1}{2}& -\frac{1}{2}\\ 0& \frac{\sqrt{3}}{2}& -\frac{\sqrt{3}}{2}\end{array}\right]\left[\begin{array}{c}{i}_{\mathrm{a}}\\ i_{\mathrm{b}}\\ i_{\mathrm{c}}\end{array}\right]$$

(1)

$$\left[\begin{array}{c}{i}_{\mathrm{sd}}\\ i_{\mathrm{sq}}\end{array}\right]=\left[\begin{array}{cc}\cos \left(\Theta \right)& \sin \left(\Theta \right)\\ -\sin \left(\Theta \right)& \cos \left(\Theta \right)\end{array}\right]\left[\begin{array}{c}{i}_{\mathsf{\alpha }}\\ i_{\mathsf{\beta }}\end{array}\right]$$

(2)

The equations for inverse Clarke transformation are presented in Equation (3):

$$\left[\begin{array}{c}{u}_{\mathsf{\alpha }}\\ u_{\mathsf{\beta }}\end{array}\right]=\left[\begin{array}{cc}\cos \left(\Theta \right)& -\sin \left(\Theta \right)\\ \sin \left(\Theta \right)& \cos \left(\Theta \right)\end{array}\right]\left[\begin{array}{c}{u}_{\mathrm{ds}}\\ u_{\mathrm{qs}}\end{array}\right]$$

(3)

The transform from the stationary αβ-axis frame to the stationary three-axis, three-phase reference frame of the stator is presented in Equation (4):

$$\left[\begin{array}{c}{u}_{\mathrm{a}}\\ u_{\mathrm{b}}\\ u_{\mathrm{c}}\end{array}\right]=\left[\begin{array}{cc}1& 0\\ -\frac{1}{2}& \frac{\sqrt{3}}{2}\\ -\frac{1}{2}& -\frac{\sqrt{3}}{2}\end{array}\right]\left[\begin{array}{c}{u}_{\mathsf{\alpha }}\\ u_{\mathsf{\beta }}\end{array}\right]$$

(4)

Requirements for the central unit:

• Performing complex mathematical calculations;
• high computing performance;
• appropriate hardware resources, e.g., input/output (I/O) ports, counters, PWM modulator, ADC, serial bus;
• dedication to control three-phase motors.

One of the systems that meets these requirements is the TMS320F2812 signal processor. This processor is a dedicated system for controlling three-phase motors [21].

The MAB28 (Megatron, Munich, Germany) absolute encoder was used for experimental research, which has the following properties:

• Small dimensions;
• 12-bit resolution;
• +5 V supply voltage;
• electrically erasable programmable read-only memory (EEPROM);
• serial bus.

Figure 2 shows how to connect the MAB28 encoder to the TMS320F2812 signal processor [22].

The motor speed measurement consists of:

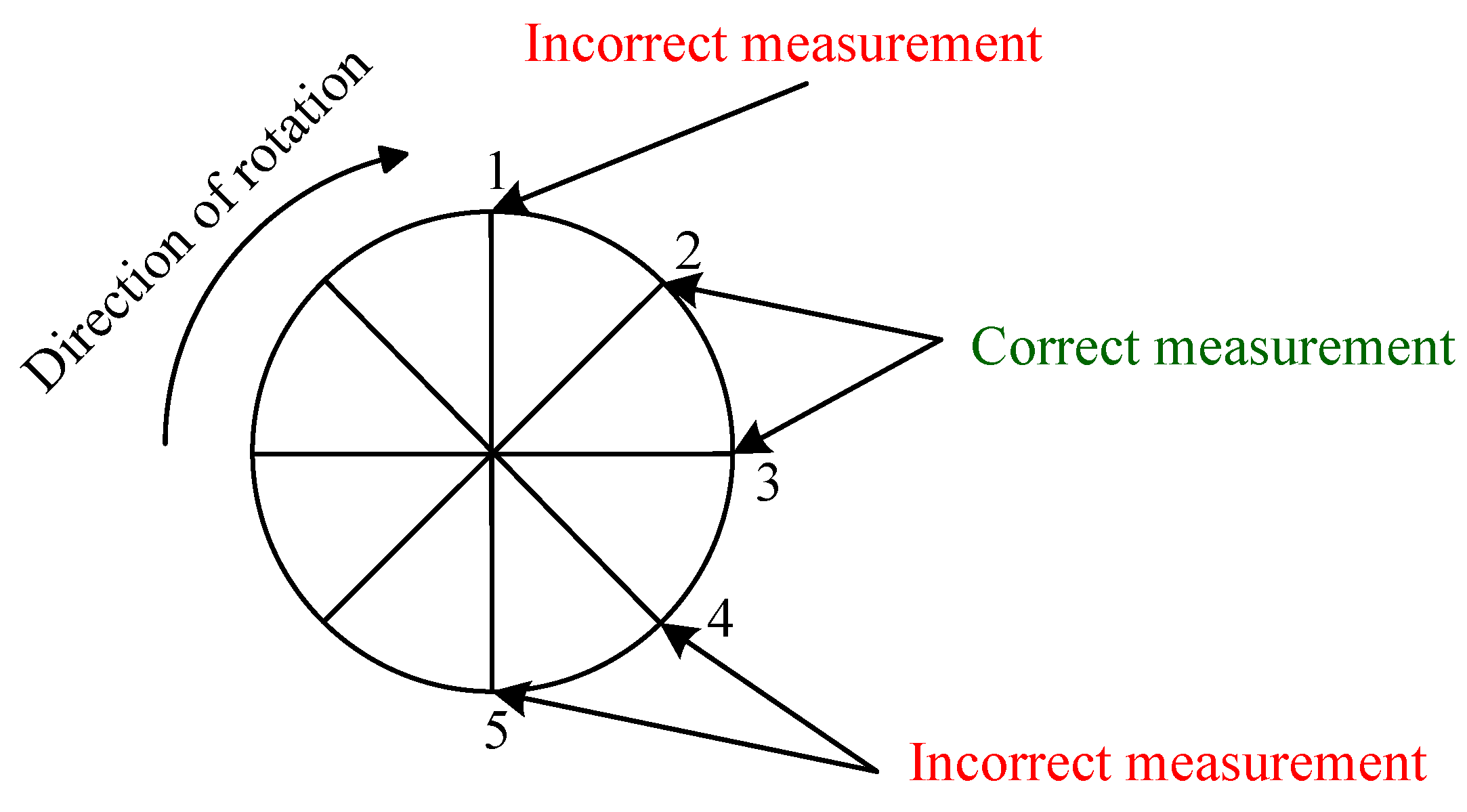
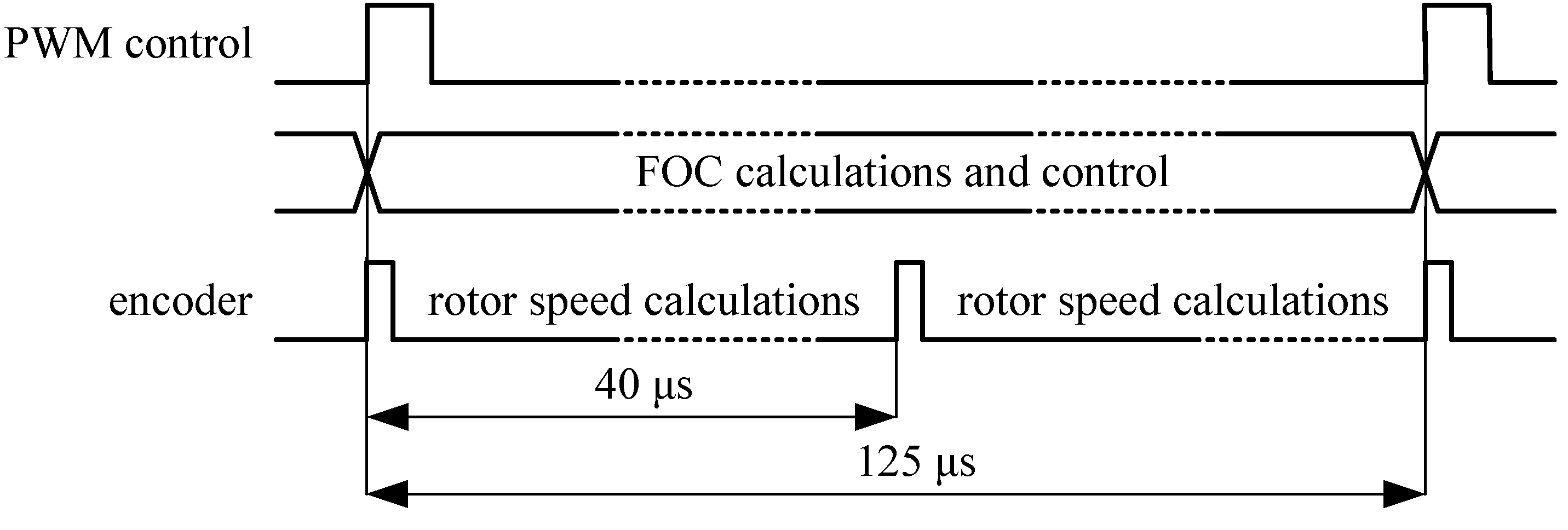
• Reading in the fixed time interval t_rpm of two motor shaft positions (position₁, position₂);
• calculation of the obtained geometric angle increment in time unit per rotational speed.

The calculation of the rotational speed ω_rpm (in revolutions per minute) was based on the equation (Equation (5)):

$${\omega }_{\mathrm{rpm}}=\frac{positio{n}_1-positio{n}_2}{2^{12}}\cdot \frac{60}{t_{\mathrm{rpm}}}$$

(5)

Division by 2¹² (4096) was required because the MAB28 encoder has 12-bit resolution. The position₁ and position₂ took values from 0 to 4095.

The shield of the cable from the signal processor side was connected to the digital ground, while the shield from the encoder side was connected to the metal enclosure of the encoder. The encoder housing was also connected to the metal enclosure of the PMSM. The author's experience shows that if there is no connection between the metal enclosure of the encoder and the digital ground, the number of incorrect encoder readings increases rapidly. Connecting the encoder with a shielded cable reduced the frequency of incorrect readings of the encoder position, but did not completely eliminate them. The incorrect operation of the encoder is shown in Figure 3.

The measurements with numbers 1, 4, and 5 were incorrect, while measurements with numbers 2 and 3 were correct. The incorrect measurement of the shaft position results in miscalculation of the shaft position angle. This, in turn, causes motor malfunction manifested by a temporary increase in current consumption by the motor and adversely impacts motor performance. The complete elimination of erroneous readings of the encoder position can take place on the program path. Equation (6) shows how to calculate the shaft position angle Θ for a 12-bit MAB28 encoder:

$$\Theta =\frac{position}{2^{12}}\cdot 360$$

(6)

The programmed elimination of erroneous readings of the encoder position should be adapted to the maximum motor speed. Suppose that the motor has a maximum speed of ω_max = 3000 rpm. Thus, the time of one turn was obtained by Equation (7):

$$t_{\mathrm{rpm}}=\frac{60}{{\omega }_{\max }}=20ms$$

(7)

The motor was controlled by the PWM with the frequency of 8 kHz, so the interruption from the PWM module was made every t_PWM = 125 µs. Therefore, information about the angle of the shaft position can be taken at t_enc = 40 µs (Figure 4).

The number of measurements of the angle of the shaft position for the maximum speed ω_max = 3000 rpm was calculated by Equation (8):

$$n{o}_{\mathsf{\Theta }}=\frac{t_{\mathrm{rpm}}}{t_{\mathrm{enc}}}=500$$

(8)

or, for the maximum speed of the motor and the encoder reading at t_enc = 40 µs, the increment of the shaft position angle by Equation (9) was obtained:

$$\mathsf{\Delta }\mathsf{\Theta }=\frac{t_{\mathrm{enc}}}{t_{\mathrm{rpm}}}\cdot 360=0.72°$$

(9)

In the case of a 12-bit encoder and an angle change of ΔΘ = 0.72°, the increment of the encoder value by Equation (10) was obtained:

$$\mathsf{\Delta }position=\frac{2^{12}\cdot \mathsf{\Delta }\mathsf{\Theta }}{360}=8$$

(10)

Equation (9) can be determined for the correct measurement of the angle of the motor shaft position. The current position of the encoder (position_i) reading was correct when:

$$\mathsf{\Delta }position=\left|positio{n}_{\mathrm{i}}-positio{n}_{\mathrm{i}-1}\right|\le 8$$

(11)

The time t_rpm changes as the speed changes, so a different angle ΔΘ increase was obtained. Calculating the correct position of the encoder in the event of an erroneous reading is a serious problem. An algorithm was proposed in which the increment of the encoder value (Δposition_new) is calculated on an ongoing basis, and the information on the previous increment of the encoder value (Δposition_old) is additionally stored. If the “new” increment of the encoder value does not satisfy the Equation (11), then the correct value of the encoder position needs to be determined. This can be calculated from Equation (12):

$$positio{n}_{\mathrm{i}}=positio{n}_{\mathrm{i}-1}+\mathsf{\Delta }positio{n}_{\mathrm{old}}$$

(12)

The new increment of the encoder position is:

$$\mathsf{\Delta }positio{n}_{\mathrm{new}}=\mathsf{\Delta }positio{n}_{\mathrm{old}}$$

(13)

The digital signal processor (DSP) calculates the PMSM speed and calculates how much the encoder position should change using Equations (7)–(11). If the encoder gives the wrong position, Equation (11) is not correct. Then, the correct encoder position is determined from the Equation (12).

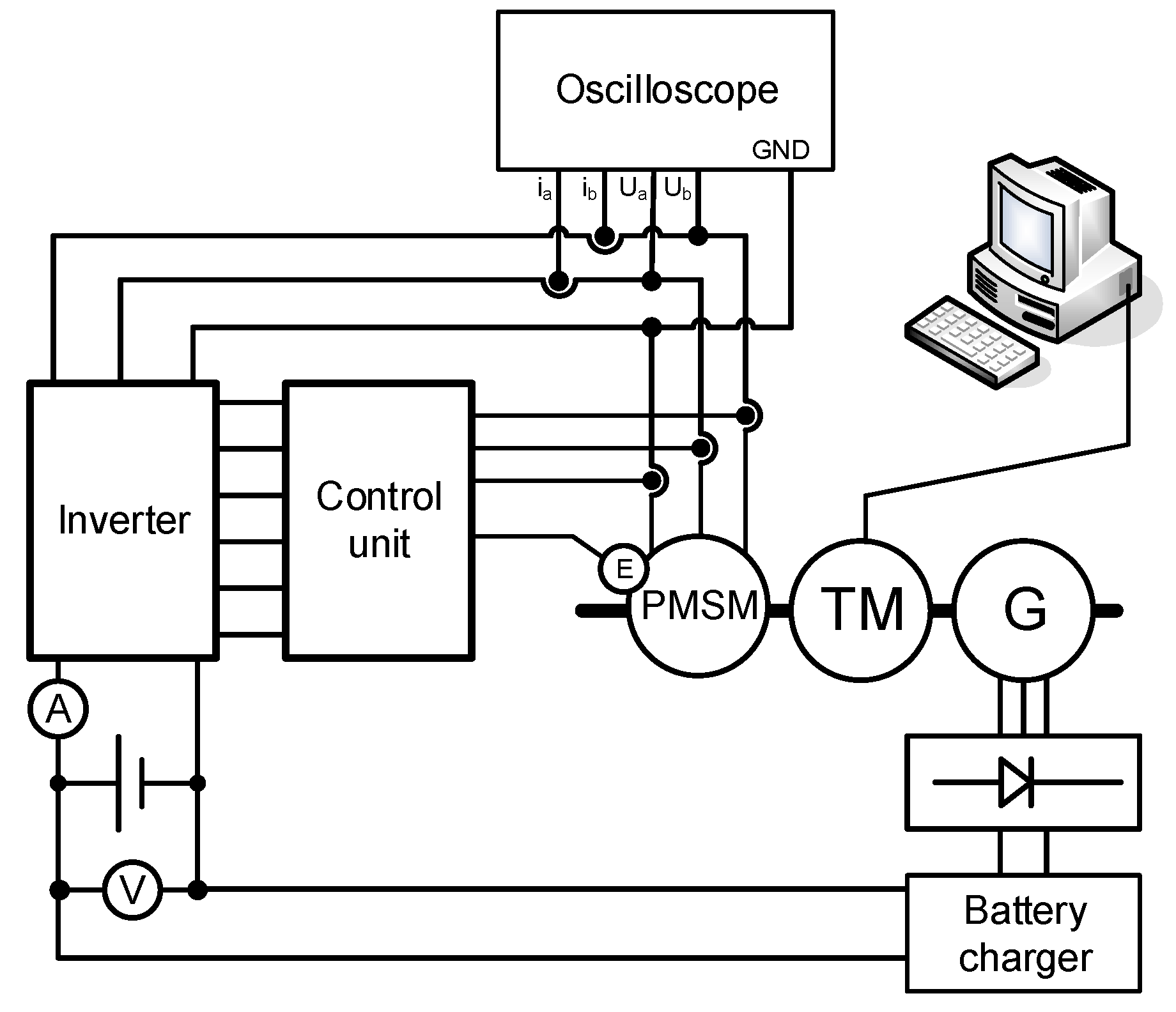
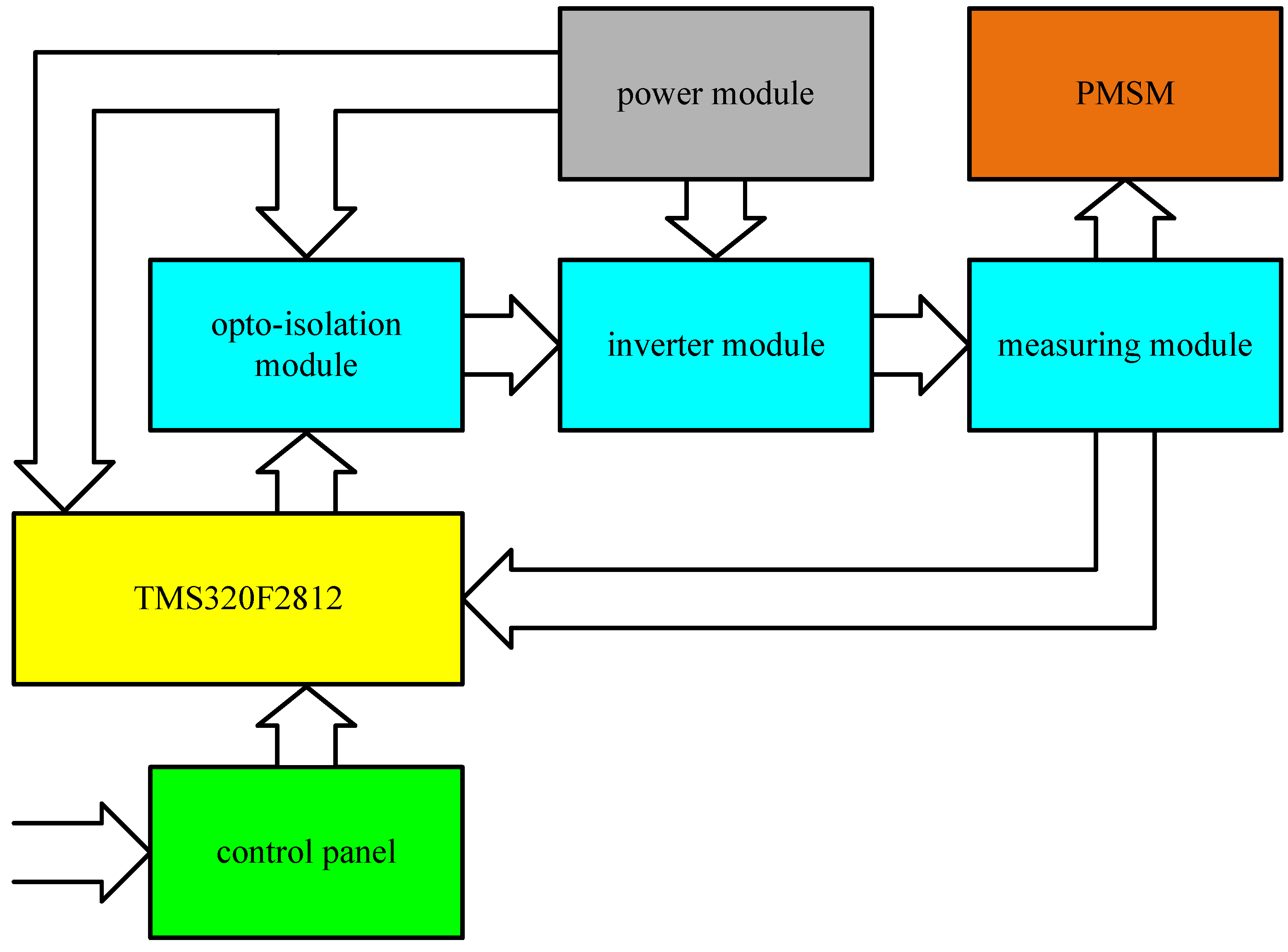
3. Materials and Methods

To perform the planned experiments, a laboratory setup was prepared (Figure 5).

The PMSM was linked to the torque measuring device (TM), generator (G), and encoder (E) by means of a common shaft. A three-phase 1-kW Brushless DC Motor (BLDC) motor worked as the generator. A DATAFLEX 22/20 (KTR, Germany) device placed on the torque-measuring shaft was used for torque sensing [23]. A detailed block diagram of the control unit is presented in Figure 6.

The control unit consist of:

• Control panel;
• development board with TMS320F2812;
• opto-isolation module;
• inverter module;
• measuring module;
• power module.

The parameters of the motor are summarized in

Table 1. PMSM nameplate.

Parameter	Value
Number of pole pairs	3
Rated voltage	48 V
Rated current	25 A
Rated speed	1000 rpm
Maximal current	35 A
Torque	6 Nm
Rated power	1 kW

.

The picture view of the experimental setup is presented in Figure 7.

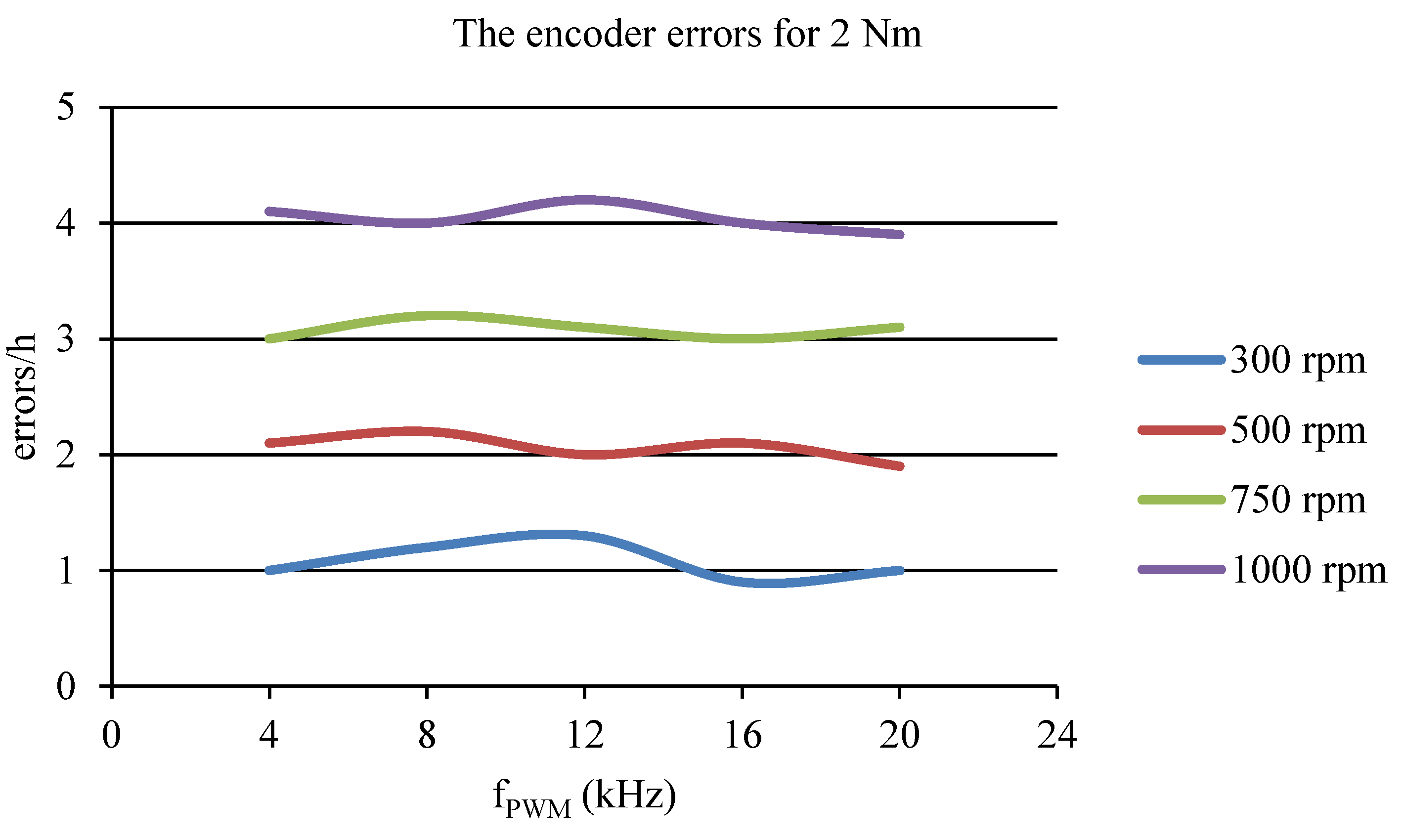
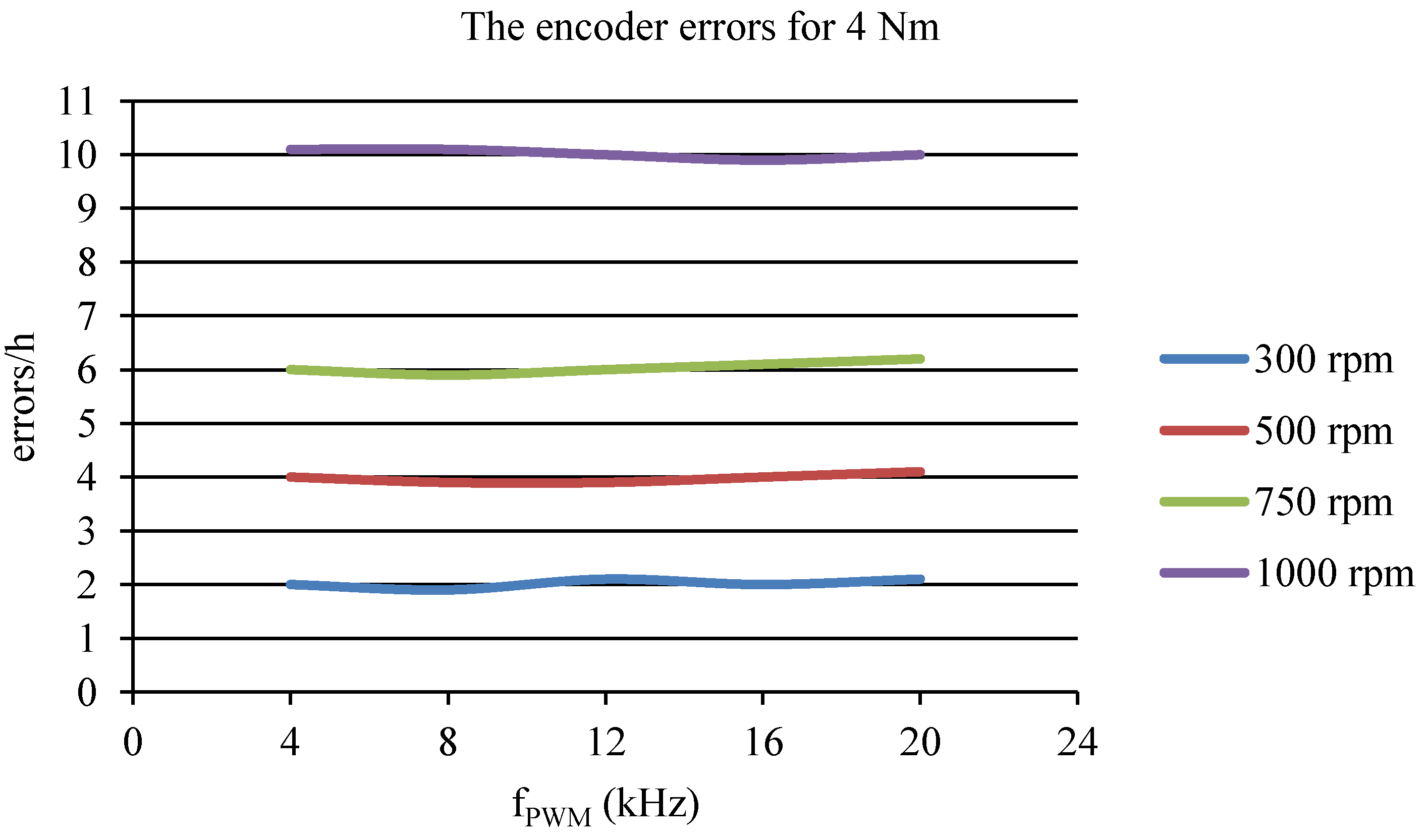
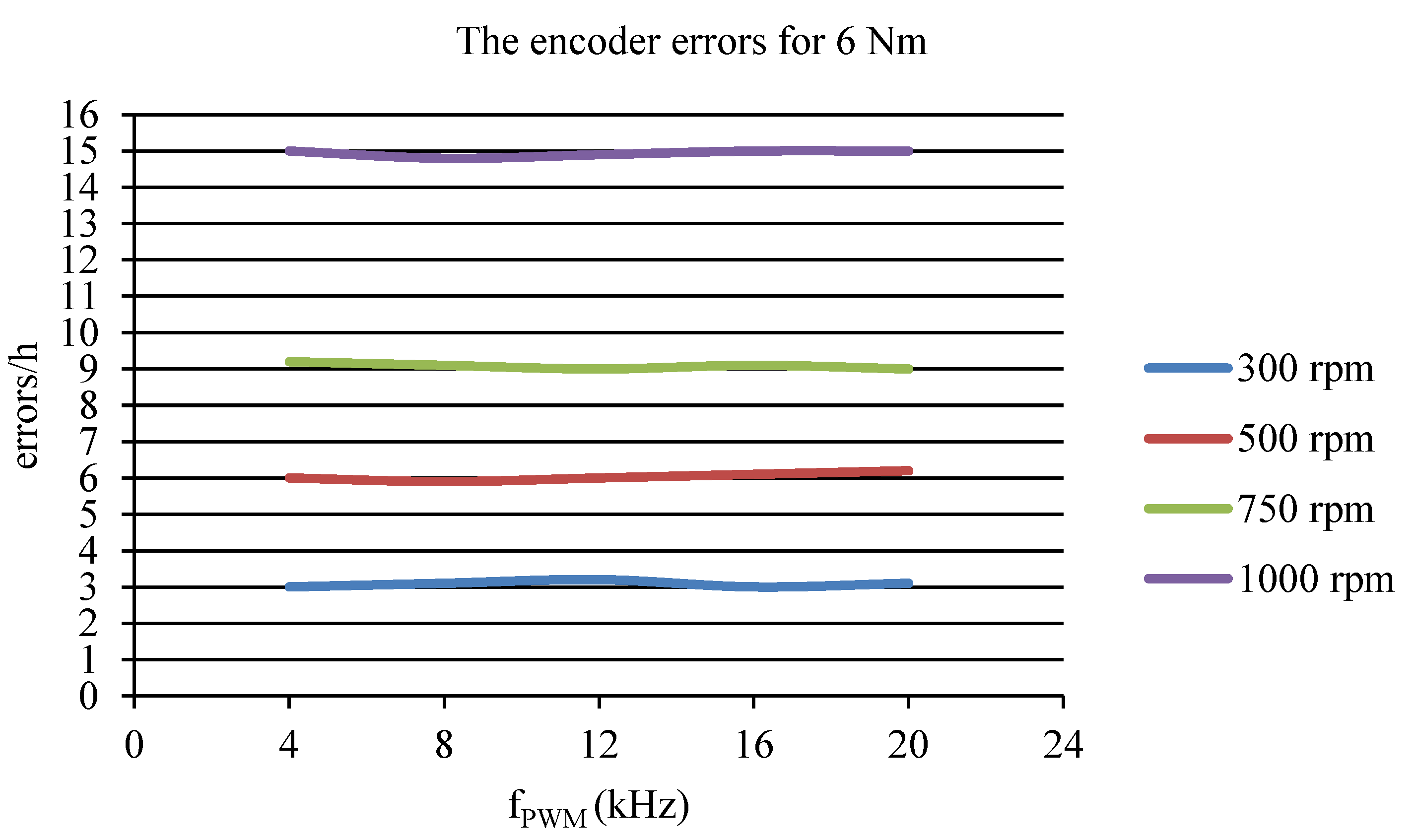
4. Results

The laboratory setup presented in Figure 5 was used to perform a series of experiments. Measurements of the encoder were taken for changes of three parameters of the system:

• The PWM control frequency for the motor in the range of 4–20 kHz with increments of 4 kHz;
• the rotation speed for the motor at 300, 500, 750, and 1000 rpm;
• the load torque for the motor at 2, 4, and 6 Nm.

The control algorithm was modified in order to count the errors of the absolute encoder for 24 h. The number of errors was presented on the display. The measurements were taken for 24 h for each initially preset rotation speed, each frequency, and each load torque, so they covered the full range of the motor operation. The number of errors during the 24-h measurement was calculated as an average number of errors per hour. Then, the average number of encoder errors per hour for 2 Nm was calculated (

Table 2. The average number of encoder errors per hour for 2 Nm.

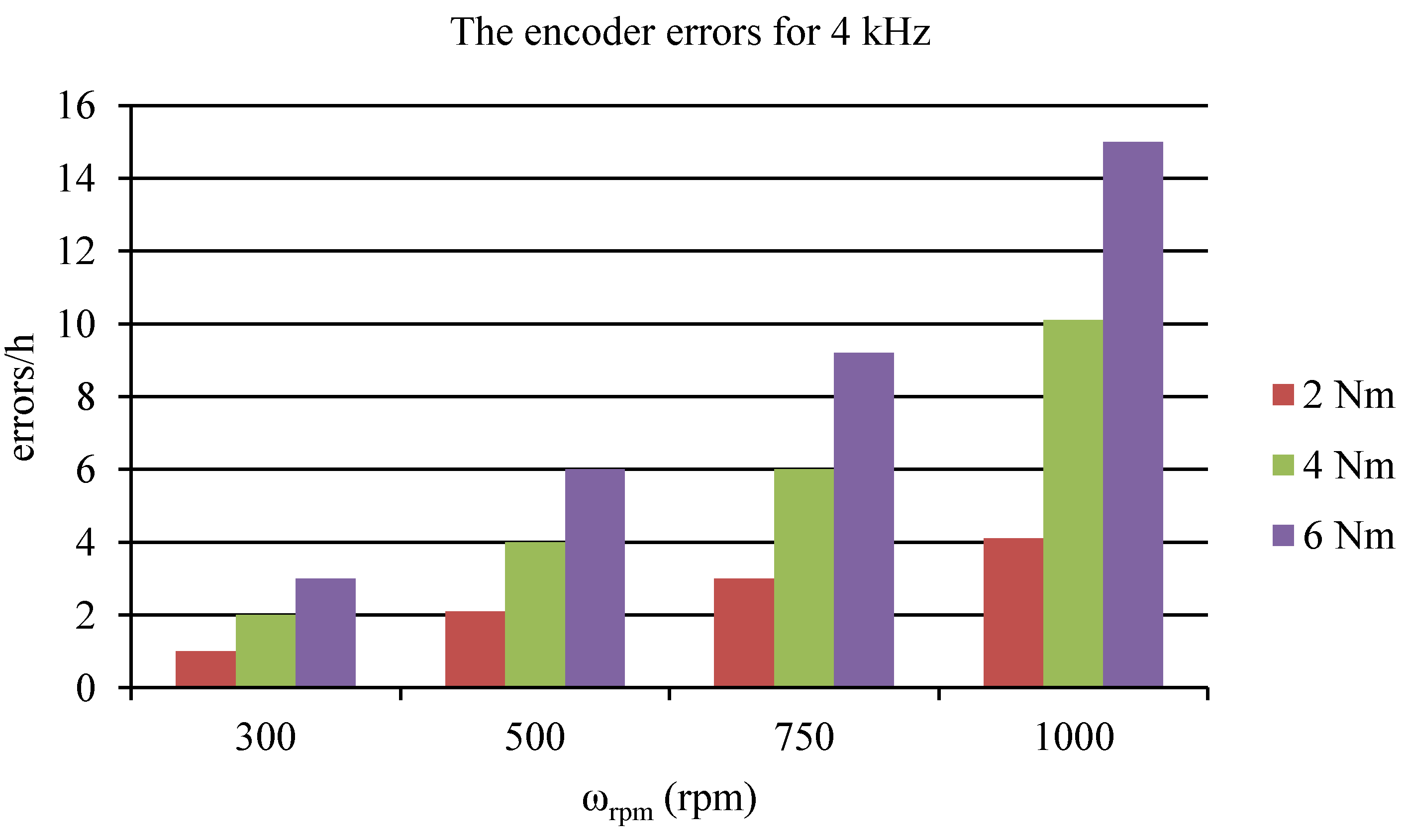
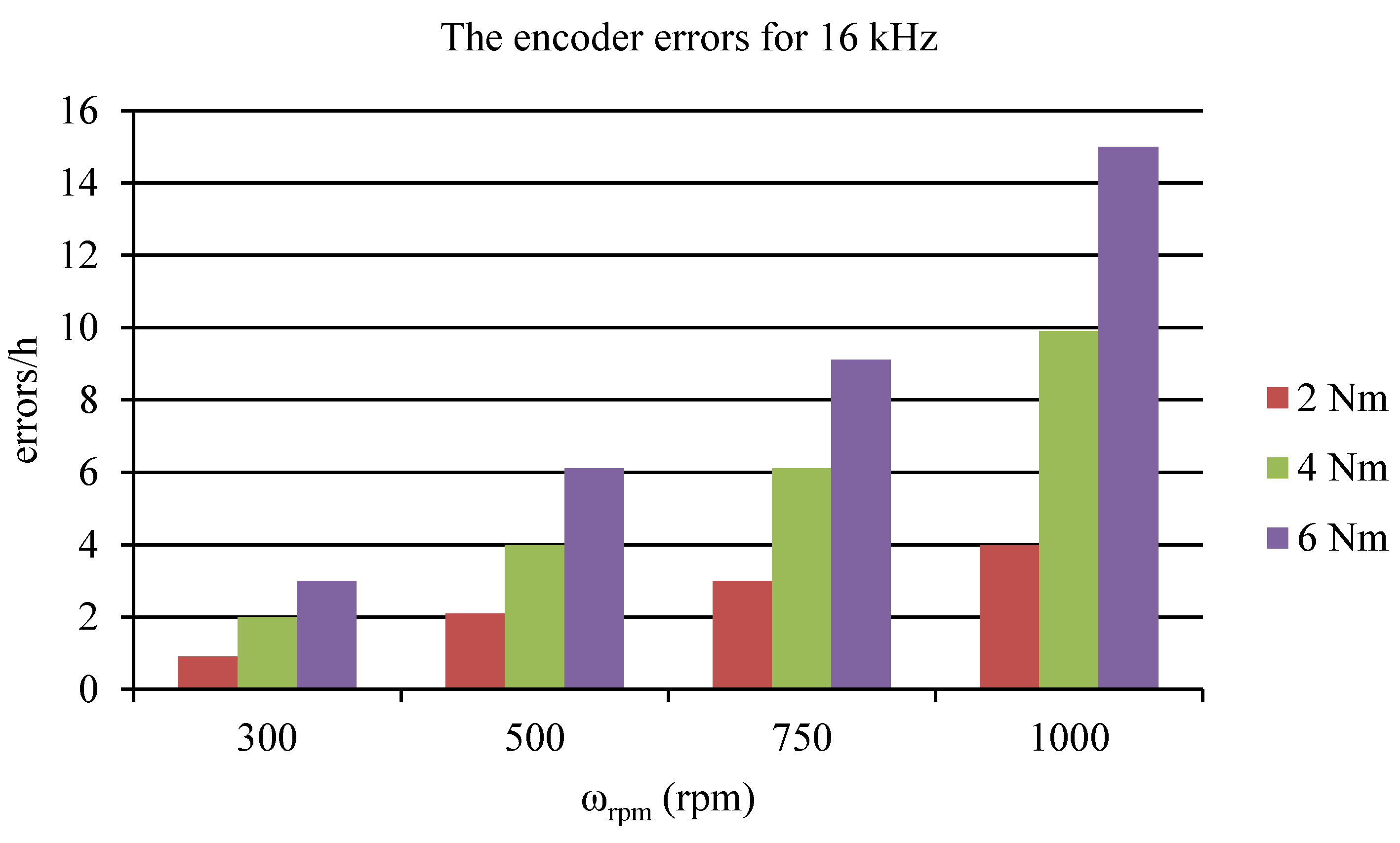
Speed	Frequency fPWM
ωrpm	4 kHz	8 kHz	12 kHz	16 kHz	20 kHz
300	1	1.2	1.3	0.9	1
500	2.1	2.2	2	2.1	1.9
750	3	3.2	3.1	3	3.1
1000	4.1	4	4.2	4	3.9

).

The encoder errors for 2 Nm is shown in Figure 8. We can observe that the number of encoder errors depends little on the PWM frequency. The number of errors increased with the motor speed.

The average number of encoder errors per hour for 4 Nm is presented in

Table 3. The average number of encoder errors per hour for 4 Nm.

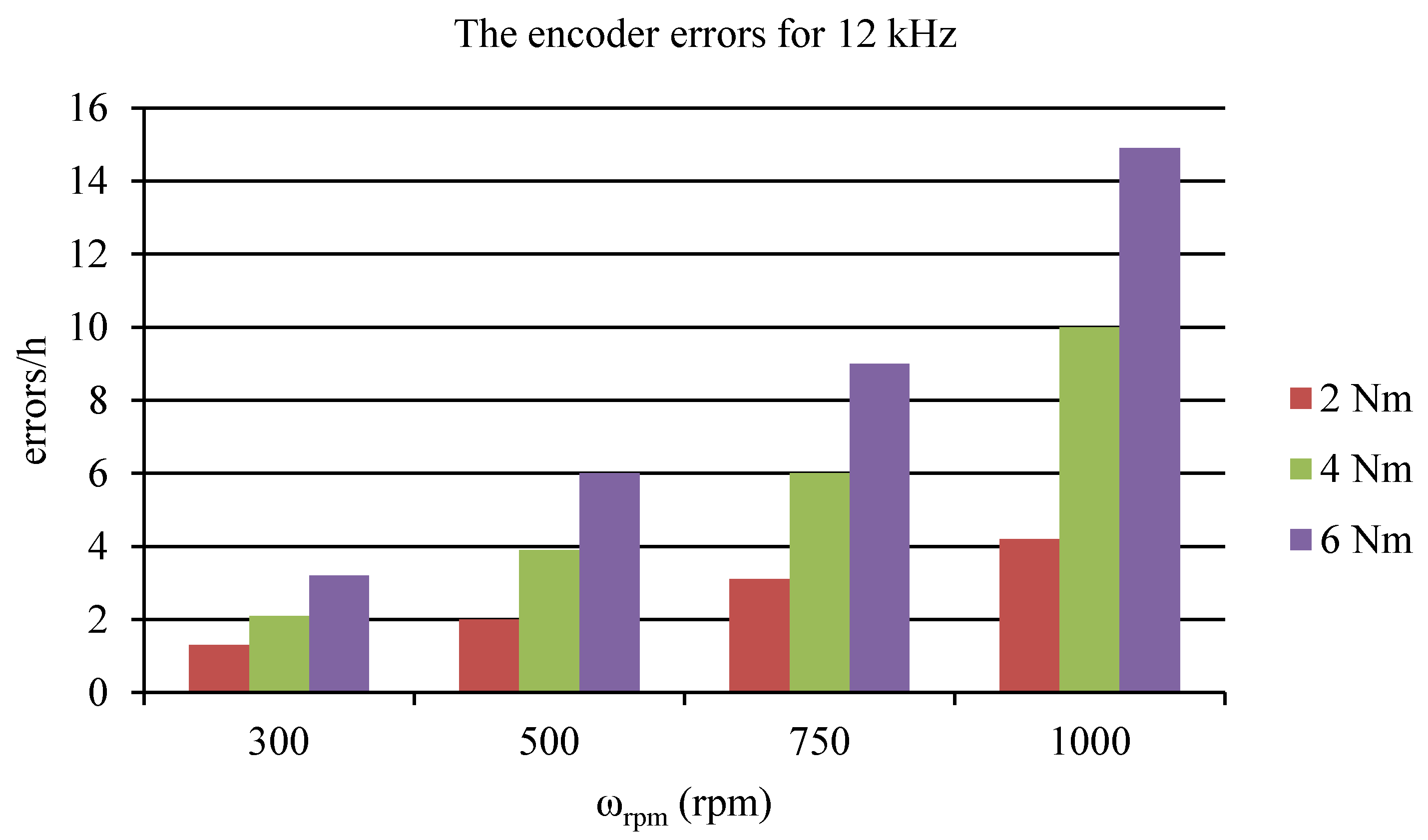
Speed	Frequency fPWM
ωrpm	4 kHz	8 kHz	12 kHz	16 kHz	20 kHz
300	2	1.9	2.1	2	2.1
500	4	3.9	3.9	4	4.1
750	6	5.9	6	6.1	6.2
1000	10.1	10.1	10	9.9	10

.

The encoder errors for 4 Nm is shown in Figure 9. We can observe that the number of encoder errors depends little on the PWM frequency. The number of errors increased with the motor speed.

The average number of encoder errors per hour for 6 Nm was presented in

Table 4. The average number of encoder errors per hour for 6 Nm.

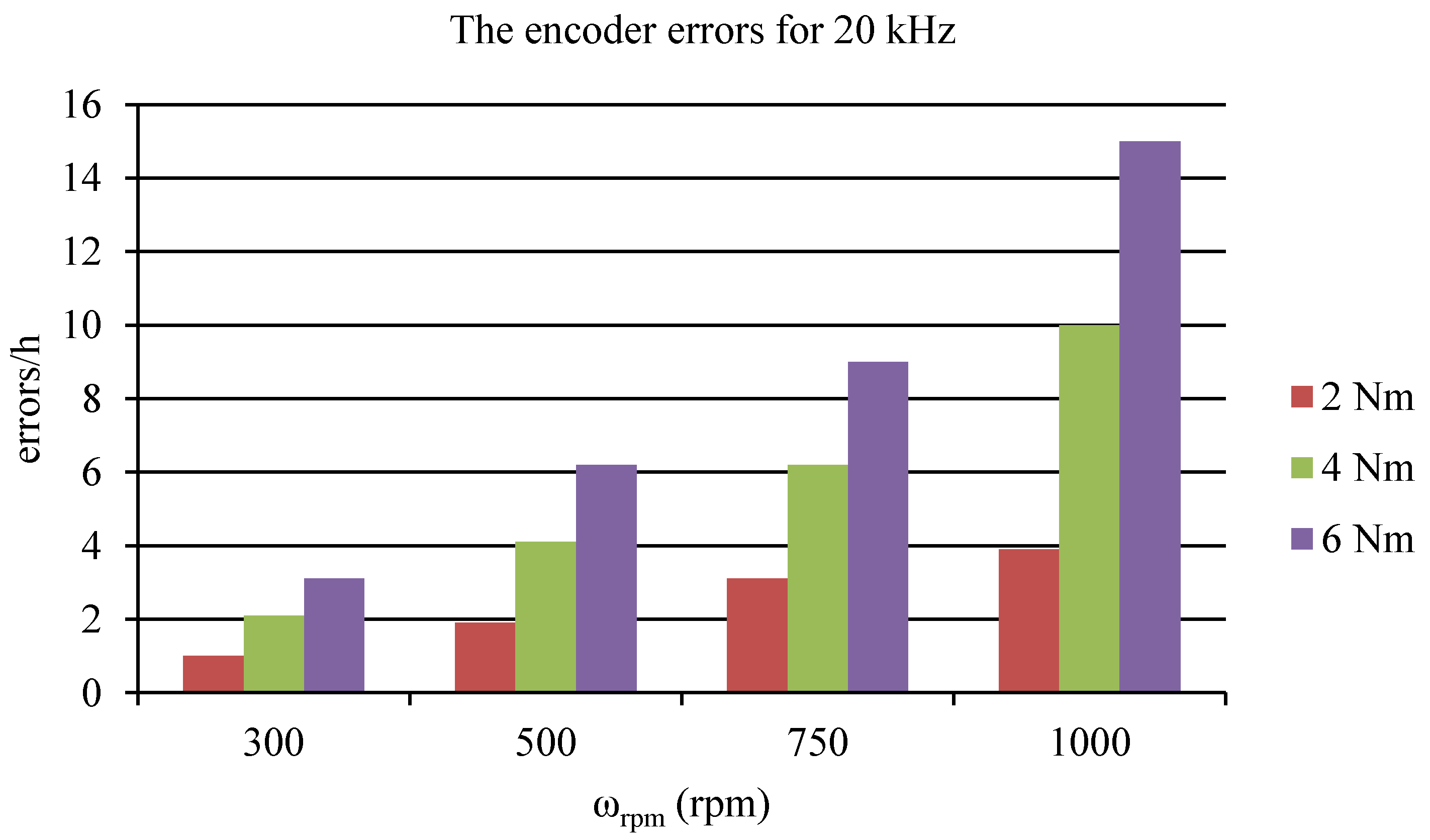
Speed	Frequency fPWM
ωrpm	4 kHz	8 kHz	12 kHz	16 kHz	20 kHz
300	3	3.1	3.2	3	3.1
500	6	5.9	6	6.1	6.2
750	9.2	9.1	9	9.1	9
1000	15	14.8	14.9	15	15

.

The encoder errors for 6 Nm is shown in Figure 10.

We can observe that the number of encoder errors depends little on the PWM frequency. The number of errors increased with the motor speed. The encoder errors for 4 kHz is shown in Figure 11.

The encoder errors for 8 kHz is shown in Figure 12.

The encoder errors for 12 kHz is shown in Figure 13.

The encoder errors for 16 kHz is shown in Figure 14.

The encoder errors for 20 kHz is shown in Figure 15.

We can observe that the number of encoder errors depends on the load torque for each frequency. The number of errors increased with the load torque for each frequency. Additionally, we can observe that the number of errors increased with the motor speed for each frequency.

5. Discussion

For the tested MAB28 absolute encoder, the average number of errors per hour was practically independent of frequency. A change in the PWM frequency had a weak effect on the number of encoder errors because it had little effect on the change of the PMSM motor current at constant load torque. The PMSM current was affected by the load torque. The number of encoder errors increased with increasing speed and with increasing load torque. Therefore, it can be concluded that an increase in rotational speed or an increase in load torque causes an increase in motor current. As the current consumed by the motor increases, the noise generated by the motor increases. This causes the encoder to operate under adverse conditions. This, in turn, causes the encoder to provide the wrong motor shaft position from time to time. For the correct operation of the drive system, correct the incorrect position of the drive shaft read from the encoder.

6. Conclusions

The paper described how to deal with an encoder operating in the presence of interference, which, from time to time, returns to the wrong position of the motor shaft position. The investigations were carried out for the PMSM with a power of 1 kW, a rated speed of 1000 rpm, and a rated torque of 6 Nm. The PWM frequency was varied within the range of 4 to 20 kHz with increments of 4 kHz with load torques of 2, 4, and 6 Nm, as well as rotation speeds of 300, 500, 750, and 1000 rpm.

Taking the control algorithm into account, the above dependencies can be protected against incorrect reading of the encoder position, which is a key matter in the vector control of the PMSM motor. The author experimentally verified how control of the motor’s operation is adversely influenced if the above dependences are not taken into account. Controlling the motor without accounting for the aforementioned dependences leads to unstable operation characterized by temporary jerkiness and increased power consumption. It can be said that any encoder used to build the drive system will occasionally give the wrong position of the shaft. The number of these errors will depend on the encoder itself and the conditions under which it will work. Unfortunately, in practical applications, this important problem related to the reliability of the drive system is often overlooked.

The aim of this paper was to show that the PWM switching frequency does not affect the numbers of errors from encoder. The article also showed how to deal with the situation when the encoder gives the wrong position of the motor shaft. The original scientific contribution was to propose an original method for determining the correct position of the motor shaft. This method uses an absolute encoder that works in the presence of interference, which sometimes causes the encoder to return in the wrong position. Based on the PMSM speed, it is possible to determine what the encoder position should be during the next reading. Based on the position read from the encoder and the calculated one, it can be determined when the encoder gives the wrong position. If the position read from the encoder is incorrect, then the calculated encoder position should be used for further calculations of the FOC algorithm. The application of the proposed method is of practical importance because it can be used in industry.