A Subthreshold Bootstrapped SAPTL-Based Adder Design
Abstract
:1. Introduction
2. Proposed Subthreshold Adder Design
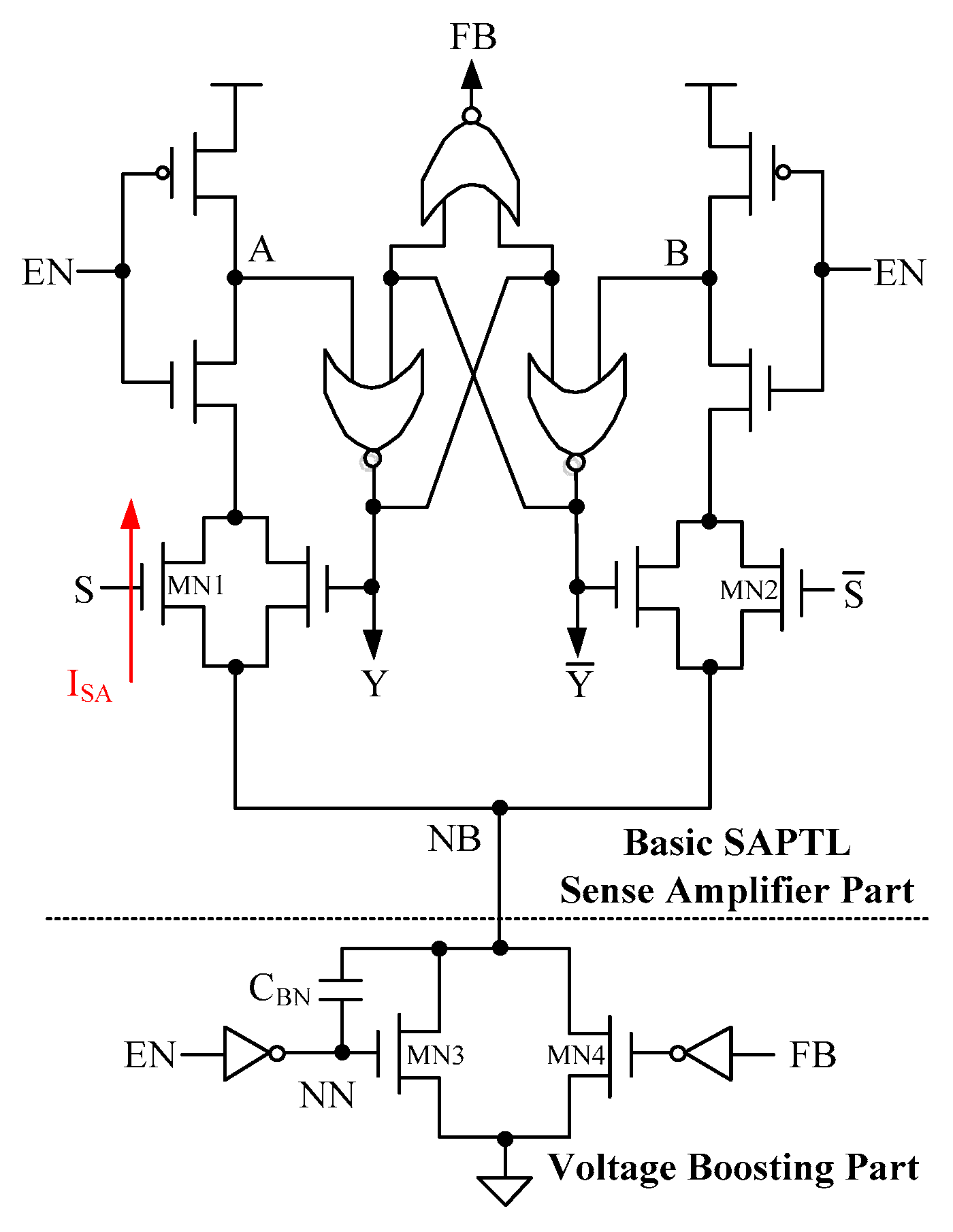
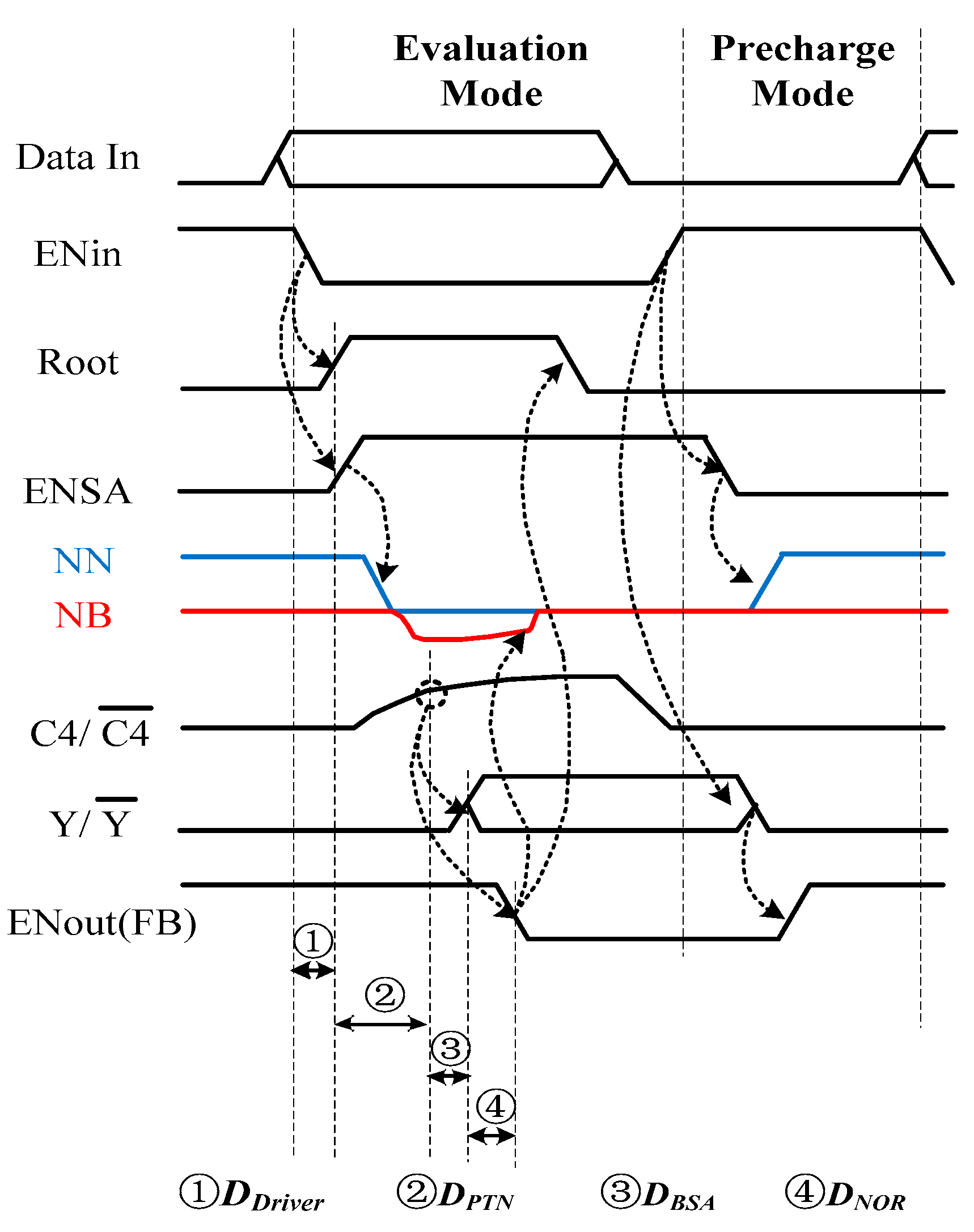
2.1. Bootstrapped Sense Amplifier
- EN = 0. BSA is in the pre-charge mode. 1 and, thus, the outputs 0. FB = 1. MN3 is on and MN4 is off, making and . A voltage equal to is thus applied across .
- EN = 1. BSA is in the evaluation mode. Before the differential inputs become valid, and MN3 turns off, then the capacitive coupling through will force to be boosted below 0. After the input signals become valid, of MN1 is thus enlarged effectively and makes MN1 faster. At the same time, of MN1 is also increased and, hence, of MN1 is reduced slightly by forward body biasing, accelerating MN1 further. Either or will be pulled down below 0 to generate two inverse outputs through the cross-coupled latch. Then FB will turn to 0 and turn on MN4 to reset the value of to 0. This procedure is to prevent the undesired leakage of MN2 from pulling down because of MN2 is larger than 0 after the evaluation is finished if is not reset.
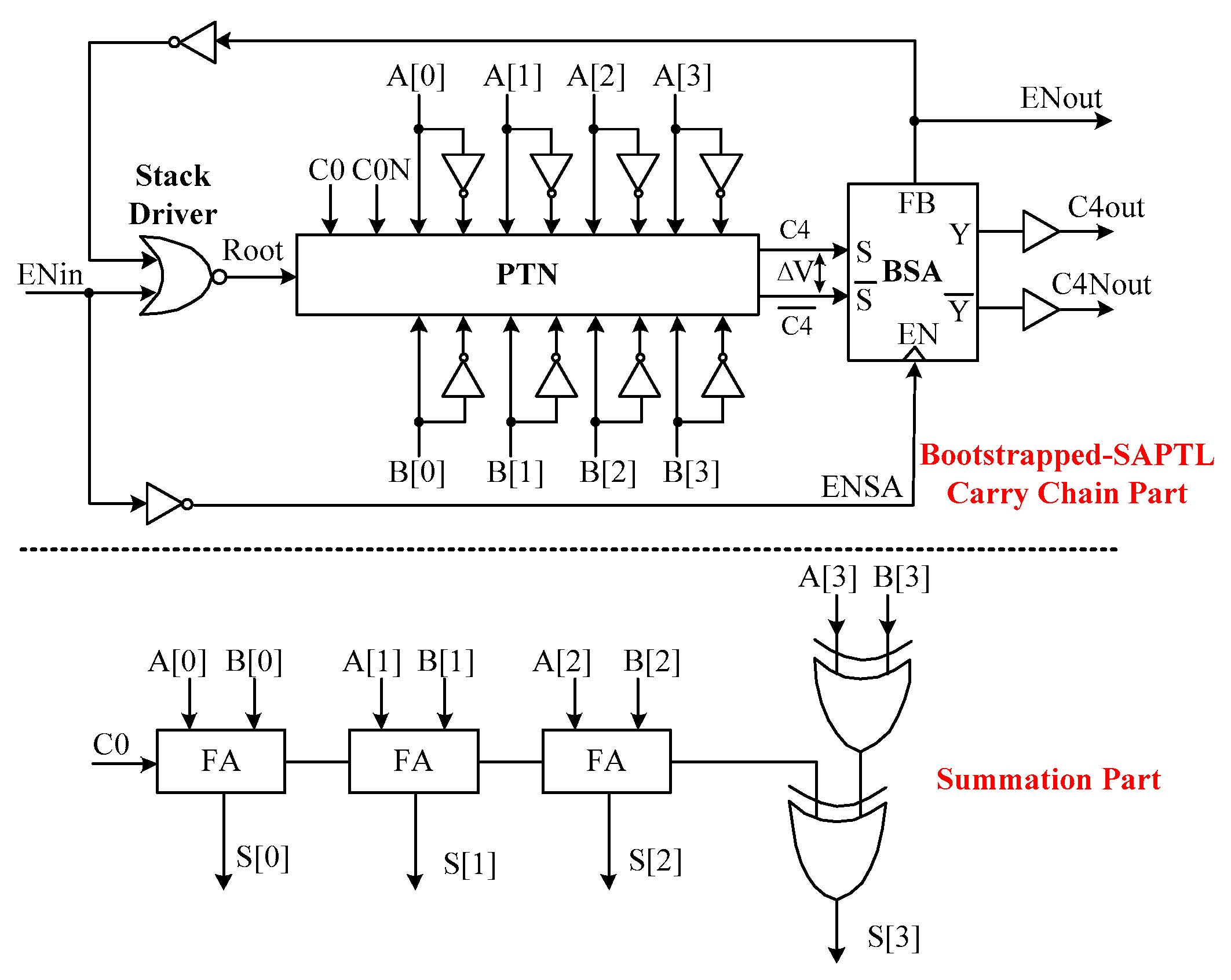
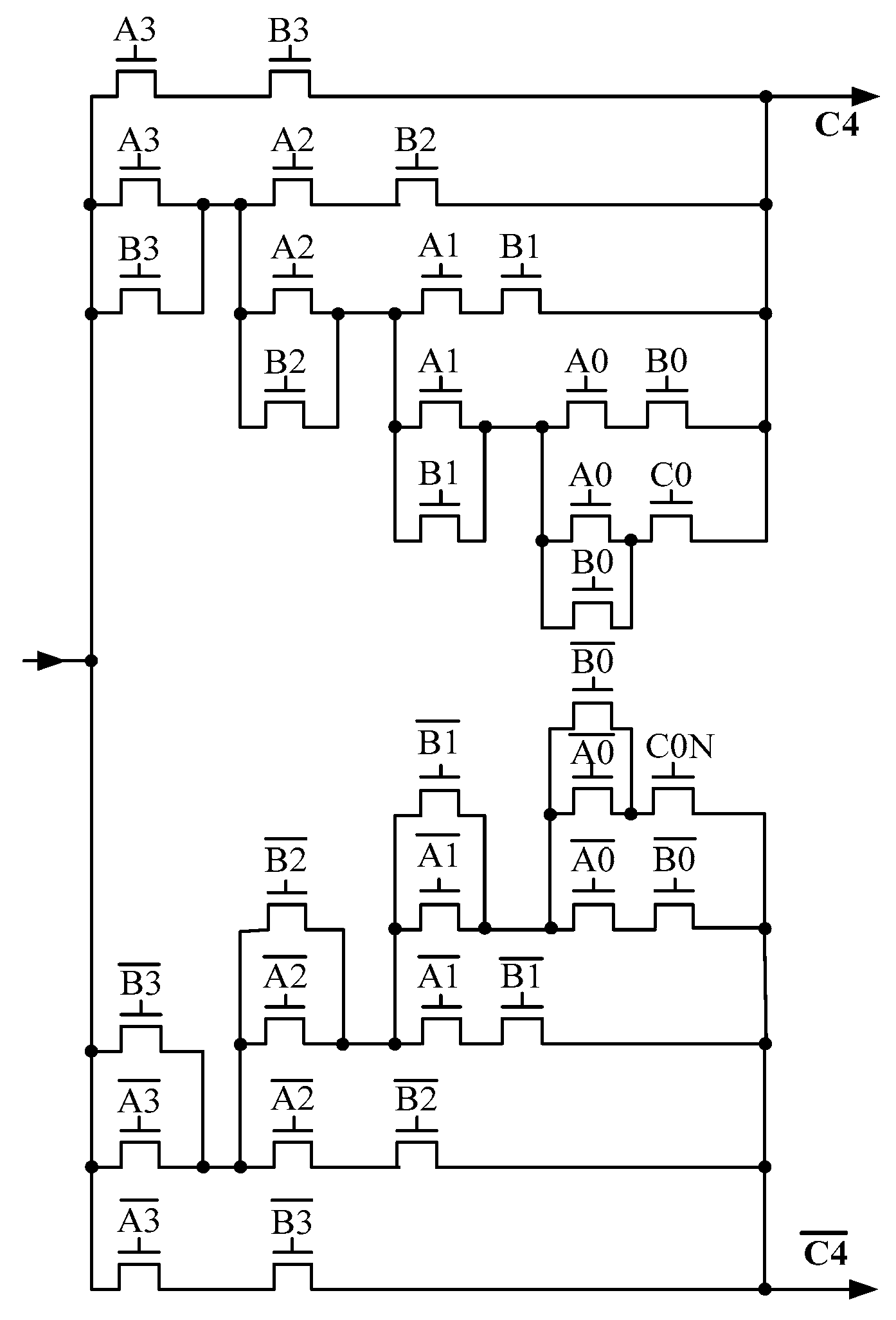
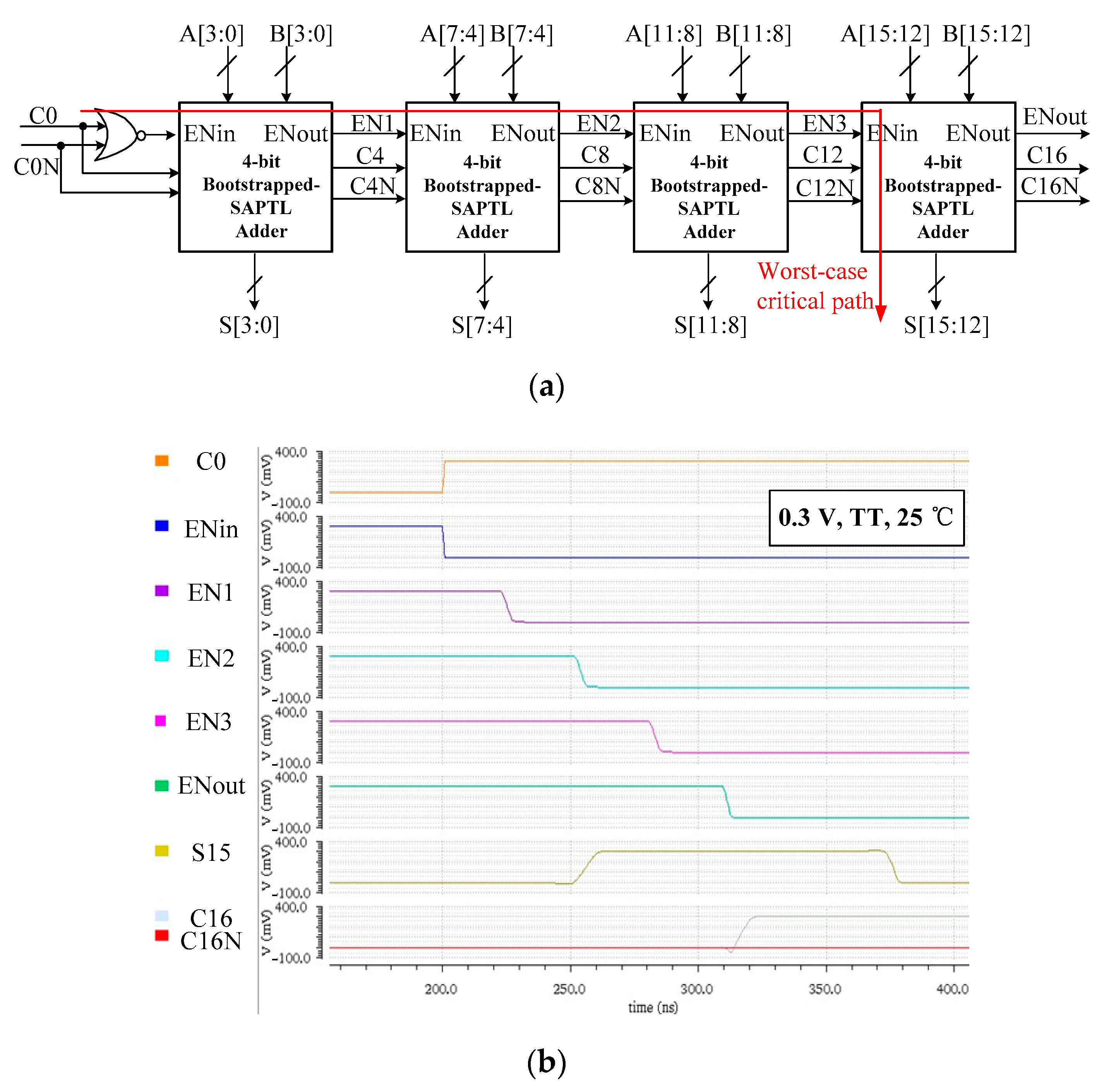
2.2. The Adder Architecture Based on Bootstrapped-SAPTL
3. Experiment Results
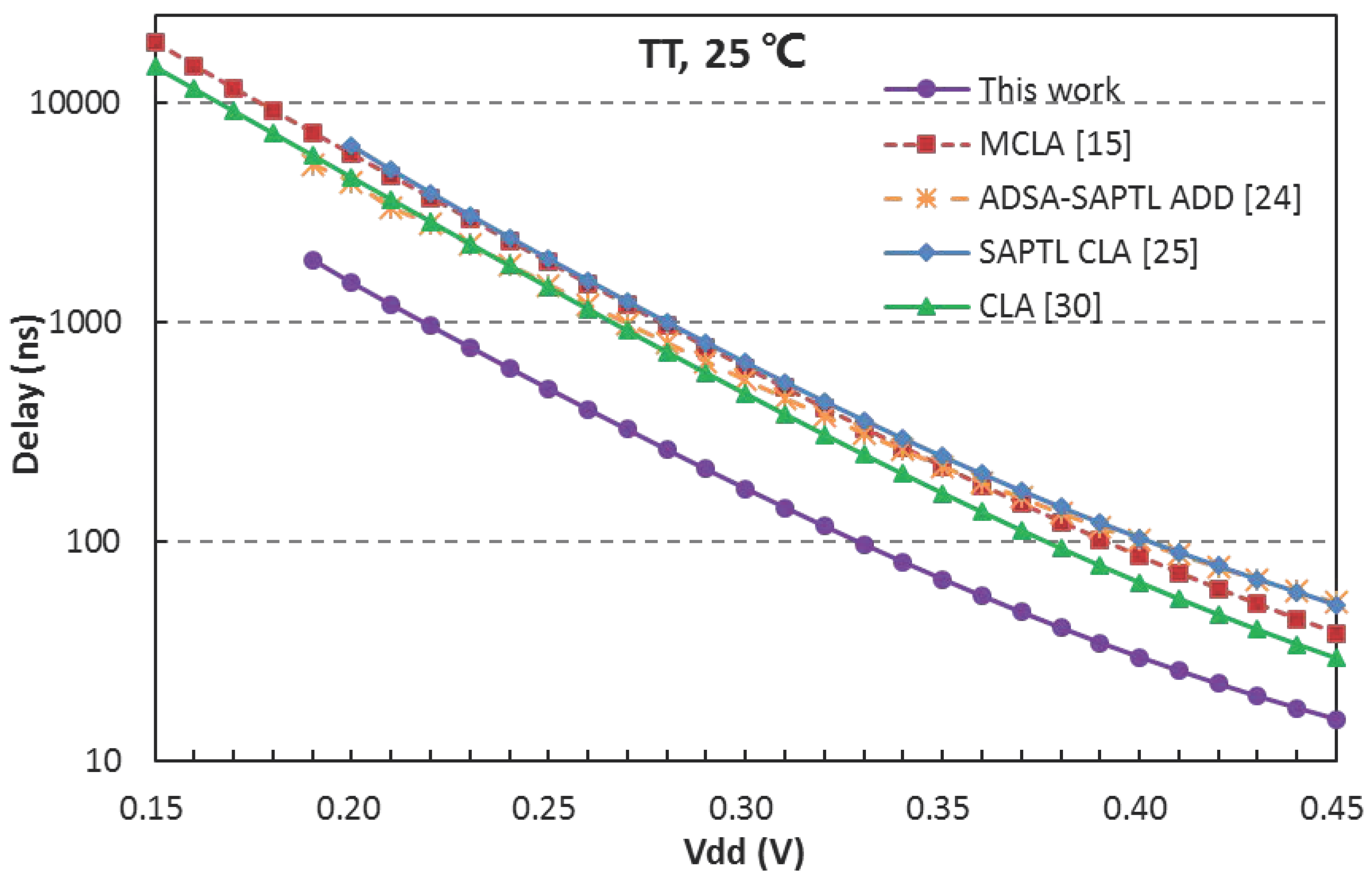
3.1. Comparison with Other Works
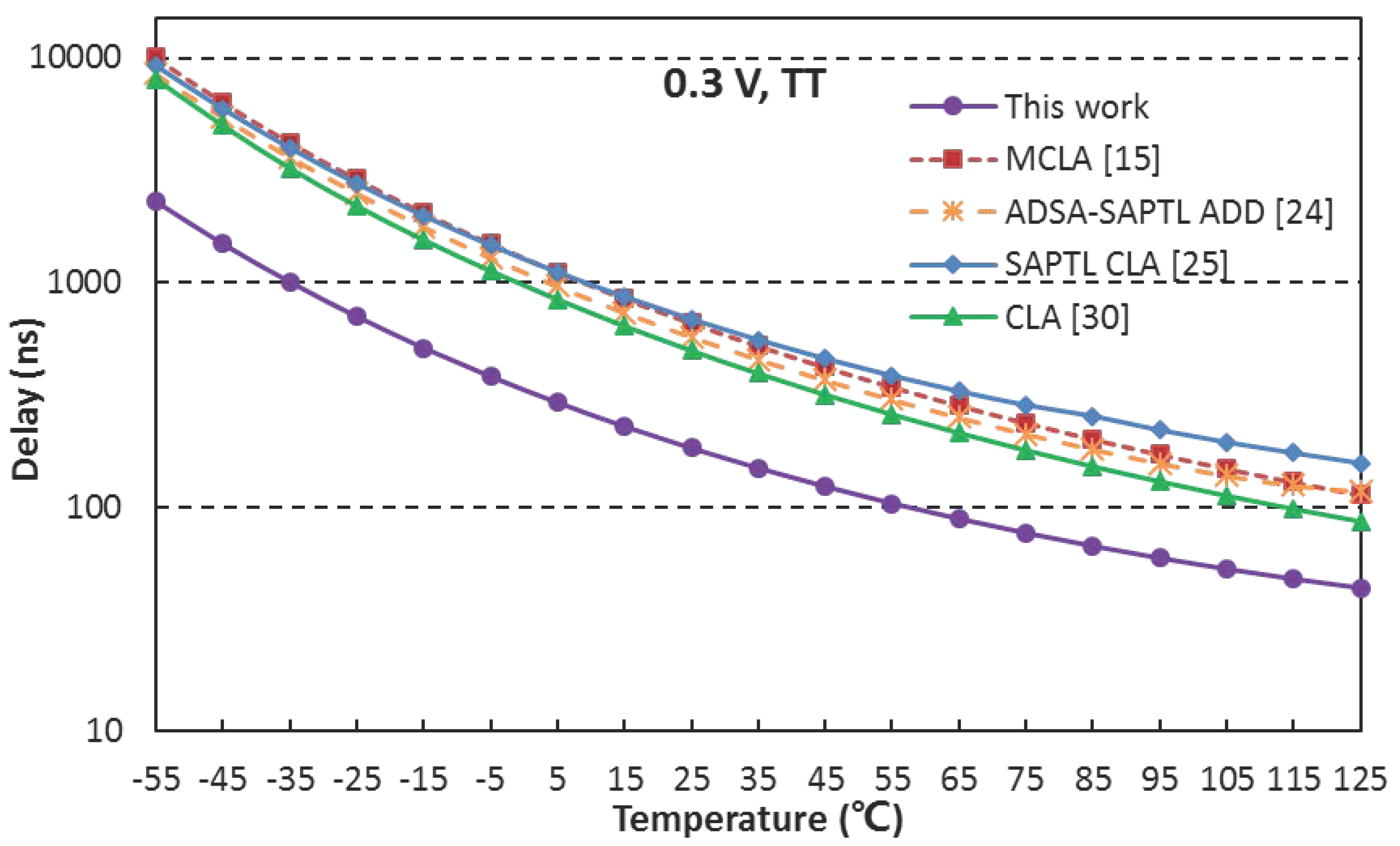
- The proposed adder used 38% fewer transistors than ADSA-SAPTL ADD [24], 48% fewer than SAPTL CLA [25], and 35% fewer than the conventional CLA [30], which manifested the proposed architecture’s advantage on the area. But the proposed adder used more transistors than Reference [15], which meant extra area overhead.
- The bootstrapped SAPTL adder provided the best performance, 72% faster than the MCLA [15]. The maximum operating frequency of the proposed adder at 0.3 V (TT corner, 25 °C) achieved 5.5 MHz.
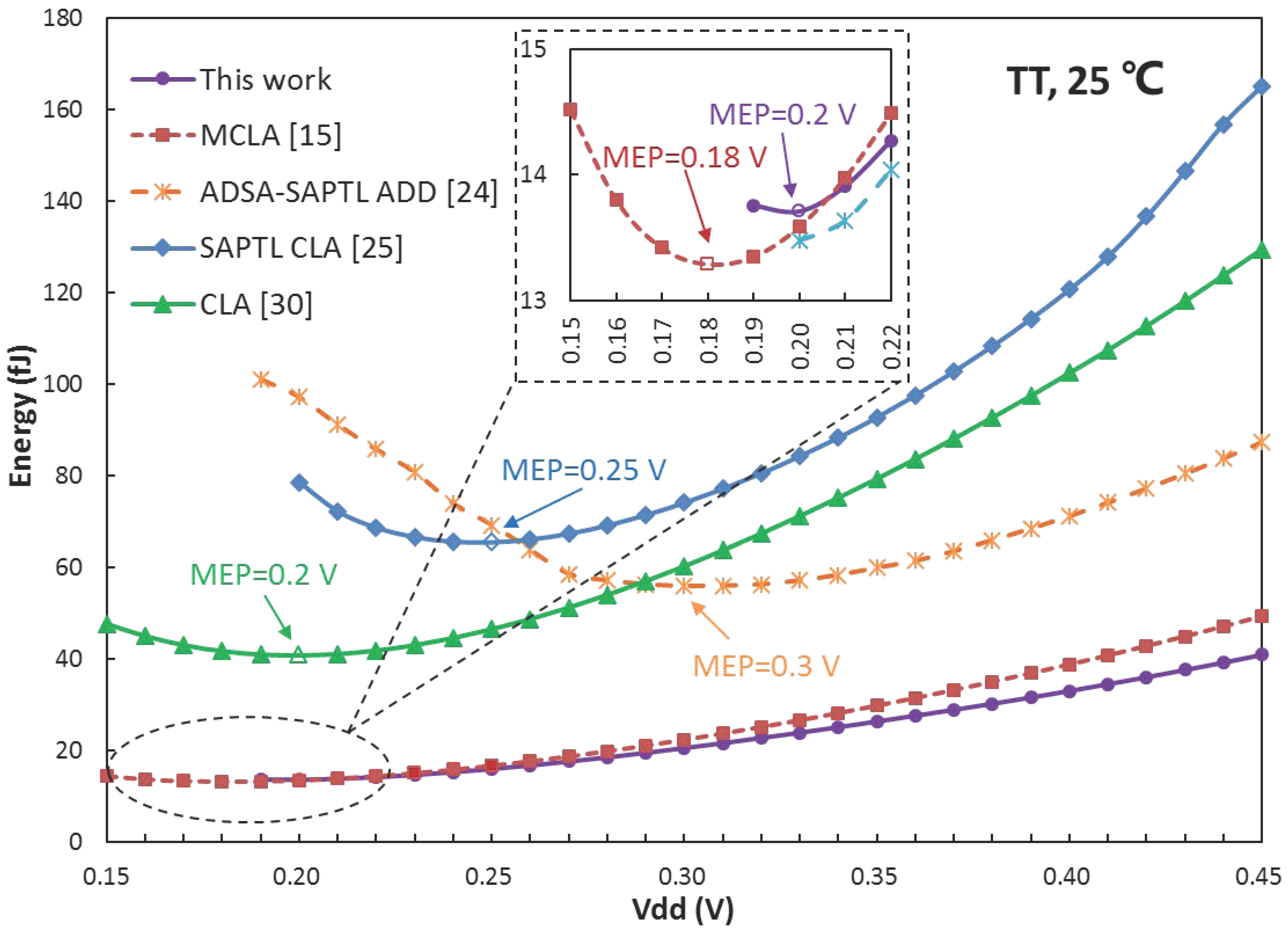
- From the perspective of energy consumption, the bootstrapped SAPTL adder cost the lowest energy, 8.1% lower than the MCLA despite a larger area overhead.
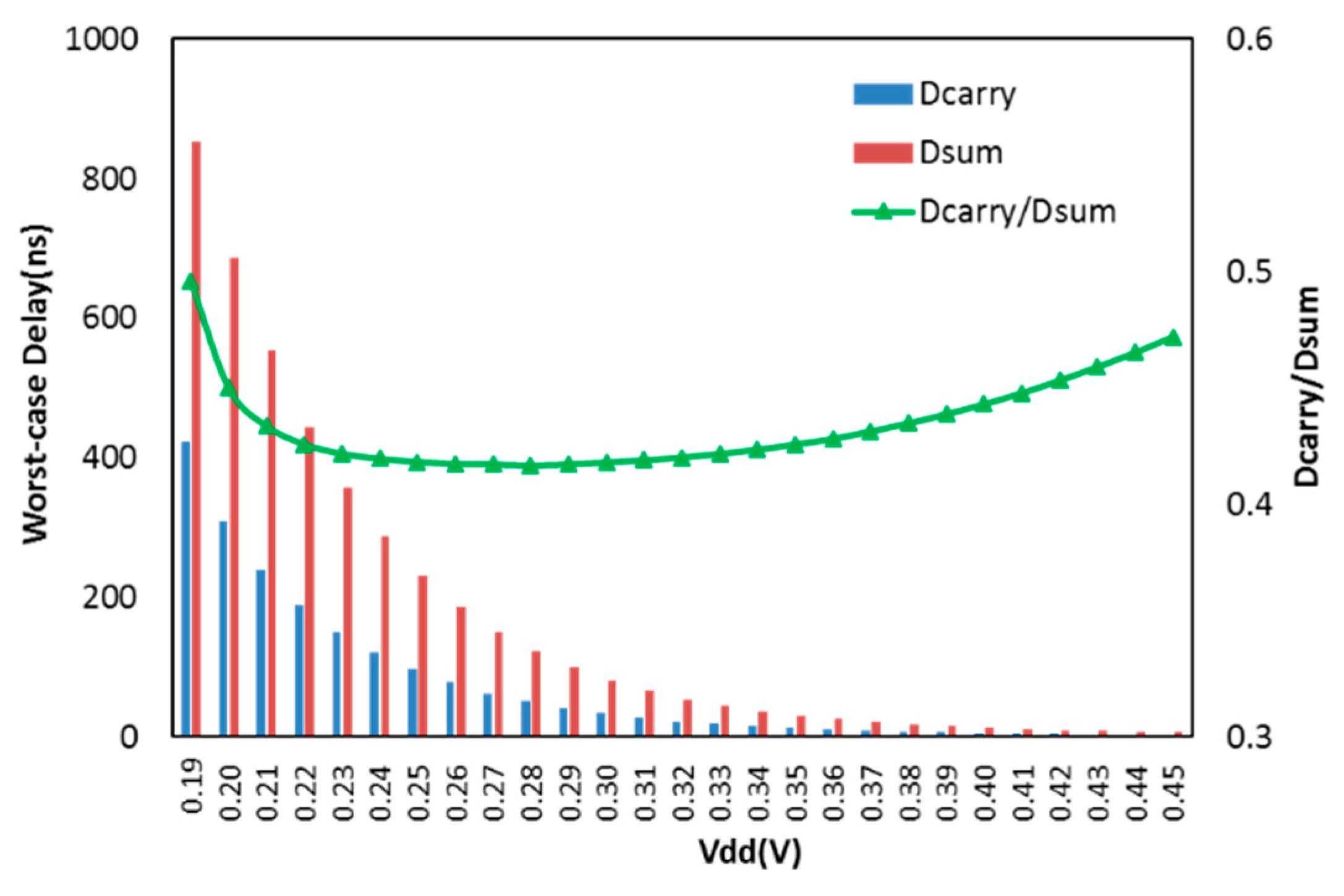
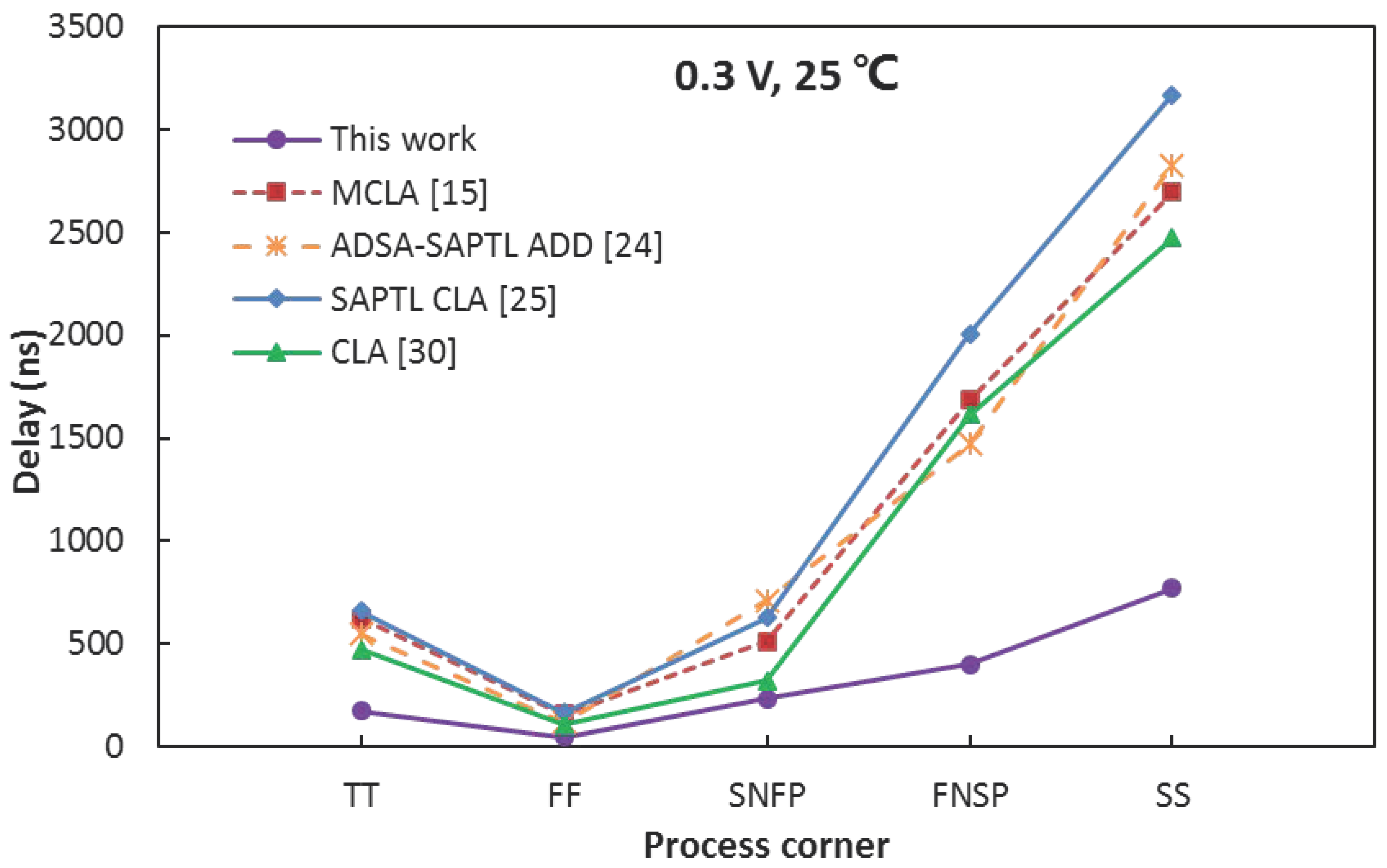
3.2. Worst-Case Delay versus Supply Voltage
3.3. Energy Consumption versus Supply Voltage
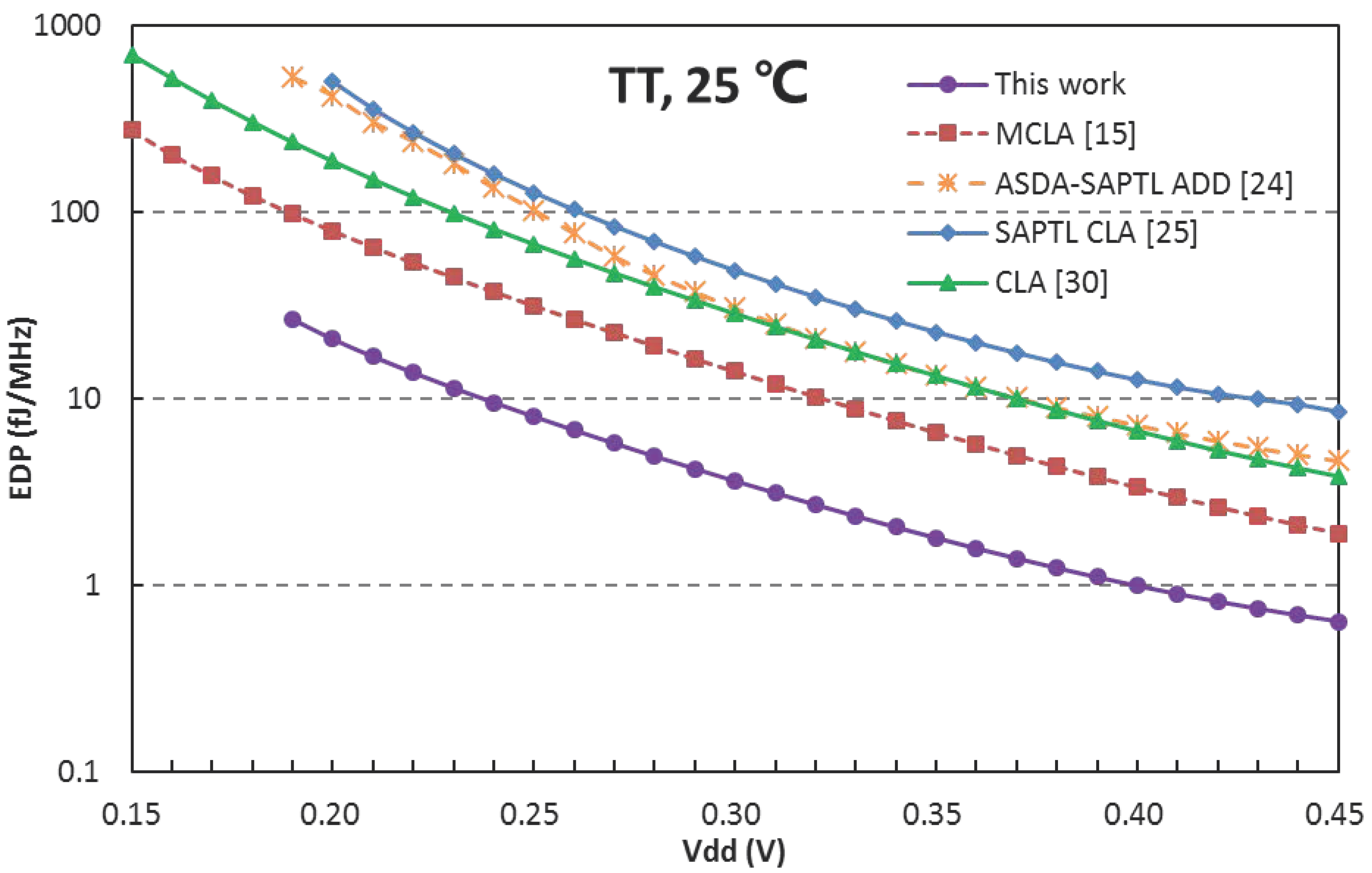
3.4. Energy-Delay Production versus Supply Voltage
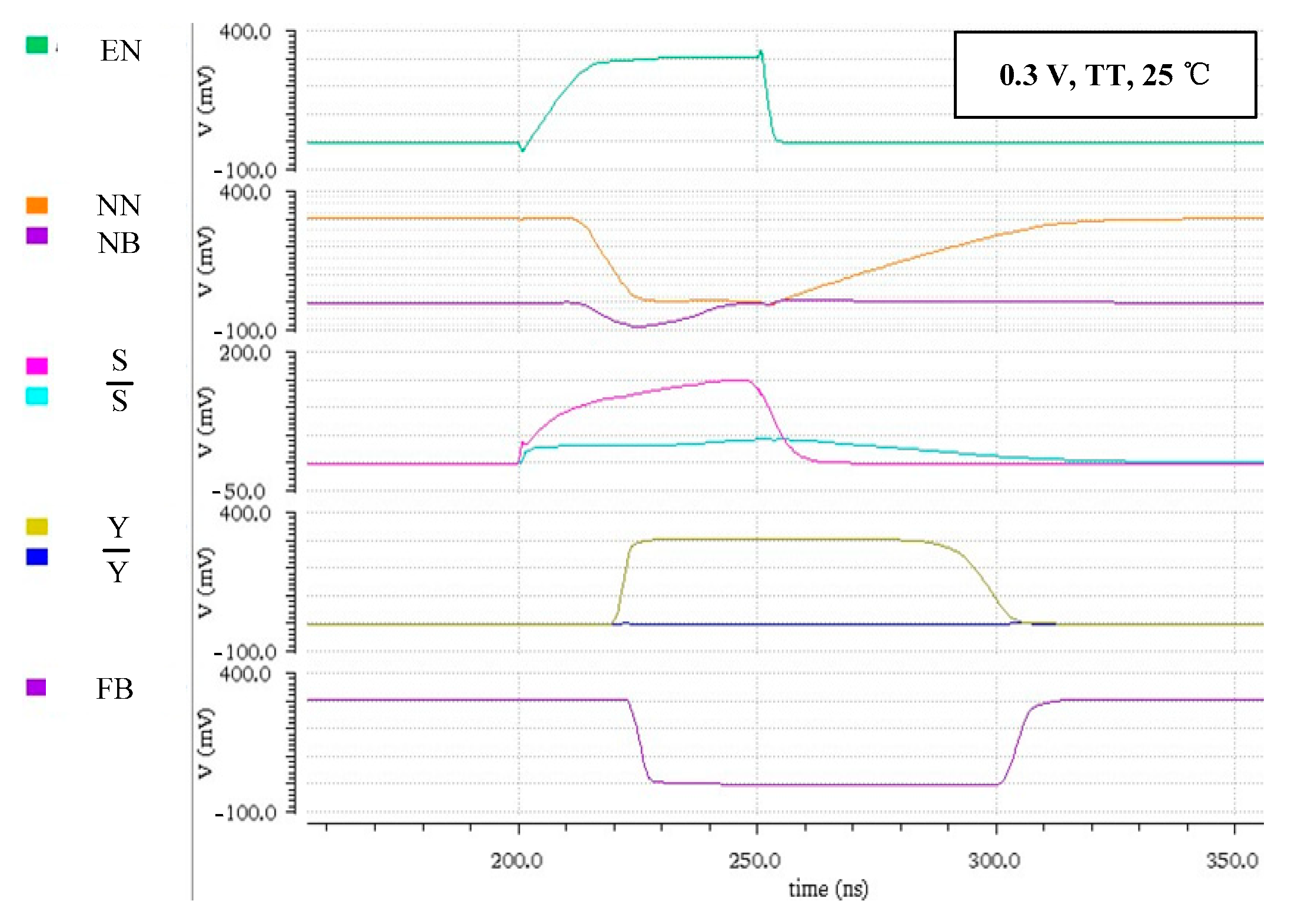
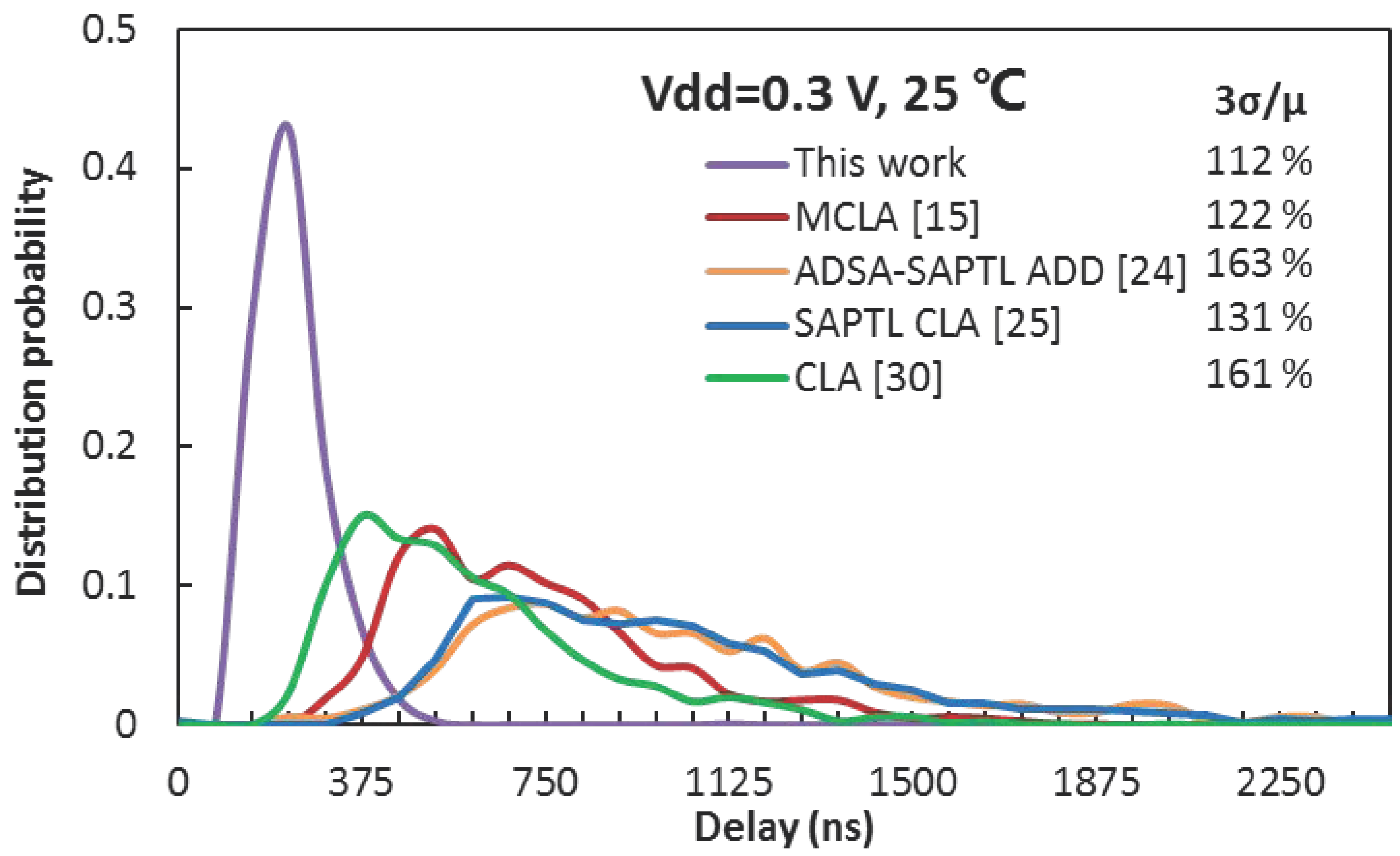
3.5. Simulation Results of Process and Temperature Variations
3.6. Post-Layout Simulation Result
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lee, I.; Sylvester, D.; Blaauw, D. Subthreshold voltage reference with scalable output voltage for low-power IoT systems. IEEE J. Solid State Circuits 2017, 52, 1443–1449. [Google Scholar] [CrossRef]
- Sridhara, K.; Biradar, G.S.; Yanamshetti, R. Subthreshold leakage power reduction in VLSI circuits: A survey. In Proceedings of the International Conference on Communication and Signal Processing, Melmaruvathur, India, 6–8 April 2016; pp. 1120–1124. [Google Scholar] [CrossRef]
- Dokic, B.; Pajkanovic, A. Low power CMOS sub-threshold circuits. In Proceedings of the 36th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 20–24 May 2013; pp. 60–65. [Google Scholar] [CrossRef]
- Wang, A.; Chandrakasan, A. A 180-mV subthreshold FFT processor using a minimum energy design methodology. IEEE J. Solid State Circuits 2005, 40, 310–319. [Google Scholar] [CrossRef]
- Verma, N.; Kwong, J.; Chandrakasan, A.P. Nanometer MOSFET variation in minimum energy subthreshold circuits. IEEE Trans. Electron. Devices 2008, 55, 163–174. [Google Scholar] [CrossRef]
- Keane, J.; Eom, H.; Kim, T.H.; Sapatnekar, S.; Kim, C. Stack sizing for optimal current drivability in subthreshold circuits. IEEE Trans. Very Large Scale Integr. VLSI Syst. 2008, 16, 598–602. [Google Scholar] [CrossRef]
- Hanson, S.; Zhai, B.; Seok, M.; Cline, B.; Zhou, K.; Singhal, M.; Minuth, M.; Olson, J.; Nazhandali, L.; Austin, T. Exploring variability and performance in a sub-200-mV processor. IEEE J. Solid State Circuits 2008, 43, 881–891. [Google Scholar] [CrossRef]
- Calhoun, B.H.; Chandrakasan, A.P. Ultra-dynamic voltage scaling (UDVS) using sub-threshold operation and local voltage dithering. IEEE J. Solid State Circuits 2006, 41, 238–245. [Google Scholar] [CrossRef]
- Bo, Z.; Hanson, S.; Blaauw, D.; Sylvester, D. Analysis and mitigation of variability in subthreshold design. In Proceedings of the 2005 International Symposium on Low Power Electronics and Design, San Diego, CA, USA, 8–10 August 2005; pp. 20–25. [Google Scholar] [CrossRef]
- Dorosti, H.; Teymouri, A.; Fakhraie, S.M.; Salehi, M. Ultralow-Energy Variation-Aware Design: Adder Architecture Study. IEEE Trans. Very Large Scale Integr. VLSI Syst. 2016, 24, 1165–1168. [Google Scholar] [CrossRef]
- Pradhan, S.N.; Rai, V.; Chakraborty, A. Design of high speed and low power full adder in subthreshold region. In Proceedings of the 2016 International Conference on Microelectronics, Computing and Communications (MicroCom), Durgapur, India, 23–25 January 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Jafari, M.; Imani, M.; Ansari, M.; Fathipour, M.; Sehatbakhsh, N. Design of an ultra-low power 32-bit adder operating at subthreshold voltages in 45-nm FinFET. In Proceedings of the International Conference on Design & Technology of Integrated Systems in Nanoscale Era, Abu Dhabi, UAE, 26–28 March 2013; pp. 167–168. [Google Scholar] [CrossRef]
- Attarzadeh, H.; Aunet, S.; Ytterdal, T. An ultra-low-power/high-speed 9-bit adder design: Analysis and comparison Vs. technology from 130nm-LP to UTBB FD-SOI-28nm. In Proceedings of the 2015 Nordic Circuits and Systems Conference (NORCSA), Oslo, Norway, 26–28 October 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Granhaug, K.; Aunet, S. Six Subthreshold Full Adder Cells characterized in 90 nm CMOS technology. In Proceedings of the 2016 IEEE Design and Diagnostics of Electronic Circuits and Systems, Prague, Czech Republic, 18–21 April 2006; pp. 25–30. [Google Scholar] [CrossRef]
- Ghobadi, N.; Majidi, R.; Mehran, M.; Afzali-Kusha, A. Low Power 4-Bit Full Adder Cells in Subthreshold Regime. In Proceedings of the 18th Iranian Conference on Electrical Engineering, Isfahan, Iran, 11–13 May 2010; pp. 362–367. [Google Scholar] [CrossRef]
- Pakniyat, E.; Talebiyan, S.R.; Morad, M.J.A. Design of High performance and Low Power 16T Full Adder Cell for Sub-threshold Technology. In Proceedings of the 2015 International Conference on Technology, Communication and Knowledge (ICTCK), Mashhad, Iran, 11–12 November 2015; pp. 79–85. [Google Scholar] [CrossRef]
- Tamang, D.; Pandey, V.; Singh, N.K. A Sub-Threshold Operation of XOR based Energy Efficient Full Adder. In Proceedings of the 2016 International Conference on Communication and Signal Processing (ICCSP), Melmaruvathur, India, 6–8 April 2016; pp. 1066–1069. [Google Scholar] [CrossRef]
- Monteiro, J.; Guntzel, J.L.; Agostini, L. A1CSA: An energy-efficient fast adder architecture for cell-based VLSI design. In Proceedings of the 18th IEEE International Conference on Electronics, Circuits, and Systems, Beirut, Lebanon, 11–14 December 2011; pp. 442–445. [Google Scholar] [CrossRef]
- Tran, A.T.; Baas, B.M. Design of an energy-efficient 32-bit adder operating at subthreshold voltages in 45-nm CMOS. In Proceedings of the International Conference on Communications and Electronics, Nha Trang, Vietnam, 11–13 August 2010; pp. 87–91. [Google Scholar] [CrossRef]
- Gupta, P.; Munje, I.; Kaswan, N.; Asati, A.; Gupta, A. Analysis & Implementation of Ultra Low Power 4-bit CLA in Subthreshold Regime. In Proceedings of the 2014 International Conference on Circuits, Power and Computing Technologies (ICCPCT), Nagercoil, India, 20–21 March 2014; pp. 1074–1076. [Google Scholar] [CrossRef]
- Alarcón, L.P.; Liu, T.T.; Pierson, M.D.; Rabaey, J.M. Exploring very low-energy logic: A case study. J. Low Power Electron. 2007, 3, 223–233. [Google Scholar] [CrossRef]
- Markovic, D.; Wang, C.C.; Alarcón, L.P.; Liu, T.T.; Rabaey, J.M. Ultralow-power design in near-threshold region. Proc. IEEE 2010, 98, 237–252. [Google Scholar] [CrossRef]
- Ho, W.G.; Chong, K.S.; Gwee, B.H.; Chang, J.S.; Sun, Y.; Chang, K.L. Improved Asynchronous-Logic Dual-Rail Sense Amplifier-Based Pass Transistor Logic with High Speed and Low Power Operation. In Proceedings of the 2011 IEEE International Symposium of Circuits and Systems (ISCAS), Rio de Janeiro, Brazil, 15–18 May 2011; pp. 1936–1939. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, Y.; Chen, L.; Zhang, X.; Shi, W. SAPTL–based Robust Sub-threshold Adder Circuit Design. In Proceedings of the 13th IEEE International Conference on Solid-State and Integrated Circuit Technology (ICSICT), Hangzhou, China, 25–28 October 2016; pp. 1–3. [Google Scholar] [CrossRef]
- Dang, F.; Wang, Y.; Liu, Y.; Jia, S.; Zhang, X. Design on Multi-bit Adder Using Sense Amplifier-Based Pass Transistor Logic for Near-Threshold Voltage Operation. In Proceedings of the 2015 IEEE 11th International Conference on ASIC (ASICON), Chengdu, China, 3–6 November 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Alarcón, L.P.; Liu, T.T.; Rabaey, J.M. A low-leakage parallel CRC generator for ultra-low power applications. In Proceedings of the 2011 IEEE International Symposium of Circuits and Systems (ISCAS), Rio de Janeiro, Brazil, 15–18 May 2011; pp. 2063–2066. [Google Scholar] [CrossRef]
- Alarcón, L.P. Sense Amplifier-based Pass Transistor Logic. Ph.D. Thesis, University of California at Berkeley, Berkeley, CA, USA, 2010. [Google Scholar]
- Kao, J.T.; Chandrakasan, A.P. Dual-threshold voltage techniques for low-power digital circuits. IEEE J. Solid State Circuits 2000, 35, 1009–1018. [Google Scholar] [CrossRef]
- Nabavi, M.; Ramezankhani, F.; Shams, M. Optimum pMOS-to-nMOS Width Ratio for Efficient Subthreshold CMOS Circuits. IEEE Trans. Electron. Devices 2016, 63, 916–924. [Google Scholar] [CrossRef]
- Weste, N.; Harris, D. CMOS VLSI Design: A Circuits and Systems Perspective, 4th ed.; Addison-Wesley: Boston, MA, USA, 2011; pp. 443–468. [Google Scholar]
- Wang, A.; Calhoun, B.H.; Chandrakasan, A.P. Minimizing Energy Consumption. In Sub-Threshold Design for Ultra Low-Power Systems; Chandrakasan, A.P., Ed.; Springer: Boston, MA, USA, 2006; pp. 42–48. [Google Scholar]

| Circuit Module | Width/Length of PMOS | Width/Length of NMOS | Fingers |
|---|---|---|---|
| Stack driver (plvt) | 750 nm/130 nm | 150 nm/130 nm | 1 |
| PTN (nlvt) | - | 150 nm/130 nm | 1 |
| PMOS capacitor in BSA | 1.1 μm/1.1 μm | - | 1 |
| INV in BSA | 560 nm/130 nm | 150 nm/130 nm | 1 |
| NOR in BSA | 300 nm/130 nm | 150 nm/130 nm | 1 |
| Other transistors in BSA | 150 nm/130 nm | 150 nm/130 nm | 1 |
| FA | 900 nm/130 nm | 150 nm/130 nm | 1 |
| XOR | 600 nm/130 nm | 150 nm/130 nm | 1 |
| Reference | [15] | [24] | [25] | [30] | This work |
|---|---|---|---|---|---|
| Transistor number | 420 (1×) | 1056 (2.51×) | 1260 (3.00×) | 1000 (2.38×) | 648 + 4 MOS-caps (1.55×) |
| Worst-case delay (ns) | 623.62 (1×) | 547.25 (0.88×) | 658.19 (1.06×) | 474.01 (0.76×) | 175.48 (0.28×) |
| Energy (fJ) | 22.45 (1×) | 55.99 (2.49×) | 74.15 (3.30×) | 60.37 (2.69×) | 20.63 (0.92×) |
| Energy-delay production (fJ/MHz) | 14.00 (1×) | 30.64 (2.19×) | 48.81 (3.49×) | 28.62 (2.04×) | 3.62 (0.26×) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Wu, Y.; Chen, L. A Subthreshold Bootstrapped SAPTL-Based Adder Design. Electronics 2019, 8, 1161. https://doi.org/10.3390/electronics8101161
Zhang Q, Wu Y, Chen L. A Subthreshold Bootstrapped SAPTL-Based Adder Design. Electronics. 2019; 8(10):1161. https://doi.org/10.3390/electronics8101161
Chicago/Turabian StyleZhang, Qi, Yuping Wu, and Lan Chen. 2019. "A Subthreshold Bootstrapped SAPTL-Based Adder Design" Electronics 8, no. 10: 1161. https://doi.org/10.3390/electronics8101161
APA StyleZhang, Q., Wu, Y., & Chen, L. (2019). A Subthreshold Bootstrapped SAPTL-Based Adder Design. Electronics, 8(10), 1161. https://doi.org/10.3390/electronics8101161




