Comparison of Measurement Methods of LV Grid Access Impedance in the Frequency Range Assigned to Nb‑Plc Technologies
Abstract
:1. Introduction
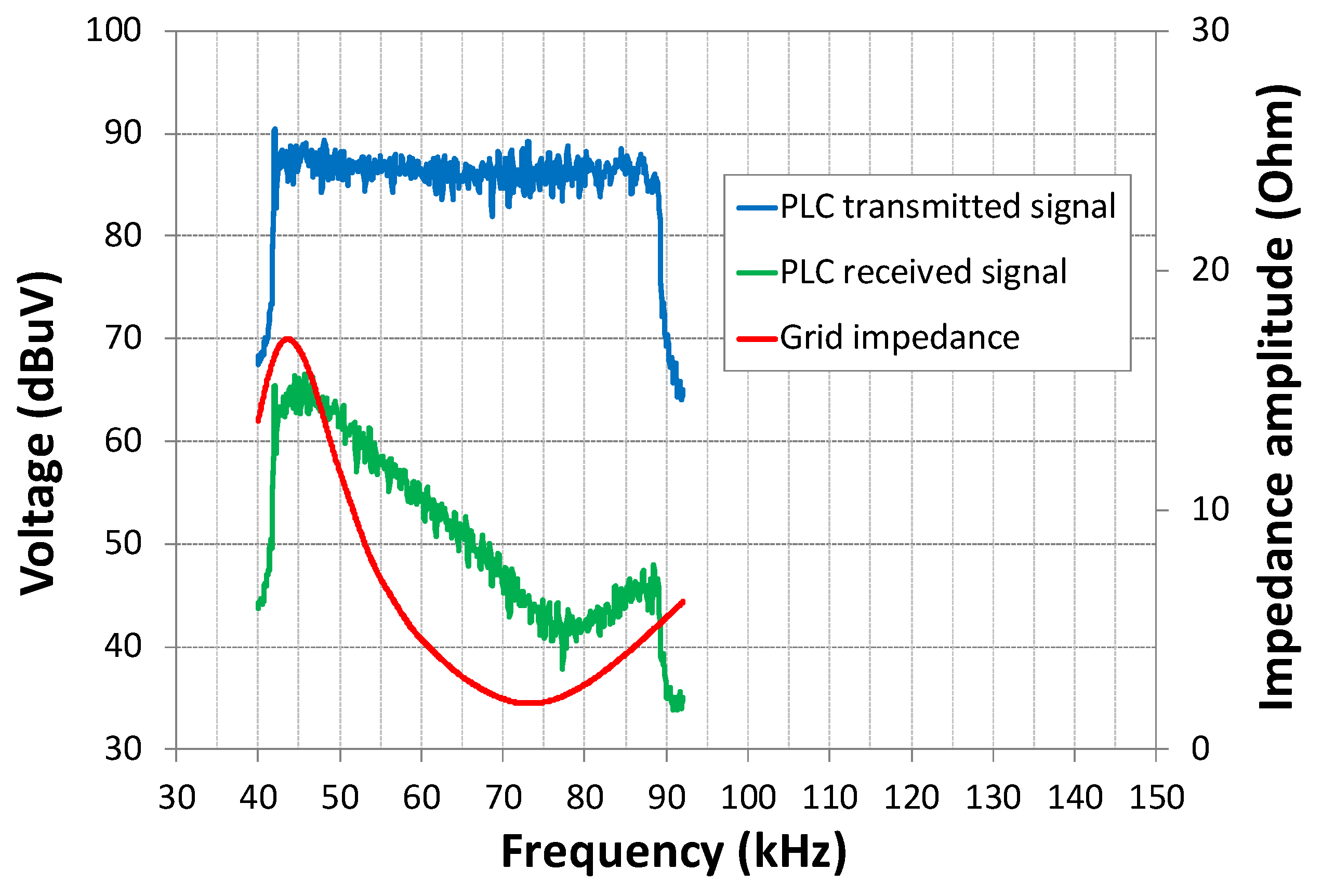
2. The Effects of the Grid Impedance on Narrow Band-Power Line Communications (NB-PLC)
3. Method I: IGOR-Meter
3.1. Measurement Setup for the IGOR-Meter
3.2. Data Processing
3.3. Advantages and Limitations
4. Method II: UPV/EHU Method
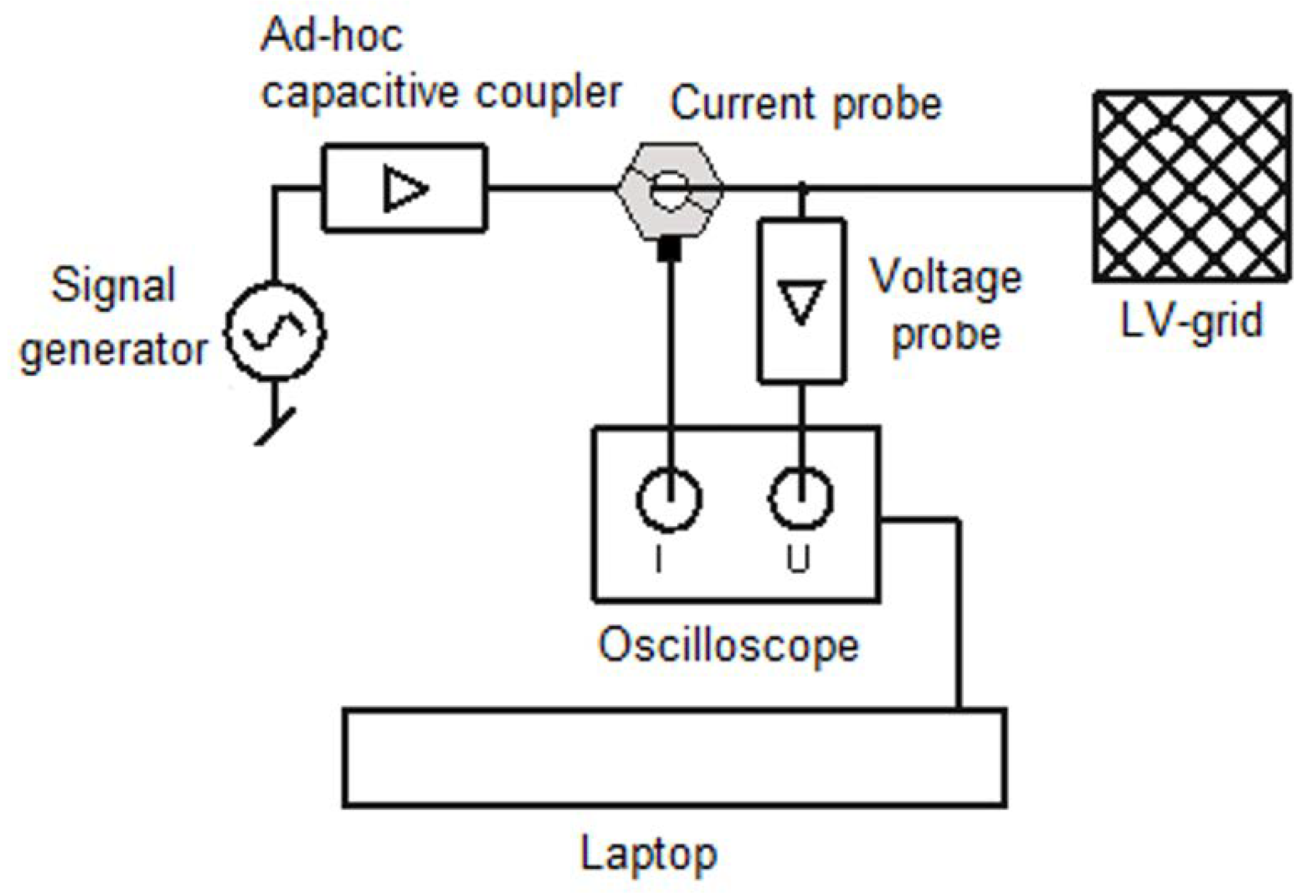
4.1. Fundamentals of the Method
4.2. Signal Processing
4.3. Advantages and Limitations
5. Method III: TUD Method
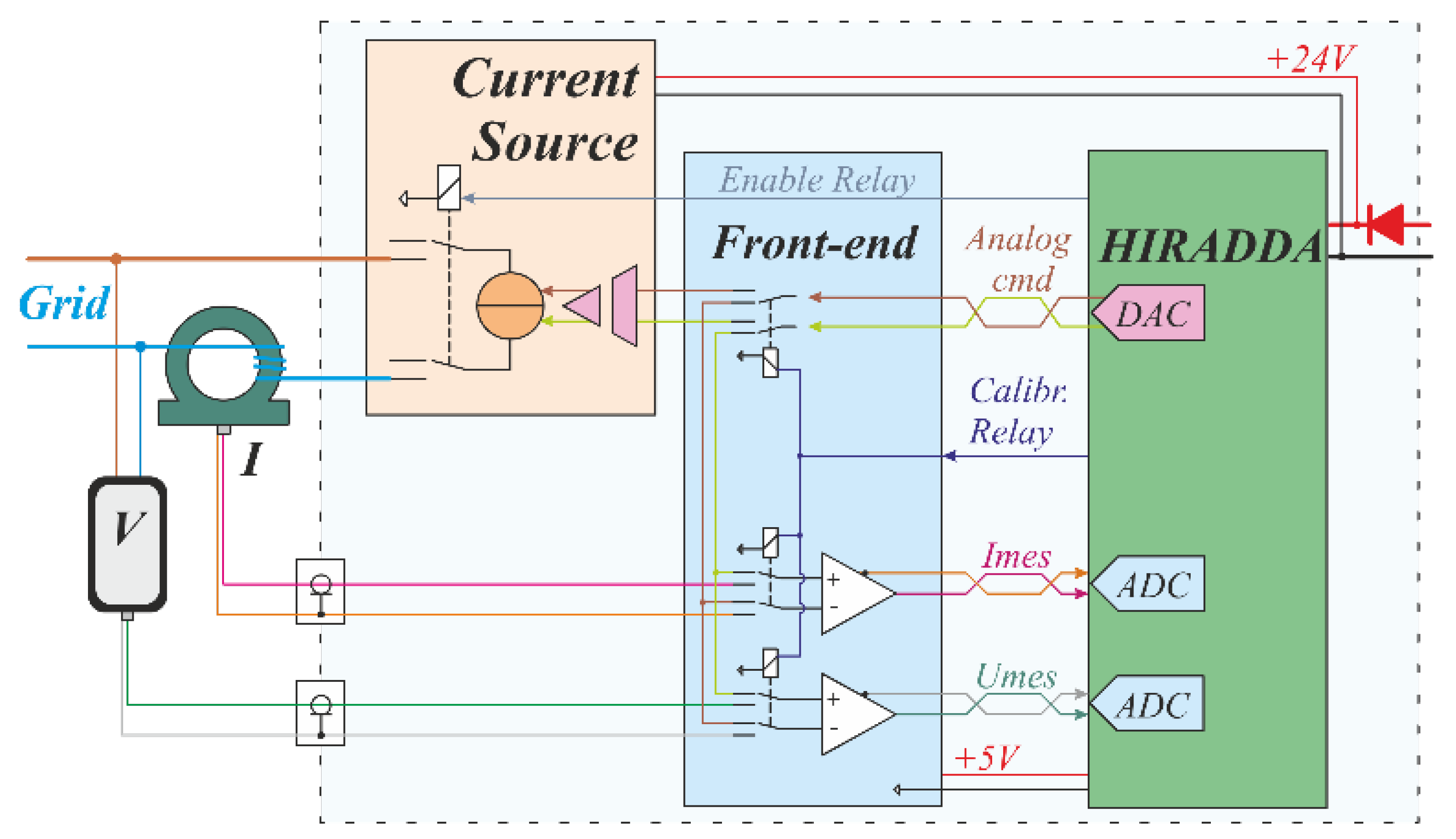
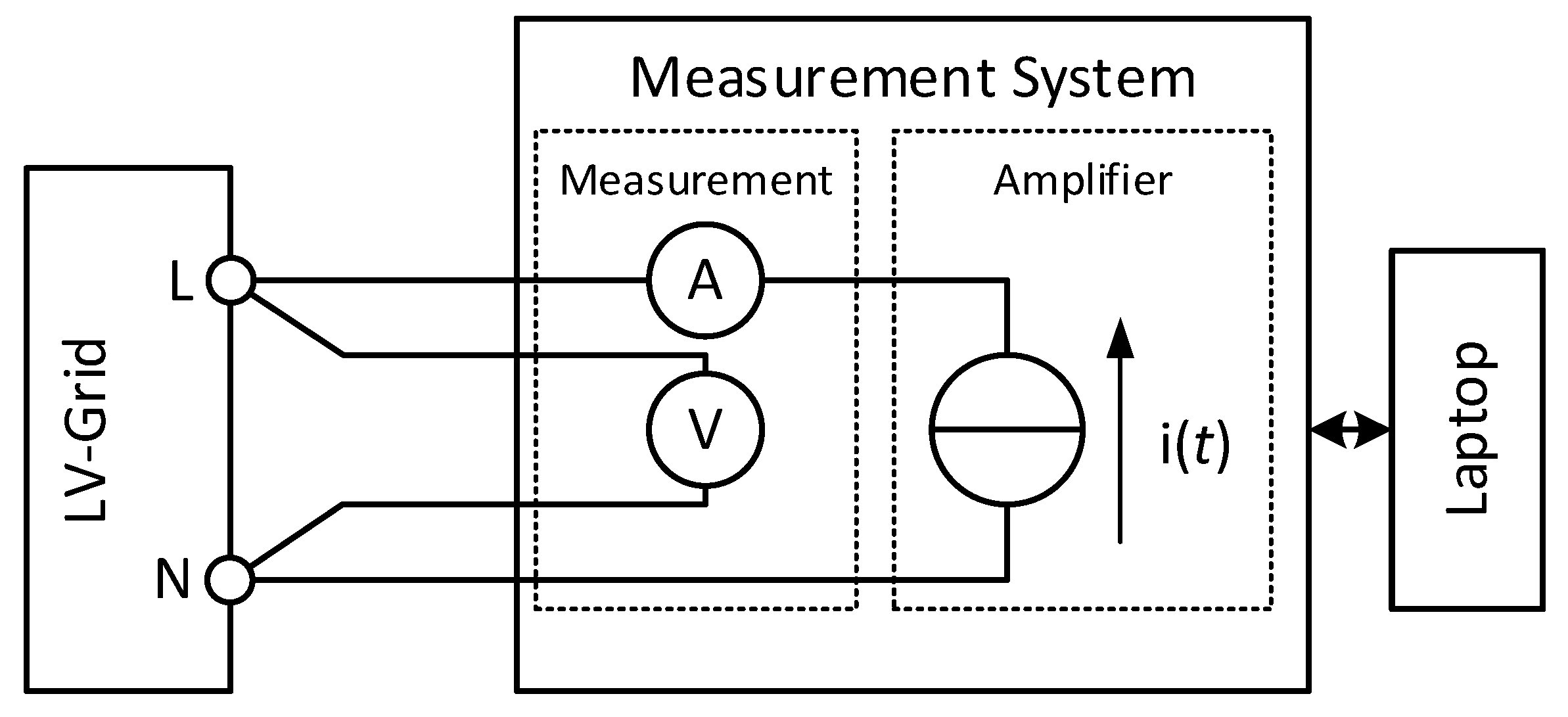
5.1. Hardware
- Linear amplifier current source for grid excitation
- Integrated voltage and current measurement
- Additional voltage input for external current probes
- Automated power supply disconnection and buffering capacitor
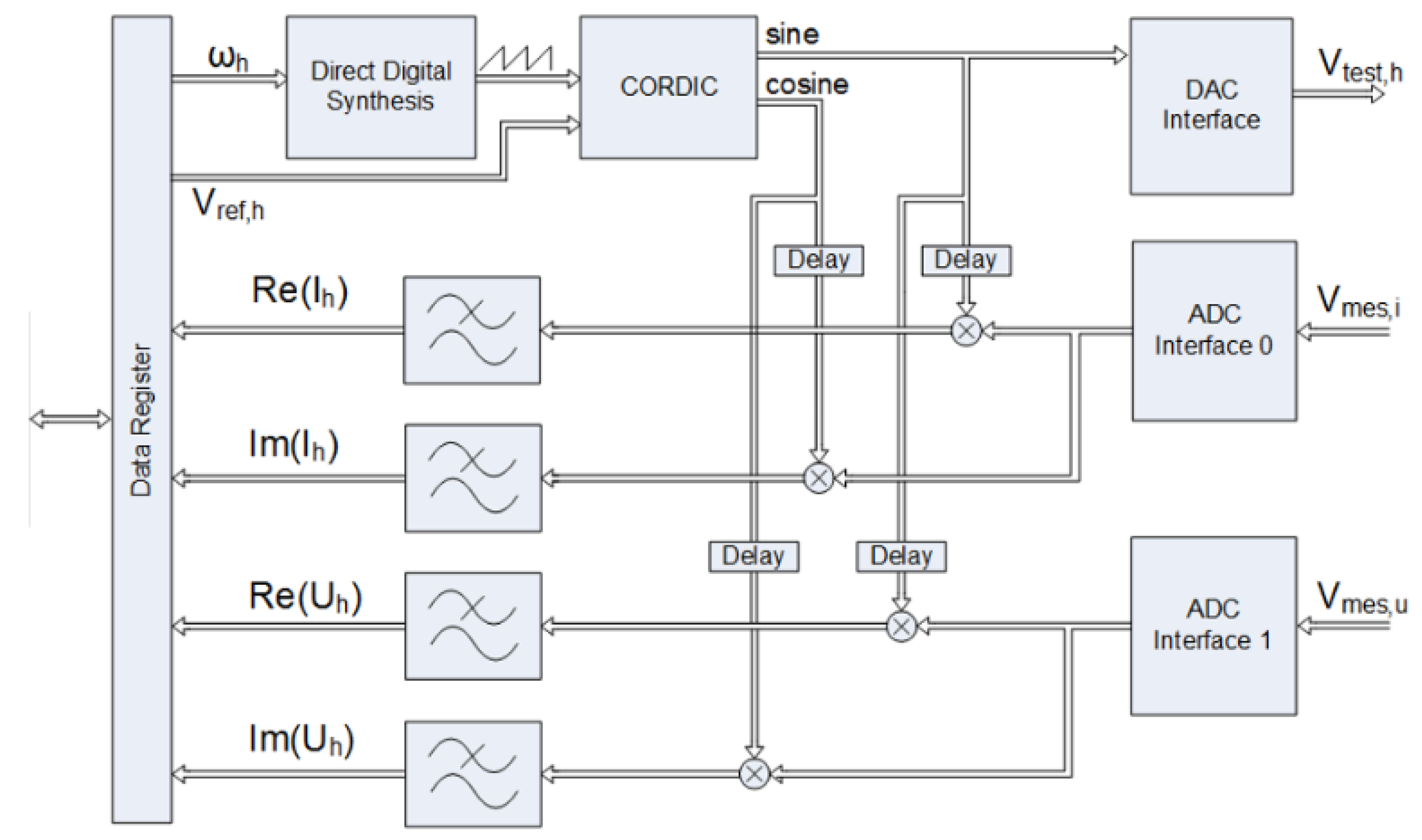
5.2. Measurement Algorithm
5.3. Advantages and Limitations
6. Comparison of the Measurement Methods
7. Results and Analysis
7.1. Measurement Scenario
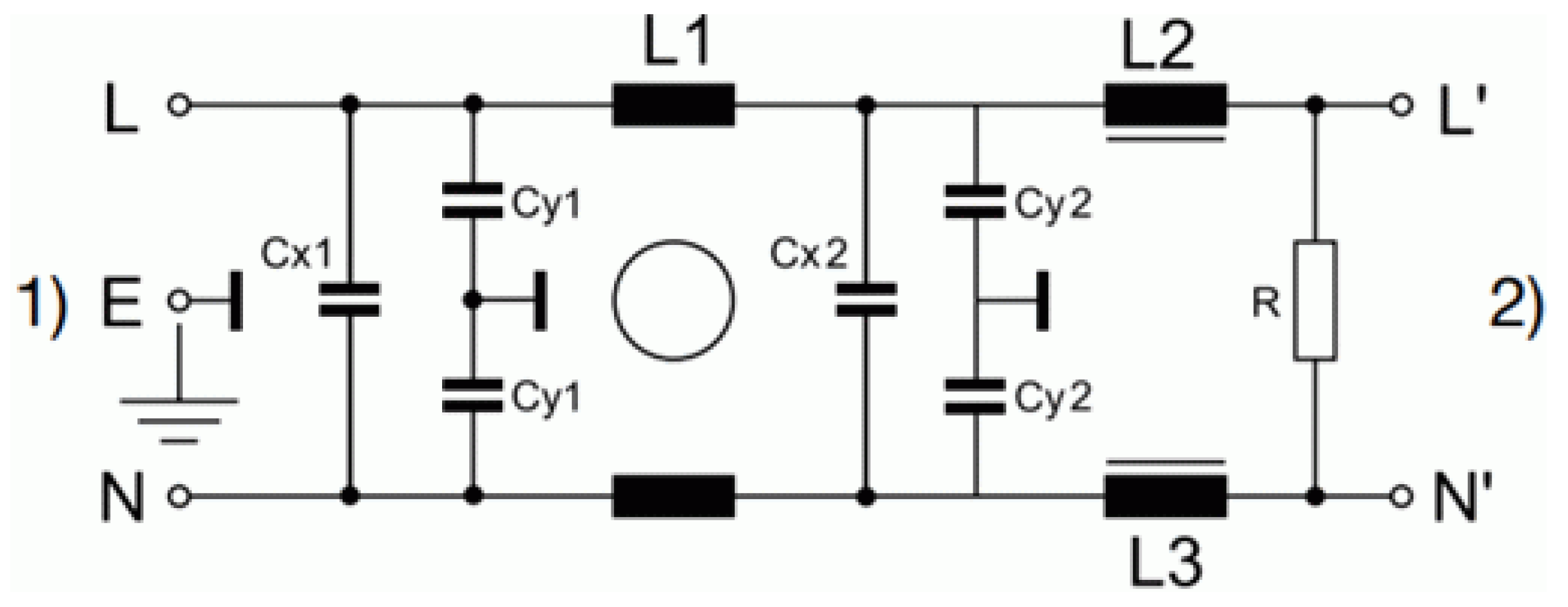
7.2. References for the Validation of the Methods
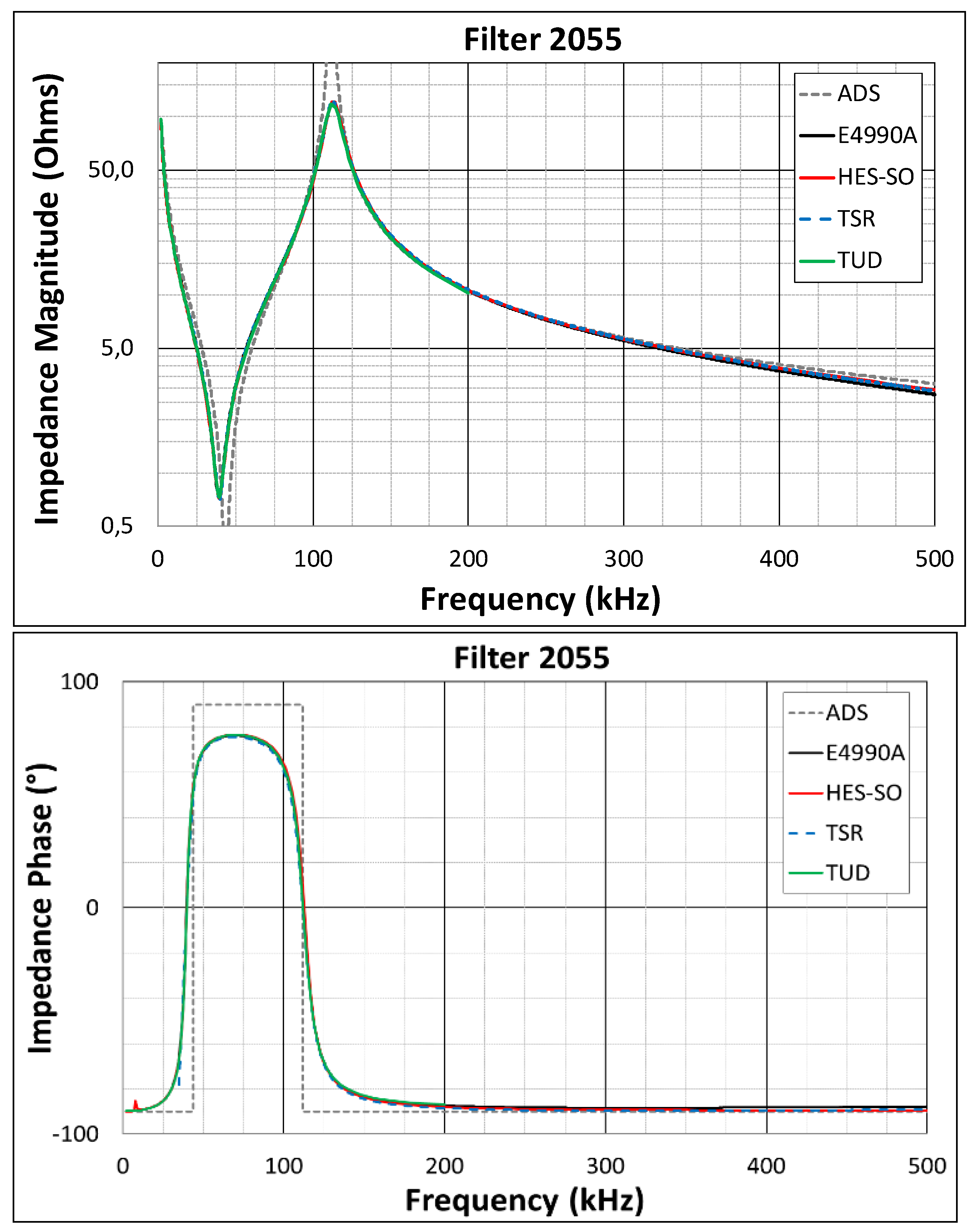
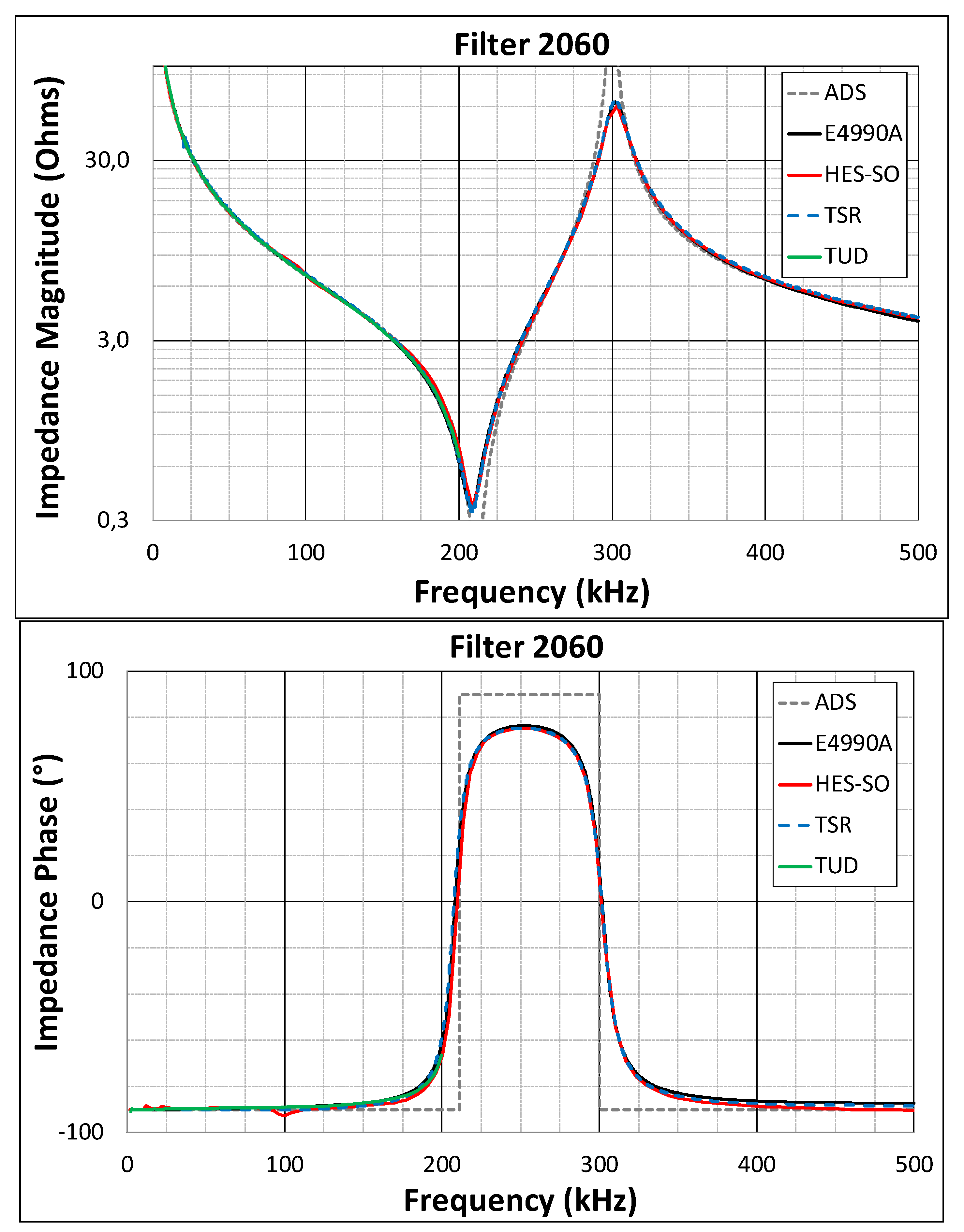
7.3. Results of the Comparison
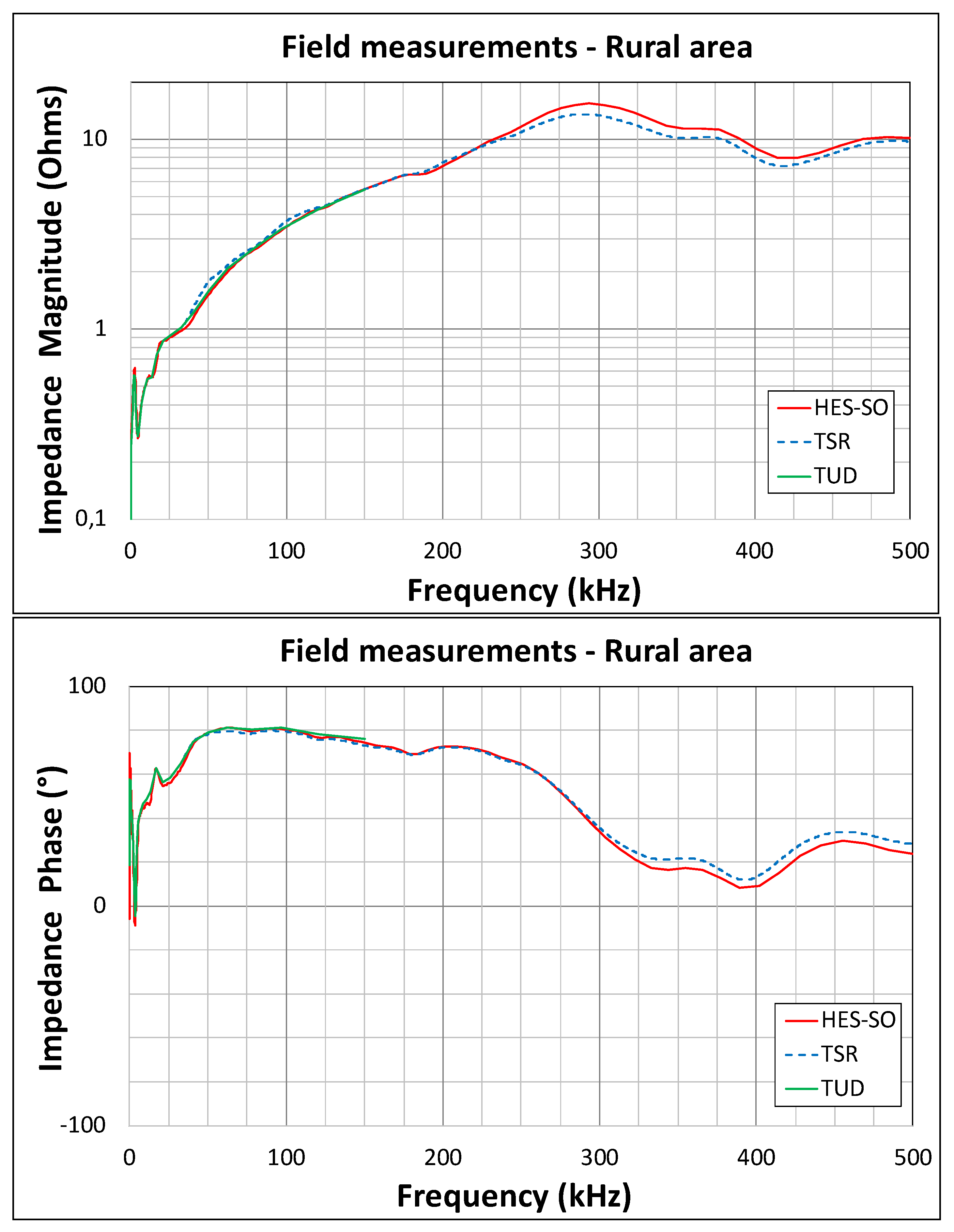
7.4. Use of the Measurement Methods in the Field
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- CENELEC. Study report III. In Electromagnetic Interference between Electrical Equipment/Systems in the Frequency Range below 150 kHz; SC205A/Sec0400/R, October 2015; NSAI: Nashua, NH, USA, 2015. [Google Scholar]
- IEC/TR. 60725:2012 Consideration of Reference Impedances and Public Supply Network Impedances for Use in Determining Disturbance Characteristics of Electrical Equipment Having a Rated Current ≤75 A per Phase. Available online: https://webstore.iec.ch/publication/3092 (accessed on 20 July 2019).
- EN 61000-4-7:2002 + A1:2009: Electromagnetic Compatibility (EMC)—Part 4-7: Testing and Measurement Techniques and Interharmonics Measurements. Available online: https://webstore.iec.ch/publication/4228 (accessed on 20 July 2019).
- Wang, J.; Tyuryukanov, I.; Monti, A. Design of a Novel Robust Current Controller for Grid-Connected Inverter Against Grid Impedance Variations. Int. J. Electr. Power Energy Syst. 2019, 110, 454–466. [Google Scholar] [CrossRef]
- Monteiro, H.L.M.; Duque, C.A.; Silva, L.R.M.; Meyer, J.; Stiegler, R.; Testa, A.; Ribeiro, P.F. Harmonic impedance measurement based on short time current injections. Electr. Power Syst. Res. 2017, 148, 108–116. [Google Scholar] [CrossRef]
- Liu, N.; Aljankawey, A.; Diduch, C.; Chang, L.; Su, J. Passive Islanding Detection Approach Based on Tracking the Frequency-Dependent Impedance Change. IEEE Trans. Power Deliv. 2015, 30. [Google Scholar] [CrossRef]
- Vijayakumari, A.; Devarajan, A.T.; Devarajan, N. Decoupled control of grid connected inverter with dynamic online grid impedance measurements for micro grid applications. Int. J. Electr. Power Energy Syst. 2015, 68, 1–14. [Google Scholar] [CrossRef]
- International Electrotechnical Commission, “IEC/TS 62578 Ed. 2.0: 2015 Power electronics systems and equipment—Operation conditions and characteristics of active infeed converter (AIC) applications including design recommendations for their emission values below 150 kHz.”. 2015. Available online: https://webstore.iec.ch/publication/22135 (accessed on 20 July 2019).
- Rönnberg, S.K.; Amaris, M.H.J.B.H.; Chang, G.W.; Gu, I.Y.H.; Kocewiak, Ł.H.; Meyer, J.; Olofsson, M.; Ribeiro, P.F.; Desmet, J. On waveform distortion in the frequency range of 2 kHz–150 kHz—Review and research challenges. Electr. Power Syst. Res. 2017, 150, 1–10. [Google Scholar] [CrossRef]
- Kotsampopoulos, P.; Rigas, A.; Kirchhof, J.; Messinis, G.; Dimeas, A.; Hatziargyriou, N.; Rogakos, V.; Andreadis, K. EMC Issues in the Interaction Between Smart Meters and Power-Electronic Interfaces. IEEE Trans. Power Deliv. 2017, 32, 822–831. [Google Scholar] [CrossRef]
- Hallak, G.; Bumiller, G. Data rate optimization on PLC devices with current controller for low access impedance. In Proceedings of the 2016 International Symposium on Power Line Communications and its Applications (ISPLC), Bottrop, Germany, 29 March–1 April 2016. [Google Scholar]
- Lopes, P.A.C.; Pinto, J.M.M.; Gerald, J.B. Dealing with Unknown Impedance and Impulsive Noise in the Power-Line Communications Channel. IEEE Trans. Power Deliv. 2013, 28. [Google Scholar] [CrossRef]
- Zhai, M.-Y. Transmission Characteristics of Low-Voltage Distribution Networks in China Under the Smart Grids Environment. IEEE Trans. Power Deliv. 2011, 26, 173–180. [Google Scholar] [CrossRef]
- Pasdar, A.M.; Cavdar, I.H.; Sozer, Y. Power-Line Impedance Estimation at FCC Band Based on Intelligent Home Appliances Status Detection Algorithm Through Their Individual Energy and Impedance Signatures. IEEE Trans. Power Deliv. 2014, 29, 1407–1416. [Google Scholar] [CrossRef]
- Lampe, L.; Tonello, A.M.; Swart, T.G. Power Line Communications. Principles, Standards and Applications from Multimedia to Smart Grid, 2nd ed.Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- CENELEC. Signalling on Low-Voltage Electrical Installations in the Frequency Range 3 kHz to 148.5 kHz; Part 1: General requirements, frequency bands and electromagnetic disturbances; CENELEC: Brussels, Belgium, 2011. [Google Scholar]
- Cano, C.; Pittolo, A.; Malone, D.; Lampe, L.; Tonello, A.M.; Dabak, A.G. State of the art in power line communications: From the applications to the medium. IEEE J. Sel. Areas Commun. 2016, 34, 1935–1952. [Google Scholar] [CrossRef]
- Arechalde, I.; Castro, M.; García-Borreguero, I.; Sendín, A.; Urrutia, I.; Fernandez, A. Performance of PLC communications in frequency bands from 150 kHz to 500 kHz. In Proceedings of the 2017 IEEE International Symposium on Power Line Communications and its Applications (ISPLC), Madrid, Spain, 3–5 April 2017. [Google Scholar]
- Sendin, A.; Kim, I.H.; Bois, S.; Munoz, A.; Llano, A. Prime v1. 4 evolution: A future proof of reality beyond metering. In Proceedings of the 2014 IEEE International Conference on Smart Grid Communications (SmartGridComm), Venice, Italy, 3–6 November 2014; pp. 332–337. [Google Scholar]
- López, G.; Matanza, J.; de la Vega, D.; Castro, M.; Arrinda, A.; Moreno, J.I.; Sendin, A. The Role of Power Line Communications in the Smart Grid Revisited: Applications, Challenges, and Research Initiatives. IEEE Access 2019, 7, 117346–117368. [Google Scholar] [CrossRef]
- Fernandez, I.; Uribe-Pérez, N.; Eizmendi, I.; Angulo, I.; de la Vega, D.; Arrinda, A.; Arzuaga, T. Characterization of non-intentional emissions from distributed energy resources up to 500 kHz: A case study in Spain. Int. J. Electr. Power Energy Syst. 2019, 105, 549–563. [Google Scholar] [CrossRef]
- Fernández, I.; de la Vega, D.; Arrinda, A.; Angulo, I.; Uribe-Pérez, N.; Llano, A. Field Trials for the Characterization of Non-Intentional Emissions at Low-Voltage Grid in the Frequency Range Assigned to NB PLC Technologies. Electronics 2019, 8, 1044. [Google Scholar] [CrossRef]
- Llano, A.; de la Vega, D.; Angulo, I.; Marron, L. Impact of Channel Disturbances on Current Narrowband Power Line Communications and Lessons to Be Learnt for the Future Technologies. IEEE Access 2019, 7, 83797–83811. [Google Scholar] [CrossRef]
- Fernández, I.; Angulo, I.; Arrinda, A.; de la Vega, D.; Arechalde, I.; Uribe-Perez, N.; Arzuaga, T. Proceedings of the Characterization of the Frequency-Dependent Transmission Losses of the Grid up to 500 kHz (CIRED-2019), Madrid, Spain, 3–6 June 2019.
- International Telecommunications Union. ITU-T Rec. G.9903: Narrowband Orthogonal Frequency Division Multiplexing Power Line Communication Transceivers for G3-PLC Networks. Available online: http://www.itu.int/rec/T-REC-G.9903 (accessed on 20 July 2019).
- PRIME Alliance Technical Working Group. PRIME 1.4 White Paper. Available online: http://www.prime-alliance.org/wp-content/uploads/2014/10/whitePaperPrimeV1p4_final.pdf (accessed on 20 July 2019).
- Cortes, J.A.; Sanz, A.; Estopiñán, P.; Garcia, J.I. Analysis of Narrowband Power Line Communication Channels for Advanced Metering Infrastructure. EURASIP J. Adv. Signal Process. 2015, 2015. [Google Scholar] [CrossRef]
- Fernández, I.; Arrinda, A.; Angulo, I.; de la Vega, D.; Uribe-Pérez, N.; Llano, A. Field Trials for the Empirical Characterization of the Low Voltage Grid Access Impedance from 35 kHz to 500 kHz. IEEE Access 2019, 7, 85786–85795. [Google Scholar] [CrossRef]
- Chu, G.; Li, J.; Liu, W. Narrow band power line channel characteristics for low voltage access network in China. In Proceedings of the International Symposium on Power Line Communications and Its Applications (ISPLC), Johannesburg, South Africa, 24–27 March 2013. [Google Scholar]
- Hooijen, O.G. A channel model for the residential power circuit used as a digital communications medium. IEEE Trans. Electromagn. Compat. 1998, 40, 331–336. [Google Scholar] [CrossRef]
- Vines, R.M.; Trussell, H.J.; Shuey, K.C.; O’Neal, J.B. Impedance of the Residential Power-Distribution Circuit. IEEE Trans. Electromagn. Compat. 1985, 1, 6–12. [Google Scholar] [CrossRef]
- Tonello, A.M.; Pittolo, A. Considerations on Narrowband and Broadband Power Line Communication for Smart Grids. In Proceedings of the 2015 IEEE International Conference on Smart Grid Communications (SmartGridComm), Miami, FL, USA, 2–5 November 2015. [Google Scholar] [CrossRef]
- Atayero, A.A.; Alatishe, A.; Ivanov, Y.A. Power line communication technologies: modeling and simulation of prime physical layer. World Congr. Eng. Comput. Sci. 2012, 2, 931–936. [Google Scholar]
- Karakash, J.J. Transmission Lines and Filter Networks; MacMillan: Beijing, China, 1950. [Google Scholar]
- Mlynek, P.; Koutny, M.; Misurec, J.; Kolka, Z. Measurements and evaluation of PLC modem with G3 and PRIME standards for Street Lighting Control. In Proceedings of the 18th IEEE International Symposium on Power Line Communications and Its Applications, Glasgow, UK, 30 March–2 April 2014. [Google Scholar] [CrossRef]
- Meyer, J.; Khokhlov, V.; Klatt, M.; Blum, J.; Waniek, C.; Wohlfahrt, T.; Myrzik, J. Overview and Classification of Interferences in the Frequency Range 2–150 kHz (Supraharmonics). In Proceedings of the 2018 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Amalfi, Italy, 20–22 June 2018. [Google Scholar] [CrossRef]
- Körner, P.M.; Stiegler, R.; Meyer, J.; Wohlfahrt, T.; Waniek, C.; Myrzik, J.M.A. Acoustic noise of massmarket equipment caused by supraharmonics in the frequency range 2 to 20 kHz. In Proceedings of the 2018 18th International Conference on Harmonics and Quality of Power (ICHQP), Ljubljana, Slovenia, 13–16 May 2018; pp. 1–6. [Google Scholar]
- López, G.; Moreno, J.I.; Sánchez, E.; Martínez, C.; Martín, F. Noise Sources, Effects and Countermeasures in Narrowband Power-Line Communications Networks: A Practical Approach. Energies 2017, 10, 1238. [Google Scholar] [CrossRef]
- Mlynek, P.; Fujdiak, R.; Misurec, J.; Slacik, J. Experimental measurements of noise influence on narrowband Power Line Communication. In Proceedings of the 2016 8th International Congress on Ultra Modern Telecommunications and Control Systems and Workshops (ICUMT), Lisbon, Portugal, 18–20 October 2016. [Google Scholar] [CrossRef]
- Aloui, A.; Rhouma, O.B.; Rebai, C. Impact of equalization on hybrid communication system for smart grid. In Proceedings of the 2017 International Symposium on Networks, Computers and Communications (ISNCC), Marrakech, Morocco, 16–18 May 2017. [Google Scholar] [CrossRef]
- Nikfar, B.; Bumiller, G. Real-time synchronization and multiband detection for narrowband power line communication. In Proceedings of the 2017 IEEE International Symposium on Power Line Communications and its Applications (ISPLC), Madrid, Spain, 3–5 April 2017. [Google Scholar] [CrossRef]
- Nikfar, B.; Bumiller, G.; Vinck, A.J.H. An adaptive pursuit strategy for dynamic spectrum assignment in narrowband PLC. In Proceedings of the 2017 IEEE International Symposium on Power Line Communications and its Applications (ISPLC), Madrid, Spain, 3–5 April 2017. [Google Scholar] [CrossRef]
- Available online: IEC 61000-2-2:2002+AMD1:2017+AMD2:2018 CSV (Consolidated Version) Electromagnetic compatibility (EMC)—Environment—Compatibility levels for low-frequency conduced disturbances and signaling in public low-voltage power supply systems. Available online: https://webstore.iec.ch/publication/63116 (accessed on 20 July 2019).
- Hallak, G.; Nieß, C.; Bumiller, G. Accurate Low Access Impedance Measurements with Separated Load Impedance Measurements on the Power-Line Network. IEEE Trans. Instrum. Meas. 2018, 67, 2282–2293. [Google Scholar] [CrossRef]
- Stiegler, R.; Meyer, J.; Schegner, P.; Chakravorty, D. Measurement of network harmonic impedance in presence of electronic equipment. In Proceedings of the IEEE International Workshop on Applied Measurements for Power Systems (AMPS), Aachen, Germany, 23–25 September 2015. [Google Scholar]
- Sigle, M.; Liu, W.; Karlsruhe, K.D. On the impedance of the low-voltage distribution grid at frequencies up to 500 kHz. In Proceedings of the 2012 IEEE International Symposium on Power Line Communications and Its Applications, Beijing, China, 27–30 March 2012; pp. 30–34. [Google Scholar]
- Zhao, H.; Zhang, W.; Wang, Y. An Effective Method to Calculate Frequency Response of Distribution Networks for PLC Applications. Electronics 2019, 8, 649. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, W.; Wang, Y. Characteristic Impedance Analysis of Medium-Voltage Underground Cables with Grounded Shields and Armors for Power Line Communication. Electronics 2019, 8, 571. [Google Scholar] [CrossRef]
- Roggo, D.; Marendaz, L.; Furrer, D. On-Line 2 to 150 kHz Grid Impedance Meter. In Proceedings of the Paper 1417, CIRED Conference 2013, Stockholm, Sweden, 10–13 June 2013. [Google Scholar]
- Capponi, L.; Fernández, I.; Roggo, D.; Arrinda, A.; Angulo, I.; de la Vega, D. Comparison of Measurement Methods of Grid Impedance for Narrow Band-PLC up to 500 kHz. In Proceedings of the IEEE 9th International Workshop on Applied Measurements for Power Systems (AMPS), Bologna, Italy, 26–28 September 2018. [Google Scholar]
- Roggo, D.; Horta, R.; Capponi, L.; Eggenschwiler, L.; Decorvet, F.; Pellodi, C.; Buholzer, F. Electromagnetic interferences in Smart Grid applications: A case study with PLC Smart Meters and PV energy generation. In Proceedings of the Paper 1285, CIRED Conference 2017, Glasgow, UK, 12–15 June 2017. [Google Scholar]
- Zurich Instruments. Principles of Lock-in Detection and the State of the Art. Available online: www.zhinst.com/applications/principles-of-lock-in-detection (accessed on 20 July 2019).
- Fernández, I.; Arrinda, A.; Angulo, I.; Alberro, M.; Montalbán, J.; de la Vega, D. Measurement method for the characterization of the grid impedance of LV networks for the frequency range for NB-PLC up to 500 kHz. In Proceedings of the CENELEC SC205A WG11 6th Meeting, Viena, Austria, 2 October 2018; Available online: https://collaborate.iec.ch/#/pages/workspaces/402718/documents/97024 (accessed on July 2019).
- Fernández, I.; Alberro, M.; Montalbán, J.; Arrinda, A.; Angulo, I.; de la Vega, D. A new voltage probe with improved performance at the 10 kHz–500 kHz frequency range for field measurements in LV networks. Measurement 2019, 145, 519–524. [Google Scholar] [CrossRef]
- Keysight Tecnhologies. Advanced Design System (ADS). Available online: https://www.keysight.com/en/pc-1297113/advanced-design-system-ads (accessed on 20 July 2019).
- Keysight Tecnhologies. E4990A Impedance Analyzer. Data sheet. Available online: https://www.keysight.com/en/pd-2405177-pn-E4990A (accessed on 20 July 2019).
- Farias, L.D.; Monteiro, L.; Leme, M.; Stevan, S. Empirical Analysis of the Communication in Industrial Environment Based on G3-Power Line Communication and Influences from Electrical Grid. Electronics 2018, 7, 194. [Google Scholar] [CrossRef]
- Zhu, Q.; Chen, Z.; He, X. Resource Allocation for Relay-Based OFDMA Power Line Communication System. Electronics 2019, 8, 125. [Google Scholar] [CrossRef]
- Bernacki, K.; Wybrańczyk, D.; Zygmanowski, M.; Latko, A.; Michalak, J.; Rymarski, Z. Disturbance and Signal Filter for Power Line Communication. Electronics 2019, 8, 378. [Google Scholar] [CrossRef]
- Varajão, D.; Araújo, R.E.; Miranda, L.; Lopes, J.P. EMI Filter Design for a Single-stage Bidirectional and Isolated AC–DC Matrix Converter. Electronics 2018, 7, 318. [Google Scholar] [CrossRef]
- Wu, C.; Gao, F.; Dai, H.; Wang, Z. A Topology-Based Approach to Improve Vehicle-Level Electromagnetic Radiation. Electronics 2019, 8, 364. [Google Scholar] [CrossRef]
| Method I (HES-SO) | Method II (UPV/EHU) | Method III (TUD) | ||
|---|---|---|---|---|
| Weight | Plugged: 12 Kg Battery powered 25 Kg | 5 Kg | 20 Kg | |
| Supply | Plugged. Optional: battery during measurement | Battery powered (only signal generator is currently plugged) | Plugged, but internally powered during measurement | |
| Need to synchronize to mains | No need of synchronization | No need of synchronization | Synchronized to mains | |
| Coupling to grid | Connection | Direct connection | Via capacitive coupler | Direct connection |
| Probes | External (Optional: Internal) | External | Internal (Optional: External) | |
| Connection for measurement | 4-wire (current injection and voltage measurement separately) | 4-wire (current injection and voltage measurement separately) | 4-wire (current injection and voltage measurement separately) | |
| Excitation source | Type and amplitude | Current (200 mA linear) | Voltage (configurable up to 10 Vpp) | Current (3 Arms linear) |
| Frequency sweep | Single frequency steps (configurable) | Single tone – continuous sweep (sweep time config., typ.: 1 sec) | Single frequency steps | |
| Signal acquis, | Sampling frequency | 4 MSample/s | 3.9 MSample/s | 10 MSample/s |
| Amplitude resolution | 24 bits (adjusted to mains amplitude) | 15 bits/channel (adjusted to the excitation level) | 16 bits (adjusted to mains amplitude) | |
| Suppression of fundamental | None | Filtering of 50/60 Hz and low-order harmonics | None | |
| Signal processing | Signal processing | Dual-Phase Demodulation (Lock-In Amplifier Detection) | Fourier analysis (FFT) | Fourier analysis (DFT) |
| Time windowing | -- | Configurable: Rectangular/Gaussian (Typ.: 20 ms window, 5 ms sliding window) | Rectangular, 200 ms (10 fundamental cycles length) | |
| Analysis in frequency domain | Bandwidth | 1 kHz–500 kHz | 20 kHz–500 kHz | 0 kHz–200 kHz |
| Frequency resolution | Configurable, from 5 Hz to 50 Hz | Configurable. Typical: 50 Hz. Best resolution: 5 Hz | 5 Hz | |
| Measurement time | From 1 to 3 min (related to resolution in frequency) | Configurable (related to sweep time). Typical: 2 s | Several minutes | |
| Accuracy | Methodology | Measurement emulation (HiRADDA + acquisition interface) of 1 Ω load. Tolerance on external probes considered | Comparison to impedance precision meter in measurements of precision resistances (0.5 to 50 Ω) | Measurement of a metrological calibrated 1 Ω Shunt |
| Maximum error (for the whole frequency range) | In amplitude: ±6% In phase: ±10° | In amplitude: ±3% for Z > 10 Ω, ±6% for Z < 10 Ω In phase: ±5° | In amplitude: ±10% for Z < 0.2 Ω ±5% for 0.2 Ω ≤ Z < 0.5 Ω ±3% for Z > 0.5 Ω In phase: ±10° for Z < 0.2 Ω ±5° for 0.2 Ω ≤ Z< 0.5 Ω ±8° for Z > 50 Ω | |
| Method I (HES-SO) | Method II (UPV/EHU) | Method III (TUD) | |
|---|---|---|---|
| Advantages |
|
|
|
| Limitations |
|
|
|
| Relative Amplitude Error | Phase Error | |||||
|---|---|---|---|---|---|---|
| Freq (kHz) | HES-SO | UPV/EHU | TUD | HES-SO | UPV/EHU | TUD |
| 10 | 0.17% | - | 0.18% | 0.44° | - | 0.00° |
| 40 | 2.57% | 3.19% | 2.56% | 1.13° | 5.86° | 1.53° |
| 80 | 2.21% | 0.12% | 0.13% | 0.52° | 0.87° | 0.41° |
| 120 | 4.51% | 0.35% | 2.42% | 0.57° | 0.43° | 0.47° |
| 160 | 0.52% | 0.93% | 2.30% | 0.56° | 0.50° | 0.28° |
| 200 | 0.37% | 1.00% | 2.89% | 0.66° | 0.26° | 0.50° |
| 240 | 0.79% | 0.97% | - | 0.75° | 0.02° | - |
| 280 | 1.33% | 1.80% | - | 0.83° | 0.01° | - |
| 320 | 1.91% | 2.16% | - | 0.94° | 0.11° | - |
| 360 | 2.82% | 2.59% | - | 1.05° | 0.17° | - |
| 400 | 3.78% | 2.88% | - | 1.32° | 0.75° | - |
| 440 | 4.51% | 4.07% | - | 1.50° | 0.69° | - |
| 480 | 5.49% | 4.47% | - | 1.65° | 0.92° | - |
| Average | 2.38% | 2.04% | 1.75% | 0.92° | 0.88° | 0.53° |
| Relative Amplitude Error | Phase Error | |||||
|---|---|---|---|---|---|---|
| Freq (kHz) | HES-SO | UPV/EHU | TUD | HES-SO | UPV/EHU | TUD |
| 10 | 2.53% | - | 0.47% | 0.01° | - | 0.00° |
| 40 | 0.99% | 0.49% | 0.39% | 0.21° | 1.07° | 0.16° |
| 80 | 1.43% | 1.37% | 0.10% | 0.08° | 0.91° | 0.21° |
| 120 | 0.98% | 1.59% | 0.29% | 1.06° | 0.46° | 0.08° |
| 160 | 3.13% | 2.58% | 0.62% | 1.41° | 0.19° | 0.19° |
| 200 | 17.24% | 2.52% | 7.82% | 6.06° | 1.87° | 5.38° |
| 240 | 3.68% | 0.03% | - | 1.01° | 0.34° | - |
| 280 | 0.68% | 1.32% | - | 1.56° | 0.19° | - |
| 320 | 1.21% | 1.87% | - | 1.07° | 0.16° | - |
| 360 | 1.04% | 2.94% | - | 1.94° | 0.07° | - |
| 400 | 1.55% | 3.23% | - | 2.35° | 0.27° | - |
| 440 | 2.37% | 3.65% | - | 2.73° | 0.31° | - |
| 480 | 3.23% | 4.50% | - | 3.07° | 0.58° | - |
| Average | 3.08% | 2.17% | 1.62% | 1.73° | 0.54° | 1.01° |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández, I.; de la Vega, D.; Roggo, D.; Stiegler, R.; Capponi, L.; Angulo, I.; Meyer, J.; Arrinda, A. Comparison of Measurement Methods of LV Grid Access Impedance in the Frequency Range Assigned to Nb‑Plc Technologies. Electronics 2019, 8, 1155. https://doi.org/10.3390/electronics8101155
Fernández I, de la Vega D, Roggo D, Stiegler R, Capponi L, Angulo I, Meyer J, Arrinda A. Comparison of Measurement Methods of LV Grid Access Impedance in the Frequency Range Assigned to Nb‑Plc Technologies. Electronics. 2019; 8(10):1155. https://doi.org/10.3390/electronics8101155
Chicago/Turabian StyleFernández, Igor, David de la Vega, Dominique Roggo, Robert Stiegler, Lino Capponi, Itziar Angulo, Jan Meyer, and Amaia Arrinda. 2019. "Comparison of Measurement Methods of LV Grid Access Impedance in the Frequency Range Assigned to Nb‑Plc Technologies" Electronics 8, no. 10: 1155. https://doi.org/10.3390/electronics8101155
APA StyleFernández, I., de la Vega, D., Roggo, D., Stiegler, R., Capponi, L., Angulo, I., Meyer, J., & Arrinda, A. (2019). Comparison of Measurement Methods of LV Grid Access Impedance in the Frequency Range Assigned to Nb‑Plc Technologies. Electronics, 8(10), 1155. https://doi.org/10.3390/electronics8101155






