Power-Time Exploration Tools for NMP-Enabled Systems
Abstract
1. Introduction
2. Previous Works and Problem Statements
3. Proposed Power-Time Exploration
3.1. Power-Time Optimization
3.2. Power-Time Cost Using Easy-to-Use Lambda for Design Decision
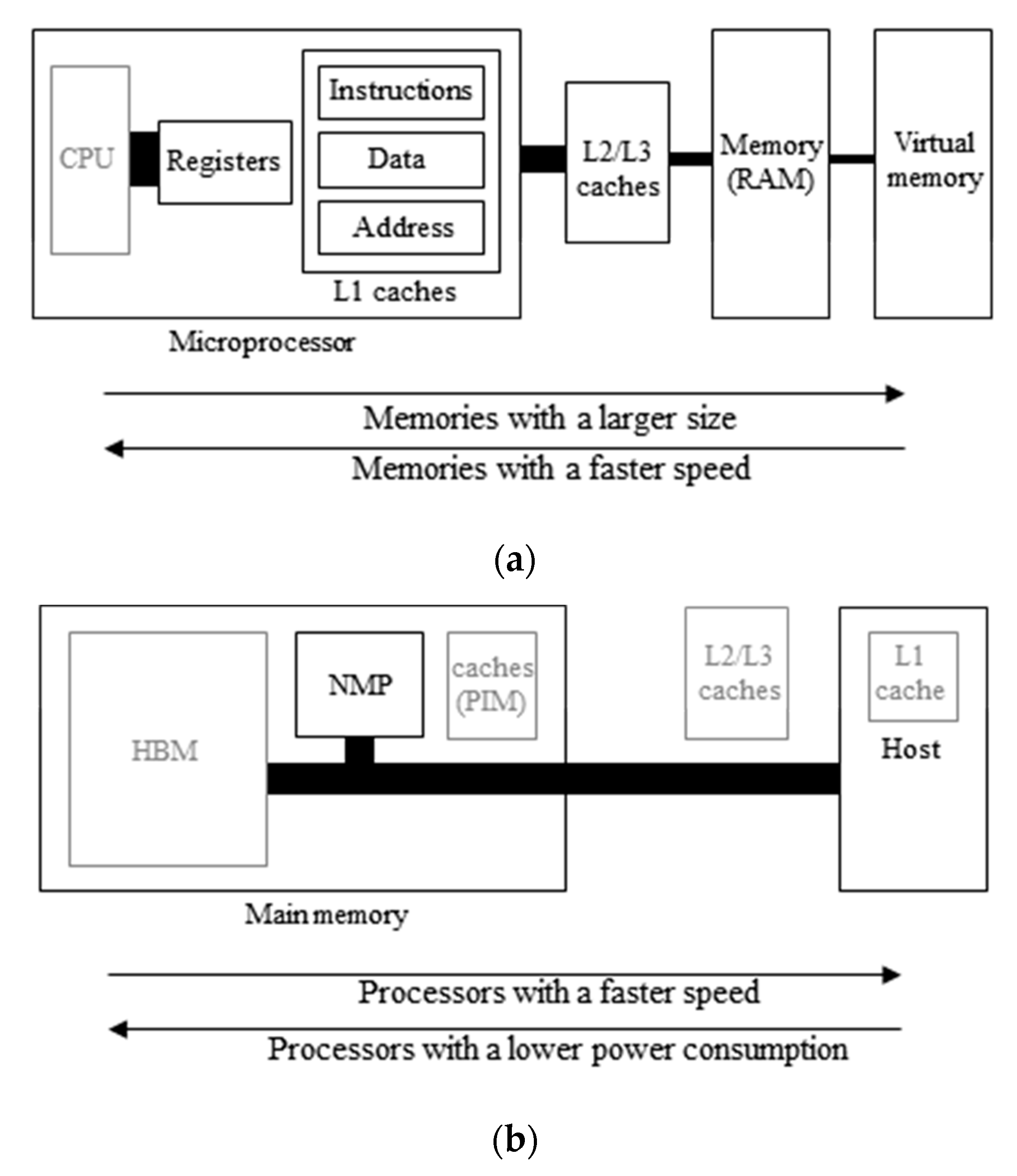
4. Evaluation Environment
4.1. NMP-Enabled System Organization
4.2. Simulation Environment
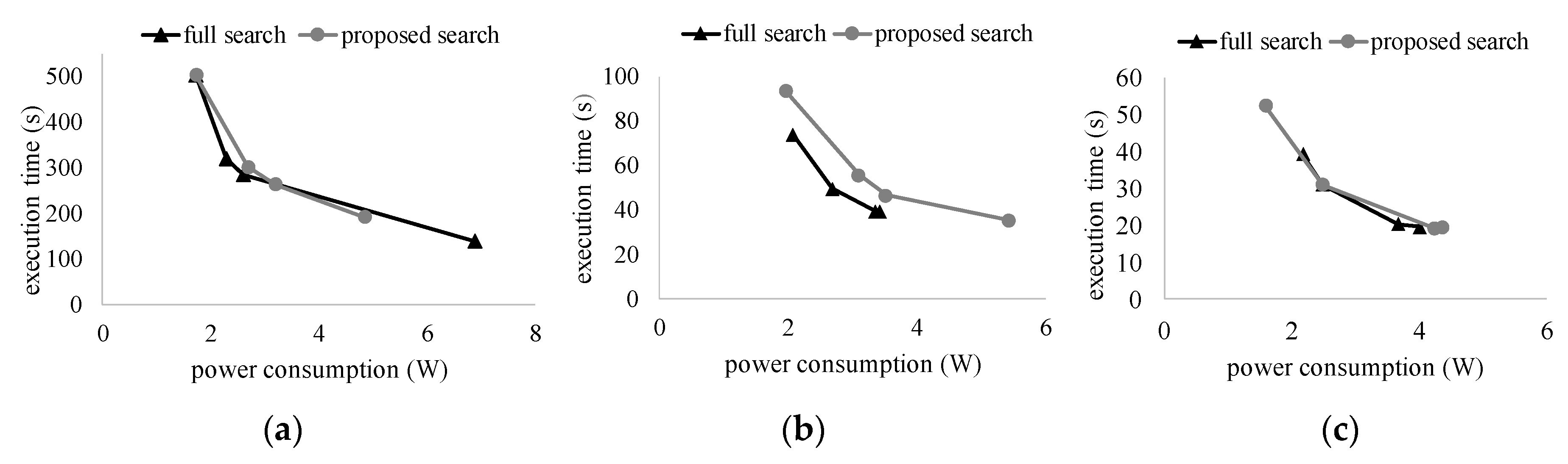
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Standard, J. High Bandwidth Memory (hbm) Dram; JEDEC: Arlington, VA, USA, 2013. [Google Scholar]
- Pawlowski, J.T. Hybrid memory cube (hmc). In Proceedings of the 2011 IEEE Hot Chips 23 Symposium (HCS), Stanford, CA, USA, 17–19 August 2011; pp. 1–24. [Google Scholar]
- Stone, H.S.; Turek, J.; Wolf, J.L. Optimal partitioning of cache memory. IEEE Trans. Comput. 1992, 41, 1054–1068. [Google Scholar] [CrossRef]
- Jeong, J.; Dubois, M. Cache replacement algorithms with nonuniform miss costs. IEEE Trans. Comput. 2006, 55, 353–365. [Google Scholar] [CrossRef]
- Cai, Y.; Schmitz, M.T.; Ejlali, A.; Al-Hashimi, B.M.; Reddy, S.M. Cache size selection for performance, energy and reliability of time-constrained systems. In Proceedings of the 2006 Asia and South Pacific Design Automation Conference, Yokohama, Japan, 24–27, January 2006; pp. 923–928. [Google Scholar]
- Al-Zoubi, H.; Milenkovic, A.; Milenkovic, M. Performance evaluation of cache replacement policies for the spec cpu2000 benchmark suite. In Proceedings of the 42nd Annual Southeast Regional Conference, Huntsville, AL, USA, 2–3 April 2004; pp. 267–272. [Google Scholar]
- Monchiero, M.; Canal, R.; Gonzalez, A. Power/performance/thermal design-space exploration for multicore architectures. IEEE Trans. Parallel Distrib. Syst. 2008, 19, 666–681. [Google Scholar] [CrossRef]
- Hanumaiah, V.; Vrudhula, S. Energy-efficient operation of multicore processors by dvfs, task migration, and active cooling. IEEE Trans. Comput. 2014, 63, 349–360. [Google Scholar] [CrossRef]
- Zhang, D.; Jayasena, N.; Lyashevsky, A.; Greathouse, J.L.; Xu, L.; Ignatowski, M. Top-PIM: Throughput-oriented programmable processing in memory. In Proceedings of the 23rd International Symposium on High-Performance Parallel and Distributed Computing, Vancouver, BC, Canada, 23–27 June 2014; pp. 85–98. [Google Scholar]
- Scrbak, M.; Greathouse, J.L.; Jayasena, N.; Kavi, K. Dvfs space exploration in power constrained processing-in-memory systems. In Proceedings of the International Conference on Architecture of Computing Systems, Vienna, Austria, 3–6 April 2017; pp. 221–233. [Google Scholar]
- Kang, Y.; Huang, W.; Yoo, S.-M.; Keen, D.; Ge, Z.; Lam, V.; Pattnaik, P.; Torrellas, J. Flexram: Toward an advanced intelligent memory system. In Proceedings of the 1999 IEEE International Conference on Computer Design: VLSI in Computers and Processors, Austin, TX, USA, 10–13 October 2012; pp. 5–14. [Google Scholar]
- Draper, J.; Chame, J.; Hall, M.; Steele, C.; Barrett, T.; LaCoss, J.; Granacki, J.; Shin, J.; Chen, C.; Kang, C.W.; et al. The architecture of the diva processing-in-memory chip. In Proceedings of the 16th International Conference on Supercomputing, New York, NY, USA, 22–26 June 2002; pp. 14–25. [Google Scholar]
- Gries, M.; Cabré, P.; Gago, J. Performance Evaluation and Feasibility Study of Near-data Processing on DRAM Modules (DIMM-NDP) for Scientific Applications; Huawei Technologies Duesseldorf GmbH, Munich Research Center (MRC): München, Germany, 2019. [Google Scholar]
- Pugsley, S.H.; Jestes, J.; Zhang, H.; Balasubramonian, R.; Srinivasan, V.; Buyuktosunoglu, A.; Davis, A.; Li, F. Ndc: Analyzing the impact of 3d-stacked memory+ logic devices on mapreduce workloads. In Proceedings of the 2014 IEEE International Symposium on Performance Analysis of Systems and Software (ISPASS), Monterey, CA, USA, 23–25 March 2014; pp. 190–200. [Google Scholar]
- Islam, M.; Scrbak, M.; Kavi, K.M.; Ignatowski, M.; Jayasena, N. Improving node-level mapreduce performance using processing-in-memory technologies. In Proceedings of the European Conference on Parallel Processing, Porto, Portugal, 25–26 August 2014; pp. 425–437. [Google Scholar]
- Ahn, J.; Hong, S.; Yoo, S.; Mutlu, O.; Choi, K. A scalable processing-in-memory accelerator for parallel graph processing. ACM SIGARCH Comput. Archit. News 2015, 43, 105–117. [Google Scholar] [CrossRef]
- Scrbak, M.; Islam, M.; Kavi, K.M.; Ignatowski, M.; Jayasena, N. Processing-in-memory: Exploring the design space. In Proceedings of the International Conference on Architecture of Computing Systems, Porto, Portugal, 24–27 March 2015; pp. 43–54. [Google Scholar]
- Xu, L.; Zhang, D.P.; Jayasena, N. Scaling deep learning on multiple in-memory processors. In Proceedings of the 3rd Workshop on Near-Data Processing, Waikiki, HI, USA, 5–9 December 2015. [Google Scholar]
- Vincon, T.; Koch, A.; Petrov, I. Moving Processing to Data: On the Influence of Processing in Memory on Data Management. arXiv 2019, arXiv:190504767. Available online: https://arxiv.org/abs/1905.04767 (accessed on 15 August 2019).
- Mutlu, O.; Ghose, S.; Gómez-Luna, J.; Ausavarungnirun, R. Processing data where it makes sense: Enabling in-memory computation. Microprocess. Microsyst. 2019, 67, 28–41. [Google Scholar] [CrossRef]
- Awan, J.; Ohara, M.; Ayguade, E.; Ishizaki, K.; Brorsson, M.; Vlassov, V. Identifying the potential of near data processing for apache spark. In Proceedings of the International Symposium on Memory Systems, Alexandria, VA, USA, 2–5 October 2017; pp. 60–67. [Google Scholar]
- Dysart, T.; Kogge, P.; Deneroff, M.; Bovell, E.; Briggs, P.; Brockman, J.; Jacobsen, K.; Juan, Y.; Kuntz, S.; Lethin, R.; et al. Highly scalable near memory processing with migrating threads on the emu system architecture. In Proceedings of the Sixth Workshop on Irregular Applications: Architectures and Algorithms, Salt Lake City, UT, USA, 13–18 November 2016; pp. 2–9. [Google Scholar]
- Wiegand, T.; Schwarz, H.; Joch, A.; Kossentini, F.; Sullivan, G.J. Rate-constrained coder control and comparison of video coding standards. IEEE Trans. Circuits Syst. Video Technol. 2003, 13, 688–703. [Google Scholar] [CrossRef]
- Binkert, N.; Beckmann, B.; Black, G.; Reinhardt, S.K.; Saidi, A.; Basu, A.; Hestness, J.; Hower, D.R.; Krishna, T.; Sardashti, S.; et al. The gem5 simulator. ACM SIGARCH Comput. Archit. News 2011, 39, 1–7. [Google Scholar] [CrossRef]
- Li, S.; Ahn, J.H.; Strong, R.D.; Brockman, J.B.; Tullsen, D.M.; Jouppi, N.P. Mcpat: An integrated power, area, and timing modeling framework for multicore and manycore architectures. In Proceedings of the 42nd Annual IEEE/ACM International Symposium on Microarchitecture, New York, NY, USA, 12–16 December 2009; pp. 469–480. [Google Scholar]
- Spiliopoulos, V.; Bagdia, A.; Hansson, A.; Aldworth, P.; Kaxiras, S. Introducing dvfs-management in a full-system simulator. In Proceedings of the 2013 IEEE 21st International Symposium on Modelling, Analysis and Simulation of Computer and Telecommunication Systems, San Francisco, CA, USA, 14–16 August 2013; pp. 535–545. [Google Scholar]
- O’Connor, M. Highlights of the high-bandwidth memory (hbm) standard. In Proceedings of the Memory Forum Workshop, Minneapolis, MN, USA, 14 June 2014. [Google Scholar]
- Jeddeloh, J.; Keeth, B. Hybrid memory cube new dram architecture increases density and performance. In Proceedings of the 2012 symposium on VLSI technology (VLSIT), Honolulu, HI, USA, 12–14 June 2012; pp. 87–88. [Google Scholar]
- Bienia, C.; Kumar, S.; Singh, J.P.; Li, K. The parsec benchmark suite: Characterization and architectural implications. In Proceedings of the 17th International Conference on Parallel architectures and Compilation Techniques, Toronto, ON, Canada, 25–29 October 2008; pp. 72–81. [Google Scholar]
- Woo, S.C.; Ohara, M.; Torrie, E.; Singh, J.P.; Gupta, A. The splash-2 programs: Characterization and methodological considerations. In Proceedings of the 22nd Annual International Symposium on Computer Architecture, S. Margherita Ligure, Italy, 22–24 June 1995; pp. 24–36. [Google Scholar]
- Chatfield, K.; Simonyan, K.; Vedaldi, A.; Zisserman, A. Return of the devil in the details: Delving deep into convolutional nets. arXiv 2014, arXiv:1405.3531. Available online: https://arxiv.org/abs/1405.3531 (accessed on 15 August 2019).

| Components | Host | NMP |
|---|---|---|
| CPU core parameters | Out-of-order issue 1 core, 192 entry ROB | In-order issue 1 core |
| L1 cache | 32 KB 2 cycle access 2 way I cache and D cache | |
| L2 cache | 1 MB 20 cycle access 8 ways | none |
| 200 MHz | 400 MHz | 600 MHz | 800 MHz | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| λ | Tasks | Power | Time | λ | Tasks | Power | Time | λ | Tasks | Power | Time | λ | Tasks | Power | Time | ||
| PARSEC | 1 GHz | 32.40 | 4 | 1.97 | 93.32 | 15.69 | 4 | 3.10 | 55.72 | 10.38 | 6 | 1.83 | 63.42 | 8.13 | 6 | 2.07 | 56.20 |
| 2 GHz | 25.99 | 3 | 2.45 | 60.27 | 12.99 | 4 | 2.79 | 48.76 | 8.85 | 4 | 3.51 | 37.95 | 7.11 | 4 | 4.15 | 32.27 | |
| 3 GHz | 16.79 | 3 | 3.04 | 58.85 | 8.46 | 4 | 3.53 | 46.61 | 5.80 | 4 | 4.57 | 35.97 | 4.68 | 4 | 5.34 | 29.97 | |
| 4 GHz | 13.21 | 3 | 3.57 | 58.21 | 6.67 | 3 | 6.06 | 33.08 | 4.58 | 4 | 5.43 | 35.44 | 3.70 | 4 | 6.07 | 28.80 | |
| SPLASH-2 | 1 GHz | 20.08 | 4 | 1.59 | 52.34 | 10.79 | 4 | 2.48 | 30.98 | 7.23 | 4 | 3.16 | 23.97 | 5.44 | 5 | 2.94 | 24.39 |
| 2 GHz | 15.98 | 3 | 2.02 | 35.41 | 8.75 | 4 | 2.28 | 28.91 | 5.97 | 4 | 3.04 | 21.14 | 4.58 | 4 | 3.70 | 17.23 | |
| 3 GHz | 10.08 | 3 | 2.51 | 34.24 | 5.55 | 3 | 4.23 | 19.29 | 3.80 | 4 | 3.87 | 20.05 | 2.92 | 4 | 4.77 | 16.15 | |
| 4 GHz | 7.76 | 3 | 2.79 | 33.65 | 4.28 | 3 | 4.79 | 18.70 | 2.94 | 4 | 4.36 | 19.50 | 2.26 | 4 | 5.41 | 15.60 | |
| VGG-F | 1 GHz | 157.67 | 8 | 1.73 | 502.40 | 75.12 | 8 | 2.69 | 301.22 | 47.68 | 8 | 3.41 | 234.28 | 34.33 | 8 | 3.95 | 201.01 |
| 2 GHz | 129.16 | 7 | 2.88 | 275.42 | 63.50 | 8 | 2.49 | 272.95 | 41.66 | 8 | 3.23 | 206.06 | 31.04 | 8 | 3.83 | 172.79 | |
| 3 GHz | 83.83 | 7 | 3.76 | 264.18 | 41.58 | 8 | 3.20 | 263.58 | 27.48 | 8 | 4.23 | 196.69 | 20.63 | 8 | 5.06 | 163.42 | |
| 4 GHz | 66.01 | 7 | 4.32 | 258.10 | 32.90 | 8 | 3.65 | 258.52 | 21.85 | 8 | 4.86 | 191.63 | 16.47 | 8 | 5.85 | 158.35 | |
| 200 MHz | 400 MHz | 600 MHz | 800 MHz | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| λ | Tasks | Power | Time | λ | Tasks | Power | Time | λ | Tasks | Power | Time | λ | Tasks | Power | Time | ||
| PARSEC | 1 GHz | 36.21 | 4 | 2.05 | 97.51 | 16.65 | 6 | 1.52 | 86.66 | 10.13 | 4 | 3.12 | 45.72 | 6.86 | 4 | 3.71 | 38.09 |
| 2 GHz | 26.97 | 3 | 2.40 | 60.49 | 12.99 | 4 | 2.79 | 48.76 | 8.33 | 4 | 3.69 | 36.05 | 6.00 | 6 | 2.10 | 43.33 | |
| 3 GHz | 19.59 | 3 | 2.39 | 56.72 | 9.56 | 3 | 4.03 | 32.13 | 6.22 | 4 | 3.81 | 32.50 | 4.55 | 4 | 4.68 | 26.15 | |
| 4 GHz | 14.15 | 3 | 2.56 | 54.84 | 6.95 | 3 | 4.44 | 30.24 | 4.55 | 3 | 6.00 | 22.05 | 3.35 | 4 | 5.20 | 24.38 | |
| SPLASH-2 | 1 GHz | 24.39 | 4 | 1.68 | 57.82 | 11.56 | 4 | 2.56 | 32.33 | 7.28 | 5 | 2.60 | 29.56 | 5.15 | 5 | 3.13 | 24.13 |
| 2 GHz | 17.92 | 3 | 1.99 | 35.65 | 8.75 | 4 | 2.28 | 28.91 | 5.69 | 4 | 2.89 | 20.13 | 4.17 | 4 | 3.55 | 16.17 | |
| 3 GHz | 12.96 | 3 | 1.95 | 33.89 | 6.38 | 3 | 3.34 | 18.70 | 4.19 | 4 | 3.09 | 19.27 | 3.09 | 4 | 3.62 | 14.74 | |
| 4 GHz | 9.34 | 3 | 2.07 | 33.01 | 4.62 | 3 | 3.64 | 17.82 | 3.04 | 3 | 4.99 | 12.76 | 2.26 | 4 | 4.21 | 14.46 | |
| VGG-F | 1 GHz | 177.08 | 8 | 1.83 | 545.91 | 79.18 | 8 | 2.89 | 327.21 | 46.51 | 9 | 2.56 | 304.15 | 30.15 | 9 | 3.08 | 249.71 |
| 2 GHz | 133.49 | 7 | 2.76 | 286.90 | 63.50 | 8 | 2.49 | 272.95 | 40.19 | 8 | 3.31 | 200.06 | 28.53 | 8 | 4.00 | 163.61 | |
| 3 GHz | 97.29 | 7 | 2.78 | 265.13 | 47.11 | 7 | 4.60 | 154.34 | 30.40 | 8 | 3.38 | 181.97 | 22.04 | 8 | 4.18 | 145.52 | |
| 4 GHz | 36.21 | 4 | 2.05 | 97.51 | 16.65 | 6 | 1.52 | 86.66 | 10.13 | 4 | 3.12 | 45.72 | 6.86 | 4 | 3.71 | 38.09 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rhee, C.E.; Park, S.-W.; Choi, J.; Jung, H.; Lee, H.-J. Power-Time Exploration Tools for NMP-Enabled Systems. Electronics 2019, 8, 1096. https://doi.org/10.3390/electronics8101096
Rhee CE, Park S-W, Choi J, Jung H, Lee H-J. Power-Time Exploration Tools for NMP-Enabled Systems. Electronics. 2019; 8(10):1096. https://doi.org/10.3390/electronics8101096
Chicago/Turabian StyleRhee, Chae Eun, Seung-Won Park, Jungwoo Choi, Hyunmin Jung, and Hyuk-Jae Lee. 2019. "Power-Time Exploration Tools for NMP-Enabled Systems" Electronics 8, no. 10: 1096. https://doi.org/10.3390/electronics8101096
APA StyleRhee, C. E., Park, S.-W., Choi, J., Jung, H., & Lee, H.-J. (2019). Power-Time Exploration Tools for NMP-Enabled Systems. Electronics, 8(10), 1096. https://doi.org/10.3390/electronics8101096






