LOS-Based Equal Gain Transmission and Combining in General Frequency-Selective Ricean Massive MIMO Channels
Abstract
1. Introduction
2. System Model
3. LOS-Based EGT/EGC and Power Scaling Laws
3.1. The Scenario without Correlation
3.2. The Scenario with Correlation
4. Cooperative Relaying Systems
4.1. The Scenario with Decode-and-Forward Protocol
4.2. The Scenario with Amplify-and-Forward Protocol
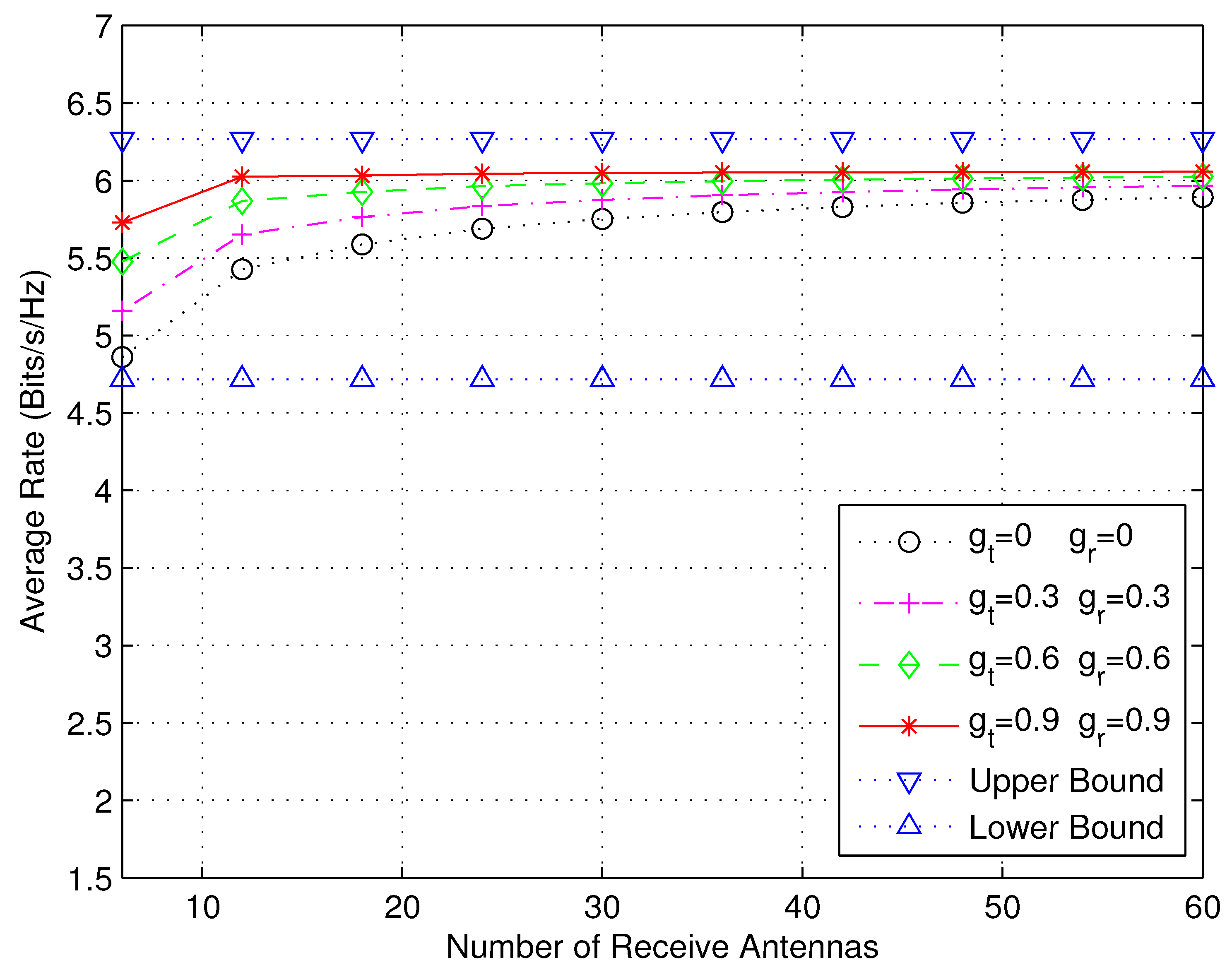
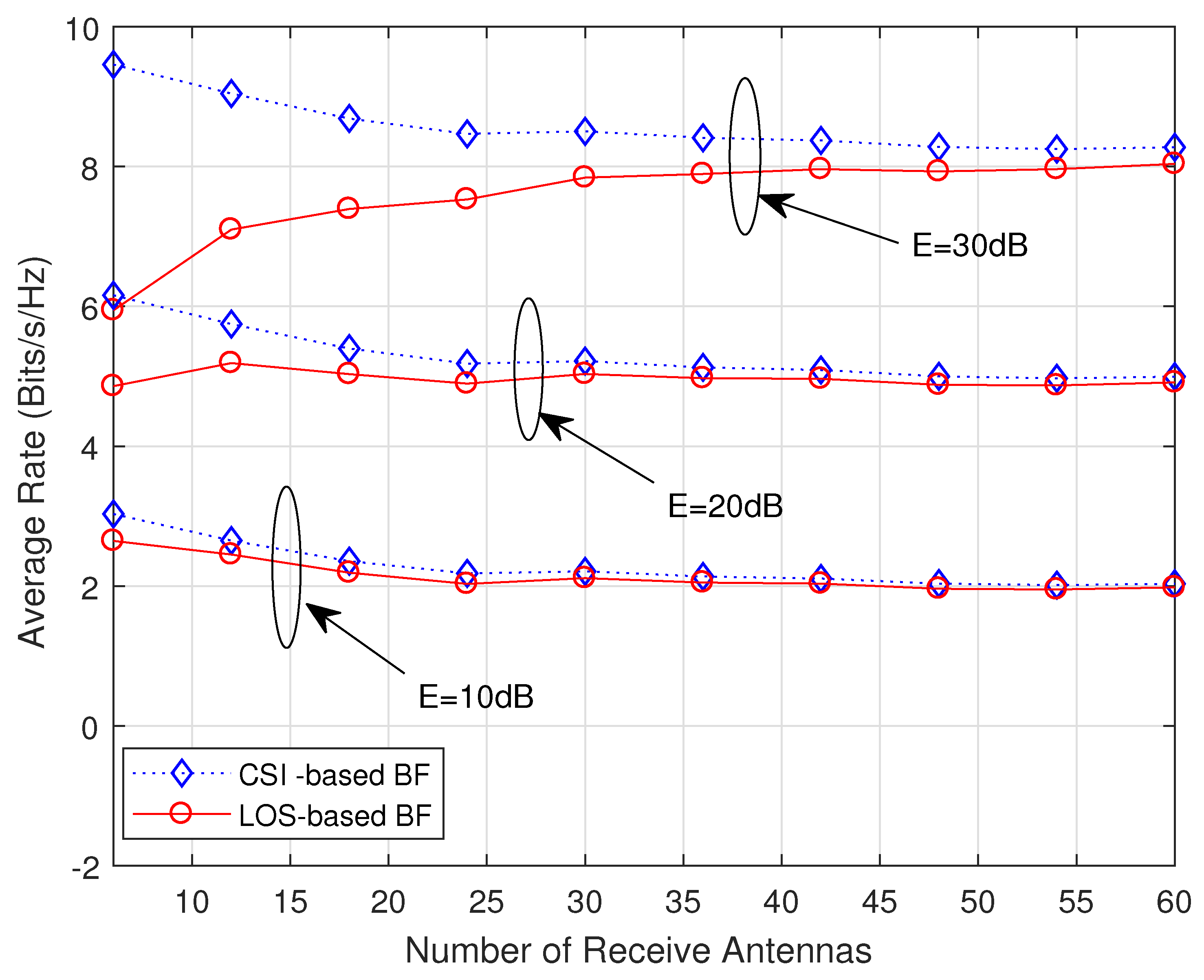
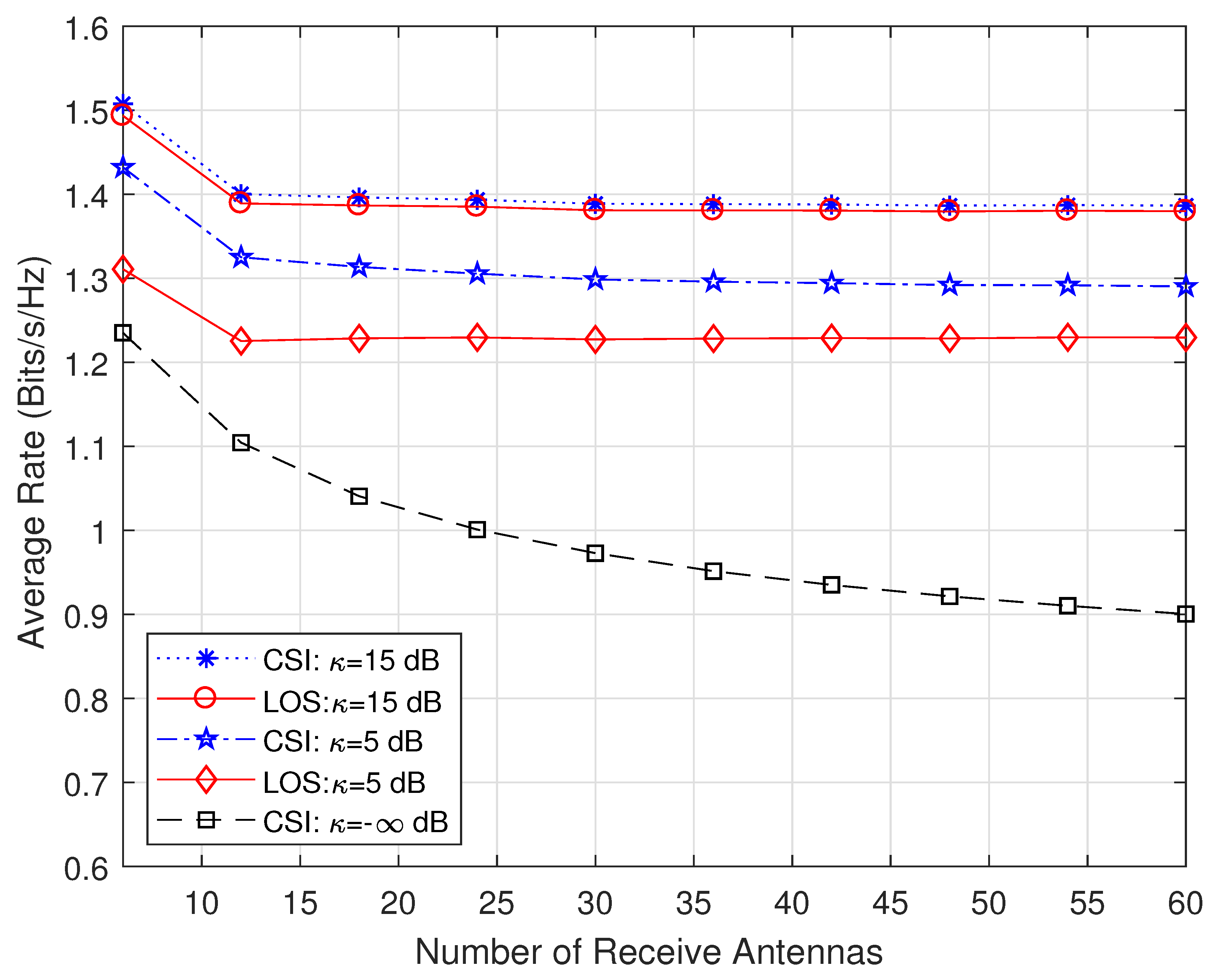
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shafi, M.; Molisch, A.F.; Smith, P.J.; Haustein, T.; Zhu, P.; Silva, P.D.; Tufvesson, F.; Benjebbour, A.; Wunder, G. 5G: A tutorial overview of standards, trials, challenges, deployment, and practice. IEEE J. Sel. Areas Commun. 2017, 35, 1201–1221. [Google Scholar] [CrossRef]
- Marzetta, T.L. Noncooperative cellular wireless with unlimited numbers of base station antennas. IEEE Trans. Wirel. Commun. 2010, 9, 3590–3600. [Google Scholar] [CrossRef]
- Ngo, H.Q.; Larsson, E.G.; Marzetta, T.L. Energy and spectral efficiency of very large multiuser MIMO systems. IEEE Trans. Commun. 2013, 61, 1436–1449. [Google Scholar]
- Liu, W.; Han, S.; Yang, C. Energy efficiency scaling law of massive MIMO systems. IEEE Trans. Commun. 2017, 65, 107–121. [Google Scholar] [CrossRef]
- Yang, H.; Marzetta, T.L. Performance of conjugate and zero-forcing beamforming in large-scale antenna systems. IEEE J. Sel. Areas Commun. 2013, 31, 172–179. [Google Scholar] [CrossRef]
- Zhang, Q.; Jin, S.; Wong, K.-K.; Zhu, H.; Matthaiou, M. Power scaling of uplink massive MIMO systems with arbitrary-rank channel means. IEEE J. Sel. Top. Signal Process. 2014, 62, 966–981. [Google Scholar] [CrossRef]
- Rana, M.M.; Kim, J. Fundamentals of Channel Estimations for Mobile Communications-Existing and New Techniques of a LTE SC-FDMA System; LAMBERT Academic Publishing: Saarbrucken, Germany, 2012; ISBN 978-3-8454-3137-6. [Google Scholar]
- Rusek, F.; Persson, D.; Lau, B.K.; Larsson, E.G.; Marzetta, T.L.; Edfors, O.; Tufvesson, F. Scaling up MIMO: Opportunities and challenges with very large arrays. IEEE Signal Proc. Mag. 2013, 30, 40–60. [Google Scholar] [CrossRef]
- Yue, D.-W.; Zhang, Y.; Jia, Y.-N. Beamforming based on specular component for massive MIMO systems in Rician fading. IEEE Wirel. Commun. Lett. 2015, 4, 197–200. [Google Scholar] [CrossRef]
- Yue, D.-W.; Yan, Q. Beamforming only based on specular component for downlink massive MIMO systems. Wirel. Pers. Commun. 2017, 95, 1799–1810. [Google Scholar] [CrossRef]
- Yue, D.-W.; Meng, Z. LOS component-based equal gain combining for Ricean links in uplink massive MIMO. In Proceedings of the 2016 Sixth International Conference on Instrumentation & Measurement, Computer, Communication and Control (IMCCC), Harbin, China, 21–23 July 2016; pp. 476–481. [Google Scholar]
- Yue, D.-W.; Zhang, Q.T. Generic approach to the performance anaysis of correlated transmit/receive diversity MIMO systems with/without co-channel interference. IEEE Trans. Inf. Theory 2010, 56, 1147–1157. [Google Scholar] [CrossRef]
- Yue, D.-W. Specular component-based beamforming for broadband massive MIMO systems with doubly-ended correlation. Electron. Lett. 2016, 52, 1082–1084. [Google Scholar] [CrossRef]
- McKay, M.R.; Collings, I.B. On the capacity of frenquency-flat and frequency-selective Rician MIMO channels with single-ended correlation. IEEE Trans. Wirel. Commun. 2006, 5, 2038–2043. [Google Scholar] [CrossRef]
- Dinis, R.; Montezuma, P. Iterative receiver based on the EGC for massive MIMO schemes using SC-FDE modulations. Electron. Lett. 2016, 52, 972–974. [Google Scholar] [CrossRef]
- Love, D.J.; Heath, R.W. Equal gain transmission in multiple-input multiple-output wireless systems. IEEE Trans. Commun. 2003, 51, 1102–1110. [Google Scholar] [CrossRef]
- Zheng, X.; Xie, Y.; Li, J.; Stoica, P. MIMO transmit beamforming under uniform elemental power constraint. IEEE Trans. Signal Process. 2007, 55, 5395–5406. [Google Scholar] [CrossRef]
- Fu, H.; Crussière, M.; Hélard, M. BER analysis for equal gain transmission in downlink multiuser MIMO systems. IEEE Wirel. Commun. Lett. 2015, 4, 533–536. [Google Scholar] [CrossRef]
- Jin, S.; Gao, X.; You, X. On the ergodic capacity of rank-1 Ricean fading MIMO channels. IEEE Trans. Inf. Theory 2003, 53, 502–517. [Google Scholar] [CrossRef]
- Bölcskei, H.; Borgmann, M.; Paulraj, A.J. Impact of the propagation environment on the the performance of space-frequency coded MIMO-OFDM. IEEE J. Sel. Areas Commun. 2003, 21, 427–439. [Google Scholar] [CrossRef]
- Chen, J. When does asymptotic orthogonality exist for very large arrays? In Proceedings of the Global Communications Conference (GLOBECOM), Atlanta, GA, USA, 9–13 December 2013; pp. 4251–4255. [Google Scholar]
- Tulino, A.M.; Verdu, S. Random matrix theory and wireless communications. Found. Trends Commun. Inf. Theory 2004, 1, 1–182. [Google Scholar] [CrossRef]
- Wang, C.-X.; Ge, X.; Cheng, X.; Zhang, G.; Thompson, J. Cooperative MIMO channel models: A survey. IEEE Commun. Mag. 2010, 48, 80–87. [Google Scholar] [CrossRef]
- Ngo, H.Q.; Suraweera, H.A.; Matthaiou, M.; Larsson, E.G. Multipair full-duplex relaying with massive arrays and linear processing. IEEE J. Sel. Areas Commun. 2014, 32, 1721–1736. [Google Scholar] [CrossRef]
- Suraweera, H.A.; Krikidis, I.; Yuen, C. Antenna selection in the full-duplex multi-antenna relay channel. In Proceedings of the 2013 IEEE International Conference on Communications (ICC), Budapest, Hungary, 9–13 June 2013; pp. 4823–4828. [Google Scholar]
- Durisi, G.; Tarable, A.; Camarda, C.; Devassy, R.; Montorsi, G. Capacity bounds for MIMO microwave backhaul links affected by phase noise. IEEE Trans. Commun. 2014, 62, 920–929. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Q.; Sun, Y.; Yue, D.-W. LOS-Based Equal Gain Transmission and Combining in General Frequency-Selective Ricean Massive MIMO Channels. Electronics 2019, 8, 79. https://doi.org/10.3390/electronics8010079
Yan Q, Sun Y, Yue D-W. LOS-Based Equal Gain Transmission and Combining in General Frequency-Selective Ricean Massive MIMO Channels. Electronics. 2019; 8(1):79. https://doi.org/10.3390/electronics8010079
Chicago/Turabian StyleYan, Qiuna, Yu Sun, and Dian-Wu Yue. 2019. "LOS-Based Equal Gain Transmission and Combining in General Frequency-Selective Ricean Massive MIMO Channels" Electronics 8, no. 1: 79. https://doi.org/10.3390/electronics8010079
APA StyleYan, Q., Sun, Y., & Yue, D.-W. (2019). LOS-Based Equal Gain Transmission and Combining in General Frequency-Selective Ricean Massive MIMO Channels. Electronics, 8(1), 79. https://doi.org/10.3390/electronics8010079




