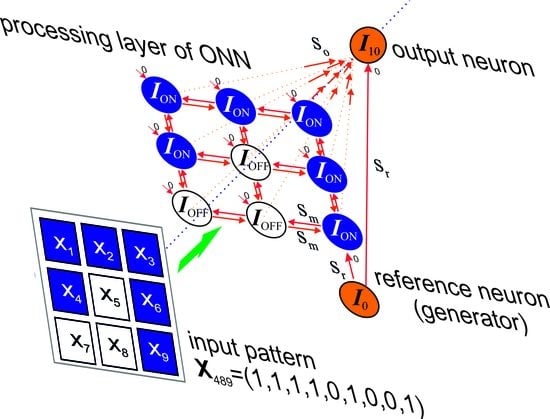
A Model of an Oscillatory Neural Network with Multilevel Neurons for Pattern Recognition and Computing
Abstract
1. Introduction
2. Materials and Methods
2.1. Oscillator Circuit and Method of ONN Organization
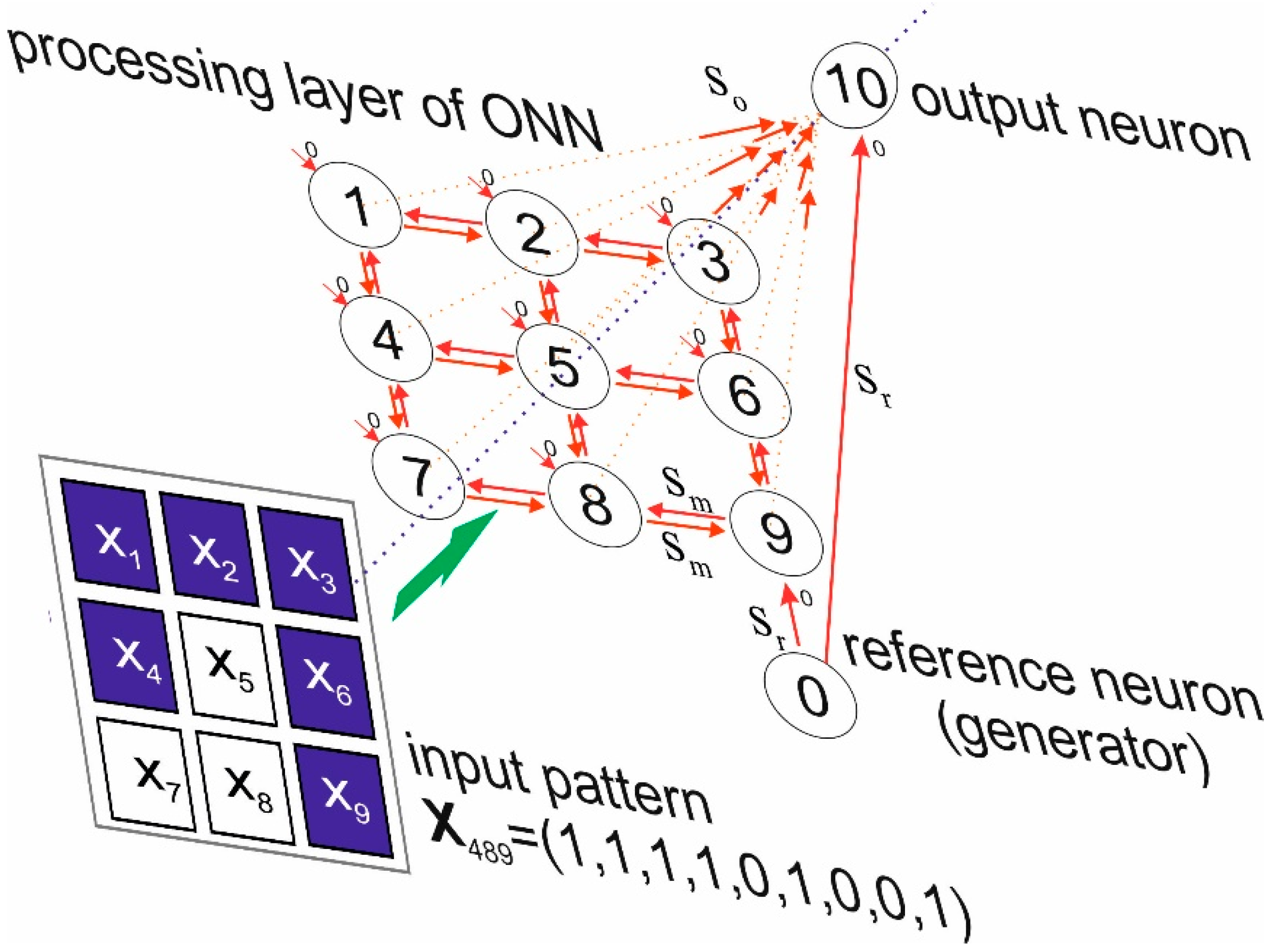
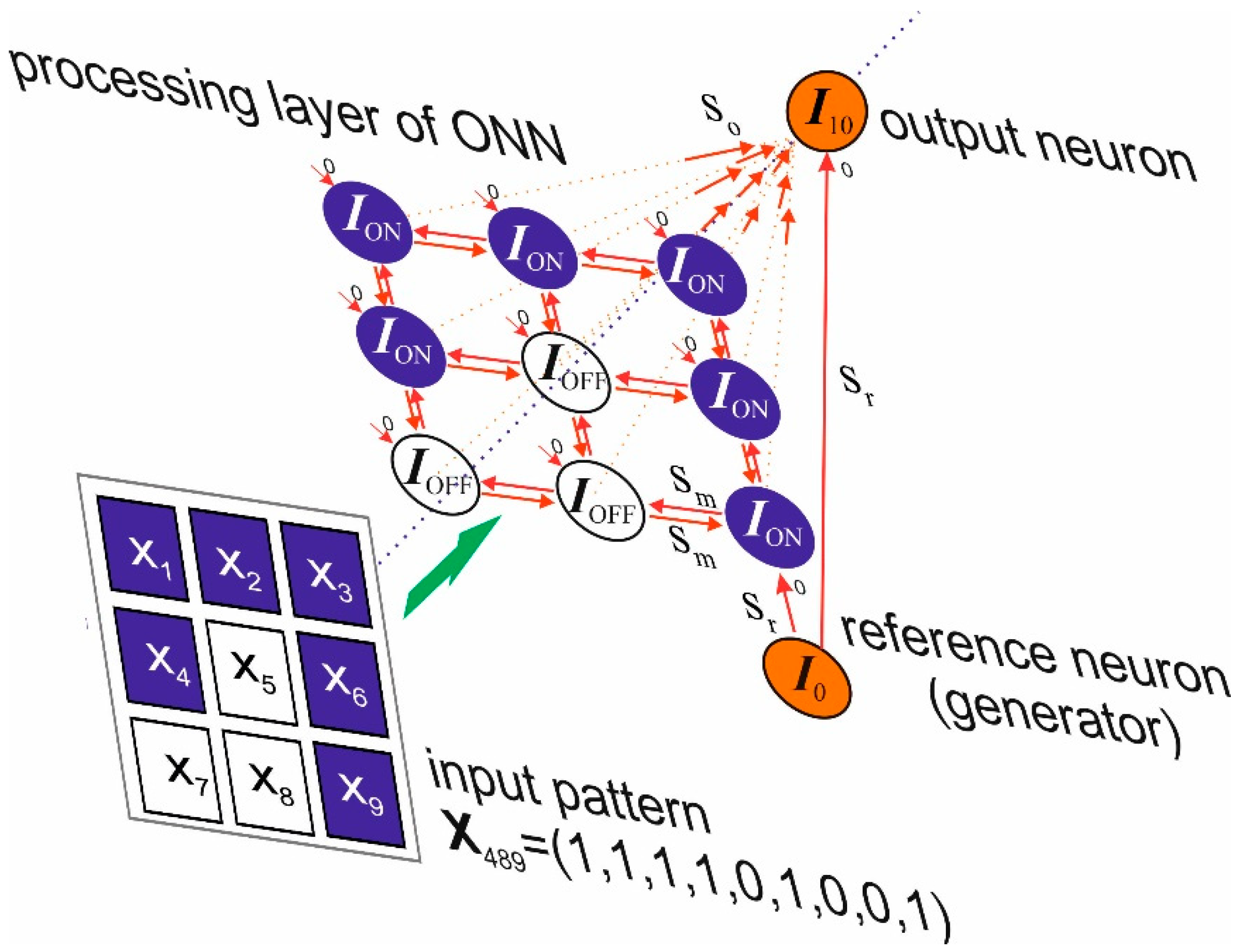
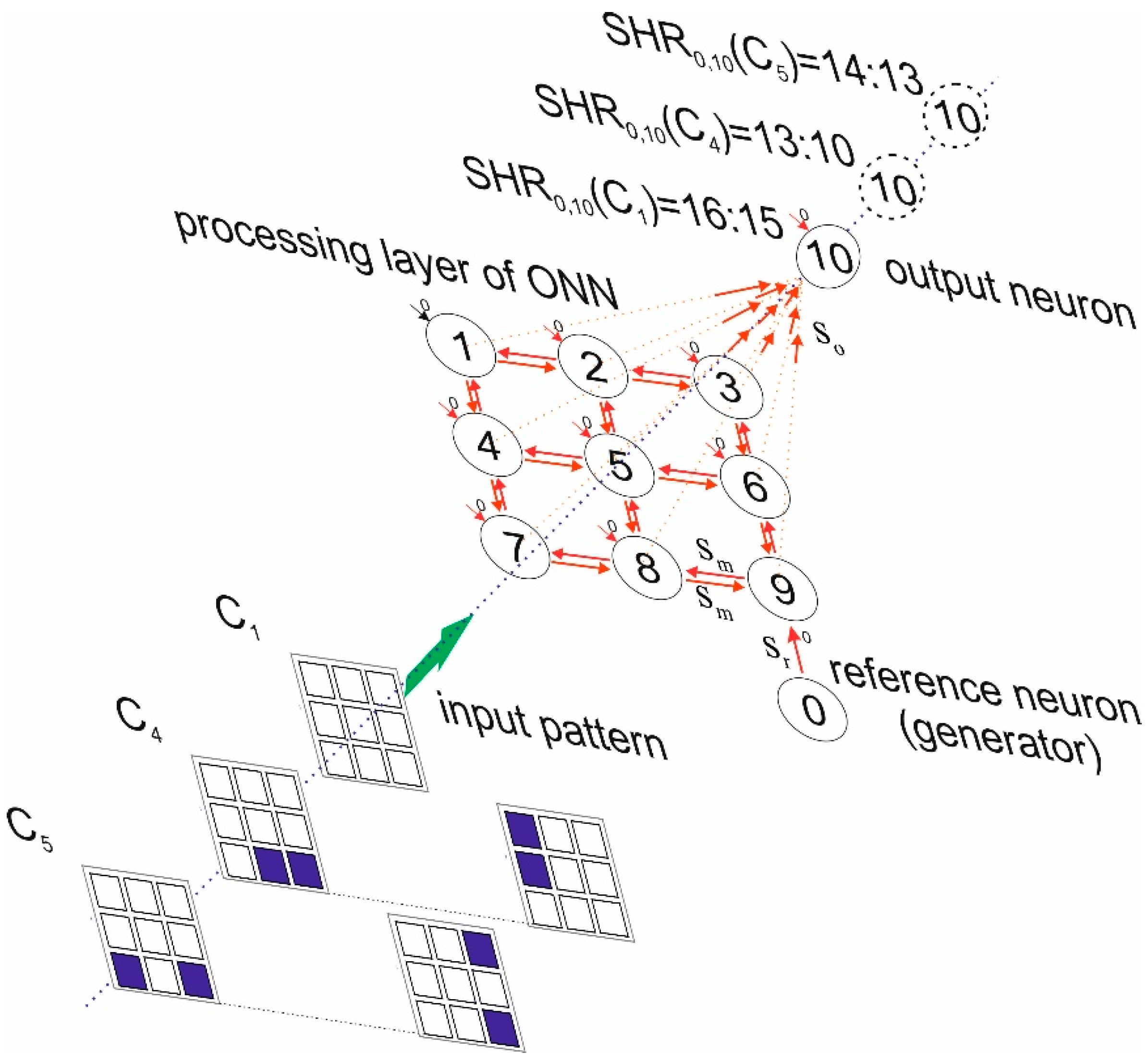
2.2. ONN Structure
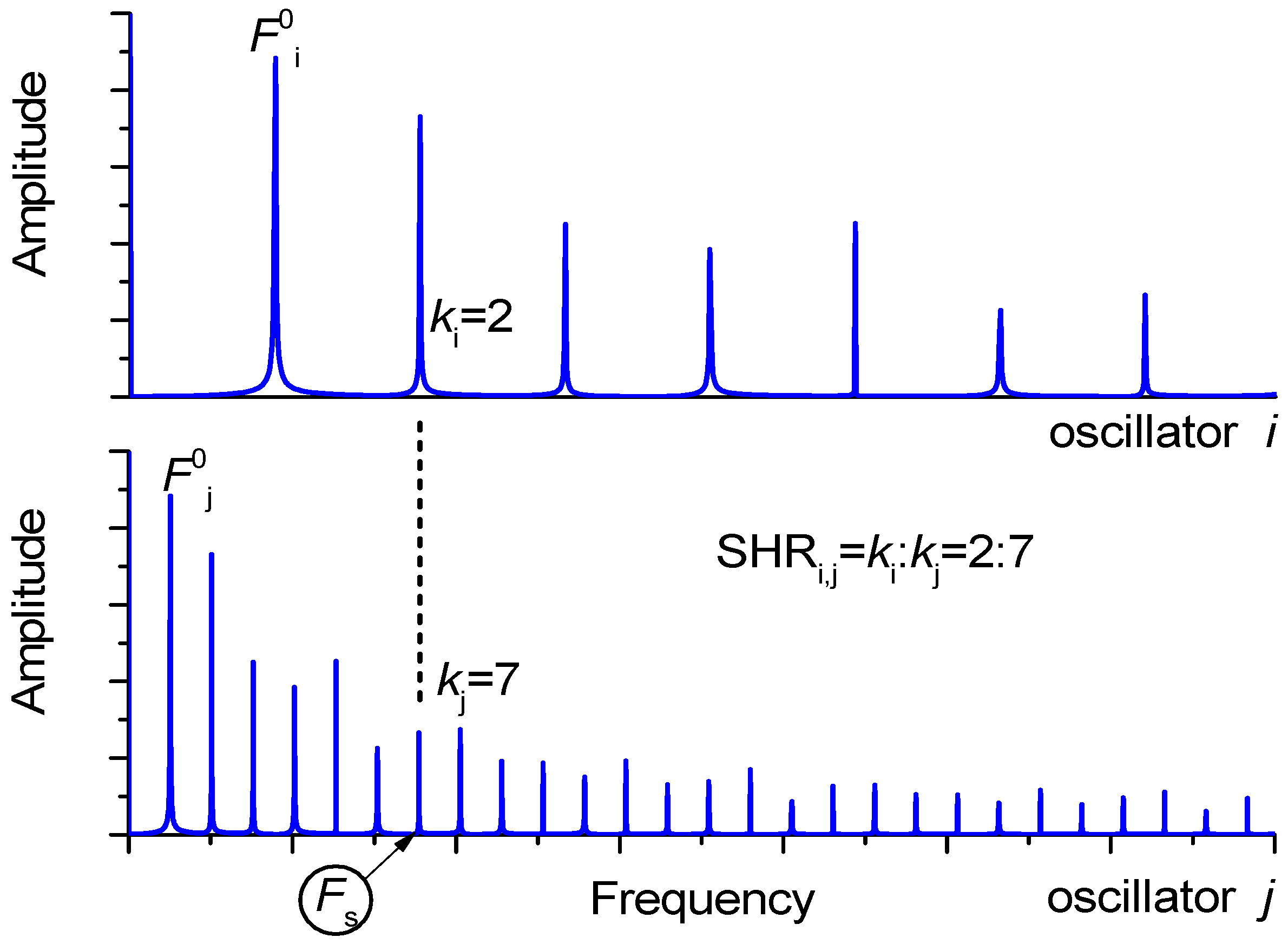
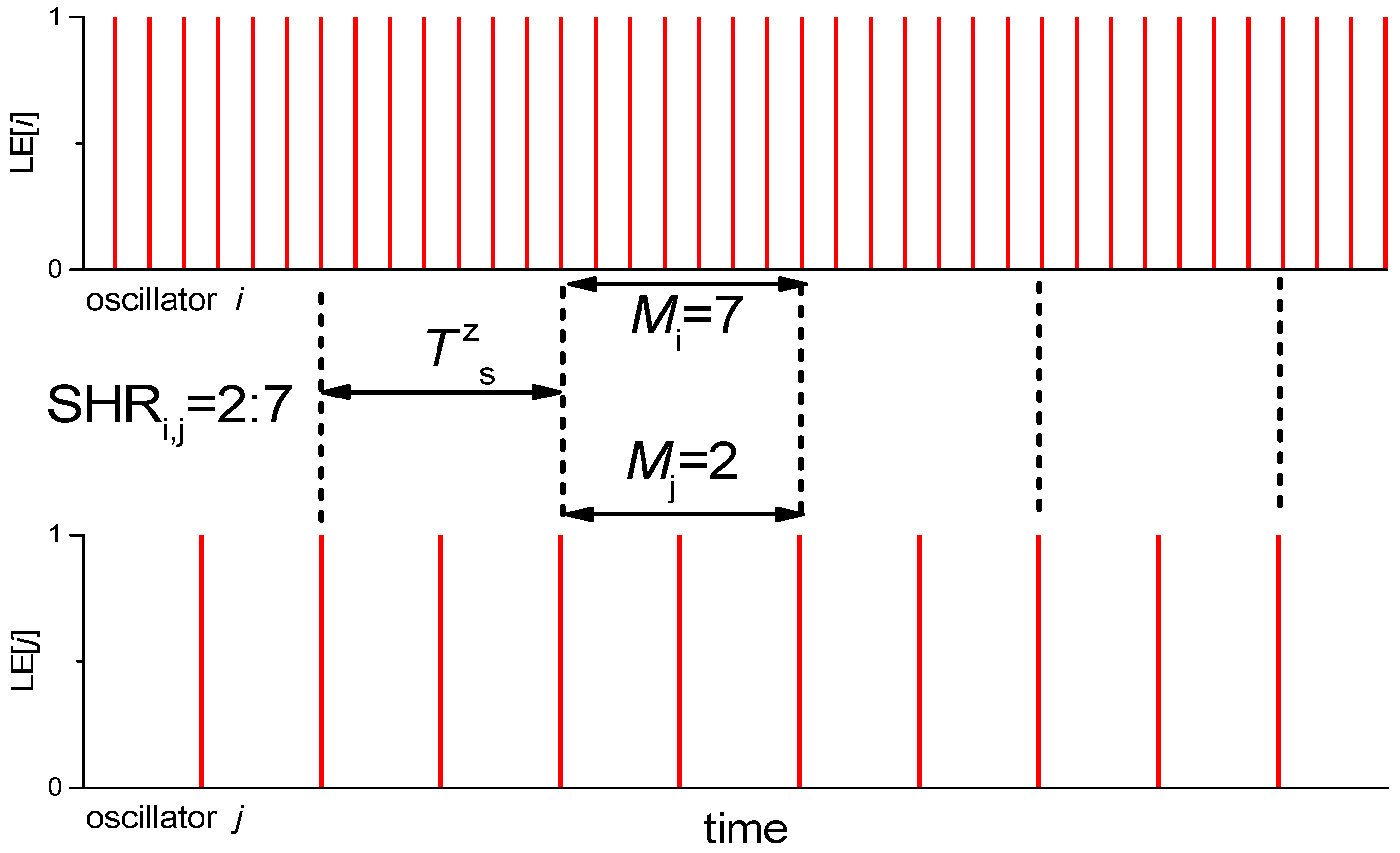
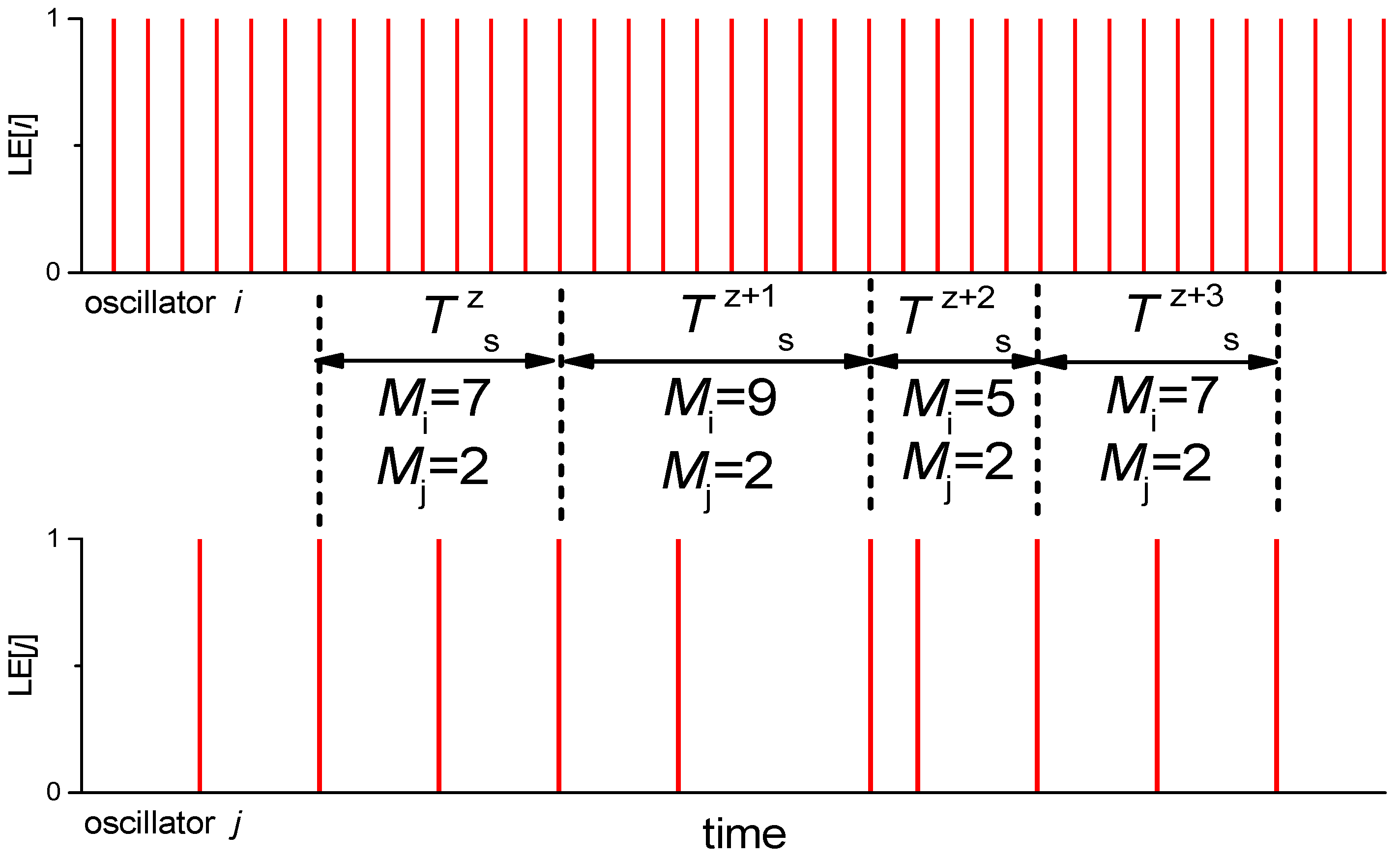
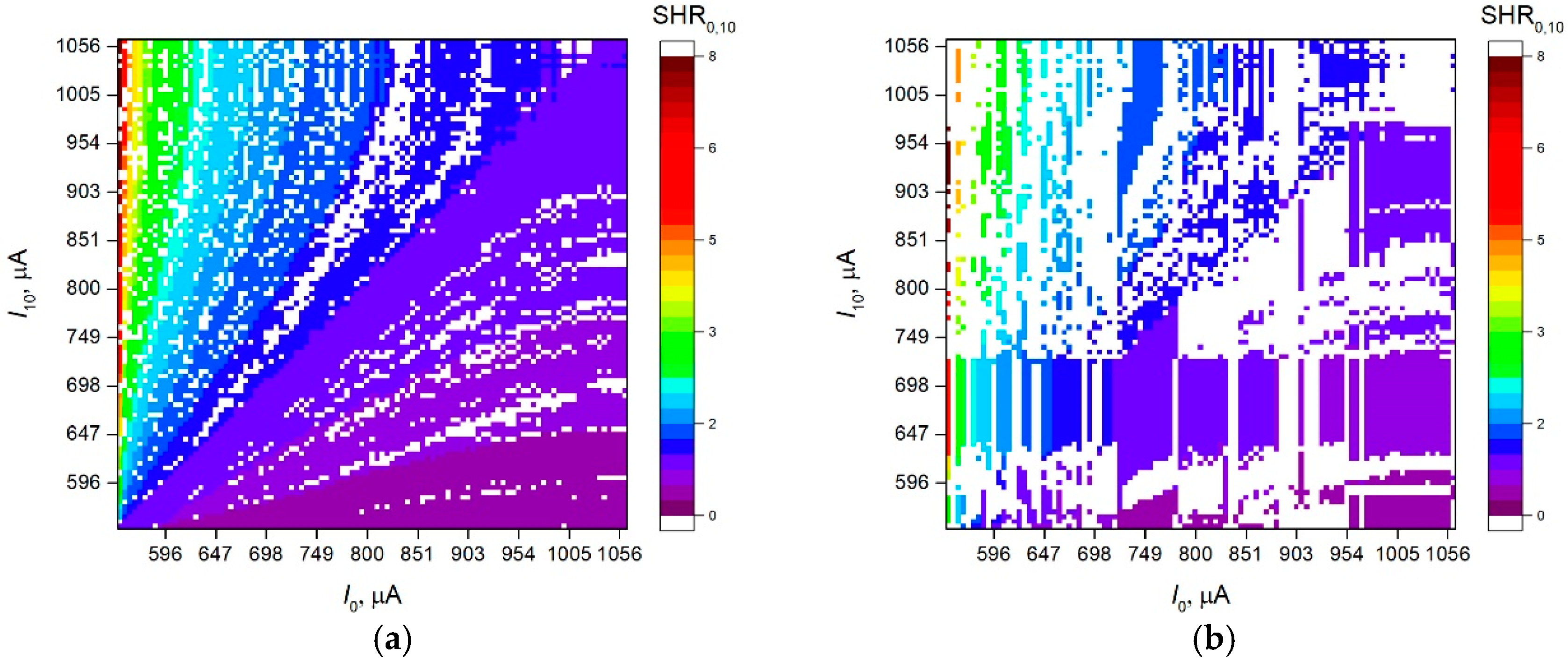
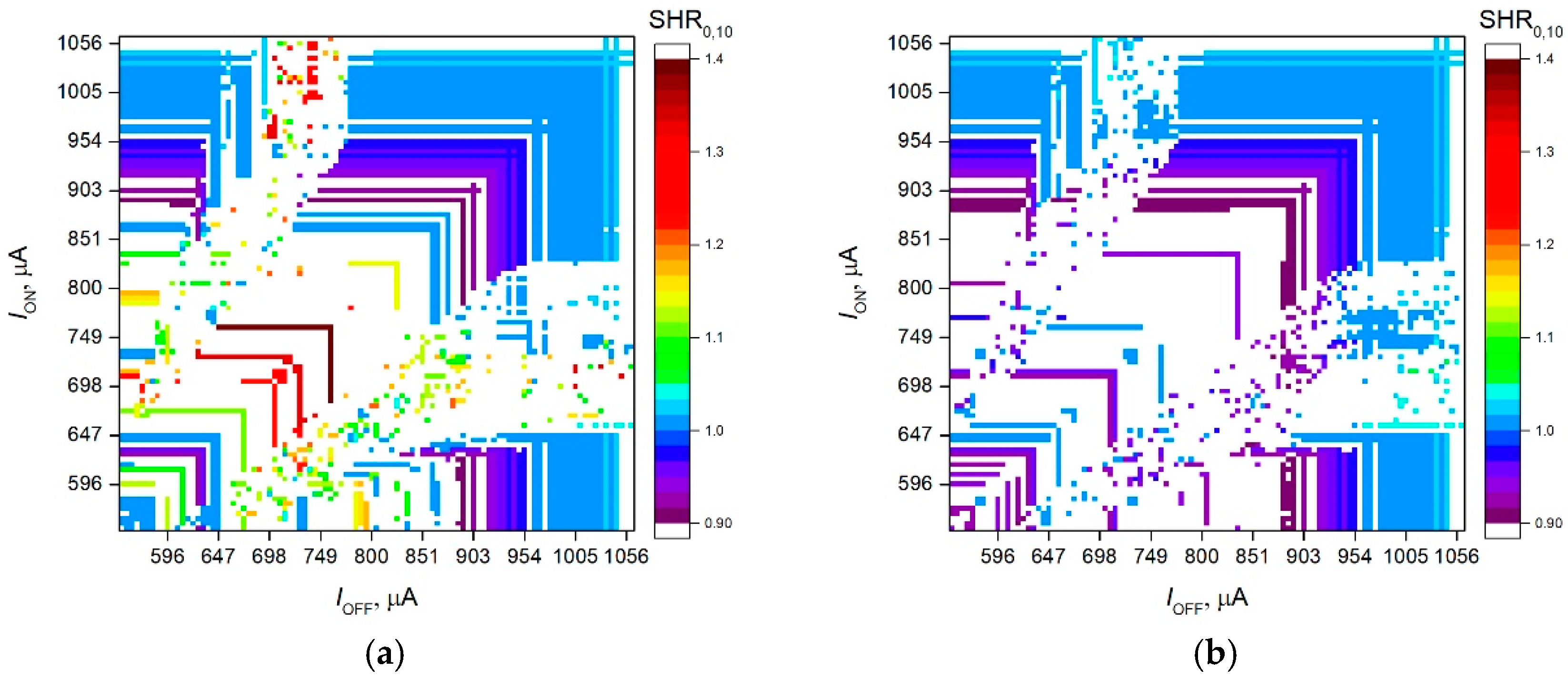
2.3. Method of Synchronization Order Definition
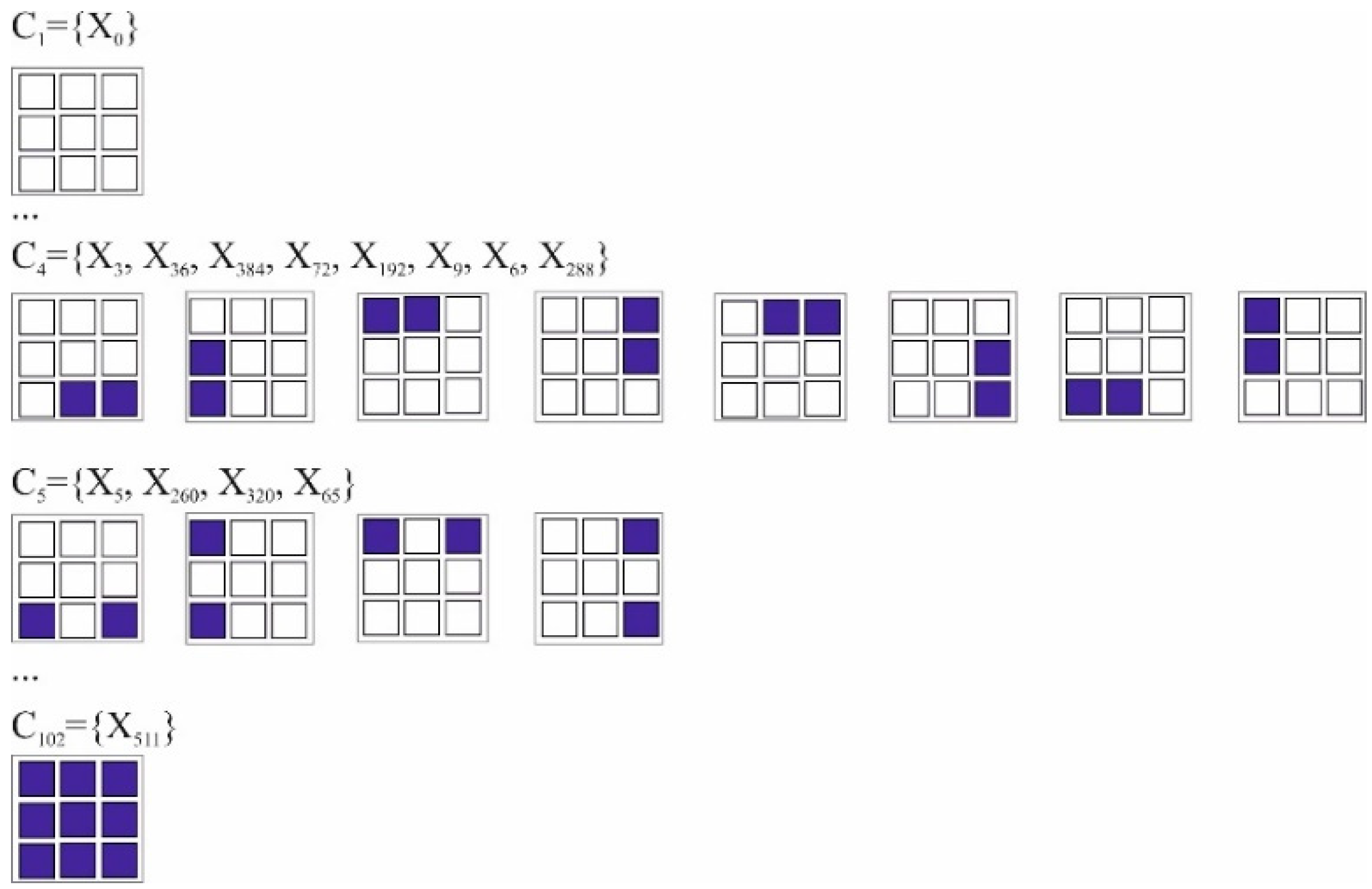
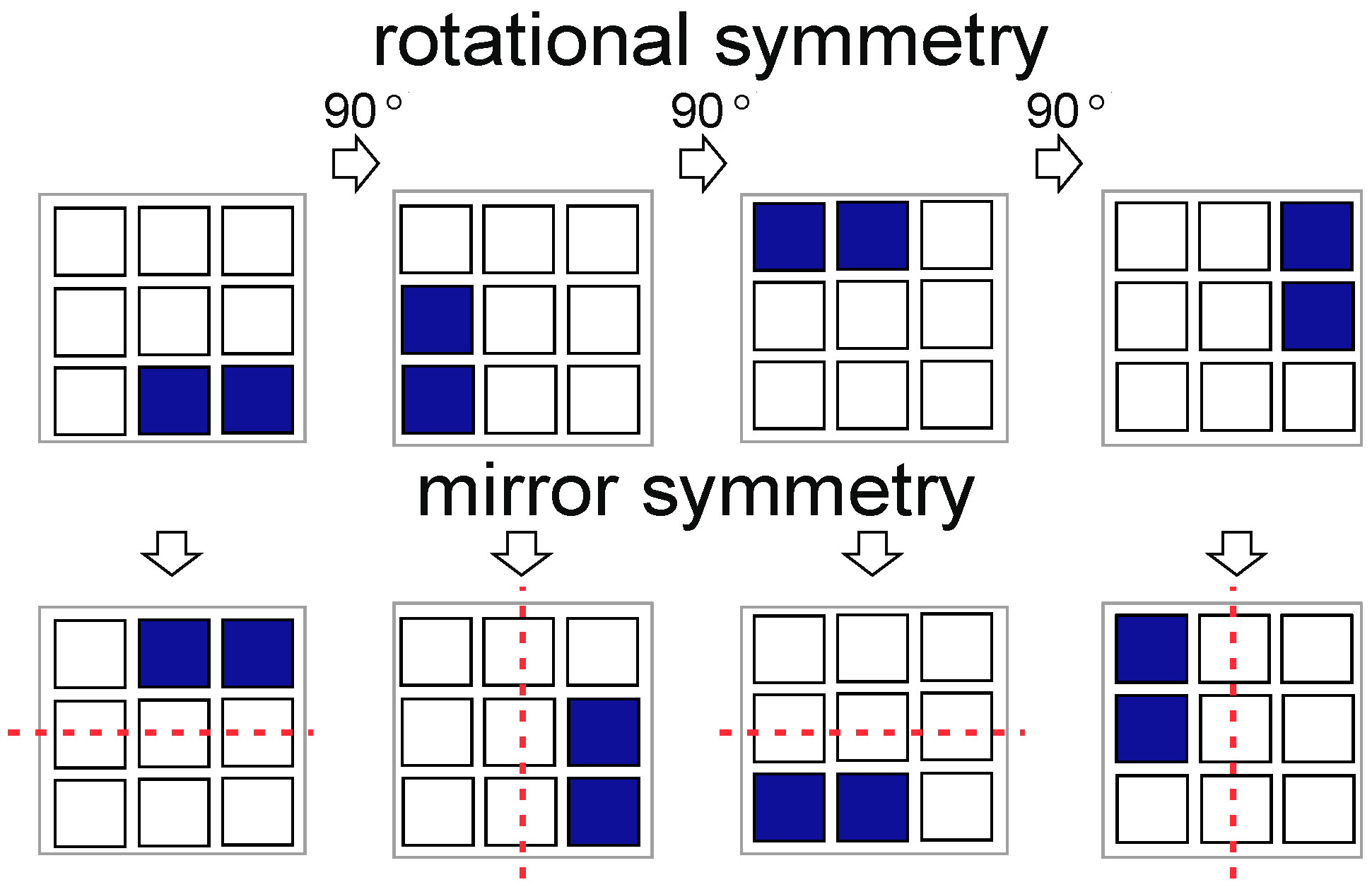
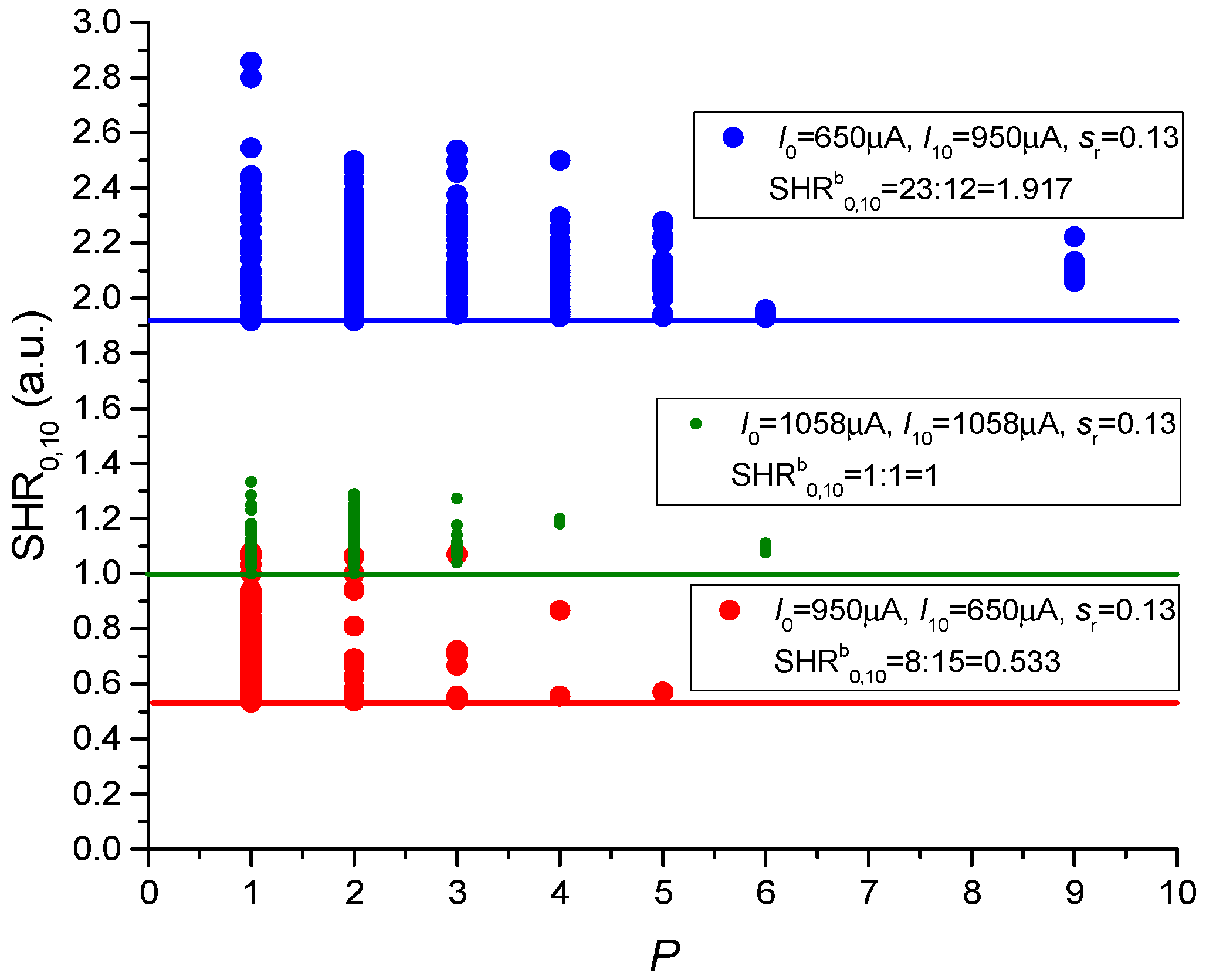
2.4. Pattern Classifier Implementation and Problem Definition
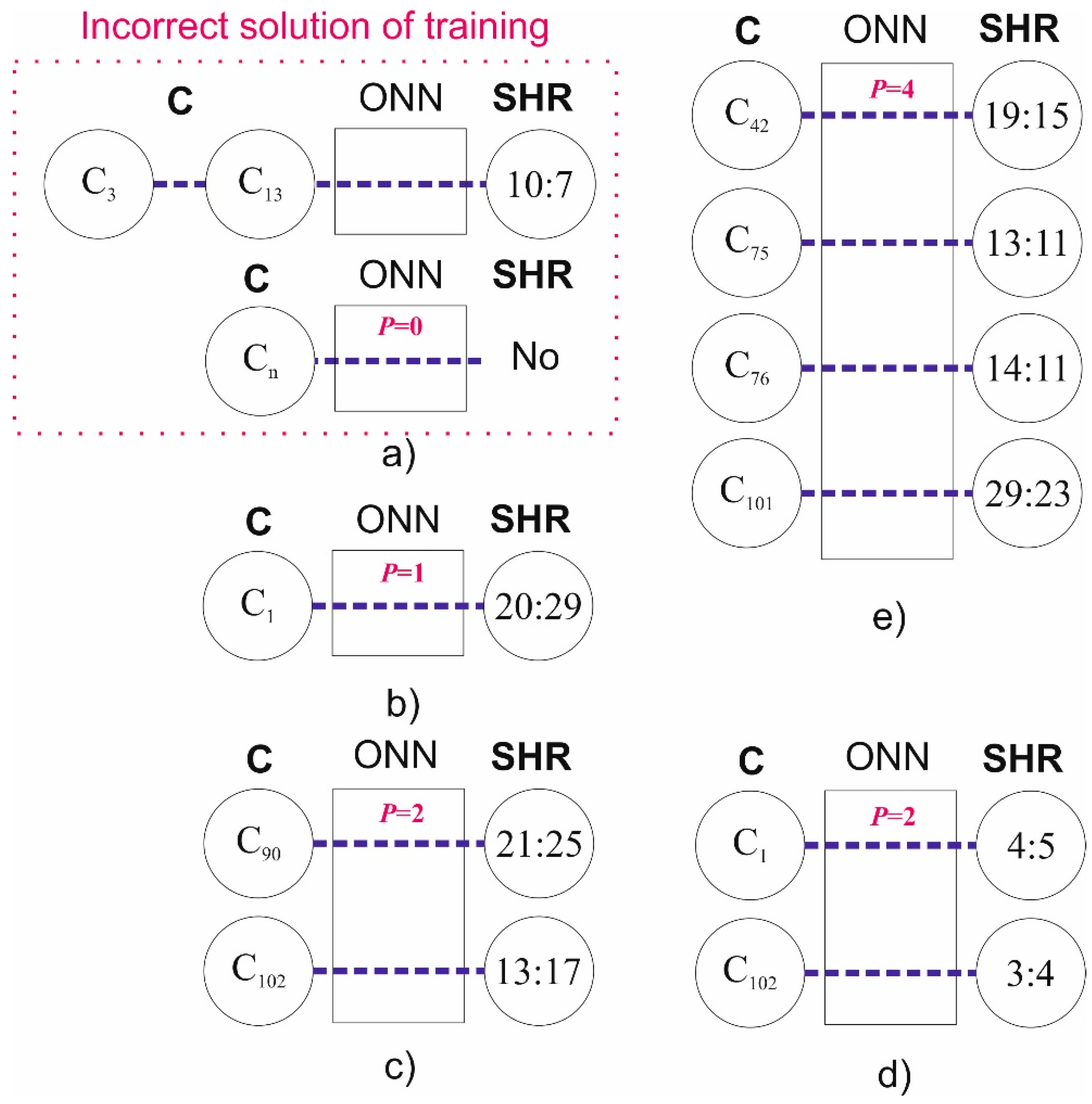
- Synchronization of oscillators No.0 and No.10 with the corresponding value of SHR0,10 and η > ηth, exists only for one specific class Cj with number j = m out of 102 classes:Here we have to show the solutions of this problem with various values of m.
- There is a set of classes C = {CZ1, CZ2 … CZP}, where Z1, Z2 … ZP are arbitrary non-repeating indices, where the number is P < 102. When inputting this set into the oscillator system, it comes to the synchronization states corresponding to the set SHR = {SHR(1)0,10, SHR(2)0,10 … SHR(P)0,10}. The set SHR does not have the same elements, i.e., each class of figures from set C corresponds to a unique synchronization order SHR0,10. By analogy with (4) the problem may be expressed as:
- III.
- The third variant of the problem corresponds to a fully trained network when it solves problem II for all possible input classes Cj, when P = 102.
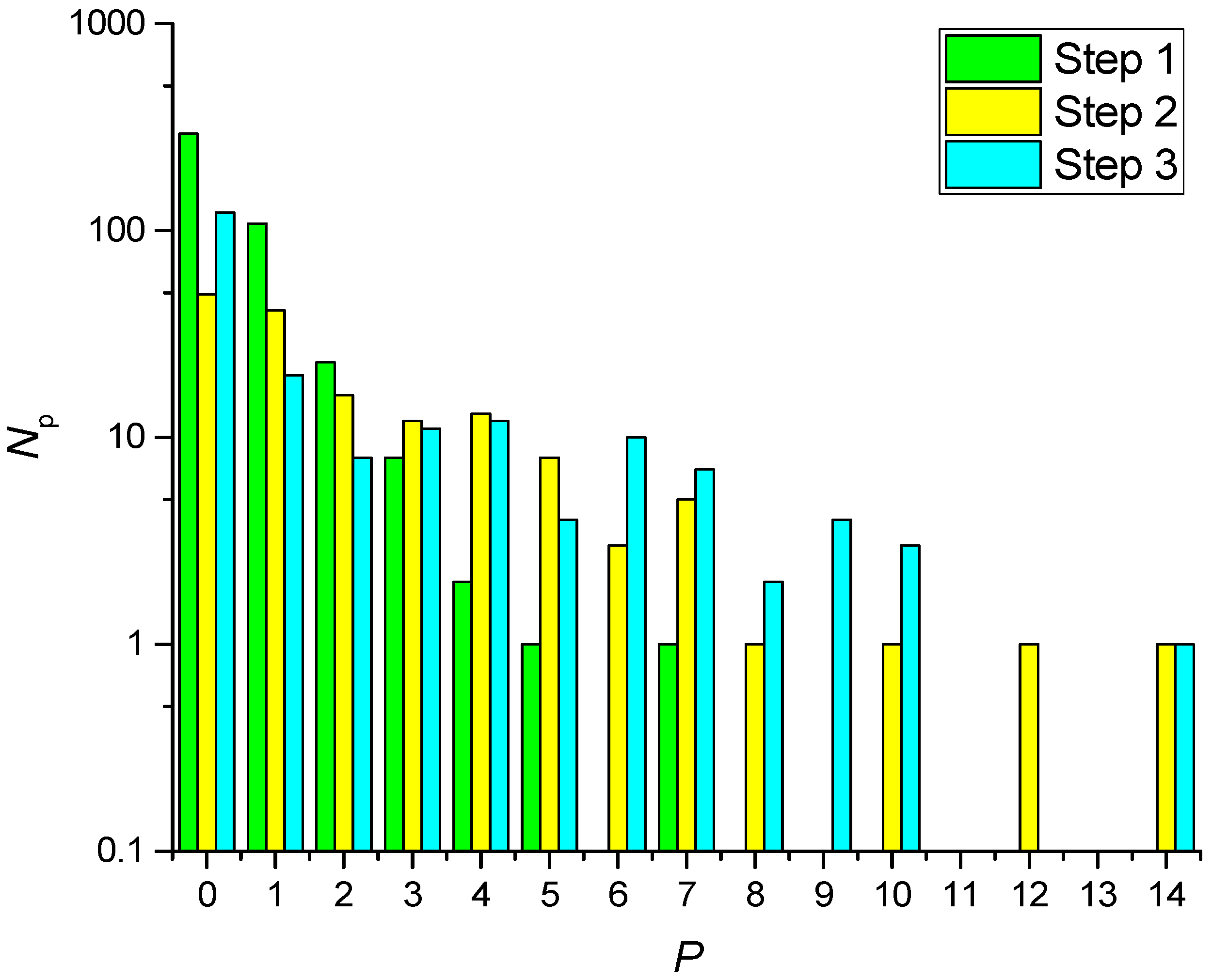
2.5. Technique for ONN Training
- Step 1:
- Random searching of parameters (ION, IOFF, I0, I10, sr, so, sm) in the maximal range of their variations and finding the values meeting the maximum value P. The number of searching attempts is 1000.
- Step 2:
- Narrowing of the parameters ranges by 5 times with their symmetric distribution in relation to the results of the previous step. The number of searching attempts is 1000.
- Step 3:
- Narrowing of the parameters ranges by 25 times with their symmetric distribution in relation to the results of the previous step. The number of searching attempts is 1000.
3. Results
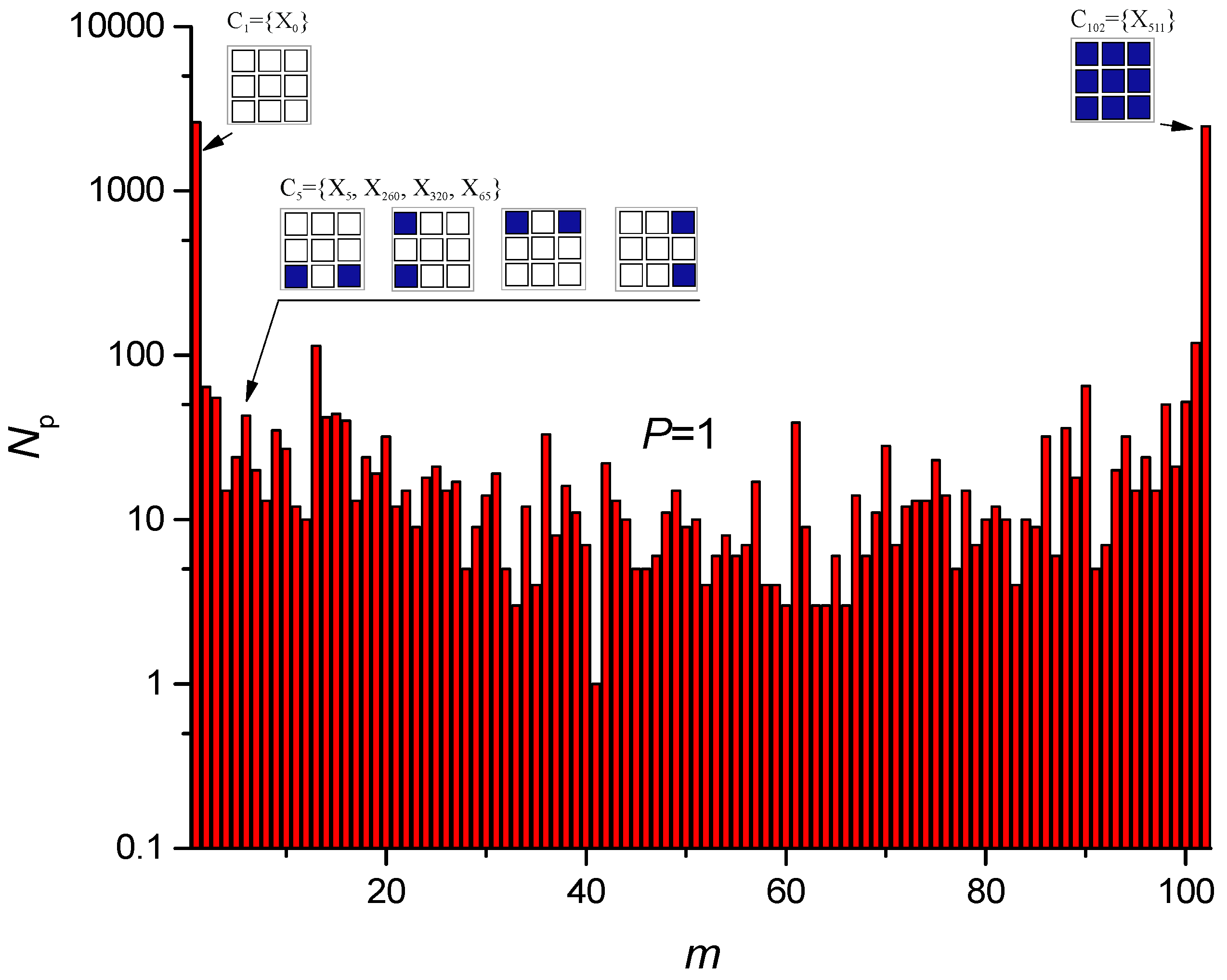
3.1. Solution of Problem I
3.2. Solution of Problem II
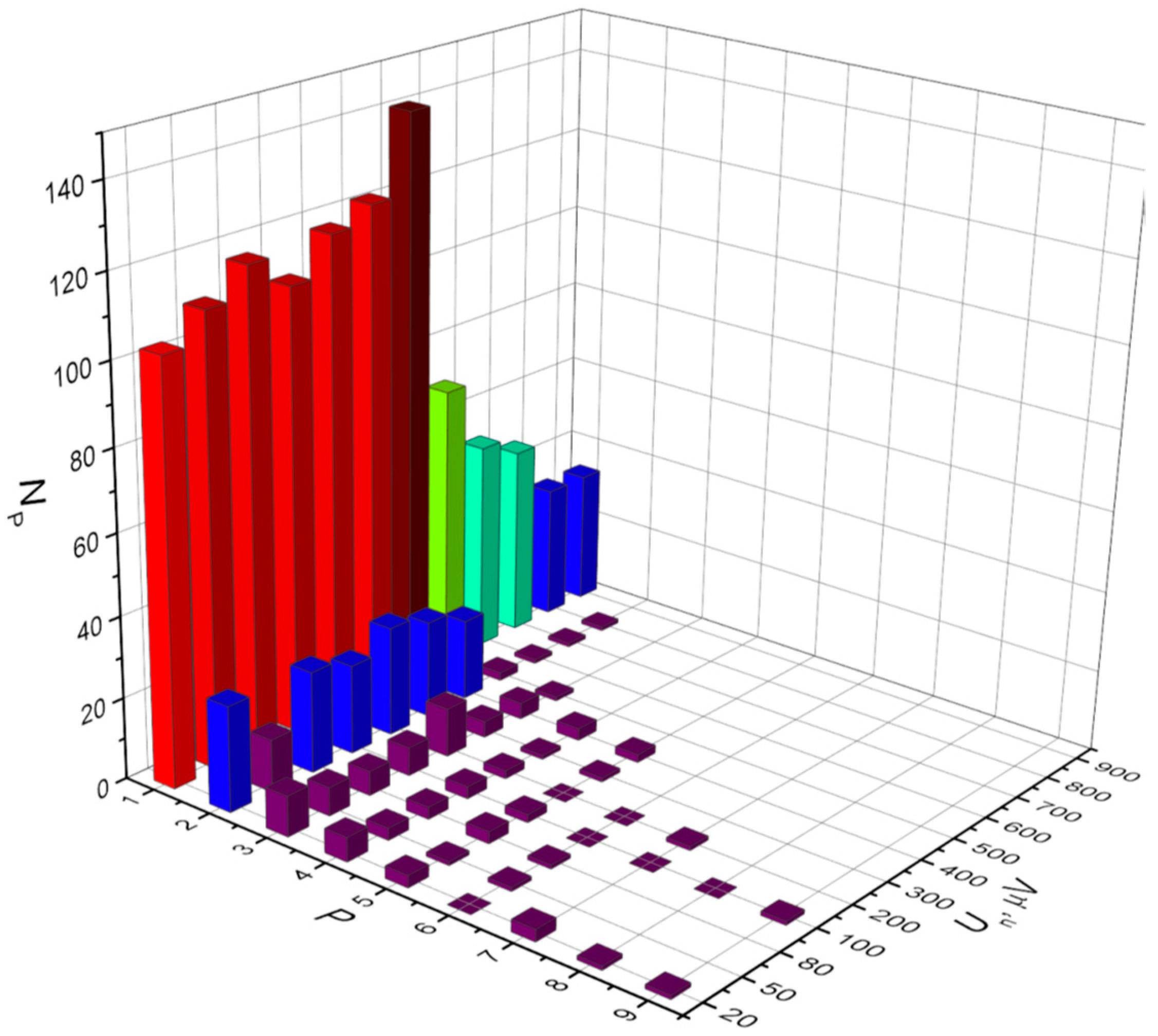
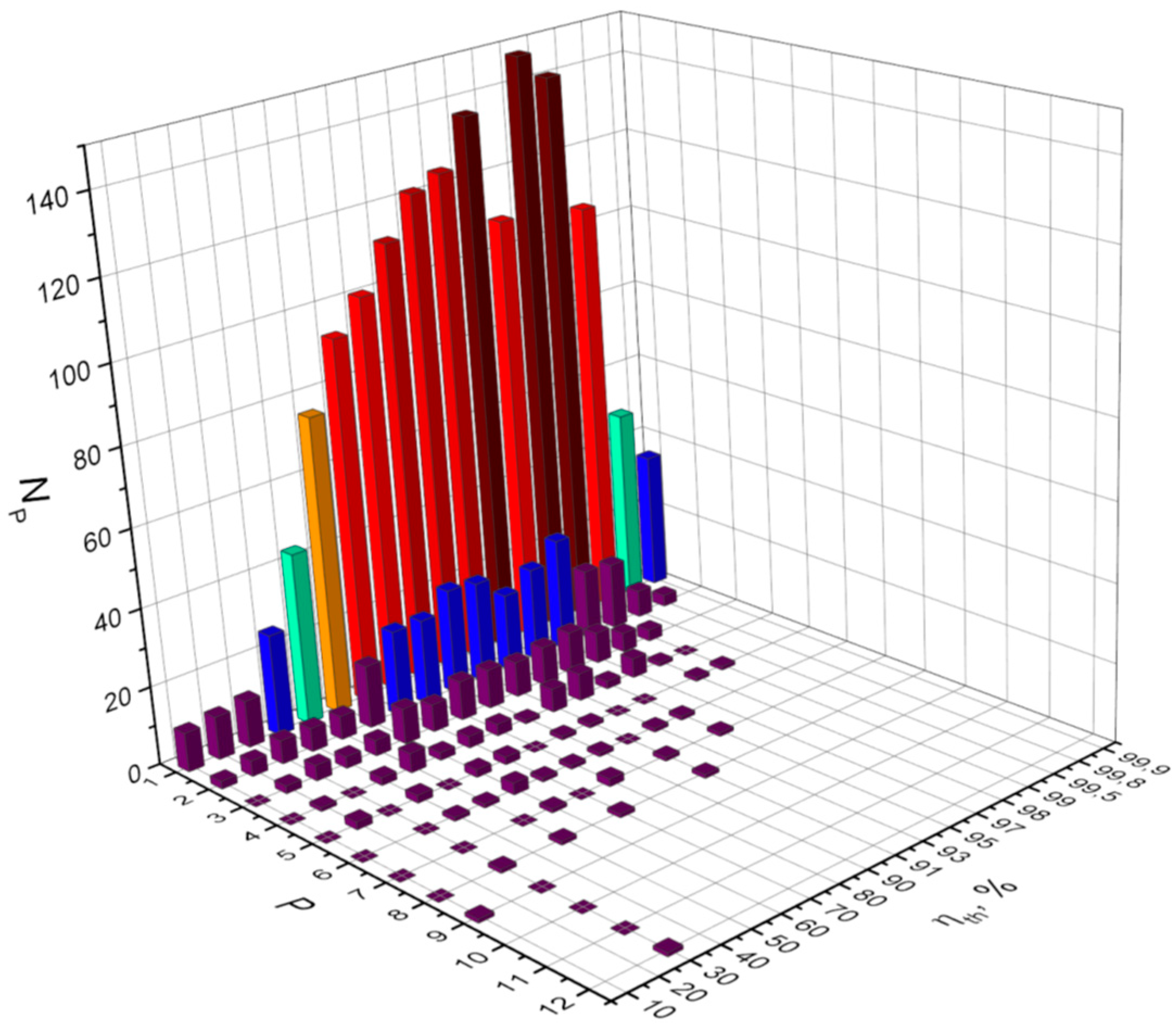
3.3. Solution of Problem III
3.4. Study of the Noise Effect on the Training Results
3.5. Examination of the Synchronization Threshold on the Training Result
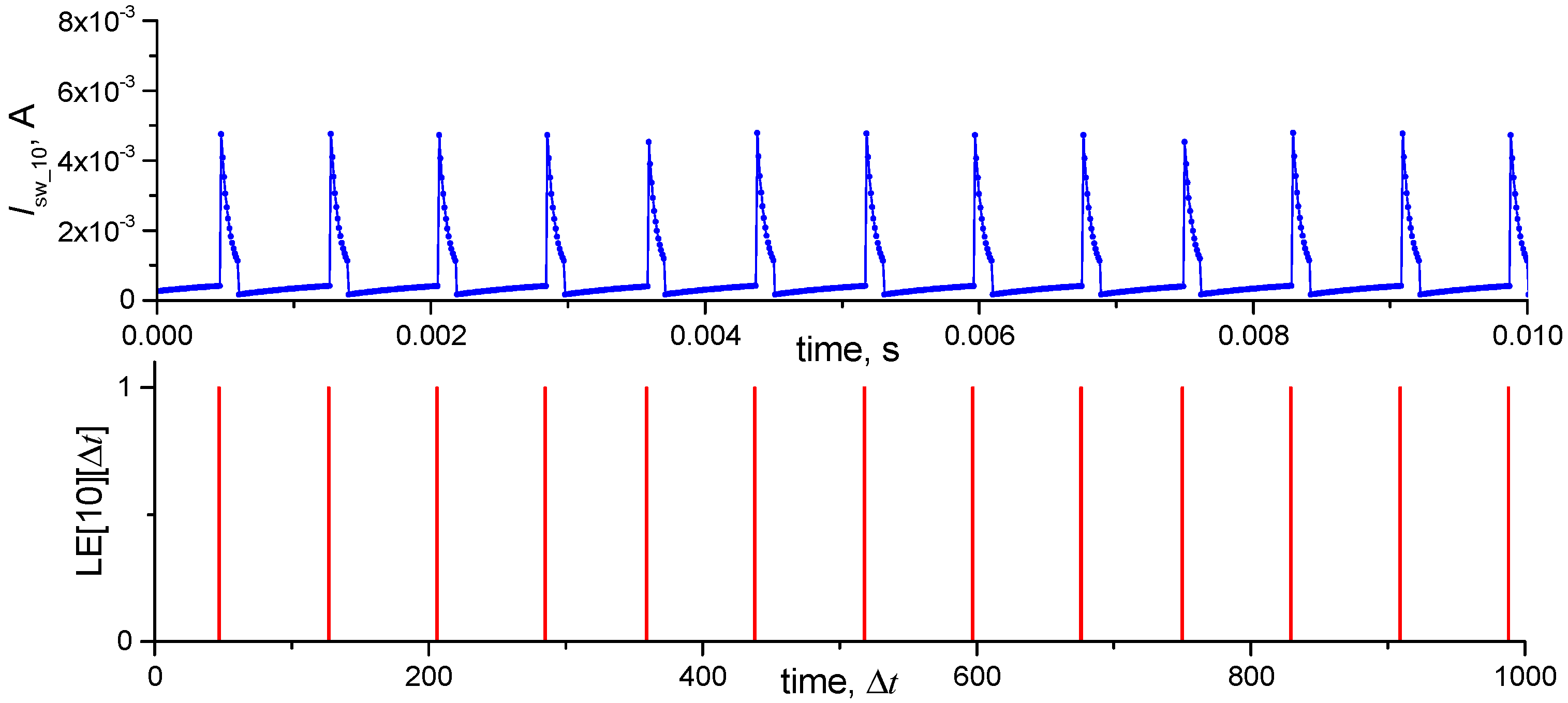
3.6. Study of the Dynamics of the Neural Network
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
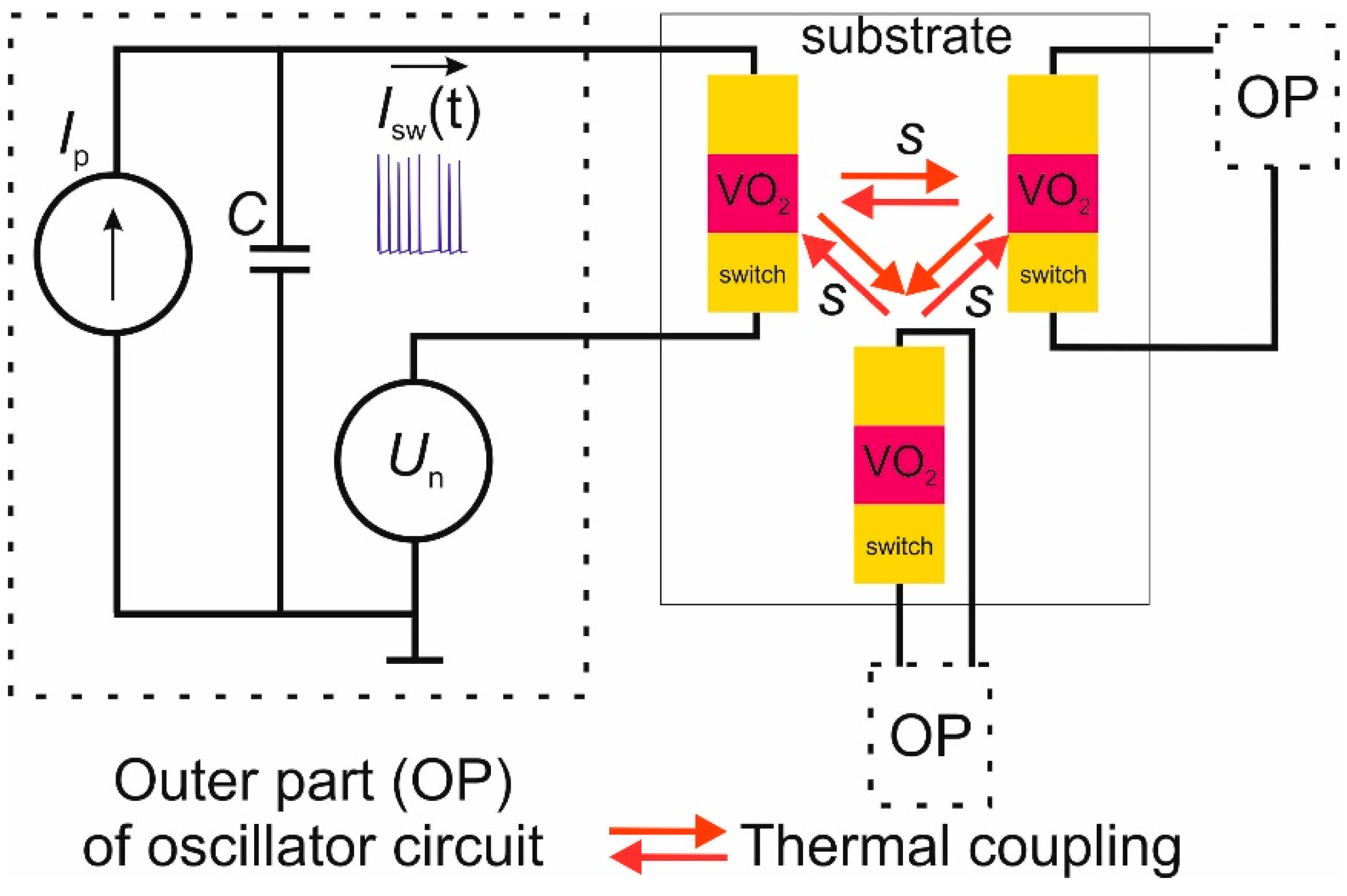
Appendix A.1. Model Circuit of a Coupled Oscillators-Based Neural Network
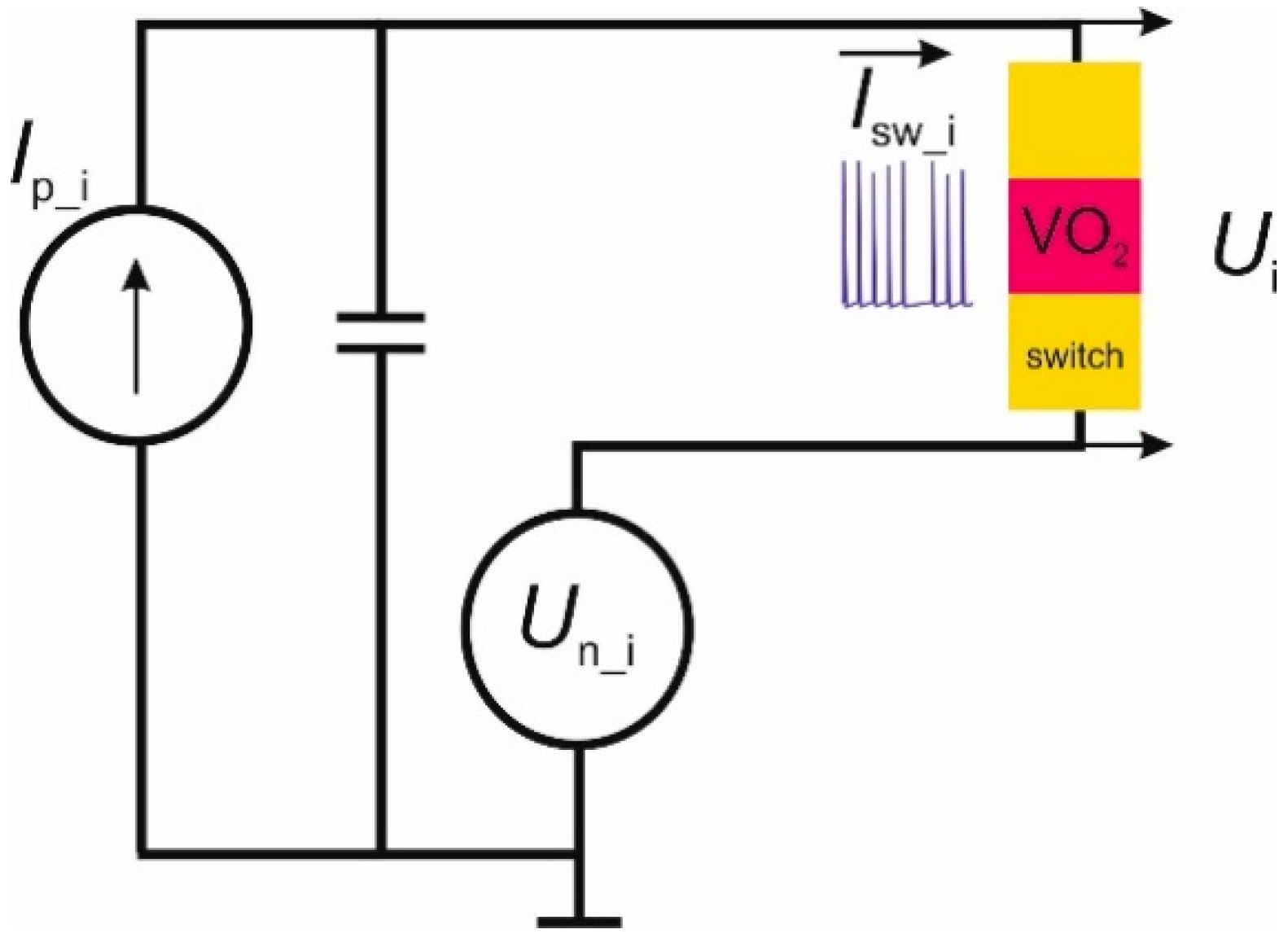
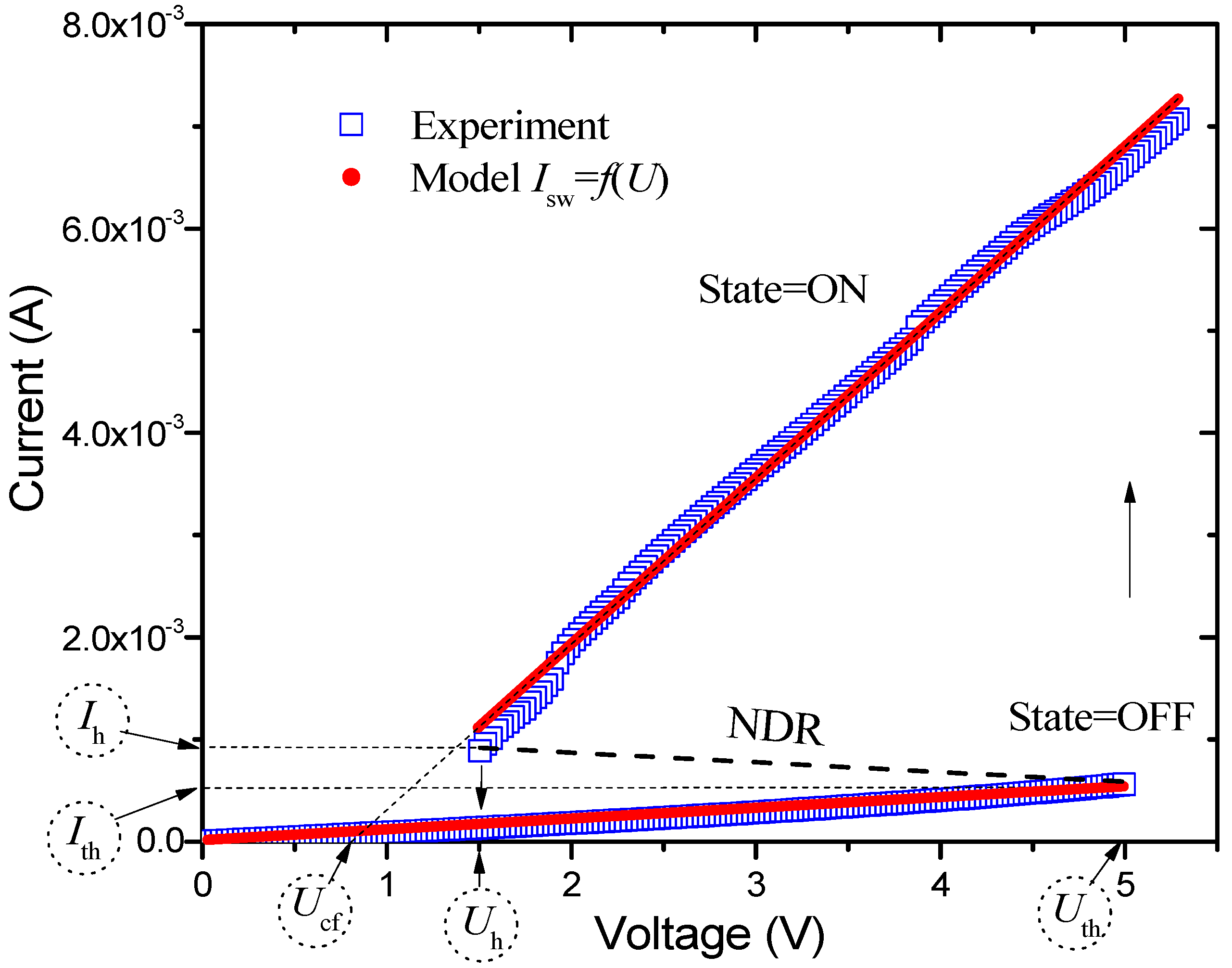
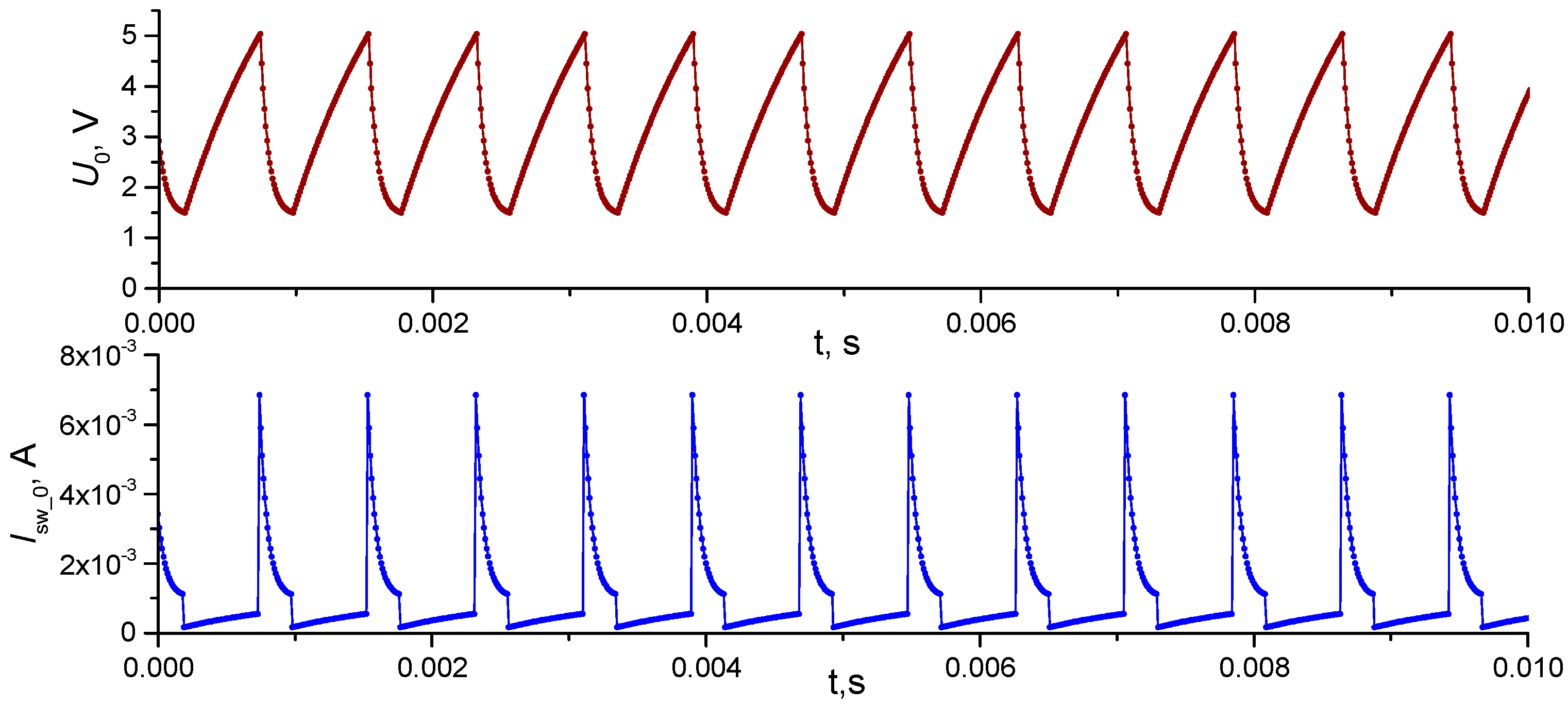
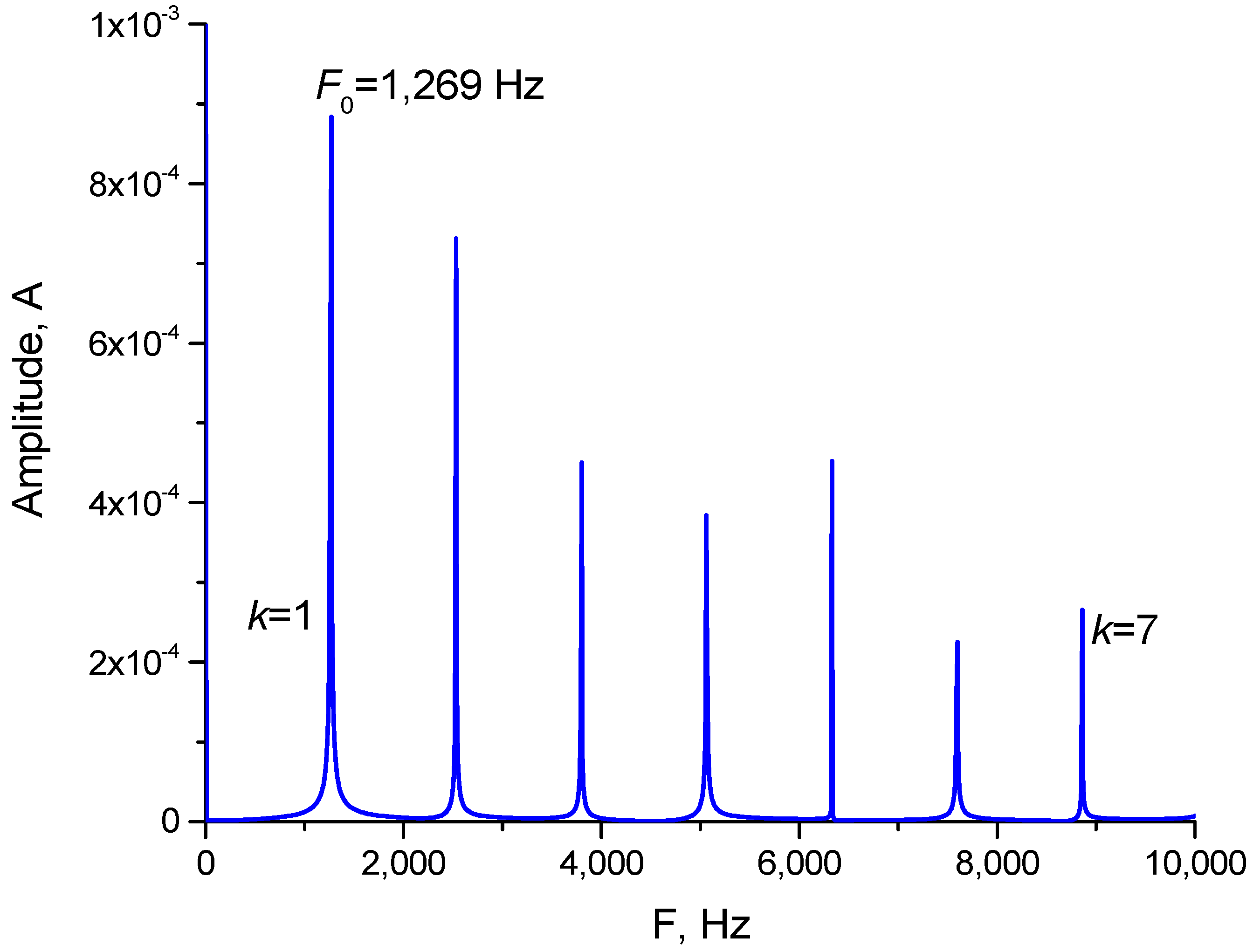
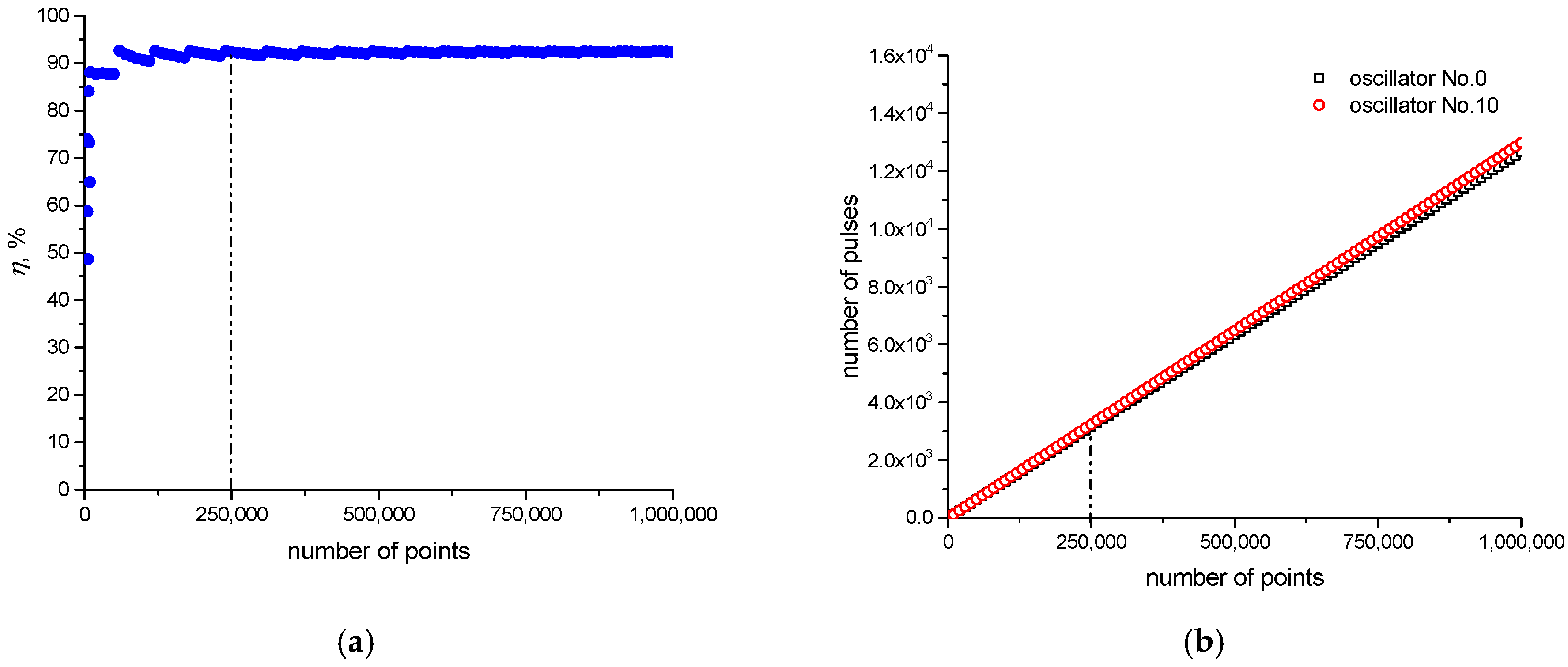
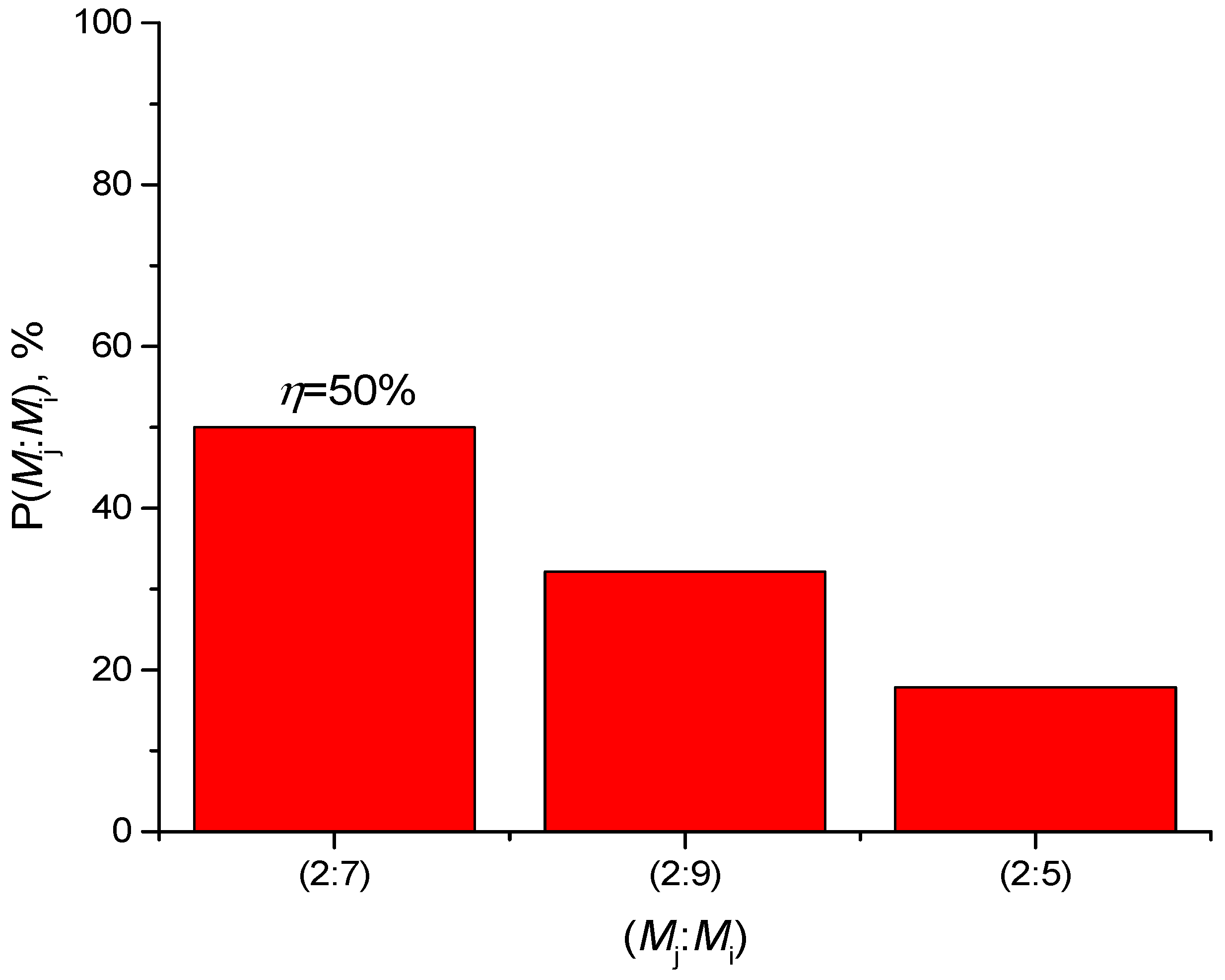
Appendix A.2. Dependence of SHR0,10 and η on the Number of Pulses in the Oscillogram
References
- Freeman, W.J. Spatial properties of an EEG event in the olfactory bulb and cortex. Electroencephalogr. Clin. Neurophysiol. 1978, 44, 586–605. [Google Scholar] [CrossRef]
- Von der Malsburg, C. The Correlation Theory of Brain Function. In Models of Neural Networks; Springer: New York, NY, USA, 1994; pp. 95–119. [Google Scholar]
- Gray, C.M.; Singer, W. Stimulus-specific neuronal oscillations in orientation columns of cat visual cortex. Proc. Natl. Acad. Sci. USA 1989, 86, 1698–1702. [Google Scholar] [CrossRef] [PubMed]
- Eckhorn, R.; Bauer, R.; Jordan, W.; Brosch, M.; Kruse, W.; Munk, M.; Reitboeck, H.J. Coherent oscillations: A mechanism of feature linking in the visual cortex? Biol. Cybern. 1988, 60, 121–130. [Google Scholar] [CrossRef] [PubMed]
- Burton, S.D.; Ermentrout, G.B.; Urban, N.N. Intrinsic heterogeneity in oscillatory dynamics limits correlation-induced neural synchronization. J. Neurophysiol. 2012, 108, 2115–2133. [Google Scholar] [CrossRef] [PubMed]
- White, J.A.; Chow, C.C.; Rit, J.; Soto-Treviño, C.; Kopell, N. Synchronization and Oscillatory Dynamics in Heterogeneous, Mutually Inhibited Neurons. J. Comput. Neurosci. 1998, 5, 5–16. [Google Scholar] [CrossRef] [PubMed]
- Akam, T.; Kullmann, D.M. Oscillations and Filtering Networks Support Flexible Routing of Information. Neuron 2010, 67, 308–320. [Google Scholar] [CrossRef] [PubMed]
- Kuzmina, M.; Manykin, E.; Surina, I. Oscillatory network with self-organized dynamical connections for synchronization-based image segmentation. Biosystems 2004, 76, 43–53. [Google Scholar] [CrossRef]
- Corinto, F.; Bonnin, M.; Gilli, M. Weakly Connected Oscillatory Network Models for Associative and Dynamic Memories. Int. J. Bifurc. Chaos 2007, 17, 4365–4379. [Google Scholar] [CrossRef]
- Nikonov, D.E.; Csaba, G.; Porod, W.; Shibata, T.; Voils, D.; Hammerstrom, D.; Young, I.A.; Bourianoff, G.I. Coupled-Oscillator Associative Memory Array Operation for Pattern Recognition. IEEE J. Explor. Solid-State Comput. Devices Circuits 2015, 1, 85–93. [Google Scholar] [CrossRef]
- Hoppensteadt, F.C.; Izhikevich, E.M. Pattern recognition via synchronization in phase-locked loop neural networks. IEEE Trans. Neural Netw. 2000, 11, 734–738. [Google Scholar] [CrossRef]
- Acebrón, J.A.; Bonilla, L.L.; Pérez Vicente, C.J.; Ritort, F.; Spigler, R. The Kuramoto model: A simple paradigm for synchronization phenomena. Rev. Mod. Phys. 2005, 77, 137–185. [Google Scholar] [CrossRef]
- Klinshov, V.V.; Nekorkin, V.I. Synchronization of delay-coupled oscillator networks. Physics-Uspekhi 2013, 56, 1217–1229. [Google Scholar] [CrossRef]
- Vassilieva, E.; Pinto, G.; Acacio de Barros, J.; Suppes, P. Learning Pattern Recognition Through Quasi-Synchronization of Phase Oscillators. IEEE Trans. Neural Netw. 2011, 22, 84–95. [Google Scholar] [CrossRef] [PubMed]
- Hagerstrom, A.M.; Murphy, T.E.; Roy, R.; Hövel, P.; Omelchenko, I.; Schöll, E. Experimental observation of chimeras in coupled-map lattices. Nat. Phys. 2012, 8, 658–661. [Google Scholar] [CrossRef]
- Vodenicarevic, D.; Locatelli, N.; Abreu Araujo, F.; Grollier, J.; Querlioz, D. A Nanotechnology-Ready Computing Scheme based on a Weakly Coupled Oscillator Network. Sci. Rep. 2017, 7, 44772. [Google Scholar] [CrossRef]
- Romera, M.; Talatchian, P.; Tsunegi, S.; Abreu Araujo, F.; Cros, V.; Bortolotti, P.; Trastoy, J.; Yakushiji, K.; Fukushima, A.; Kubota, H.; et al. Vowel recognition with four coupled spin-torque nano-oscillators. Nature 2018, 563, 230–234. [Google Scholar] [CrossRef]
- Pikovsky, A.; Rosenblum, M.; Kurths, J. Synchronization: A Universal Concept in Nonlinear Sciences; Cambridge University Press: Cambridge, UK, 2001; ISBN 9780521533522. [Google Scholar]
- Velichko, A.; Belyaev, M.; Putrolaynen, V.; Perminov, V.; Pergament, A. Thermal coupling and effect of subharmonic synchronization in a system of two VO2 based oscillators. Solid-State Electron. 2018, 141, 40–49. [Google Scholar] [CrossRef]
- Sakai, J. High-efficiency voltage oscillation in VO2 planer-type junctions with infinite negative differential resistance. J. Appl. Phys. 2008, 103, 103708. [Google Scholar] [CrossRef]
- Shukla, N.; Parihar, A.; Freeman, E.; Paik, H.; Stone, G.; Narayanan, V.; Wen, H.; Cai, Z.; Gopalan, V.; Engel-Herbert, R.; et al. Synchronized charge oscillations in correlated electron systems. Sci. Rep. 2015, 4, 4964. [Google Scholar] [CrossRef]
- Maffezzoni, P.; Daniel, L.; Shukla, N.; Datta, S.; Raychowdhury, A. Modeling and Simulation of Vanadium Dioxide Relaxation Oscillators. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 2207–2215. [Google Scholar] [CrossRef]
- Belyaev, M.A.; Boriskov, P.P.; Velichko, A.A.; Pergament, A.L.; Putrolainen, V.V.; Ryabokon, D.V.; Stefanovich, G.B.; Sysun, V.I.; Khanin, S.D. Switching Channel Development Dynamics in Planar Structures on the Basis of Vanadium Dioxide. Phys. Solid State 2018, 60, 447–456. [Google Scholar] [CrossRef]
- Boriskov, P.P.; Velichko, A.A.; Pergament, A.L.; Stefanovich, G.B.; Stefanovich, D.G. The effect of electric field on metal-insulator phase transition in vanadium dioxide. Tech. Phys. Lett. 2002, 28, 406–408. [Google Scholar] [CrossRef]
- Datta, S.; Shukla, N.; Cotter, M.; Parihar, A.; Raychowdhury, A. Neuro Inspired Computing with Coupled Relaxation Oscillators. In Proceedings of the 51st Annual Design Automation Conference on Design Automation Conference—DAC ’14; ACM Press: New York, NY, USA, 2014; pp. 1–6. [Google Scholar]
- Parihar, A.; Shukla, N.; Datta, S.; Raychowdhury, A. Exploiting Synchronization Properties of Correlated Electron Devices in a Non-Boolean Computing Fabric for Template Matching. IEEE J. Emerg. Sel. Top. Circuits Syst. 2014, 4, 450–459. [Google Scholar] [CrossRef]
- Shukla, N.; Parihar, A.; Cotter, M.; Barth, M.; Li, X.; Chandramoorthy, N.; Paik, H.; Schlom, D.G.; Narayanan, V.; Raychowdhury, A.; et al. Pairwise coupled hybrid vanadium dioxide-MOSFET (HVFET) oscillators for non-boolean associative computing. In 2014 IEEE International Electron Devices Meeting; IEEE: San Francisco, CA, USA, 2014; pp. 28.7.1–28.7.4. [Google Scholar]
- Velichko, A.; Belyaev, M.; Putrolaynen, V.; Pergament, A.; Perminov, V. Switching dynamics of single and coupled VO2-based oscillators as elements of neural networks. Int. J. Mod. Phys. B 2017, 31, 1650261. [Google Scholar] [CrossRef]
- Ghosh, S. Generation of high-frequency power oscillation by astable mode arcing with SCR switched inductor. IEEE J. Solid-State Circuits 1984, 19, 269–271. [Google Scholar] [CrossRef]
- Chen, C.L.; Mathews, R.H.; Mahoney, L.J.; Calawa, S.D.; Sage, J.P.; Molvar, K.M.; Parker, C.D.; Maki, P.A.; Sollner, T.C.L.G. Resonant-tunneling-diode relaxation oscillator. Solid-State Electron. 2000, 44, 1853–1856. [Google Scholar] [CrossRef]
- Sharma, A.A.; Bain, J.A.; Weldon, J.A. Phase Coupling and Control of Oxide-Based Oscillators for Neuromorphic Computing. IEEE J. Explor. Solid-State Comput. Devices Circuits 2015, 1, 58–66. [Google Scholar] [CrossRef]
- Locatelli, N.; Cros, V.; Grollier, J. Spin-torque building blocks. Nat. Mater. 2014, 13, 11–20. [Google Scholar] [CrossRef]
- Velichko, A.; Belyaev, M.; Putrolaynen, V.; Boriskov, P. New Method of the Pattern Storage and Recognition in Oscillatory Neural Networks Based on Resistive Switches. Electronics 2018, 7, 266. [Google Scholar] [CrossRef]
- Velichko, A.A.; Stefanovich, G.B.; Pergament, A.L.; Boriskov, P.P. Deterministic noise in vanadium dioxide based structures. Tech. Phys. Lett. 2003, 29, 435–437. [Google Scholar] [CrossRef]
- Velichko, A.; Belyaev, M.; Putrolaynen, V.; Perminov, V.; Pergament, A. Modeling of thermal coupling in VO2-based oscillatory neural networks. Solid-State Electron. 2018, 139, 8–14. [Google Scholar] [CrossRef]
- Velichko, A.; Putrolaynen, V.; Belyaev, M. Effects of Higher Order and Long-Range Synchronizations for Classification and Computing in Oscillator-Based Spiking Neural Networks. arXiv, 2018; arXiv:1804.03395. [Google Scholar]
- Belyaev, M.; Velichko, A.; Putrolaynen, V.; Perminov, V.; Pergament, A. Electron beam modification of vanadium dioxide oscillators. Phys. Status Solidi Curr. Top. Solid State Phys. 2017, 14. [Google Scholar] [CrossRef]
- Reljan-Delaney, M.; Wall, J. Solving the linearly inseparable XOR problem with spiking neural networks. In 2017 Computing Conference; IEEE: London, UK, 2017; pp. 701–705. [Google Scholar]
- Callan, R. The Essence of Neural Networks; Prentice Hall Europe: Upper Saddle River, NJ, USA, 1999; ISBN 013908732X. [Google Scholar]
- Collins, J.J.; Chow, C.C.; Imhoff, T.T. Stochastic resonance without tuning. Nature 1995, 376, 236–238. [Google Scholar] [CrossRef] [PubMed]
- Kawaguchi, M.; Mino, H.; Durand, D.M. Stochastic Resonance Can Enhance Information Transmission in Neural Networks. IEEE Trans. Biomed. Eng. 2011, 58, 1950–1958. [Google Scholar] [CrossRef] [PubMed]
- Uzuntarla, M.; Cressman, J.R.; Ozer, M.; Barreto, E. Dynamical structure underlying inverse stochastic resonance and its implications. Phys. Rev. E 2013, 88, 42712. [Google Scholar] [CrossRef] [PubMed]
- Parzen, E. Modern Probability Theory and Its Applications; Wiley: Hoboken, NJ, USA, 1992; ISBN 9780471572787. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Velichko, A.; Belyaev, M.; Boriskov, P. A Model of an Oscillatory Neural Network with Multilevel Neurons for Pattern Recognition and Computing. Electronics 2019, 8, 75. https://doi.org/10.3390/electronics8010075
Velichko A, Belyaev M, Boriskov P. A Model of an Oscillatory Neural Network with Multilevel Neurons for Pattern Recognition and Computing. Electronics. 2019; 8(1):75. https://doi.org/10.3390/electronics8010075
Chicago/Turabian StyleVelichko, Andrei, Maksim Belyaev, and Petr Boriskov. 2019. "A Model of an Oscillatory Neural Network with Multilevel Neurons for Pattern Recognition and Computing" Electronics 8, no. 1: 75. https://doi.org/10.3390/electronics8010075
APA StyleVelichko, A., Belyaev, M., & Boriskov, P. (2019). A Model of an Oscillatory Neural Network with Multilevel Neurons for Pattern Recognition and Computing. Electronics, 8(1), 75. https://doi.org/10.3390/electronics8010075