An Oscillatory Neural Network Based Local Processing Unit for Pattern Recognition Applications
Abstract
1. Introduction
2. Weakly Coupled Oscillatory Neural Network and Pattern Recognition
3. Topology of the Proposed ONN System
3.1. Network Initialization
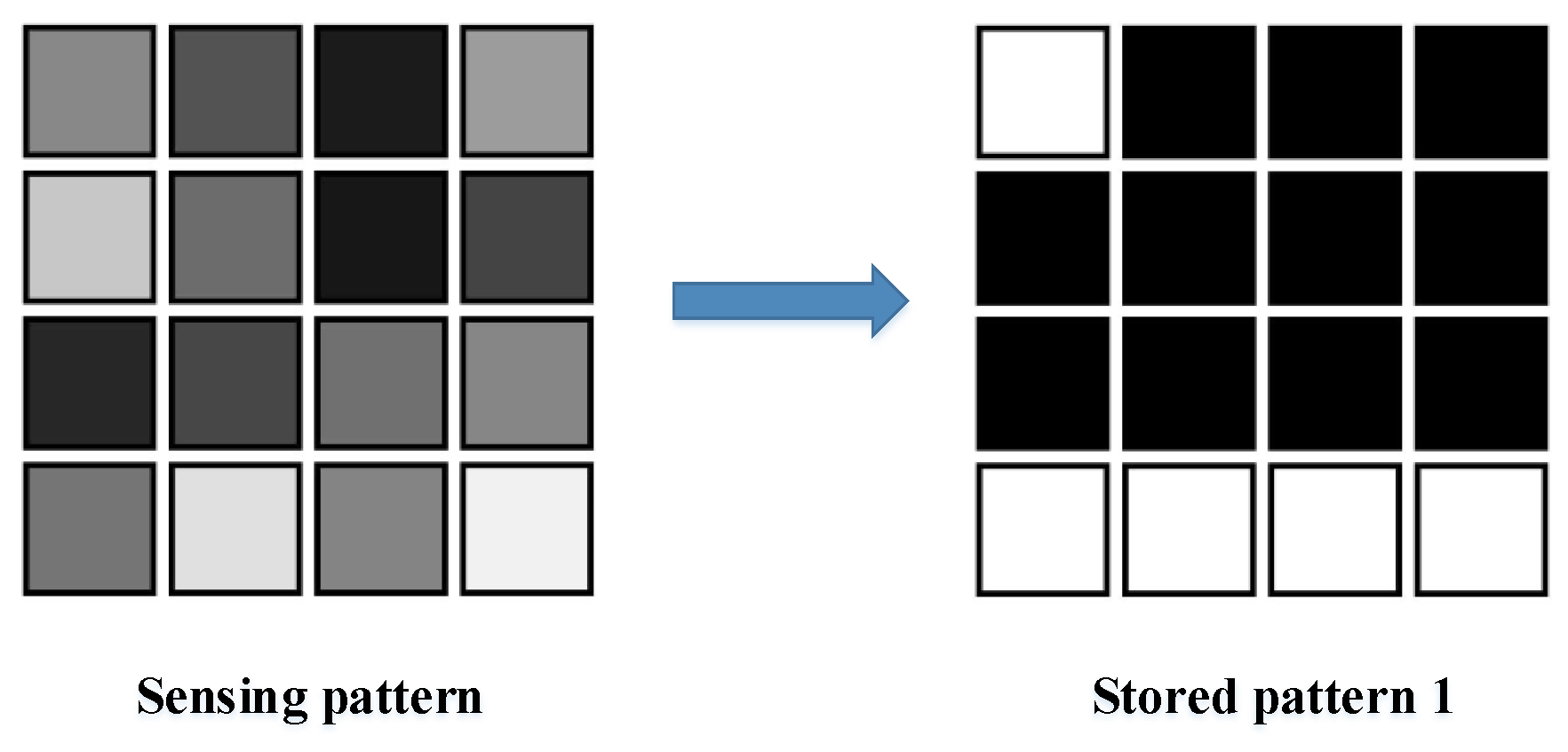
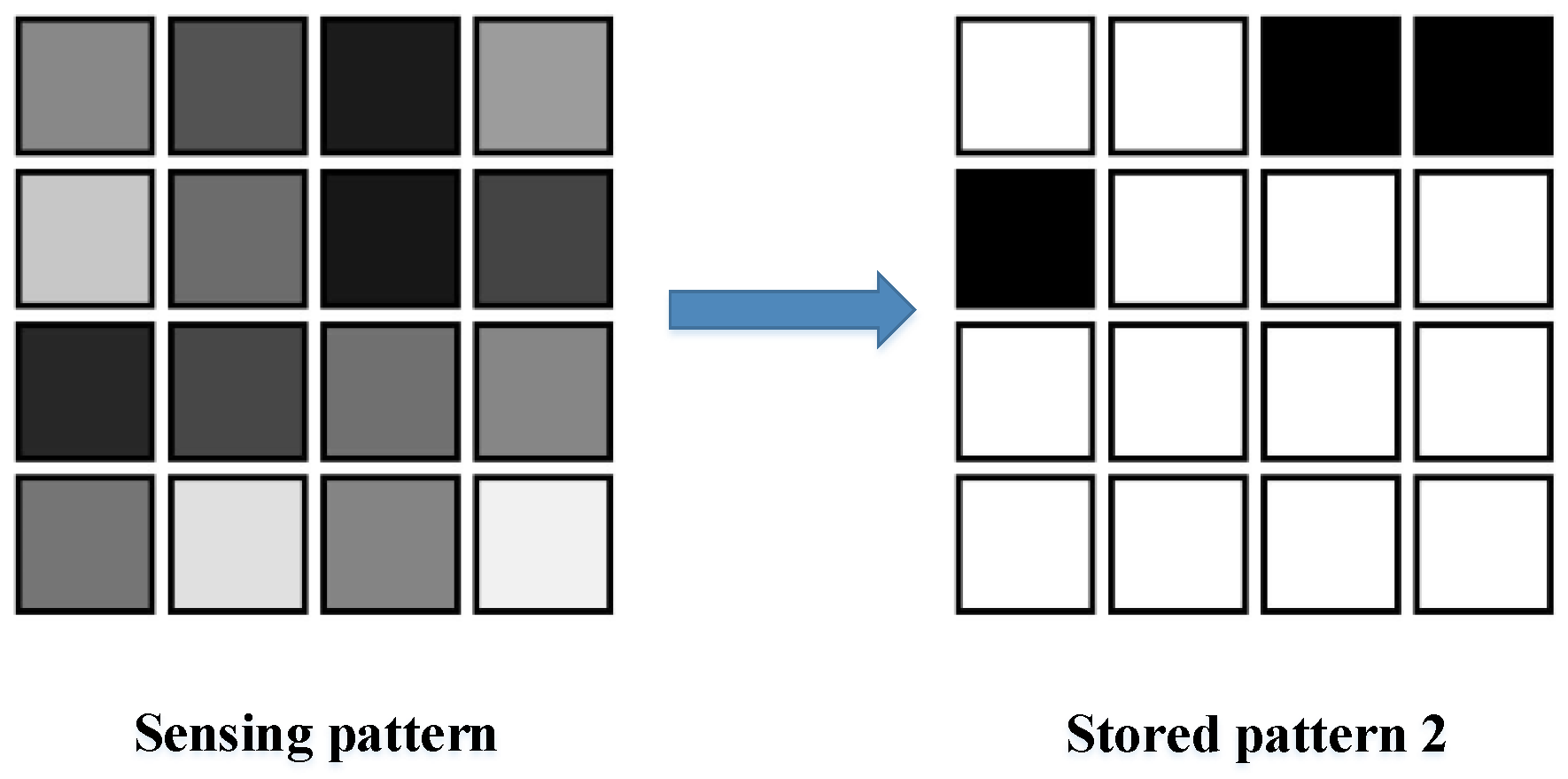
3.2. Pattern Recognition
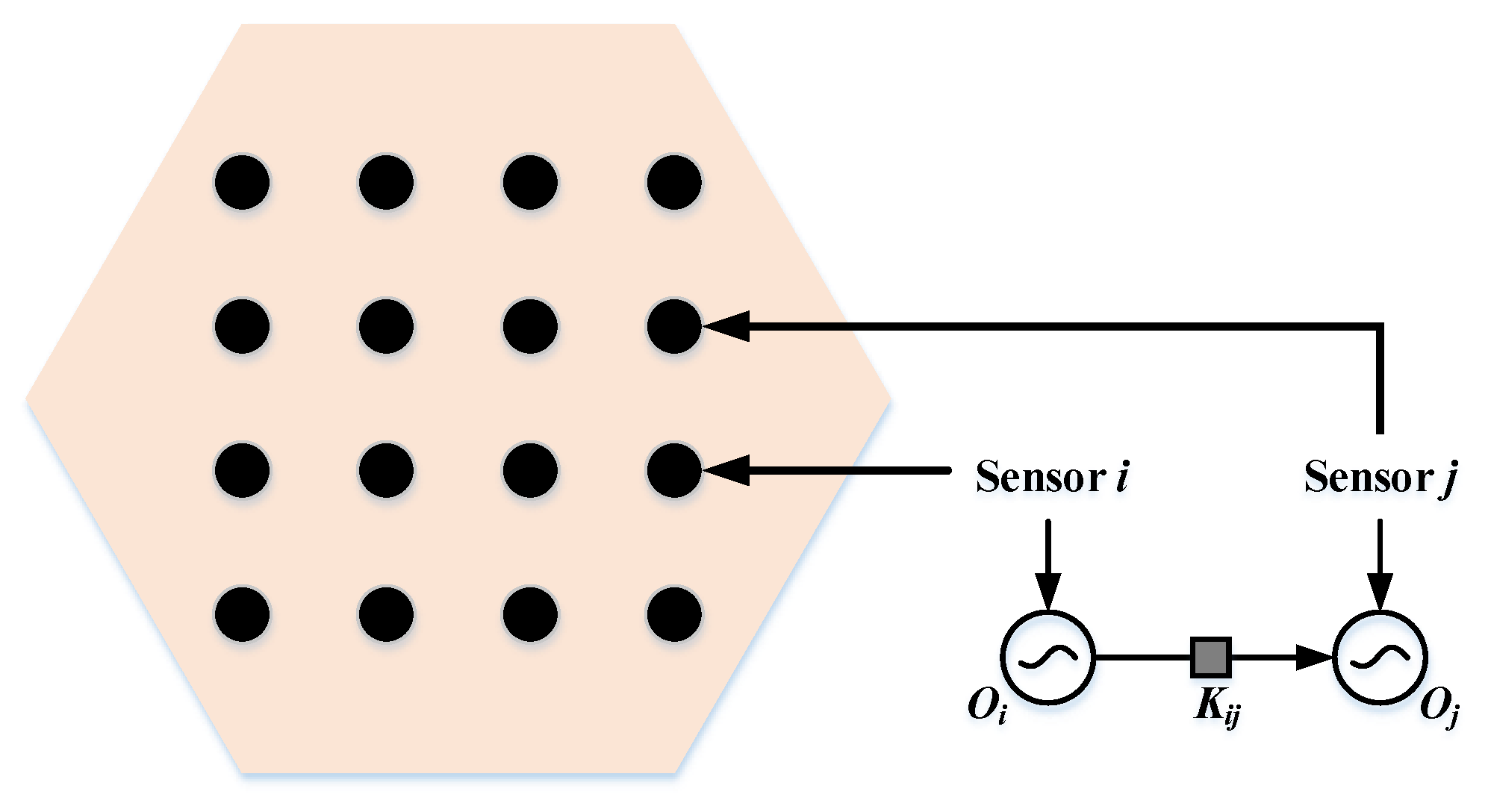
4. Hierarchical Clustering of Impedance Sensing Grid
4.1. Hierarchical Associative Memory Model
4.2. Sensing Device
4.3. Comparison with Other Algorithms
5. Validation of the Proposed Approach
6. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ONN | Oscillator neural network |
| AM | Associative memory |
Appendix A
References
- Bauer, H.; Patel, M.; Veira, J. The Internet of Things: Sizing Up the Opportunity. Section: The Technological Challenges. 2014. Available online: https://www.mckinsey.com/industries/semiconductors/our-insights/the-internet-of-things-sizing-up-the-opportunity (accessed on 30 October 2018).
- Baum, A. A Link to the Internet-of-Things, White Paper, Texas Instruments. 2014. Available online: http://www.ti.com/lit/wp/swry009/swry009.pdf (accessed on 30 October 2018).
- Haider, M.R.; Islam, S.K.; Mahfouz, M.R. A low-voltage low-power injection-locked oscillator for wearable health monitoring systems. Analog Integr. Circuits Signal Process. 2011, 66, 145–154. [Google Scholar] [CrossRef]
- Haider, M.R.; Islam, S.K.; Mostafa, S.; Zhang, M.; Oh, T. Low-Power Low-Voltage Current Read-out Circuit for Inductively-Powered Implant System. IEEE Trans. Biomed. Circuits Syst. 2010, 4, 205–213. [Google Scholar] [CrossRef] [PubMed]
- Haider, M.R.; Holleman, J.; Mostafa, S.; Islam, S.K. Low-power biomedical signal monitoring system for implantable sensor applications. Int. J. High Speed Electron. Syst. 2011, 20, 115–128. [Google Scholar] [CrossRef]
- Li, Y.-G.; Haider, M.R.; Massoud, Y. A low-noise gain-tunable amplifier for large array biopotential recording system. Analog Integr. Circuits Signal Process. 2013, 74, 485–489. [Google Scholar] [CrossRef]
- Li, Y.-G.; Ma, Q.; Haider, M.R.; Massoud, Y. An ultra-low-power bioamplifier for implantable large-scale recording of neural activity. In Proceedings of the IEEE Wireless and Microwave Technology Conference (WAMICON2013), Orlando, FL, USA, 7–9 April 2013. [Google Scholar]
- Quadir, M.S.E.; Haider, M.R.; Massoud, Y. A low-power low-noise bioamplifier for multielectrode neural recording systems. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS2012), Seoul, Korea, 20–23 May 2012; pp. 2557–2560. [Google Scholar]
- Ma, Q.; Haider, M.R.; Shrestha, V.L.; Massoud, Y. Bursting Hodgkin-huxley model-based ultra-low-power neuromimetic silicon neuron. Analog Integr. Circuits Signal Process. 2012, 73, 329–337. [Google Scholar] [CrossRef]
- Li, Y.-G.; Haider, M.R. A low-power neuromorphic CMOS sensor circuit for the implanted biomolecular detections. In Proceedings of the IEEE Sensor Conference, Baltimore, MD, USA, 3–6 November 2013. [Google Scholar]
- Arifuzzman, A.K.M.; Islam, M.S.; Haider, M.R. A neuron model based ultra-low current sensor system for bio-applications. J. Sens. 2016, 2016. [Google Scholar] [CrossRef]
- Ma, Q.; Haider, M.R. A low-power, low-noise bioinspired bandpass biopotential amplifier-filter bank for implantable bio-sensor. In Proceedings of the IEEE Sensor Conference, Baltimore, MD, USA, 3–6 November 2013. [Google Scholar]
- Ma, Q.; Li, Y.-G.; Haider, M.R.; Massoud, Y. A low-power neuromorphic bandpass filter for biosignal processing. In Proceedings of the IEEE Wireless and Microwave Technology Conference (WAMICON2013), Orlando, FL, USA, 7–9 April 2013. [Google Scholar]
- Li, Y.-G.; Ma, Q.; Haider, M.R.; Massoud, Y. Ultra-low-power high sensitivity spike detectors based on modified nonlinear energy operator. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS2013), Beijing, China, 19–23 May 2013; pp. 137–140. [Google Scholar]
- Li, Y.-G.; Massoud, Y.; Haider, M.R. Low-power high-sensitivity spike detectors for implantable VLSI neural recording microsystems. Analog Integr. Circuits Signal Process. 2014, 80, 449–457. [Google Scholar] [CrossRef]
- Li, Y.-G.; Haider, M.R.; Massoud, Y. An efficient orthogonal pulse set generator for high-speed sub-GHz UWB communications. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS2014), Melbourne, Australia, 1–5 June 2014. [Google Scholar]
- Marvel, S.A.; Strogatz, S.H. Invariant submanifold for series arrays of Josephson junctions. Chaos 2009, 19, 013132. [Google Scholar] [CrossRef]
- Bennett, M.; Schatz, M.F.; Rockwood, H.; Wiesenfeld, K. Huygens’s clocks. Proc. Math. Phys. Eng. Sci. 2002, 458, 563–579. [Google Scholar] [CrossRef]
- Winfree, A.T. Biological rhythms and the behavior of populations of coupled oscillators. J. Theor. Biol. 1967, 16, 15–42. [Google Scholar] [CrossRef]
- Breakspear, M.; Heitmann, S.; Daffertshofer, A. Generative models of cortical oscillations: Neurobiological implications of the Kuramoto model. Front. Hum. Neurosci. 2010, 4, 190. [Google Scholar] [CrossRef] [PubMed]
- Fang, Y.; Yashin, V.V.; Levitan, S.P.; Balazs, A.C. Pattern recognition with ‘materials that compute’. Sci. Adv. 2016, 2, e1601114. [Google Scholar] [CrossRef] [PubMed]
- Wong, M.H.Y.; Lee, R.S.T.; Liu, J.N.K. Wind shear forecasting by Chaotic Oscillatory-based Neural Networks (CONN) with Lee Oscillator (retrograde signalling) model. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–8 June 2008; pp. 2040–2047. [Google Scholar]
- Chen, K.; Wang, D.L. A dynamically coupled neural oscillator network for image segmentation. Neural Netw. 2002, 15, 423–439. [Google Scholar] [CrossRef]
- Hoppensteadt, F.C.; Izhikevich, E.M. Pattern recognition via synchronization in phase-locked loop neural networks. IEEE Trans. Neural Netw. 2000, 11, 734–738. [Google Scholar] [CrossRef] [PubMed]
- Vodenicarevic, D.; Locatelli, N.; Grollier, J.; Querlioz, D. Synchronization detection in networks of coupled oscillators for pattern recognition. In Proceedings of the 2016 International Joint Conference on Neural Networks, Vancouver, BC, Canada, 24–29 July 2016; pp. 2015–2022. [Google Scholar]
- Sookhak, M.; Akhunzada, A.; Gani, A.; Khan, M.K.; Anuar, N.B. Towards dynamic remote data auditing in computational clouds. Sci. World J. 2014, 2014, 269357. [Google Scholar] [CrossRef]
- Csaba, G.; Ytterdal, T.; Porod, W. Oscillatory neural network from ring oscillators. In Proceedings of the CNNA 2016 15th International Workshop on Cellular Nanoscale Networks and their Applications, Dresden, Germany, 23–25 August 2016; pp. 1–2. [Google Scholar]
- Cotter, M.J.; Fang, Y.; Levitan, S.P.; Chiarulli, D.M.; Narayanan, V. Computational architectures based on coupled oscillators. In Proceedings of the VLSI (ISVLSI) 2014 IEEE Computer Society Annual Symposium on IEEE, Tampa, FL, USA, 9–11 July 2014; pp. 130–135. [Google Scholar]
- Shi, R.; Jackson, T.C.; Swenson, B.; Kar, S.; Pileggi, L. On the design of phase locked loop oscillatory neural networks: Mitigation of transmission delay effects. In Proceedings of the Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 2039–2046. [Google Scholar]
- Andrej, K.; George, T.; Sanketh, S.; Thomas, L.; Rahul, S.; Li, F.F. Large-scale Video Classification with Convolutional Neural Networks. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1725–1732. [Google Scholar]
- Yan, F. Hierarchical Associative Memory Based on Oscillatory Neural Network. Ph.D. Thesis, University of Pittsburgh, Pittsburgh, PA, USA, 2013. [Google Scholar]
- Vassilieva, E.; Pinto, G.; De Barros, J.A.; Suppes, P. Learning pattern recognition through quasi-synchronization of phase oscillators. IEEE Trans. Neural Netw. 2011, 22, 84–95. [Google Scholar] [CrossRef]
- Itoh, M.; Chua, L.O. Star cellular neural networks for associative and dynamic memories. Int. J. Bifurc. Chaos 2004, 14, 1725–1772. [Google Scholar] [CrossRef]
- Hoppensteadt, F.C.; Izhikevich, E.M. Oscillatory neurocomputers with dynamic connectivity. Phys. Rev. Lett. 1999, 82, 2983. [Google Scholar] [CrossRef]
- Acebrón, J.A.; Bonilla, L.L.; Vicente, C.J.P.; Ritort, F.; Spigler, R. The Kuramoto model: A simple paradigm for sychronization phenomena. Rev. Mod. Phys. 2005, 77, 137–185. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, Z.; Yu, C. Finite time synchronization of networked Kuramoto-like oscillators. In Proceedings of the Control Conference (AuCC), Newcastle, Australia, 3–4 November 2016; pp. 81–86. [Google Scholar]
- Kuramoto, Y. Chemical Oscillations, Waves, and Turbulences; Spinger: New York, NY, USA, 1984. [Google Scholar]
- Izhikevich, E.M.; Kuramoto, Y. Weakly coupled oscillators. Encycl. Math. Phys. 2006, 5, 448. [Google Scholar]
- Swisher, S.L.; Lin, M.C.; Liao, A.; Leeflang, E.J.; Khan, Y.; Pavinatto, F.J.; Mann, K.; Naujokas, A.; Young, D.; Roy, S.; et al. Impedance sensing device enables early detection of pressure ulcers in vivo. Nat. Commun. 2015, 6, 7575. [Google Scholar] [CrossRef] [PubMed]
- Orosz, G.; Moehlis, J.; Ashwin, P. Designing the dynamics of globally coupled oscillators. Prog. Theor. Phys. 2009, 122, 611–630. [Google Scholar] [CrossRef]
- Terence, S.; Sukthankar, R.; Mullin, M.; Baluja, S. High-performance Memory-Based Face Recognition for Visitor Identification. Technical Report, Just Research. 1999. Available online: https://www.ri.cmu.edu/pub_files/pub1/sim_terence_1999_1/sim_terence_1999_1.pdf (accessed on 30 October 2018).
- ATT Cambridge Image Database. Available online: http://www.cl.cam.ac.uk/research/dtg/attarchive/facedatabase.html (accessed on 30 October 2018).
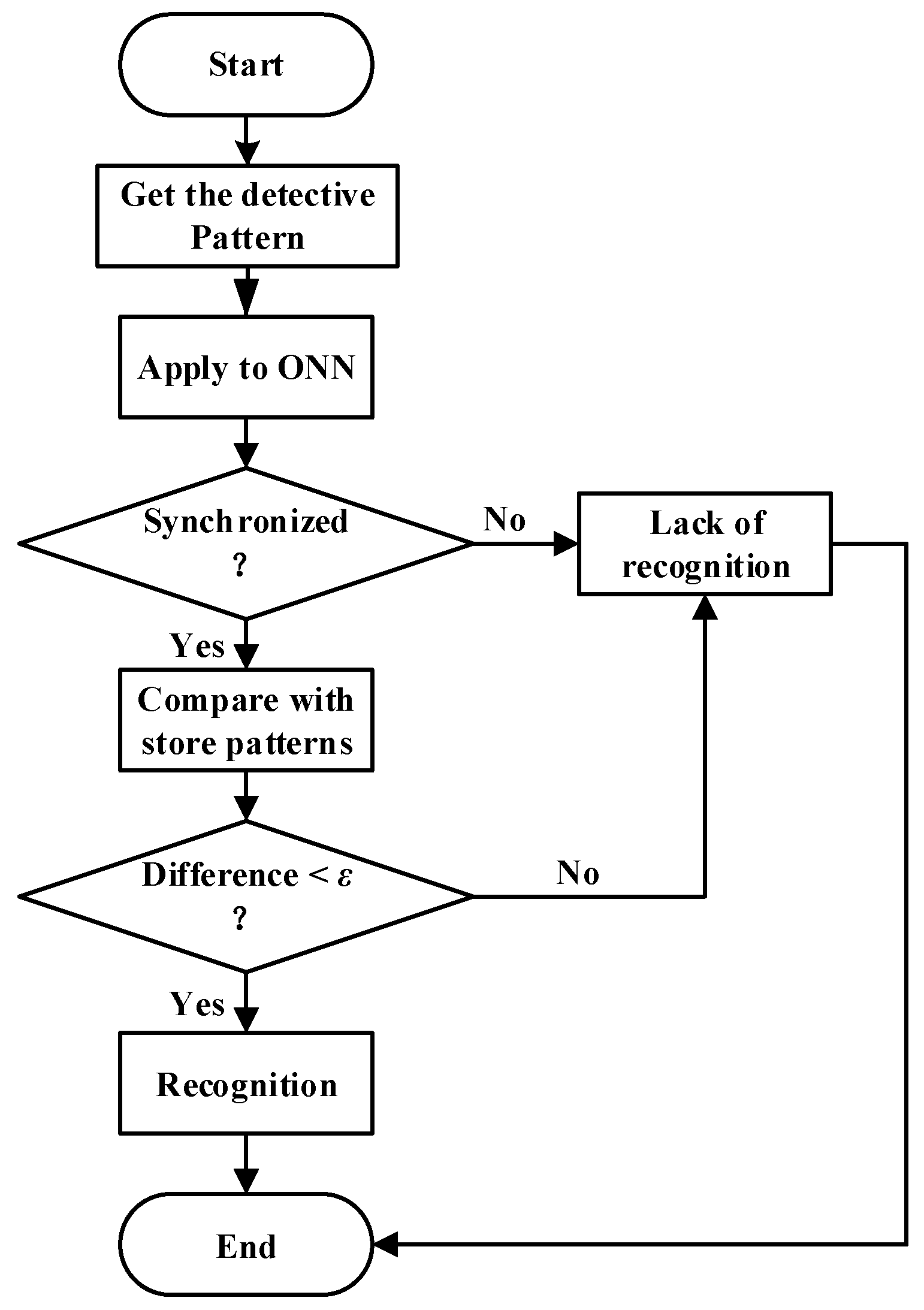

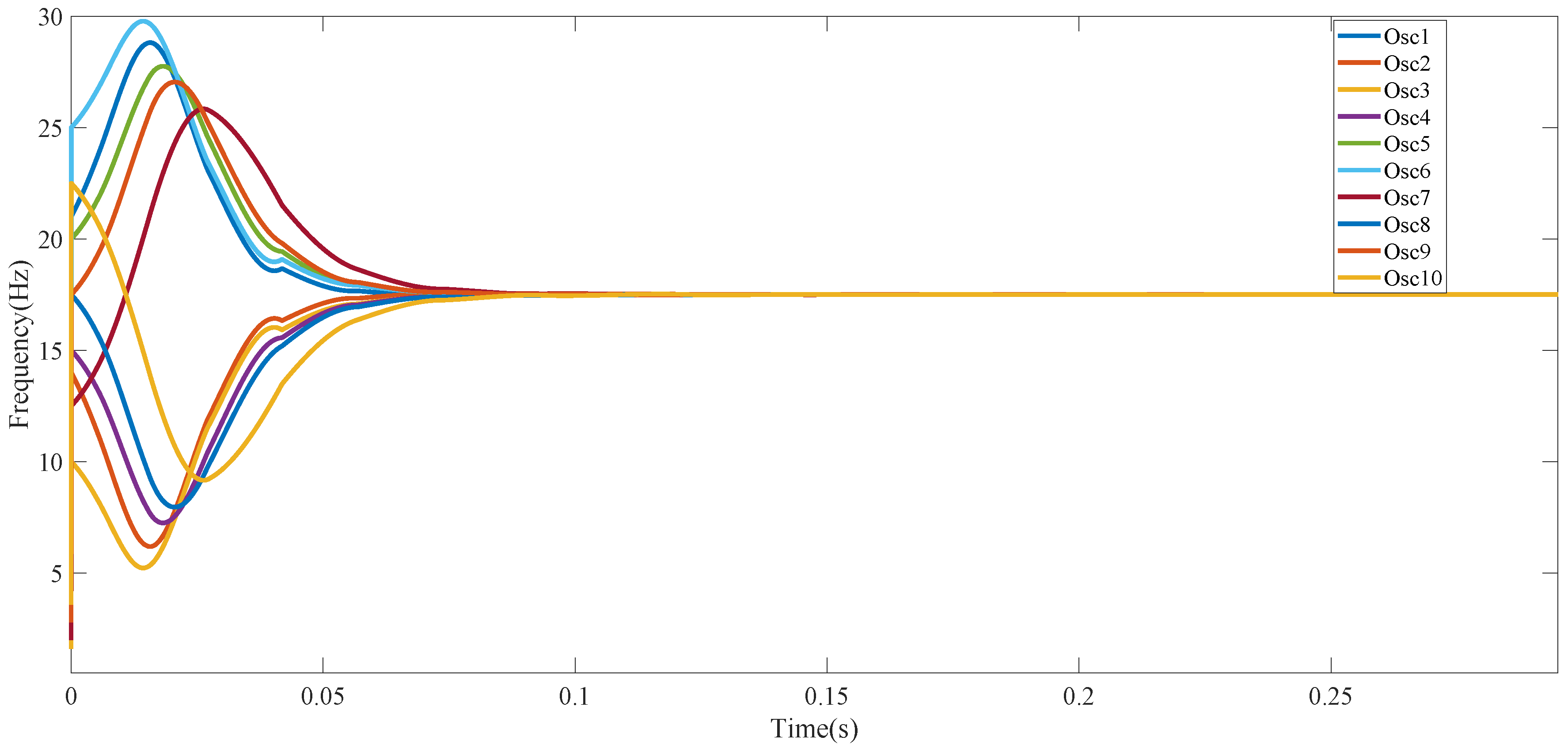
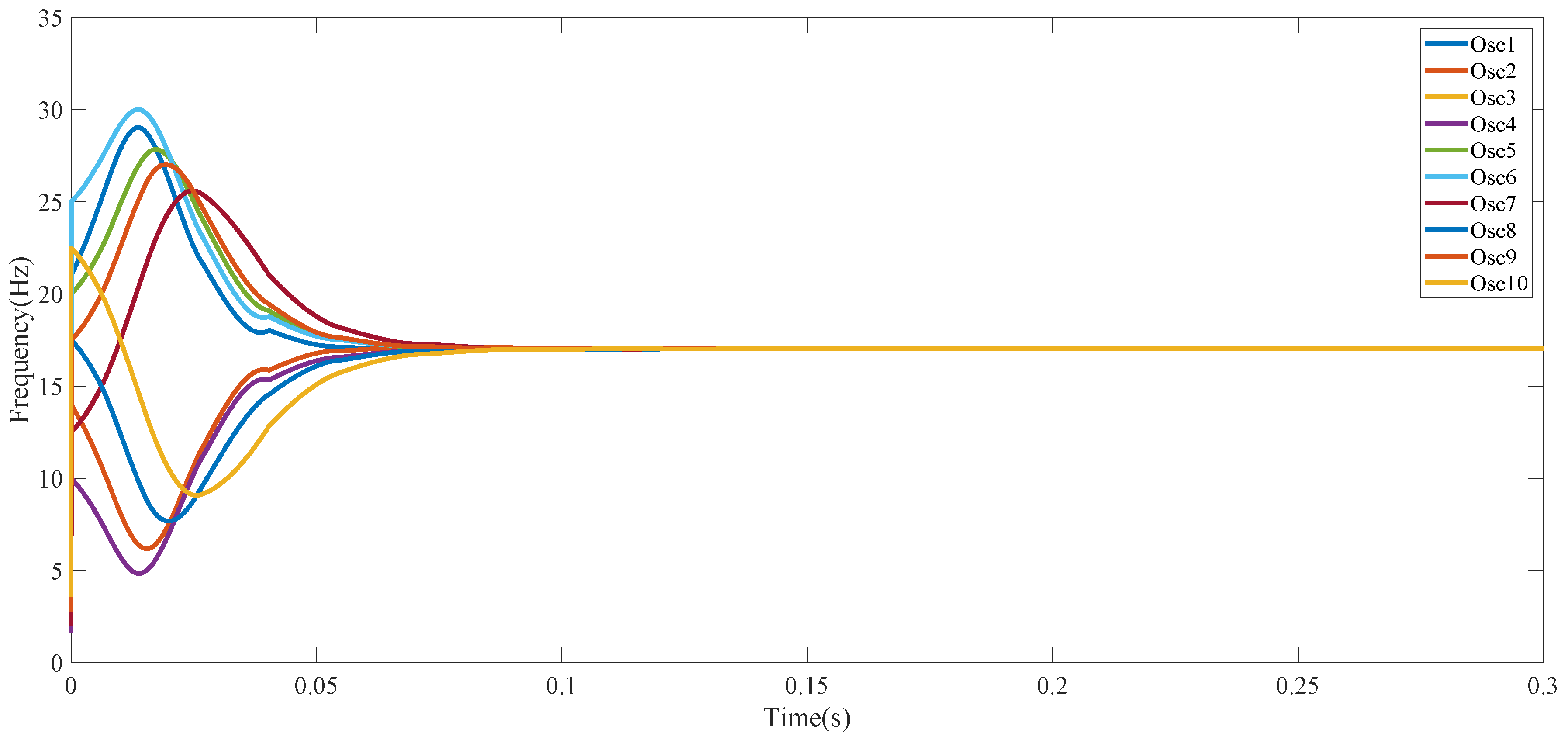
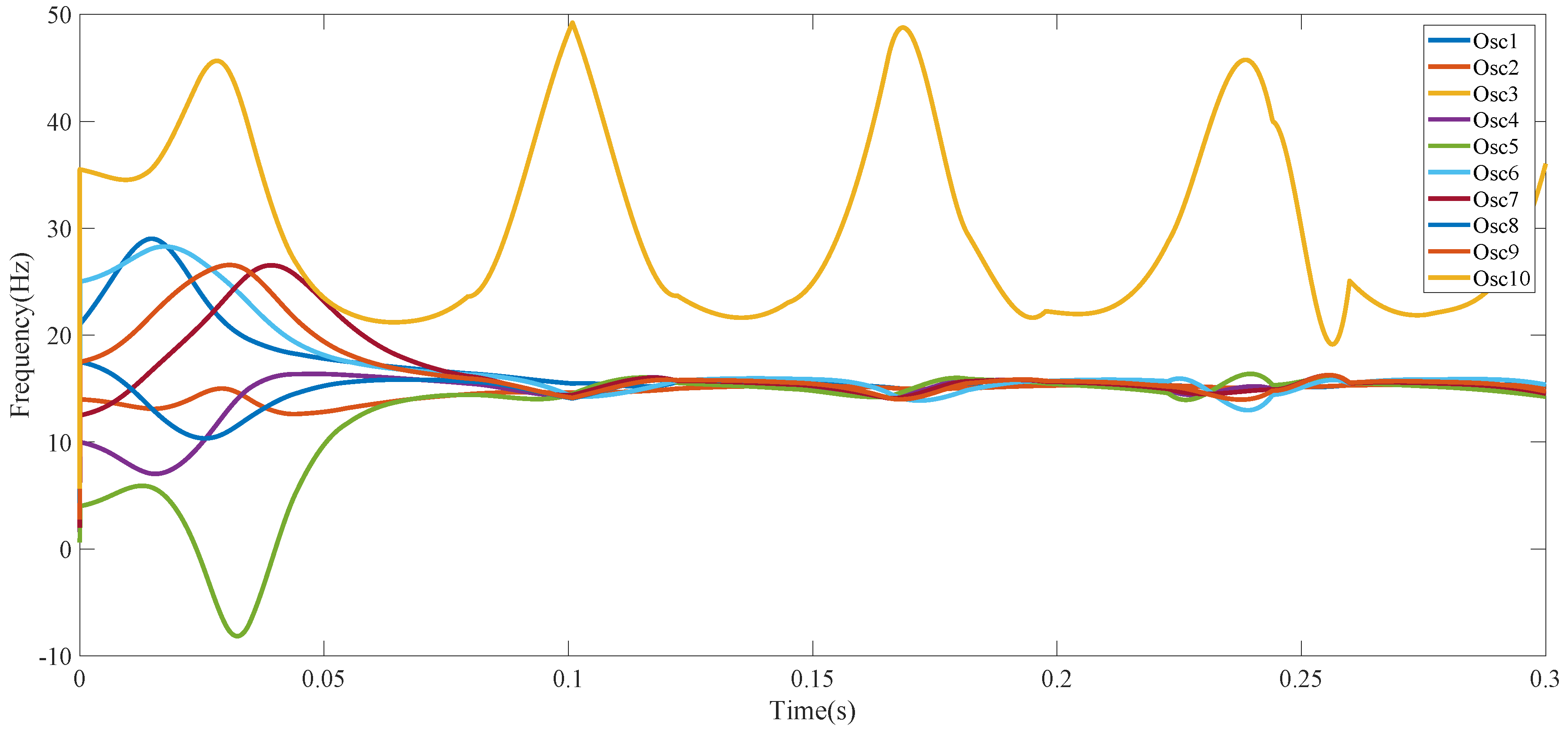

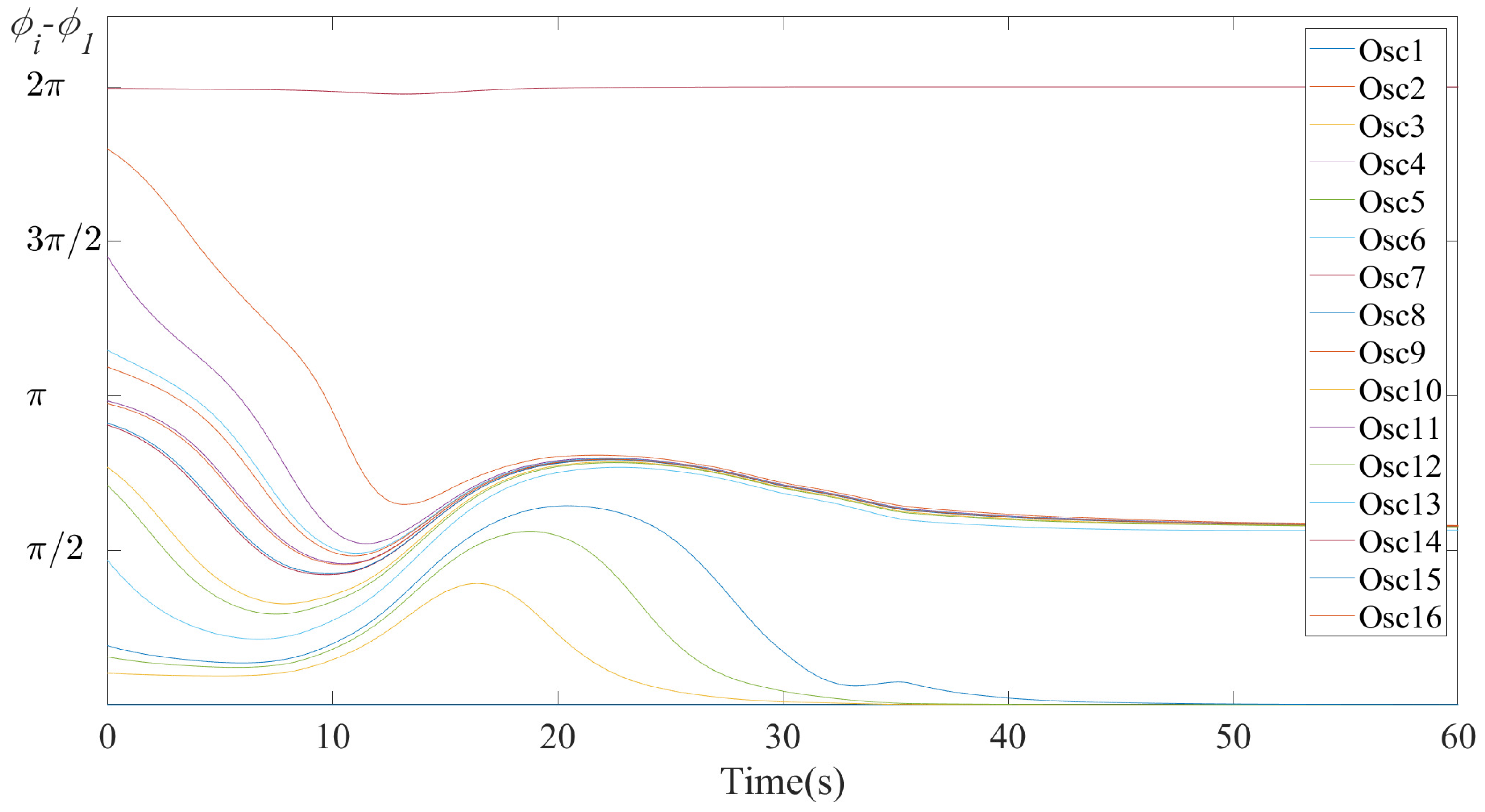
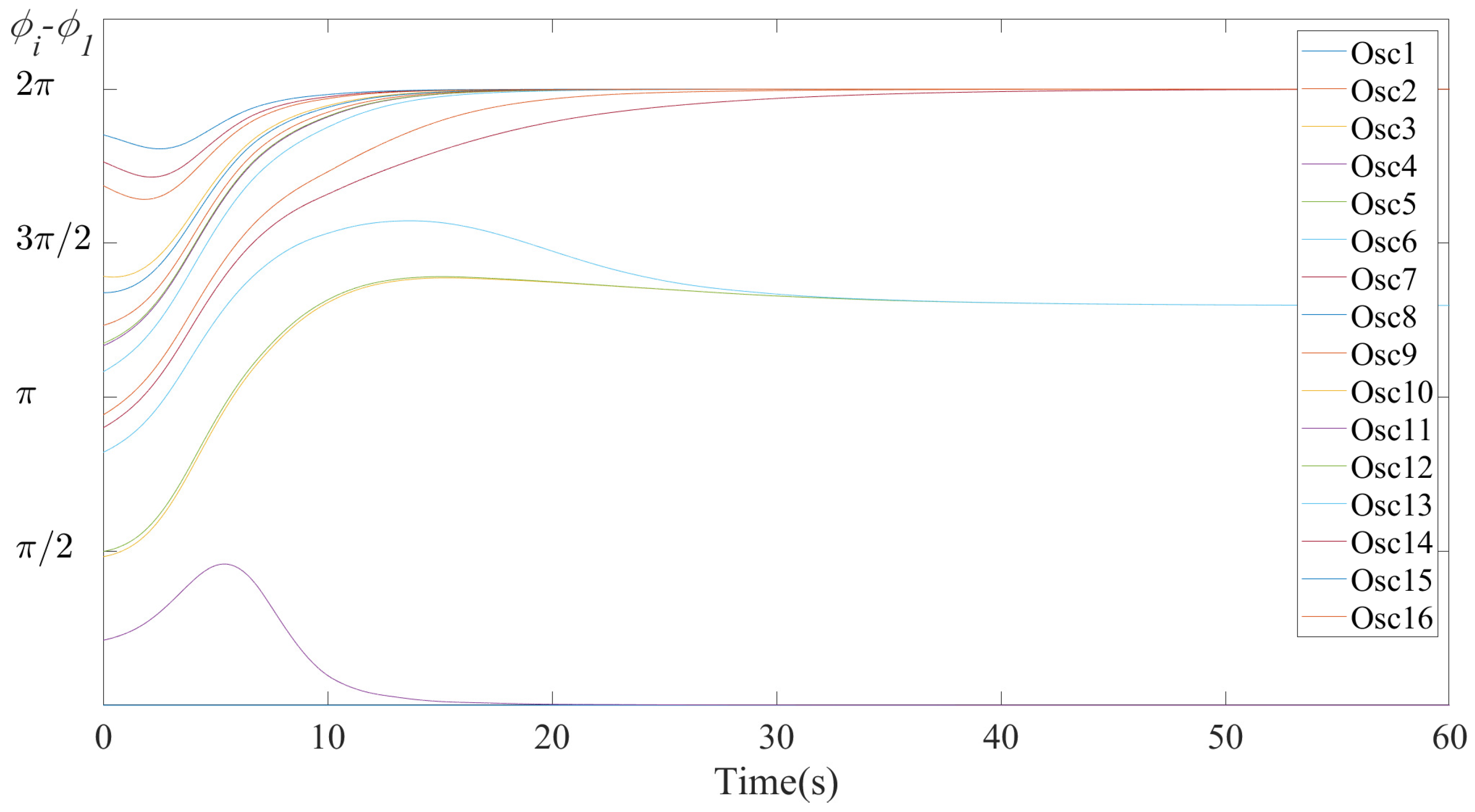

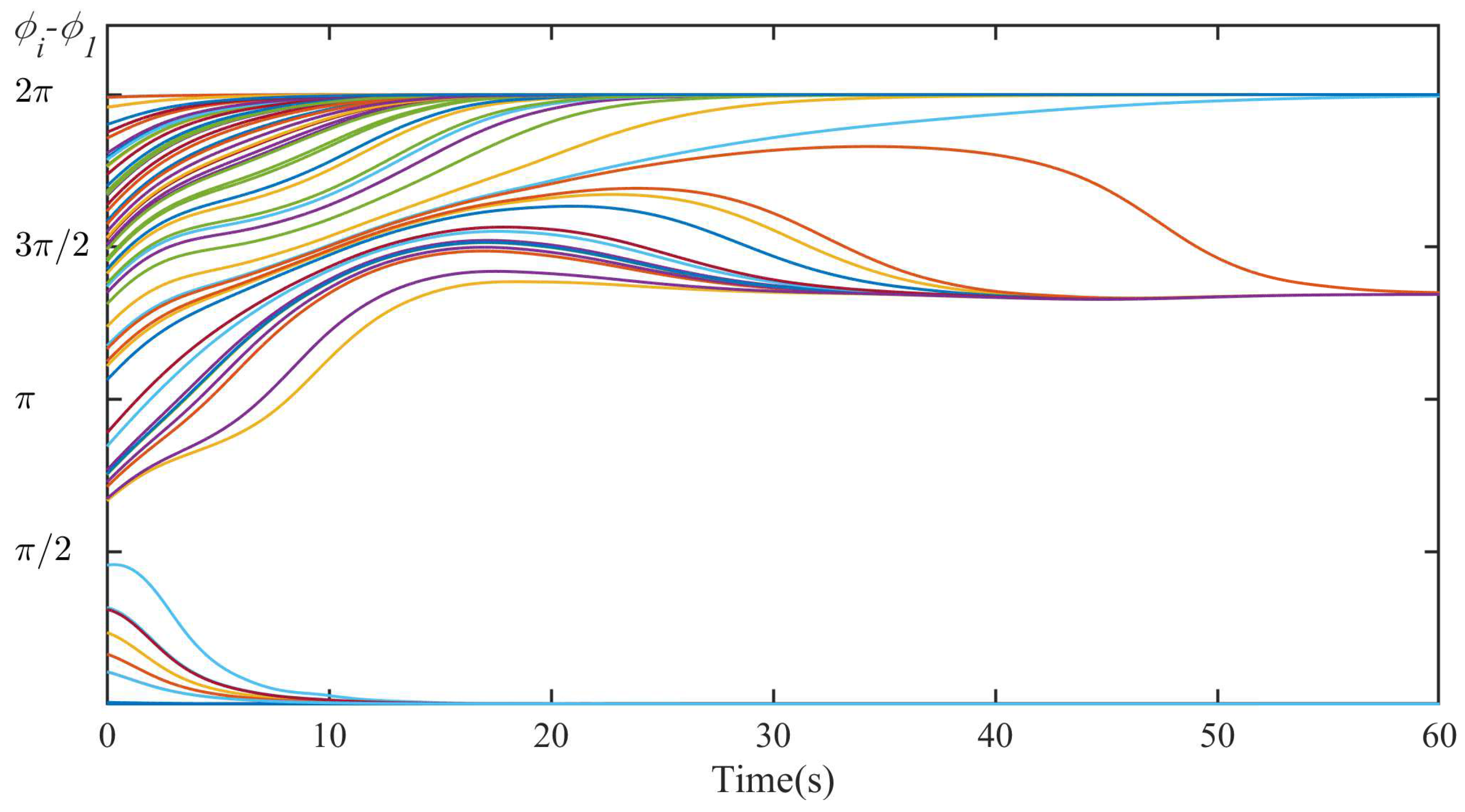
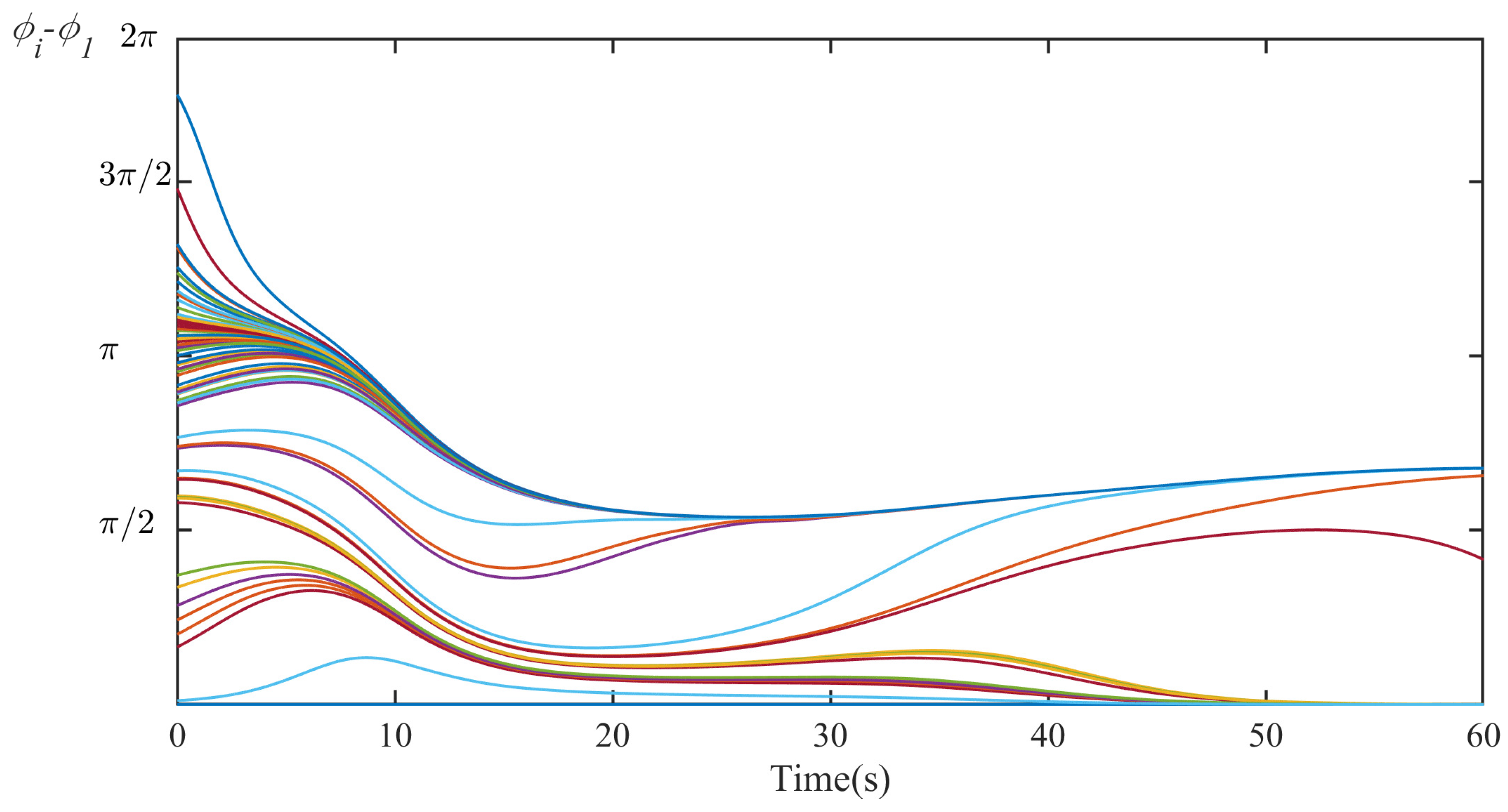
| Synchronization Pattern | Convergence Time (s) | Convergence Frequency (Hz) |
|---|---|---|
| Stored | 1.576800 × 10−1 | 17.5 |
| Recognition | 1.731000 × 10−1 | 17 |
| Recognition upper threshold | 2.742600 × 10−1 | 19.3 |
| Recognition lower threshold | 1.841300 × 10−1 | 16.5 |
| Lack of Recognition | No Convergence | No Convergence |
| ONN Characteristics | Hierarchical AM Model | Single AM Model |
|---|---|---|
| No. of layers | 2 | 1 |
| No. of oscillators | ||
| No. of oscillators in each layer | n | |
| Connections (Number of weights) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Haider, M.R.; Massoud, Y.; Alexander, J.I.D. An Oscillatory Neural Network Based Local Processing Unit for Pattern Recognition Applications. Electronics 2019, 8, 64. https://doi.org/10.3390/electronics8010064
Zhang T, Haider MR, Massoud Y, Alexander JID. An Oscillatory Neural Network Based Local Processing Unit for Pattern Recognition Applications. Electronics. 2019; 8(1):64. https://doi.org/10.3390/electronics8010064
Chicago/Turabian StyleZhang, Ting, Mohammad R. Haider, Yehia Massoud, and J. Iwan D. Alexander. 2019. "An Oscillatory Neural Network Based Local Processing Unit for Pattern Recognition Applications" Electronics 8, no. 1: 64. https://doi.org/10.3390/electronics8010064
APA StyleZhang, T., Haider, M. R., Massoud, Y., & Alexander, J. I. D. (2019). An Oscillatory Neural Network Based Local Processing Unit for Pattern Recognition Applications. Electronics, 8(1), 64. https://doi.org/10.3390/electronics8010064






