1. Introduction
It is expected that the amount of mobile wireless traffic in 2020 will be 1000 times higher than that of 2010 [
1,
2,
3]. Along with the dramatic growth in the demand for wireless communications, performance requirements for data rate, spectral efficiency and energy efficiency are also getting higher [
4,
5,
6]. To meet these growing demand and performance requirements for wireless communications, massive multi-input multi-output (m-MIMO) technology was proposed as one of the key technologies for the next generation cellular networks, known as fifth generation (5G) systems [
7,
8,
9,
10]. It is known that m-MIMO systems, whose transmitter or receiver is equipped with massive number of antennas, can improve the spectral efficiency and save energy in wireless communication systems [
10,
11,
12]. As a result, m-MIMO systems have recently attracted many researchers and engineers in many aspects. Multi-user m-MIMO technology, in which a base station (BS) uses a large number of antennas to serve many pieces of user equipment (UE) simultaneously on the same time-frequency resource, is one example that is actively studied to be practically adopted in 5G systems [
13,
14,
15]. The distributed antenna system (DAS) has also been considered a key technology for feasible deployment of 5G systems [
16,
17,
18]. In DAS configuration, there exist a digital unit (DU) and multiple radio units (RUs) in a cell, where each RU is connected to DU via fiber optic links. The DU manages RUs in a centralized manner, by which RUs can transmit and receive signals in a cooperative manner.
The key requirement for enjoying the benefit of m-MIMO technology is to obtain the accurate channel state information (CSI) for each link at the BS, or at RUs in DAS environment. In the frequency-division duplex (FDD) approach, UEs estimate downlink (DL) channels by using DL pilot signals, or sounding reference signals (SRS), transmitted from the BS [
19]. The required number of DL pilots in an FDD based approach is proportional to the number of BS antennas multiplied by the number of served UEs, which complicates the adoption of such a DL channel estimation in massive MIMO environments. Thus, the m-MIMO systems typically employ the time-division duplex (TDD) approach to estimate the DL channel. In the TDD approach, UEs estimate DL channels by sending mutually orthogonal uplink (UL) pilot signals (SRS) to BS based on the DL and UL channel reciprocity within the channel coherence interval [
9]. The total number of UL pilots required in such a TDD based approach is proportional to the number of served UEs irrespective of the number of BS antennas [
7,
9].
For a given length of sequence, say
M, we may generate at most
M orthogonal sequences. Conventionally, pilot sequences are mutually orthogonal, so the maximum number of pilot sequences is limited by
M. If the number of UEs in simultaneous service exceeds
M, we need to reuse some or all of the already generated orthogonal sequences. This results in the so-called pilot contamination problem [
20] due to the violation of orthogonality between pilot sequences. The pilot contamination mainly limits the performance improvement of m-MIMO systems [
7,
15]. Most of the prior works that proposed to resolve this problem have considered the use of mutually orthogonal SRS sequences. They include pilot signal coordination [
21], blind channel estimation with data samples [
22] and cooperative multi-cell precoding in m-MIMO systems [
23]. The number of mutually orthogonal SRS sequences is mainly limited by the length of the base sequence. In Long Term Evolution (LTE)/Long Term Evolution-Advanced (LTE-A) systems, the number of orthogonal SRS sequences is 16, which is not suitable for serving a large number of users in m-MIMO environments [
24,
25]. Using long pilot sequences may reduce the pilot contamination, but they replace data sequences and reduce channel spectral efficiency and throughput. If pilot sequences are made too long, they may occupy even the restricted band, which must be prevented. Thus, it may be desirable to generate a larger number of SRS sequences without increasing the sequence length.
For this purpose, we propose a mechanism for generating SRS sequences with a lower level of pilot contamination which is suitable for serving a large number of UEs. In the proposed mechanism, a phase rotation is applied to the base sequence without increasing the sequence length. The resultant SRS sequences may be mutually correlated and thus still incur a pilot contamination as the number of UEs grows and exceeds the length of base sequence. This results in high channel estimation error when a linear estimation based on the orthogonality of SRS sequences is used. To resolve this problem, we propose a two-step channel estimation algorithm by which the least square (LS) estimation [
26] is first applied and the minimum mean squared error (MMSE) estimation [
27] is additionally applied only to the group of UEs using mutually correlated SRS sequences. The proposed
correlation-aided channel estimation shows the improved performance in the channel estimation. It is shown that the proposed SRS combined with the supplemental channel estimation algorithm guarantees lower mean squared error (MSE) in channel estimation, which alleviates the pilot contamination problem.
The rest of the paper is organized as follows. In
Section 2, we introduce the system model in consideration. In
Section 3, a brief review of SRS sequences in conventional LTE/LTE-A systems is provided. We introduce the generation of proposed SRS sequences and the analysis on the resultant correlation in
Section 4. In
Section 5, we propose the two-step channel estimation algorithm composed of an LS estimation followed by a supplemental MMSE estimation. We also formulate and analyze the MSE obtained for SRS sequences with an LS estimation. We verify the performances in various aspects by computer simulations in
Section 6 and conclude this paper in
Section 7.
2. System Model
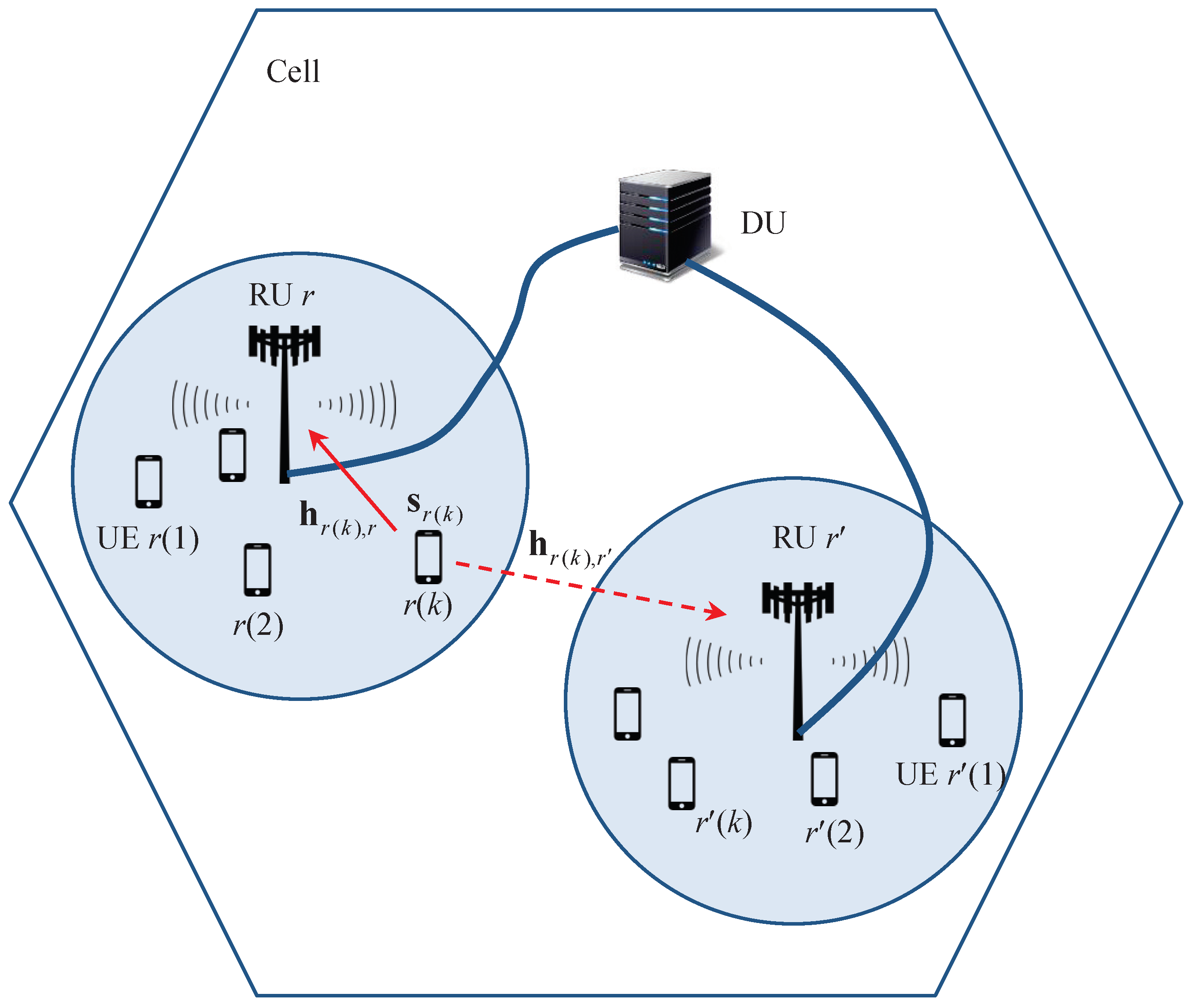
Consider a cell having a DU and
R RUs each of which serves
K UEs as shown in
Figure 1, where each RU has
transmit and receive antennas. We index RU by
, and index the UE served by RU
r as
,
. We consider orthogonal frequency division multiplexing (OFDM) communications with
subcarriers between UE and RU. We suppose the channel reciprocity, by which the DL channel from RU to UE can be estimated by using the UL pilots sent from UEs under the constraint that the time delay from the UL channel estimation to the DL transmission is less than the coherence time of the channel [
7]. Then, the UL channel estimated by sending SRS sequence from each UE to RU is used as the DL channel estimation. Let
denote the SRS sequence of UE
, where the superscript
T denotes a transpose of a vector. We also let
denote the channel gain between UE
and RU
over the
m-th subcarrier. Then, the channel gains corresponding to
M subcarriers,
,
, are estimated by using an SRS sequence.
The signal received by RU
r over the subcarrier
m is denoted by
and obtained by
where
is the zero-mean additive white Gaussian noise vector with covariance matrix
. Note that
, where
represents the large scale fading while each entry of
denotes the small scale fading represented by an independent and identically distributed (i.i.d.) zero mean complex Gaussian random variable with unit variance. Note that the large scale fading factor
, where
is a distance between UE
and RU
, and
a is an attenuation factor.
3. Conventional Channel Sounding Reference Signal in LTE/LTE-A Systems
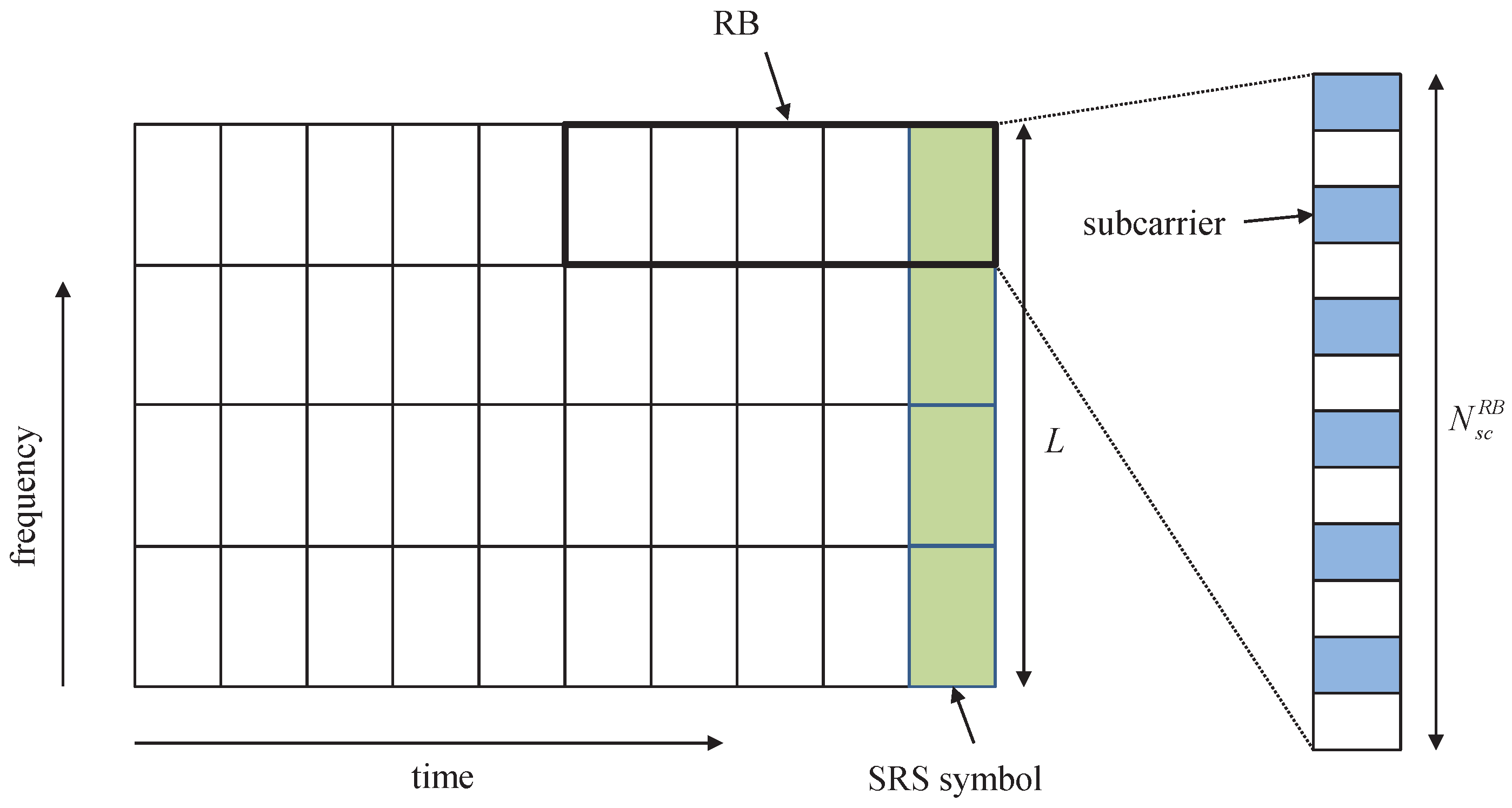
In the following, we briefly introduce the generation of SRS in conventional LTE/LTE-A systems [
24,
25]. The structure of SRS symbol is illustrated in
Figure 2. Basically, the SRS sequence is generated by a cyclic shift of a base sequence, which is obtained from Zadoff–Chu sequence [
24,
25] as presented below. Let
be the number of subcarriers per RB, where
in LTE/LTE-A systems, and
L be the number of assigned subcarriers for SRS or sounding bandwidth. Let
D be the decimation factor which is the number of SRS sequences sharing the allocated sounding bandwidth, where the length of SRS sequence is
. Note that
L is the multiple of
, i.e.,
,
, where
is the uplink system bandwidth in terms of RBs. Let
denote the length of Zadoff–Chu sequence used to generate the base sequence of length
M, where
is given by the largest prime number such that
.
Let
denote the
q-th root Zadoff–Chu sequence defined by
where
with
and
if
,
and
if
,
. The base sequence
is obtained by
Note that base sequences are divided into groups, where
u is the group number associated with the physical cell ID and the length of the SRS sequence, and
v is the base sequence number within the group. The SRS sequence
of length
M is defined by applying a cyclic shift
,
, to the base sequence
as
where
to obtain distinct values of
for different
. For any
and
chosen from
, two sequences
and
are orthogonal if
, where
if
and 0 otherwise, and the superscript
H denotes a conjugate transpose of a vector. This condition reduces to
by using Equation (
5) and the property
for all
m, which is clear from Equations (
2)–(
4).
This condition is satisfied only if is an even integer, or, in other words, is a factor of , for . Consequently, must be an integer that is greater than 7 and is a factor of .
Multiple SRS sequences are defined from a single base sequence by using different values of and the decimation factor. In LTE/LTE-A, the decimation factor of two is used and the signal occupies every second subcarrier within the allocated sounding bandwidth. By using distinct SRS sequences obtained with different values of and by using distinct sets of subcarriers as a result of decimation, multiple UEs can estimate their channel gains and can be served by RU simultaneously. In conventional LTE/LTE-A systems using and the decimation factor of two, we can obtain only 16 orthogonal sequences. In the multi-user systems with higher number of UEs than 16, we need to design a larger set of SRS sequences having low cross-correlation.
4. Proposed Channel Sounding Reference Signal for Multi-User Systems
The lack of orthogonal SRS sequences may cause the pilot contamination problem. The easy way to alleviate this is using longer SRS sequences or wider sounding bandwidth. However, this approach may result in the degraded performance of channel estimation in the frequency selective environment and the lower spectral efficiency and throughput because SRS sequences replace data sequences. Moreover, if the sounding bandwidth is too wide, SRS sequences may occupy the restricted band, which must be prohibited. Thus, we aim to generate a new set of SRS sequences showing reduced pilot contamination without increasing the sounding bandwidth or sequence length. We apply phase rotation to the LTE/LTE-A SRS sequences, which is introduced in
Section 3 to generate a new SRS sequence as
where
and
, and the last equality comes from Equation (
5). Note that
is an integer greater than 7 which can divide
as introduced in
Section 3 and
is a prime number which is smaller than
. For a given SRS sequence length
M, we may generate up to
M orthogonal sequences. However, by using Equation (
5), we can generate only eight orthogonal sequences with varying
. Thus, we use the phase rotation
,
, together with
,
, to generate
M orthogonal SRS sequences without incurring pilot contamination. If the number of UEs exceeds
M, we need to generate extra SRS sequences instead of reusing already generated ones. For this purpose, we apply additional phase rotation
,
, where
needs to be coprime with
M and thus be also coprime with
in order to make the resultant sequences distinct from already generated
M sequences. We empirically found that a prime number
smaller than
results in a good performance.
By Equations (
2)–(
4), we can rewrite Equation (
6) as
The correlation of SRS sequences
and
is defined and expanded as
where
,
and the superscript * represents the complex conjugate of a complex variable. The detailed derivation of Equation (
8) is provided in
Appendix A. It is clear that
obtained with
,
and
corresponds to the auto-correlation of
because
, where
. The cross-correlation
if
and either
or
, while
if
by the following reason.
Consider
, where
if
is a nonzero integer, and
, otherwise. If
, the rightmost side of Equation (
8) becomes
. If
or
,
is a nonzero integer because
M is a multiple of
as introduced in
Section 3, and thus
. On the other hand, if
,
cannot be a nonzero integer because
is not divisible by
, and, thus
, where
and
M are coprime and
.
Consequently, for each
p, we can generate a set of
M orthogonal SRS sequences, where
and
enables the generation of
M orthogonal sequences. Applying the phase rotation
,
, in Equation (
7) enables to obtain
sets of
M orthogonal sequences. Any two sequences obtained with different values of
p are mutually correlated.
Distinct SRS sequences generated with different
,
s and
p by Equation (
7) are assigned to different UEs. The first set of
M orthogonal sequences generated with
are assigned to the first
M UEs. Then, the next set of
M orthogonal sequences generated with
are assigned to the next
M UEs. This procedure is repeated by increasing
p until all UEs are assigned SRS sequences.
6. Numerical Results
We evaluate the performances of the proposed SRS and the proposed supplemental channel estimation algorithm in terms of MSE in the multi-user m-MIMO DAS environment. For comparison, the MSE obtained by using conventional LTE/LTE-A SRS scheme is also shown. As the proposed scheme, we consider the following three types:
- (a)
using repeatedly
M orthogonal sequences generated by varying
and
s without applying the phase rotation
in Equation (
7),
- (b)
using the phase rotation together with varying and s for SRS generation, but not using the supplemental correlation-aided channel estimation,
- (c)
using the phase rotation together with varying and s for SRS generation, and the supplemental correlation-aided channel estimation as well.
We consider the large scale fading factor between UEs and serving RU as
and the large scale fading factor between UEs and other neighboring RUs as
, i.e.,
and
for all
k,
r and
. We let
, which comes from the assumption that the distance of UE from serving RU is 1.3 times shorter than the distance from other neighboring RUs, where the attenuation factor is assumed to be
. We let each RU serve the same number of UEs. We choose
in Equations (
5) and (
7), and
when applying the phase rotation
in types (b) and (c) of the proposed scheme. We consider a block fading channel, International Telecommunication Union Radiocommunication Sector (ITU-R) Ped A and ITU-R Veh A channels [
28], where ITU-R Ped A [
29] and ITU-R Veh A channels are examples of frequency selective channels. The simulation parameters used for performance evaluation are listed in
Table 1.
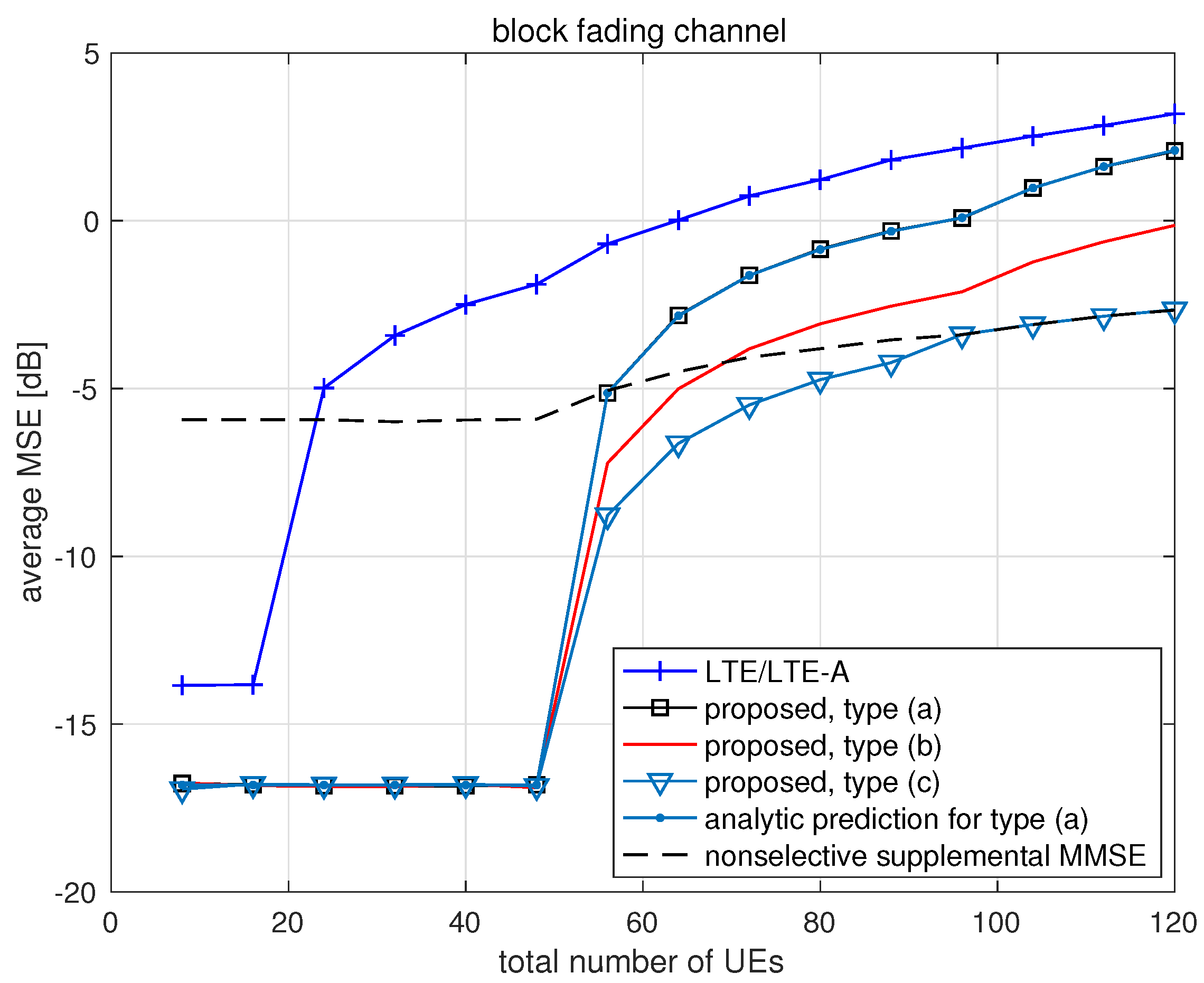
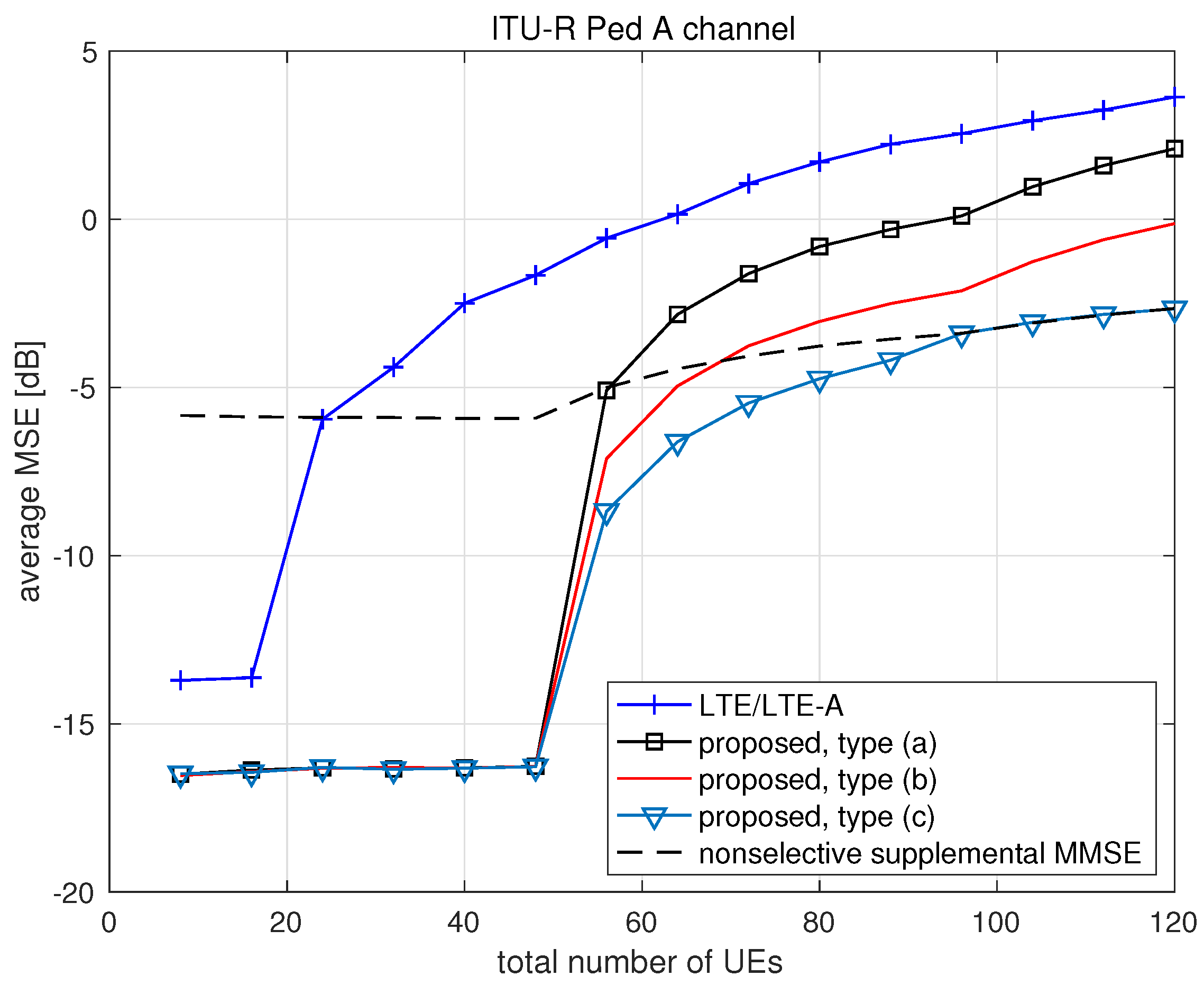
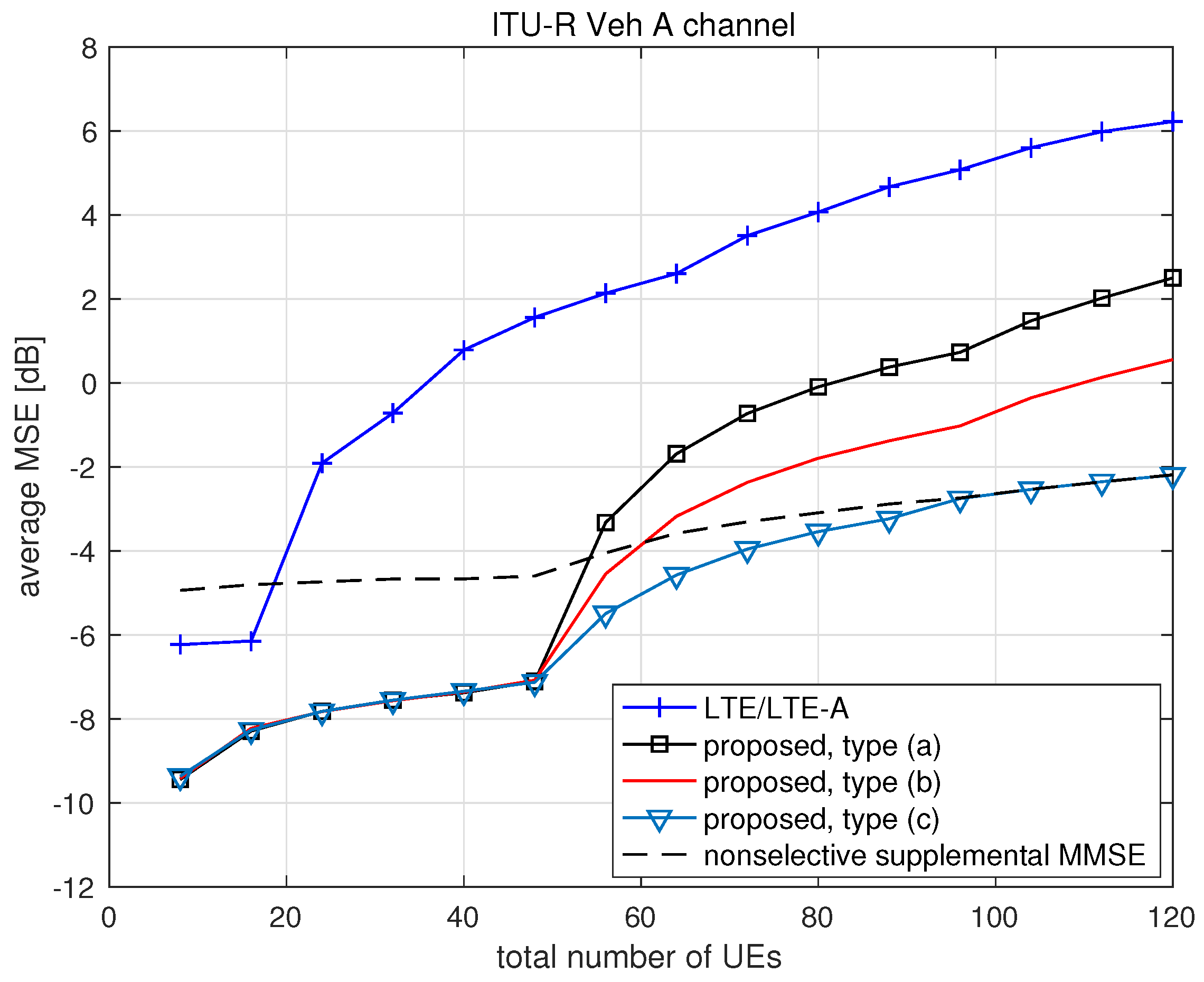
We depict the average MSE of channel estimation with respect to the total number of UEs in the cell obtained for block fading channel, ITU-R Ped A channel and ITU-R Veh A channel in
Figure 3,
Figure 4 and
Figure 5, respectively. In each figure, we plot the average MSE obtained by using conventional SRS in LTE/LTE-A systems and the proposed scheme of three types.
We also plot the average MSE obtained by applying supplemental MMSE estimation to all UEs instead of applying MMSE selectively only to UEs belonging to the second class, where the phase rotation
is applied and the corresponding curves are marked with ‘nonselective supplemental MMSE.’ In
Figure 3, we include the average MSE predicted analytically by Equation (
20) for the proposed scheme of type (a) over block fading channel.
It is observed that the channel estimation MSE obtained by using any SRS scheme rapidly increases when the number of UEs in service exceeds the number of orthogonal SRS sequences, where the conventional LTE/LTE-A scheme and the proposed scheme generate 16 and
M (=48) orthogonal SRS sequences, respectively. For more than 48 UEs, the proposed scheme also provides much lower channel estimation MSE than LTE/LTE-A scheme. Even reusing repeatedly
M (=48) orthogonal SRS sequences generated in type (a) can lower significantly the channel estimation MSE for any number of UEs. It is observed that applying phase rotation
to SRS generation further lowers the channel estimation MSE, and the use of supplemental selective MMSE estimation can even further improve the channel estimation performance at the cost of increasing complexity. Note that the computational complexity of supplemental selective MMSE estimation is, in general,
because it requires the matrix inversion, where
n is the dimension of a square matrix
. Considering, as a reference, the case that
M orthogonal sequences are repeatedly used to generate SRS sequences, the dimension of
is determined from Equation (
17) as
. Applying supplemental MMSE estimation nonselectively to all UEs degrades the performance when the number of UEs is not high enough. In
Figure 3, the analytic prediction of MSE for block fading channel is observed to match the numerical result very well. It is clear that the proposed scheme of type (c) shows the best channel estimation performance in terms of MSE for all numbers of UEs. The MSE gain of the proposed scheme of type (c) over LTE/LTE-A system is about 6 dB in block fading and ITU-R Ped A channels, and about 8 dB in ITU-R Veh A channel when serving 120 UEs through four RUs. The performance gain achieved by using the proposed scheme can be observed in block fading channel as well as frequency selective channel.
Conventional LTE/LTE-A systems may not effectively employ m-MIMO transmission for the service of a large number of UEs mainly due to the pilot contamination problem. However, the proposed SRS and the supplemental channel estimation can relieve the pilot contamination problem in a significant level. It is expected that the proposed scheme can be effectively adopted in multi-user m-MIMO systems.